2. 中国人民解放军92064部队, 广东 东莞 523900
2. The Chinese People's Liberation Army of 92064, Dongguan 523900, Guangdong, China
同时具有内部声场和外部自由声场的声振耦合系统广泛存在于汽车、飞机和潜艇等运载工具和武器平台之中。结构与声介质因振动相互作用而产生的中低频噪声会对人员及设备产生负面影响,辐射噪声影响人员舒适性和造成环境污染,在军事上,声辐射过大会影响武器系统的隐身性和自身的声呐探测距离[1]。因此在准确计算声辐射的基础上,通过适当设计材料的结构分布以使耦合系统在所关心的激励频段下具有较低的声辐射值的研究十分必要。
作为新兴的结构动力优化方法,不同于尺寸优化[2]和形状优化[3]仅能改变已知设计部件的尺寸,拓扑优化的目标是寻求最优的结构材料分布以满足性能和结构工艺等多方面要求[4]。国、内外诸多研究者在减振降噪问题上采用拓扑优化法开展了研究。在内声场优化问题中,Akl等[5]采用有限元法建立内声场声辐射模型,采用MMA法优化柔性板厚度,降低了声腔内的声辐射,数值计算结果与实验吻合较好;Dühring等[6]结合混合有限元法和MMA优化法实现在无法明确耦合边界的情况下解决声- 结构耦合优化问题;随后Kook[7]用Comsol软件实现将混合有限元法扩展至BESO优化方法中,优化结果与采用传统有限元法的文献[8]结果一致。在外声场优化问题的研究中,陈炉云等[9]结合ESO优化法和单向耦合的边界元法研究了简支板在低频率下外场声辐射优化问题;张军[10]推导了空气为声介质的有限元- 边界元耦合方法的声压级和辐射声功率灵敏度公式,并以板厚为设计变量对薄板声辐射进行优化;针对两相材料板结构的声辐射拓扑优化问题,文献[11-12]通过优化布局两种弹性材料的方式降低声辐射;此后,黄其柏在上述基础上研究了板结构声辐射计算方法和辐射特性,提出约束阻尼复合板的拓扑优化方法;Zhang等[13]采用状态空间中的复模态叠加法求解非比例全局阻尼的复合板声响应,伴随变量法进行声压灵敏度分析,通过合理分配阻尼层材料达到最小化指定点声压的目标。
目前,声振耦合方法的研究大多针对单一的有限内声场[5-8]或无限大/半无限大自由声场问题[9-13],且在处理自由声场灵敏度分析时往往忽略了声介质对结构的反作用,无法适用于内声场和外部自由声场均存在的声辐射问题和强耦合问题。基于上述问题,本文结合声振耦合有限元方程和边界元法,推导了内外声场声压的耦合计算公式,并提出一种新的强耦合声功率的灵敏度求解方法,通过不同设计条件下的声辐射优化设计结果验证了声辐射预报的准确性和灵敏度方法在优化过程中的适用性。
1 声辐射问题 1.1 声学基本方程声振耦合示意图如图 1所示,假定流体是可压缩的,无黏且无旋,忽略自由表面重力效应的均匀理想声学介质,声压满足如下的波动方程:

|
图 1 声振耦合示意 Fig. 1 Acoustic vibration coupling diagram |
| $ \nabla^{2} p_{\mathrm{f}}-\frac{1}{c_{0}^{2}} \frac{\partial^{2} p_{\mathrm{f}}}{\partial t^{2}}=0 $ | (1) |
式中:pf为介质中质点声压,c02为声波在声介质中的传播速度。当外界激励为稳态谐波激励时,流体压强pf可表示为pf=|pf|exp(-iωt),其中ω为外界谐波激励的角频率。将上式代入式(1)消去时间项,可得到Helmholtz方程:
| $ \nabla^{2} p_{\mathrm{f}}+\left(\omega / c_{0}\right)^{2} p_{\mathrm{f}}=0 $ | (2) |
在流固交界面上,应满足如下的运动学和力学条件:
| $ \nabla p_{\mathrm{f}} \boldsymbol{n}_{\mathrm{f}}+\rho_{\mathrm{f}} \ddot{\boldsymbol{u}}_{\mathrm{s}} \boldsymbol{n}_{\mathrm{f}}=0 $ | (3) |
| $ \boldsymbol{u}_{\mathrm{s}} \boldsymbol{n}_{\mathrm{s}}+\boldsymbol{u}_{\mathrm{f}} \boldsymbol{n}_{\mathrm{f}}=0 $ | (4) |
| $ \sigma_{\mathrm{s}} \mid \boldsymbol{n}_{\mathrm{s}}=-p_{\mathrm{f}} $ | (5) |
式中:ρf为流体密度,nf为耦合表面从声场指向结构的法向量,ns为耦合表面从结构指向声场的法向量,σs为结构应力,us为结构位移向量。
1.2 内声场声振耦合的有限元法结构域的平衡状态方程为
| $ \nabla \cdot \sigma_{\mathrm{s}}-\rho_{\mathrm{s}} \ddot{u}_{\mathrm{s}}=f_{\mathrm{s}} $ | (6) |
式中:ρs为结构质量密度,fs为结构所受外激励。
联立式(2)、(3)~式(6),并采用加权余量的伽辽金法可得到声振耦合的有限元方程[14]:
| $ \left(\left[\begin{array}{cc} \boldsymbol{K}_{\mathrm{s}} & \bf{0} \\ \boldsymbol{C} & \boldsymbol{K}_{\mathrm{f}} \end{array}\right]-\omega^{2}\left[\begin{array}{cc} \boldsymbol{M}_{\mathrm{s}} & -\boldsymbol{C} / \rho_{\mathrm{f}} \\ \bf{0} & \boldsymbol{M}_{\mathrm{f}} \end{array}\right]\right)\left(\begin{array}{l} \boldsymbol{u}_{\mathrm{s}} \\ \boldsymbol{p}_{\mathrm{f}} \end{array}\right)=\left[\begin{array}{l} \boldsymbol{f}_{\mathrm{s}} \\ \bf{0} \end{array}\right] $ | (7) |
式中:Ks、Kf分别为结构域和流体域的系统刚度矩阵,Ms、Mf分别为结构域和流体域系统质量矩阵,C为系统耦合矩阵。
为方便后文推导计算,式(7)可简写为
| $ \left(\boldsymbol{K}_{\mathrm{fe}}-\omega^{2} \boldsymbol{M}_{\mathrm{fe}}\right) \boldsymbol{X}_{\mathrm{fe}}=\boldsymbol{F}_{\mathrm{fe}} $ | (8) |
稳态谐激励下,为求解结构表面上受到介质的压力,需要建立介质中任一点的声压积分方程。对声压和格林函数应用格林第二公式,由Sommerfeld辐射定律,外域自由声场通过Helmholtz积分方程求解:
| $ c p_{x}=\int_{\varGamma_{\mathrm{be}}}\left(\frac{\partial G_{(x, y)}}{\partial \boldsymbol{n}_{\mathrm{f}}} p_{y}-G_{(x, y)} \frac{\partial p_{y}}{\partial \boldsymbol{n}_{\mathrm{f}}}\right) \mathrm{d} \varGamma $ | (9) |
式中:px为源点声压;py为场点声压; c为空间角系数,光滑面上取0.5,声场内取1;G(x, y)为自由空间格林函数; Γbe为自由场声辐射边界。
以二维空间为例,对于二维声场问题,格林函数G(x, y)和其对场点处的法向导数的基本阶函数如下:
| $ G_{(x, y)}=\frac{i}{4} H_{0}^{1}(k r) $ | (10) |
| $ \frac{\partial G_{(x, y)}}{\partial \boldsymbol{n}_{\mathrm{f}}}=-\frac{i k}{4} H_{1}^{1}(k r) \frac{\boldsymbol{r n}_{\mathrm{f}}}{r} $ | (11) |
式中:H01为第1类0阶Hankel函数; H11为第1类1阶Hankel函数; k为波数,其表达式为k=ω/c0; r为场点与源点的矢径; r为矢径的模。
联立式(3),式(9)~式(11),并通过Kronecker函数合并声压项得到边界积分方程:
| $ \boldsymbol{H} \boldsymbol{p}_{\mathrm{be}}-\boldsymbol{G} \boldsymbol{v}_{\mathrm{be}}=\bf{0} $ | (12) |
式中:H、G分别为采用边界积分方程得到的频率相关的矩阵,pbe、vbe分别为边界上的声压和法向速度向量。
1.4 声振耦合方程及辐射声功率当声场由有限大内声场和无限大自由声场组成时,式(8)的平衡方程须引入自由场声介质对结构表面的反作用力项为
| $ \left(\boldsymbol{K}_{\mathrm{fe}}-\omega^{2} \boldsymbol{M}_{\mathrm{fe}}\right) \boldsymbol{X}_{\mathrm{fe}}=\boldsymbol{F}_{\mathrm{fe}}+\boldsymbol{L} \boldsymbol{p}_{\mathrm{be}} $ | (13) |
式中L为结构与自由声场的边界压强与边界法向作用力的耦合矩阵。
耦合界面上任一点声介质的速度vbe用形函数Np和边界上声学单元速度vbee表示为
| $ v_{\mathrm{be}}=\boldsymbol{N}_{\mathrm{p}} \boldsymbol{v}_{\mathrm{be}}^{\mathrm{e}} $ | (14) |
由稳态谐波激励下的界面位移与界面法向速度的界面连续性条件可知:
| $ \sum\limits_{1}^{m} \int_{\varGamma_{\mathrm{e}}} N_{\mathrm{p}}^{\mathrm{T}} N_{\mathrm{p}} \mathrm{d} \varGamma \boldsymbol{v}_{\mathrm{be}}^{\mathrm{e}}=-\mathrm{i} \omega \sum\limits_{1}^{m} \int_{\varGamma_{\mathrm{e}}} N_{\mathrm{p}}^{\mathrm{T}} \boldsymbol{n}_{\mathrm{f}} N_{u} \mathrm{~d} {\varGamma} \boldsymbol{u}_{\mathrm{s}}^{\mathrm{e}} $ | (15) |
式中:Nu为结构单元的位移形函数,Γe为自由声场与结构的单元耦合边界,m为耦合边界单元总数。上式求积分并求逆移项后,将结构位移从边界单元扩充至全局响应向量Xfe得到:
| $ \boldsymbol{v}_{\mathrm{be}}=-\mathrm{i} \omega \boldsymbol{M}_{\mathrm{be}}^{-1} \boldsymbol{L}^{\mathrm{T}} \boldsymbol{X}_{\mathrm{fe}} $ | (16) |
式中:Mbe为边界质量矩阵,其表达式即为式(15)左端积分项;联立式(12)、(13)和式(16),得到修正后含外部自由声场的声振耦合方程
| $ \left[\begin{array}{cc} \boldsymbol{K}_{\mathrm{fe}}-\omega^{2} \boldsymbol{M}_{\mathrm{fe}} & -\boldsymbol{L} \\ \mathrm{i} \omega \boldsymbol{G} \boldsymbol{M}_{\mathrm{be}}^{-1} \boldsymbol{L}^{\mathrm{T}} & \boldsymbol{H} \end{array}\right]\left[\begin{array}{c} \boldsymbol{X}_{\mathrm{fe}} \\ \boldsymbol{p}_{\mathrm{be}} \end{array}\right]=\left[\begin{array}{l} \boldsymbol{F}_{\mathrm{fe}} \\ \bf{0} \end{array}\right] $ | (17) |
直接求解式(17)即可得到内外声场声压值以及结构边界位移。同式(14),采用形函数Np对自由场边界声速和声压进行采用统一的插值离散并代入上式,得到声功率W的数值计算公式为[15]
| $ W=-\frac{1}{2} \operatorname{Re}\left(\boldsymbol{p}_{\mathrm{be}}^{\mathrm{T}} \boldsymbol{M}_{\mathrm{be}} \boldsymbol{v}_{\mathrm{be}}^{*}\right) $ | (18) |
式中Re为取计算值的实部。
式(18)在声功率灵敏度求解中不便于解耦变量,为方便后文求解单元灵敏度,需要将声功率公式修改为用结构位移响应表达的方式。将边界积分方程式(12)代入上式并由复共轭矩阵乘法规则得到采用边界振速表示的结构声功率的表达式:
| $ W=-\frac{1}{2} \operatorname{Re}\left(\boldsymbol{v}_{\mathrm{be}}^{\mathrm{H}}\left(\boldsymbol{H}^{-1} \boldsymbol{G}\right)^{\mathrm{H}} \boldsymbol{M}_{\mathrm{be}} \boldsymbol{v}_{\mathrm{be}}\right) $ | (19) |
声功率灵敏度是求声功率对结构单元状态参数xi求微分,为方便计算,应使式(19)尽量简单。由实部操作符得到式(19)的简单表达式:
| $ W=-\frac{1}{2}\left(\boldsymbol{v}_{\mathrm{be}}^{\mathrm{H}} \boldsymbol{A v}_{\mathrm{be}}\right) $ | (20) |
其中
| $ \boldsymbol{A}=\frac{1}{2}\left(\left(\boldsymbol{H}^{-1} \boldsymbol{G}\right)^{\mathrm{H}} \boldsymbol{M}_{\mathrm{be}}+\left(\left(\boldsymbol{H}^{-1} \boldsymbol{G}\right)^{\mathrm{H}} \boldsymbol{M}_{\mathrm{be}}\right)^{\mathrm{H}}\right) $ |
将式(16)代入式(20),得到辐射声功率关于Xfe的关系式:
| $ W=-\frac{1}{2}\left(\boldsymbol{X}_{\mathrm{fe}}^{\mathrm{H}} \boldsymbol{Q X}_{\mathrm{fe}}\right) $ | (21) |
其中
| $ \boldsymbol{Q}=\overline{\left(\mathrm{i} \omega \boldsymbol{M}_{\mathrm{be}}^{-1} \boldsymbol{L}^{\mathrm{T}}\right)} \boldsymbol{A}\left(\mathrm{i} \omega \boldsymbol{M}_{\mathrm{be}}^{-1} \boldsymbol{L}^{\mathrm{T}}\right) $ |
拓扑优化问题需要对目标函数相对设计变量的灵敏度进行分析,由辐射声功率的表达式可知,在外载荷和辐射边界不发生变化的情况下,辐射声功率仅与结构表面法向速度vbe有关,即是结构响应Xfe的函数。Kang等[16-17]利用伴随变量法(AVM)推导出广义结构响应函数g(Xfe)的灵敏度分析方法,该方法明确指出灵敏度依赖于结构位移响应的幅值,随后他们团队采用这种伴随变量法计算仅考虑单向耦合的声压灵敏度[13],取得了一定的成果。本文将该方法推广到强耦合的声功率灵敏度分析中。
2.1 声功率单元灵敏度的AVM方法在本文中,首先将AVM方法扩展到重介质的灵敏度分析中。对于依赖于位移响应Xfe的结构响应g(Xfe),其目标函数可以通过引入两个拉格朗日乘子的和改写为
| $ \begin{aligned} g=& g\left(\boldsymbol{X}_{\mathrm{fe}}\right)+\boldsymbol{\mu}_{1}^{\mathrm{T}}\left(\boldsymbol{K}_{\mathrm{d}} \boldsymbol{X}_{\mathrm{fe}}-\boldsymbol{L} \boldsymbol{p}_{\mathrm{be}}-\boldsymbol{F}\right)+\\ & \boldsymbol{\mu}_{2}^{\mathrm{T}}\left(\boldsymbol{K}_{\mathrm{d}} \boldsymbol{X}_{\mathrm{fe}}-\boldsymbol{L} \boldsymbol{p}_{\mathrm{be}}-\boldsymbol{F}\right)^{\mathrm{H}} \end{aligned} $ | (22) |
式中,Kd= Kfe-ω2 Mfe。上式中存在与Xfe不统一的变量pbe,联立式(12)和式(16)可得
| $ \boldsymbol{L} \boldsymbol{p}_{\mathrm{be}}=\boldsymbol{B} \boldsymbol{X}_{\mathrm{fe}} $ | (23) |
式中,B =-iω LH-1 GMbe-1 LT。式(23)代入式(22)得到目标函数灵敏度与Xfe有关的函数:
| $ \begin{gathered} g=g\left(\boldsymbol{X}_{\mathrm{fe}}\right)+\mu_{1}^{\mathrm{T}}\left(\boldsymbol{K}_{\mathrm{d}} \boldsymbol{X}_{\mathrm{fe}}-\boldsymbol{B} \boldsymbol{X}_{\mathrm{fe}}-\boldsymbol{F}\right)+ \\ \boldsymbol{\mu}_{2}^{\mathrm{T}}\left(\boldsymbol{K}_{\mathrm{d}} \boldsymbol{X}_{\mathrm{fe}}-\boldsymbol{B} \boldsymbol{X}_{\mathrm{fe}}-\boldsymbol{F}\right)^{\mathrm{H}} \end{gathered} $ | (24) |
将式(24)两边对设计变量xi求导,可得
| $ \begin{aligned} \frac{\mathrm{d} g}{\mathrm{~d} x_{i}}=& \boldsymbol{\mu}_{1}^{\mathrm{T}} \frac{\partial \boldsymbol{K}_{\mathrm{d}}}{\partial x_{i}} \boldsymbol{X}_{\mathrm{fe}}+\boldsymbol{\mu}_{2}^{\mathrm{T}} \frac{\partial\left(\boldsymbol{K}_{\mathrm{d}}\right)^{\mathrm{H}}}{\partial x_{i}} {\overline{\boldsymbol{X}}}_{\mathrm{fe}}+\\ & \frac{\partial \boldsymbol{X}_{\mathrm{fe}}^{\mathrm{R}}}{\partial x_{i}}\left(\frac{\partial g}{\partial \boldsymbol{X}_{\mathrm{fe}}^{\mathrm{R}}}+\boldsymbol{\mu}_{1}^{\mathrm{T}}\left(\boldsymbol{K}_{\mathrm{d}}-\boldsymbol{B}\right)+\boldsymbol{\mu}_{2}^{\mathrm{T}}\left(\boldsymbol{K}_{\mathrm{d}}-\boldsymbol{B}\right)^{\mathrm{H}}\right)+\\ & \frac{\partial \boldsymbol{X}_{\mathrm{fe}}^{\mathrm{I}}}{\partial x_{i}}\left(\frac{\partial g}{\partial \boldsymbol{X}_{\mathrm{fe}}^{\mathrm{I}}}+\mathrm{i} \boldsymbol{\mu}_{1}^{\mathrm{T}}\left(\boldsymbol{K}_{\mathrm{d}}-\boldsymbol{B}\right)-\mathrm{i} \boldsymbol{\mu}_{2}^{\mathrm{T}}\left(\boldsymbol{K}_{\mathrm{d}}-\boldsymbol{B}\right)^{\mathrm{H}}\right) \end{aligned} $ | (25) |
令伴随向量满足以下方程:
| $ \left\{\begin{array}{l} \boldsymbol{\mu}_{1}^{\mathrm{T}}\left(\boldsymbol{K}_{\mathrm{d}}-\boldsymbol{B}\right)=\frac{1}{2}\left(-\frac{\partial g}{\partial \boldsymbol{X}_{\mathrm{fe}}^{\mathrm{R}}}+\mathrm{i} \frac{\partial g}{\partial \boldsymbol{X}_{\mathrm{fe}}^{\mathrm{I}}}\right) \\ \boldsymbol{\mu}_{2}^{\mathrm{T}}\left(\boldsymbol{K}_{\mathrm{d}}-\boldsymbol{B}\right)^{\mathrm{H}}=\frac{1}{2}\left(-\frac{\partial g}{\partial \boldsymbol{X}_{\mathrm{fe}}^{\mathrm{R}}}-\mathrm{i} \frac{\partial g}{\partial \boldsymbol{X}_{\mathrm{fe}}^{\mathrm{I}}}\right) \end{array}\right. $ | (26) |
式中μ1、μ2满足μ1=(μ2)H。式(25)可以化简为
| $ \begin{aligned} \frac{\mathrm{d} g}{\mathrm{~d} x_{i}}=& 2 \operatorname{Re}\left(\boldsymbol{\mu}_{1}^{\mathrm{T}} \frac{\partial \boldsymbol{K}_{\mathrm{d}}}{\partial x_{i}} \boldsymbol{X}_{\mathrm{fe}}\right)=\\ & 2 \operatorname{Re}\left(\boldsymbol{\mu}_{1}^{\mathrm{T}}\left(\frac{\partial \boldsymbol{K}_{\mathrm{fe}}}{\partial x_{i}}-\omega^{2} \frac{\partial \boldsymbol{M}_{\mathrm{fe}}}{\partial x_{i}}\right) \boldsymbol{X}_{\mathrm{fe}}\right) \end{aligned} $ | (27) |
由声振耦合方程(17)求解的Xfe是复向量,将其分解为实部与虚部之和的形式代入式(21),得到辐射声功率的表达式:
| $ \begin{gathered} W=-\frac{1}{2}\left(\left(\boldsymbol{X}_{\mathrm{fe}}^{\mathrm{R}}\right)^{\mathrm{T}} \boldsymbol{Q} \boldsymbol{X}_{\mathrm{fe}}^{\mathrm{R}}+\mathrm{i}\left(\boldsymbol{X}_{\mathrm{fe}}^{\mathrm{R}}\right)^{\mathrm{T}} \boldsymbol{Q} \boldsymbol{X}_{\mathrm{fe}}^{\mathrm{I}}-\right. \\ \left.\mathrm{i}\left(\boldsymbol{X}_{\mathrm{fe}}^{\mathrm{I}}\right)^{\mathrm{T}} \boldsymbol{Q} \boldsymbol{X}_{\mathrm{fe}}^{\mathrm{R}}+\left(\boldsymbol{X}_{\mathrm{fe}}^{\mathrm{I}}\right)^{\mathrm{T}} \boldsymbol{Q} \boldsymbol{X}_{\mathrm{fe}}^{\mathrm{I}}\right) \end{gathered} $ | (28) |
式中()R、()I分别为取实部和虚部。式(28)对Xfe求导得到:
| $ \begin{aligned} \frac{\partial W}{\partial X_{\mathrm{fe}}^{\mathrm{R}}}=&-\frac{1}{2}\left(\left(\boldsymbol{X}_{\mathrm{fe}}^{\mathrm{R}}\right)^{\mathrm{T}} \boldsymbol{Q}^{\mathrm{T}}+\left(\boldsymbol{X}_{\mathrm{fe}}^{\mathrm{R}}\right)^{\mathrm{T}} \boldsymbol{Q}+\right.\\ &\left.\mathrm{i}\left(\boldsymbol{X}_{\mathrm{fe}}^{\mathrm{I}}\right)^{\mathrm{T}} \boldsymbol{Q}^{\mathrm{T}}-\mathrm{i}\left(\boldsymbol{X}_{\mathrm{fe}}^{\mathrm{I}}\right)^{\mathrm{T}} \boldsymbol{Q}\right) \end{aligned} $ | (29) |
| $ \begin{gathered} \frac{\partial W}{\partial \boldsymbol{X}_{\mathrm{fe}}^{\mathrm{I}}}=-\frac{1}{2}\left(\mathrm{i}\left(\boldsymbol{X}_{\mathrm{fe}}^{\mathrm{R}}\right)^{\mathrm{T}} \boldsymbol{Q}-\mathrm{i}\left(\boldsymbol{X}_{\mathrm{fe}}^{\mathrm{R}}\right)^{\mathrm{T}} \boldsymbol{Q}^{\mathrm{T}}+\right. \\ \left.\left(\boldsymbol{X}_{\mathrm{fe}}^{\mathrm{I}}\right)^{\mathrm{T}} \boldsymbol{Q}^{\mathrm{T}}+\left(\boldsymbol{X}_{\mathrm{fe}}^{\mathrm{I}}\right)^{\mathrm{T}} \boldsymbol{Q}\right) \end{gathered} $ | (30) |
将式(29)、(30)代入式(26)可得到伴随向量的表达式:
| $ \boldsymbol{\mu}_{1}^{\mathrm{T}}\left(\boldsymbol{K}_{\mathrm{d}}-\boldsymbol{B}\right)=\frac{1}{4}\left(-2\left(\boldsymbol{X}_{\mathrm{fe}}^{\mathrm{R}}\right)^{\mathrm{T}} \boldsymbol{Q}+\mathrm{i}\left(\boldsymbol{X}_{\mathrm{fe}}^{\mathrm{I}}\right)^{\mathrm{T}}\left(\boldsymbol{Q}+\boldsymbol{Q}^{\mathrm{T}}\right)\right) $ | (31) |
求解式(31)即可得到拉格朗日乘子μ1,进而辐射声功率灵敏度可由式(27)得出
| $ \begin{aligned} \frac{\mathrm{d} W}{\mathrm{~d} x_{i}}=&-\frac{1}{2} \operatorname{Re}\left(\left(-2\left(\boldsymbol{X}_{\mathrm{fe}}^{\mathrm{R}}\right)^{\mathrm{T}} \boldsymbol{Q}+\mathrm{i}\left(\boldsymbol{X}_{\mathrm{fe}}^{\mathrm{I}}\right)^{\mathrm{T}}\left(\boldsymbol{Q}+\boldsymbol{Q}^{\mathrm{T}}\right)\right) \times\right.\\ &\left.\left(\boldsymbol{K}_{\mathrm{d}}-\boldsymbol{B}\right)^{-1}\left(\frac{\partial \boldsymbol{K}_{\mathrm{fe}}}{\partial x_{i}}-\omega^{2} \frac{\partial \boldsymbol{M}_{\mathrm{fe}}}{\partial x_{i}}\right) \boldsymbol{X}_{\mathrm{fe}}\right) \end{aligned} $ | (32) |
由上述伴随变量法的推导过程可以发现,该方法推导过程较为繁琐,中间变量较多,容易出错。因此,本文提出更为简洁高效的直接求导法求解辐射声功率灵敏度。
2.2 声功率单元灵敏度的直接求导法式(21)中的辐射声功率W直接对单元变量xi求导,并由实部操作符得到声功率的简单形式:
| $ \frac{\partial W}{\partial x_{i}}=-\frac{1}{2}\left(\frac{\partial \boldsymbol{X}_{\mathrm{fe}}^{\mathrm{H}}}{\partial x_{i}} \boldsymbol{Q} \boldsymbol{X}_{\mathrm{fe}}+\boldsymbol{X}_{\mathrm{fe}}^{\mathrm{H}} \boldsymbol{Q} \frac{\partial \boldsymbol{X}_{\mathrm{fe}}}{\partial x_{i}}\right)=-\operatorname{Re}\left(\boldsymbol{X}_{\mathrm{fe}}^{\mathrm{H}} \boldsymbol{Q} \frac{\partial \boldsymbol{X}_{\mathrm{fe}}}{\partial x_{i}}\right) $ | (33) |
式(13)和式(23)分别对xi求导得到:
| $ \left\{\begin{array}{l} \frac{\partial \boldsymbol{K}_{\mathrm{d}}}{\partial x_{i}} \boldsymbol{X}_{\mathrm{fe}}+\boldsymbol{K}_{\mathrm{d}} \frac{\partial \boldsymbol{X}_{\mathrm{fe}}}{\partial x_{i}}-\boldsymbol{L} \frac{\partial \boldsymbol{p}_{\mathrm{be}}}{\partial x_{i}}=\bf{0} \\ \boldsymbol{L} \frac{\partial \boldsymbol{p}_{\mathrm{be}}}{\partial x_{i}}=\boldsymbol{B} \frac{\partial \boldsymbol{X}_{\mathrm{fe}}}{\partial x_{i}} \end{array}\right. $ | (34) |
由式(34)得到:
| $ \frac{\partial \boldsymbol{X}_{\mathrm{fe}}}{\partial x_{i}}=-\left(\boldsymbol{K}_{\mathrm{d}}-\boldsymbol{B}\right)^{-1} \frac{\partial \boldsymbol{K}_{\mathrm{d}}}{\partial x_{i}} \boldsymbol{X}_{\mathrm{fe}} $ | (35) |
将式(35)代入式(33)得到辐射声功率的单元灵敏度公式:
| $ \frac{\partial W}{\partial x_{i}}=\operatorname{Re}\left(\boldsymbol{X}_{\mathrm{fe}}^{\mathrm{H}} \boldsymbol{Q}\left(\boldsymbol{K}_{\mathrm{d}}-\boldsymbol{B}\right)^{-1}\left(\frac{\partial \boldsymbol{K}_{\mathrm{fe}}}{\partial x_{i}}-\omega^{2} \frac{\partial \boldsymbol{M}_{\mathrm{fe}}}{\partial x_{i}}\right) \boldsymbol{X}_{\mathrm{fe}}\right) $ | (36) |
对比本文的直接求导法和AVM法可以发现,本文方法的推导过程较为简洁高效,中间变量少。最终的灵敏度公式中的各矩阵都在AVM法的最终公式中出现,不需要计算额外的变量,说明灵敏度计算量也并未增加。
2.3 目标函数与优化算法体积约束条件下,以辐射声功率C最小化为目标函数,则结构拓扑优化数学模型为:
| $ \left\{\begin{array}{l} \min (C) \\ \text { s. t. : } \\ \qquad\left[\begin{array}{ll} \boldsymbol{K}_{\mathrm{fe}}-\omega^{2} \boldsymbol{M}_{\mathrm{fe}} & \boldsymbol{L} \\ -\mathrm{i} \omega \boldsymbol{G} \boldsymbol{M}_{\mathrm{be}}^{-1} \boldsymbol{L} & \boldsymbol{H} \end{array}\right]\left[\begin{array}{l} \boldsymbol{X}_{\mathrm{fe}} \\ \boldsymbol{p}_{\mathrm{be}} \end{array}\right]=\left[\begin{array}{l} \boldsymbol{F}_{\mathrm{fe}} \\ \bf{0} \end{array}\right] \\ \qquad V^{*}-\sum\limits_{i=1}^{N} V_{i} x_{i}=0 \quad x_{i} \in\left\{x_{\min }, 1\right\} \end{array}\right. $ | (37) |
式中:V*为结构有效体积,xi为单元状态变量(取xmin或1)。
在涉及到特征值问题的优化中,低密度区域容易产生局部模态。在使用BESO优化方法时,Huang等[18]对质量和刚度采用相同的罚函数幂率,该模型对部分优化问题是有效的。但是在计算中发现,采用这种方法后有些优化问题在失效单元区域仍然会出现局部模态,这导致优化过程中结构拓扑突变,迭代不稳定难以收敛。Pedersen[19]提出线性化单元刚度的方法,该方法可以使单元在极低密度时仍然能保持较高的刚度质量比,可有效避免伪本征模,使优化结果更加合理,罚函数模型如下:
| $ \left\{\begin{array}{l} \rho_{i}=x_{i} \rho^{0}, 0<x_{\min } \leqslant x_{i} \leqslant 1.0 \\ E_{i}=x_{i}^{p} E^{0}, 0.1 \leqslant x_{i} \leqslant 1.0 \\ E_{i}=\frac{x_{i}}{100} E^{0}, x_{\min } \leqslant x_{i} \leqslant 0.1 \end{array}\right. $ | (38) |
式中:ρ0为结构初始密度,E0为结构初始弹性模量,p为罚因子。
结合BESO方法中单元状态变量xi仅可取xmin或1的特点,同时为保证罚函数模型的连续性,本文提出以下改进的罚函数模型:
| $ \left\{\begin{array}{l} \rho_{i}=x_{i} \rho^{0} \\ E_{i}=\left[\frac{x_{\min } / 100-x_{\min }^{\mathrm{p}}}{1-x_{\min }^{\mathrm{p}}}\left(1-x_{i}^{\mathrm{p}}\right)+x_{i}^{\mathrm{p}}\right] E^{0} \end{array}\right. $ | (39) |
拓扑优化过程中需要采用基于半径滤波法和单元灵敏度历史平均方法等来避免“孤立网格”和加速收敛。具体的耦合优化的计算流程如下:
1) 初始化结构参数。定义初始耦合域的物理参数、定义BESO算法的各初始参数;
2) 生成数值网格、生成单元矩阵和耦合矩阵并组装生成有限元声振耦合方程,生成结构外表面边界元的各矩阵;
3) 根据步骤2)计算各矩阵,求解系统响应。根据式(38)计算单元灵敏度。进行灵敏度过滤和灵敏度历史平均[20];
4) 判断失效单元是否与声学单元相邻,如果相邻,则将失效单元转变为声学单元,并更新结构域和流体域;
5) 根据更新后的各域,识别结构域和流体域的耦合单元和耦合边界;
6) 进行收敛性判断,如不满足收敛条件,则重复步骤2)~步骤5),直到满足收敛条件。
3 数值算例 3.1 声辐射数值计算结果验证为验证本文文建立的声振耦合方程的正确性,设置验证算例。无限大水中放置一个内径为1.0 m外径为1.2 m的铝质圆环,结构密度为2 700 kg/m3,弹性模量为69 GPa,泊松比为0.3,内声场和外声场介质为水,其密度为1 000 kg/m3,声速为1 450 m/s。圆环内侧顶点处施加频率为10 Hz,幅值为1 N,方向为y轴方向的激励力。
采用Matlab编程计算圆环内外的耦合声场,并与无反射边界法的计算计算结果进行对比。在无反射边界中,取圆环外侧半径5 m的同心圆为外侧计算域,外边界设置为无反射边界,材料属性和其他边界条件与声振耦合法相同,两种方式的声压计算结果如图 2所示。对比可知,本文的声振耦合法与无反射边界法计算的内、外场声压分布基本一致。
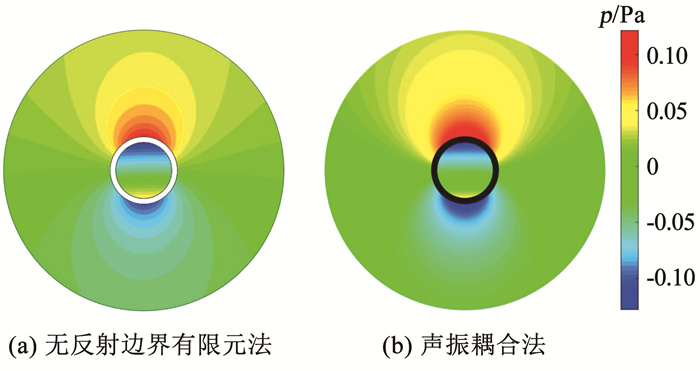
|
图 2 圆环内外声场声压分布 Fig. 2 Distribution of sound pressure inside and outside the ring |
图 3给出圆环外边界声压实部的分布曲线,为方便比较,设置起始点为圆环左侧中点(与图 3中弧度为0处相对应),沿顺时针方向。两种数值方法计算的整体匹配度较好,但在谷值处误差相对较大,原因在于有限元的无反射边界对正入射波吸收性较好,但对倾斜入射波有一定的反射作用,因此与实际值有一定误差。此外可明显看出无反射边界法的曲线在对称节点上的声压值略微不对称,而边界条件和外载荷均是对称,其边界声压实部也应该是对称的。出现这种现象的原因是划分有限元网格无法做到完全对称,造成一定的误差。因此,可以认为采用声振耦合方程可获得良好的声压预报结果。
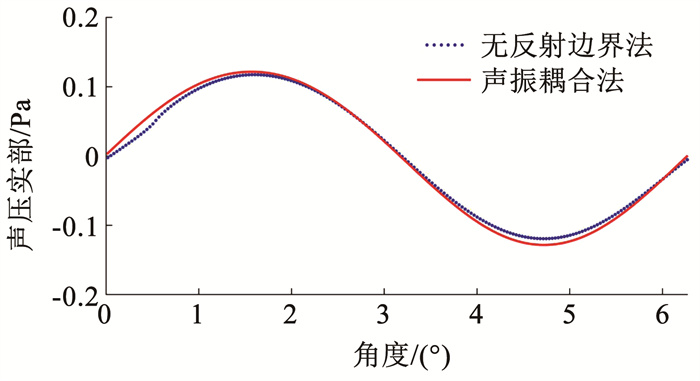
|
图 3 结构表面声压实部分布 Fig. 3 Real part of sound pressure around the structure interface |
图 4为算例1的设计模型,设计域为一外部半径3.0 m,内部半径2.0 m的半圆环,外圈厚度0.1 m部分为非设计域,初始设计域为全设计域的80%(即图中半径2.2 m部分),半圆环两侧的底部固定约束,内部流体的底部边界为零声压边界。内外声场的声介质均为水,声介质属性和结构材料属性同声辐射数值计算结果。内声场中点Pin点为一幅值大小为100 Pa的声压激励,激励频率为125 Hz。本算例以结构外表面辐射声功率最小化为目标函数,设置目标体积为全结构域的80%不变。计算域用最大0.03 m尺寸的四边形四节点等参数单元离散,过滤半径rmin=0.1 m,罚函数因子p=3,xmin=0.000 1。

|
图 4 拱形梁设计模型 Fig. 4 Design model of arch beam |
为验证本文所提灵敏度方法的设计效果,同条件下采用AVM灵敏度法进行对比。迭代过程的声功率级和灵敏度计算消耗时间如图 5所示,其中基准声功率为1×10-12 W。两种方法的目标函数在迭代过程中除了在开始有小幅波动之外,均很快达到平稳状态,说明两种灵敏度方法的鲁棒性较好,且最终的优化目标函数一致。对比两种方法在迭代过程中灵敏度部分消耗的时间可以发现,两种灵敏度求解方法在每一个迭代步中的分析时间没有明显差异。从式(32)和式(36)看出,两个灵敏度计算公式都包含相似的变量,因此计算时间没有太大差异。
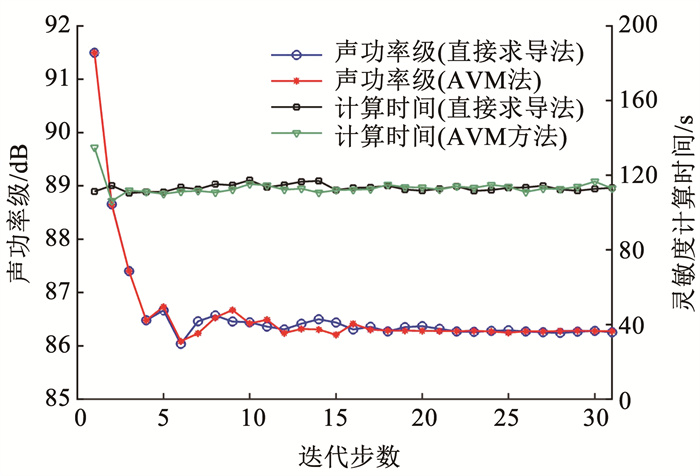
|
图 5 目标函数和灵敏度计算时间的迭代曲线 Fig. 5 Evolution histories of objective function andsensitivity calculation time |
结构对外声辐射情况也体现在外部声场的声压级分布情况上。图 6为优化前、后结构拓扑图与内部声场和部分外部声场的声压级响应分布,外部声场截取10 m×6 m范围。对比内部声场,优化前、后仅分布范围改变,强度未发生明显变化,但从外部声场的声压级分布可以看出,初始设计的外声场存在大范围的高声压级区域。优化设计模型中,该区域声压级明显低于初始设计,这也印证了优化后结构的声辐射得到有效的降低。

|
图 6 优化前、后结构拓扑和声压级分布 Fig. 6 Structural topology and sound pressure level distribution before and after optimization |
算例1为铝在水介质中的声辐射优化,为研究不同声介质和结构材料的优化效果,算例2的设计模型同算例1,改变声介质和结构材料。初始设计域为全设计域,半圆环两侧的底部固定约束,流体下边界为刚性边界。圆环内部和外部辐射声场的声介质均为空气,密度为1.21 kg/m3,声速为343 m/s。结构的材料密度为800 kg/m3,弹性模量为2 GPa,泊松比为0.3。声压激励源位于圆心处Pin点,幅值大小为100 Pa,激励频率为205 Hz。以结构外表面辐射声功率最小化为目标函数,设置目标体积为全结构域的65%。单次迭代的体积缩减率为2%,过滤半径rmin=0.1 m,罚函数因子p=3,xmin=0.000 1。
为方便对比外声场情况,截取外部半径为6 m的圆环区域。图 7为优化前、后同色度范围的声压级分布图和结构拓扑形态。结构拓扑的边界清晰,且较为规整,内部声场和外部声场的声压级得到大幅的降低。这与图 8的迭代曲线相对应,结构拓扑渐变稳定,迭代曲线未出现大幅波动,声功率级从初始的104.8 dB降低至62.1 dB,降低幅度达到40.7%。从优化前、后内部声场的分布情况看,由激励源声波、边界反射声波以及结构振动辐射声波相互叠加形成环形的低声压带,由于结构拓扑的改变,低声压带分布位置和个数发生改变。为方便观察内部声压带与外部辐射声场的关系,图 7还给出声压级高对比图,从图中圈出部分可以看出,圆环内边界上的声压带个数与外声场高(或低)声压是对应的。

|
图 7 优化前、后结构拓扑和声压级分布 Fig. 7 Structural topology andsound pressure level distribution before and after optimization |
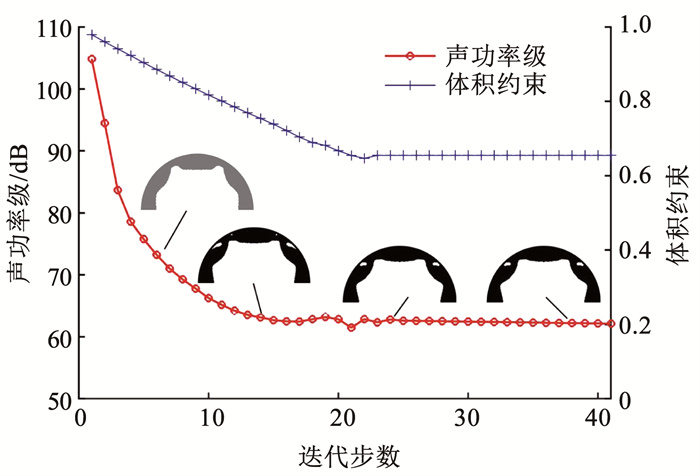
|
图 8 目标函数和约束体积的优化迭代曲线 Fig. 8 Evolution histories of objective function and volumefraction |
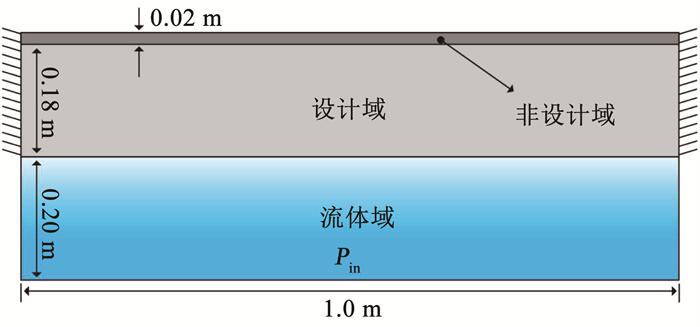
图 9为算例3的设计模型,结构域为1.0 m×0.2 m的固支梁,梁顶部0.02 m部分为非设计域,初始设计域即为全设计域,结构密度为2 700 kg/m3,弹性模量为69 GPa,泊松比为0.3,设置目标体积为全结构域的85%。结构域下侧声介质域为1.0 m×0.2 m的矩形域,声介质为水,梁上侧声介质为空气,各介质属性与上文相同。声压激励源为矩形流体域的下边界,幅值大小为100 Pa,激励频率为1 940 Hz。同样以声功率最小化为目标函数。设计域离散为200×40个四边形单元,体积缩减率设置为1%,过滤半径rmin=0.015 m,罚函数因子p=3,xmin=0.000 1。
|
图 9 固支梁设计模型 Fig. 9 Design model of fixed beam |
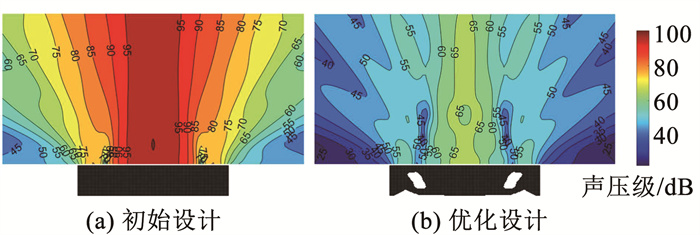
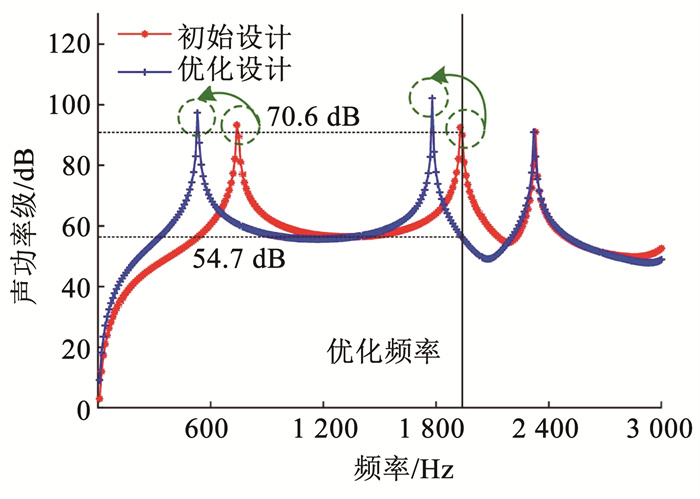
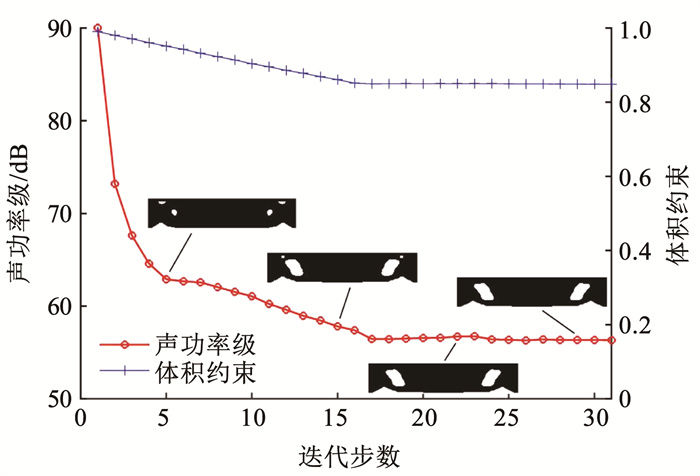
截取固支梁上方2.0 m×1.0 m区域的声压级分布来比较优化结果,如图 10所示。可以看出,优化后的外声场声压得到明显降低。图中的等值线上数值表明,初始设计的辐射声场最大声压级达到100 dB,且占据固支梁上方的大部分区域,优化构型的最大辐射声压级降低至65 dB,降低幅度约35%。图 11显示了两种模型在不同激励频率下的声功率级曲线,激励频率位于初始设计模型的第2个响应峰值处,优化后的结构辐射声功率峰值频率降低,避开激励频率所在位置,使其位于响应谷值附近,声功率级从初始的70.6 dB降低至54.7 dB,降低幅度达22.5%。图 12为优化迭代曲线,与前文一致,迭代曲线平缓,结构拓扑形式未发生突变,说明本文算法的稳定性较好。
|
图 10 优化前、后结构拓扑和声压级分布 Fig. 10 Structural topology and sound pressure level distribution before and afterthe optimization |
|
图 11 声功率频率响应曲线 Fig. 11 Frequencyresponse curves of sound power |
|
图 12 目标函数和约束体积的优化迭代曲线 Fig. 12 Evolution histories of objective function and volume fraction |
1) 建立的含内部声场的强耦合有限元/边界元模型计算精度较高,可用于求解耦合系统的声辐射问题。
2) 提出的直接求导法与经典的伴随变量法得到的优化结果一致,且鲁棒性较好。
3) 本文的线性化刚度模型和灵敏度分析法适用于不同结构材料与声介质问题,因此使用本文的优化算法可以得到最优拓扑。
| [1] |
VASCONCELOS R O, AMORIM M C P, LADICH F. Effects of ship noise on the detectability of communication signals in the lusitanian toadfish[J]. Journal of Experimental Biology, 2007, 210: 2104. DOI:10.1242/jeb.004317 |
| [2] |
蔡保佩. 基于粒子群算法的刚架结构的优化[D]. 大连: 大连理工大学, 2014. CAI Baopei. Optimization of the frame based on particle swarm algorithm[D]. Dalian: Dalian University of Engineering, 2014 |
| [3] |
陈龙, 张高朋. 基于灵敏度分析的三维结构等几何形状优化方法[J]. 中国机械工程, 2017, 28(14): 1723. CHEN Long, ZHANG Gaopeng. Three dimensional structural shape optimization based on sensitivity analysis using isogeometric analysis[J]. China Mechanical Engineering, 2017, 28(14): 1723. DOI:10.3969/j.issn.1004-132X.2017.14.015 |
| [4] |
许智生, 黄其柏, 赵志高, 等. 基于拓扑优化方法的安静结构设计[J]. 华中科技大学学报(自然科学版), 2010, 38(4): 91. XU Zhisheng, HUANG Qibai, ZHAO Zhigao, et al. Quiet structure design based on topology optimization[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2010, 38(4): 91. |
| [5] |
AKL W, EL-SABBAGH A, AL-MITANI K, et al. Topology optimization of a plate coupled with acoustic cavity[J]. International Journal of Solids and Structures, 2009, 46(10): 2060. DOI:10.1016/j.ijsolstr.2008.05.034 |
| [6] |
DVHRING M B, JENSEN J S, SIGMUND O. Acoustic design by topology optimization[J]. Journal of Sound and Vibration, 2008, 317(3/4/5): 557. DOI:10.1016/j.jsv.2008.03.042 |
| [7] |
KOOK J. Evolutionary topology optimization for acoustic-structure interaction problems using a mixed u/p formulation[J]. Mechanics Based Design of Structures and Machines, 2019, 47(3): 356. DOI:10.1080/15397734.2018.1557527 |
| [8] |
VICENTE W M, PICELLI R, PAVANELLO R, et al. Topology optimization of frequency responses of fluid-structure interaction systems[J]. Finite Elements in Analysis and Design, 2015, 98: 1. DOI:10.1016/j.finel.2015.01.009 |
| [9] |
陈炉云, 王德禹. 基于渐进结构优化的结构- 声拓扑优化研究[J]. 声学学报, 2008, 33(5): 456. CHEN Luyun, WANG Deyu. Structural-acoustic topology optimization analysis based on evolutionary structural optimization method[J]. Acta Acoustica, 2008, 33(5): 456. DOI:10.3321/j.issn:0371-0025.2008.05.012 |
| [10] |
张军. 声学- 结构灵敏度及结构- 声学优化设计研究[D]. 大连: 大连交通大学, 2006 ZHANG Jun. Researchon acoustic-structure sensitivity and structure-acoustic optimization design[D]. Dalian: Dalian Jiaotong University, 2006 |
| [11] |
DU Jianbin, OLHOFF N. Minimization of sound radiation from vibration bi-material structures using topology optimization[J]. Structural Multidisciplinary Optimization, 2007, 33: 305. DOI:10.1007/s00158-006-0088-9 |
| [12] |
XU Z S, HUANG Q B, ZHAO Z G. Topology optimization of composite material plate with respect to sound radiation[J]. Engineering Analysis with Boundary Elements, 2011, 35(1): 61. DOI:10.1016/j.enganabound.2010.05.013 |
| [13] |
ZHANG Xiaopeng, KANG Zhan. Topology optimization of damping layers for minimizing sound radiation of shell structures[J]. Journal of Sound and Vibration, 2013, 332(10): 2500. DOI:10.1016/j.jsv.2012.12.022 |
| [14] |
SANDBERG G, WERNBERG P A, DAVIDSSON P. Fundamentals of fluid-structure interaction[M]. Vienna: Springer, 2008. DOI:10.1007/978-3-211-89651-8_2
|
| [15] |
PETERS H, KESSISSOGLOU N, MARBURG S. Modal decomposition of exterior acoustic-structure interaction[J]. Journal of the Acoustical Society of America, 2013, 133(5): 2668. DOI:10.1121/1.4796114 |
| [16] |
KANG Zhan, ZHANG Xiaopeng, JIANG Shigang, et al. On topology optimization of damping layer in shell structures under harmonic excitations[J]. Structural and Multidisciplinary Optimization, 2012, 46(1): 51. DOI:10.1007/s00158-011-0746-4 |
| [17] |
ZHANG Xiaopeng, KANG Zhan. Vibration suppression using integrated topology optimization of host structures and damping layers[J]. Journal of Vibration & Control, 2014, 22: 1. DOI:10.1177/1077546314528368 |
| [18] |
HUANG X, XIE Y M. Bi-directional evolutionary topology optimization of continuum structures with one or multiple materials[J]. Computational Mechanics, 2009, 43(3): 393. DOI:10.1007/s00466-008-0312-0 |
| [19] |
PEDERSEN N L. Maximization of eigenvalues using topology optimization[J]. Structural and Multidisciplinary Optimization, 2000, 20(1): 2. DOI:10.1007/s001580050130 |
| [20] |
HUANG X, XIE Y M. Convergent and mesh-independent solutions for the bi-directional evolutionary structural optimization method[J]. Finite Elements in Analysis and Design, 2007, 43(14): 1039. DOI:10.1016/j.finel.2007.06.006 |
 2021, Vol. 53
2021, Vol. 53


