2. 中国科学院 微电子研究所, 北京 100029
2. Institute of Microelectronics, Chinese Academy of Sciences, Beijing 100029, China
基于MEMS加速度计的尺寸、成本功耗等方面的优势,其广泛应用于物联网、智能穿戴设备[1-2],尤其在SLAM(simultaneous localization and mapping)、姿态识别、跌倒检测等应用中对IMU(inertial measurement unit)设备的姿态角精确计算有重要作用[3-4]。但是由于加速度计的安装偏差、尺度因子、零偏和随机噪声等因素的影响,其输出存在一定的误差[5-6]。因此需要建立校准补偿模型以实现稳定、高精度的加速度输出。
传统分立式标定校准依赖于大型转台设备,价格昂贵、操作方法复杂,标定精度取决于转台设备,不利于大批量的生产使用。为了降低校准对大型设备的依赖,颜开思等[7]提出借助于立方体治具将加速度计依次旋转90°,旋转6次,依此求得模型参数;为了解决六面体算法中治具所处平面可能不水平的问题,陆续有学者[8-11]提出九位置法、十位置法,十二面体法、二十四位置法等,将相差45°,90°,180°的两面求均值作为其中一组数据来抵消水平夹角问题,但均需要依赖治具。Lötters等[12]首次提出基于模观测的加速度计标定方法,将标定问题转化为优化问题,其关键在于非线性方程组的求解,最为常见的为迭代法、牛顿法[13],其缺点为迭代结果严重依赖于初值的选取。Cheuk等[14-15]提出在多组任意位置下观测数据来求解模型参数,摆脱了治具的限制,但仍无法解决初值依赖问题。
针对LM算法过度依赖初值的问题,本文结合了LM算法与最小二乘法算法,在初值预估不准确情况下,实现误差模型参数的精确标定,并在标定后的姿态解算中,精度能达到与传统标定方法相同的量级。
1 加速度计误差补偿模型根据误差产生原因,MEMS三轴加速度计误差主要来源于轴间非正交误差、尺度因子、零偏和噪声的随机游走,可以建立如下误差模型:
| $ \left[\begin{array}{c} O_{x} \\ O_{y} \\ O_{z} \end{array}\right]=\left[\begin{array}{ccc} S_{x x} & K_{y z} & K_{z y} \\ K_{x z} & S_{y y} & K_{z x} \\ K_{x y} & K_{y x} & S_{z z} \end{array}\right] *\left(\left[\begin{array}{c} R_{x} \\ R_{y} \\ R_{z} \end{array}\right]+\left[\begin{array}{c} B_{x} \\ B_{y} \\ B_{z} \end{array}\right]+\left[\begin{array}{c} \nu_{x} \\ \nu_{y} \\ \nu_{z} \end{array}\right]\right) $ | (1) |
式中:O=[Ox Oy Oz]T,R=[Rx Ry Rz]T,B=[Bx By Bz]T分别为测量值、真实值和零偏;ν=[νx νy νz]T为白噪声,一般可忽略;Tk=
| $ \theta^{\mathrm{cal}}=\left[K_{y z}, K_{z y}, K_{z x}, S_{x x}, S_{y y}, S_{z z}, B_{x}, B_{y}, B_{z}\right] $ | (2) |
加速度计处于静止状态下,只受到重力,理论上加速度计的任意姿态下,各轴输出数据的模等于1 g,因此有
| $ \begin{aligned} \|g\|^{2}=&\|\boldsymbol{O}\|^{2}=\left\|\boldsymbol{T}_{k} * \boldsymbol{T}_{s}(\boldsymbol{R}+\boldsymbol{B})\right\|^{2}=\\ &\left\|h\left(\boldsymbol{R}, \boldsymbol{\theta}^{\text {cal }}\right)\right\|^{2} \end{aligned} $ | (3) |
为求解误差模型中θcal参数,可以利用多组静态观测数据使用最小二乘法对多元方程求解;也可以通过构建椭球模型近似等效加速度计误差模型,通过大量静态观测数据拟合求解椭球参数来近似求解误差模型参数,这些已有方法将在下文具体说明。针对LM算法过度依赖初值的问题,本文提出的LM& 最小二乘法自校准法在LM&最小二乘法自校准法的实现中进行详细阐述,并在实验验证与分析中进行相关实验结果的呈现。
2 已有方法求解模型参数 2.1 十二面体法求参在十二面体法[16]求解加速度计误差模型参数中,需要将被测加速度计固定在治具中,依次旋转0°,90°,180°,270°,如图 1所示。将所得到的12组数据分为2组,按照加速度计误差补偿模型的误差模型,将观测数据代入,通过最小二乘法,求得两组参数,再对参数进行加权获得最后的加速度计误差模型参数:
| $ \boldsymbol{\theta}^{\mathrm{cal}}=\alpha \boldsymbol{\theta}_{1}^{\mathrm{cal}}+\beta \boldsymbol{\theta}_{2}^{\mathrm{cal}} $ | (4) |
在忽略轴间偏差,即三轴之间均正交的情况下,加速度计任意静止状态输出数据的模为定值g,在三轴正交坐标系中表现为一椭球面上的点[17],即:
| $ \begin{gathered} a_{1} x^{2}+a_{2} y^{2}+a_{3} z^{2}+a_{4} x y+a_{5} x z+a_{6} y z+ \\ a_{7} x+a_{8} y+a_{9} z \end{gathered} $ | (5) |
| $ [\boldsymbol{X}-\boldsymbol{C}] \boldsymbol{M}[\boldsymbol{X}-\boldsymbol{C}]^{\mathrm{T}}=1+\boldsymbol{C M C}^{\mathrm{T}} $ | (6) |
| $ \boldsymbol{M}=\left[\begin{array}{ccc} a_{1} & a_{4} / 2 & a_{5} / 2 \\ a_{4} / 2 & a_{2} & a_{6} / 2 \\ a_{5} / 2 & a_{6} / 2 & a_{3} \end{array}\right] $ | (7) |
式中:X为椭球面上的数据,C为椭球球心,M为所求参数矩阵。通过最小二乘法对大量静止状态样本数据进行拟合得到椭球球心即零偏,椭球在各个轴上的投影为尺寸因子。
3 LM& 最小二乘法自校准法的实现 3.1 LM算法LM(levenberg-marquardt)算法[18-20]是介于牛顿法和梯度下降法之间的非线性优化算法,广泛应用于非线性最小化的求解。在对于模型参数求解问题中,如式(8),LM算法通过将状态转移矩阵中Hessian矩阵近似为Jacobian矩阵的方式,如式(9)、(10),解决了梯度下降法收敛速度缓慢的问题,避免了牛顿法求解高阶非线性问题时复杂二阶导数计算过程,以及Hessian非满秩和非正定情况。LM算法最终训练形式通过如下进行拟合求参:
| $ F(\boldsymbol{x}, \boldsymbol{\omega})=\sum\limits_{j=1}^{M} \sum\limits_{i=1}^{M} E_{i, j}^{2} $ | (8) |
| $ \boldsymbol{H} \approx \boldsymbol{J}^{\mathrm{T}} \boldsymbol{J}+\mu \boldsymbol{I} $ | (9) |
| $ x_{k+1}=x_{k}-\left(\boldsymbol{J}^{\mathrm{T}} \boldsymbol{J}+\mu \boldsymbol{I}\right) * g_{k} $ | (10) |
| $ d_{k}\left(u_{k}\right)=-\left(\boldsymbol{J}^{\mathrm{T}} \boldsymbol{J}+\mu_{k} \boldsymbol{I}\right)^{-1} \boldsymbol{J}_{k}^{\mathrm{T}} F_{k} $ | (11) |
式中:x为输入参数向量,ω为待求参数向量,N为待求参数向量个数,E为目标函数残差,M为离散非线性系统采样点个数。
利用LM算法求解加速度计误差模型参数,需要构建目标函数以及残差。由加速度计误差补偿模型可知,加速度计处于静止状态下,只受到重力,因此将式(3)作为目标函数。
为求解误差模型中θcal参数,需要求解式(2)非线性输出方程,即需要多组不同姿态的静态观测数据。由于上述的各类误差导致加速度计各轴输出数据的模值不等于g,因此构造目标函数残差方程(12),通过对目标函数最小化实现模型参数的求解。
| $ E_{k}(\theta)=\sum\limits_{i}^{M}\left(\|g\|^{2}-\left\|h\left(\boldsymbol{R}, \boldsymbol{\theta}^{\mathrm{cal}}\right)\right\|^{2}\right) $ | (12) |
LM算法拥有高斯- 牛顿算法快速收敛的优点,也在梯度下降法的基础上解决了负梯度收敛缓慢的问题,但是其本身因在泰勒展开式中忽略了高阶项,在一定情况下会出现收敛缓慢的情况。另外LM算法高度依赖初值的设定,所以在单次加速度误差模型参数的求解中,由于初值的设定不准会导致模型参数拟合不准确。
因此,为实现加速度计应用过程中的闭环校准,就需要对加速度计误差模型的初值进行实时修正,确保LM算法可以迅速收敛。本文通过对加速度计任意位置下的静态数据样本进行滤波、筛选、截断,获取可用于最小二乘法的姿态数据,即加速度计某个轴垂直于水平面,另外两个轴平行水平面的姿态。与已有初值相关数据共同求解修正初值,并以此初值为LM算法训练初值,进行训练拟合,获得最终加速度计误差模型参数。
如图 2所示,为本文所提出的加速度计LM& 最小二乘法自校准法的流程图。主要过程分为3个部分:数据采集处理、模型参数初值修正、模型参数训练拟合。
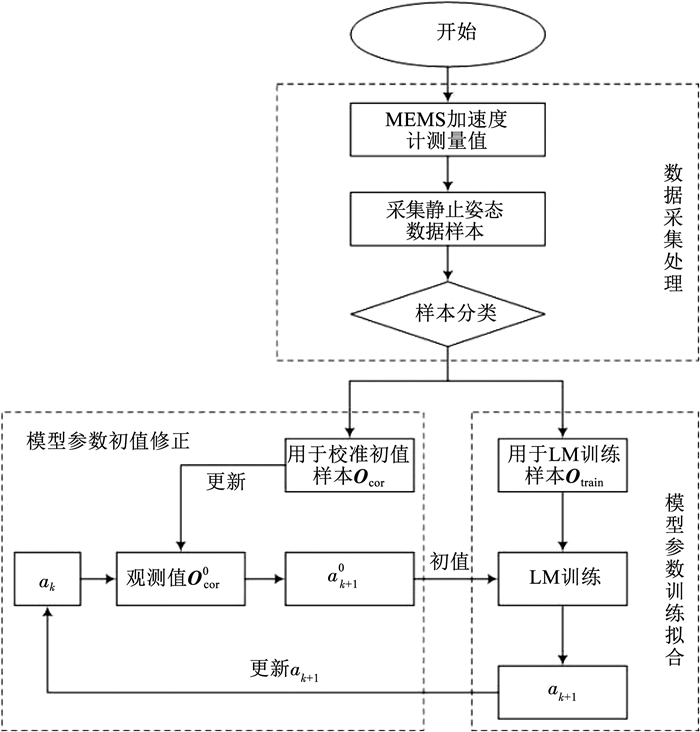
|
图 2 MEMS加速度计自校准流程 Fig. 2 Flow chart of self-calibration of MEMS accelerometer |
1) 采集加速度计静止姿态数据样本需要满足如下条件。
① 加速度计连续静止Twait。对连续采集到的Twait*f采集频率个数据,均需要满足|ζ(k)| < δ1,其中ζ(k)如式(13)所示,为加速度计各轴输出数据模值与重力加速度g的差,δ1为判断加速度计静止的阈值。
| $ \zeta(t)=\sqrt{\operatorname{var}\left(\boldsymbol{O}_{x}\right)^{2}+\operatorname{var}\left(\boldsymbol{O}_{y}\right)^{2}+\operatorname{var}\left(\boldsymbol{O}_{z}\right)^{2}}-g $ | (13) |
② 压力传感器输出的标准差P(t) < δ2。针对本文实验对象为智能鞋垫,以k个鞋垫内嵌压力传感器输出的标准差作为检测算子,检测鞋垫是否处于静止姿态,δ2为检测阈值。
| $ P(t)=\sqrt{\sum\limits_{1}^{k}\left[\operatorname{var}\left(p_{k}^{t}\right)-u\right]^{2}} $ | (14) |
③ 保证训练样本丰富性。所获得的静止姿态数据样本不与已存在样本重复,即需式(15)中,γ>δ3, 以保证解算结果精准。
| $ \gamma=\sum\limits_{\varTheta}\left(h_{i}\left(\boldsymbol{R}, \boldsymbol{\theta}^{\text {cal }}\right)-h_{j}\left(\boldsymbol{R}, \boldsymbol{\theta}^{\text {cal }}\right)\right), i \neq j \in \varTheta $ | (15) |
2) 加速度计静止姿态数据样本预处理。
① 滤波。对收集到的静止姿态数据样,通过式(13)进行滤波和提取有效数据,如图 3所示为采集到加速度计的原始静态数据样本与滤波后的静止姿态数据。

|
图 3 滤波和截断前、后数据对比 Fig. 3 Comparison of data before and after filtering and truncation |
② 分类。为获得最小二乘法所需要的静止姿态数据样本,需要从所有样本中筛选出加速度计某个轴垂直于地面,即输出接近|g|,另外2个轴输出接近为0的数据集合,在所有观测样本中找到满足式(16)的样本作为Ocor, 用以修正每次迭代的初值;其余静止姿态数据样本作为Otrain, 用来LM算法训练。
| $ \left|O_{i j}-g\right|<\sigma \&\&\left|O_{i j+1}\right|<\sigma \&\&\left|O_{i j-1}\right|<\sigma $ | (16) |
将误差模型(1)转换为
| $ \left[\boldsymbol{R}_{x}, \boldsymbol{R}_{y}, \boldsymbol{R}_{z}\right]=\left[O_{x}, O_{y}, O_{z}, 1\right] *\left[\begin{array}{ccc} S_{x x} & K_{y z} & K_{z y} \\ K_{x z} & S_{y y} & K_{z x} \\ K_{x y} & K_{y x} & S_{z z} \\ B_{x} & B_{y} & B_{z} \end{array}\right] $ | (17) |
通过最小二乘法求解多元方程参数得到:
| $ \left[\begin{array}{ccc} S_{x x} & K_{y z} & K_{z y} \\ K_{x z} & S_{y y} & K_{z x} \\ K_{x y} & K_{y x} & S_{z z} \\ B_{x} & B_{y} & B_{z} \end{array}\right]=\left[\boldsymbol{O}_{m \times 4}^{\mathrm{T}} \boldsymbol{O}_{m \times 4}\right]^{-1} \boldsymbol{O}_{m \times 4}^{\mathrm{T}} \boldsymbol{R}_{m \times 3} $ | (18) |
为求解全部模型参数,需要m>6, 修正第k+1次迭代的Ocor样本数可以小于6,即根据检测到的姿态部分代替原有数据,实现ak+10的修正,得到的参数Tk需要进一步初等变换,获得9参数模型。
3.2.1.3 模型参数训练拟合将上述修正的初值ak+10作为第k+1次LM算法迭代的初值就行训练拟合,参考LM算法所述原理,最终得到模型参数ak+1。
对于LM算法训练样本Otrain在非相关样本数m>6即可收敛,这获利于初值修正。
3.2.2 算法步骤步骤1 获取参考初值ak+10, 根据理论值,计算得到a0对应的测量值矩阵Ok。
步骤2 收集加速度计静止数据样本,需满足式(13)~(15)。
步骤3 根据式(16),对步骤2中收集到的静止姿态样本分类。
1) 用于修正第k+1次迭代模型初值的观测样本Ocor。
2) 用于训练拟合第k+1次模型参数ak+1的观测样本Otrain。
步骤4 通过Ocor修正第k+1次模型参数初值ak+10:将步骤3中的Ocor替换Ok中相应姿态数据,通过式(18)重新计算ak+10。
步骤5 以ak+10为第k+1次LM迭代的初值,按式(12)通过Otrain样本进行训练,拟合得k+1次迭代后模型参数ak+1。
4 实验验证与分析本文实验以自主研发的多传感器集成的智能鞋垫为被测对象,内置三轴加速度计、4组柔性压力传感器以及低功耗蓝牙片上系统、无线充电模块,如图 4所示。以蓝牙传输的方式将鞋垫数据实时传输到终端,传输频率为20 Hz。

|
图 4 被测对象智能鞋垫与立方体治具 Fig. 4 Measured object of smart insole and cube fixture |
根据已有方法求解模型参数所述,设计如下实验验证环节。
4.1 实验步骤 4.1.1 LM训练法1) 收集同一时段任意静止姿态加速度计输出数据M组。
2) 给定随机误差模型参数初值(0~1),通过LM算法,以M组数据进行训练求解误差模型参数。
4.1.2 LM& 最小二乘法自校准法1) 在为期30 d正常使用智能鞋垫的情况下,按照4.2所述条件每3 d自动检测收集任意静止姿态加速度数据M组。
2) 根据LM算法,对第1次M组样本数据给定随机模型参数初值(随机范围0~1),使用LM算法进行训练,得到初始误差模型参数。
3) 根据基于LM& 最小二乘法自校准法,对后续9次样本数据依次以前一次训练得到的参数为初值进行迭代训练,更新得到最终误差模型参数。
4.1.3 十二面体法1) 将鞋垫固定在治具上,保持鞋垫与治具水平与对齐。
2) 连接蓝牙设备,并根据图 1按照x, y, z轴旋转0°,90°,180°,270°,每个状态保持1 min。
3) 根据十二面体法求解加速度计误差模型参数。
4.1.4 椭球拟合法1) 采集智能鞋垫任意静止姿态加速度数据M组。
2) 根据椭球拟合法求解椭球拟合方程系数,并求解出椭球中心(即偏差)和椭球半径(即尺寸因子)。
4.2 实验结果1) LM& 最小二乘法自校准法所得结果如图 5(a)所示,在多次、长时间的循环迭代中,由初值设定不准引起的误差模型参数的估计误差在迭代中逐步消除,3次迭代后,由初值设定失误引起的模型参数平均相对误差降低95%。优化初值后,提高了参数训练的运算速度,训练时间由25 s降低到平均0.4 s,如图 5(b)所示。

|
图 5 LM& 最小二乘法校准法迭代过程中参数变化 Fig. 5 Parameters variation of LM& least squares method during iteration |
2) 如表 1所示为4种校准方式下获取的加速度计误差模型参数及其参数的相对误差。十二面体法、椭球拟合法、单纯LM方法与LM& 最小二乘法自校准法分别求解得到误差模型中12、6、9、9个参数。
| 表 1 本文方法与其他方法标定结果对比 Tab. 1 Comparison of calibration results between proposed method and other methods |
其中十二面体法、椭球法以及LM迭代法3种校准方法均对该加速度计在y轴方向存在较大零偏具有一致性描述。
3) 椭球拟合法模拟出加速度计数据样本构成的椭球面,如图 6所示,数据样本越丰富,椭球拟合法越精准。本实验中48组样本拟合得到的零偏和尺寸因子6个参数。采用椭球拟合法对加速度数据进行补偿,见表 2,补偿后三轴相对误差分别为-83.36%,12.80%,3.70%,存在一定误差。

|
图 6 椭球拟合球面图 Fig. 6 Ellipsoid fitting spherical graph |
| 表 2 椭球拟合法补偿后的相对误差 Tab. 2 Relative error of ellipsoid fitting method after compensation |
4) LM& 最小二乘法自校准法构建的误差模型对加速度计进行补偿,所得结果见表 3,相对误差分别为18.110%,4.300%,0.316%,相对椭圆拟合法精度有明显升高。进一步解算姿态角度,如图 7所示,解算所得各轴角度误差为0.363 5°,0.699 6°,0.643 3°,误差小于1°,可实现误差补偿后的姿态解算精度与传统标定方法十二面体法同等量级。
| 表 3 本文方法补偿后误差 Tab. 3 Error of proposed method after compensation |

|
图 7 本文方法补偿加速度计后的姿态角度 Fig. 7 Posture angle of accelerometer after compensated by proposed method |
结合不同方法的标定结果对比,可以得到本文提出的LM& 最小二乘法自校准法的优势如下:
1) 在不断LM迭代拟合过程中,加入了初值修正的步骤,优化解决了LM算法过度依赖初值的问题。并在可穿戴设备长期使用过程中采集校准数据,不需要人工设定姿态,实现了对加速度计实时校准。
2) 对于椭圆拟合法,只能解算出6项参数,并且需要大量的静态样本对椭球拟合才能达到解算的精度,通过对比其解算得到的加速度数据,仍有较大误差。LM& 最小二乘法自校准法需要静态观测样本少,且可解算出9种误差参数,参数相对误差更低。
3) 传统十二面体法可以解算误差模型中所有参数,精度相对较高,但是需要相关立方体治具,需要人工固定,也需要相对水平的测试平台。本文提出的LM& 最小二乘法自校准法可以实现实时采集,实时解算的效果,且在一定程度上脱离了治具的束缚。以本文方法对加速度计标定后,解算出角度值与十二面体法解算出角度值误差均小于1°,说明本文方法可以达到传统标定方法相同量级的精度。
5 结论1) 为保证MEMS持续、高精度的输出,本文建立了基于LM算法的加速度自校准模型,根据静态加速度计三轴输出模等于1 g,将标定问题转换为非线性方程优化问题。为解决LM算法过分依赖初值,导致拟合模型参数误差较大的问题。本文提出对静止姿态数据预处理,筛选出加速度计某个轴输出接近g,另外2个轴输出接近为0的静止姿态数据,通过最小二乘法修正初值。
2) 实际测试结果表明,由于初值的修正,与单纯LM校准算法比,本文方法降低了对初值的依赖,提高了训练效率。与椭球拟合法相比,本文方法标定时间短、精度高,解算参数的静止姿态观测样本数量需求不高。
3) 与传统十二面体校准法相比,本文方法不需要转台与治具,并能达到与传统校准方法相同的精度,并可以实现加速度计的实时自校准,针对可穿戴设备在未来能起到更广泛的应用。
4) 综上所述,本文所阐述的方法融合了传统误差模型参数求解的方法与人工智能训练的方法的优点。传统误差模型求解方程的算法可以为了数据训练提供更精准的收敛方向,LM算法则摆脱了治具的限制,为加速度的自校准提供了新的方向。
| [1] |
潘家瑶. 基于惯性传感器的可穿戴设备智能控制技术的研究与实现[J]. 信息技术与信息化, 2018(11): 58. PAN Jiayao. Research and realization of intelligence control technique of wearable devices based on inertial sensors[J]. Information Technology & Informatization, 2018(11): 58. DOI:10.3969/j.issn.1672-9528.2018.11.015 |
| [2] |
IGNACIO C V A, BELLA P, MANUEL T F, et al. Inertial sensors embedded in smartphones as a tool for fatigue assessment based on acceleration in survivors of breast cancer[J]. Physical Therapy, 2020, 100(3): 447. DOI:10.1093/ptj/pzz173 |
| [3] |
曹玉珍, 蔡伟超, 程旸. 基于MEMS加速度传感器的人体姿态检测技术[J]. 纳米技术与精密工程, 2010, 8(1): 37. CAO Yuzhen, CAI Weichao, CHENG Yang. Body posture detection technique based on MEMS acceleration sensor[J]. Nanotechnology and Precision Engineering, 2010, 8(1): 37. DOI:10.13494/j.npe.2010.008 |
| [4] |
赵祥欣. 基于三维加速度传感器的跌倒监测研究[D]. 杭州: 浙江大学, 2008 ZHAO Xiangxin. The research of fall detection based on tri-axial accelerometer[D]. Hangzhou: Zhejiang University, 2008. |
| [5] |
许鹏, 陈琳, 王娟. MEMS加速度计的误差补偿方法[J]. 微纳电子技术, 2016, 53(7): 467. XU Peng, CHEN Lin, WANG Juan. Method of the error compensation for MEMS accelerometers[J]. Micronanoelectronic Technology, 2016, 53(7): 467. DOI:10.13250/j.cnki.wndz.2016.07.008 |
| [6] |
彭孝东, 张铁民, 李继宇, 等. 三轴数字MEMS加速度计现场标定方法[J]. 振动、测试与诊断, 2014, 34(3): 544. DOI:10.3969/j.issn.1004-6801.2014.03.024 |
| [7] |
颜开思, 李岁劳, 龚柏春, 等. 基于平台和正六面体的惯导系统现场标定技术[J]. 测控技术, 2011, 30(5): 106. YAN Kaisi, LI Suilao, GONG Bochun, et al. Calibration techniques for inertial navigation system based on platform and regular hexahedron[J]. Measurement & Control Technology, 2011, 30(5): 106. DOI:10.3969/j.issn.1000-8829.2011.05.025 |
| [8] |
付强, 戴晓斌. 基于加速度计阵列的多轴向振动台校准研究[J]. 强度与环境, 2018, 45(6): 10. FU Qiang, DAI Xiaobin. Research on calibration technology of multi-axial vibration table based on accelerometer array[J]. Structure & Environment Engineering, 2018, 45(6): 10. DOI:10.19447/j.cnki.11-1773/v.2018.06.002 |
| [9] |
邱浩阳, 虞水俊. 惯导平台加速度计静态多位置模观测标定方法[J]. 导航与控制, 2013, 12(2): 63. QIU Haoyang, YU Shuijun. Accelerometer multi-position norm-observed calibration method of GINS on fixed base[J]. Navigation and Control, 2013, 12(2): 63. DOI:10.3969/j.issn.1674-5558.2013.02.013 |
| [10] |
孙佳, 邹靖, 胡桐. 基于24位置的MEMS惯性传感器快速标定方法[J]. 压电与声光, 2019, 41(3): 440. SUN Jia, ZOU Jing, HU Tong. A fast calibration method for MEMS Inertial sensors based on 24-position[J]. Piezoelectrics & Acoustooptics, 2019, 41(3): 440. DOI:10.11977/j.issn.1004-2474.2019.03.027 |
| [11] |
孙枫, 曹通. 基于Kalman滤波的加速度计十位置标定方法[J]. 系统工程与电子技术, 2011, 33(10): 2272. SUN Feng, CAO Tong. Ten-position calibration for accelerometer based on Kalman filter[J]. Systems Engineering and Electronics, 2011, 33(10): 2272. DOI:10.3969/j.issn.1001-506X.2011.10.26 |
| [12] |
LÖTTERS J C, SCHIPPER J, VELTINK P H, et al. Procedure for in-use calibration of triaxial accelerometers in medical applications[J]. Sensors amd Actuators A: Physical, 1998, 68(1/2/3): 221. DOI:10.1016/S0924-4247(98)00049-1 |
| [13] |
徐琛梅. 关于非线性方程的牛顿迭代格式初始值选取的注记[J]. 大学数学, 2019, 35(2): 110. XU Chenmei. Notes of the initial value selection for newton iterative schemes of nonlinear equations[J]. College Mathematics, 2019, 35(2): 110. |
| [14] |
TEDALDI D, PRETTO A, MENEGATTI E. A robust and easy to implement method for IMU calibration without external equipments[C]//Proceedings of the International Conference on Robotics and Automation. Hong Kong: IEEE, 2013. DOI: 10.1109/ICRA.2014.6907297
|
| [15] |
CHEUK C M, LAU T K, LIN K W, et al. Automatic calibration for inertial measurement unit[C]//Proceedings of the 12th International Conference on Control Automation Robotics & Vision (ICARCV). Guangzhou: IEEE, 2012. DOI: 10.1109/ICARCV.2012.6485340
|
| [16] |
刘宇, 余跃, 路永乐, 等. MEMS加速度计混合误差标定补偿方案[J]. 压电与声光, 2018, 40(4): 589. LIU Yu, YU Yue, LU Yongle, et al. A mixing error calibration and compensation scheme for MEMS accelerometer[J]. Piezoelectrics & Acoustooptics, 2018, 40(4): 589. DOI:10.11977/j.issn.1004-2474.2018.04.026 |
| [17] |
张海鹏, 李杰, 张波, 等. 基于椭球拟合的MEMS倾角仪现场快速标定系统[J]. 中国测试, 2019, 45(2): 94. |
| [18] |
OSBORNE M R. Nonlinear least squares—the Levenberg algorithm revisited[J]. Journal of the Australian Mathematical Society, 1976, 19(3): 343. DOI:10.1017/S033427000000120X |
| [19] |
何郁波, 董晓亮. 关于非线性不等式组Levenberg-Marquardt算法的收敛性[J]. 数学杂志, 2012, 32(1): 25. HE Yubo, DONG Xiaoliang. On the convergence of levenberg-marquardt method for nonlinear inequalities[J]. Journal of Mathematics, 2012, 32(1): 25. DOI:10.3969/j.issn.0255-7797.2012.01.004 |
| [20] |
冀祥麟, 韦增欣. 一种广义BFGS Levenberg-Marquardt算法[J]. 广西科学, 2016, 23(5): 428. JI Xianglin, WEI Zengxin. A generalized BFGS Levenberg-Marquardt algorithm[J]. Guangxi Sciences, 2016, 23(5): 428. DOI:10.13656/j.cnki.gxkx.20161121.003 |
 2021, Vol. 53
2021, Vol. 53



