2. 中国科学院大学,北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
无拖曳卫星采用位于星体内部的质量块作为理想的宁静参考源,通过测量质量块与卫星之间的状态偏差实现卫星的超高精度控制[1-2].由于几乎消除了作用在质量块上的外部非保守力扰动,无拖曳控制技术逐渐成为地球重力场测量、空间引力波探测等超高精度空间科学卫星的首选方案[3].
质量块是保证卫星实现超稳超静的关键部件[4].对于多质量块无拖曳卫星,由于质量块总自由度数远多于卫星的自由度数[5],使得多质量块无拖曳卫星的控制策略更为复杂.无拖曳控制器是实现无拖曳卫星极低的残余加速度要求的基础.对于执行深空任务的无拖曳卫星,因为空间环境较近地更为干净,其残余加速度要求也更为严格[6].例如对运行在日地L1点的LISA Pathfinder卫星,残余加速度要求为30×10-15 m · s-2 · Hz-1/2[7].而在如LISA、太极计划等空间引力波探测任务中,残余加速度要求达到前所未有的3×10-15 m · s-2 · Hz-1/2[8].这给控制器的设计带来了极大挑战,也是目前深空探测无拖曳卫星的研究重点.
深空探测无拖曳卫星一般用于超高精度的空间科学任务,例如空间引力波探测任务,通常包含多个质量块,模型复杂且控制难度大.文献[9]基于鲁棒控制设计了LISA Pathfinder卫星的无拖曳与姿态控制系统(drag-free and attitude control system, DFACS),在轨运行结果表明控制器具有充足的稳定裕度和良好的抗干扰能力.文献[10]则基于PID控制的原理设计了LISA Pathfinder卫星的干扰抑制系统(disturbance reduction system, DRS).该方案需要分别调试15个控制回路的PID控制参数以及高阶衰减滤波器,且难以有效利用频域信息.文献[11]介绍了在频域利用定量反馈理论(quantitative feedback theory, QFT)设计LISA Pathfinder构型卫星无拖曳控制系统的方法.该方法利用QFT技术调节控制器参数从而实现性能与稳定性之间的平衡.文献[12]则利用自抗扰控制技术(active disturbance rejection control, ADRC)设计了相同构型卫星的无拖曳与悬浮控制器,控制器阶数较低,但需要调节的参数较多,且噪声抑制能力在部分回路较弱.
由于无拖曳卫星的各项控制指标均在频域给出,基于频域的控制器设计方法可以充分利用各项性能指标,从而高效率地设计出符合要求的无拖曳控制器.基于H∞范数的H∞控制理论一直在鲁棒控制中占据重要地位,具有鲁棒性以及抗干扰能力强的优点[13].此外,H∞控制器可以在频域中进行设计,物理意义明确,很适合用于无拖曳卫星的控制器设计.因此,本文通过在频域推导的一系列灵敏度函数与补灵敏度函数约束,基于H∞鲁棒控制理论提出了一种无拖曳控制系统的快速设计方法,避免了经验试凑,大大降低了设计的复杂度.首先,本文考虑深空环境下的双质量块无拖曳卫星,将控制系统划分为3个控制回路,并制定了各回路的解耦与控制策略; 再基于卫星的频域科学指标与扰动和噪声的频谱模型构建了每个回路的灵敏度函数与补灵敏度函数设计约束,避免了混合灵敏度问题中加权函数阵难以选取的缺点,从而快速且准确地设计出既具有鲁棒稳定性又符合抗干扰要求的无拖曳与姿态控制系统; 最后的仿真结果证明了所提出的设计方法的有效性.
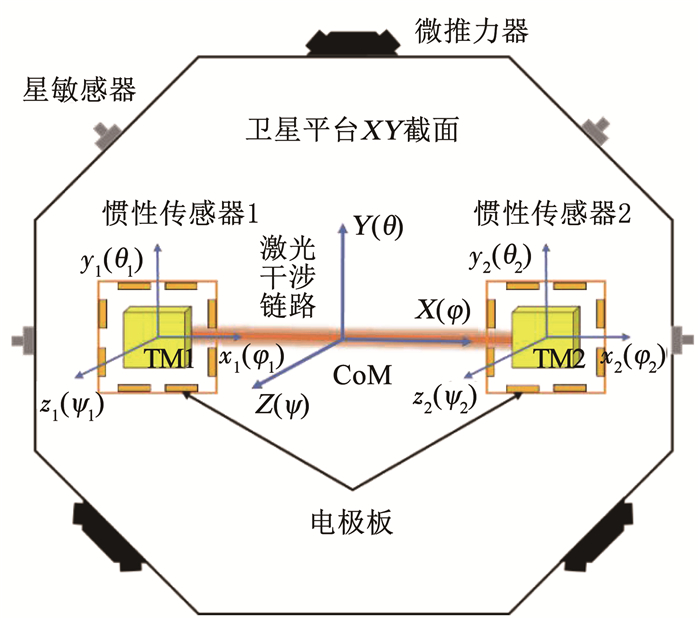
1 双质量块无拖曳卫星动力学模型图 1展示了本文研究的无拖曳卫星的构型示意图.卫星内含有两个测试质量块,左侧为TM1,右侧为TM2.惯性传感器将质量块与外界隔离,用于测量质量块相对于卫星的位置和姿态,同时还作为驱动质量块的执行机构.卫星(除两个质量块以外部分,下同)上装配有微推力器和星敏感器,分别用于驱动卫星跟随质量块运动以及测量卫星的姿态.
|
图 1 双质量块无拖曳卫星布局示意 Fig. 1 Schematic of drag-free satellite with two test masses |
卫星运行在黄道面内的日心圆轨道上,轨道半径为1 AU.科学模式下,卫星本体系的Z轴指向太阳,保持对日定向的姿态.
参照LISA Pathfinder任务,两质量块之间连线为激光干涉链路,即敏感轴方向.总的科学指标要求为在测量频段1 mHz≤f≤30 mHz上,沿TM1的x1轴方向的残余加速度为
| $ S_{\rm{a}}^{1/2}(f) \le 3 \times {10^{ - 14}}\left( {1 + {{[f/3{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{mHz}}]}^2}} \right){\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{m}} \cdot {{\rm{s}}^{ - 2}} \cdot {\rm{H}}{{\rm{z}}^{ - 1/2}}. $ |
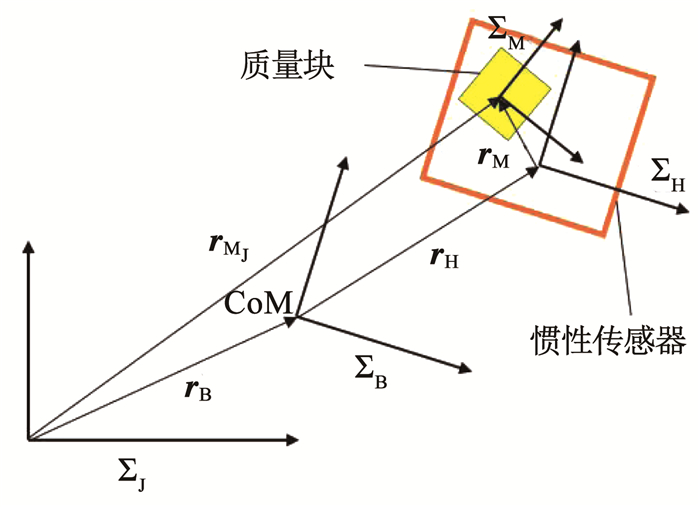
引力波探测等科学任务对超稳超静的要求,决定了卫星工作时不能使用太阳能帆板以及反作用飞轮、陀螺等运动机构.此外,卫星的温控精度极高,可以忽略热膨胀影响.因此可以使用刚体动力学理论来对卫星进行建模.图 2以单个质量块为例,对建模过程中使用到的坐标系和向量进行了说明.
|
图 2 坐标系与向量示意 Fig. 2 Definition of coordinate frames and vectors |
根据牛顿第二定律,卫星和质量块在日心惯性系下的运动方程为:
| $ \left\{ \begin{array}{l} {\left. {{{\mathit{\boldsymbol{\ddot r}}}_{\rm{B}}}} \right|_{\rm{J}}} = {\mathit{\boldsymbol{g}}_{\rm{B}}} + {\mathit{\boldsymbol{a}}_{{\rm{SP}}}} + {\mathit{\boldsymbol{a}}_{{\rm{Mu\_}}{{\rm{M}}_1}}}\mathit{\boldsymbol{ + }}{\mathit{\boldsymbol{a}}_{{\rm{Mu\_}}{{\rm{M}}_2}}} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{a}}_{\rm{T}}} + {\mathit{\boldsymbol{a}}_{{\rm{N\_T}}}} + {\mathit{\boldsymbol{a}}_{{{\rm{M}}_1} - {\rm{B}}}} + {\mathit{\boldsymbol{a}}_{{{\rm{M}}_2}{\rm{\_B}}}} + {\mathit{\boldsymbol{a}}_{{\rm{DIS}}\_{\rm{B}}}},\\ {\left. {\mathit{\boldsymbol{\ddot r}}_{{{\rm{M}}_1}{\rm{J}}}^{\rm{J}}} \right|_{\rm{J}}} = {\mathit{\boldsymbol{g}}_{{{\rm{M}}_1}}} + {\mathit{\boldsymbol{a}}_{{{\rm{H}}_1}\_{{\rm{M}}_1}}} + {\mathit{\boldsymbol{a}}_{{\rm{N}}\_{{\rm{H}}_1}}} + {\mathit{\boldsymbol{a}}_{{\rm{B}} - {{\rm{M}}_1}}} + {\mathit{\boldsymbol{a}}_{{\rm{DIS}}\_{{\rm{M}}_1}}},\\ {\left. {\mathit{\boldsymbol{\ddot r}}_{{{\rm{M}}_2}{\rm{J}}}^{\rm{J}}} \right|_{\rm{J}}} = {\mathit{\boldsymbol{g}}_{{{\rm{M}}_2}}} + {\mathit{\boldsymbol{a}}_{{{\rm{H}}_2}{\rm{\_}}{{\rm{M}}_2}}} + {\mathit{\boldsymbol{a}}_{{\rm{N}}\_{{\rm{H}}_2}}} + {\mathit{\boldsymbol{a}}_{{\rm{B}} - {{\rm{M}}_2}}} + {\mathit{\boldsymbol{a}}_{{\rm{DIS}}\_{{\rm{M}}_2}}}. \end{array} \right. $ | (1) |
式中:
由欧拉动力学方程,在卫星和质量块的本体系下有:
| $ \left\{ \begin{array}{l} \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{I}}_{\rm{B}}}{{\mathit{\boldsymbol{\dot \omega }}}_{\rm{B}}} + {\mathit{\boldsymbol{\omega }}_{\rm{B}}} \times {\mathit{\boldsymbol{I}}_{\rm{B}}}{\mathit{\boldsymbol{\omega }}_{\rm{B}}} = {\mathit{\boldsymbol{M}}_{{\rm{G}}\_{\rm{B}}}} + {\mathit{\boldsymbol{M}}_{{\rm{SP}}}} + {\mathit{\boldsymbol{M}}_{{\rm{DIS}}\_{\rm{B}}}} + {\mathit{\boldsymbol{M}}_{\rm{T}}} + }\\ {{\mathit{\boldsymbol{M}}_{{{\rm{N}}_ - }{\rm{T}}}} + {\mathit{\boldsymbol{M}}_{{\rm{Mu}} - {{\rm{M}}_1}}} + {\mathit{\boldsymbol{M}}_{{\rm{Mu}} - {{\rm{M}}_2}}} + {\mathit{\boldsymbol{M}}_{{{\rm{M}}_1} - {\rm{B}}}} + {\mathit{\boldsymbol{M}}_{{{\rm{M}}_2}\_{\rm{B}}}},} \end{array}\\ {\mathit{\boldsymbol{I}}_{{{\rm{M}}_1}}}\mathit{\boldsymbol{\dot \omega }}_{{{\rm{M}}_1}{\rm{J}}}^{{{\rm{M}}_1}} + \mathit{\boldsymbol{\omega }}_{{{\rm{M}}_1}{\rm{J}}}^{{{\rm{M}}_1}} \times {\mathit{\boldsymbol{I}}_{{{\rm{M}}_1}}}\mathit{\boldsymbol{\omega }}_{{{\rm{M}}_1}{\rm{J}}}^{{{\rm{M}}_1}} = {\mathit{\boldsymbol{M}}_{{{\rm{G}}_ - }{{\rm{M}}_1}}} + {\mathit{\boldsymbol{M}}_{{{\rm{H}}_1}{\rm{\_}}{{\rm{M}}_1}}} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{M}}_{{\rm{N}}\_{{\rm{H}}_1}}} + {\mathit{\boldsymbol{M}}_{{\rm{B}} - {{\rm{M}}_1}}} + {\mathit{\boldsymbol{M}}_{{\rm{DIS\_}}{{\rm{M}}_1}}},\\ {\mathit{\boldsymbol{I}}_{{{\rm{M}}_2}}}\mathit{\boldsymbol{\dot \omega }}_{{{\rm{M}}_2}{\rm{J}}}^{{{\rm{M}}_2}} + \mathit{\boldsymbol{\omega }}_{{{\rm{M}}_2}{\rm{J}}}^{{{\rm{M}}_2}} \times {\mathit{\boldsymbol{I}}_{{{\rm{M}}_2}}}\mathit{\boldsymbol{\omega }}_{{{\rm{M}}_2}{\rm{J}}}^{{{\rm{M}}_2}} = {\mathit{\boldsymbol{M}}_{{\rm{G}}\_{{\rm{M}}_2}}} + {\mathit{\boldsymbol{M}}_{{{\rm{H}}_2}{\rm{\_}}{{\rm{M}}_2}}} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{M}}_{{\rm{N}}\_{{\rm{H}}_2}}} + {\mathit{\boldsymbol{M}}_{{\rm{B}} - {{\rm{M}}_2}}} + {\mathit{\boldsymbol{M}}_{{\rm{DIS}}\_{{\rm{M}}_2}}}. \end{array} \right. $ | (2) |
式中:IB、IM1、IM2分别为卫星、质量块1和质量块2的转动惯量; MSP、MT、MN_T分别为太阳光压力矩、微推力器的控制力矩以及推力矩噪声; MH1_M1、MH2_M2、MN_H1、MN_H2分别为电极笼子施加给质量块的静电控制力矩以及噪声; MMu_M1、MMu_M2分别为静电控制力对卫星的反作用力引起的力矩; MM1-B=-M B-M1、MM2-B=-MB-M2为质量块与卫星之间的耦合; MDIS_B、MDIS_M1、MDIS_M2为卫星和质量块受到的其他直接扰动力矩.
1.1.2 相对运动学模型无拖曳卫星的惯性传感器一般固连在卫星上,因此惯性传感器相对于卫星的角速度ωH=0.以其中一个质量块为例,其绝对角速度在惯性系下可以表示为
| $ \mathit{\boldsymbol{\omega }}_{{\rm{MJ}}}^{\rm{J}} = \mathit{\boldsymbol{\omega }}_{\rm{B}}^{\rm{J}} + \mathit{\boldsymbol{\omega }}_{\rm{H}}^{\rm{J}} + \mathit{\boldsymbol{\omega }}_{\rm{M}}^{\rm{J}} = {\mathit{\boldsymbol{T}}_{{\rm{JB}}}}{\mathit{\boldsymbol{\omega }}_{\rm{B}}} + {\mathit{\boldsymbol{T}}_{{\rm{JM}}}}{\mathit{\boldsymbol{\omega }}_{\rm{M}}}. $ | (3) |
式中:ωB为卫星相对于惯性系的角速度在卫星本体系下的表示; ωM为质量块相对于惯性传感器的角速度在质量块本体系下的表示; TXY为坐标系Y到X的坐标变换矩阵.再利用坐标变化,得到质量块绝对角速度在质量块本体系下的表示
| $ \mathit{\boldsymbol{\omega }}_{{\rm{MJ}}}^{\rm{M}} = {\mathit{\boldsymbol{T}}_{{\rm{MB}}}}{\mathit{\boldsymbol{\omega }}_{\rm{B}}} + {\mathit{\boldsymbol{\omega }}_{\rm{M}}}. $ | (4) |
然后,分别对式(3)和(4)求导得到
| $ {\mathit{\boldsymbol{\dot \omega }}_{{\rm{MJ}}}^{\rm{J}} = {\mathit{\boldsymbol{T}}_{{\rm{JB}}}}{{\mathit{\boldsymbol{\dot \omega }}}_{\rm{B}}} + {\mathit{\boldsymbol{T}}_{{\rm{JM}}}}\left( {{{\mathit{\boldsymbol{\dot \omega }}}_{\rm{M}}} + {\mathit{\boldsymbol{\omega }}_{{\rm{MJ}}}} \times {\mathit{\boldsymbol{\omega }}_{\rm{M}}}} \right),} $ | (5) |
| $ {\mathit{\boldsymbol{\dot \omega }}_{{\rm{MJ}}}^{\rm{M}} = {\mathit{\boldsymbol{T}}_{{\rm{MB}}}}{{\mathit{\boldsymbol{\dot \omega }}}_{\rm{B}}} + \left( {{\mathit{\boldsymbol{T}}_{{\rm{JM}}}}{\mathit{\boldsymbol{\omega }}_{\rm{M}}}} \right) \times {\mathit{\boldsymbol{\omega }}_{\rm{M}}} + {{\mathit{\boldsymbol{\dot \omega }}}_{\rm{M}}}.} $ | (6) |
由图 2所示的几何关系,可以得到质量块在惯性系下的位置表示
| $ \mathit{\boldsymbol{r}}_{{\rm{MJ}}}^{\rm{J}} = {\mathit{\boldsymbol{r}}_{\rm{B}}} + {\mathit{\boldsymbol{T}}_{{\rm{JB}}}}{\mathit{\boldsymbol{r}}_{\rm{H}}} + {\mathit{\boldsymbol{T}}_{{\rm{JB}}}}{\mathit{\boldsymbol{T}}_{{\rm{BH}}}}{\mathit{\boldsymbol{r}}_{\rm{M}}}. $ | (7) |
对式(7)在惯性系下求导,分别得到质量块相对于惯性系的速度以及加速度
| $ {\left. {\mathit{\boldsymbol{\dot r}}_{{\rm{MJ}}}^{\rm{J}}} \right|_{\rm{J}}} = {\left. {{{\mathit{\boldsymbol{\dot r}}}_{\rm{B}}}} \right|_{\rm{J}}} + {\mathit{\boldsymbol{T}}_{{\rm{JB}}}}{\mathit{\boldsymbol{\omega }}_{\rm{B}}} \times {\left. {{\mathit{\boldsymbol{r}}_{{\rm{MB}}}}} \right|_{\rm{B}}} + {\left. {{\mathit{\boldsymbol{T}}_{{\rm{JH}}}}{{\mathit{\boldsymbol{\dot r}}}_{\rm{M}}}} \right|_{\rm{H}}}, $ | (8) |
| $ \begin{array}{l} {\left. {\mathit{\boldsymbol{\ddot r}}_{{\rm{MJ}}}^{\rm{J}}} \right|_{\rm{J}}} = {\left. {{{\mathit{\boldsymbol{\ddot r}}}_{\rm{B}}}} \right|_{\rm{J}}} + {\mathit{\boldsymbol{T}}_{{\rm{JB}}}}\left( {{\mathit{\boldsymbol{\omega }}_{\rm{B}}} \times \left( {{\mathit{\boldsymbol{\omega }}_{\rm{B}}} \times {\mathit{\boldsymbol{r}}_{{\rm{MB}}}}} \right) + {{\mathit{\boldsymbol{\dot \omega }}}_{\rm{B}}} \times {\mathit{\boldsymbol{r}}_{{\rm{MB}}}}} \right) + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\left. {2{\mathit{\boldsymbol{T}}_{{\rm{JH}}}}{{\left( {{\mathit{\boldsymbol{T}}_{{\rm{HB}}}}{\mathit{\boldsymbol{\omega }}_{\rm{B}}}} \right)}^ \times }{{\mathit{\boldsymbol{\dot r}}}_{\rm{M}}}} \right|_{\rm{H}}} + {\left. {{\mathit{\boldsymbol{T}}_{{\rm{JH}}}}{{\mathit{\boldsymbol{\ddot r}}}_{\rm{M}}}} \right|_{\rm{H}}}. \end{array} $ | (9) |
式中rMB=rH+TBHrM;
将式(3)~(9)分别代入式(1)和式(2)对应项中,并加以整理即可完成双质量块无拖曳卫星动力学模型的建立,如式(10)所示:
| $ \left[ {\begin{array}{*{20}{c}} {{m_{\rm{B}}}{\mathit{\boldsymbol{E}}_{3 \times 3}}}&{{{\bf{0}}_{3 \times 3}}}&{{{\bf{0}}_{3 \times 3}}}&{{{\bf{0}}_{3 \times 3}}}&{{{\bf{0}}_{3 \times 3}}}&{{{\bf{0}}_{3 \times 3}}}\\ {{{\bf{0}}_{3 \times 3}}}&{{\mathit{\boldsymbol{I}}_{\rm{B}}}}&{{{\bf{0}}_{3 \times 3}}}&{{{\bf{0}}_{3 \times 3}}}&{{{\bf{0}}_{3 \times 3}}}&{{{\bf{0}}_{3 \times 3}}}\\ {{\mathit{\boldsymbol{T}}_{{{\rm{H}}_{\rm{1}}}{\rm{J}}}}{m_{{{\rm{M}}_1}}}}&{ - {m_{{{\rm{M}}_1}}}{\mathit{\boldsymbol{T}}_{{{\rm{H}}_1}{\rm{B}}}}{\bf{r}}_{{{\rm{M}}_1}{\rm{B}}}^ \times }&{{m_{{{\rm{M}}_1}}}{\mathit{\boldsymbol{E}}_{3 \times 3}}}&{{{\bf{0}}_{3 \times 3}}}&{{{\bf{0}}_{3 \times 3}}}&{{{\bf{0}}_{3 \times 3}}}\\ {{{\bf{0}}_{3 \times 3}}}&{{\mathit{\boldsymbol{I}}_{{{\rm{M}}_1}}}{\mathit{\boldsymbol{T}}_{{{\rm{M}}_1}{\rm{B}}}}}&{{{\bf{0}}_{3 \times 3}}}&{{\mathit{\boldsymbol{I}}_{{{\rm{M}}_1}}}}&{{{\bf{0}}_{3 \times 3}}}&{{{\bf{0}}_{3 \times 3}}}\\ {{\mathit{\boldsymbol{T}}_{{{\rm{H}}_{\rm{2}}}{\rm{J}}}}{m_{{{\rm{M}}_2}}}}&{ - {m_{{{\rm{M}}_2}}}{\mathit{\boldsymbol{T}}_{{{\rm{H}}_2}{\rm{B}}}}\mathit{\boldsymbol{r}}_{{{\rm{M}}_2}{\rm{B}}}^ \times }&{{{\bf{0}}_{3 \times 3}}}&{{{\bf{0}}_{3 \times 3}}}&{{m_{{{\rm{M}}_2}}}{\mathit{\boldsymbol{E}}_{3 \times 3}}}&{{{\bf{0}}_{3 \times 3}}}\\ {{{\bf{0}}_{3 \times 3}}}&{{\mathit{\boldsymbol{I}}_{{{\rm{M}}_2}}}{\mathit{\boldsymbol{T}}_{{{\rm{M}}_2}{\rm{B}}}}}&{{{\bf{0}}_{3 \times 3}}}&{{{\bf{0}}_{3 \times 3}}}&{{{\bf{0}}_{3 \times 3}}}&{{\mathit{\boldsymbol{I}}_{{{\rm{M}}_2}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\ddot r}}}_{\rm{B}}}}\\ \cdot \\ {{\mathit{\boldsymbol{\omega }}_{\rm{B}}}}\\ {{{\mathit{\boldsymbol{\ddot r}}}_{{{\rm{M}}_1}}}}\\ \cdot \\ {{\mathit{\boldsymbol{\omega }}_{{{\rm{M}}_1}}}}\\ {{{\mathit{\boldsymbol{\ddot r}}}_{{{\rm{M}}_2}}}}\\ {{\mathit{\boldsymbol{\omega }}_{{{\rm{M}}_2}}}} \end{array}} \right] +\\ \left[ {\begin{array}{*{20}{c}} {{{\bf{0}}_{3 \times 1}}}\\ {\mathit{\boldsymbol{\omega }}_{\rm{B}}^ \times {\mathit{\boldsymbol{I}}_{\rm{B}}}{\mathit{\boldsymbol{\omega }}_{\rm{B}}}}\\ {{m_{{{\rm{M}}_1}}}{\mathit{\boldsymbol{T}}_{{{\rm{H}}_1}{\rm{B}}}}{{\left( {\mathit{\boldsymbol{\omega }}_{\rm{B}}^ \times } \right)}^2}{\mathit{\boldsymbol{r}}_{{{\rm{M}}_1}{\rm{B}}}} + 2{m_{{{\rm{M}}_1}}}{{\left( {{\mathit{\boldsymbol{T}}_{{{\rm{H}}_1}{\rm{B}}}}{\mathit{\boldsymbol{\omega }}_{\rm{B}}}} \right)}^ \times }{{\mathit{\boldsymbol{\dot r}}}_{{{\rm{M}}_1}}}}\\ {{\mathit{\boldsymbol{I}}_{{{\rm{M}}_1}}}{{\left( {{\mathit{\boldsymbol{T}}_{{{\rm{M}}_1}{\rm{B}}}}{\mathit{\boldsymbol{\omega }}_{\rm{B}}}} \right)}^ \times }{\mathit{\boldsymbol{\omega }}_{{{\rm{M}}_1}}} + \mathit{\boldsymbol{\omega }}_{{\rm{J}}{{\rm{M}}_1}}^ \times {\mathit{\boldsymbol{I}}_{{{\rm{M}}_1}}}{\mathit{\boldsymbol{\omega }}_{{\rm{J}}{{\rm{M}}_1}}}}\\ {{m_{{{\rm{M}}_2}}}{\mathit{\boldsymbol{T}}_{{{\rm{H}}_2}{\rm{B}}}}{{\left( {\mathit{\boldsymbol{\omega }}_{\rm{B}}^ \times } \right)}^2}{\mathit{\boldsymbol{r}}_{{{\rm{M}}_2}{\rm{B}}}} + 2{m_{{{\rm{M}}_2}}}{{\left( {{\mathit{\boldsymbol{T}}_{{{\rm{H}}_2}{\rm{B}}}}{\mathit{\boldsymbol{\omega }}_{\rm{B}}}} \right)}^ \times }{{\mathit{\boldsymbol{\dot r}}}_{{{\rm{M}}_2}}}}\\ {{\mathit{\boldsymbol{I}}_{{{\rm{M}}_2}}}{{\left( {{\mathit{\boldsymbol{T}}_{{{\rm{M}}_1}{\rm{B}}}}{\mathit{\boldsymbol{\omega }}_{\rm{B}}}} \right)}^ \times }{\mathit{\boldsymbol{\omega }}_{{{\rm{M}}_2}}} + \mathit{\boldsymbol{\omega }}_{{\rm{J}}{{\rm{M}}_2}}^ \times {\mathit{\boldsymbol{I}}_{{{\rm{M}}_2}}}{\mathit{\boldsymbol{\omega }}_{{\rm{J}}{{\rm{M}}_2}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{F}}_{\rm{B}}}}\\ {{\mathit{\boldsymbol{M}}_{\rm{B}}}}\\ {{\mathit{\boldsymbol{T}}_{{{\rm{H}}_1}{\rm{J}}}}{\mathit{\boldsymbol{F}}_{{{\rm{M}}_1}}}}\\ {{\mathit{\boldsymbol{M}}_{{{\rm{M}}_1}}}}\\ {{\mathit{\boldsymbol{T}}_{{{\rm{H}}_2}{\rm{J}}}}{\mathit{\boldsymbol{F}}_{{{\rm{M}}_2}}}}\\ {{\mathit{\boldsymbol{M}}_{{{\rm{M}}_2}}}} \end{array}} \right]. $ | (10) |
式中:ωJM=TMBωB+ωM; FB、FM1、FM2和MB、MM1、MM2分别为卫星、TM1和TM2受到的合力以及合力矩; 此外,矢量叉乘a×b=a×·b,式中a×=
上述动力学模型建立方法具有通用性.对于不同构型的无拖曳卫星仅需改变质量块个数以及相应的坐标变换矩阵.
1.2 动力学方程线性化为进行控制器设计,需要对动力学方程进行线性化.无拖曳模式下,卫星相对于轨道系的姿态角为θB小量,于是卫星本体角速度
1) 卫星本体角速度
2) ΣJ和ΣB的坐标转换矩阵TJB=E3×3+θB×. 质量块相对于卫星的姿态运动为小量,则有
1) 质量块相对于电极笼子的角速度:
2) ΣM和ΣB的坐标转换矩阵TMB=E3×3+θM×.
式中, E3×3为三维单位阵.
无拖曳与姿态控制系统涉及到的动力学模型包括卫星的姿态运动以及质量块的相对运动.因此,结合上述近似并且忽略状态变量的二阶小项,可以将式(10)所示的非线性模型简化为如下形式:
| $ \left[ {\begin{array}{*{20}{l}} {{{\mathit{\boldsymbol{\ddot \theta }}}_{\rm{B}}}}\\ {{{\mathit{\boldsymbol{\ddot X}}}_{\rm{M}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{B}}_{{\rm{ATT}}}}}&{{\mathit{\boldsymbol{0}}_{3 \times 12}}}\\ {{\mathit{\boldsymbol{B}}_1}}&{{\mathit{\boldsymbol{E}}_{12 \times 12}}} \end{array}} \right]\left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{a}}_{{\rm{SC}}}}}\\ {{\mathit{\boldsymbol{a}}_{{\rm{TM}}}}} \end{array}} \right]. $ | (11) |
其中,
| $ {\mathit{\boldsymbol{B}}_{{\rm{ATT}}}} = \left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{0}}_{3 \times 3}}}&{{\mathit{\boldsymbol{E}}_{3 \times 3}}} \end{array}} \right]. $ | (12) |
| $ {\mathit{\boldsymbol{B}}_1} = \left[ {\begin{array}{*{20}{c}} { - {\mathit{\boldsymbol{E}}_{3 \times 3}}}&{\mathit{\boldsymbol{r}}_{{{\rm{M}}_1}{\rm{B}}}^ \times }\\ {{{\bf{0}}_{3 \times 3}}}&{ - {\mathit{\boldsymbol{E}}_{3 \times 3}}}\\ { - {\mathit{\boldsymbol{E}}_{3 \times 3}}}&{\mathit{\boldsymbol{r}}_{{{\rm{M}}_2}{\rm{B}}}^ \times }\\ {{{\bf{0}}_{3 \times 3}}}&{ - {\mathit{\boldsymbol{E}}_{3 \times 3}}} \end{array}} \right]. $ | (13) |
式中:θB为卫星姿态; XM= [rM1 θM1 rM2 θM2]T分别为两个质量块的相对位移和相对姿态; aSC=[aB αB]T为作用在卫星上的合加速度和合角加速度; aM=[aM1 αM1 aM2 αM2]T为作用在两个质量块上的合加速度和合角加速度.
2 双质量块无拖曳卫星控制策略设计 2.1 无拖曳与悬浮控制自由度选择由于卫星只有6个自由度,根据无拖曳技术的原理,卫星最多能实现6个方向的无拖曳控制.因此,对于存在多个质量块的无拖曳卫星,在设计控制器之前,首先要确定无拖曳控制自由度以及悬浮控制自由度.
本研究中设计TM1为完全无拖曳控制,TM2为完全静电悬浮控制.因此可定义如式(14)所示的选择矩阵,将控制系统划分为卫星姿态控制回路、无拖曳控制回路以及静电悬浮控制回路.
| $ {\mathit{\boldsymbol{S}}_{{\rm{DF}}}} = \left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{E}}_{6 \times 6}}}&{{{\bf{0}}_{6 \times 6}}} \end{array}} \right],{\mathit{\boldsymbol{S}}_{{\rm{SUS}}}} = \left[ {\begin{array}{*{20}{l}} {{{\bf{0}}_{6 \times 6}}}&{{\mathit{\boldsymbol{E}}_{6 \times 6}}} \end{array}} \right]. $ | (14) |
从而得到无拖曳控制坐标和悬浮控制坐标
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{X}}_{{\rm{DF}}}} = {\mathit{\boldsymbol{S}}_{{\rm{DF}}}}{\mathit{\boldsymbol{X}}_{\rm{M}}} = {\left[ {\begin{array}{*{20}{l}} {{x_1}}&{{y_1}}&{{z_1}}&{{\varphi _1}}&{{\theta _1}}&{{\psi _1}} \end{array}} \right]^{\rm{T}}},\\ {\mathit{\boldsymbol{X}}_{{\rm{SUS}}}} = {\mathit{\boldsymbol{S}}_{{\rm{SUS}}}}{\mathit{\boldsymbol{X}}_{\rm{M}}} = {\left[ {\begin{array}{*{20}{l}} {{x_2}}&{{y_2}}&{{z_2}}&{{\varphi _2}}&{{\theta _2}}&{{\psi _2}} \end{array}} \right]^{\rm{T}}}. \end{array} \right. $ | (15) |
再将式(11)中的各外力和外力矩作用展开,可以得到3个控制回路的动力学模型:
| $ \begin{array}{l} \left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\ddot \theta }}}_{\rm{B}}}}\\ {{{\mathit{\boldsymbol{\ddot X}}}_{{\rm{DF}}}}}\\ {{{\mathit{\boldsymbol{\ddot X}}}_{{\rm{SUS}}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{B}}_{{\rm{ATT}}}}}&{{{\bf{0}}_{3 \times 6}}}&{{{\bf{0}}_{3 \times 6}}}\\ {{\mathit{\boldsymbol{S}}_{{\rm{DF}}}}{\mathit{\boldsymbol{B}}_1}}&{{\mathit{\boldsymbol{E}}_{6 \times 6}}}&{{{\bf{0}}_{6 \times 6}}}\\ {{\mathit{\boldsymbol{S}}_{{\rm{SUS}}}}{\mathit{\boldsymbol{B}}_1}}&{{{\bf{0}}_{6 \times 6}}}&{{\mathit{\boldsymbol{E}}_{6 \times 6}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{a}}_{{\rm{SC}}}}}\\ {{\mathit{\boldsymbol{S}}_{{\rm{DF}}}}{\mathit{\boldsymbol{a}}_{{\rm{TM}}}}}\\ {{\mathit{\boldsymbol{S}}_{{\rm{SUS}}}}{\mathit{\boldsymbol{a}}_{{\rm{TM}}}}} \end{array}} \right] = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{B}}_{{\rm{ATT}}}}}&{{{\bf{0}}_{3 \times 6}}}&{{{\bf{0}}_{3 \times 6}}}\\ {{\mathit{\boldsymbol{B}}_{{\rm{DF}}}}}&{{\mathit{\boldsymbol{E}}_{6 \times 6}}}&{{{\bf{0}}_{6 \times 6}}}\\ {{\mathit{\boldsymbol{B}}_{{\rm{SUS}}}}}&{{{\bf{0}}_{6 \times 6}}}&{{\mathit{\boldsymbol{E}}_{6 \times 6}}} \end{array}} \right]\left( {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{u}}_{{\rm{THR}}}}}\\ {{\mathit{\boldsymbol{u}}_{{\rm{E}}{{\rm{S}}_{{\rm{DF}}}}}}}\\ {{\mathit{\boldsymbol{u}}_{{\rm{E}}{{\rm{S}}_{{\rm{SUS}}}}}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{n}}_{{\rm{THR}}}}}\\ {{\mathit{\boldsymbol{n}}_{{\rm{E}}{{\rm{S}}_{{\rm{DF}}}}}}}\\ {{{\bf{n}}_{{\rm{E}}{{\rm{S}}_{{\rm{SUS}}}}}}} \end{array}} \right] + } \right.\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{d}}_{\rm{B}}}}\\ {{\mathit{\boldsymbol{d}}_{{\rm{DF}}}}}\\ {{\mathit{\boldsymbol{d}}_{{\rm{SUS}}}}} \end{array}} \right]} \right) + \left[ {\begin{array}{*{20}{c}} {{{\bf{0}}_{3 \times 6}}}&{{{\bf{0}}_{3 \times 6}}}&{{{\bf{0}}_{3 \times 6}}}\\ {{{\bf{0}}_{6 \times 6}}}&{ - {\mathit{\boldsymbol{k}}_{{\rm{DF}}}}}&{{{\bf{0}}_{6 \times 6}}}\\ {{{\bf{0}}_{6 \times 6}}}&{{{\bf{0}}_{6 \times 6}}}&{ - {\mathit{\boldsymbol{k}}_{{\rm{SUS}}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{\theta }}_{\rm{B}}}}\\ {{\mathit{\boldsymbol{X}}_{{\rm{DF}}}}}\\ {{\mathit{\boldsymbol{X}}_{{\rm{SUS}}}}} \end{array}} \right] \end{array} $ | (16) |
式中:uTHR、uESDF、uESSUS分别为微推进器对卫星的推力加速度以及无拖曳和悬浮控制自由度上的静电控制加速度; nTHR、nESDF、nESSUS分别为微推进器噪声、无拖曳和悬浮控制自由度上的电容噪声; dB、dDF、dSUS分别为卫星、无拖曳和悬浮控制自由度上受到其他扰动加速度; -ki·xi为卫星和质量块之间的耦合加速度且ki < 0[14].
2.2 动力学解耦从式(16)可以看出,无拖曳控制回路的6个自由度之间互相耦合.对于双质量块无拖曳卫星,由于输入数量远多于控制量,无法采取传统的解耦控制方式.因此,采用输入解耦的方式,定义如下关系
| $ {\mathit{\boldsymbol{u}}_{{\rm{THR }}}} = \mathit{\boldsymbol{B}}_{{\rm{DF }}}^{ - 1}{\mathit{\boldsymbol{u}}_{\rm{T}}},{\mathit{\boldsymbol{n}}_{{\rm{THR }}}} = \mathit{\boldsymbol{B}}_{{\rm{DF}}}^{ - 1}{\mathit{\boldsymbol{n}}_{\rm{T}}},{\mathit{\boldsymbol{d}}_{\rm{B}}} = \mathit{\boldsymbol{B}}_{{\rm{DF}}}^{ - 1}{\mathit{\boldsymbol{d}}_{{\rm{SC}}}}. $ | (17) |
则式(16)可以重新整理为
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\ddot \theta }}}_{\rm{B}}}}\\ {{{\mathit{\boldsymbol{\ddot X}}}_{{\rm{DF}}}}}\\ {{\mathit{\boldsymbol{X}}_{{\rm{SUS}}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{B}}_{{\rm{ATT}}}}\mathit{\boldsymbol{B}}_{{\rm{DF}}}^{ - 1}}&{{{\bf{0}}_{3 \times 6}}}&{{{\bf{0}}_{3 \times 6}}}\\ {{\mathit{\boldsymbol{E}}_{6 \times 6}}}&{{\mathit{\boldsymbol{E}}_{6 \times 6}}}&{{{\bf{0}}_{6 \times 6}}}\\ {{\mathit{\boldsymbol{B}}_{{\rm{SUS}}}}\mathit{\boldsymbol{B}}_{{\rm{DF}}}^{ - 1}}&{{{\bf{0}}_{6 \times 6}}}&{{\mathit{\boldsymbol{E}}_{6 \times 6}}} \end{array}} \right]\left( {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{u}}_{\rm{T}}}}\\ {{\mathit{\boldsymbol{u}}_{{\rm{E}}{{\rm{S}}_{{\rm{DF}}}}}}}\\ {{\mathit{\boldsymbol{u}}_{{\rm{E}}{{\rm{S}}_{{\rm{SUS}}}}}}} \end{array}} \right] + } \right.\\ \left. {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{n}}_{\rm{T}}}}\\ {{\mathit{\boldsymbol{n}}_{{\rm{E}}{{\rm{S}}_{{\rm{DF}}}}}}}\\ {{\mathit{\boldsymbol{n}}_{{\rm{E}}{{\rm{S}}_{{\rm{SUS}}}}}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{d}}_{{\rm{SC}}}}}\\ {{\mathit{\boldsymbol{d}}_{{\rm{DF}}}}}\\ {{\mathit{\boldsymbol{d}}_{{\rm{SUS}}}}} \end{array}} \right]} \right) + \left[ {\begin{array}{*{20}{c}} {{{\bf{0}}_{3 \times 6}}}&{{{\bf{0}}_{3 \times 6}}}&{{{\bf{0}}_{3 \times 6}}}\\ {{{\bf{0}}_{6 \times 6}}}&{ - {\mathit{\boldsymbol{k}}_{{\rm{DF}}}}}&{{{\bf{0}}_{6 \times 6}}}\\ {{{\bf{0}}_{6 \times 6}}}&{{{\bf{0}}_{6 \times 6}}}&{ - {\mathit{\boldsymbol{k}}_{{\rm{DF}}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{\theta }}_{\rm{B}}}}\\ {{\mathit{\boldsymbol{X}}_{{\rm{DF}}}}}\\ {{\mathit{\boldsymbol{X}}_{{\rm{SUS}}}}} \end{array}} \right]. \end{array} $ | (18) |
从而实现了无拖曳回路上的解耦.再对上式进行拉式变换有
| $ \begin{array}{l} \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{\theta }}_{\rm{B}}}}\\ {{\mathit{\boldsymbol{X}}_{{\rm{DF}}}}}\\ {{\mathit{\boldsymbol{X}}_{{\rm{SUS}}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{G}}_{{\rm{SC}}}}{\mathit{\boldsymbol{B}}_{{\rm{ATT}}}}\mathit{\boldsymbol{B}}_{{\rm{DF}}}^{ - 1}}&{{\mathit{\boldsymbol{\theta }}_{3 \times 6}}}&{{{\bf{0}}_{3 \times 6}}}\\ {{\mathit{\boldsymbol{G}}_{{\rm{DF}}}}}&{{\mathit{\boldsymbol{G}}_{{\rm{DF}}}}}&{{{\bf{0}}_{6 \times 6}}}\\ {{\mathit{\boldsymbol{G}}_{{\rm{SUS}}}}{\mathit{\boldsymbol{B}}_{{\rm{SUS}}}}\mathit{\boldsymbol{B}}_{{\rm{DF}}}^{ - 1}}&{{{\bf{0}}_{6 \times 6}}}&{{\mathit{\boldsymbol{G}}_{{\rm{SUS}}}}} \end{array}} \right]\left( {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{u}}_{\rm{T}}}}\\ {{\mathit{\boldsymbol{u}}_{{\rm{E}}{{\rm{S}}_{{\rm{DF}}}}}}}\\ {{\mathit{\boldsymbol{u}}_{{\rm{E}}{{\rm{S}}_{{\rm{SUS}}}}}}} \end{array}} \right] + } \right.\\ \left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{n}}_{\rm{T}}}}\\ {{\mathit{\boldsymbol{n}}_{{\rm{E}}{{\rm{S}}_{{\rm{DF}}}}}}}\\ {{\mathit{\boldsymbol{n}}_{{\rm{E}}{{\rm{S}}_{{\rm{SUS}}}}}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{d}}_{{\rm{SC}}}}}\\ {{\mathit{\boldsymbol{d}}_{{\rm{DF}}}}}\\ {{\mathit{\boldsymbol{d}}_{{\rm{SUS}}}}} \end{array}} \right]} \right). \end{array} $ | (19) |
式中:Gi为各回路传递函数,
由此可以看出无拖曳回路已经解耦成了6个无阻尼的二阶系统.但是BATTBDF-1在姿态控制回路上引入了来自无拖曳回路控制输出的交叉耦合.这是解耦带来的代价.
2.3 反馈控制策略从式(19)中可以看到,无拖曳控制与卫星姿态控制共有9个自由度,而微推力器只能提供6个方向的控制.若两个控制回路均采用微推力器作为执行机构,则会造成低频时无拖曳控制器与姿态控制器的冲突.对此,文献[15]设计了式(20)所示的反馈控制器结构
| $ \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{u}}_{\rm{T}}}}\\ {{\mathit{\boldsymbol{u}}_{{\rm{E}}{{\rm{S}}_{{\rm{DF}}}}}}}\\ {{\mathit{\boldsymbol{u}}_{{\rm{E}}{{\rm{S}}_{{\rm{SUS}}}}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{{\bf{0}}_{6 \times 3}}}&{ - {\mathit{\boldsymbol{C}}_{{\rm{DF}}}}}&{{{\bf{0}}_{6 \times 3}}}\\ { - {\mathit{\boldsymbol{C}}_{{\rm{ATT}}}}}&{{{\bf{0}}_{6 \times 6}}}&{{{\bf{0}}_{6 \times 6}}}\\ {{{\bf{0}}_{6 \times 6}}}&{{{\bf{0}}_{6 \times 6}}}&{ - {\mathit{\boldsymbol{C}}_{{\rm{SUS}}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{\theta }}_{\rm{B}}}}\\ {{\mathit{\boldsymbol{X}}_{{\rm{DF}}}}}\\ {{\mathit{\boldsymbol{X}}_{{\rm{SUS}}}}} \end{array}} \right]. $ | (20) |
该反馈控制结构可以解释为:
1) 无拖曳控制器CDF通过微推力器反馈控制无拖曳自由度;
2) 静电悬浮控制器CSUS通过悬浮自由度上的静电驱动装置反馈控制悬浮自由度;
3) 姿态控制器CATT通过无拖曳自由度上的静电驱动装置控制TM1的姿态,再通过无拖曳控制回路间接实现对卫星姿态的控制.
为消除式(20)所示的反馈控制结构引入的耦合项BATTBDF-1,考虑该矩阵的伪逆,同时考虑各测量机构的测量噪声,得到最终的闭环结构见图 3及式(21).

|
图 3 闭环回路示意 Fig. 3 Closed loop structure |
至此,整个卫星的控制系统划分为了质量块的无拖曳控制回路和悬浮控制回路以及卫星的姿态控制回路,共包含15个解耦的闭环回路.对该闭环模型具有如下说明:
1) 无拖曳回路由6个解耦的无阻尼二阶系统构成,完全由微推进系统控制; 悬浮控制回路完全由相应自由度上的静电驱动装置实现闭环控制;
2) 卫星的姿态控制回路则以TM1自由度上的静电驱动器为执行机构.当星敏感器测量到卫星的姿态偏差时,误差信号反馈给姿态控制器,通过静电驱动装置输出静电力直接控制TM1的姿态.随后无拖曳控制回路再实现卫星对TM1的跟踪,从而间接实现了卫星的姿态控制;
3) 由于姿态控制器的输出会直接作用在处于无拖曳状态的TM1上,因此必须保证姿态控制器的带宽远低于无拖曳控制器的带宽.这样既保证了敏感轴在测量带宽上的信号读出不受影响,又在频域上实现了无拖曳控制与姿态控制的解耦.
2.4 扰动与噪声的频谱模型根据文献[16],对于深空任务的无拖曳卫星,卫星受到的扰动主要是微推进器的噪声和太阳光压.质量块则受到多种直接扰动,本文只考虑其中的主导项,包括卫星与质量块之间的耦合以及惯性传感器的驱动噪声.此外还考虑了各测量机构的测量噪声.
| $ \left\{ {\begin{array}{*{20}{l}} {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{\theta }}_{\rm{B}}}}\\ {{\mathit{\boldsymbol{X}}_{{\rm{DF}}}}}\\ {{\mathit{\boldsymbol{X}}_{{\rm{SUS}}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{G}}_{{\rm{SC}}}}{\mathit{\boldsymbol{B}}_{{\rm{ATT}}}}\mathit{\boldsymbol{B}}_{{\rm{DF}}}^{ - 1}}&{{{\bf{0}}_{3 \times 6}}}&{{{\bf{0}}_{3 \times 6}}}\\ {{\mathit{\boldsymbol{G}}_{{\rm{DF}}}}}&{{\mathit{\boldsymbol{G}}_{{\rm{DF}}}}}&{{{\bf{0}}_{6 \times 6}}}\\ {{\mathit{\boldsymbol{G}}_{{\rm{SUS}}}}{\mathit{\boldsymbol{B}}_{{\rm{SUS}}}}\mathit{\boldsymbol{B}}_{{\rm{DF}}}^{ - 1}}&{{{\bf{0}}_{6 \times 6}}}&{{\mathit{\boldsymbol{G}}_{{\rm{SUS}}}}} \end{array}} \right]\left( {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{u}}_{\rm{T}}}}\\ {{\mathit{\boldsymbol{u}}_{{\rm{E}}{{\rm{S}}_{{\rm{DF}}}}}}}\\ {{\mathit{\boldsymbol{u}}_{{\rm{E}}{{\rm{S}}_{{\rm{SUS}}}}}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{n}}_{\rm{T}}}}\\ {{\mathit{\boldsymbol{n}}_{{\rm{E}}{{\rm{S}}_{{\rm{DF}}}}}}}\\ {{\mathit{\boldsymbol{n}}_{{\rm{E}}{{\rm{S}}_{{\rm{SUS}}}}}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{d}}_{{\rm{SC}}}}}\\ {{\mathit{\boldsymbol{d}}_{{\rm{DF}}}}}\\ {{\mathit{\boldsymbol{d}}_{{\rm{SUS}}}}} \end{array}} \right]} \right),}\\ {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{u}}_{\rm{T}}}}\\ {{\mathit{\boldsymbol{u}}_{{\rm{E}}{{\rm{S}}_{{\rm{DF}}}}}}}\\ {{\mathit{\boldsymbol{u}}_{{\rm{E}}{{\rm{S}}_{{\rm{SUS}}}}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{{\bf{0}}_{6 \times 3}}}&{ - {\mathit{\boldsymbol{C}}_{{\rm{DF}}}}}&{{{\bf{0}}_{6 \times 3}}}\\ {{{\left( { - {\mathit{\boldsymbol{B}}_{{\rm{ATT}}}}\mathit{\boldsymbol{B}}_{{\rm{DF}}}^{ - 1}} \right)}^{ - 1}}{\mathit{\boldsymbol{C}}_{{\rm{ATT}}}}}&{{{\bf{0}}_{6 \times 6}}}&{{{\bf{0}}_{6 \times 6}}}\\ {{{\bf{0}}_{6 \times 6}}}&{{{\bf{0}}_{6 \times 6}}}&{ - {{\bf{C}}_{{\rm{SUS}}}}} \end{array}} \right]\left( {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{\theta }}_{\rm{B}}}}\\ {{\mathit{\boldsymbol{X}}_{{\rm{DF}}}}}\\ {{\mathit{\boldsymbol{X}}_{{\rm{SUS}}}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{n}}_{{\rm{STR}}}}}\\ {{\mathit{\boldsymbol{n}}_{{\rm{DF}}}}}\\ {{\mathit{\boldsymbol{n}}_{{\rm{SUS}}}}} \end{array}} \right]} \right).} \end{array}} \right. $ | (21) |
将单位白噪声通过低通滤波器,可以对上述扰动与噪声的频域特性进行建模.为使本文研究更具有实际意义,参考目前最先进的无拖曳卫星LISA Pathfinder任务公开的噪声水平,给出了各扰动与噪声的幅值谱密度.
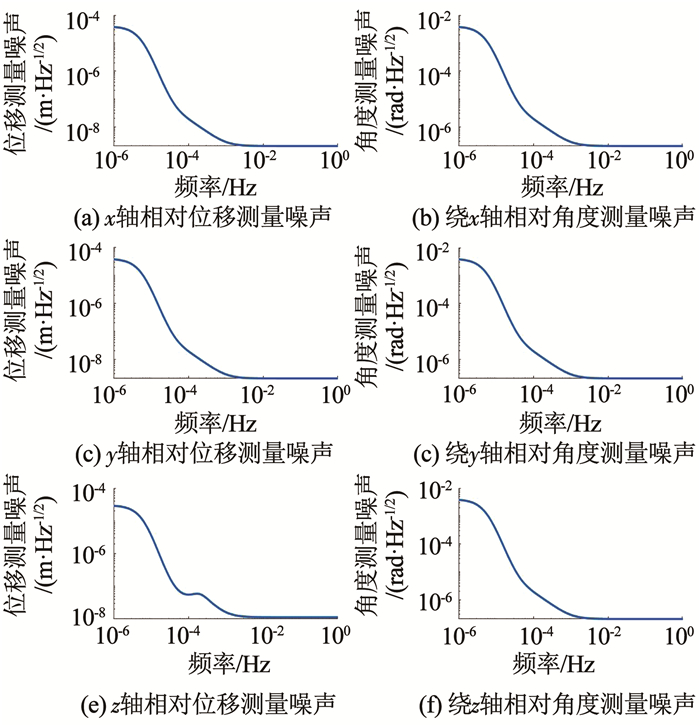
惯性传感器各轴的测量噪声见图 4.星敏感器测量噪声的幅值谱密度为1×10-4 rad · Hz-1/2,在频谱图中为一条直线,不在这里给出.
|
图 4 惯性传感器各轴的测量噪声 Fig. 4 Measurement noises on each axis of inertial sensor |
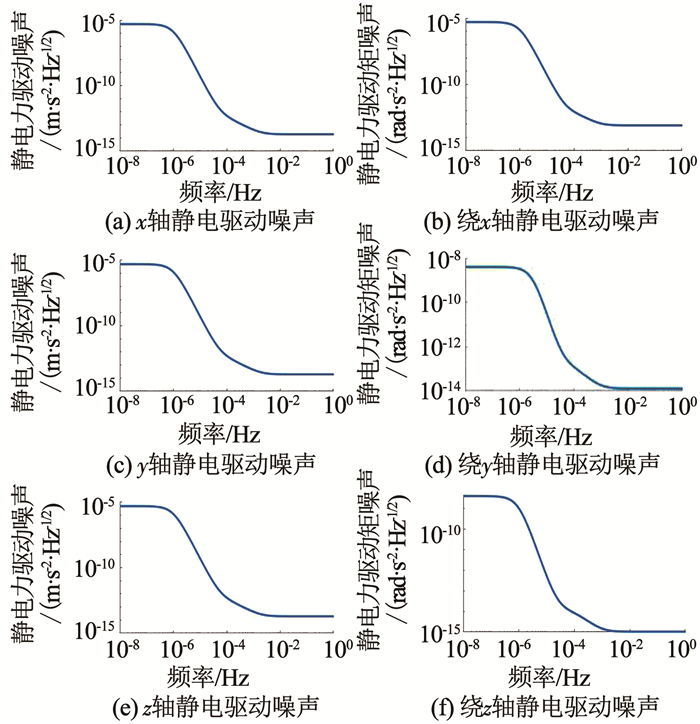
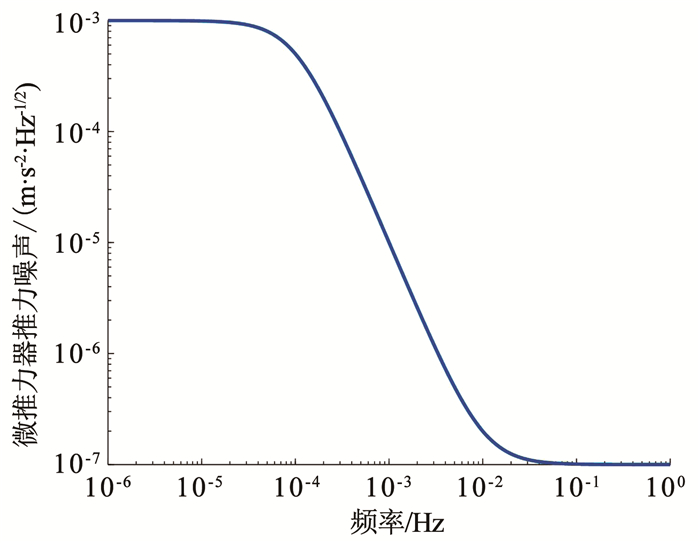
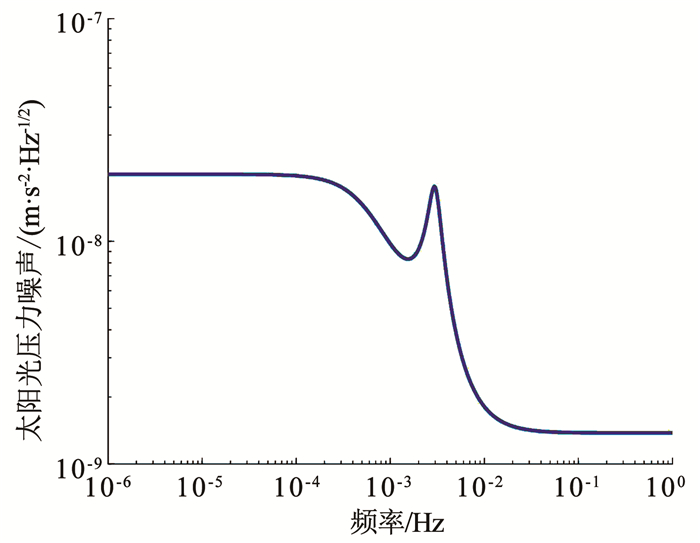
质量块各轴受到的静电驱动噪声见图 5.微推力器推力噪声的频域特性见图 6.卫星受到的太阳光压波动力的频域特性见图 7,其常值分量假设已被微推力器的常值输出抵消.
|
图 5 质量块各轴受到的力和力矩噪声 Fig. 5 Force and torque noises on each axis of test mass |
|
图 6 微推力器噪声模型 Fig. 6 Noise model of micro-thruster |
|
图 7 太阳光压噪声模型 Fig. 7 Noise model of solar pressure |
为设计出符合无拖曳水平要求的控制系统,需要将总残余加速度指标分解为对质量块各轴的性能指标要求[9-10],见表 1.
| 表 1 测量频段内的频谱性能指标 Tab. 1 Spectrum specifications within measurement bandwidth |
同时,在测量频段以下(f≤1 mHz),对于质量块的平动最大值约束为Xmax≤±10 μm; 转动的最大值约束分别为Xmax≤±1 mrad.
因此,无拖曳与姿态控制系统设计的目标是使所设计的15个自由度上的控制器能够抑制各类扰动与噪声的作用,达到上述控制性能指标要求.
3.2 控制器约束设计对于单输入单输出(single-input single-output, SISO)系统,灵敏度函数S(s)与补灵敏度函数T(s)的定义如式(22)和式(23)所示:
| $ {S(s) = \frac{1}{{1 + G(s)C(s)}},} $ | (22) |
| $ {T(s) = \frac{{G(s)C(s)}}{{1 + G(s)C(s)}}.} $ | (23) |
式中, G(s)为被控对象的传递函数,C(s)为控制器.
对于传递函数为H(s)的系统,若输入信号的幅值谱密度为X(f),则输出信号的幅值谱密度Y(f)可以表示为
| $ Y(f) = |H(j2{\rm{ \mathsf{ π} }}f)|X(f). $ | (24) |
式中, H(j2πf)为系统的频率特性.特别地,当输入信号为单位功率谱密度的白噪声时有
| $ Y(f) = |H(j2{\rm{ \mathsf{ π} }}f)|. $ | (25) |
结合表 1在频域给出的性能指标要求、工程设计准则、稳定裕度要求以及式(22)~(25),可以推得对每个SISO控制回路上的灵敏度函数Sspec和补灵敏度函数Tspec约束.这些约束将成为H∞控制器设计的基础.
由于,对于每个控制回路均有稳定裕度与鲁棒性的要求,从而在15个控制自由度上有
| $ {{S_{{\rm{spec}}}} \le 3{\kern 1pt} {\kern 1pt} {\rm{dB,}}} $ | (26) |
| $ {{T_{{\rm{spec}}}} \le 3{\kern 1pt} {\kern 1pt} {\rm{dB}}{\rm{.}}} $ | (27) |
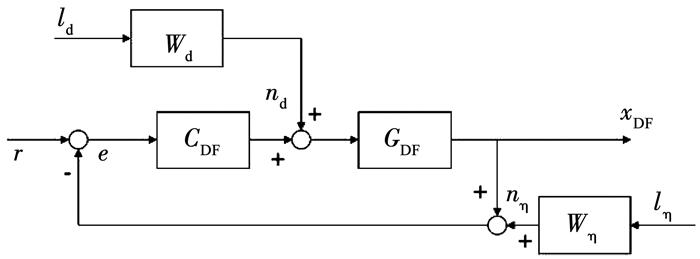
图 8展示了解耦后的无拖曳控制单输入单输出回路.ld和lη为单位功率谱密度的白噪声; Wd和Wη分别为图 4~7中所示的扰动与噪声的成形滤波器.nd和nη表示加权后的实际扰动与噪声.
|
图 8 带有噪声成形滤波器的无拖曳单输入单输出回路 Fig. 8 Drag-free single-input single-output (SISO) loop with noise shape filters |
1) Sspec:扰动噪声抑制.结合式(21)所示的闭环传递函数,作用在无拖曳控制回路上的扰动力主要为微推力器噪声、太阳光压以及无拖曳控制回路上的静电驱动噪声.由图 8可以得到扰动作用到无拖曳回路上的输出为
| $ \left| {{G_{{\rm{DF}}}}{S_{{\rm{DF}}}}\left( {{n_{\rm{T}}} + {d_{{\rm{SC}}}} + {n_{{\rm{E}}{{\rm{S}}_{{\rm{DF}}}}}}} \right)} \right| = \left| {{x_{\rm{d}}}} \right|. $ | (28) |
xd必须小于表 1中回路输出约束xreq,于是可以得到灵敏度函数约束为
| $ \left| {{S_{{\rm{spec}}}}} \right| \le \left| {\frac{{{x_{{\rm{req}}}}}}{{{G_{{\rm{DF}}}}\left( {{n_{\rm{T}}} + {d_{{\rm{SC}}}} + {n_{{\rm{E}}{{\rm{S}}_{{\rm{DF}}}}}}} \right)}}} \right|. $ | (29) |
2) Tspec1:测量噪声抑制.测量噪声对于无拖曳回路的影响主要来自惯性传感器的测量噪声,可以表示为
| $ \left| {{T_{{\rm{DF}}}}{\eta _{{\rm{DF}}}}} \right| \le \left| {{x_{{\rm{req}}}}} \right|. $ | (30) |
因此可以得到补灵敏度函数约束为
| $ \left| {{T_{{\rm{spec}}}}} \right| \le \left| {\frac{{{x_{{\rm{req}}}}}}{{{\eta _{{\rm{DF}}}}}}} \right|. $ | (31) |
3) Tspec2:微推力器连续两次控制最大推力变化限制.测量噪声会引起控制输出的跳变.在工程上,对于单个微推力器,两次指令之间的推力最大变化不得超过30 μN.根据文献[11]可以将其转换为如下补灵敏度函数约束
| $ \left| {{T_{{\rm{spec}}2}}} \right| \le \left| {\frac{{{G_{{\rm{DF}}}}{u_{{\rm{step}}}}}}{{{\eta _{{\rm{DF}}}}}}} \right|. $ | (32) |
在式(21)中,矩阵BSUSBDF-1会引入无拖曳回路的控制信号到悬浮控制回路中.从而使得悬浮控制回路会受到所有噪声的作用,这些噪声必须由惯性传感器提供的微弱静电力加以抑制.
1) Sspec1:扰动噪声抑制.对于悬浮自由度,闭环传递函数的分析表明, 起主导作用的噪声来自静电驱动噪声和微推力器噪声,因此可以得到
| $ \left| {{S_{{\rm{spec1 }}}}} \right| \le \left| {\frac{{{x_{{\rm{req }}}}}}{{{G_{{\rm{SUS }}}}\left( {{n_{{\rm{E}}{{\rm{S}}_{{\rm{SUS}}}}{\rm{ }}}} + {n_{{\rm{T }}}}} \right)}}} \right|{\rm{.}} $ | (33) |
2) Sspec2:测量频段以下的扰动噪声抑制.在测量频段以下,质量块的相对位移与相对姿态均有最大值限制,于是有
| $ \left| {{S_{{\rm{spec2 }}}}} \right| \le \left| {\frac{{{x_{\max }}}}{{{G_{{\rm{SUS }}}}\left( {{n_{{\rm{E}}{{\rm{S}}_{{\rm{SUS}}}}{\rm{ }}}} + {n_{{\rm{T }}}}} \right)}}} \right|{\rm{.}} $ | (34) |
3) Tspec1:测量噪声抑制.闭环传递函数分析表明无拖曳方向的测量噪声对于悬浮控制回路的影响远小于悬浮方向的测量噪声,于是有
| $ \left| {{T_{{\rm{spec}}1}}} \right| = \left| {\frac{{{G_{{\rm{SUS}}}}{C_{{\rm{SUS}}}}}}{{1 + {G_{{\rm{SUS}}}}{C_{{\rm{SUS}}}}}}} \right| \le \left| {\frac{{{x_{{\rm{req}}}}}}{{{\eta _{{\rm{SUS}}}}}}} \right|. $ | (35) |
4) Tspec2:测量噪声引起的悬浮控制回路控制输出的限制.测量噪声引起的控制器输出可以表示为
| $ \left| {{C_{{\rm{SUS}}}}{S_{{\rm{SUS}}}}{\eta _{{\rm{SUS}}}}} \right| = \left| {{u_{\rm{d}}}} \right|. $ | (36) |
根据表 1中静电驱动装置的输出限制可以得到补灵敏度函数约束为
| $ \left| {{T_{{\rm{spec}}2}}} \right| \le \left| {\frac{{{G_{{\rm{SUS}}}}{u_{{\rm{req}}}}}}{{{\eta _{{\rm{SUS}}}}}}} \right|. $ | (37) |
5) Tspec3:测量频段以下的测量噪声抑制为
| $ \left| {{T_{{\rm{spec3 }}}}} \right| \le \left| {\frac{{{x_{\max }}}}{{{\eta _{{\rm{SUS}}}}}}} \right|.. $ | (38) |
6) Tspec4:扰动噪声引起的悬浮控制回路控制输出的限制为
| $ \left| {{T_{{\rm{spec4 }}}}} \right| \le \left| {\frac{{{u_{{\rm{req }}}}}}{{\left( {{n_{\rm{T}}} + {n_{{\rm{E}}{{\rm{S}}_{{\rm{SUS }}}}}}} \right)}}} \right|. $ | (39) |
卫星的姿态在测量带宽内的性能指标由无拖曳回路质量块的性能指标推导而来[11],即
| $ {\varphi _{{\rm{req}}}} = {B_{{\rm{ATT}}}}B_{{\rm{DF}}}^{ - 1}{X_{{\rm{req}} - {\rm{DF}}}}. $ | (40) |
1) Sspec:扰动噪声抑制.对于卫星姿态,微推进器的噪声已经被无拖曳回路抑制,主要的扰动来源为静电驱动噪声,从而姿态控制回路上的灵敏度函数约束为
| $ \left| {{S_{{\rm{spec}}}}} \right| \le \left| {\frac{{{\varphi _{\rm{d}}}}}{{{G_{{\rm{SC}}}}{n_{{\rm{E}}{{\rm{S}}_{{\rm{DF}}}}}}}}} \right|. $ | (41) |
2) Tspec1:测量噪声抑制.测量噪声主要来自星敏感器,惯性传感器的读出噪声已经被无拖曳回路抑制,从而有
| $ \left| {{T_{{\rm{spec}}1}}} \right| \le \left| {\frac{{{\varphi _{{\rm{req}}}}}}{{{\eta _{{\rm{STR}}}}}}} \right|. $ | (42) |
3) Tspec2:测量噪声引起的姿态控制回路控制输出的限制
| $ \left| {{T_{{\rm{spec}}2}}} \right| \le \left| {\frac{{{G_{{\rm{SC}}}}{u_{{\rm{req}}}}}}{{{\eta _{{\rm{STR}}}}}}} \right|. $ | (43) |
无拖曳与姿态控制系统的设计目的是抑制各类扰动与噪声的作用,在实现鲁棒稳定性的同时达到高精度的性能要求.混合灵敏度H∞控制器十分适合此类控制任务设计.但是其设计过程存在加权函数阵难以选取,且需要大量经验以及理论知识去调试的缺点[17-19].利用上述Sspec和Tspec设计规范可以快速指导权函数阵选取,提高了控制器设计效率.
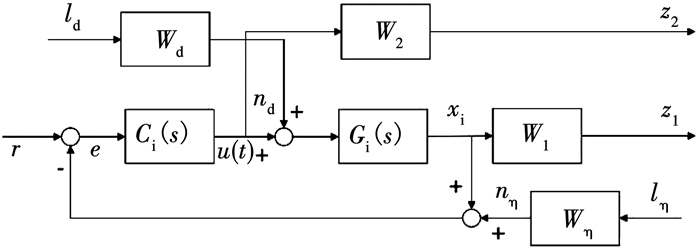
S/T和KS/T混合灵敏度问题常常会产生零极点对消问题,使得小扰动输入导致系统输出的大改变.GS/T加权方式则可以避免这一问题[20].采用输入解耦的方式,式(21)已经将系统解耦成了15个SISO回路.在此基础上,可以将控制器设计问题转化为如图 9所示的GS/T混合灵敏度问题.
|
图 9 GS/T混合灵敏度结构设计 Fig. 9 Schematic of GS/T mixed-sensitivity design |
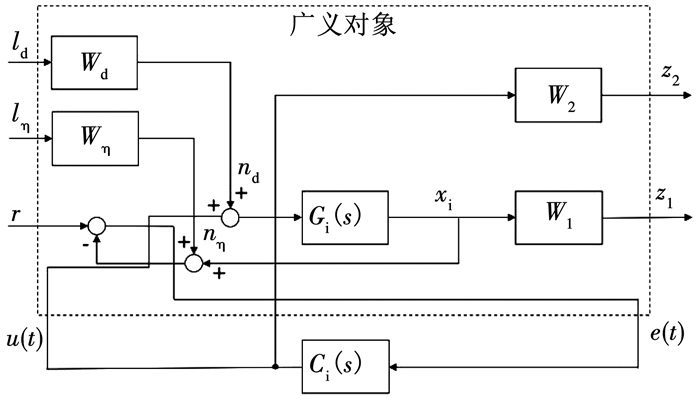
将图 9转化为图 10所示的标准H∞控制的二端口结构.图中,广义噪声输入
|
图 10 整理成标准二端口形式 Fig. 10 Transformed into standard two-port structure |
根据GS/T混合灵敏度控制问题,各回路的控制器设计即可转化为配置加权函数阵W1(s)和W2(s),寻找控制器Ci(s)使得闭环系统稳定且最小化广义输入
| $ \mathop {\min }\limits_{{C_i}} \left\| {\begin{array}{*{20}{c}} {{W_1}(s)G(s)S(s)}\\ {{W_2}(s)T(s)} \end{array}} \right\| \le 1. $ | (44) |
式中:G(s)S(s)为扰动输入到对象输出的传递函数,W1(s)G(s)S(s)代表扰动的衰减特性, W2(s)T(s)代表了乘性不确定性下的鲁棒稳定性约束.
H∞混合灵敏度设计的难点在于权函数的选取.利用上节推导的一系列控制约束,可以快速对加权函数阵进行选取,避免了经验整定权函数参数,提高了控制系统设计效率.根据鲁棒控制第一定理有
| $ \left\{ {\begin{array}{*{20}{l}} {\bar \sigma (S(j\omega )) \le \left| {{G^{ - 1}}W_1^{ - 1}(j\omega )} \right|,\quad \forall \omega ;}\\ {\bar \sigma (T(j\omega )) \le \left| {W_2^{ - 1}(j\omega )} \right|,\quad \forall \omega .} \end{array}} \right. $ | (45) |
式中
| $ \left\{ {\begin{array}{*{20}{l}} {|S(j\omega )| \le \min \left\{ {\left| {{S_{{\rm{spec}}}}} \right|,1{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{mHz}} \le f \le 30{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{mHz}}} \right\}}\\ {|T(j\omega )| \le \min \left\{ {\left| {{T_{{\rm{spec}}}}} \right|,1{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{mHz}} \le f \le 30{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{mHz}}} \right\}} \end{array}} \right. $ | (46) |
|
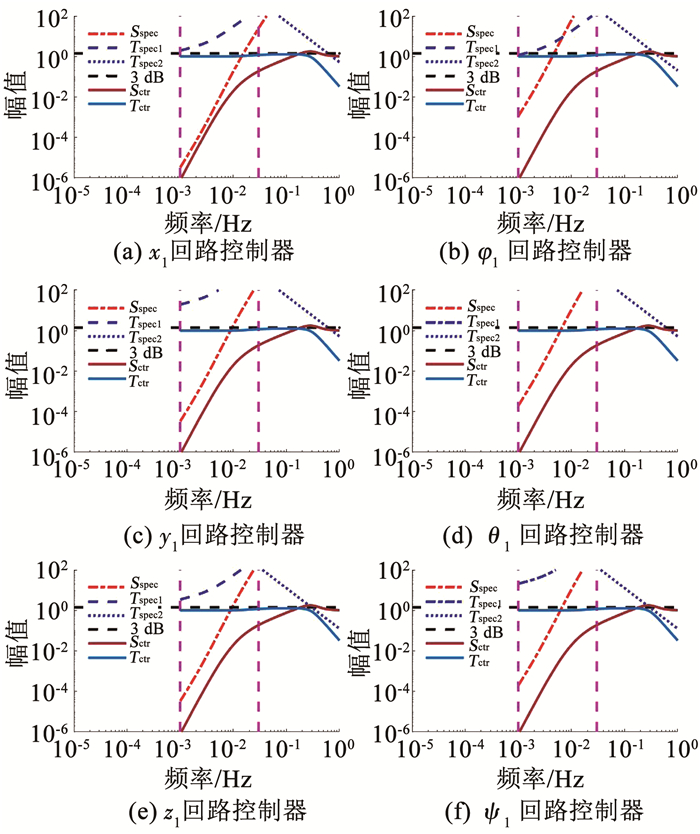
图 11 无拖曳回路控制器设计结果 Fig. 11 Controller designs for drag-free loops |
|
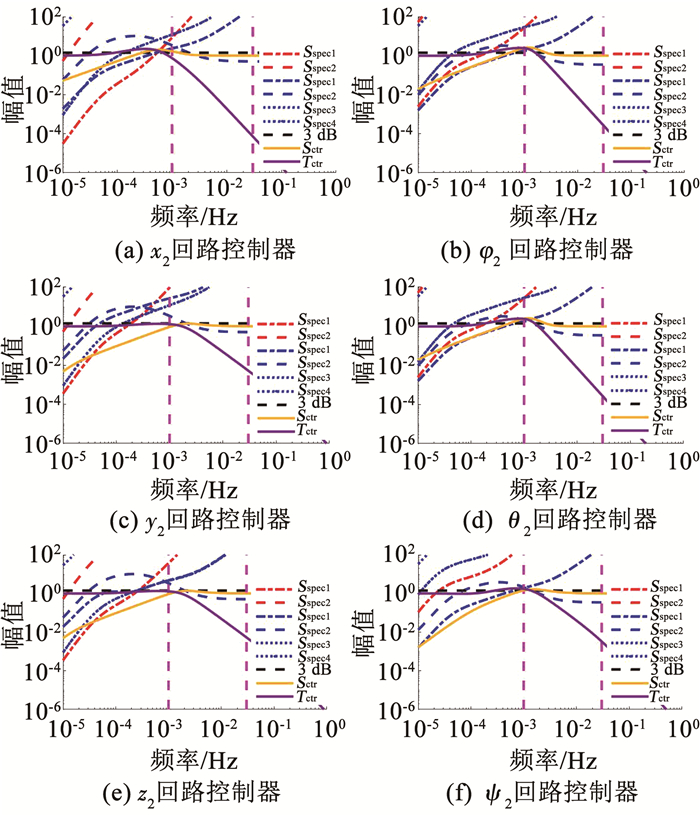
图 12 悬浮回路控制器设计结果 Fig. 12 Controller designs for suspension loops |
式中:min{|Sspec|, 1 mHz≤f≤30 mHz}为各回路推导的一系列灵敏度函数约束在测量频段上的最小值; min{|Tspec, 1 mHz≤f≤30 mHz}为各回路推导的一系列补灵敏度函数的最小值.
结合式(45)和式(46)即可得到W1(s)和W2(s)的设计初值,如式(47)所示,避免了一般性经验的试凑.
| $ \left\{ {\begin{array}{*{20}{l}} {{W_{10}}(s) = \frac{{G(s)}}{{\min \left\{ {{S_{{\rm{spec }}}}(s)} \right\}}},}\\ {{W_{20}}(s) = \frac{1}{{\min \left\{ {{T_{{\rm{spec }}}}(s)} \right\}}}.} \end{array}} \right. $ | (47) |
对于无拖曳控制回路,min{Sspec}和min{Tspec}分别为Sspec和Tspec1.但是表示测量噪声抑制能力的Tspec1的幅值在测量频段上大于1,因此在这里不起决定作用,可以考虑将补灵敏度函数的加权因子设计为空,这样同时可以降低控制器阶数.由此可以设计加权函数阵的初值见式(48).
| $ \left\{ {\begin{array}{*{20}{l}} {{W_{10{\rm{DF}}}}(s) = \frac{{{G_{{\rm{DF}}}}(s)}}{{{S_{{\rm{spec}}}}(s)}},}\\ {{W_{20{\rm{DF}}}}(s) = [{\kern 1pt} {\kern 1pt} {\kern 1pt} ].} \end{array}} \right. $ | (48) |
再进一步依据Tspec2在1 Hz处确定的补灵敏度函数幅值上界,调节W10DF的截止频率,实现推力跳变限制约束.最后为使得到的设计结果尽可能满足3 dB的稳定裕度限制,可以进一步调节在靠近3 dB约束时W10DF的下降斜率.最终的设计结果如图 11所示.
悬浮控制回路与姿态控制回路可以类似设计得到.根据上述分析,依据Sspec和Tspec可以很容易调节加权函数实现约束、稳定裕度以及控制器复杂度之间的折衷.总的来说,在设计加权函数阵时,要在测量带宽上尽可能满足所有的约束.同时尽量降低W1(s)和W2(s)的阶数,使得最终设计的控制器的阶数不至于过高.
从图 3中可以看出,各控制回路之间仍有耦合.如无拖曳回路的控制输出会前馈耦合到悬浮控制回路; 姿态控制回路与无拖曳控制之间也需要在频域上进一步解耦.因此,有必要按照下述顺序设计各个回路的控制器.
1) 不考虑姿态回路的耦合,首先设计最重要的无拖曳控制器.
2) 考虑无拖曳回路控制信号的耦合,设计6个悬浮回路自由度上的控制器; 由于耦合的存在,设计W1(s)在低频段的幅值尽可能大,从而确保悬浮控制器具有足够的抗干扰能力.
3) 姿态控制要求相对较低,最后进行设计.但要保证姿态控制回路的带宽远低于无拖曳控制回路,从而避免姿态控制对于无拖曳输出的影响.本研究中,姿态控制带宽约为0.7 mHz,无拖曳控制带宽约为2.1 Hz,从而使得步骤1)的假设是合理的.
5 仿真校验图 13所示为搭建的无拖曳与姿态控制系统仿真平台.左侧模块为各扰动和噪声的加权函数,右侧模块分别为姿态控制回路、无拖曳控制回路以及悬浮控制回路.

|
图 13 无拖曳与姿态控制系统仿真平台 Fig. 13 Simulation platform for drag-free and attitude control system (DFACS) |
为充分表现TM1和TM2的相对运动演化规律并绘制准确的功率谱密度曲线,设置仿真时间为120 h.其余仿真参数见表 2.
| 表 2 仿真参数设置 Tab. 2 Simulation parameters setting |
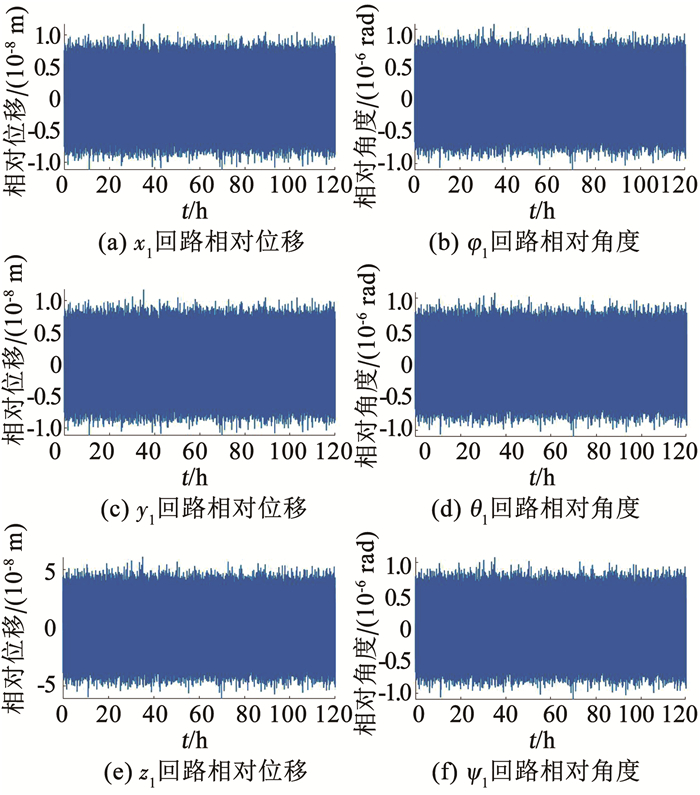
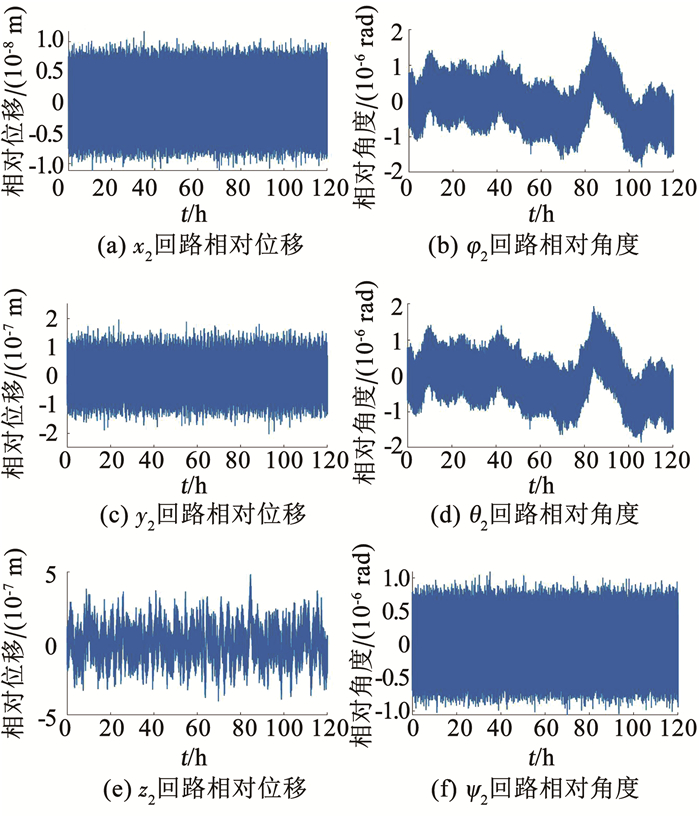
TM1和TM2相对运动的时域演化规律见图 14~15.可以看出,在设计的无拖曳与姿态控制系统作用下,TM1和TM2均处于稳定状态.不论是无拖曳控制的TM1还是悬浮控制的TM2的相对运动均未超出最大值限制.表明质量块在控制系统的作用下很好地抵消了扰动与噪声的作用,没有与包覆质量块的惯性传感器相撞,具有相应的微重力水平.
|
图 14 无拖曳控制回路的相对运动 Fig. 14 Relative motions of drag-free control loops |
|
图 15 悬浮控制回路的相对运动 Fig. 15 Relative motions of suspension control loops |
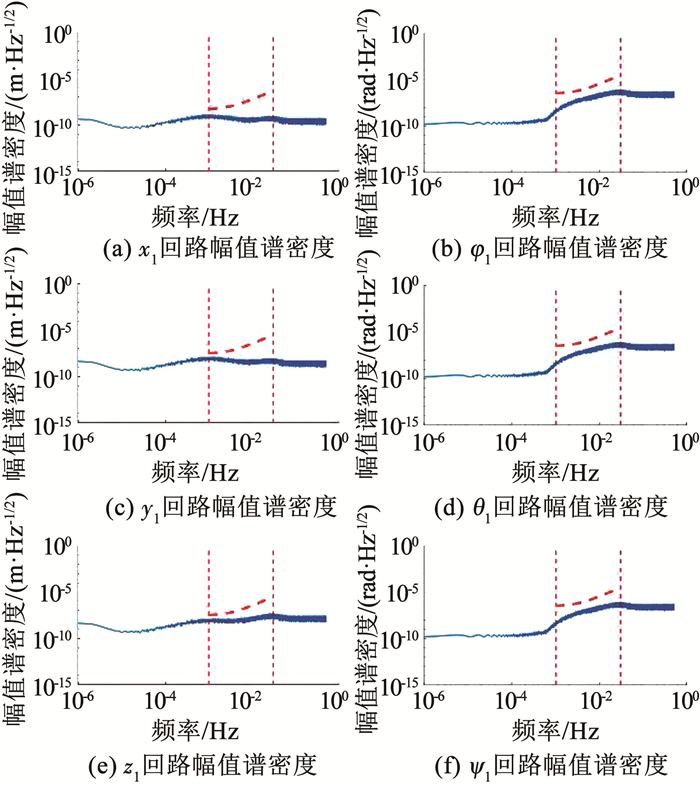
图 16和图 17所示为TM1和TM2状态响应的幅度谱密度曲线.红色虚线为表 1所述测量带宽内各轴的性能指标,蓝色曲线为状态响应的幅度谱密度.可以看出,无拖曳各轴的频域特性距离性能指标均存在一定裕度.要求最为严苛的敏感轴x1方向也通过配置Sctr实现了低频段的抗干扰能力.
|
图 16 无拖曳控制性能指标仿真结果 Fig. 16 Simulation results of drag-free control performances |
|
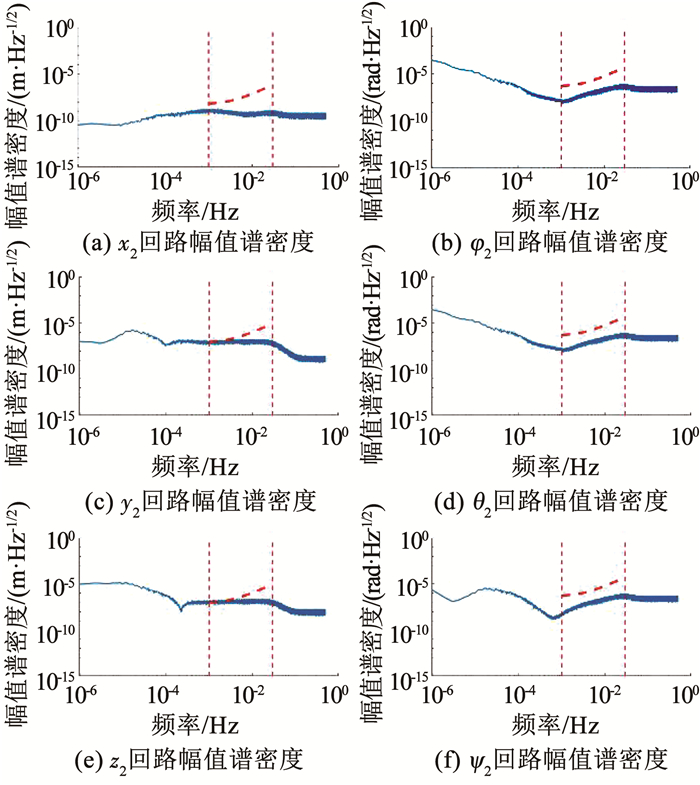
图 17 悬浮控制性能指标仿真结果 Fig. 17 Simulation results of suspension control performances |
悬浮控制回路y2和z2轴在低频段的频域性能超出了约束.由于悬浮控制回路对于系统噪声的敏感,使得无法通过提高控制器带宽的方式来改善性能.但是该方向只会通过交叉耦合的方式对敏感轴的残余加速度造成影响,所以y2和z2轴的结果是容许的.
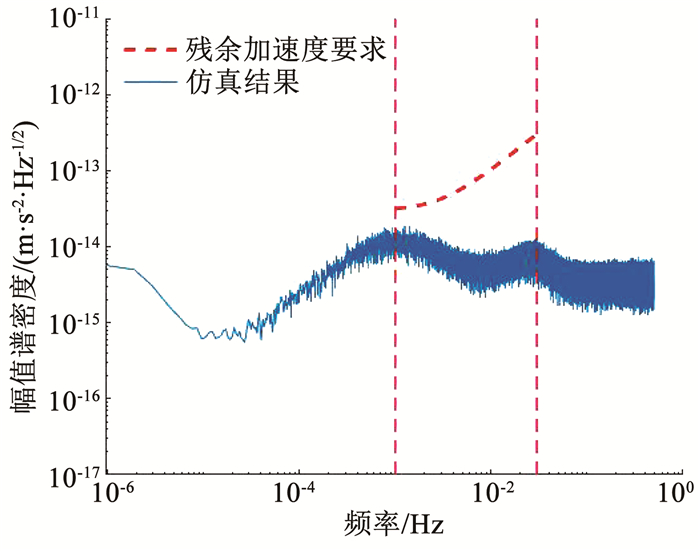
依据式(1)可以计算敏感轴x1方向残余加速度的仿真结果.图 18中红色虚线为残余加速度要求,可以看出,以表 1所示的分解指标为参考而设计的无拖曳与姿态控制系统实现了本研究要求的3×10-14(1+[f/3 mHz]2)m·s-2·Hz-1/2的无拖曳水平.
|
图 18 敏感轴方向残余加速度仿真结果 Fig. 18 Simulation results of residual acceleration along sensitive axis |
图 13所示的仿真平台是依据闭环全系统模型搭建的,考虑了各回路间的耦合.最后的仿真结果符合指标要求,表明本文在设计过程中提出的解耦分析与假设是合理的,进行的解耦设计过程是有效的.
最后,根据设计的无拖曳与姿态控制系统,进一步分析了实现中国科学院空间引力波探测太极计划要求的3×10-15(1+[f/8 mHz]4)m·s-2·Hz-1/2残余加速度的可能性.
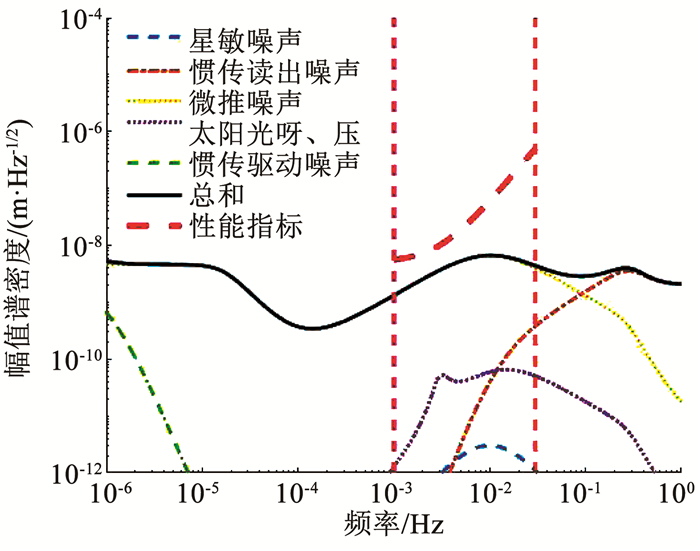
通过闭环传递函数分析,图 19所示为在控制器作用下,各扰动和噪声对敏感轴x1方向相对位移的影响.可以看出,在测量带宽以内,主要的影响来自于微推力器噪声,其次是惯性传感器的读出噪声.因此,考虑将微推力器噪声减小1个数量级,并且沿敏感轴方向采用测量噪声更低的激光干涉测量方式.此外,禁止电容系统在x1方向施加任何力,从而消除该轴上的驱动噪声.利用图 13所示仿真平台,再次进行仿真,得到了图 20所示的残余加速度水平.
|
图 19 沿敏感轴方向的传递函数分析 Fig. 19 Transfer function analysis along sensitive axis |

|
图 20 减小微推力器噪声后的敏感轴残余加速度 Fig. 20 Residual acceleration along sensitive axis with reduced micro-thruster noise |
根据仿真结果可以说明,若在未来的工程设计中,能够在目前微推力器的噪声水平上继续下降1个数量级,即根据图 6,达到1 μN·Hz-1/2@1 mHz的水平并且不激活沿敏感轴方向的电极片,采用激光干涉测量敏感轴方向的相对状态偏差,将有可能实现空间引力波探测太极计划要求的残余加速度水平.
6 结论本文以深空环境下的双质量块无拖曳卫星为研究对象,基于构建的频域设计规范快速且有效地解决了其复杂多变量高精度控制问题.通过将15个自由度划分成3个控制回路,并结合噪声的频谱模型以及频域科学指标构建了每个控制回路的灵敏度函数与补灵敏度函数设计约束,准确地指导了混合灵敏度GS/T问题中的加权函数设计,完成了卫星无拖曳与姿态控制系统的设计.仿真校验结果表明基于频域规范设计的控制系统不仅具有鲁棒稳定性并且实现了深空探测无拖曳卫星的抗干扰性要求,满足各项无拖曳水平要求.
此外,利用所设计的无拖曳控制系统,进一步通过传递函数分析发现了影响敏感轴无拖曳性能的主要扰动来源.给出了未来实现空间引力波探测太极计划要求的残余加速度水平的工程建议.
本文介绍的建模与控制器设计方法虽然针对LISA Pathfinder任务类别的无拖曳卫星,但也可以推广到任意构型的无拖曳卫星,具有通用性.
| [1] |
LANGE B. The control and use of drag-free satellite[D]. Stanford: Stanford University, 1964
|
| [2] |
HAINES R. Development of a drag-free control system[C]//14th Annual AIAA/USU Conference on Small Satellite. Utah: [s.n.], 2000
|
| [3] |
DITTUS H, LÄMMERZAHL C, TURYSHEV S G. Lasers, clocks and drag-free control: exploration of relativistic gravity in space[M]. Berlin: Springer, 2008: 341.
|
| [4] |
施梨, 曹喜滨, 张锦绣, 等. 无阻力卫星发展现状[J]. 宇航学报, 2010, 31(5): 1511. SHI Li, CAO Xibin, ZHANG Jinxiu, et al. Survey of drag-free satellite[J]. Journal of Astronautics, 2010, 31(5): 1511. DOI:10.3873/j.issn.1000-1328.2010.06.001 |
| [5] |
WEBER W J, CAVALLERI A, DOLESI R, et al. Position sensor for LISA drag-free control[J]. Classical and Quantum Gravity, 2002, 19(7): 1751. DOI:10.1088/0264-9381/19/7/371 |
| [6] |
邹奎, 苟兴宇, 薛大同. 重力梯度卫星无拖曳控制技术[J]. 空间控制技术与应用, 2017, 43(2): 28. ZOU Kui, GOU Xingyu, XUE Datong. An overview on drag-free control for gravitational gradiometry satellites[J]. Aerospace Control and Application, 2017, 43(2): 28. DOI:10.3969/j.issn.1674-1579.2017.02.005 |
| [7] |
ARMANO M, AUDLEY H, BAIRD J, et al. LISA Pathfinder platform stability and drag-free performance[J]. Physical Review D, 2019, 99(8): 082001. DOI:10.1103/PhysRevD.99.082001 |
| [8] |
LUO Ziren, GUO Zongkuan, JIN Gang, et al. A brief analysis to Taiji: science and technology[J]. Results in Physics, 2019, 16: 102918. DOI:10.1016/j.rinp.2019.102918 |
| [9] |
GATH P, FICHTER W, ZIEGLER T, et al. Feedback controller design for the basic science mode of the LISA Pathfinder mission[J]. IFAC Proceedings Volumes, 2004, 37(6): 839. DOI:10.1016/S1474-6670(17)32282-6 |
| [10] |
MAGHAMI P G, O'DONNELL J R, HSU O H, et al. Drag-free performance of the ST7 disturbance reduction system experiment on LISA Pathfinder[C]//10th International ESA Conference on Guidance, Navigation and Control System. Salzburg: European Space Agency, 2017
|
| [11] |
WU Shufan, FERTIN D. Spacecraft drag-free attitude control system design with Quantitative Feedback Theory[J]. Acta Astronautica, 2008, 62(12): 668. DOI:10.1016/j.actaastro.2008.01.038 |
| [12] |
章楚.基于自抗扰控制方法的无拖曳控制研究[D].北京: 中国科学院大学, 2019 ZHANG Chu. Drag-free control based on active disturbance rejection control paradigm[D]. Beijing: University of Chinese Academy of Sciences, 2019 |
| [13] |
刘康志, 姚郁. 线性鲁棒控制[M]. 北京: 科学出版社, 2013: 352.
|
| [14] |
ZHOU Jiaxing, LIU Lei, WANG Zhigang. Modeling and analysis of ultra-low frequency dynamics of drag-free satellites[J]. Microgravity Science and Technology, 2019, 31: 151. DOI:10.1007/s12217-019-9672-7 |
| [15] |
GATH P, FICHTER W, KERSTEN M, et al. Drag-free and attitude control system design for the LISA Pathfinder Mission[C]//AIAA Guidance, Navigation, and Control Conference and Exhibit. Providence: AIAA, 2004. DOI: 10.2514/6.2004-5430
|
| [16] |
SCHUMAKER B L. Disturbance reduction requirement for LISA[J]. Classical and Quantum Gravity, 2003, 20(20). DOI:10.1088/0264-9381/20/10/327 |
| [17] |
MIRANDA M F, TAKAHASHI R H C, JOTA F G. H∞ controllers with integral action: an experimental evaluation[J]. Proceedings of the Institution of Mechanical Engineers, 2010, 224(1): 21. DOI:10.1243/09596518JSCE867 |
| [18] |
ORTEGA M G, VARGAS M, CASTANO F, et al. Improved design of the weighting matrices for the S/KS/T mixed sensitivity problem-application to a multivariable thermodynamic system[J]. IEEE Transactions on Control Systems Technology, 2006, 14(1): 82. DOI:10.1109/TCST.2005.860518 |
| [19] |
ORTEGA M G, RUBIO F R. Systematic design of weighting matrices for the H∞ mixed sensitivity problem[J]. Journal of Process Control, 2004, 14(1): 89. DOI:10.1016/S0959-1524(03)00035-0 |
| [20] |
CHRISTEN U, GEERING H P. Inverting and noninverting H∞ controllers[J]. Systems & Control Letters, 1997, 30(1): 31. DOI:10.1016/S0167-6911(96)00074-6 |
 2021, Vol. 53
2021, Vol. 53


