有监督的模式识别过于依赖有标签的训练样本的数量.一方面,在现实生活中为样本打标签十分耗费资源和时间; 另一方面,这种完全由样本的数量和质量决定的学习方式非常容易导致过拟合.由于监督学习的局限性和不便利性,大量的研究者开始探索无监督和半监督的学习方法.如主动学习,它不是将所有样本打上标签,而是提出一些标注请求,将一些经过筛选的数据提交给相关领域专家进行标注.
域自适应或迁移学习,因为不需要大量的数据标注,近年来受到研究者的广泛关注.在域自适应的问题中,将需要进行识别的数据集称为测试集.测试集中的数据全部没有标签时称为无监督域自适应[1-2],测试集中有少部分数据有标签时则称为半监督域自适应[3-4].与主动学习不一样的是,不需要采取人工辅助的方式为样本打上标签,用于训练做训练集的源域中已经拥有大量有标签的数据,但是源域的数据和真正需要进行分类的目的域数据并不是同分布的.所以域自适应主要解决两个域分布适应的问题,从而借助源域中大量有标签的数据集对目的域的数据进行识别.目前传统的域自适应算法的相关研究工作主要分为以下3种方式:1)数据分布的适应:即通过某种变换直接将两个域的分布拉近或者选择出分布相似的公共特征,主要通过最大平均差异(maximum mean discrepancy, MMD)[5]度量变换后的两个域的相似性,例如TCA[6]、TJM[7]、JDA[8]和JGSA[9].TCA首先提出通过一个特征映射使得映射后的两个域的边缘分布接近,JDA同时考虑了边缘分布适配和条件分布适配.其他部分方法基于TCA和JDA做出了扩展,例如TJM在TCA中加入了源域样本选择,ARTL[10]将JDA嵌入结构风险最小化框架.2)子空间学习:包括低维统计特征的子空间对齐(SA[11]、SDA[12]和RTML[13])和低维流形结构的子空间对齐(GFK[14]和DIP[15]).3)表示学习:在子空间学习的基础上通过源域样本表示目的域样本(DTSL[16]和LSDT[17]).
1 域适应表示学习算法本文的方法基于表示学习,与现有表示学习方法思想相同:都是在子空间学习的基础上引入表示矩阵以更好地减少两个域的分布差异.但是现有方法通常只采用一个单一的表示矩阵来建立两个域之间的映射关系.本文的方法与之不同:1)本文改进地采用两个不同的表示矩阵,分别用源域表示目的域和用目的域表示源域; 2)同时提出两个表示矩阵各自的最优化约束设计,使得源域和目的域最优地相互表示,从而减少域差异,实现借助源域数据对目的域无标签数据的分类.
1.1 源域有监督子空间学习域自适应问题最关键的是减小两个域的差异.通常可以通过寻求一个两域的共同子空间去实现两域之间的迁移.由于源域具有可靠的真实标签,首先在源域学习一个标签引导的子空间.模型如式(1)所示
| $ \begin{array}{l} \begin{array}{*{20}{c}} {\mathop {\min }\limits_{P,C} \frac{1}{2}\left\| {{\mathit{\boldsymbol{P}}^{\rm{T}}}{\mathit{\boldsymbol{X}}_{\rm{s}}} - \left( {{\mathit{\boldsymbol{Y}}_{\rm{s}}} + \mathit{\boldsymbol{D}} \odot \mathit{\boldsymbol{C}}} \right)} \right\|_F^2,}\\ {{\rm{ s}}{\rm{.t}}{\rm{. }}\mathit{\boldsymbol{C}} \ge 0,} \end{array}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{D}}_{i,j}} = \left\{ {\begin{array}{*{20}{l}} { + 1,{\mathit{\boldsymbol{Y}}_{\rm{s}}}\{ i,j\} = 1;}\\ { - 1,{\rm{ 其他}}{\rm{. }}} \end{array}} \right. \end{array} $ | (1) |
式中:⊙是Hadamard乘积运算,P∈Rm×d是共同的子空间,Xs∈Rm×ns是源域的数据,Ys∈Rsd×n是源域标签矩阵,m是样本特征的维度,ns代表源域样本的数目,d是共同子空间的维度.C∈Rsd×n是松弛标签矩阵,加入松弛标签C是为了更自由地获得共同子空间.
1.2 构建表示矩阵通常引入表示矩阵可以促进共同子空间的学习.常见的方法是使用一个表示矩阵,即单一方向地用源域的数据表示目的域数据,或者目的域数据表示源域数据,例如DTSL和LSDT.但这样的表示方式下,两个域的有用信息很难被完全保留.这是因为源域和目标域的特征分布不同,两个域需要保留的信息不同,而使用同一个表示矩阵不能很好地保留两个域特有的有用信息和结构特征.尤其是,当带有标签的源域样本单方向地靠近目的域数据时,会对源域的基本结构造成一定的破坏.
于是本文提出在源域和目的域采用两个不同的表示矩阵来表示另一个域.即在源域存在一个表示矩阵去表示目的域的特征,同时在目的域存在另一个表示矩阵去表示源域的特征.该模型如式(2)(3)所示
| $ {{\mathit{\boldsymbol{P}}^{\rm{T}}}{\mathit{\boldsymbol{X}}_{\rm{s}}}{\mathit{\boldsymbol{Z}}_{\rm{s}}} = {\mathit{\boldsymbol{P}}^{\rm{T}}}{\mathit{\boldsymbol{X}}_{\rm{t}}},} $ | (2) |
| $ {{{\left( {{\mathit{\boldsymbol{P}}^{\rm{T}}}{\mathit{\boldsymbol{X}}_{\rm{s}}}} \right)}^{\rm{T}}} = {\mathit{\boldsymbol{Z}}_{\rm{t}}}{{\left( {{\mathit{\boldsymbol{P}}^{\rm{T}}}{\mathit{\boldsymbol{X}}_{\rm{t}}}} \right)}^{\rm{T}}}.} $ | (3) |
式中:Zs∈Rns×nt是作用于源域的表示矩阵; Zt∈Rns× nt是作用于目的域的表示矩阵; Xt∈Rtm×n是目的域的样本,nt代表目的域样本的数目.对于分布不同的两个域,按照各自特征去学习不同的表示矩阵有助于对齐两个域的分布,同时保存自己特有的信息.
2 表示矩阵的约束设计共同子空间和合理的两个表示矩阵可以减小两个域差异的同时尽可能地保存两个域的原始有用信息.为了得到尽可能最优的两个表示矩阵,对上面提出的两个表示矩阵进行了相应的约束设计,进而借助它们学习到有利于域适应的共同子空间.由于两个表示矩阵需要保留的特征不同,应该按条件对它们施加不同的约束.在两个域分布差异尽可能小的公共子空间上,目的域数据通过表示矩阵可以被源域的数据线性表示,如式(2)所示.也就是说,目的域中的每个样本都可以视作是源域样本的线性组合.再则考虑到源域的数据具有可靠的标签,对源域表示矩阵进行按列稀疏约束,表示为
| $ \mathop {\min }\limits_{\mathit{\boldsymbol{P}},{\mathit{\boldsymbol{Z}}_{\rm{t}}}} {\left\| {{\mathit{\boldsymbol{Z}}_{\rm{t}}}} \right\|_1},{\rm{s}}.{\rm{ t}}{\rm{. }}{\mathit{\boldsymbol{P}}^{\rm{T}}}{\mathit{\boldsymbol{X}}_{\rm{s}}}{\mathit{\boldsymbol{Z}}_{\rm{s}}} = {\mathit{\boldsymbol{P}}^{\rm{T}}}{\mathit{\boldsymbol{X}}_{\rm{t}}}. $ | (4) |
式中‖·‖1表示1-范数.这样目的域的样本可以由更少的源域样本线性组合,保留了数据局部结构的同时能够更确切地分类.
但是同一类别往往有很多样本,当某一个样本由同一类样本线性组合表示的时候并不会丢失可判别性,反而会提高可判别性并降低过拟合的风险.受这个思路和最优传输理论[18]的启发,本文采用group-lasso作为Zs表示矩阵的稀疏约束,对表示矩阵按类别进行稀疏约束,同一类别采用2-范数降低稀疏约束强度,表示为
| $ \sum\limits_j {\sum\limits_{cl} {{{\left\| {{\mathit{\boldsymbol{Z}}_{\rm{s}}}\left( {{\tau _{cl}},j} \right)} \right\|}_2}} } , $ |
式中,‖·‖2表示2-范数,τcl是源域第cl类数据对应表示矩阵Zs中相应行的组合,j代表样本特征维度的第j维.综上,源域表示矩阵Zs受到的稀疏约束由式(4)改进为式(5).
| $ \mathop {\min }\limits_{\mathit{\boldsymbol{P}},{\mathit{\boldsymbol{Z}}_{\rm{s}}}} {\left\| {{\mathit{\boldsymbol{Z}}_{\rm{s}}}} \right\|_{{\rm{group - lasso}}}},{\rm{s}}.{\rm{ t}}{\rm{. }}{\mathit{\boldsymbol{P}}^{\rm{T}}}{\mathit{\boldsymbol{X}}_{\rm{s}}}{\mathit{\boldsymbol{Z}}_{\rm{s}}} = {\mathit{\boldsymbol{P}}^{\rm{T}}}{\mathit{\boldsymbol{X}}_{\rm{t}}}, $ | (5) |
其中,
为了更好地保留数据的结构信息,最理想的情况是源域中相同类别的数据被目的域中的数据用同一种线性表示方式所表示.例如作用在目的域的表示矩阵的秩降低到等于类别数,即说明同一类样本拥有同样的线性表示方式.于是作用于目的域的表示矩阵应该受到低秩约束,如式(6)所示
| $ \mathop {\min }\limits_{\mathit{\boldsymbol{P}},{\mathit{\boldsymbol{Z}}_{\rm{t}}}} {\left\| {{\mathit{\boldsymbol{Z}}_{\rm{t}}}} \right\|_*},{\rm{s}}.{\rm{t}}.{\left( {{\mathit{\boldsymbol{P}}^{\rm{T}}}{\mathit{\boldsymbol{X}}_{\rm{s}}}} \right)^{\rm{T}}} = {\mathit{\boldsymbol{Z}}_{\rm{t}}}{\left( {{\mathit{\boldsymbol{P}}^{\rm{T}}}{\mathit{\boldsymbol{X}}_{\rm{t}}}} \right)^{\rm{T}}}. $ | (6) |
将式(1)~(3)、(5)和(6)合并,得到最终的模型,总模型为
| $ \begin{array}{*{20}{c}} {\mathop {\min }\limits_{\mathit{\boldsymbol{P}},\mathit{\boldsymbol{C}},{\mathit{\boldsymbol{Z}}_s},{\mathit{\boldsymbol{Z}}_1}} \frac{1}{2}\left\| {{\mathit{\boldsymbol{P}}^{\rm{T}}}{\mathit{\boldsymbol{X}}_{\rm{s}}} - \left( {{\mathit{\boldsymbol{Y}}_{\rm{s}}} + \mathit{\boldsymbol{D}} \odot \mathit{\boldsymbol{C}}} \right)} \right\|_F^2 + }\\ {\alpha {{\left\| {{\mathit{\boldsymbol{Z}}_{\rm{s}}}} \right\|}_{{\rm{group }} - {\rm{lass}}}} + \beta {{\left\| {{\mathit{\boldsymbol{Z}}_{\bf{t}}}} \right\|}_*},}\\ {{\rm{ s}}{\rm{. t}}{\rm{. }}{\mathit{\boldsymbol{P}}^{\rm{T}}}{\mathit{\boldsymbol{X}}_{\rm{s}}}{\mathit{\boldsymbol{Z}}_{\rm{s}}} = {\mathit{\boldsymbol{P}}^{\rm{T}}}{\mathit{\boldsymbol{X}}_{\rm{t}}},}\\ {{{\left( {{\mathit{\boldsymbol{P}}^{\rm{T}}}{\mathit{\boldsymbol{X}}_{\rm{s}}}} \right)}^{\rm{T}}} = {Z_{\bf{t}}}{{\left( {{\mathit{\boldsymbol{P}}^{\rm{T}}}{\mathit{\boldsymbol{X}}_{\bf{t}}}} \right)}^{\rm{T}}},C \ge 0.} \end{array} $ | (7) |
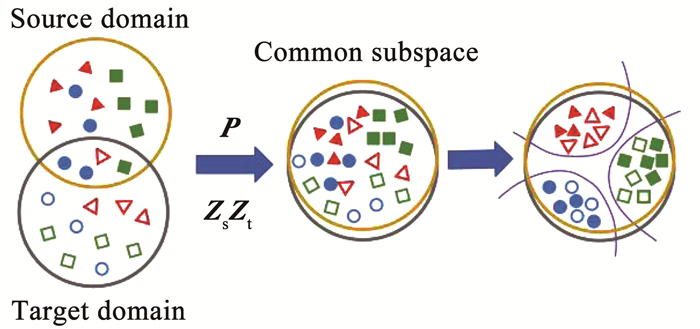
其中,α和β是超参数.总模型示意图如图 1所示.
|
图 1 模型示意 Fig. 1 Schematic diagram of model |
式(7)的最优化问题是非凸的,求解只能保证局部最优而不是全局最优.为了解决这个问题, 利用不精确拉格朗日乘子法(IALM)将该问题转换成凸问题,转换如下:
| $ \begin{array}{*{20}{c}} {\mathop {\min }\limits_{\mathit{\boldsymbol{P}},\mathit{\boldsymbol{C}},{\mathit{\boldsymbol{Z}}_{\rm{s}}},{\mathit{\boldsymbol{Z}}_{\rm{t}}}} \frac{1}{2}\left\| {{\mathit{\boldsymbol{P}}^{\rm{T}}}{\mathit{\boldsymbol{X}}_{\rm{s}}} - \left( {{\mathit{\boldsymbol{Y}}_{\rm{s}}} + \mathit{\boldsymbol{D}} \odot \mathit{\boldsymbol{C}}} \right)} \right\|_F^2 + }\\ {\alpha {{\left\| {{\mathit{\boldsymbol{Z}}_2}} \right\|}_{{\rm{group - lasso}}}} + \beta {{\left\| {{\mathit{\boldsymbol{Z}}_1}} \right\|}_*},}\\ {{\rm{ s}}{\rm{. t}}{\rm{. }}{\mathit{\boldsymbol{P}}^{\rm{T}}}{\mathit{\boldsymbol{X}}_{\rm{s}}}{\mathit{\boldsymbol{Z}}_{\rm{s}}} = {\mathit{\boldsymbol{P}}^\mathit{\boldsymbol{T}}}{\mathit{\boldsymbol{X}}_{\rm{t}}},}\\ {{{\left( {{\mathit{\boldsymbol{P}}^{\rm{T}}}{\mathit{\boldsymbol{X}}_{\rm{s}}}} \right)}^{\rm{T}}} = {\mathit{\boldsymbol{Z}}_{\rm{t}}}{{\left( {{\mathit{\boldsymbol{P}}^{\rm{T}}}{\mathit{\boldsymbol{X}}_{\rm{t}}}} \right)}^{\rm{T}}},}\\ {{\mathit{\boldsymbol{Z}}_{\rm{s}}} = {\mathit{\boldsymbol{Z}}_2},{\mathit{\boldsymbol{Z}}_{\rm{t}}} = {\mathit{\boldsymbol{Z}}_1},\mathit{\boldsymbol{C}} \ge 0.} \end{array} $ | (8) |
可以通过增广拉格朗日乘子法,进一步将式(8)转换为
| $ \begin{array}{l} L = \frac{1}{2}\left\| {{\mathit{\boldsymbol{P}}^{\rm{T}}}{\mathit{\boldsymbol{X}}_{\rm{s}}} - \left( {{\mathit{\boldsymbol{Y}}_{\rm{s}}} + \mathit{\boldsymbol{D}} \odot \mathit{\boldsymbol{C}}} \right)} \right\|_F^2 + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \beta {\left\| {{\mathit{\boldsymbol{Z}}_1}} \right\|_*} + \alpha {\left\| {{\mathit{\boldsymbol{Z}}_2}} \right\|_{{\rm{group }} - {\rm{lasso}}}} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left\langle {{\mathit{\boldsymbol{Y}}_1},{\mathit{\boldsymbol{P}}^{\rm{T}}}{\mathit{\boldsymbol{X}}_{\rm{s}}}{\mathit{\boldsymbol{Z}}_{\rm{s}}} - {\mathit{\boldsymbol{P}}^{\rm{T}}}{\mathit{\boldsymbol{X}}_{\rm{t}}}} \right\rangle + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left\langle {{\mathit{\boldsymbol{Y}}_2},{{\left( {{\mathit{\boldsymbol{P}}^{\rm{T}}}{\mathit{\boldsymbol{X}}_{\rm{s}}}} \right)}^{\rm{T}}} - {\mathit{\boldsymbol{Z}}_{\rm{t}}}{{\left( {{\mathit{\boldsymbol{P}}^{\rm{T}}}{\mathit{\boldsymbol{X}}_{\rm{t}}}} \right)}^{\rm{T}}}} \right\rangle + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left\langle {{\mathit{\boldsymbol{Y}}_3},{\mathit{\boldsymbol{Z}}_{\rm{t}}} - {\mathit{\boldsymbol{Z}}_1}} \right\rangle + \left\langle {{\mathit{\boldsymbol{Y}}_4},{\mathit{\boldsymbol{Z}}_{\rm{s}}} - {\mathit{\boldsymbol{Z}}_2}} \right\rangle + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{\mu }{2}\left\| {{\mathit{\boldsymbol{P}}^{\rm{T}}}{\mathit{\boldsymbol{X}}_s}{\mathit{\boldsymbol{Z}}_{\rm{s}}} - {\mathit{\boldsymbol{P}}^{\rm{T}}}{\mathit{\boldsymbol{X}}_{\rm{t}}}} \right\|_F^2 + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{\mu }{2}\left\| {{{\left( {{\mathit{\boldsymbol{P}}^{\rm{T}}}{\mathit{\boldsymbol{X}}_{\rm{s}}}} \right)}^{\rm{T}}} - {\mathit{\boldsymbol{Z}}_{\rm{t}}}{{\left( {{\mathit{\boldsymbol{P}}^{\rm{T}}}{\mathit{\boldsymbol{X}}_{\rm{t}}}} \right)}^{\rm{T}}}} \right\|_F^2 + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{\mu }{2}\left\| {{\mathit{\boldsymbol{Z}}_{\rm{t}}} - {\mathit{\boldsymbol{Z}}_1}} \right\|_F^2 + \frac{\mu }{2}\left\| {{\mathit{\boldsymbol{Z}}_{\rm{s}}} - {\mathit{\boldsymbol{Z}}_2}} \right\|_F^2. \end{array} $ | (9) |
式中,μ是惩罚参数; Y1、Y2、Y3和Y4代表拉格朗日乘子,在优化求解过程中,每次更新其中一个变量并固定其余变量迭代求解.
4 理论分析Ben-David[19]定理提出源域分类器在目的域中的误差上限,即借助源域有标签的样本训练得到的分类器来识别无标签的目的域样本的误差上限.如式(10)所示
| $ \begin{array}{*{20}{c}} {{ \epsilon _{\rm{T}}}(h) \le { \epsilon _{\rm{S}}}(h) + {d_1}\left( {{\mathit{\boldsymbol{D}}_{\rm{S}}},{\mathit{\boldsymbol{D}}_{\rm{T}}}} \right) + }\\ {\min {{\rm{E}}_{{\mathit{\boldsymbol{D}}_{\rm{S}}}}}\left[ {\left| {{f_{\rm{S}}}(X) - {f_{\rm{T}}}(X)} \right|} \right],}\\ {{{\rm{E}}_{{\mathit{\boldsymbol{D}}_{\rm{T}}}}}\left[ {\left| {{f_{\rm{S}}}(X) - {f_{\rm{T}}}(X)} \right|} \right].} \end{array} $ | (10) |
式中:
由于标签函数是已知的,所以min EDS [|fS(X)-fT(X)|], EDT[|fS(X)-fT(X)|]是一个常量.从式(10)可以推出,若需减小目的域分类误差,则需要减小
在3个迁移学习常用的数据集上开展实验进行验证.1)COIL20数据集将1 440张灰度图片分成了两个域:COIL1(C1)和COIL2(C2).该数据集的样本有20个类别,COIL20数据集的部分示例见图 2.2)Office-Caltech 10[10]是最广泛使用的数据集,一共分为4个域:Caltech(C)、Amazon(A)、DSLR(D)和Webcam(W).本文的实验使用了该数据集800维的SURF特征和4 096维的DeCAF特征.3)ImageCLEF-DA[16]由3个数据集共同的12类数据组成,3个数据集分别是:Caltech-256(C)、ImageNet ILSVRC 2012(I)和VOC 2012(P).可构建6个跨域任务:C→I、C→P、I→C、I→P、P→C和P→I.

|
图 2 COIL20数据集部分示例 Fig. 2 Example images from COIL20 |
与以下10种传统迁移学习方法进行了对比,包括:TCA[6]、GFK[14]、JDA[8]、SA[11]、DTSL[16]、CORAL[20]、BDA[21]、DICD[22]、KOT[23]和DST-ELM[24],同时还与以下2种深度方法也进行了对比:AlexNet[25]和JDOT[26].实验结果见表 1~5,其中识别准确率的最好值与次好值分别通过加粗和下划线表示.从实验结果来看,本文的方法超过了很多的传统迁移学习方法和一些深度方法,其中包括一些比较先进的传统迁移学习方法如DST-ELM和深度方法如JDOT等,这体现了本文方法的有效性.
| 表 1 在COIL20数据集上的准确率 Tab. 1 Accuracy on COIL20 |
在COIL20数据集构建两个跨域任务:COIL1→COIL2和COIL2→COIL1.其中,COIL1由角度为[0°, 85°]∪[180°, 265°]的灰度图像组成,而COIL2则由[90°, 175°]∪[270°, 355°]的灰度图像组成.实验结果如表 1所示,本文算法的平均准确率达89.3%, 比CORAL准确率高了7.3%.JDA简单地考虑边缘分布和条件分布适配反而比DTSL和CORAL效果好.由于两个域的差异仅仅来自图片的拍摄角度不同,所以该任务比其他数据集简单,过度拟合和破坏源域的基本结构反而会降低在该数据集的识别准确性.而本文采用group-lasso作为表示矩阵的稀疏约束,可以降低过拟合风险,从实验结果可以验证本文模型的有效性和鲁棒性.
在Office-Caltech 10数据集上,不论使用SURF特征还是DeCAF特征,本文算法都超过了对比的算法.采用SURF特征的平均准确率为51.2%,使用DeCAF特征,本文模型的平均准确率达90.6%,分别如表 2和表 3所示.与DTSL对比,使用SURF特征,本文模型的准确率提升了4.5%,如果使用DeCAF深度特征,本文模型将准确率从83.8%提升到了90.6%.由于DTSL只使用了一个表示矩阵,对源域的基本结构造成了一定的破坏,很难保存所有目的域的有用信息.所以本文模型采用两个表示矩阵解决了相关问题,从而提升了准确率.DICD通过MMD测量来减小两个域之间的差异,虽然考虑了减小类内距离和扩大类间距离,但是只通过MMD距离来判断差距也会对结构造成一定的破坏,本文算法在这个数据集上的效果仍然高于DICD,这也验证了本文算法具有不错的可判别性.
| 表 2 在Office-Caltech 10 (SURF)数据集上的准确率 Tab. 2 Accuracy on Office-Caltech 10(SURF) |
| 表 3 在Office-Caltech 10 (DeCAF)数据集上的准确率 Tab. 3 Accuracy on Office-Caltech 10(DeCAF) |
传统的方法在Office-Caltech 10数据集使用DeCAF特征都取得了不错的结果.虽然本文的方法与一些先进的传统方法(如DST-ELM)对比只提升了一点,但是与某些先进的深度方法(如JDOT)做对比时,本文的方法仍能显示出一定的优势,如表 4所示.
| 表 4 在Office-Caltech 10 (DeCAF)数据集上与深度方法对比准确率 Tab. 4 Comparison of accuracy of proposed method and deep methods on Office-Caltech 10 |
在ImageCLEF-DA数据集,使用ResNet50网络提取的深度特征.显然,本文算法的效果优于所有对比的算法.实验结果如表 5所示.
| 表 5 在ImageCLEF-DA数据集上的准确率 Tab. 5 Accuracy on ImageCLEF-DA |
为了进一步验证对作用于源域的表示矩阵施加group-lasso约束是否可以提高模型的识别准确率,进行了消融实验.RLlow-rank模型只对Zt矩阵进行低秩约束,对Zs矩阵不做约束.RLsparse模型对Zs矩阵做1-范数稀疏约束.RLgroup-lasso模型对Zs矩阵采用group-lasso约束.RLjoint1模型对Zs和Zt两个表示矩阵分别做1-范数和低秩约束,而RLjoint2模型对Zs和Zt两个表示矩阵分别做group-lasso和低秩约束.实验结果如表 6所示.通过对比RLgroup-lasso和RLsparse两个模型的实验结果,可以明显得出在域自适应表示学习中,稀疏约束采用group-lasso优于使用1-范数.通过RLjoint1的实验结果,仅仅对作用于源域的表示矩阵Zs采用group-lasso约束的分类准确率甚至高于同时使用1-范数和低秩约束.对比RLgroup-lasso和RLjoint2模型的实验结果,对Zt的低秩约束也是必不可少的,能够更好地保留样本特征的结构,从而提高准确率.
| 表 6 Office-Caltech 10 (SURF)数据集上消融实验的结果 Tab. 6 Results of ablation experiments on Office-Caltech 10(SURF) |
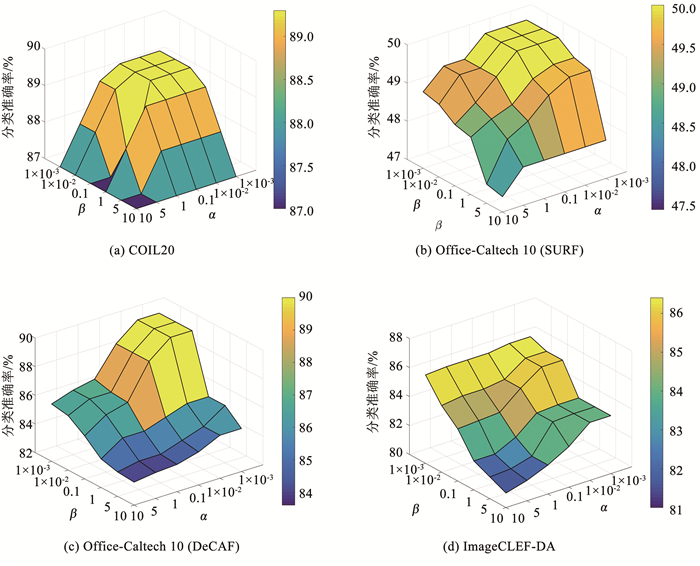
由式(7)可知,本文的总模型含有两个超参数α和β.为了分析不同参数对模型识别准确率的影响,在COIL20、Office-Caltech 10和ImageCLEF-DA 3个数据集进行了参数敏感度实验:在离散数据集[0.001, 0.01, 0.1, 1, 5, 10]的范围内改变两个超参数的值,观察识别准确率的变化,实验结果见图 3.从图 3可以观察到,参数α和β的取值在0.001~10大范围变化,对识别准确率造成的影响依然很小.所以虽然本文的模型需要调试两个超参数,但是两个超参数的选择却较简单,在相对大的范围内取值,都可以使本文的模型分类准确率达到一个很好的效果.
|
图 3 参数敏感度分析 Fig. 3 Parameter sensitivity analysis |
针对无监督域自适应问题,本文提出了一个新颖的表示学习算法.为了在学得的共同子空间下更好地保留源域和目的域样本的特有特征和结构,使用两个不同的表示矩阵分别作用于两个域,同时基于线性表示和最优传输相关理论为这两个表示矩阵设计不同的约束.大量的实验验证了本文模型的有效性和鲁棒性,在多个数据集上,本文方法的识别精度超过了很多先进的无监督域自适应方法.
| [1] |
LIU Hong, LONG Mingsheng, WANG Jianmin, et al. Transferable adversarial training: a general approach to adapting deep classifiers[C]// International Conference on Machine Learning. Long Beach: PMLR, 2019: 1
|
| [2] |
CHEN Yu, YANG Chunling, ZHANG Yan, et al. Deep conditional adaptation networks and label correlation transfer for unsupervised domain adaptation[J]. Pattern Recognition, 2020, 98: 107072. DOI:10.1016/j.patcog.2019.107072 |
| [3] |
ZHANG Lei, WANG Shanshan, HUANG Guangbin, et al. Manifold criterion guided transfer learning via intermediate domain generation[J]. IEEE Transactions on Neural Networks and Learning Systems, 2019, 30(12): 59. DOI:10.1109/TNNLS.2019.2899037 |
| [4] |
PEREIRA L A, TORRES R D S. Semi-supervised transfer subspace for domain adaptation[J]. Pattern Recognition, 2018, 75: 235. DOI:10.1016/j.patcog.2017.04.011 |
| [5] |
GRETTON A, BORGWARDT K, RASCH M, et al. A kernel method for the two-sample-problem[C]// International Conference on Neural Information Processing Systems. Cambridge: MIT Press, 2006: 513
|
| [6] |
PAN S J, TSANG I W, KWOK J T, et al. Domain adaptation via transfer component analysis[J]. IEEE Transactions on Neural Networks, 2011, 22(2): 199. DOI:10.1109/tnn.2010.2091281 |
| [7] |
LONG Mingsheng, WANG Jianmin, DING Guiguang, et al. Transfer joint matching for unsupervised domain adaptation[C]// 2014 IEEE Conference on Computer Vision and Pattern Recognition. Piscataway: IEEE, 2014: 1. DOI: 10.1109/CVPR.2014.183
|
| [8] |
LONG Mingsheng, WANG Jianmin, DING Guiguang, et al. Transfer feature learning with joint distribution adaptation[C]//2013 IEEE International Conference on Computer Vision. Piscataway: IEEE, 2013: 1. DOI: 10.1109/ICCV.2013.274
|
| [9] |
ZHANG Jing, LI Wanqing, OGUNBONA P. Joint geometrical and statistical alignment for visual domain adaptation[C]//2017 IEEE Conference on Computer Vision and Pattern Recognition. Piscataway: IEEE, 2017: 2. DOI: 10.1109/CVPR.2017.547
|
| [10] |
LONG Mingsheng, WANG Jianmin, DING Guiguang, et al. Adaptation regularization: a general framework for transfer learning[J]. IEEE Transactions on Knowledge and Data Engineering, 2014, 26(5): 1076. DOI:10.1109/TKDE.2013.111 |
| [11] |
FERNANDO B, HABRARD A, SEBBAN M, et al. Unsupervised visual domain adaptation using subspace alignment[C]//2013 IEEE International Conference on Computer Vision. Piscataway: IEEE, 2013: 1. DOI: 10.1109/ICCV.2013.368
|
| [12] |
SUN Baochen, SAENKO K. Subspace distribution alignment for unsupervised domain adaptation[C]//Proceedings of British Machine Vision Conference. Berlin: Springer, 2015: 24. DOI: 10.5244/C.29.24
|
| [13] |
DING Zhengming, FU Yun. Robust transfer metric learning for image classification[J]. IEEE Transactions on Image Processing, 2017, 26(2): 660. DOI:10.1109/TIP.2016.2631887 |
| [14] |
GONG Boqing, SHI Yuan, SHA Fei, et al. Geodesic flow kernel for unsupervised domain adaptation[C]// 2012 IEEE Conference on Computer Vision and Pattern Recognition. Piscataway: IEEE, 2012: 1. DOI: 10.1109/CVPR.2012.6247911
|
| [15] |
BAKTASHMOTLAGH M, HARANDI M T, LOVELL B C, et al. Unsupervised domain adaptation by domain invariant projection[C]//International Conference on Computer Vision. Piscataway: IEEE, 2013: 1. DOI: 10.1109/ICCV.2013.100
|
| [16] |
XU Yong, FANG Xiaozhao, WU Jian, et al. Discriminative transfer subspace learning via low-rank and sparse representation[J]. IEEE Transactions on Image Processing, 2016, 25(2): 850. DOI:10.1109/TIP.2015.2510498 |
| [17] |
ZHANG Lei, ZUO Wangmeng, ZHANG D. LSDT: latent sparse domain transfer learning for visual adaptation[J]. IEEE Transactions on Image Processing, 2016, 25(3): 1177. DOI:10.1109/TIP.2016.2516952 |
| [18] |
COURTY N, FLAMARY R, TUIA D, et al. Optimal transport for domain adaptation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2016, 39(9): 1853. DOI:10.1109/TPAMI.2016.2615921 |
| [19] |
BEN-DAVID S, BLITZER J, CRAMMER K, et al. A theory of learning from different domains[J]. Machine Learning, 2010, 79(1/2): 151. DOI:10.1007/s10994-009-5152-4 |
| [20] |
SUN Baochen, FENG Jiashi, SAENKO K. Return of frustratingly easy domain adaptation[C]// Thirtieth AAAI Conference on Artificial Intelligence. Palo Alto: AAAI, 2016: 2058
|
| [21] |
WANG Jindong, CHEN Yiqiang, HAO Shuji, et al. Balanced distribution adaptation for transfer learning[C]// 2017 IEEE International Conference on Data Mining. Piscataway: IEEE, 2017: 1129. DOI: 10.1109/ICDM.2017.150
|
| [22] |
LI Shuang, SONG Shiji, HUANG Gao, et al. Domain invariant and class discriminative feature learning for visual domain adaptation[J]. IEEE Transactions on Image Processing, 2018, 27(9): 4260. DOI:10.1109/TIP.2018.2839528 |
| [23] |
ZHANG Zhen, WANG Mianzhi, HUANG Yan, et al. Aligning infinite-dimensional covariance matrices in reproducing kernel Hilbert spaces for domain adaptation[C]// 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Piscataway: IEEE, 2018: 3437. DOI: 10.1109/CVPR.2018.00362
|
| [24] |
CHEN Yiming, SONG Shiji, LI Shuang, et al. Domain space transfer extreme learning machine for domain adaptation[J]. IEEE Transactions on Cybernetics, 2019, 49(5): 1909. DOI:10.1109/TCYB.2018.2816981 |
| [25] |
KRIZHEVSKY A, SUTSKEVER I, HINTON G E. ImageNet classification with deep convolutional neural networks[J]. Communications of the ACM, 2017, 60(6): 84. DOI:10.1145/3065386 |
| [26] |
COURTY N, FLAMARY R, HABRARD A, et al. Joint distribution optimal transportation for domain adaptation[Z]. arXiv: 1705.08848
|
 2021, Vol. 53
2021, Vol. 53


