在城市街道等密集行人场景中，自动驾驶车辆、机器人等运动主体需要根据其他行人的位置规划自身路径，通过对目标的位置预测得以保持安全距离并排除风险因素，行人未来位置预测的准确性对于运动主体的决策系统至关重要^[1].行人轨迹预测是一项复杂任务，由于每个行人自身的运动习惯有着天然差异，并且群体环境中存在人与人的交互，个人的运动模式会受到周围行人隐含的影响，人们会遵循社会规则方面的常识来调整自己的路线，运动主体需要预测他人的动作和社会行为^[2].构建具有较高可解释性和泛化能力的行人交互模式是轨迹预测问题的重点.

早期的行人轨迹预测使用手工设计特征的方法构建社会力量(social force, SF)^[3-4]模型，由此表示行人在运动过程中相互吸引和排斥的情况，然而完全依靠手工设计特征难以表示复杂场景中隐含的交互行为.近年来以数据驱动为主导的循环神经网络(recurrent neural network, RNN)编解码结构广泛应用于轨迹预测任务，具有代表性的是Alahi等^[5]使用长短期记忆网络(long short-term memory, LSTM)^[6]编码器-解码器结构，通过社交池化(social-pooling)获取不同距离行人间的依赖关系，从而表现个体间隐含的交互信息; Gupta等^[7]将轨迹预测看作序列生成问题，使用生成对抗网络(generative adversarial networks, GAN)体现轨迹的多模态性质，并且对历史轨迹编码进行最大池化(max-pooling)，生成社交可接受的轨迹; 在考虑多种物理特征的方面，Hasan等^[8]将获取的行人头部朝向特征纳入编码过程，其结果证实对周围行人的关注程度与自身视线方向具有高度相关性; 张志远等^[9]使用行人间的距离及方向信息构建注意力模型，并使用生成对抗方法训练轨迹生成; Amirian等^[10]使用infoGAN结构，通过优化输入隐含变量与输出轨迹分布的互信息来提升轨迹生成效果，并根据行人间的位置、方向、可接近的最小距离等物理特征进行注意力池化.

图神经网络(graph neural network, GNN)将深度学习应用在非欧几里得结构上，构建顶点和边表示对象间的关系，展现出良好的鲁棒性和可解释性，因此通过图拓扑结构建模行人之间的交互模式是一种有效的方式.Vemula等^[11]在轨迹预测问题上使用时空图网络构建交互模型，使预测目标对周围行人分配不同软注意力权重，获取时间和空间上的轨迹交互信息; 由于行人运动具有时间连续性，空间上的行人交互模式不仅与当前位置有关，还应考虑历史影响，Huang等^[12]基于图注意力网络(graph attention network, GAT)^[13]对周围行人分配注意力以进行运动LSTM编码; Kosaraju等^[14]使用图注意力网络表示空间交互关系，通过Bicycle-GAN生成多模态预测; Mohamed等^[15]根据行人位置构建邻接矩阵，通过图卷积神经网络(graph convolutional network, GCN) ^[16]构建交互模式，并使用时间外推卷积神经网络进行轨迹预测.然而，使用图注意力网络进行注意力分配由于依赖于高维特征间的相关性，其过程并不直观，且没有考虑图的结构关系; 另一方面，由于正常人眼关注度高的区域主要分布在视野中部，并且双眼水平视场角约为188°，在行走状态下人眼存在较大盲区，现有图网络所分配得到的交互注意力往往会错误地将盲区中的行人纳入其中.

考虑到图网络在建立交互模型中所具有的优势及存在的问题，本文提出一种新的基于图卷积神经网络的轨迹预测模型(trajectory prediction graph convolutional network, TP-GCN)用于构建行人间的交互模式并进行轨迹预测.算法使用图卷积神经网络处理编码过的高维行人轨迹特征，从而构建行人间的交互模式，根据盲区信息优化图卷积神经网络的邻接矩阵，并加强了对自身隐含交互模式的获取，同时使用深度图信息最大化方法将图结构的局部特征和整体特征间的互信息最大化，优化图网络的特征提取效果.在公开数据集上进行实验，结果表明本文算法可以取得较精确的预测效果，同时具有较强泛化效果及可解释性.

1 图卷积神经网络

卷积神经网络(convolutional neural network, CNN)利用固定尺寸的卷积核在图像上进行卷积操作并平移，从而提取图像中的所需特征.图卷积神经网络的原理与CNN类似，并将欧氏空间的卷积操作推广到非欧空间，对图结构中顶点的特征进行提取，以完成后续的顶点分类等任务.具体地，若无向图G=(V, E)中有n个顶点，顶点为V={V_i| $\forall $ i∈{1, 2, …, n}}，连接顶点的边为E={e_ij|$\forall $i, j∈{1, 2, …, n}}，每个顶点包含d维特征，则根据各顶点V之间的边E构成的n×n维的邻接矩阵A，通过训练卷积核系数，计算中心顶点的邻接顶点与卷积核的卷积结果，从而实现特征提取.单层GCN结构如式(1)所示

$ {H^{l + 1}} = \sigma \left( {{{\mathit{\boldsymbol{\tilde D}}}^{ - \frac{1}{2}}}\mathit{\boldsymbol{\tilde A}}{{\mathit{\boldsymbol{\tilde D}}}^{ - \frac{1}{2}}}{H^l}W_{\rm{g}}^l} \right), $

(1)

式中：$\mathit{\boldsymbol{\tilde A}} = \mathit{\boldsymbol{A}} + \mathit{\boldsymbol{I}}, \mathit{\boldsymbol{A}} $为图的邻接矩阵，I为单位矩阵; $ {{\mathit{\boldsymbol{\tilde D}}}^{ - \frac{1}{2}}}\mathit{\boldsymbol{\tilde A}}{{\mathit{\boldsymbol{\tilde D}}}^{ - \frac{1}{2}}}$为规范化对称邻接矩阵; H^l为l层顶点的特征; W_g^l为l层的图卷积权重，其将对应图顶点的特征维数d进行变换; σ为激活函数.

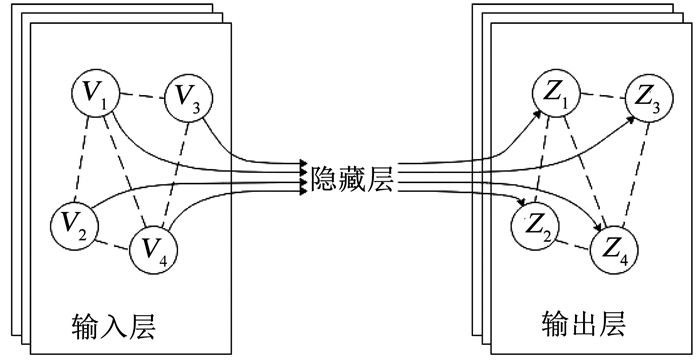
两层图卷积网络示意图如图 1所示，其中每层顶点的连接关系均由共享的邻接矩阵$ {\mathit{\boldsymbol{\tilde A}}}$表示，输入特征为V，通过两层GCN得到输出Z，如式(2)所示

$ Z = f(V,\mathit{\boldsymbol{\tilde A}}) = \sigma \left( {\mathit{\boldsymbol{\tilde A}}\sigma \left( {\mathit{\boldsymbol{\tilde A}}VW_{\rm{g}}^0} \right)W_{\rm{g}}^1} \right), $

(2)

式中f为两层GCN的特征传播公式.

2 本文算法

行人轨迹预测任务定义为，假设场景中有n个行人，通过给定t=1, 2, …, T_obs时刻场景内全部行人的观测轨迹坐标X=X₁, X₂, …, X_n，预测t=T_obs+ 1, …, T_final时刻全部行人的未来轨迹坐标$ \hat{X}=\hat{X}_{1}$, $ \hat{X}_{2}, \cdots, \hat{X}_{n}$.每个行人i=1, 2, …, n在t=1, 2, …, T_obs, T_obs+1, …, T_final时刻的真实坐标为X_i^t=(x_i^t, y_i^t)，行人i=1, 2, …, n在t=T_obs+1, …, T_final时刻的预测坐标为$\hat{X}_{i}^{t}=\left(\hat{x}_{i}^{t}, \hat{y}_{i}^{t}\right) $，预测时长为T_pred=T_final-T_obs.

轨迹预测任务中任意时刻的每个行人i都与不同数量和运动状态的其他行人存在交互关系，行人间内在的影响方式复杂且随时间而变化，若以向量表示每个行人的运动状态，那么同一时刻相关联的所有行人构成了一组典型的图结构数据.

本文提出的轨迹预测模型TP-GCN中，将行人作为图结构中的顶点，利用GCN在图结构中良好的特征提取能力来获取行人间的交互关系，并通过最大互信息优化方法进一步提升GCN的运算效果，从而完成轨迹预测.算法框图见图 2.

如图 2所示，TP-GCN由4个模块构成，分别为：1)轨迹编码模块：将原始轨迹使用LSTM编码得到轨迹运动特征; 2)图卷积神经网络交互模块：通过原始轨迹计算改进的邻接矩阵，将轨迹运动特征输入GCN计算轨迹交互特征; 3)互信息最大化图网络模块：最大化GCN输出中局部特征与全局特征间的互信息，从而优化GCN的特征提取效果; 4)轨迹预测模块：将提取的轨迹运动特征与轨迹交互特征进行LSTM解码，得到轨迹预测结果.

2.1 轨迹编码模块

该模块的输入为多帧历史轨迹图像，每帧历史轨迹图像包括若干条轨迹，各帧间轨迹的数目相同，轨迹编码模块对每条轨迹的相对位置变化进行M-LSTM编码，输出轨迹运动特征.为了获取单一轨迹中具有较强表达能力的特征^{[5, 7-8]}，首先将前后帧之间单个轨迹的相对位置变化ΔX_i^t=(x_i^t－x_i^t－1, y_i^t－y_i^t－1)编码为固定长度的运动向量q_i^t, 如式(3)所示

$ q_i^t = \phi \left( {\Delta X_i^t,{\mathit{\boldsymbol{W}}_{\rm{q}}}} \right), $

(3)

式中，ϕ为相对位置编码函数，W_q为相对位置编码权重.随后使用LSTM结构进行M-LSTM编码以获取轨迹运动特征m_i^t，如式(4)所示

$ m_i^t = {f_{{\rm{M}} - {\rm{LSTM}}}}\left( {m_i^{t - 1},q_i^t,{\mathit{\boldsymbol{W}}_{\rm{m}}}} \right), $

(4)

式中：f_M-LSTM为编码器M-LSTM; m_i^t-1为M-LSTM在t-1时刻的隐藏状态，隐藏层单元个数为32;W_m为M-LSTM的编码权重.

2.2 图卷积神经网络交互模块

由于行人的轨迹受到周围行人运动模式隐含的影响，仅对每个轨迹分别进行编码难以完整表达场景内多个轨迹的复杂运动模式，需要构建合理的模型表达行人间交互模式.使用图结构G^t=(V^t, E^t)建立t时刻行人间的交互模型，将行人作为图结构中顶点的集合V^t，行人间的交互关系为边的集合E^t，其表达式为

$ {V^t} = \left\{ {V_i^t\mid \quad \forall i \in \{ 1,2, \cdots ,n\} } \right\}, $

(5)

$ {E^t} = \left\{ {e_{ij}^t\mid \quad \forall i,j \in \{ 1,2, \cdots ,n\} } \right\}. $

(6)

式中：V_i^t为第i个顶点所具有的特征; e_ij^t为顶点之间值为0或1的边，若i与j间存在交互关系则为1，否则为0.

将每一个时间点中顶点V^t的连接关系E^t表示为邻接矩阵A^t，所有时刻邻接矩阵的集合为A.行人间相互的影响程度随着距离的增加而减小^[15]，本文将邻接矩阵A^t中的边e_ij^t根据距离不同分配的权重a_ij^t，如式(7)所示

$ a_{ij}^t = \left\{ {\begin{array}{*{20}{l}} {1/{{\left\| {X_i^t - X_j^t} \right\|}_2},{{\left\| {X_i^t - X_j^t} \right\|}_2} \ne 0;}\\ {0,{\rm{ 其他}}{\rm{. }}} \end{array}} \right. $

(7)

由于个体在运动中存在较大盲区，为了避免盲区中行人的干扰，故应主动筛除为盲区中的其他行人分配交互权重的情况，本文中假设行人的盲区范围为速度方向两侧各＞90°的范围.如图 3所示，在t时刻，X₁=(x₁, y₁)，X₂=(x₂, y₂)，ΔX₁=(x₁^′, y₁^′)，ΔX₂=(x₂^′, y₂^′)，背向而行的两个行人均处于对方的盲区中.

此时两个行人的速度向量与相对位置向量满足式(8)

$ \left[ {\Delta {X_1}\left( {{X_1} - {X_2}} \right)} \right]\left[ {\Delta {X_2}\left( {{X_1} - {X_2}} \right)} \right] < 0. $

(8)

由以上情况推广，根据位置和速度方向信息，将行人背离情况下的边权重a_ij^t设置为0，此时a_ij^t如式(9)所示

$ a_{ij}^t = \left\{ {\begin{array}{*{20}{l}} {1/{{\left\| {X_i^t - X_j^t} \right\|}_2},}\\ {\left[ {\Delta X_i^t\left( {X_i^t - X_j^t} \right)} \right]\left[ {\Delta X_j^t\left( {X_i^t - X_j^t} \right)} \right] > 0;}\\ {0,{\rm{ 其他}}{\rm{. }}} \end{array}} \right. $

(9)

将经过M-LSTM编码的轨迹运动特征m_i^t作为图卷积网络中顶点的输入特征V_i^t，因为LSTM的记忆门使得若干时刻前m_i的影响依然保留，而行人在此段时间中的轨迹隐式地表现了其他轨迹的交互影响，间接体现了交互模式，故在图网络中对中心顶点分配额外权重，增加对行人自身所含的隐式交互信息的提取，得到t时刻改进的邻接矩阵A_o^t，如式(10)所示

$ \mathit{\boldsymbol{A}}_{\rm{o}}^t = {\mathit{\boldsymbol{\tilde D}}^{ - \frac{1}{2}}}{\mathit{\boldsymbol{\tilde A}}^t}{\mathit{\boldsymbol{\tilde D}}^{ - \frac{1}{2}}} + k\mathit{\boldsymbol{I}}\mathit{\boldsymbol{.}} $

(10)

式中, k为中心顶点额外权重系数，本文使用k=2;I为单位矩阵.

本文将两层图卷积网络相叠加，通过两层GCN结构得到第i条轨迹的输出特征

$ Z_i^t = {f^\prime }\left( {V_i^t,\mathit{\boldsymbol{A}}_{\rm{o}}^t} \right) = \sigma \left( {\mathit{\boldsymbol{A}}_{{\rm{o}}i}^t\sigma \left( {\mathit{\boldsymbol{A}}_{\rm{o}}^tV_i^t\mathit{\boldsymbol{W}}_{\rm{g}}^0} \right)\mathit{\boldsymbol{W}}_{\rm{g}}^1} \right). $

(11)

式中，σ为激活函数PReLU; W_g⁰、W_g¹为第1、2层GCN的权重.场景内的整体输出Z^t为

$ {Z^t} = f\left( {{V^t},\mathit{\boldsymbol{A}}_{\rm{o}}^t} \right) = \sigma \left( {\mathit{\boldsymbol{A}}_{\rm{o}}^t\sigma \left( {\mathit{\boldsymbol{A}}_{\rm{o}}^t{V^t}\mathit{\boldsymbol{W}}_{\rm{g}}^0} \right)\mathit{\boldsymbol{W}}_{\rm{g}}^1} \right). $

(12)

对图网络输出Z_i^t进行S-LSTM编码，从而得到轨迹交互特征

$ s_i^t = {f_{{\rm{S}} - {\rm{LSTM}}}}\left( {s_i^{t - 1},Z_i^t,{\mathit{\boldsymbol{W}}_{\rm{s}}}} \right). $

(13)

式中：f_S-LSTM为编码器S-LSTM; s_i^t-1为S-LSTM在t-1时刻的隐藏状态，隐藏层单元个数为32;W_s为S-LSTM编码权重.

2.3 互信息最大化图网络模块

由于受到周围行人和潜在社交规则的影响，群体中个体的运动模式倾向于场景内所有个体的平均运动模式.本文使用深度图信息最大化方法^[17]最大化GCN输出局部特征与全局特征间的互信息，使得局部特征可以获得接近全局特征的向量表示，也就意味着在行人间的交互模型中，每个个体行人学习到了场景内全体行人所共有的运动模式.

本文的深度图信息最大化方法中，局部特征为第2层GCN的输出特征Z_i^t，全局特征为所有局部特征Z^t的平均值${{\vec S}_t} $，表示为

$ {{\vec S}^t} = R\left( {{Z^t}} \right) = {\mathop{\rm softmax}\nolimits} \left( {\frac{1}{n}\sum\limits_{i = 1}^n {Z_i^t} } \right), $

(14)

式中R为读取函数.

为了使局部特征Z_i^t与全局特征${{\vec S}_t} $间的互信息最大化，首先利用腐蚀函数C在保留原有图结构中顶点的连接方式的前提下添加扰动，对每个顶点的特征进行随机排序，从而制作负样本$\left(\tilde{V}_{i}^{t}, \boldsymbol{A}_{\mathrm{o}}^{l}\right)= $ $ C\left(V_{i}^{t}, \boldsymbol{A}_{\mathrm{o}}^{t}\right)$; 然后负样本通过两层GCN，得到局部特征$ \tilde{Z}_{i}^{t}=f\left(\tilde{V}_{i}^{t}, \boldsymbol{A}_{\mathrm{o}}^{t}\right)$; 随后使用判别器D判别局部特征Z_i^t、$\tilde{Z}_{i}^{t} $包含于全局特征${{\vec S}_t} $所在范围的概率分数，即判别$ D\left(Z_{i}^{t}, \vec{S}^{t}\right) $与$ D\left(\tilde{Z}_{i}^{t}, \vec{S}^{t}\right)$; 最后通过训练使判别器尽可能给正样本打高分且给负样本打低分，完成对GCN特征提取效果的优化，训练判别器的损失函数L_inf如式(15)所示

$ \begin{array}{l} {L_{{\rm{inf}}}} = \frac{1}{{2n}}\left( {\sum\limits_{i = 1}^n f \left( {\mathit{\boldsymbol{V}},{\mathit{\boldsymbol{A}}_{\rm{o}}}} \right)\left[ {\log D\left( {{Z_i},\vec S} \right)} \right] + } \right.\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {\sum\limits_{j = 1}^n f \left( {\mathit{\boldsymbol{\tilde V}},{\mathit{\boldsymbol{A}}_{\rm{o}}}} \right)\left[ {\log \left( {1 - D\left( {{{\tilde Z}_j},\vec S} \right)} \right)} \right]} \right). \end{array} $

(15)

2.4 轨迹预测模块

为了表示真实场景中的不确定性，本文从标准正态分布N(0, 1)中抽取噪声z ^[7]，将z与轨迹运动特征和轨迹社交特征叠加，得到T_obs时刻的轨迹解码特征$ d_{i}^{T_{\mathrm{obs}}}=m_{i}^{T_{\mathrm{obs}}}\left\|s_{i}^{T_{\mathrm{obs}}}\right\| z$.使用D-LSTM将$ d_{i}^{T_{\mathrm{obs}}}$解码得到下一时刻的轨迹解码特征$ d_{i}^{T_{\mathrm{obs}}+1}$，如式(16)所示

$ d_i^{{T_{{\rm{obs}}}} + 1} = {f_{{\rm{D}} - {\rm{LSTM}}}}\left( {d_i^{{T_{{\rm{obs}}}}},q_i^{{T_{{\rm{obs}}}}},{\mathit{\boldsymbol{W}}_{\rm{d}}}} \right). $

(16)

式中：f_D-LSTM为解码器D-LSTM; $q_{i}^{T_{\mathrm{obs}}} $为式(4)中编码过的运动向量，T_obs+1时刻起所使用的位置为预测位置; W_d为D-LSTM权重.利用$ d_{i}^{T_{\mathrm{obs}}+1}$计算每个时间点的预测未来轨迹

$ \hat X_i^{{T_{{\rm{obs}}}} + 1} = \left( {\hat x_i^{{T_{{\rm{obs}}}} + 1},\hat y_i^{{T_{{\rm{obs}}}} + 1}} \right) = \delta \left( {d_i^{{T_{{\rm{obs}}}} + 1}} \right). $

(17)

式中δ为线性层.因为未来轨迹存在多种合理分布，本文使用多样损失函数^{[7, 12]}生成多个轨迹样本，进而选取轨迹样本中与真实轨迹间L2距离最小的预测轨迹，多样损失函数L_variety如式(18)所示

$ {L_{{\rm{variety }}}} = \mathop {\min }\limits_p {\left\| {{X_i} - \hat X_i^{(p)}} \right\|_2}. $

(18)

式中：X_i为t=T_obs+1, …, T_final时刻真实未来轨迹序列; $\hat{X}_{i}^{p} $为t=T_obs+1, …, T_final时刻的预测序列; p为训练时生成的样本数，本文使用p=20.本文在训练神经网络模型的同时，使用深度图信息最大化方法对模型进行优化，最终损失函数如式(19)所示

$ L_{\text {total }}=L_{\text {variety }}+L_{\text {inf }} $

(19)

3 实验与分析

实验基于PyTorch 1.1建立网络模型，使用Adam优化器进行参数优化，LSTM学习率为0.01，GCN学习率为0.03，判别器D学习率为0.001，批处理大小为64，训练数据集训练轮数为500，单个RTX 2 080 Ti GPU进行训练，生成测试样本数N=20.

本文在公开轨迹预测数据集ETH^[18]和UCY^[19]上进行实验，ETH包含ETH和HOTEL 2个子数据集，UCY包含UNIV、ZARA1和ZARA2 3个子数据集，所有数据集均使用俯拍视角，包含了不同场景中1 500多名行人的运动轨迹.使用世界坐标系，将行人表示为坐标点，获取时间间隔为0.4 s的坐标序列.保留同时存在n个目标的序列，即每段序列中行人的数量保持不变.采用留一法^[5]，即在4个数据集上进行训练和验证，在剩下的一个数据集上进行测试.

本文使用两种基本评价指标：

1) 平均偏移误差(ADE)：全部时间点的预测序列与真实序列间的均方误差，单位为m.

2) 最终偏移误差(FDE)：预测结束时刻的预测序列与真实序列间的误差，单位为m.

3.1 定量分析

定量分析使用不同算法在相同数据集上进行对比实验，并使用除去了部分模块的本文算法进行消融实验，具体分析如下.

3.1.1 算法对比

为评估TP-GCN的准确性，选取了多种对比算法，分别是S-LSTM^[5]、S-Atten ^[11]、S-GAN^[7]、SoPhie^[2]、Next^[20]、S-ways^[10]、Social-BiGAT^[14]、STGAT^[12]，观测时长T_obs=8(3.2 s)，预测时长T_pred=12(4.8 s)，使用ADE和FDE进行评价，所有生成多样本轨迹的算法均产生20个预测样本，本文算法与其他对比算法在5个数据集上的预测精度比较结果见表 1，表中黑体为表现最好的预测结果.

由表 1可以看出，TP-GCN在HOTEL和UNIV数据集上两个指标均优于其他所有算法，并在5个数据集的平均ADE和FDE并列第一.相较于SoPhie和Next使用环境信息和行人姿态信息，TP-GCN仅使用坐标序列信息而没有使用环境信息，更利于在多种场景中泛化; TP-GCN在ETH数据集上效果一般，原因在于ETH的测试集较小，各种算法普遍在ETH数据集上效果一般，但相较于使用图网络的Social-BiGAT和STGAT，TP-GCN在HOTEL、UNIV、ZARA1和ZARA2这4个数据集上表现更好，同时取得了良好的稳定性.与对比算法相比，一方面，本算法使用图卷积神经网络建立交互模式，利用盲区信息筛除错误交互行为的干扰，并且加强了对行人自身运动习惯的挖掘，使算法具有较强的可解释性; 另一方面，本算法通过深度图信息最大化方法，使得场景中个体行人与全体行人间的运动模式一致程度更高，从而在多种场景下依然具有较好的鲁棒性.综上所述，本文算法的总体预测精度较高.

3.1.2 消融实验

为评估TP-GCN各个部分的作用，调整多个指定模块，其中算法1去掉最大互信息模块，算法2去掉邻接矩阵A，算法3没有使用盲区信息优化A，算法4单位矩阵系数k=0，算法5训练样本数p=1，测试样本数N=1，算法6训练样本数p=1，测试样本数N=20，观测时长T_obs=8(3.2 s)，预测时长T_pred=12(4.8 s)，使用ADE和FDE进行评价，本文算法与调整指定模块后的算法在5个数据集上的预测精度比较结果见表 2.表中黑体为表现最好的预测结果.

由表 2可以看出，与算法1做对比，由于最大互信息模块进行了图网络输出结果的局部特征和全局特征间的互信息最大化，使得受到周围行人交互影响的个体行人运动模式更趋近于周围所有人的平均运动模式，符合环境中集体所默认的潜在社交规则，TP-GCN的预测结果全面优于对比算法1.与算法2、3、4做对比，TP-GCN通过构建基于盲区信息的邻接矩阵并外加单位矩阵构建交互模式，既考虑了周围其他行人直接的交互影响，又提取了自身所受到的隐式交互影响.3种对比算法整体表现均不如TP-GCN，而值得注意的是算法3和4在UNIV数据集中表现优于本文算法，本文理解为由于此数据集中行人远密集于其他数据集并且行人转头环顾四周情况明显增多，周围行人的直接交互影响更为明显，在此情景下本文算法单位矩阵权重过大且盲区范围过大，但另一方面，这也恰恰说明交互权重在密集场景中的重要性.与算法5、6做对比，TP-GCN考虑了轨迹的多样性和不确定性，预测效果明显优于算法5和算法6，在同为产生20个预测样本的情况下比算法6的ADE提升了8.5%，FDE提升了15.3%.通过消融实验的对比结果可知，本文所使用算法的预测精度较高.

3.2 定性分析

通过对轨迹序列进行可视化，进一步分析本文所提出算法的可解释性.从ZARA2测试数据集中提取本文算法所使用和生成的轨迹，实线轨迹为观察轨迹，时长为3.2 s，点划线轨迹为真实未来轨迹，虚线为预测未来轨迹，时长为4.8 s，轨迹可视化结果见图 4.

从图 4(a)、(b)中可以观察到，在密集行人场景中，处于图像右侧的个体行人自右向左运动，左侧的群体行人并排自左向右运动，此时右侧行人通过，由于右侧行人经过了左侧行人原本朝向的方向，左侧群体的路径受到了轻微影响.从图 4(c)、(d)中可观察到，处于相向行走的两组行人，相遇时两组人依照社会规则相互绕行，期间基本没有改变组内个体间的距离关系; 另一方面，预测最终时刻行人的盲区范围如图中矩型阴影范围所示，由于此时背向而行的行人位于彼此的盲区之中，没有相互的交互影响，故而视觉盲区中的交互信息被筛除，行人保持原有方向运动.从图 4(e)、(f)中可以看出，图 4(e)右侧的两名并行的行人和图 4(f)右侧同向而行的3个行人，受到周围不经过自身路线的行人影响较小，即原本沿近乎直线行走的行人，能够察觉附近的行人不妨碍自身运动时，行人可以保持原有路线运动，这也与人的运动习惯相符.通过分析预测结果，证明本文算法能够基于交互信息做出与真实行为接近的符合行人习惯的预测.

4 结论

本文提出了一种基于视觉盲区信息和互信息最大化图卷积神经网络的算法TP-GCN来建立行人间的交互模式并进行轨迹预测.该算法克服了图注意力网络构建交互模式不直观的问题，筛除了盲区中行人的交互影响，综合考虑了行人间直接的交互模式和隐含的交互信息，并使得个体运动符合群体运动的社交规则，具有良好的可解释性和泛化性能.在公开数据集ETH和UCY上与目前先进的算法进行对比，本文算法的整体预测精度较高，同时消融实验和预测轨迹的可视化也显示了本文算法的有效性及良好的可解释性.