2. 西北工业大学 航空学院,西安 710072;
3. 西北工业大学 机电学院,西安 710072
2. School of Aeronautics, Northwestern Polytechnical University, Xi'an 710072, China;
3. School of Mechanical Engineering, Northwestern Polytechnical University, Xi'an 710072, China
一个产品的主要功能是靠若干关键功能零件的装配结构实现的,关键功能零件的设计是产品设计的核心,同时也是重用过程中最重要的设计资源.然而,当前存在的主要方式是由设计人员根据产品设计情况与自身设计经验进行人工识别,费时费力还具有很强的主观性,缺少自动识别和发现装配体模型中关键零件的手段和方法.在重用装配体模型结构时需要人工分析与查找,降低了模型的重用效率,增加了模型重用难度和时间成本.所以在产品设计过程中,查找到已有模型的关键功能零件对产品设计重用具有重要意义.
在三维装配模型重用时,相较于装配体模型检索,识别出嵌入在装配体模型中的隐性知识(可重用局部结构[1-4]或者关键功能零件[5])更为重要.对于设计新手而言,快速识别出具有关键功能的零件是很困难的.Belhagj等[6]通过提取装配体模型各零件间的邻接关系构建属性邻接矩阵,综合考虑零件边界面数、零件的邻接零件数和零件体积进行评价,获得各零件在装配体模型中所占的重要度.Ma等[7]提出了一种同时考虑顾客需求和产品可靠性的零件识别方法,但该方法识别出的是根据客户要求需要改善的局部零件,并不一定是关键功能零件.董士龙等[8]提出了通过产品零件的无向连接图,找出复杂产品中的“连接关键件”和“识别关键件”.许评等[9]进一步利用复杂网络理论从装配拓扑结构方面评价零件的重要程度筛选关键零件.但这两种方法都忽略零件自身属性的影响,评价结果存在误差.为了从装配模型中识别具有关键功能的重要结构单元,Han等[10]建立了一个双层关键功能零件的评价模型,从装配拓扑结构和零件多源属性两个方面综合评价装配零件,评定装配体的关键功能零件.这类识别隐性知识的方法需要进行大量的专家打分工作,对于用户或者设计新手而言很难操作.并且不同类型的模型在分析时需要考虑的因素也不尽相同,使用同一评价标准影响结果准确度.
为改善以上情况,本文提出了一种较“专家打分法”更为客观的识别方法,以装配体模型自身数据作为驱动代替主观赋值,获得零件重要度评价所需权重参数.利用复杂网络对装配体模型进行表示,使用粗糙集理论在子装配零件的装配拓扑结构层和零件自身属性层两个层面对装配体模型进行知识挖掘,获得相对约简属性及其对应属性权重,综合评价后获得关键功能零件的排序.经蜗轮蜗杆减速器模型验证,本文的方法实用可靠,具有较大的工程应用价值.
1 粗糙集理论粗糙集理论是由波兰数学家Pawlak于1982年提出的,它是一个处理不确定性和不完整性的数学工具.该理论依靠数据本身驱动,对问题的不确定性的描述或处理更加客观[11].
定义1 (信息系统)信息系统作为主要处理对象可被视为是一个四元组,现有系统S={U, A, V, f},其中U={x1, x2, …, xn}为对象的非空有限集合,称为论域,A是属性集合,V是对应各属性的取值集合,f是U×A→V的映射,是一个信息函数,即为每个对象的每个属性赋予一个信息值.若
常用的属性约减算法为启发式算法,先求解决策信息表的相对核,然后再往相对核中添加重要的属性,从而最后获得相对约简集.
定义2 (相对核)在知识表达系统S={U, A}中,x, y∈U,对于任意子集
| $ \operatorname{IND}(I)=\{(x, y) \in U \otimes U \mid a(x)=a(y), \forall a \in A\}. $ |
给定一个知识库K={U, S}和知识库上的2个等价关系
| $ \operatorname{POS}_{\operatorname{IND}(P-\mid R\})}(\operatorname{IND}(Q)) \neq \operatorname{POS}_{\operatorname{IND}(P)}(\operatorname{IND}(Q)) $ |
则称R为P中Q必要的,P中所有Q必要的知识组成的集合称为P的Q核,或称为P的相对于Q的核,也可称为P的相对Q核,记为COREQ(P).
定义3 (重要度)若条件属性集C={c1, c2, …, cm}, D为决策属性集,B为相对核,则属性ci的重要度定义为
| $ \operatorname{sig}\left(c_{i}, B\right)=\left|\operatorname{POS}_{B \cup\left\{c_{i}\right\}}(D)\right|-\left|\operatorname{POS}_{B}(D)\right|. $ |
定义4 (相对约简)给定一个知识库K={U, S}和知识库上的2个等价关系
1) G是Q独立的,即G是P的Q独立子集;
2) POSG(Q)=POSP(Q).
则称G是P的一个Q约简,或称G是P相对于Q的一个约简,记为G∈REDQ(P).其中,REDQ(P)表示P的全体Q约简组成的集合.
本文使用的是基于Pawlak属性重要度的属性约简算法[11],其伪代码如下:
| 表 |
获得属性约减后,使用基于重要度的属性权重计算方法对每个条件属性的权重w(c)进行计算,其公式为
| $ w(c)=\frac{\operatorname{sig}(c, B)}{\sum\limits_{a \in C} \operatorname{sig}(a, B)}, $ |
式中sig(c, B)为属性c的重要度.
1.2 连续属性离散化连续属性的离散化可以缩减运算时间,还能在一定程度上抑制噪声,使数据具有更强的抗干扰性,是数据处理非常重要的环节.一个装配体模型包含的零件种类、大小各不相同,导致提取的数据分布密度是不均匀的,需要对信息系统进行离散化处理.本文采用基于动态层次聚类的离散化算法,无需用户提供簇的数目或聚集度的阈值等信息,可以自动地调整阈值的步长[12].其简要介绍如下:
设
| $ \alpha_{i}=\frac{\operatorname{card}\left(\bar{C}_{i}\right)}{\operatorname{card}(U)}. $ |
式中
因为决策表中属性之间出现不相容情况可视为统计独立的,所以,整个决策表的不相容度αT可表示为
事实上,决策表中不同属性之间的相容度存在一定差异.因此,在实际处理中,要求每个属性的不相容度αi落在
| $ \left|\alpha_{i}-\hat{\alpha}\right| \leqslant \beta, $ |
式中β为预先给定的误差.
基于动态层次聚类的连续属性离散化算法[12]
具体步骤如下:
第1步 为αT、β和δ进行赋值;
第2步 计算;
第3步 对于i=1, 2, …, m,重复以下过程:
a) 对条件属性ci以及初始阈值δi,通过层次聚类法可得属性ci关于论域U的一种划分;
b) 计算该属性的不相容度αi;
c) 判断
d) 若
第4步 输出满足误差条件的划分后的决策表.
2 基于粗糙集的装配模型关键功能零件识别装配体中的零件可分为两大类: 1)紧固零件:用于紧固连接的一类零件,主要包括螺栓、螺钉、螺母、垫片、键、销、轴承等起紧固、密封作用的零件; 2)功能零件:除紧固零件外的、具有一定的功能特性的零部件.其中,将具有较高重要度空间位置、较高装配影响范围及关键自身特性(加工、装配中的属性等)的功能零件视为关键功能零件.
为实现关键功能零件的识别,本文从装配模型的装配网络拓扑结构(简称“拓扑”层)和零件自身属性(简称“零件属性”层)两个层面考虑,利用粗糙集理论及相关方法计算各零件重要度评价所需权重参数,最终通过综合评价获得关键子装配功能零件的重要度排序,其流程见图 1.整个过程主要包括3个阶段.
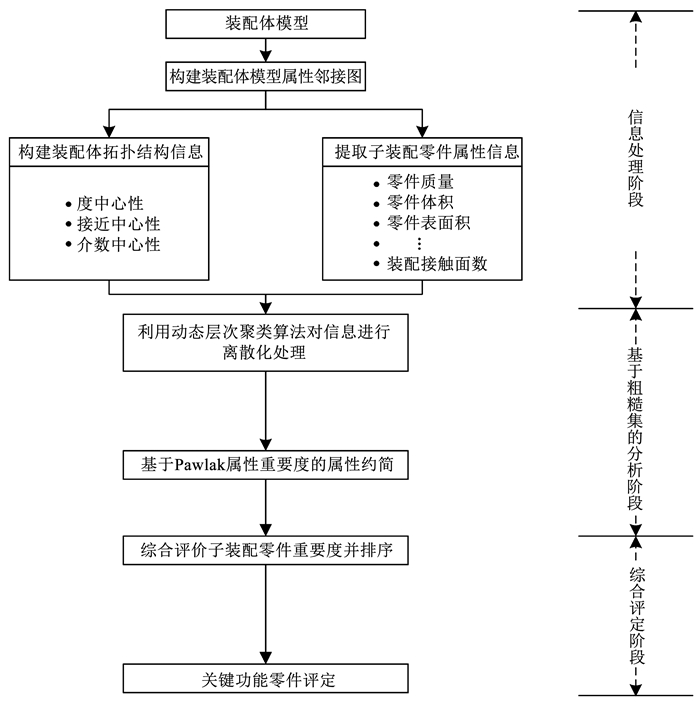
|
图 1 关键子装配零件评定流程 Fig. 1 Evaluation process of key subassembly functional parts |
1) 信息处理阶段:提取子装配零件属性信息,包括零件质量、零件体积和零件表面积等,根据子装配零件邻接矩阵计算拓扑结构信息包含的相关属性(例如:度中心性、接近中心性和介数中心性);
2) 基于粗糙集的分析阶段:利用基于动态层次聚类的方法对拓扑层信息和零件属性层信息分别进行离散化处理,通过基于Pawlak属性重要度的属性约简方法对离散化后的各属性进行约简,获得最终评定所需属性及各属性权重;
3) 综合评定阶段:依据子装配零件在拓扑层与属性层的重要度评价结果,实现装配体中功能零件重要度的综合排序.最后,筛选、评定装配体中具有较高重要度的功能零件作为该装配体的关键功能零件.
2.1 装配模型数学表示假设一个三维CAD装配模型P由N个子装配零件组成,则P={p1, p2, …, pN},其中,不同子装配零件之间具有复杂的装配约束关系.利用复杂网络的相关理论和方法[13],可以建立复杂机械产品的装配模型,表示为
| $ G=(V, E, V A, E A). $ |
式中:V={p1, p2, …, pN}为节点集合即子装配零件集合,E={(pi, pj)|pi∈V, pj∈V}为节点间的连接关系即子装配零件间的装配约束关系. VA、EA分别表示子装配零件属性邻接图中的节点属性和边属性.VA是一个五元组,VA=(ptype, pnum, pra, ppnum, pwei, pvol),其中每一项代表零件的一个属性.ptype为零件类型,如功能件、连接件等; pnum为与该零件接触的面数量; pra为零件的相对表面积; ppnum为与该零件接触的零件数量; pwei为零件重量; pvol为该零件的体积.EA为边属性集合,主要包括零件对之间的连接类型、接触面的类型等装配关系.
2.2 装配模型的拓扑结构特性分析在装配模型中,根据零件间是否存在邻接关系可构建关于零件的属性邻接矩阵A[10].若零件i和零件j之间存在面接触连接关系,则aij=1;否则,aij=0.零件邻接矩阵A可表示为N×N的方阵,其中N为零件个数,有
| $ \boldsymbol{A}=\left(a_{i j}\right)_{N \times N}. $ |
在复杂网络中,节点的重要性不但与自身的属性有关联,也与该节点邻居节点关系有关.节点在复杂网络系统的重要程度可以通过节点的度数中心性、紧密度中心性和介数等参数进行有效衡量[14].
1) 度中心性(Di)
零件i的度中心性(即度数)表示在装配体中与零件i存在面接触关系的零件总数.度数越大,表明零件i在装配体中连接的零件越多.零件i的度数由属性邻接矩阵A计算可得
| $ D_{i}=\sum\limits_{j=1}^{n} a_{i j}. $ | (1) |
2) 接近中心性(Ci)
接近中心性用来度量网络中节点通过网络对其他节点施加影响的能力[15].节点越居于网络中心,说明该节点在网络中就越重要.接近中心性的数值越大,表明该零件对与之相连接的零件的影响能力越大,也说明该零件在装配体中越重要.
| $ C_{i}=\frac{n-1}{\sum\limits_{j=1}^{n} d_{i j}}, $ | (2) |
式中dij为节点i到节点j的最短距离,可采用Dijkstra算法计算[16].
3) 介数中心性(Bi)
节点介数中心性表示节点在整个复杂网络结构中的影响范围程度.介数的值越大,表示该节点在网络中的影响力越大.在装配模型中,零件介数可用来表征零件对装配体中其他零件的影响范围程度.零件节点i的介数越大,说明零件i在装配体中的影响范围越大.
| $ B_{i}=\sum\limits_{u <v} \frac{m_{u v}^{i}}{g_{u v}}, $ | (3) |
式中guv为节点u到节点v之间最短路径数,muvi为节点u和节点v之间经过节点i的最短路径数.
4) 聚集系数(Cli)
聚集系数(也称群聚系数、集群系数)是用来描述网络中的节点之间结集成团的程度的系数.具体来说,是一个节点的邻接节点间相互连接的程度.该系数越大,表明零件i与相邻零件j的聚集程度越高.
| $ C l_{i}=\frac{2 \tau_{i}}{k_{i}\left(k_{i}-1\right)}, $ | (4) |
式中ki为与节点i相邻的节点个数,τi为与节点i存在邻接关系的边数.
2.3 关键子装配功能零件识别方法从拓扑结构和零件属性两个方面分别进行重要度评价,最终获得零件的综合重要度评价.
对于拓扑层,重要度评价公式如下:
| $ W_{{\rm{t}}, i}=w_{{\rm{t}}1} \frac{D_{i}}{\sum\limits_{i=1}^{N} D_{i}}+w_{{\rm{t}}2} \frac{C_{i}}{\sum\limits_{i=1}^{N} C_{i}}+w_{{\rm{t}}3} \frac{B_{i}}{\sum\limits_{i=1}^{N} B_{i}}+w_{{\rm{t}}4} \frac{C l_{i}}{\sum\limits_{i=1}^{N} C l_{i}}, $ | (5) |
式中:Wt, i为零件i在拓扑层的重要度; Di、Ci、Bi和Cli分别为零件i的度中心性、接近中心性、介数中心性和聚集系数; wt1、wt2、wt3和wt4为拓扑层属性对应的权重,且满足wt1+wt2+wt3+wt4=1.
零件在装配体中的重要性不仅表现在装配拓扑结构方面,还反映在零件自身属性的差异.对于复杂机械产品,零件的重要性主要表现在零件的装配接触面数、表面积、体积、材料及重量等属性方面[10].对于零件属性层,重要度可表示为
| $ \begin{array}{c} W_{\mathrm{s}, i}=w_{\mathrm{s} 1} \frac{p_{\mathrm{num}, i}}{\sum\limits_{i=1}^{N} p_{\mathrm{num}, i}}+w_{\mathrm{s} 2} \frac{p_{\mathrm{ra}, i}}{\sum\limits_{i=1}^{N} p_{\mathrm{ra}, i}}+w_{\mathrm{s} 3} \frac{p_{\mathrm{pnum}, i}}{\sum\limits_{i=1}^{N} p_{\mathrm{pnum}, i}}+ \\ w_{\mathrm{s} 4} \frac{p_{\mathrm{wei}, i}}{\sum\limits_{i=1}^{N} p_{\mathrm{wei}, i}}+w_{\mathrm{s} 5} \frac{p_{\mathrm{vol}, i}}{\sum\limits_{i=1}^{N} p_{\mathrm{vol}, i}}, \end{array} $ | (6) |
式中Ws, i为零件i在属性层的重要度; ws1、ws2、ws3、ws4和ws5为零件属性层属性对应的权重,满足ws1+ws2+ws3+ws4+ws5=1.
在装配体对应的复杂网络图中,通过从装配拓扑层和零件属性层两个层面实现装配体中零件i在装配结构中的重要度评价Wi,计算方法为
| $ {W_i} = {\omega _1}\frac{{{W_{{\rm{s}},i}}}}{{\sum\limits_{i = 1}^N {{W_{{\rm{s}},i}}} }} + {\omega _2}\frac{{{W_{{\rm{t}},i}}}}{{\sum\limits_{i = 1}^N {{W_{{\rm{t}},i}}} }}, $ | (7) |
式中Ws, i为第i个零件的零件属性层重要度; Wt, i为第i个零件的拓扑层重要度; ω1和ω2为权重, 满足ω1+ω2=1.
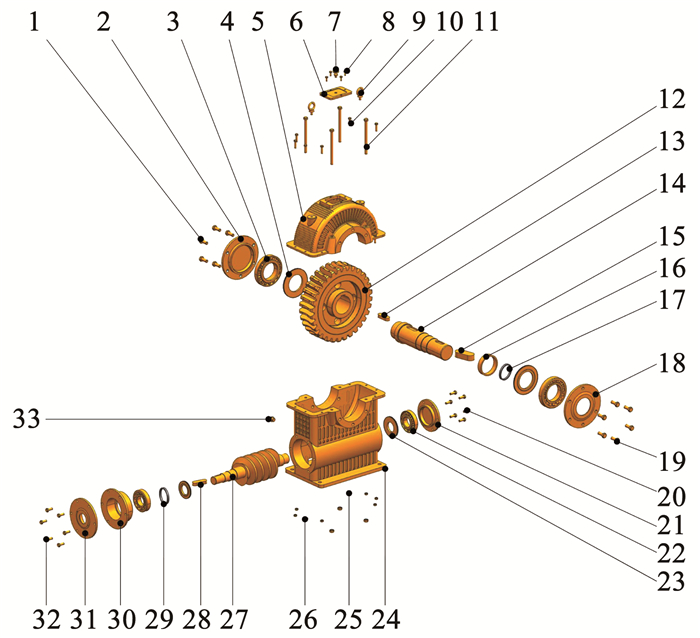
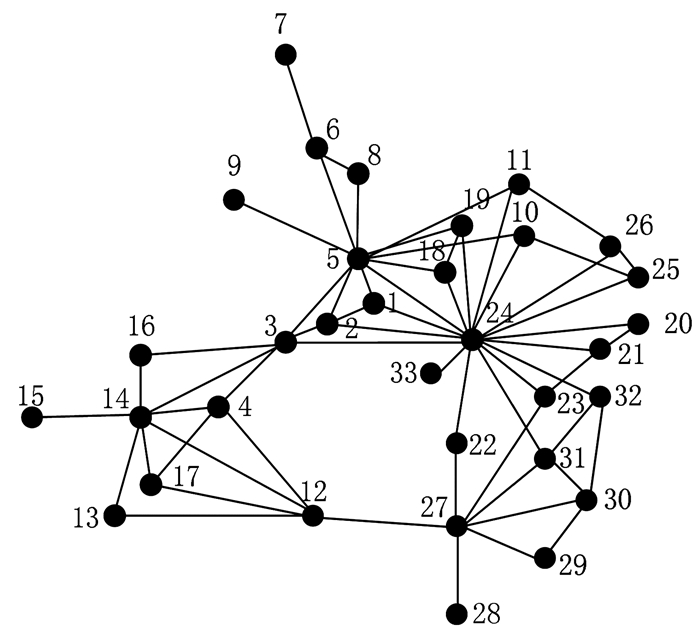
3 算法验证本文以蜗轮蜗杆减速器为例对本文方法进行验证,其装配结构见图 2.根据各子装配零件间是否存在接触关系可得到装配体的零件属性邻接图(图 3)[4, 10],蜗轮蜗杆减速器各组成零件的详细信息可见表 1.
|
图 2 蜗轮蜗杆减速器模型装配示意 Fig. 2 Schematic diagram of worm gear reducer model |
|
图 3 蜗轮蜗杆减速器零件属性邻接图 Fig. 3 Part attribute adjacency of worm gear reducer model |
| 表 1 蜗轮蜗杆减速器装配零件信息表 Tab. 1 Assembly parts information of worm gear reducer model |
按照式(1)~(4)以及该模型的属性邻接矩阵计算蜗轮蜗杆减速器模型各零件的拓扑层信息Dpi、Cpi、Bpi和Clpi,并将这些信息作为决策信息表的条件属性(C); 根据零件名称确定其是否为功能件,并作为决策信息表的决策属性(D).其中0表示该零件不是功能零件,1表示该零件为功能零件.构建的蜗轮蜗杆减速器拓扑层的信息决策表见表 2.
| 表 2 蜗轮蜗杆减速器模型拓扑层信息决策表 Tab. 2 Decision information table for topological layer data of worm gear reducer model |
对表 2进行离散化处理,根据经验,参数选择为α=0.02,β=0.5.离散化结果见表 3.
| 表 3 拓扑层数据离散化结果 Tab. 3 Discrete results of topological layer data |
对表 3中数据进行属性约简,其结果及对应的属性权重见表 4.
| 表 4 拓扑层数据属性约简结果及属性权重 Tab. 4 Attribute reduction results and attribute weights for topology layer data |
在文献[10]中,因其未考虑属性“聚集系数”,故其权重为0,其他拓扑层各属性权重均来自专家评价.本文使用粗糙集理论对拓扑层各属性进行约简,结果为{“度中心性(Dp)”、“接近中心性(Cp)”}.对约减结果进行权重计算,接近中心性属性的权重较大,为wt2=0.513 5;而度中心性(Dc)的权重为wt1=0.486 5.
3.2 装配体零件属性层信息分析本文中,提取子装配零件的自身属性作为条件属性,主要包括零件装配接触面数量(C1)、接触面表面积和(C2)、接触零件数(C3)、零件重量(C4)和零件体积(C5)5个方面,决策属性(D)与表 2相同,构建的蜗轮蜗杆减速器零件属性层信息决策表见表 5.
| 表 5 蜗轮蜗杆减速器零件属性层属性信息决策表 Tab. 5 Decision information table for part attribute layer data of worm gear reducer model |
对表 5中数据进行离散化处理,其参数选择为α=0.02,β=0.5.离散化结果见表 6.
| 表 6 零件属性层信息离散化结果 Tab. 6 Discrete results of part attribute layer data |
根据表 6数据进行属性约简,其结果及对应的属性权重见表 7.
| 表 7 零件属性层数据属性约简结果及属性权重 Tab. 7 Attribute reduction results and attribute weights for part attribute layer data |
需要指出的是,对于零件属性层,文献[10]未考虑属性“接触零件数量(C3)”,故其权重为0.而其他属性依然使用专家评价方法进行赋权.本文的属性约简结果为{“零件接触面数(C1)”、“接触表面积(C2)”、“接触零件数量(C3)”},属性“零件重量(C4)”和“零件体积(C5)”被约简,因此其权重为0.
在实际情况中,拓扑层和零件属性层所需考虑属性存在重复问题,且各属性在衡量零件重要度过程中并不一定具有相等的作用,而属性约简的引入恰好可以减少数据冗余,提高计算效率.并且本文对于各权重的确定均来自于模型数据本身,而不依赖于专家的先验知识,具有更强的客观性.
3.3 关键功能零件综合重要度评定利用复杂网络和粗糙集理论计算得到式(5)、(6)所需参数后,需要进一步计算得到式(7)中的ω1和ω2.
本文将式(5)、(6)中计算所得的Wt, i和Ws, i作为一个新的决策信息表中的条件属性(C),将表 2中的决策属性(D)作为新决策信息表中的决策属性,利用前文介绍的粗糙集分析方法,可获得这两种条件属性(Wt, i和Ws, i)的属性权重,结果见表 8.
| 表 8 权重的决策信息表 Tab. 8 Decision information table for weights |
对表 8中数据进行离散化处理,参数选择为α=0.02,β=0.5.离散化结果见表 9.
| 表 9 权重的离散化结果 Tab. 9 Discrete results of weights |
经过属性约简获得拓扑层和零件属性层各自权重,与其在文献[10]中的数值进行比较,结果见表 10.
| 表 10 与文献[10]的属性权重对比结果 Tab. 10 Comparison of attribute weights |
由表 10可见,不同于文献[10]中基于专家打分方法的权重分配ω1>ω2,本文计算得到的拓扑层和零件属性层权重相等,均为0.500 0.
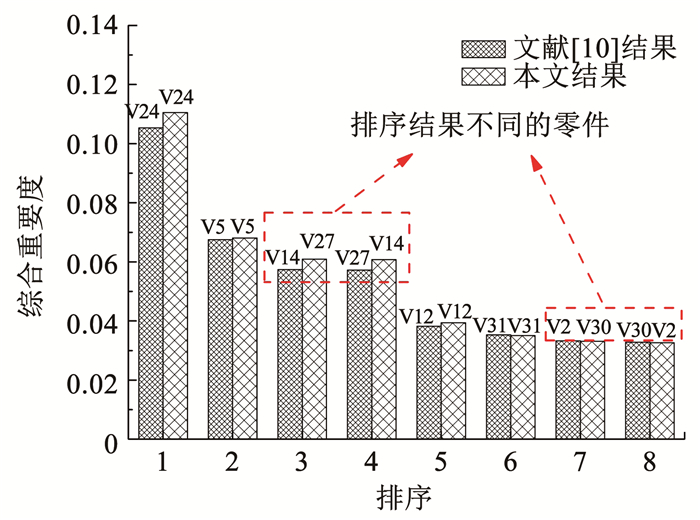
根据式(7)可得到最终的功能零件重要度排序,选定重要度较高的功能零件作为装配体的关键子装配功能零件.由表 11可知,本文与文献[10]的排序结果基本一致,关键功能零件均为箱座(V24)、闷盖(V5)、蜗杆(V27)和蜗轮轴(V14).
| 表 11 关键零件排序结果比较 Tab. 11 Comparison of key functional parts ranking results |
由图 4可知,蜗杆(V27)和蜗轮轴(V14)的排序虽然不同,但因其权重仅相差0.000 1,所以二者重要度可视为同等重要.同理,闷盖Ι(V2)和套杯(V30)的权重仅相差0.001,二者重要度非常接近.总体来说,利用两种不同方法获取的零件重要度的排序基本一致.
两种方法所选权重ω1和ω2虽不同,但获得的排序结果基本一致,原因可能在于该权重并不局限于一个固定值,而是在某一范围内均有效.事实上,对于不同类型的装配体模型,每个属性的权重也应略有不同,如果使用相同的权重进行计算,则结果将出现一定偏差.
4 结论为提高装配体模型重用水平,降低专家系统判断的主观性,本文引入粗糙集相关理论实现了以数据驱动的关键功能零件识别方法.该方法首先使用复杂网络对装配体模型进行描述; 然后,利用粗糙集相关理论对属性进行约减并计算属性权重; 最后,通过综合评价筛选出关键功能的零件.该方法突破了先验知识的限制,利用装配体模型自身的数据信息即可自动判断关键功能零件,为模型局部重用提供关键指导.
同时,该方法具有较高的柔性,能够适应各类机械领域三维CAD复杂装配体中关键功能零件的识别.可以针对每一类模型提供更加匹配的权重数据进行计算,发掘蕴藏在装配体结构中的关键功能零件,能够帮助设计人员尤其是设计新手快速定位复杂三维CAD装配模型中的重要的、可重用的零件,提高三维CAD装配模型的重用和自主设计的质量.
| [1] |
张杰, 左咪, 杨瑞康, 等. 基于属性相似性的三维装配体通用设计单元发掘方法[J]. 计算机集成制造系统, 2016, 22(9): 2072. ZHANG Jie, ZUO Mi, YANG Ruikang, et al. Method to discover common design units from three-dimensional assembly models based on attribute similarity analysis[J]. Computer Integrated Manufacturing Systems, 2016, 22(9): 2072. DOI:10.13196/j.cims.2016.09.003 |
| [2] |
BAI Jing, LUO Haonan, QIN Feiwei. Design pattern modeling and extraction for CAD models[J]. Advances in Engineering Software, 2016, 93: 30. DOI:10.1016/j.advengsoft.2015.12.005 |
| [3] |
MA Lujie, HUANG Zhengdong, WU Qingsong. Extracting common design patterns from a set of solid models[J]. Computer-Aided Design, 2009, 41(12): 952. DOI:10.1016/j.cad.2009.05.007 |
| [4] |
MA Lujie, HUANG Zhengdong, WANG Yanwei. Automatic discovery of common design structures in CAD models[J]. Computers and Graphics, 2010, 34(5): 545. DOI:10.1016/j.cag.2010.06.002 |
| [5] |
ZHANG Jie, PANG Jiazhen, YU Jianfeng, et al. An efficient assembly retrieval method based on Hausdorff distance[J]. Robotics and Computer-Integrated Manufacturing, 2018, 51: 103. DOI:10.1016/j.rcim.2017.11.012 |
| [6] |
BELHAGJ I, TRIGUI M, BENAMARA A. Subassembly generation algorithm from a CAD model[J]. The International Journal of Advanced Manufacturing Technology, 2016, 87(9): 2829. DOI:10.1007/s00170-016-8637-x |
| [7] |
MA Hongzhan, CHU Xuening, XUE Deyi, et al. Identification of to-be-improved components for redesign of complex products and systems based on fuzzy QFD and FMEA[J]. Journal of Intelligent Manufacturing, 2019, 30(2): 623. DOI:10.1007/s10845-016-1269-z |
| [8] |
董士龙, 古天龙, 徐周波. 基于识别关键件的子装配体识别方法[J]. 桂林电子科技大学学报, 2015, 35(2): 147. DONG Shilong, GU Tianlong, XU Zhoubo. Subassembly identify method based on identify key part[J]. Journal of Guilin University of Electronic Technology, 2015, 35(2): 147. DOI:10.3969/j.issn.1673-808X.2015.02.012 |
| [9] |
许评, 李玉鹏, 莫宇迪, 等. 基于复杂网络的复杂机械产品关键零件识别[J]. 组合机床与自动化加工技术, 2018(10): 51. XU Ping, LI Yupeng, MO Yudi, et al. Identification of key parts within complex mechanical products based on complex networks[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2018(10): 51. DOI:10.13462/j.cnki.mmtamt.2018.10.014 |
| [10] |
HAN Zhoupeng, MO Rong, CHANG Zhiyong, et al. Key assembly structure identification in complex mechanical assembly based on multi-source information[J]. Assembly Automation, 2017, 37(2): 208. DOI:10.1108/AA-09-2016-121 |
| [11] |
PAWLAK Z. Rough sets[J]. International Journal of Computer & Information Sciences, 1982, 11(5): 341. DOI:10.1007/BF01001956 |
| [12] |
苗夺谦, 李道国. 粗糙集理论、算法与应用[M]. 北京: 清华大学出版社, 2008. MIAO Duoqian, LI Daoguo. Rough sets theory, algorithms and applications[M]. Beijing: Tsinghua University Press, 2008. |
| [13] |
NEWMAN M E J. The structure and function of complex networks[J]. SIAM Review, 2003, 45(2): 167. DOI:10.1137/S003614450342480 |
| [14] |
FREEMAN L C. Centrality in social networks conceptual clarification[J]. Social Networks, 1978, 1(3): 215. DOI:10.1016/0378-8733(78)90021-7 |
| [15] |
SABIDUSSI G. The centrality index of a graph[J]. Psychometrika, 1966, 31(4): 581. DOI:10.1007/bf02289527 |
| [16] |
DIJKSTRA E W. A note on two problems inconnexion with graphs[J]. Numerische Mathematik, 1959, 1: 269. DOI:10.1007/BF01386390 |
 2021, Vol. 53
2021, Vol. 53