高速化成为轨道交通发展趋势,作为高速化的核心装备,时速300~350 km/h高速动车组成为中国重点发展主导车型,需求旺盛,市场巨大.高速铝合金车体是高速动车组国产化自主研制需突破的九大关键技术之一.因轨道车辆车体构件尺寸大,形状复杂,尺寸和形状精度要求高,制造难度大,多采用拉弯工艺对铝合金型材进行成形[1].对于复杂截面、变曲率、成形精度要求高的铝合金型材结构件,传统拉弯成形已不能满足现代化生产.为了提高型材弯曲件的精度,降低生产成本,目前主要以试验和数值模拟为主[2-4].
近年来,北京航空航天大学[5-7]采用有限元模拟法和试验对型材拉弯成形性做了大量研究,分析了不同工艺参数对成形质量的影响.燕山大学[8-9]建立了型材转台式拉弯解析模型,对成形过程作了详细的理论分析.吉林大学[10-12]对各类复杂截面的碳钢、不锈钢进行了拉弯成形研究,探索了成形精度的关键影响因素,提出了钢型材畸变和回弹等缺陷的控制方法.
高速动车组车顶弯梁、端顶弯梁、侧墙柱及端角柱等都是复杂截面铝型材车体构件,其弯曲成形和钢型材弯曲成形存在很大差异[13],钢型材的成形理论和规律不能直接应用于铝型材的成形,因此探索铝合金型材成形规律及缺陷控制方法成为行业重大需求.
图 1为L型截面铝合金型材车门立柱,位于每节车体两端,是高速动车组侧墙组件中的一个重要构件.车门立柱在实际生产时常常出现截面畸变和回弹缺陷,导致轮廓精度差,无法与车门配合,影响车体安全性和气密性.

|
图 1 L型截面铝合金车门立柱 Fig. 1 L-section aluminum alloy door column |
本文采用ABAQUS有限元模拟软件对高速动车组L型截面铝合金门立柱拉弯成形精度进行研究,探索开口复杂截面变曲率铝合金型材拉弯成形过程中缺陷产生原因,优选成形方案和工艺参数,修正拉弯胎模具型面,有效控制成形缺陷,构件成形精度得到进一步提高.通过实际生产验证,证实了所提方法的可行性.
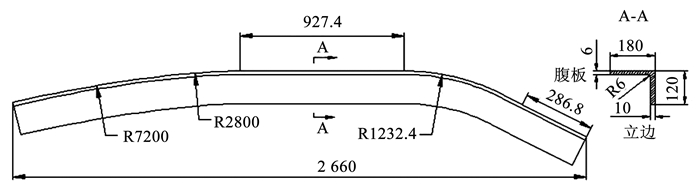
1 门立柱拉弯成形分析及建模 1.1 门立柱结构分析门立柱构件由铝型材弯曲而成,两端为圆弧段,中央为直线段,如图 2所示,其腹板壁厚6 mm,立边壁厚10 mm,在成形精度方面要求腹板畸变小于1 mm;两段圆弧区域立边畸变分别小于1.2 mm.由图可见该件截面呈L型,属于开口型截面,加上该件立边较高,长度较长、外轮廓曲率变化复杂以及纵向左右不对称,使得拉弯后构件容易出现截面畸变、直线段平面度差和两端回弹大等成形缺陷.
|
图 2 构件的几何结构(mm) Fig. 2 Geometry structure of component (mm) |
基于弯曲工程理论[14-15],分别对小曲率和大曲率型材拉弯成形过程进行理论分析,推导截面的应力应变分布表达式和回弹半径变化关系式.
型材小曲率弯曲时,假定型材横截面底部单元在反向加载时为弹性变形,忽略包申格效应.
预拉阶段,对型材两端施加轴向拉力T,使截面预拉应力超过弹性极限σ0,至屈服极限,σT=σ0.2.
弯曲阶段,型材截面内应变均为单向拉应变,可以近似认为截面应变在横截面高度方向呈线性分布,有
补拉阶段,截面内应力可近似认为沿截面高度方向呈线性分布,截面应力
回弹阶段,型材小曲率拉弯变形过程与板料压弯过程类似,曲率半径变化可由板料压弯回弹半径一般表达式变换,即
| $ \Delta r = {r_h} - {r_q} = \frac{{{\rm{ }}{r_q}\left( {{\sigma _w} - {\sigma _n}} \right)}}{{hE - {r_q}\left( {{\sigma _w} - {\sigma _n}} \right)}}{\rm{ }} \approx \\{\rm{ }}\frac{{r_q^2Dh/{R_C}}}{{hE - {r_q}Dh/{R_C}}} = \frac{{r_q^2D}}{{{\rm{ }}E{R_C} - {r_q}D}}. $ | (1) |
式中:rq、rh分别为卸载时型材底部回弹前、后半径; h为型材截面高度; σw、σn分别为卸载前型材顶部和底部单元所受应力; RC为补拉后应变中性层曲率半径; D为材料的塑性模量.
型材小曲率拉弯时卸载回弹受材料性能E,拉弯曲率半径rq影响.
型材大曲率弯曲时,型材底部区域先拉伸至屈服,之后受到反向载荷的作用进入压缩塑性变形阶段,需要考虑包申格效应.
预拉阶段,预拉力作用下,截面内的应力分布保持一致,外层和内层材料的轴向应力
弯曲阶段,型材中性应力层外层区域继续受拉,顶部单元受到拉应力沿着曲线增大为σw2,中性应力层内层区域反向加载,型材底部单元的应力减小为σn2.
补拉阶段,近似认为截面应变在横截面高度方向呈线性分布,由图 3几何关系,z处的材料所受应力

|
图 3 拉弯几何关系 Fig. 3 Geometric relationship of profiles in stretch bending |
回弹阶段,外层材料一直处于单向拉伸状态,外层材料的弹性收缩应变与外层所受应力呈反比关系.回弹时型材外层材料弹性收缩应变、内层材料弹性拉伸应变分别为
| $ \Delta {\varepsilon _w} = - {\rm{ }}\frac{{{\sigma _w}}}{E}, $ | (2) |
| $ \Delta {\varepsilon _n} \approx {\rm{ }}\frac{{{\sigma _w}\left( {\rho - {r_q}} \right){\rm{ }}}}{{E\left( {h + {r_q} - \rho } \right)}}. $ | (3) |
式中:E为材料弹性模量,ρ为应变中性层半径,rq为型材回弹前半径,h为型材截面高度, σw为回弹前型材外层材料的应力.
回弹后型材回弹半径变化关系式为
| $ \begin{array}{l} \Delta r = {r_h} - {r_q} \approx \frac{{{\rm{ }}{r_q}\left[ {h\Delta {\varepsilon _n} - {r_q}(\Delta {\varepsilon _\omega } - \Delta {\varepsilon _n})} \right]{\rm{ }}}}{{h\left( {{\rm{ }}1 + {\rm{ }}\frac{{{r_q} - \rho {\rm{ }}}}{\rho }} \right){\rm{ }} + {r_q}(\Delta {\varepsilon _\omega } - \Delta {\varepsilon _n})}}{\rm{ }} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{ }}\frac{{\rho 2{\sigma _w}}}{{E\left( {h + {r_q} - \rho } \right) - \rho {\sigma _w}}}. \end{array} $ | (4) |
式中:回弹半径与材料性能E,型材截面高度h,拉弯曲率半径rq和拉伸量有关.
1.3 有限元模型铝合金材料为6005A,性能数据如下:密度ρ为2.6×10-9 t/mm3;弹性模量E为70 000 MPa;泊松比μ为0.3;屈服强度σs为139.5 MPa;硬化系数K为401.5 MPa;应变强化系数n为0.2.考虑材料各向异性,采用Krupkowsky准则描述材料的真实应力-应变塑性变形关系:
| $ \sigma = K{\left( {{\varepsilon _0} + {\varepsilon _p}} \right)^n}, $ | (5) |
| $ {\varepsilon _0} = {\rm{ }}n{\rm{ }}\sqrt {\frac{{{\sigma _{\rm{s}}}}}{K}} . $ | (6) |
式中:σ为真实应力,ε0为初始塑性应变,εp为塑性应变,K为硬化系数,σs为极限屈服应力,n为应变强化系数.
门立柱采用张臂式拉弯机拉弯成形,基于构件特征,建立如图 4所示的拉弯有限元模型.模型包括拉弯模具、夹钳、型材.由于腹板和立边板料不等厚,考虑到板厚方向应力会对模拟的精度有一定影响,本文采用实体板料网格单元模拟.在型材截面厚度方向上均使用5个积分点组成的4层实体单元.型材与拉弯模具之间罚接触,摩擦系数取0.1.

|
图 4 门立柱拉弯有限元模型 Fig. 4 Numerical simulation model of door column stretch bending |
根据模拟,拉弯成形中拉伸量的选取对最后成形效果有显著影响,在防止构件过分减薄的前提下,增大拉伸量有利于提高拉弯成形精度.初选如下拉弯工艺参数:预拉量1%,包覆拉伸量7.5%,补拉量0.5%,图 5为模拟结果.拉弯后,构件最大等效塑性应变为13.85%.L型截面门立柱的截面畸变主要为腹板塌陷和立边内凹,其中腹板塌陷出现在中央直线段区域,立边内凹主要出现在圆弧段区域.此外,在夹钳应力卸载后,构件不对称、两端回弹量不一样.其中小圆弧端的回弹量较大,达到9.616 mm,大圆弧端的回弹达到6.41 mm,如图 6所示.构件出现明显截面畸变并且回弹较大,因此必须优化工艺,控制成形精度.

|
图 5 等效塑性应变模拟结果,截面畸变 Fig. 5 Simulation results of equivalent strain, and cross-section distortions: (a) web collapse in straight section, (b) concave deformation of vertical edge in arc segment |

|
图 6 卸载后型材回弹量(mm) Fig. 6 Spring-back amount after unloading (mm) |
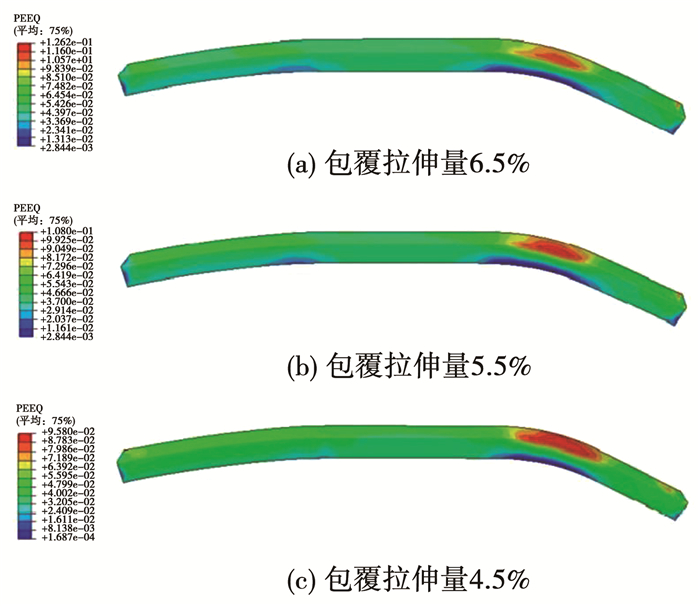
铝型材拥有良好的延展性,但延伸率太大会导致型材局部区域过分减薄甚至拉裂,影响整体强度.上述模拟结果发现原方案拉伸量过大.由于包覆拉伸量对成形精度影响最为显著,保持预拉量、补拉量不变,分别取1%、0.5%,包覆拉伸量选择4.5%、5.5%、6.5%进行模拟,结果见图 7.其中包覆拉伸量为4.5%时,小圆弧段区域最大塑性应变为9.58%,满足延伸率控制要求且最为安全.
|
图 7 不同包覆拉伸量下等效塑性应变分布 Fig. 7 Equivalent strain distribution of components under different wrap-elongations |
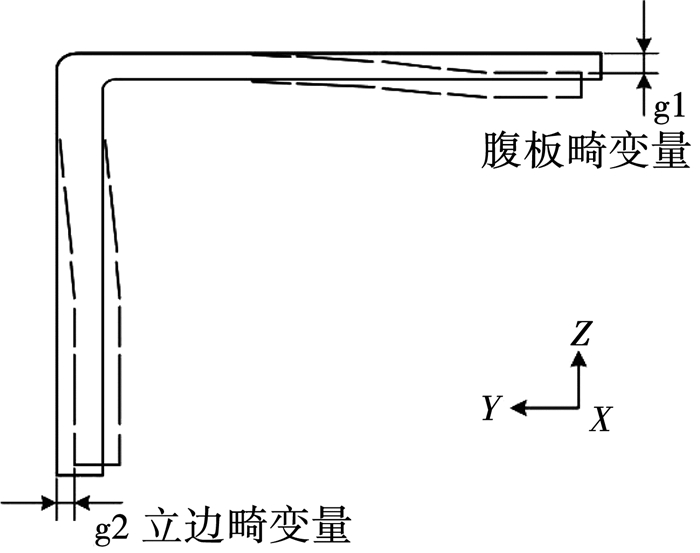
L型截面铝合金型材门立柱的截面畸变主要为腹板塌陷和立边内凹,见图 8.由于L型截面构件为非对称截面,在夹钳拉伸力和弯矩作用下,直线段处腹板单元的受力状态为y向受拉,z向受压,立边单元y向受压,z向受拉.
|
图 8 L型截面门立柱的截面畸变 Fig. 8 Cross-section distortion of L-section door column |
拉弯时直线段区域的腹板有立边一端,受到立边作用力的影响向上凸起,而腹板无立边一端在夹钳弯矩的作用下向下贴模,总体表现为直线段区域腹板塌陷,如图 5(a)所示.
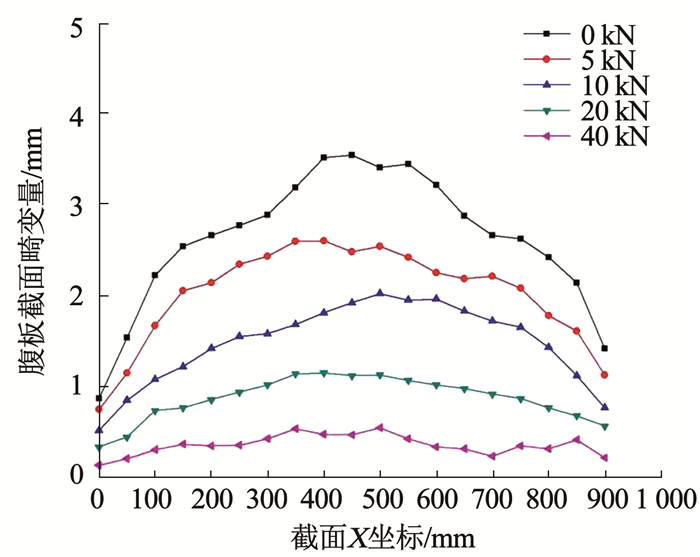
根据直线段区域截面畸变的产生原因,在该区域设置背压板,限制该区域的立边拱起.压板的载荷大小将直接影响腹板上沿y轴各单元z向的应力分布,采用不同的背压力模拟拉弯过程,由图 9可知提高压板载荷能够减小直线段畸变.
|
图 9 不同背压力下直线段区域的腹板截面畸变对比 Fig. 9 Comparison of distortion of web plate in straight section under different back pressures |
构件立边的截面畸变主要集中于圆弧段区域,由于拉弯过程中构件的立边出现减薄,导致立边底部和拉弯模具底部之间存在间隙,见图 5(b).由于立边底部未能接触受力,刚度不足、导致“立边失稳”,立边底部向模具方向倾斜.
根据立边截面畸变的产生原因,本文提出一种控制立边畸变的方法:即记录型材与模具底部对应点的间隙值gi,将原轮廓对应点等量偏移gi,光顺后的模具底部轮廓线,尽量确保在拉弯成形中立边与模具底部能够保持相互接触,图 10为拉弯模具优化前后底部轮廓变化.
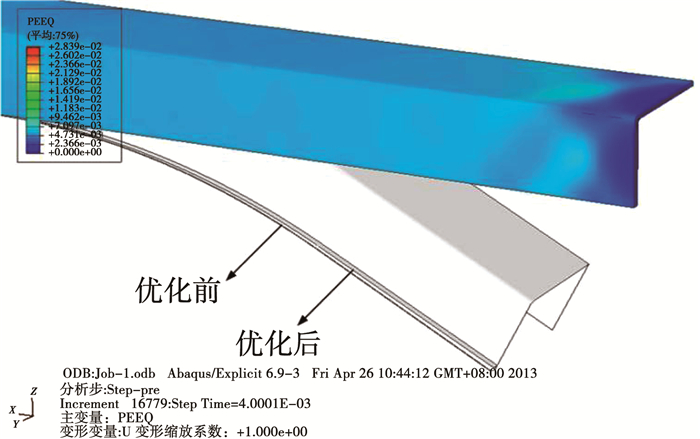
|
图 10 优化前后拉弯模具底部轮廓对比 Fig. 10 Comparison of bottom profiles of stretch bending die before and after optimization |
通过优化,测量构件各面的立边截面畸变值,图 11表明,立边截面畸变最大值由3.73 mm下降至1.68 mm,满足精度要求.
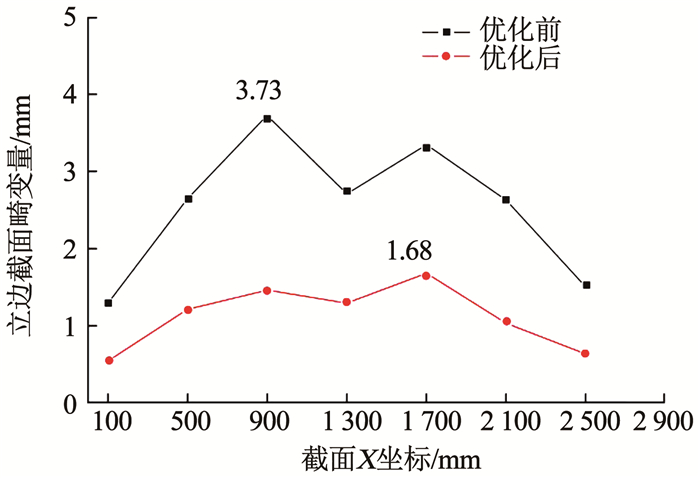
|
图 11 优化前后立边截面畸变值对比 Fig. 11 Comparison of distortion values of vertical edge section before and after optimization |
构件的回弹导致门立柱外轮廓发生改变,会严重影响门立柱的贴模度,故回弹量的大小是考察门立柱成形质量的一项重要指标.构件的回弹定义如图 12所示,采用构件回弹前后半径R的变化和构件两端的间隙S来描述回弹大小.
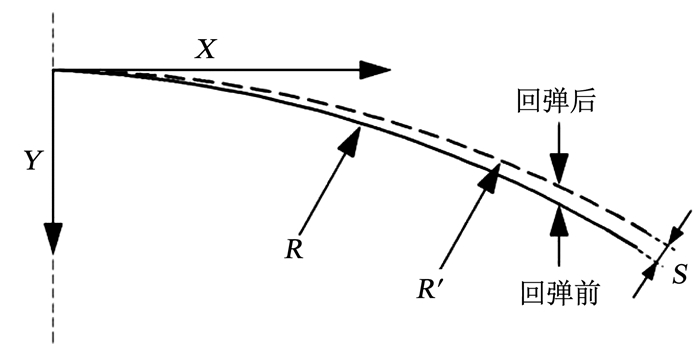
|
图 12 回弹定义示意 Fig. 12 Definition of spring-back |
考虑到回弹变形大,本文采用一种基于数值模拟的虚拟迭代修模方法控制构件回弹.算法采用几何补偿法[16-19],图 13为几何补偿法示意.下面进行算法理论分析.
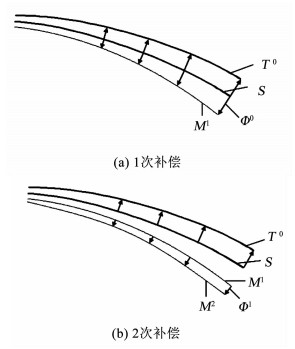
|
图 13 回弹补偿基本原理 Fig. 13 Basic principle of spring-back compensation |
在数值模拟分析中,构件轮廓线分布着有限个网格节点.理想构件形状S是由n个节点依次连接而成,回弹后形状变为T,即
| $ S = \{ {s_i}\left| s \right. \in {\mathit{\Omega} ^3},1 \le i \le n\} , $ | (7) |
| $ T = \{ {t_i}\left| t \right. \in {\mathit{\Omega} ^3},1 \le i \le n\} . $ | (8) |
对于节点i,回弹后形状由si变为ti,补偿后形状M为
| $ M = S - \mu (T - S). $ | (9) |
式中, μ为补偿因子,一般取0.8~1.5.各点的偏差补偿值Φ
| $ {M^2} = {M^1} - \mu ({T^1} - S). $ | (10) |
逐步迭代补偿,存在如下递推关系:
| $ {M^{j + 1}} = {M^j} - \mu ({T^j} - S), $ | (11) |
| $ \mathit{\Phi} _i^j = - \mu (t_i^j - {s_i}). $ | (12) |
式中, j为迭代次数.当形状偏差

|
图 14 补偿前后拉弯模具外轮廓线对比 Fig. 14 Comparison of outer contours of stretch bending die before and after compensation |
|
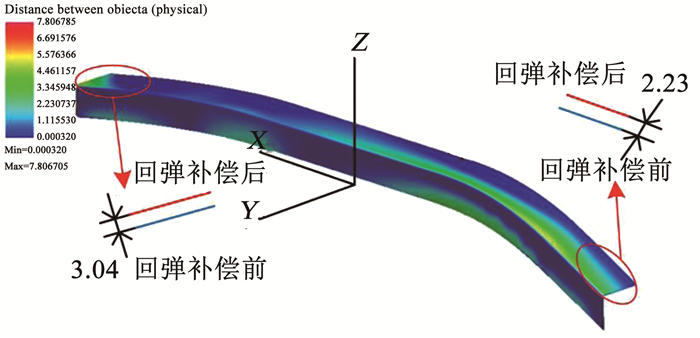
图 15 回弹补偿构件与标准件轮廓对比(mm) Fig. 15 Comparison of contours between compensated component and standard component (mm) |
在Cyril Bath公司生产的数控拉弯机上进行拉弯试验.根据上述模拟结果,修正模具轮廓型面、重新构造拉弯胎具,设置背压板并优化工艺参数.压板压力由5 kN增大至40 kN,发现直线段最大腹板畸变由3.81 mm降低为0.86 mm;两段圆弧区域的截面立边畸变分别由2.81 mm和2.93 mm降低至0.95 mm和1.1 mm.
腹板和立边优化前后试验结果对比见图 16,构件的截面尺寸精度得到很大改善.在应力卸载后,构件外轮廓形状偏差较小,满足小于3 mm的设计指标,门立柱的成形精度达到要求.图 17为轮廓精度良好的门立柱.

|
图 16 试验结果对比 Fig. 16 Comparison of experiment results: (a) before the optimization of web, (b) optimized web, (c) before the optimization of vertical edge, (d) optimized edge |

|
图 17 轮廓精度良好的门立柱 Fig. 17 Door column with high accuracy |
1) 对拉弯成形工艺进行理论分析,基于简单的线性强化模型和力学假定,建立回弹半径变化的数学模型,给出回弹半径的变化规律,即截面高度增加,回弹半径变小;随着拉伸量增大,回弹半径变小;不同构件材料力学性能参数E不同,回弹半径也不同.
2) 变曲率L型截面铝合金门立柱在拉弯成形时容易出现腹板塌陷,在直线段处设置背压板,背压力从5 kN增大至40 kN,直线段区域腹板截面畸变值下降大约77%. 3)优化门立柱拉弯模具轮廓线,确保构件立边与拉弯模具底部保持接触,增加立边结构强度,使圆弧段的立边截面畸变值下降大约66%. 4)为避免壁厚过分减薄导致结构强度降低,铝合金型材拉弯时包覆拉伸量不宜超过5.5%.
| [1] |
梁继业, 邓钢, 方斌. L型截面铝型材拉弯成形截面畸变缺陷控制研究[J]. 锻压技术, 2016, 41(12): 42. LIANG Jiye, DENG Gang, FANG Bin. Section distortion control for L-section aluminum profile part in the stretch-bending process[J]. Forging & Stamping Technology, 2016, 41(12): 42. DOI:10.13330/j.issn.1000-3940.2016.12.007 |
| [2] |
ELSHARKAWY A A, EL DOMIATY A A. Determination of stretch-bendability limits and springback for T-section beams[J]. Journal of Materials Processing Technology, 2001, 110(3): 265. DOI:10.1016/S0924-0136(00)00885-2 |
| [3] |
YU Chenglong, LI Xiaoqiang. Theoretical analysis on spring-back of L-section extrusion in rotary stretch bending process[J]. Transactions of Nonferrous Metals Society of China, 2011, 21(12): 2705. DOI:10.1016/S1003-6326(11)61113-8 |
| [4] |
CORONA E. A simple analysis for bend stretch forming of aluminum extrusions[J]. International Journal of Mechanical Sciences, 2004, 46(3): 433. DOI:10.1016/j.ijmecsci.2004.03.010 |
| [5] |
刁可山, 周贤宾, 金朝海. 铝合金型材拉弯成形研究进展[J]. 塑性工程学报, 2003, 10(6): 38. DIAO Keshan, ZHOU Xianbin, JIN Chaohai. The study on stretch bending process for aluminum extrusions[J]. Journal of Plasticity Engineering, 2003, 10(6): 38. DOI:10.3969/j.issn.1007-2012.2003.06.010 |
| [6] |
周贤宾, 刁可山, 李晓星, 等. 闭截面型材的拉弯成形性[J]. 北京航空航天大学学报, 2006, 32(10): 1168. ZHOU Xianbin, DIAO Keshan, LI Xiaoxing, et al. Stretch-bending formability of profile[J]. Journal of Beijing University of Aeronautics and Astronautics, 2006, 32(10): 1168. DOI:10.3969/j.issn.1001-5965.2006.10.009 |
| [7] |
金朝海, 周贤宾. 基于PS2F的铝型材拉弯回弹研究[J]. 塑性工程学报, 2007, 14(3): 1. JIN Chaohai, ZHOU Xianbin. PS2F-based study on spring-back in stretch-wrap bending of aluminum profiles[J]. Journal of Plasticity Engineering, 2007, 14(3): 1. DOI:10.3969/j.issn.1007-2012.2007.03.001 |
| [8] |
钱志平.型材拉弯的智能化控制工艺理论研究[D].秦皇岛: 燕山大学, 2009 QIAN Zhiping. Research on the theory and technology of intelligent control for profile stretch-bending[D]. Qinhuangdao: Yanshan University, 2009 |
| [9] |
赵军, 殷璟, 马瑞, 等. 小曲率平面弯曲弹复方程[J]. 中国科学技术科学, 2011, 54: 2386. ZHAO Jun, YIN Jing, MA Rui, et al. Springback equation of small curvature plane bending[J]. Science China Technological Sciences, 2011, 54: 2386. DOI:10.1007/s11431-011-4447-4 |
| [10] |
GU Zhengwei, LV Mengmeng, LI Xin, et al. Stretch-bending of Z-section stainless steel profile[J]. Journal of Iron and Steel Research, 2016, 23(6): 525. DOI:10.1016/s1006-706x(16)30083-8 |
| [11] |
谷诤巍, 吕萌萌, 李欣, 等. 数控拉弯工艺中型材变形量的影响因素[J]. 吉林大学学报(工学版), 2016, 46(4): 1190. GU Zhengwei, LV Mengmeng, LI Xin, et al. Influence factors of profile deformation in NC stretch bending[J]. Journal of Jilin University (Engineering and Technology Edition), 2016, 46(4): 1190. DOI:10.13229/j.cnki.jdxbgxb201604026 |
| [12] |
谷诤巍, 张文学, 吕萌萌, 等. 宽翼边U型截面不锈钢型材拉弯成形缺陷控制[J]. 吉林大学学报(工学版), 2017, 47(4): 1165. GU Zhengwei, ZHANG Wenxue, LV Mengmeng, et al. Stretch bending defect control of U-section stainless steel profile with wide flange[J]. Journal of Jilin University (Engineering and Technology Edition), 2017, 47(4): 1165. DOI:10.13229/j.cnki.jdxbgxb201704022 |
| [13] |
GU Zhengwei, LV Mengmeng, LI Xin, et al. Stretch bending defects control of L-section aluminum components with variable curvatures[J]. The International Journal of Advanced Manufacturing Technology, 2015, 85: 1053. DOI:10.1007/s00170-015-8010-5 |
| [14] |
ZHANG Z T, LEE D. Development of a new model for plane strain bending and spring back analysis[J]. Journal of Materials Engineering and Performance, 1995, 4(3): 291. DOI:10.1007/bf02649066 |
| [15] |
LEU D K. A simplified approach for evaluating bend ability and spring-back in plastic bending of anisotropic sheet metals[J]. Journal of Materials Processing Technology, 1997, 66(1/2/3): 9. DOI:10.1016/s0924-0136(96)02453-3 |
| [16] |
GAN Wei, WAGONER R H. Die design method for sheet springback[J]. International Journal of Mechanical Sciences, 2004, 46(7): 1097. DOI:10.1016/j.ijmecsci.2004.06.006 |
| [17] |
CHENG Hangshawn, CAO Jian, XIA Z C. An accelerated springback compensation method[J]. International Journal of Mechanical Sciences, 2007, 49(3): 267. DOI:10.1016/j.ijmecsci.2006.09.008 |
| [18] |
MEINDERS T, BURCHITZ I A, BONTE M H A, et al. Numerical product design: springback prediction, compensation and optimization[J]. International Journal of Machine Tools and Manufacture, 2008, 48(5): 499. DOI:10.1016/j.ijmachtools.2007.08.006 |
| [19] |
LI Gui, LIU Yuqi, DU Ting, et al. Algorithm research and system development on geometrical springback compensation system for advanced high-strength steel parts[J]. The International Journal of Advanced Manufacturing Technology, 2014, 70: 413. DOI:10.1007/s00170-013-5230-4 |
 2021, Vol. 53
2021, Vol. 53


