2. 重庆邮电大学 信息无障碍与服务机器人工程技术研究中心,重庆 400065
2. Engineering Research Center for Information Accessibility and Service Robots, Chongqing University of Posts and Telecommunications, Chongqing 400065, China
视觉里程计(VO)是一种利用视觉传感器信息对机器人或其他载体进行准确的位姿估计的方法,相比于使用激光传感器的方法,视觉信息更加丰富,可用于三维重建、物体识别、语义分割等.同时,因其成本低、体积小、精度高等优点,而广泛地应用于机器人自主导航、自动驾驶、增强现实等领域[1-4].
近年来,许多精度高、效率快的视觉里程计方法被提出来,可以将其大致分为3类.第1类是基于特征点法的视觉里程计[4-6],这些方法通过提取和匹配相邻图像的特征点,建立重投影优化函数来估计帧间运动.第2类是基于直接法的视觉里程计[7-9],根据灰度不变假设,建立光度误差函数来估计帧间运动.第3类是将直接法与特征点法融合的视觉里程计,Forster等[10]提出一种半直接法视觉里程计(SVO),通过对图像中的特征点块进行匹配来计算位姿,加快了计算精度与速度.这些传统的算法都基于静态环境假设,忽略了动态物体对运动估计的影响,从而导致计算结果在动态环境下有较大的误差.
在动态环境下,一般可采用随机采样一致性(RANSAC)或鲁棒Huber函数等概率方法将动态部分当作噪声剔除掉.当动态物体在图像中占比较大时,则无法通过概率方法剔除,需要将动、静态物体区分开来,使用静态部分估算位姿,避免动态物体造成的误差.Besco等[11]提出的DynaSLAM算法采用深度学习结合几何的方法检测动态物体,该方法能准确剔除动态物体,具有较高的精度,但是该算法需要GPU加速,无法达到实时性与便携性.Li等[12]使用边缘点静态权重的方法判别动态点,该方法拥有较大的像素级噪声,容易导致动、静态点判断错误,且仅使用了部分图像信息,位姿估计精度较差.Jaimez等[13]和Scona等[14]采用聚类的方法,通过构建背景分割优化函数来分离动、静态物体,然而该类方法在高动态环境下,不能有效地剔除动态对象,且无法进行准确的位姿估计.
本文提出一种融合边缘信息的稠密视觉里程计算法,利用边缘信息对光照变化和运动模糊不敏感的特性,弥补直接法的缺点.同时,在几何纹理较少的环境下,加大直接法在计算中的占比,从而减小边缘信息缺失导致的误差.本文的主要贡献如下:1)将边缘对齐的Distance Transform(DT)误差引入残差模型中,增加算法在不同环境的鲁棒性;2)引入平均背景深度,加大动态部分残差,以辅助运动分割;3)将带有边缘信息的加权聚类残差加入到位姿估计的非线性优化函数中,提高位姿估算的精度.实验结果表明,本文算法在动态环境下能准确剔除动态物体,并在位姿估算中具有较高的精度.
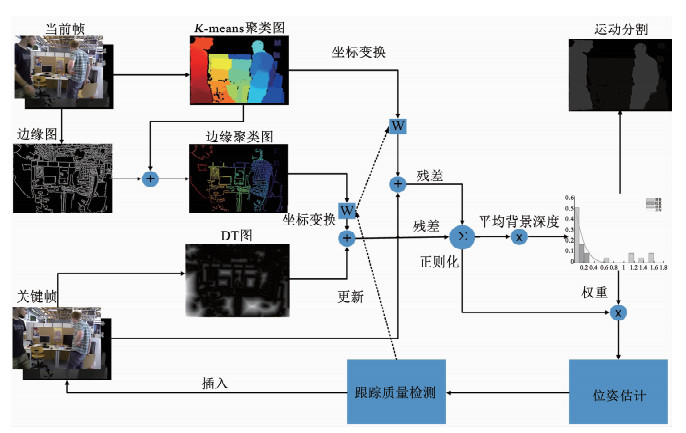
1 算法框架本文算法的全过程见图 1.首先,使用K-means聚类法将图像分为N个集群.然后,将聚类后的边缘图与灰度图分别坐标变换到关键帧及其DT图上,构建基于聚类的残差模型.接着,根据聚类残差建立基于t分布的非参数统计模型,并通过分段阈值函数分离出动态物体并得到残差权重.最后,将加权残差加入到优化函数中进行位姿估算,并将得到的位姿进行跟踪质量检查,更新下次迭代的变换矩阵或关键帧.
|
图 1 算法框架 Fig. 1 Algorithm framework |
本文算法引入了边缘信息,对当前帧进行边缘提取与聚类后,计算出融合DT误差的残差模型,通过平均背景深度扩大动、静部分残差差距来辅助运动分割,并将边缘对齐作为约束加入到位姿估计中以获得更准确的估算结果.
2 融合边缘信息的视觉里程计使用RGB-D传感器,每一个时间帧都可以获得一个灰度图Ic和一个深度图Zc.深度信息用于计算场景聚类、参与构建残差模型并计算平均背景深度.灰度信息用于提取边缘信息,并结合深度信息构建光度及几何一致性误差与DT误差.
2.1 相机运动模型使用图像对应的三维点坐标P=(X, Y, Z)和深度Z=Zc(p)可通过投影函数π计算出图像的像素坐标p=(x, y)为
| $ p = \pi \left( P \right) = \left( {\frac{{X{f_x}}}{Z} + {c_x}, \frac{{Y{f_y}}}{Z} + {c_y}} \right), $ | (1) |
式中, fx和fy为焦距,cx和cy为标准针孔相机模型定义的光学中心.另外,为了将像素坐标p反投影为三维坐标点P,定义逆投影函数π-1为
| $ P = {\pi ^{ - 1}}\left( {p, Z} \right) = \left( {\frac{{x - {c_x}}}{{{f_x}}}Z, \frac{{y - {c_y}}}{{{f_y}}}Z, Z} \right). $ | (2) |
两个图像帧之间的相对运动可以表示为变换矩阵T∈SE(3),其中包含3×3的旋转矩阵R3×3∈SO(3)和3×1的平移向量t3×1∈R3.通过上一帧的三维坐标点Pc-1以及两帧间的变换矩阵T,可以计算出当前帧的三维坐标点Pc为
| $ {P_{\rm{c}}} = {\mathit{\boldsymbol{T}}_{{\rm{cc - 1}}}}{P_{{\rm{c - 1}}}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{R}}_{{\rm{cc - 1}}}}}&{{\mathit{\boldsymbol{t}}_{{\rm{cc - 1}}}}}\\ 0&1 \end{array}} \right]{P_{{\rm{c - 1}}}}. $ | (3) |
刚体运动有6个自由度,可使用李代数se(3)中的ξ∈R6来表示李群SE(3)中的变换矩阵T∈R4×4.定义坐标变换函数ω为
| $ {p_{\rm{c}}} = \omega \left( {{\xi _{{\rm{cc - 1}}}}, {p_{{\rm{c - 1}}}}} \right) = \pi \left( {{\mathit{\boldsymbol{T}}_{{\rm{cc - 1}}}}{\pi ^{ - 1}}\left( {{p_{{\rm{c - 1}}}}, {Z_{{\rm{c - 1}}}}\left( {{p_{{\rm{c - 1}}}}} \right)} \right)} \right), $ | (4) |
式中, ξcc-1是Tcc-1的李代数,pc-1和pc分别是相邻两帧对应的像素点坐标.
2.2 场景聚类为了获得稠密的运动分割,有的方法直接采用像素点进行权重计算[12],逐点分割未考虑到像素点之间的空间关系,不可避免地会产生噪声,导致精度下降.本文参考Jaimez等[13, 15]的方法采用K-means聚类法,利用深度信息和逆投影函数π-1得到三维空间点坐标,通过计算每一个三维空间点距离集群中心点的距离,来确定该空间点属于哪一个集群,属于同一个集群的点一般为同一个刚体.使用集群计算能够避免产生像素级噪声,简化运动分割问题.
2.3 残差模型 2.3.1 光度及几何误差为了识别环境中的动、静态部分,需要计算每个集群的残差大小,然后进行运动分割.首先,将当前帧Fc完成聚类后坐标变换到关键帧Fk.然后,根据光度及几何一致性构建误差模型:
| $ \begin{array}{l} \mathit{r}_{\rm{Z}}^\mathit{i}\left( \mathit{\boldsymbol{\xi }} \right) = {\mathit{Z}_{\rm{k}}}\left( {\omega \left( {{\mathit{\boldsymbol{\xi }}_{{\rm{kc}}}}, p_{\rm{c}}^i} \right)} \right) - \\ \;\;\;\;\;\;\;\;\;\;\;|{\mathit{\boldsymbol{T}}_{{\rm{kc}}}}{\pi ^{ - 1}}\left( {p_{\rm{c}}^i, {Z_{\rm{c}}}\left( {p_{\rm{c}}^i} \right)} \right){|_{\rm{Z}}}, \end{array} $ | (5) |
| $ \mathit{r}_{\rm{Z}}^\mathit{i}\left( \mathit{\boldsymbol{\xi }} \right) = {I_{\rm{k}}}\left( {\omega \left( {{\mathit{\boldsymbol{\xi }}_{{\rm{kc}}}}, {Z_{\rm{c}}}\left( {p_{\rm{c}}^i} \right)} \right)} \right) - {I_{\rm{c}}}\left( {p_{\rm{c}}^i} \right). $ | (6) |
式中:rIi和rZi分别表示点i对应的光度误差与深度误差,|· |Z表示三维坐标点的Z坐标值.ξkc为当前帧到关键帧坐标变换的李代数,由匀速运动假设ξcc-1=ξc-1c-2可得ξkc=ξkc-1ξc-2c-1,这个假设值一般接近于相机运动的最终估计值,从而可减少收敛时间并避免陷入局部最优解.
2.3.2 边缘对齐误差Schenk等[16]对比了多种边缘检测算法的性能,本文借鉴他们的方法对当前帧Fc进行边缘提取.然后,将边缘点按照集群分类,并将边缘坐标变换到关键帧的DT图以计算边缘对齐误差.基于边缘对齐的误差模型为
| $ \mathit{r}_{\rm{E}}^\mathit{i}\left( \mathit{\xi } \right) = D{T_{\rm{k}}}\left( {\omega \left( {{\mathit{\boldsymbol{\xi }}_{{\rm{kc}}}}, p_{\rm{c}}^i} \right)} \right), $ | (7) |
式中, rEi表示边缘点i对应的DT误差,DTk表示关键帧的DT误差函数.根据关键帧提取的边缘,可以很快速地计算出DT图[17],如图 2所示,(a)为原始灰度图,(b)为边缘检测图,(c)为由边缘得到的DT图,其中距离边缘远的像素呈白色.

|
图 2 DT计算 Fig. 2 Calculation of distance transform (DT) |
直接法基于灰度不变假设,所以导致rIi受光照变化影响较大,且对于运动模糊图像的处理也会产生较大误差,而边缘信息对于光照变化以及图像模糊不敏感.因此,通过引入基于边缘对齐的误差模型rEi,来提高算法的鲁棒性.同时,在纹理单一的环境中,直接法可以避免边缘过少导致算法精度下降的问题[18].
将边缘对齐误差引入到光度及几何误差中构建融合边缘信息的残差模型,能够计算出更准确的残差.但是,背景的遮挡区域往往会导致残差模型具有较高的值,类似于Jaimez等[13]的方法,为降低遮挡的影响,定义残差模型为
| $ {\mathit{r}_n}\left( \mathit{\boldsymbol{\xi }} \right) = \frac{{\sum\nolimits_{i = 1}^{{S_n} - {O_n}} {\left( {{\alpha _{\rm{I}}}r_{\rm{I}}^i + r_{\rm{Z}}^i/{{\bar Z}_n}} \right)} }}{{{S_n} - {O_n}}} + \frac{{\sum\nolimits_{i = 1}^{{E_n} - {O_n}} {{\alpha _{\rm{E}}}r_{\rm{E}}^i} }}{{{E_n} - {O_n}}}. $ | (8) |
式中:rn表示第n个集群的残差值,Sn表示第n个集群中所有深度有效的像素个数,On表示第n个集群中遮挡的像素个数,En表示第n个集群中所有深度有效的边缘点,Zn为第n个集群的平均深度,αI与αE分别表示光度误差与DT误差在残差模型中所占权重.为了加强算法应对各种环境的鲁棒性,构建权重公式为
| $ {\alpha _{\rm{E}}} = \frac{{\eta {v_{\rm{c}}}\sum\nolimits_{n = 1}^N {{E_n}} }}{{\sum\nolimits_{n = 1}^N {{S_n}} }}{\alpha _{\rm{I}}}. $ | (9) |
式中:vc为相机运动速度,N为集群总数量,η为由αI到αE的尺度系数.在边缘信息丰富(边缘点占比高)或相机运动速度较快时(容易产生模糊图像),αE有较大值,相反,αE较小时边缘信息影响较小.
使用原始集群残差往往准确率不高,运动分割效果较差.因此,参考Jaimez等[13]的方法进行残差正则化,对连续的集群偏向于相似的运动分割,建立最小化模型来求取正则化残差公式为
| $ \begin{array}{l} E\left( {{\mathit{r}_n}} \right) = {\lambda _{\rm{R}}}\sum\limits_{m = 1}^N {{G_{mn}}{{\left( {{r_n} - {r_m}} \right)}^2}} \\ \;\;\;\;\;\;\;\;\;\;\;\;\;{\lambda _{\rm{T}}}{\left( {{r_n} - {r_{n, c - 1}}} \right)^2}. \end{array} $ | (10) |
式中,Gmn为聚类连通函数,为1表示m与n集群连通; rn, c-1表示上一帧中第n个集群的残差值,因为在时间上,物体都是趋于保持移动或静止的.通过求解最小问题来得到最佳rn,正则化后的残差模型与动态物体有较高的相关性.
2.3.4 平均背景深度辅助运动分割为了减少场景的错误分割与过度分割,提高运动分割的准确性,本文引入平均背景深度来辅助算法进行运动分割.动态物体一般都为独立的刚体且远离背景,通过扩大远离背景部分的集群残差,使得靠近背景的集群偏向于分割为静态部分,而远离背景的集群有更大几率被判定为动态部分.定义平均背景深度为
| $ {{\mathit{\bar Z}}_{{\rm{b, c}}}} = {\lambda _{\rm{D}}}{{\mathit{\bar Z}}_{{\rm{b, c - 1}}}} + \left( {1 - {\lambda _{\rm{D}}}} \right)\frac{{\sum\nolimits_{n = 1}^{N - {d_{c - 1}}} {{{\mathit{\bar Z}}_n}} }}{{N - {d_{c - 1}}}}. $ | (11) |
式中, Zb, c表示当前帧平均背景深度,dc-1为上一帧所分割出的动态集群数量.采用上一帧dc-1计算当前帧的平均深度原因有3点:1)相邻两帧图像的聚类与运动分割大致相同;2)可通过权重λD来降低两帧间运动分割不一致产生的误差;3)背景不会移动,只有当相机移动时,背景深度才会变化,通过引入加权Zb, c-1可使背景深度缓慢变化,符合相机缓慢移动的事实.引入平均背景深度后的残差模型为
| $ {\delta _n} = \left( {1 + |{{\mathit{\bar Z}}_\mathit{n}} - {{\mathit{\bar Z}}_{{\rm{b, c}}}}|} \right){r_n}. $ | (12) |
式中, δn为引入平均背景深度后的第n个集群的残差值,|Zn-Zb, c|表示第n个集群与背景的距离.平均背景深度的引入使得距离背景较远的动态部分有更大的残差值,而距离背景较近的动态部分本身就有较大的残差,以此来扩大动、静部分残差差距而有利于正确的运动分割.
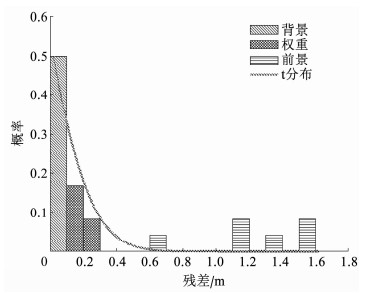
2.4 相机位姿估计动态物体的独立运动会使得两帧之间坐标变换后的动态物体图像不对齐,而导致属于该物体的集群有较大的残差,而静态集群的残差在图像对齐的情况下往往很小或接近于0.图 3是一个高度动态场景的统计残差直方图,根据聚类残差分布的普遍特征,参考文献[12, 19]的方法建立一个基于t分布的非参数统计模型
|
图 3 残差直方图与t分布曲线 Fig. 3 Residual histogram and t distribution curve |
| $ {\mathit{w}_n} = \frac{{{v_0} + 1}}{{{v_0} + {{\left( {\left( {{\delta _n} - \mu } \right)/\sigma } \right)}^2}}}, $ | (13) |
| $ \sigma = 1.4826{\rm{Median}}\left\{ {\left| {\left( {{\delta _n} - \mu } \right)} \right|} \right\}. $ | (14) |
式中:v0为t分布的自由度,它决定了分布曲线的陡峭程度; 平均值μ决定分布中心所处位置,将其设置为0表示残差小的静态集群占比较大; σ为统计方差,通过中位数绝对偏差估算得到.
如图 3所示,非参数统计模型能够较好地拟合实际实验残差的直方图.由于统计模型的概率代表了聚类的运动似然,因此可以指导场景进行运动分割.在各种复杂的场景下,采用固定阈值会使得分割效果不佳,参考Zhou等[19]的方法使用自适应阈值构建场景分割模型,残差高于自适应阈值的集群可判定为动态部分,而低于阈值的集群可作为静态部分或赋权部分加入到位姿估算中,其公式为
| $ {\varphi _n} = \left\{ \begin{array}{l} 0, {\delta _n} \ge 1/\left( {\min \left( {10, \max \left( {3.\beta v{_{\rm{c}}}\sigma } \right)} \right)} \right);\\ 1, {\delta _n} < 1/10;\\ {\mathit{w}_n}, {\rm{Others}}. \end{array} \right. $ | (15) |
式中:φn代表第n个集群的权重,为0时表示该集群为动态集群,为1时表示为静态集群; vc为相机速度; σ为统计方差; β用于调整因变量到残差尺度的系数,通过公式103×min(103, 10dc-1)计算得到.
计算出集群权重后,便可得到加权聚类残差,通过加权聚类残差来构建非线性优化函数,用以更准确地估计帧间运动.文献[13, 19]的方法表明,采用Cauchy M-estimator模型进行优化能获得较好的结果.构建融合边缘信息的加权聚类残差的非线性优化函数
| $ \begin{array}{l} \mathit{\boldsymbol{\xi = }}\mathop {{\rm{argmin}}}\limits_\mathit{\boldsymbol{\xi }} \left\{ {\sum\limits_{i = 1}^M {\left[ {F\left( {\varphi _n^ir_{\rm{Z}}^i\left( \mathit{\boldsymbol{\xi }} \right)} \right) + F\left( {{\alpha _{\rm{I}}}\varphi _n^ir_{\rm{I}}^i\left( \mathit{\boldsymbol{\xi }} \right)} \right) + } \right.} } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {\left. {F\left( {{\alpha _{\rm{E}}}\varphi _n^ir_{\rm{E}}^i\left( \mathit{\boldsymbol{\xi }} \right)} \right)} \right]} \right\}, \end{array} $ | (16) |
| $ \mathit{F}\left( r \right) = \frac{{{c^2}}}{2}\log \left( {1 + {{\left( {\frac{r}{c}} \right)}^2}} \right). $ | (17) |
式中:M表示所有深度有效的点的数量,φni表示属于第n个集群的点i的权重,参数c标记了F的转折点.通过最小化非线性优化函数求得最佳的帧间运动.
2.5 跟踪质量检测本文采用帧到关键帧的跟踪方法,只有在更新关键帧的时候才会进行复杂的DT计算,相比于传统的帧对帧计算每一帧DT的方法[20],大大提高了计算效率.另外,采用帧与关键帧的跟踪方法,可使得非刚性物体的轻微运动更加容易区分,从而降低轻微运动导致的累计误差.参考Schenk等[16]的方法,通过将先前跟踪过的N帧的边缘投影到当前帧,得到像素点重叠计数图,通过对相同重叠数构建直方图,来获取图像重叠情况,从而评估当前帧跟踪质量,公式为
| $ \sum\limits_{j = 1}^N {{\gamma _j}H\left( j \right) \le {\gamma _0}H\left( 0 \right).} $ | (18) |
式中, H(j)表示重叠数为j的点的数量,γj表示重叠数为j的点在跟踪质量评估中所占的权重.当边缘重叠的加权和小于非重叠的数量时,说明跟踪质量较差,此时将上一跟踪较好的帧更新为关键帧.
3 实验与分析本实验所用电脑配置为:CPU为英特尔i5-4210,主频为1.7 GHz,内存为4 G,不使用图形处理器(GPU)加速,在Ubuntu 16.04下进行实验.本文算法的运行基于每一时间帧的灰度与深度信息,因此主要适用于RGB-D相机.在慕尼黑工业大学提供的TUM RGB-D标准数据集[21]上进行实验,每个序列包含RGB图像、深度图像以及真实轨迹等,该数据集已被广泛用于测试各种SLAM和VO算法的准确性和性能.为了方便算法评估,将数据集分为2类:1)低动态与静态环境,此类数据集下没有移动物体或仅有少量移动物体;2)高动态环境,人或其他移动物体在图像中占比较大.同时在这2类数据集下测试来评估算法的综合性能.
本文实验取K-means聚类集群数N为24,并设置其他参数如下:1)在残差模型建立部分,如图 4所示,(a)为原始图像;仅采用几何信息进行运动分割时,即αI为0,可见(b)中由于信息不足而导致分割不完全;(c)中融合光度信息并设置较高的αI值导致光度信息占比较高而产生过度分割;(d)为融合光度信息并取合适的αI所产生的较准确的分割结果;(e)中融合边缘信息并取较高的η值时,同样会导致过度分割;(f)为最准确的分割结果,此时设置光度误差权重αI为0.15,计算DT误差权重的尺度因子η为0.35,来平衡几何、光度、边缘信息对残差模型的影响.2)在残差正则化部分,参考文献[13]的方法,将式(10)中的参数设置为λR=0.5,λT=1.5来设置空间正则化与时间正则化的权重.3)将式(11)中的λD设为0.7来计算稳定且缓慢变化的平均背景深度.4)在跟踪质量检测中,参考文献[16]的方法,将前3帧的边缘投影到当前帧进行质量评估,设置式(18)中γj=[1, 1, 1.25, 1.5],其中j∈[0, 3].以上参数为本次实验中获取的经验值,并非最优参数,但在实验中提供了良好的结果.

|
图 4 信息权重 Fig. 4 Schematic diagram of information weights |
为了评估本文算法的精度,与现存的3种算法进行了比较:包括结合场景流的VO-SF[13]、基于边缘对齐的REVO[16]以及文献[19]的方法.以上算法都是基于RGB-D数据进行实验,其中REVO仅利用边缘信息进行位姿估计,且未处理动态目标,与其进行对比的原因在于评估算法在静态环境下的精度以及效率.VO-SF与文献[19]的方法都是目前动态环境下较为先进的视觉里程计算法.
3.1 运动分割运动分割用于剔除动态部分,使视觉里程计仅使用静态部分计算相机位姿.如若分割错误,部分动态物体未被检测而加入位姿计算,会导致相机与动态物体产生错误的相对运动而造成位姿估计误差.若过度分割,将部分静态物体剔除,会使得位姿估计中可用像素信息减少而增大位姿估计误差.因此,正确的运动分割对于动态环境下的视觉里程计起到至关重要的作用.
在多种动态环境下采用VO-SF算法与本文算法进行运动分割比较实验,结果见图 5.(a)为原始RGB图,(b)为有聚类信息的边缘图,(c)为VO-SF算法运动分割结果,(d)为本文算法运动分割结果,深色为静态部分,浅色为动态部分.(1)与(2)展示了动态物体在图像像素占比较大的情况,因引入了丰富的边缘信息则相比于VO-SF有更为准确的运动分割.引入的平均背景深度能辅助运动分割,从(3)与(4)可以看出,平均背景深度加大了远离背景的物体的残差,从而避免了(3)中动、静态部分分割错误并在(4)中准确地检测出了远离相机的移动物体.(5)中椅子因靠近移动的人而被分割为动态物体,轻量的过度分割是合理的且不会影响整体的位姿估计.(6)与(7)分别为有效深度过少的图像以及相机移动过快导致的模糊图像,这两种情况会因严重的信息丢失而导致较差的分割结果,但是引入边缘信息使得本文算法在类似情况下仍优于VO-SF.

|
图 5 运动分割 Fig. 5 Motion segmentation results |
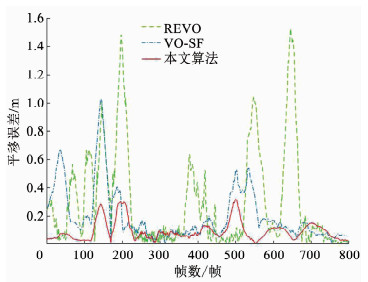
相对位姿误差(RPE)[21]用于测量每秒的平均漂移量,使用RPE对本文算法以及另外3种算法进行评估,分别在静态与低动态环境和高动态环境下进行了实验,文献[19]采用该文献部分原始数据.实验结果见表 1,在静态与低动态环境下,本文算法可能因场景过度分割而造成边缘信息减少,但光度误差能为位姿估计提供更多的约束,对比仅采用边缘信息的REVO算法也拥有较好的性能,而对比VO-SF与文献[19]的方法,本文算法明显有更优的性能.在高动态环境下,本文算法采用帧与关键帧的跟踪方法避免非刚性物体造成的累积误差,并利用平均背景深度来辅助场景分割.从表 1中可看出本文算法在高动态环境下拥有更高的精度,相比VO-SF平均精度提升了45%,相比文献[19]平均精度提升了15%.图 6通过对REVO、VO-SF与本文算法在序列fr3/walking_xyz下进行了轨迹漂移比较,可以很直观地看出本文算法精度高于其他算法.
| 表 1 平移和旋转均方根误差 Tab. 1 RMSE of translation and rotation |
|
图 6 fr3/walking_xyz下相对轨迹误差 Fig. 6 Relative trajectory error of fr3/walking_xyz |
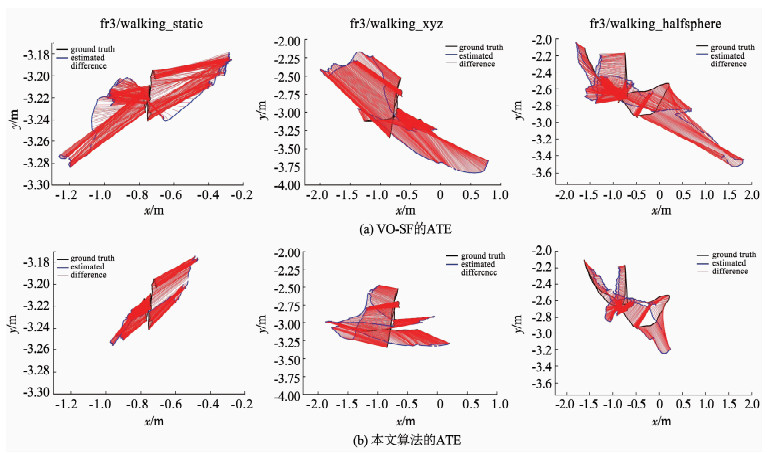
绝对轨迹误差(ATE)[21]用于测量轨迹的整体质量,使用ATE图可以直观地看出估计轨迹与真实轨迹的区别,结果见图 7.图中, (a)为VO-SF的绝对轨迹误差,(b)为本文算法的绝对轨迹误差.从图中可以看出,本文算法具有更小的轨迹误差,验证了本文算法改进的有效性.
|
图 7 不同算法的绝对轨迹误差 Fig. 7 Absolute trajectory error of different algorithms |
为了比较运行时间,在同样的实验环境,本文算法采用与其他算法相同的分辨率为320×240的QVGA图像进行实验.结果表明,在不采用GPU加速的前提下,REVO因仅采用边缘信息且未对动态物体进行处理,因此计算效率较高,平均每帧运行时间为55 ms,VO-SF平均每帧运行时间为80 ms.因本文引入边缘信息,并在插入关键帧的时候进行了更多的处理,因此运行时间比其他算法要较长,平均每帧运行时间为100 ms,基本满足实时性.
4 结论本文提出了一种融合边缘信息的稠密视觉里程计算法,将边缘信息加入到运动分割与位姿估计中,并引入平均背景深度辅助运动分割,然后利用边缘进行关键帧选择.边缘信息的融合使得算法在多种不同的环境下拥有更好的鲁棒性,同时对于几何纹理较少的环境,更多地采用光度结合深度信息来进行位姿估计,降低环境特征过少而导致的误差.在TUM公共数据集上的实验结果表明,本文算法在静态环境下以及富有挑战性的高动态环境下都能取得较好的结果,能够检测出距离相机较远的动态部分,在信息丢失、图像模糊等情况下也有更好的鲁棒性.
视觉里程计算法在各种环境下不可避免地产生误差,累积误差会导致估计位姿偏离真实位姿.因此,下一步工作将融合IMU(惯性测量单元)数据,在动态环境下为位姿求解添加更多的约束项,用以降低位姿估计误差,并考虑加入回环检测以消除累积误差,进一步提高算法精度.
| [1] |
CADENA C, CARLONE L, CARRILLO H, et al. Past, present, and future of simultaneous localization and mapping: toward the robust-perception age[J]. IEEE Transactions on Robotics, 2016, 32(6): 1309. DOI:10.1109/TRO.2016.2624754 |
| [2] |
BRESSON G, ALSAYED Z, YU Li, et al. Simultaneous localization and mapping: a survey of current trends in autonomous driving[J]. IEEE Transactions on Intelligent Vehicles, 2017, 2(3): 194. DOI:10.1109/TIV.2017.2749181 |
| [3] |
刘浩敏, 章国锋, 鲍虎军. 基于单目视觉的同时定位与地图构建方法综述[J]. 计算机辅助设计与图形学学报, 2016, 28(6): 855. LIU Haomin, ZHANG Guofeng, BAO Hujun. A survey of monocular simultaneous localization and mapping[J]. Journal of Computer-Aided Design and Computer Graphics, 2016, 28(6): 855. DOI:10.3969/j.issn.1003-9775.2016.06.001 |
| [4] |
KLEIN G, MURRAY D. Parallel tracking and mapping for small AR workspaces[C]//2007 6th IEEE and ACM International Symposium on Mixed and Augmented Reality. Nara: IEEE, 2007: 225. DOI: 10.1109/ISMAR.2007.4538852
|
| [5] |
MUR-ARTAL R, MONTIEl J M M, TARDÓS J D. ORB-SLAM: a versatile and accurate monocular SLAM system[J]. IEEE Transactions on Robotics, 2015, 31(5): 1147. DOI:10.1109/TRO.2015.2463671 |
| [6] |
MUR-ARTAL R, TARDÓS J D. ORB-SLAM2: an open-source SLAM system for monocular, stereo and RGB-D cameras[J]. IEEE Transactions on Robotics, 2016, 33(5): 1255. DOI:10.1109/TRO.2017.2705103 |
| [7] |
ENGEL J, SCHÖPS T, CREMERS D.LSD-SLAM: large-scale direct monocular SLAM[C]//Computer Vision - ECCV 2014. Cham: Springer, 2014: 834. DOI: 10.1007/978-3-319-10605-2_54
|
| [8] |
ENGEL J, STVCKLER J, CREMERS D. Large-scale direct SLAM with stereo cameras[C]//2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). Hamburg: IEEE, 2015: 1935. DOI: 10.1109/IROS.2015.7353631
|
| [9] |
ENGEL J, KOLTUN V, CREMERS D. Direct sparse odometry[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2018, 40(3): 611. DOI:10.1109/TPAMI.2017.2658577 |
| [10] |
FORSTER C, PIZZOLI M, SCARAMUZZA D. SVO: fast semi-direct monocular visual odometry[C]//2014 IEEE International Conference on Robotics and Automation (ICRA). Hong Kong: IEEE, 2014: 15. DOI: 10.1109/ICRA.2014.6906584
|
| [11] |
BESCOS B, FÁCIL J M, CIVERA J, et al. DynaSLAM: tracking, mapping, and inpainting in dynamic scenes[J]. IEEE Robotics and Automation Letters, 2018, 3(4): 4076. DOI:10.1109/LRA.2018.2860039 |
| [12] |
LI Shile, LEE D H. RGB-D SLAM in dynamic environments using static point weighting[J]. IEEE Robotics and Automation Letters, 2017, 2(4): 2263. DOI:10.1109/LRA.2017.2724759 |
| [13] |
JAIMEZ M, KERL C, GONZALEZ-JIMENEZ J, et al. Fast odometry and scene flow from RGB-D cameras based on geometric clustering[C]//2017 IEEE International Conference on Robotics and Automation (ICRA). Singapore: IEEE, 2017: 3992. DOI: 10.1109/ICRA.2017.7989459
|
| [14] |
SCONA R, JAIMEZ M, PETILLOT Y R, et al. StaticFusion: background reconstruction for dense RGB-D SLAM in dynamic environments[C]//2018 IEEE International Conference on Robotics and Automation (ICRA). Brisbane: IEEE, 2018: 3849. DOI: 10.1109/ICRA.2018.8460681
|
| [15] |
JAIMEZ M, SOUIAI M, STVCKLER J, et al. Motion cooperation: smooth piece-wise rigid scene flow from RGB-D images[C]//2015 IEEE International Conference on 3D Vision. Lyon: IEEE, 2015: 64. DOI: 10.1109/3DV.2015.15
|
| [16] |
SCHENK F, FRAUNDORFER F. Robust edge-based visual odometry using machine-learned edges[C]//2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). Vancouver: IEEE, 2017: 1297. DOI: 10.1109/IROS.2017.8202305
|
| [17] |
FELZENSZWALB P F, HUTTENLOCHER D P. Distance transforms of sampled functions[J]. Theory of Computing, 2012, 8: 415. DOI:10.4086/toc.2012.v008a019 |
| [18] |
WANG Xin, WEI Dong, ZHOU Mingcai, et al. Edge enhanced direct visual odometry[C]//British Machine Vision Conference. York: BMVA Press, 2016: 35. DOI: 10.5244/C.30.35
|
| [19] |
ZHOU Wugen, PENG Xiaodong, WANG Haijiao, et al. Nonparametric statistical and clustering based RGB-D dense visual odometry in a dynamic environment[J]. 3D Research, 2019, 10(2): 1. DOI:10.1007/s13319-019-0220-4 |
| [20] |
KUSE M, SHEN Shaojie. Robust camera motion estimation using direct edge alignment and sub-gradient method[C]//2016 IEEE International Conference on Robotics and Automation (ICRA). Stockholm: IEEE, 2016: 573. DOI: 10.1109/ICRA.2016.7487181
|
| [21] |
STURM J, ENGELHARD N, ENDRES F, et al. A benchmark for the evaluation of RGB-D SLAM systems[C]//2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, 2012: 573. DOI: 10.1109/IROS.2012.6385773
|
 2021, Vol. 53
2021, Vol. 53


