波达方向(direction-of-arrival, DOA)估计是阵列信号处理中的重要内容,在雷达、通信及医学领域有着广泛的应用.空间谱方法是DOA估计的经典方法,如多信号分类(multiple signal classification, MUSIC)方法、旋转子空间不变(estimating signal parameter via rotational invariance techniques, ESPRIT)算法等.但是,传统的空间谱方法一般假设空间噪声为高斯均匀白噪声.在实际应用中,大多数阵列信号处理中面临色噪声环境.因此,有学者提出了色噪声环境下的阵列DOA估计改进方法,主要可分为3类:参数化方法[1]、四阶累积量算法[2-3]及协方差矩阵差分法[4-5].参数化方法一般需要预先知道噪声协方差矩阵结构特征,以此来进行预白化处理;四阶累积量算法通过构造观测信号的四阶累积量来消除非高斯色噪声影响;协方差差分法一般假设色噪声协方差矩阵满足Toeplitz结构,并通过将观测信号协方差矩阵与线性变换后的协方差矩阵进行差分处理来消除色噪声影响.
上述针对色噪声环境下DOA估计算法的大多数只适用于窄带阵列,在宽带阵列中的使用受限.目前,宽带DOA估计主要解决途径有:基于频率分解的非相干信号子空间方法[6-7](incoherent signal subspace method, ISSM)及基于频率聚焦的相干信号子空间方法[8-10](coherent signal subspace method, CSSM).ISSM方法对信噪比要求较高,低信噪比条件下性能急剧下降;CSSM方法在低信噪比条件下性能优于ISSM方法,但存在的问题是需要预估或者假设信号角度,以此来构建信号子空间,这种角度估计会导致聚焦矩阵出现偏差,最终导致DOA估计误差.为避免CSSM方法中角度预估带来的失配误差,有学者提出了改进算法.文献[11]提出基于频域时延补偿的DOA估计方法(DCF),避免了角度预估的问题,但是算法复杂度较高,用于实时阵列信号处理难度较大.文献[12]提出使用阵列自相关矩阵构造聚焦矩阵,避免了角度预估带来的误差,但是算法的估计性能有所下降.
结合来看,对于色噪声下的宽带阵列DOA估计问题,研究者提出解决一些方法.文献[13]提出一种低复杂度宽带色噪声DOA估计方法,利用空间差分技术去除Toeplitz结构的色噪声,然后通过RSS方法计算通用协方差矩阵,最后应用低复杂度的PM算法估计信号DOA;但是该算法对信源数较为敏感.文献[14]提出了一种基于数据协方差矩阵修正及TOPS算法相结合的宽带DOA估计方法(data covariance matrix correction with TOPS algorithm for DOA estimation, DCT-DE),利用特殊构造矩阵将色噪声协方差矩阵从数据协方差矩阵中剔除,然后利用平方TOPS算法实现宽带DOA估计.文献[15]提出基于FOCUSS的网格角度求解算法(MMV-FOCUSS),通过差分算法去除色噪声影响并构建新观测模型,采用分布优化的方式进行DOA估计,但是算法复杂度较高.
针对色噪声背景下宽带DOA估计存在的上述问题,本文提出基于差分聚焦的宽带阵列DOA估计方法.算法首先对信号协方差矩阵进行差分处理,消除色噪声影响;然后对差分矩阵进行特征分解,以差分矩阵正特征值对应的信号子空间为基础重构观测信号模型;在此基础上,分析了无需角度预估的特征向量空间聚焦DOA估计原理,并对特征向量矩阵进行重新分块排列,简化重构聚焦矩阵.理论分析及仿真结果表明,本文算法估计精度及稳健性较好,且不需角度预估、复杂度低.
1 阵列信号模型阵列排布为一维线阵,阵元数为K,阵元间距为d.空间中有I个宽带远场信号s(t)=[s1(t), …, sI(t)]入射至阵列,且信号与噪声相互独立,入射角为θ=[θ1, …, θI],则第k个阵元输出信号xk(t)可以表征为
| $ {\mathit{\boldsymbol{x}}_k}\left( t \right) = \sum\limits_{i = 1}^I {{\mathit{\boldsymbol{s}}_i}\left( {t - {\mathit{\boldsymbol{\tau }}_{k, i}}} \right) + {\mathit{\boldsymbol{n}}_k}\left( t \right)} . $ |
式中, τk, i为信号si(t)在第k个阵元相对于首个阵元的接收时延;nk(t)为第k个阵元接收非均匀噪声矢量,并假设空间噪声场为各向同性圆形或柱形场.
将足够长时间内阵列接收到的信号分割成若干独立快拍,对每个快拍内的数据进行离散傅里叶变换(discrete Fourier transform, DFT),得到J个频域窄带信号.宽带阵列接收信号的频域表示形式如下:
| $ \begin{array}{l} \mathit{\boldsymbol{X}}\left( {{f_j}} \right) = \mathit{\boldsymbol{A}}\left( {{f_j}, \mathit{\boldsymbol{\theta }}} \right)\mathit{\boldsymbol{S}}\left( {{f_j}} \right) + \mathit{\boldsymbol{N}}\left( {{f_j}} \right), j = 1, \cdots , J;\\ \mathit{\boldsymbol{X}}\left( {{f_j}} \right) = \left[ {{\mathit{\boldsymbol{X}}_k}\left( {{f_j}} \right), \cdots , {\mathit{\boldsymbol{X}}_K}\left( {{f_j}} \right)} \right];\\ \mathit{\boldsymbol{A}}\left( {{f_j}, \mathit{\boldsymbol{\theta }}} \right) = \left[ {\mathit{\boldsymbol{a}}\left( {{f_j}, {\mathit{\boldsymbol{\theta }}_1}} \right), \cdots , \mathit{\boldsymbol{a}}\left( {{f_j}, {\mathit{\boldsymbol{\theta }}_I}} \right)} \right];\\ \mathit{\boldsymbol{S}}\left( {{f_j}} \right) = \left[ {{\mathit{\boldsymbol{S}}_i}\left( {{f_j}} \right), \cdots , {\mathit{\boldsymbol{S}}_I}\left( {{f_j}} \right)} \right];\\ \mathit{\boldsymbol{N}}\left( {{f_j}} \right) = \left[ {{\mathit{\boldsymbol{N}}_k}\left( {{f_j}} \right), \cdots , {\mathit{\boldsymbol{N}}_K}\left( {{f_j}} \right)} \right]. \end{array} $ |
式中, A(fj, θ)为频点fj处的阵列流形;a(fj, θi)为入射角为θi的信号在频点fj的方位导向矢量.
频点fj处的阵列输出信号自相关矩阵可表示为
| $ \begin{array}{l} \mathit{\boldsymbol{R}}\left( {{f_j}, \mathit{\boldsymbol{\theta }}} \right) = E\left[ {\mathit{\boldsymbol{X}}\left( {{f_j}, \mathit{\boldsymbol{\theta }}} \right){\mathit{\boldsymbol{X}}^{\rm{H}}}\left( {{f_j}, \mathit{\boldsymbol{\theta }}} \right)} \right] = \\ \mathit{\boldsymbol{A}}\left( {{f_j}, \mathit{\boldsymbol{\theta }}} \right){\mathit{\boldsymbol{R}}_{\rm{s}}}\left( {{f_j}, \mathit{\boldsymbol{\theta }}} \right){\mathit{\boldsymbol{A}}^{\rm{H}}}\left( {{f_j}, \mathit{\boldsymbol{\theta }}} \right) + \\ E\left[ {\mathit{\boldsymbol{N}}\left( {{f_j}} \right){\mathit{\boldsymbol{N}}^{\rm{H}}}\left( {{f_j}} \right)} \right] = \\ \mathit{\boldsymbol{A}}\left( {{f_j}, \mathit{\boldsymbol{\theta }}} \right){\mathit{\boldsymbol{R}}_{\rm{s}}}\left( {{f_j}, \mathit{\boldsymbol{\theta }}} \right){\mathit{\boldsymbol{A}}^{\rm{H}}}\left( {{f_j}, \mathit{\boldsymbol{\theta }}} \right) + {\mathit{\boldsymbol{Q}}_N}. \end{array} $ |
式中QN表示噪声信号协方差矩阵.高斯相关色噪声协方差矩阵QN的第(n1, n2)个元素为[16]
| $ {\mathit{\boldsymbol{Q}}_N}\left( {{n_1}, {n_2}} \right) = {\sigma ^2}{\gamma ^{\left| {{n_1} - {n_2}} \right|}}{{\rm{e}}^{\left| {j{p_i}\left( {{n_1} - {n_2}} \right)/2} \right|}}. $ |
式中σ2为噪声功率,用于调整信噪比参数;γ为回归系数,用于调整噪声相干性.
2 协方差矩阵差分理论由于假设空间噪声场为同性圆形或柱形场,因此色噪声信号协方差矩阵满足Toeplitz结构[4].可知,噪声协方差矩阵分量旋转不变,有
| $ {\mathit{\boldsymbol{Q}}_N} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{\mathit{\boldsymbol{Q}}_N}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}. $ |
式中Φ表示转置矩阵.
对协方差矩阵变化前后求差得到
| $ \begin{array}{l} \Delta \mathit{\boldsymbol{R = R}} - \mathit{\boldsymbol{ \boldsymbol{\varPhi} R \boldsymbol{\varPhi} = }}\\ \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{R}}_{\rm{S}}}{\mathit{\boldsymbol{A}}^{\rm{H}}} + {\mathit{\boldsymbol{Q}}_N} - \mathit{\boldsymbol{ \boldsymbol{\varPhi} A}}{\mathit{\boldsymbol{R}}_{\rm{S}}}{\mathit{\boldsymbol{A}}^{\rm{H}}}\mathit{\boldsymbol{ \boldsymbol{\varPhi} - \boldsymbol{\varPhi} }}{\mathit{\boldsymbol{Q}}_N}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }} = \\ \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{R}}_{\rm{S}}}{\mathit{\boldsymbol{A}}^{\rm{H}}} - \mathit{\boldsymbol{ \boldsymbol{\varPhi} A}}{\mathit{\boldsymbol{R}}_{\rm{S}}}{\mathit{\boldsymbol{A}}^{\rm{H}}}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }} = \\ \left[ {\mathit{\boldsymbol{A}}, \mathit{\boldsymbol{ \boldsymbol{\varPhi} A}}} \right]\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{R}}_{\rm{S}}}}&{}\\ {}&{ - {\mathit{\boldsymbol{R}}_{\rm{S}}}} \end{array}} \right]{\left[ {\mathit{\boldsymbol{A}}, \mathit{\boldsymbol{ \boldsymbol{\varPhi} A}}} \right]^{\rm{H}}}. \end{array} $ | (1) |
从上式可以看出,在差分协方差矩阵ΔR中,噪声分量已被消除.对[A, ΦA]进行分解,有
| $ \left[ {\mathit{\boldsymbol{A}}, \mathit{\boldsymbol{ \boldsymbol{\varPhi} A}}} \right] = \left[ {\mathit{\boldsymbol{A}}, {\mathit{\boldsymbol{A}}^*}} \right]\left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{I}}&0\\ 0&\mathit{\boldsymbol{D}} \end{array}} \right]. $ | (2) |
其中(·)*表示矩阵共轭.将式(2)代入式(1)中,可得
| $ \Delta \mathit{\boldsymbol{R}} = \left[ {\mathit{\boldsymbol{A}}, {\mathit{\boldsymbol{A}}^*}} \right]\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{R}}_{\rm{S}}}}&{}\\ {}&{ - \mathit{\boldsymbol{D}}{\mathit{\boldsymbol{R}}_{\rm{S}}}{\mathit{\boldsymbol{D}}^{\rm{H}}}} \end{array}} \right]{\left[ {\mathit{\boldsymbol{A}}, {\mathit{\boldsymbol{A}}^*}} \right]^{\rm{H}}}. $ |
从上式可以看出,A对应信源入射真实角度,而A*则对应信源入射负角度.因此,利用ΔR进行DOA估计的过程中,不可避免地会出现伪峰.
3 DOA估计方法 3.1 差分协方差矩阵特征分解针对协方差矩阵差分过程导致的伪峰问题,本文对差分矩阵ΔR进行特征分解,取正特征值对应的信号子空间作为DOA估计基础,有
| $ \Delta \mathit{\boldsymbol{R}} = \mathit{\boldsymbol{U \boldsymbol{\varLambda} }}{\mathit{\boldsymbol{U}}^{\rm{H}}} = \left[ {{\mathit{\boldsymbol{U}}_ + }, {\mathit{\boldsymbol{U}}_{\rm{n}}}, {\mathit{\boldsymbol{U}}_{\rm{ - }}}} \right]\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}\left[ {{\mathit{\boldsymbol{U}}_ + }, {\mathit{\boldsymbol{U}}_{\rm{n}}}, {\mathit{\boldsymbol{U}}_{\rm{ - }}}} \right]. $ |
式中:U+是由I个正特征值对应的特征向量构成的特征矩阵;Un对应噪声子空间;U_是由N个负特征值对应的特征向量构成的特征矩阵;Λ可分别表示为
| $ \mathit{\boldsymbol{ \boldsymbol{\varLambda} }} = {\rm{diag}}\left( {{\lambda _1}, \cdots , {\lambda _I}, \vec \sigma , - {\lambda _I}, \cdots , - {\lambda _1}} \right). $ |
从上述分析知,U+可张成导向矢量A,因此可建立新的观测模型如下:
| $ {\mathit{\boldsymbol{U}}_ + } = \mathit{\boldsymbol{Aq}}{\rm{ + }}\mathit{\boldsymbol{\varepsilon }}{\rm{.}} $ |
式中:q为新观测模型对应的信号矩阵;ε为新观测模型对应的噪声分量.新的观测模型经过差分分解处理后,不再含有色噪声分量,同时包含了全部目标方位信息,可较好用于宽带DOA估计.
3.2 DOA估计方法 3.2.1 DOA估计基本原理在构建新的观测模型基础上,本文提出特征向量信号子空间聚焦的方法进行宽带DOA估计.
首先,对于新的观测模型,信号自相关矩阵R+可表示为
| $ {\mathit{\boldsymbol{R}}_ + } = {\rm{E}}\left( {{\mathit{\boldsymbol{U}}_ + }\mathit{\boldsymbol{U}}_ + ^{\rm{H}}} \right) = \mathit{\boldsymbol{AP}}{\mathit{\boldsymbol{A}}^{\rm{H}}} + {\delta ^2}\mathit{\boldsymbol{I}}{\rm{.}} $ | (3) |
其中P表示无噪声信号自相关矩阵.P为Hermitian矩阵,因此可酉相似于对角矩阵,表示为
| $ \mathit{\boldsymbol{P}} = \mathit{\boldsymbol{VM}}{\mathit{\boldsymbol{V}}^{\rm{H}}}. $ |
式中, 矩阵V为P的特征向量矩阵;M为P的特征值矩阵.由于V为酉矩阵,因此其向量
本文以子空间Γj为聚焦空间,设定参考聚焦矩阵Ψ0,则有
| $ {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_0} = {\mathit{\boldsymbol{V}}_0}\mathit{\boldsymbol{ \boldsymbol{\varOmega} V}}_0^{\rm{H}}. $ | (4) |
式中Ω为参考聚焦矩阵Ψ0在聚焦空间Γj中的系数矩阵.聚焦矩阵为T,则T满足
| $ \begin{array}{*{20}{l}} {{\rm{min}}\left\| {{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_0} - {\mathit{\boldsymbol{T}}_j}\mathit{\boldsymbol{P}}\left( {f,\mathit{\boldsymbol{\theta }}} \right)\mathit{\boldsymbol{T}}_j^{\rm{H}}} \right\|_F^2,}\\ {{\rm{s}}.{\rm{t}}.\;\;{\mathit{\boldsymbol{T}}_j}\mathit{\boldsymbol{T}}_j^{\rm{H}} = \mathit{\boldsymbol{I}};j{\rm{ = 1}}, \cdots ,\mathit{\boldsymbol{J}}.} \end{array} $ |
按照文献[10]推导,有
| $ {\mathit{\boldsymbol{T}}_j} = \mathit{\boldsymbol{\xi V}}_j^{\rm{H}}. $ | (5) |
式中ξ为参考聚焦矩阵Ψ0的特征向量矩阵.若要实现完美聚焦,则应有
| $ \sum\limits_{j = 1}^J {\left\| {{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_0} - {\mathit{\boldsymbol{T}}_j}\mathit{\boldsymbol{P}}\left( {{f_j}, \mathit{\boldsymbol{\theta }}} \right)\mathit{\boldsymbol{T}}_j^{\rm{H}}} \right\|_F^2} = 0 $ |
上式可化为
| $ \begin{array}{l} \sum\limits_{j = 1}^J {\left\| {{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_0} - {\mathit{\boldsymbol{T}}_j}\mathit{\boldsymbol{P}}\left( {{f_j}, \mathit{\boldsymbol{\theta }}} \right)\mathit{\boldsymbol{T}}_j^{\rm{H}}} \right\|_F^2} = \\ \sum\limits_{j = 1}^J {\left\| {{\mathit{\boldsymbol{V}}_0}\mathit{\boldsymbol{ \boldsymbol{\varOmega} V}}_0^{\rm{H}} - {\mathit{\boldsymbol{T}}_j}{\mathit{\boldsymbol{V}}_j}{\mathit{\boldsymbol{M}}_j}\mathit{\boldsymbol{V}}_j^{\rm{H}}\mathit{\boldsymbol{T}}_j^{\rm{H}}} \right\|_F^2} . \end{array} $ | (6) |
式中, V0及Vj分别为频点f0及fj处的特征向量矩阵.观察式(6),为了方便计算合并,令
| $ {\mathit{\boldsymbol{T}}_j} = {\mathit{\boldsymbol{V}}_0}*\mathit{\boldsymbol{W*V}}_j^{\rm{H}}. $ |
式中W为未知矩阵.则式(6)可进一步化为
| $ \begin{array}{l} \sum\limits_{j = 1}^J {\left\| {{\mathit{\boldsymbol{V}}_0}\mathit{\boldsymbol{ \boldsymbol{\varOmega} V}}_0^{\rm{H}} - {\mathit{\boldsymbol{T}}_j}{\mathit{\boldsymbol{V}}_j}{\mathit{\boldsymbol{M}}_j}\mathit{\boldsymbol{V}}_j^{\rm{H}}\mathit{\boldsymbol{T}}_j^{\rm{H}}} \right\|_F^2} = \\ \sum\limits_{j = 1}^J {\left\| {{\mathit{\boldsymbol{V}}_0}\left( {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }} - \mathit{\boldsymbol{W}}{\mathit{\boldsymbol{M}}_j}{\mathit{\boldsymbol{W}}^{\rm{H}}}} \right)\mathit{\boldsymbol{V}}_0^{\rm{H}}} \right\|_F^2} = \\ \sum\limits_{j = 1}^J {\left\| {{\mathit{\boldsymbol{V}}_0}\mathit{\boldsymbol{BV}}_0^{\rm{H}}} \right\|_F^2} . \end{array} $ |
式中B=Ω-WMjWH.由矩阵的范数特性可将上式进一步化为
| $ \begin{array}{l} \sum\limits_{j = 1}^J {\left\| {{\mathit{\boldsymbol{V}}_0}\mathit{\boldsymbol{BV}}_0^{\rm{H}}} \right\|_F^2} = \sum\limits_{j = 1}^J {{\rm{trace}}\left( {{\mathit{\boldsymbol{V}}_0}{\mathit{\boldsymbol{B}}^{\rm{H}}}\mathit{\boldsymbol{BV}}_0^{\rm{H}}} \right)} = \\ \;\;\;\;\;\;\;\;\;\;\;\sum\limits_{j = 1}^J {{\rm{trace}}\left( {{\mathit{\boldsymbol{B}}^{\rm{H}}}\mathit{\boldsymbol{B}}} \right)} . \end{array} $ | (7) |
可知,W为酉矩阵,Mj为对角矩阵,则WMjWH亦为对角矩阵.因此,若要式(7)为0,可行解之一为
| $ \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} = \frac{1}{J}\sum\limits_{j = 1}^J {\mathit{\boldsymbol{W}}{\mathit{\boldsymbol{M}}_j}{\mathit{\boldsymbol{W}}^{\rm{H}}}} . $ |
式中Ω为对角矩阵.对照式(4),可知V0即为参考聚焦矩阵Ψ0的特征向量矩阵.因此,根据式(5),有
| $ {\mathit{\boldsymbol{T}}_j} = {\mathit{\boldsymbol{V}}_0}\mathit{\boldsymbol{V}}_j^{\rm{H}}. $ |
为避免特征分解过程中零特征值所对应的特征向量对分辨门限的影响,对聚焦矩阵进行重构.目标信号的方位区间为β,对区间范围内按角度间隔进行功率谱积分可得
| $ \mathit{\Pi }\left( {{f_i}} \right) = \int_\beta {\frac{{\mathit{\boldsymbol{a}}\left( {\mathit{\boldsymbol{\theta }}, {f_j}} \right){\mathit{\boldsymbol{a}}^{\rm{H}}}\left( {\mathit{\boldsymbol{\theta }}, {f_j}} \right)}}{{{\mathit{\boldsymbol{a}}^{\rm{H}}}\left( {\mathit{\boldsymbol{\theta }}, {f_j}} \right){\mathit{\boldsymbol{R}}_ + }\left( {{f_i}} \right)\mathit{\boldsymbol{a}}\left( {\mathit{\boldsymbol{\theta }}, {f_j}} \right)}}} {\rm{d}}\mathit{\boldsymbol{\theta }}. $ | (8) |
对Π(fj)进行特征值分解,得出其显著特征值个数ρ(即为信号数).
将V0及Vj按照对应特征值递减的顺序进行重新排列,表示为
| $ \begin{array}{l} {\mathit{\boldsymbol{V}}_0} = \left[ {{{\mathit{\boldsymbol{V'}}}_0}, {{\mathit{\boldsymbol{V''}}}_0}} \right], \\ {\mathit{\boldsymbol{V}}_j} = \left[ {{{\mathit{\boldsymbol{V'}}}_j}, {{\mathit{\boldsymbol{V''}}}_j}} \right]. \end{array} $ |
式中V′0、V′j为K*ρ矩阵,即是由信号协方差矩阵特征分解后前ρ个显著特征值对应的特征向量构成.Vj为酉矩阵,则可知
| $ {\left( {{{\mathit{\boldsymbol{V''}}}_j}} \right)^{\rm{H}}}\mathit{\boldsymbol{A}}\left( {{f_j}} \right) = {\mathit{\boldsymbol{A}}^{\rm{H}}}\left( {{f_j}} \right){{\mathit{\boldsymbol{V''}}}_j} = 0. $ |
因此,
| $ \begin{array}{l} {\mathit{\boldsymbol{T}}_j}{\mathit{\boldsymbol{P}}_j}\mathit{\boldsymbol{T}}_j^{\rm{H}} = \left[ {{{\mathit{\boldsymbol{V'}}}_0}, {{\mathit{\boldsymbol{V''}}}_0}} \right]\left[ {\begin{array}{*{20}{c}} {{{\left( {{{\mathit{\boldsymbol{V'}}}_j}} \right)}^{\rm{H}}}}\\ {{{\left( {{{\mathit{\boldsymbol{V''}}}_j}} \right)}^{\rm{H}}}} \end{array}} \right]\mathit{\boldsymbol{A}}\left( {{f_j}} \right){\mathit{\boldsymbol{R}}_s}\left( {{f_j}} \right), \\ {\mathit{\boldsymbol{A}}^{\rm{H}}}\left( {{f_j}} \right)\left[ {\begin{array}{*{20}{c}} {{{\left( {{{\mathit{\boldsymbol{V'}}}_0}} \right)}^{\rm{H}}}}\\ {{{\left( {{{\mathit{\boldsymbol{V''}}}_0}} \right)}^{\rm{H}}}} \end{array}} \right]\left[ {{{\mathit{\boldsymbol{V'}}}_j}, {{\mathit{\boldsymbol{V''}}}_j}} \right] = \\ {{\mathit{\boldsymbol{V'}}}_0}{\left( {{{\mathit{\boldsymbol{V'}}}_j}} \right)^{\rm{H}}}{\mathit{\boldsymbol{P}}_j}{{\mathit{\boldsymbol{V'}}}_j}{\left( {{{\mathit{\boldsymbol{V'}}}_0}} \right)^{\rm{H}}}. \end{array} $ |
可得重构后的聚焦矩阵
| $ {{\mathit{\boldsymbol{\bar T}}}_j} = {{\mathit{\boldsymbol{V'}}}_0}{\left( {{{\mathit{\boldsymbol{V'}}}_j}} \right)^{\rm{H}}}. $ | (9) |
从上式看出,重构后的聚焦矩阵避免了协方差分解过程中非显著特征值所对应的特征向量,提高了算法在整个信噪比范围内的适应能力及分辨性能.
因此,针对新观测模型,经过聚焦平滑处理后的信号平均自相关矩阵R+可表示为
| $ {{\mathit{\boldsymbol{\bar R}}}_ + } = \frac{1}{J}\sum\limits_{j = 1}^J {{{\mathit{\boldsymbol{\bar T}}}_j}{\mathit{\boldsymbol{R}}_ + }\left( {{f_j}, \mathit{\boldsymbol{\theta }}} \right)\mathit{\boldsymbol{\bar T}}_j^{\rm{H}}} . $ | (10) |
得到R+后,可采用子空间类方法进行DOA估计.
3.3 算法实现步骤综上,本文算法步骤总结为:
1) 将阵列接收信号分割为独立快拍片段,进行DFT处理,计算各频点处的阵列输出信号自相关矩阵R(fj, θ);
2) 根据式(1)计算差分协方差矩阵ΔR(fj, θ),并对其进行特征分解得U+;
3) 按照式(3)求取R+(fj),对R+(fj)进行特征分解,得V0与Vj;
4) 按照式(8)求取Π(fj),对Π(fj)进行特征分解,得ρ;
5) 对V0、Vj进行重新排列,得V′0、V′j,按照式(9)求Tj;
6) 按照式(10)求R+,利用子空间类方法估计DOA.
4 仿真分析本小节通过仿真比较实验,分析本文所提算法的测向准确性、角分辨能力、算法稳健性及复杂度特性.基本仿真参数为:阵元数为8,工作带宽覆盖X波段(8~12 GHz),信号带宽500 MHz,采样频率为2.4 GHz,阵元间距为2.5 cm.仿真实验将本文算法与DCT-DE算法、MMV-FOCUSS算法及文献[13]算法进行比较分析.其中,MMV-FOCUSS算法的网格间距取1°.
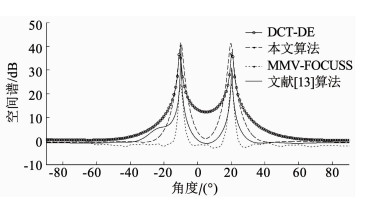
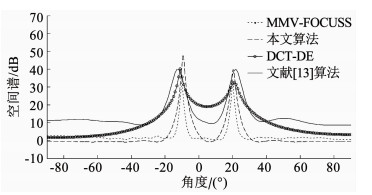
4.1 噪声背景下算法的测向精确性比较在高斯白噪声与高斯色噪声背景下,仿真比较本文算法与另外3种算法在不同噪声背景下的测向准确性.仿真实验中,设定2个独立的宽带辐射源,入射角度分别为-10°及20°,算法采用快拍数为200,白噪声信噪比设定为5 dB,色噪声信噪比设定为5 dB.4种算法的空间谱见图 1、2.
|
图 1 高斯白噪声下空间谱 Fig. 1 Spatial spectrum under Gaussian white noise |
|
图 2 高斯色噪声下空间谱 Fig. 2 Spatial spectrum under Gaussian colored noise |
从图 1看出,白噪声背景下本文算法、MMV-FOCUSS算法、DCT-DE算法及文献[13]算法均具备较好的DOA估计性能.从图 2看出,高斯色噪声背景下,文献[13]算法及DCT-DE算法谱峰出现较大偏差,MMV-FOCUSS算法测向精度稍好,但估计方差仍在2°以上,而本文算法保持较好的估计性能,测向精度较高.
4.2 噪声背景下算法的分辨能力比较本次仿真实验主要比较本文算法与其他3种算法在高斯色噪声背景下的角度分辨能力.仿真条件为:空间环境中设定两个独立的等功率辐射源,快拍数为500,噪声参数同上.入射角度间隔Δθ分别设定为Δθ=[2°, 4°, 8°, 15°],即入射角度θ为
| $ \begin{array}{l} \mathit{\boldsymbol{\theta }} = \left[ {\left( {{\mathit{\boldsymbol{\theta }}_1}, {\mathit{\boldsymbol{\theta }}_2}} \right)} \right] = \\ \left[ {\left( { - {1^ \circ }, {1^ \circ }} \right), \left( { - {2^ \circ }, {2^ \circ }} \right), \left( { - {4^ \circ }, {4^ \circ }} \right), \left( { - {7^ \circ }, {8^ \circ }} \right)} \right]. \end{array} $ |
仿真实验中,通过200次蒙特卡洛仿真实验,统计各类算法的平均分辨能力,比较分析4种算法在色噪声背景下的角度分辨性能.本文对角度分辨率η的定义为
| $ \eta {\rm{ = }}\frac{{Q\left( {{\mathit{\boldsymbol{\theta }}_1}} \right) + Q\left( {{\mathit{\boldsymbol{\theta }}_2}} \right)}}{2} - {Q_{\min }}. $ |
式中Q(θ)为根据R+计算的MUSIC谱函数.Qmin的计算式为
| $ {Q_{\min }} = \min \left[ {Q\left( \mathit{\boldsymbol{\theta }} \right)} \right], \mathit{\boldsymbol{\theta }} \in \left[ {{\mathit{\boldsymbol{\theta }}_1}, {\mathit{\boldsymbol{\theta }}_2}} \right]. $ |
可知,η代表两谱峰与峰间谷值之间的平均差,η越高,表示分辨能力越强.统计4种算法的平均分辨率见表 1.
| 表 1 算法分辨能力比较 Tab. 1 Algorithm resolution comparison |
从表 1看出,横向比较表格数据,两辐射源信号入射角度的间隔越大,则各算法的角度分辨率越高;纵向比较发现,相同的空间色噪声环境下,本文算法的角度分辨能力相较于MMV-FOCUSS及DCT-DE等算法更好.
4.3 算法稳健性分析本节对4种算法的稳健性进行仿真分析,主要包括估计方差及快拍数影响等.仿真实验中,单次估计误差<3°认为是有效实验,而估计方差及快拍数影响是对所有有效实验结果的统计.快拍数影响分析实验中,信噪比取5 dB.背景噪声为高斯色噪声,参数不变.仿真结果为200次蒙特卡洛仿真实验的统计平均.
从图 3看出,色噪声背景下,随着输入信噪比的不断提高,本文算法与MMV-FOCUSS始终保持较好的估计性能;而文献[13]算法在低信噪比条件下的估计性能较差.从图 4看出,随着快拍数的提升,文献[13]算法的性能提升较大,但总体性能差于本文算法及MMV-FOCUSS算法;在仿真所取的快拍数范围内,本文算法性能始终优于其他算法.

|
图 3 均方根误差随信噪比变化曲线 Fig. 3 Change curves of RMS error with SNR |

|
图 4 均方根误差随快拍数变化曲线 Fig. 4 Change curves of RMS error with snapshot numbers |
仿真条件设置为:设定两辐射源入射场景及三辐射源入射场景,入射角度分别为θ=[0°, 10°]及θ=[-10°, 0°, 10°],快拍数取200,信噪比取5 dB.仿真平台为MATLAB 2014a,运行于联想P1移动工作站,进行500次蒙特卡洛实验,求取算法平均运行时间,结果见表 2.
| 表 2 算法运行时间比较 Tab. 2 Comparison of algorithm runtimems |
分析表 2,本文算法的运行时间最短,MMV-FOCUSS算法的运行时间最长,而文献[13]算法与DCT_DE算法运行时间相当.从算法实现过程看,MMV-FOCUSS算法需要在每个角度间隔内进行迭代运算,造成的计算量较大;文献[13]算法在估计单频点参考聚焦矩阵的过程中,需要进行2次矩阵逆运算及4次矩阵乘法;DCT-DE算法需要进行3次特征值分解及2次矩阵乘法;本文算法需要进行3次特征值分解及1次矩阵乘法.因此,本文算法的运算复杂度相对较小.
5 结论针对色噪声背景下宽带阵列DOA估计精度差及稳健性不足的问题,本文提出基于差分聚焦的宽带阵列DOA估计方法.利用信号自相关矩阵差分去除色噪声影响并以其正特征值对应的信号子空间为基础构建新的观测模型;通过对新模型信号协方差矩阵特征向量子空间的分析,提出无需角度预估的聚焦矩阵计算方法.理论分析及仿真实验证明,色噪声背景下,本文方法相较于对比算法具有更好的估计精度及分辨率,且算法稳健性好、复杂度低.
| [1] |
STOICA P, WONG K M, WU Qiang. On a nonparametric detection method for array signal processing in correlated noise fields[J]. IEEE Transactions on Signal Processing, 1996, 44(4): 1030. DOI:10.1109/78.492564 |
| [2] |
刘庆华, 周秀清, 晋良念. 相关色噪声下无冗余累积量稀疏表示DOA估计[J]. 航空学报, 2017, 38(4): 320. LIU Qinghua, ZHOU Xiuqing, JIN Liangnian. DOA estimation using non-redundant cumulants sparse representation in correlated colored noise[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(4): 320. DOI:10.7527/S1000-6893.2016.0247 |
| [3] |
CHEN Guanghui, ZENG Xiaoping, JIAO Shuang, et al. High accuracy near-field localization algorithm at low SNR using fourth-order cumulant[J]. IEEE Communications Letters, 2020, 24(3): 553. DOI:10.1109/LCOMM.2019.2959576 |
| [4] |
PAN Meihong, ZHANG Gong, HU Zhentao, et al. Real-valued off-grid DOA estimation via iterative optimization based on covariance differencing method with spatial colored noise[J]. IET Radar, Sonar & Navigation, 2019, 13(7): 1116. DOI:10.1049/iet-rsn.2018.5404 |
| [5] |
PAULRAJ A, KAILATH T. Eigenstructure methods for direction of arrival estimation in the presence of unknown noise fields[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1986, 34(1): 13. DOI:10.1109/TASSP.1986.1164776 |
| [6] |
WAX M, SHAH T, KAILATH T. Spatio-temporal spectral analysis by eigenstructure methods[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1984, 32(4): 817. DOI:10.1109/TASSP.1984.1164400 |
| [7] |
HU Bin, LI Xuejun, CHONG P H J. Denoised modified incoherent signal subspace method for DOA of coherent signals[C]//2018 IEEE Asia-Pacific Conference on Antennas and Propagation. Auckland: IEEE, 2018: 539 DOI: 10.1109/APCAP.2018.8538143
|
| [8] |
HE Shun, YANG Zhiwei, LIAO Guisheng. DOA estimation of wideband signals based on iterative spectral reconstruction[J]. Journal of Systems Engineering and Electronics, 2017, 28(6): 1039. DOI:10.21629/JSEE.2017.06.01 |
| [9] |
EBADI Z, MOGHADDAM S S. Modified rotational signal subspace algorithm[C]// 2017 International Conference on Wireless Communications, Signal Processing and Networking. Chennai: IEEE, 2017: 2557. DOI: 10.1109/WiSPNET.2017.8300224
|
| [10] |
VALAEE S, KABAL P. Wideband array processing using a two-sided correlation transformation[J]. IEEE Transactions on Signal Processing, 1995, 43(1): 160. DOI:10.1109/78.365295 |
| [11] |
张兴良, 樊甫华. 宽带DOA估计的频域时延补偿算法[J]. 电子学报, 2018, 46(7): 1633. ZHANG Xingliang, FAN Fuhua. DOA estimation algorithm for wideband signals using time delay compensation method in frequency domain[J]. Acta Electonica Sinica, 2018, 46(7): 1633. DOI:10.3969/j.issn.0372-2112.2018.07.013 |
| [12] |
WEN Jinming, ZHOU Zhengchun, WANG Jian. A sharp condition for exact support recovery with orthogonal matching pursuit[C]//2016 IEEE International Symposium on Information Theory. Barcelona: IEEE, 2016: 2364. DOI: 10.1109/ISIT.2016.7541722
|
| [13] |
张进, 叶中付, 毛云祥. 一种有效的相关噪声背景下宽带相干信号DOA估计算法[J]. 电子学报, 2013, 41(7): 1278. ZHANG Jin, YE Zhongfu, MAO Yunxiang. An effective DOA estimation algorithm for wideband coherent signals in the background of correlated noise[J]. Acta Electronica Sinica, 2013, 41(7): 1278. DOI:10.3969/j.issn.0372-2112.2013.07.006 |
| [14] |
陈明健, 胡振彪, 黄中瑞. 空间非平稳噪声下的宽带DOA估计算法[J]. 现代雷达, 2018, 40(1): 36. CHEN Mingjian, HU Zhenbiao, HUANG Zhongrui. Direction of arrival estimation of wideband signals with sensor arrays in spatial non-stationary noise[J]. Modern Radar, 2018, 40(1): 36. DOI:10.16592/j.cnki.1004-7859.2018.01.008 |
| [15] |
潘美虹.色噪声背景下基于稀疏重构的off-grid DOA估计算法研究[D].南京: 南京航空航天大学, 2019 PAN Meihong. Off-grid DOA estimation based on sparse reconstruction in the colored noise background[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2019. DOI: 10.27239/d.cnki.gnhhu.2019.000507 |
| [16] |
PALANISAMY P, KALYANASUNDARAM N, RAGHUNANDAN A. A new DOA estimation algorithm for wideband signals in the presence of unknown spatially correlated noise[J]. Signal Processing, 2009, 89(10): 1921. DOI:10.1016/j.sigpro.2009.03.033 |
 2021, Vol. 53
2021, Vol. 53


