2. 高速铁路轨道技术国家重点实验室(中国铁道科学研究院),北京 100081;
3. 中国铁道科学研究院,北京 100081
2. State Key Laboratory for Track Technology of High-Speed Railway (China Academy of Railway Sciences)Beijing 100081, China;
3. China Academy of Railway Sciences, Beijing 100081, China
特大型缆索式桥梁,通常由斜拉索或主缆将主梁荷载传递至索塔.为满足行车平稳性和缆索受力经济性指标,工程中索塔常选用高塔身和大截面形式,增加了结构自重,极易引起基础变位,对行车平稳性产生影响.此外,在桥梁施工过程中由于桥塔的基础沉降,对主塔施工模板、钢锚梁定位和线形控制等带来影响[1],需要在施工过程中考虑由于基础沉降引起的预抬量.因此,特大型桥梁基础变位的连续监测是桥梁施工期和运营期安全的必要保证[2].目前,传统的基础变位观测通常采用精密水准测量,但由于人工监测存在工作量大、累积误差、观测周期长等不足,特别是在桥梁服役期间难以满足快速准确实时监测基础变形的要求.
近年来随着全球导航卫星系统(global navigation satellite system, GNSS)的不断发展,相较于传统变形监测方法具有灵活、方便,任何时段都能接收卫星信号,可实现长期连续监测等优点.随着采样频率的逐渐提高,GNSS技术在高层[3]和大跨度桥梁[4]的静动力响应的检测中得到了不断发展.由于GNSS技术受卫星星历误差、对流层延迟误差、多路径效应误差等因素的影响,其测量精度通常在10 mm范围内.而桥塔结构在施工和运营期间的基础变位通常是毫米级[5],直接通过GNSS采集数据无法满足基础变位实时监测和最终沉降量预测的精度需求.
GNSS技术应用于工程结构变形监测时,基线通常布设较短(如小于5 km),误差源中的卫星和接收机的时钟钟误差及对流层延迟误差可通过双差计算[6]消除;而多径干扰引起的误差是高精度动态测量的主要误差源.在动态变形监测中,由于卫星天线的位置及其周围环境基本不变,可根据多径干扰效应的重复性,利用小波降噪[7]、经验模态分解(empirical mode decomposition, EMD)[8]和滤波算法[9]等方法削弱信号误差的影响.
本文以某在建公铁两用双塔斜拉桥基础变位连续动态观测数据为例,将平稳小波变换和EMD降噪相结合,提取桥塔结构基础变位信号;通过BP神经网络建立GNSS信号与精密水准测量数据间的非线性映射网络,修正卫星信号的观测误差,最后根据非线性映射网络和修正卫星信号,实现基础变位的高精度连续监测和最终沉降量的预测.
1 基本理论 1.1 平稳小波降噪消除多径效应GNSS监测信号主要由结构实际振动、多径误差和随机噪声3部分组成.其中,多径误差主要集中在0~0.2 Hz的频带[10],常采用非线性非平稳滤波算法抑制.相较于离散小波变换在尺度间的正交小波基的非一致取样性,平稳小波变换[11](stationary wavelet transform, SWT)使用冗余离散小波基,具有平移不变性,随着SWT尺度的增大,信号和噪声所对应的小波系数分别具有增大和减小的特点.若连续进行SWT,噪声的小波系数可基本去除,可以很好地削弱离散小波变换中的振荡效应.通过SWT去除GNSS信号的多径误差的具体步骤如下[12].
1) 选择symmlets簇小波基函数,应用SWT算法分解双差伪距残差.采用文献[8]中给出的自适应方法确定小波分解层数,得到小波系数.
2) 通过阈值模平方去噪法计算每个尺度的高频次小波系数,阈值表示为
| $ TH = \sigma \sqrt {2\log L} ;\sigma = \frac{{{\rm{MAD}}}}{{0.6745}}. $ | (1) |
式中,L为信号长度,MAD为高频次系数的绝对中位差.
3) 基于SWT逆变换,根据小波分解系数重构GNSS信号,克服离散小波变换中采样间隔随分解尺度指数升高的不足.
1.2 经验模态分解降低随机噪声经验模态分解(empirical mode decomposition, EMD)是基于信号本身的局部特征时间尺度,把复杂的信号函数分解成了有限的本征模态函数(intrinsic mode function, IMF)之和.EMD方法不受Heisenberg测不准原理的限制,能够获得很高的频率分辨率,且该方法基于信号自身的特征进行分解,不需要预先定义基函数,具有很好的自适应性,基本分解过程参见文献[13-14].
通过经验模态分解,含噪声信号x(t)分解成从高频到低频的本征模态IMFi和残值分量rn,即
| $ \mathit{x}\left( t \right) = \sum\limits_{i = 1}^n {{\rm{IM}}{{\rm{F}}_i}} \left( t \right) + {r_n}\left( t \right). $ | (2) |
信号经分解后得到有限个从高到低的频率,阶数小的对应于信号中的高频成分,阶数大的对应于低频成分.一般认为高频成分包含的是信号尖锐部分或噪声,而低频成分中噪声影响很小.基于EMD降噪的主要思想是:对于大多数被噪声污染的信号,其主要能量集中在低频段,越往高频段,其含有的能量就越少.但该方法在直接舍弃若干阶高频成分的同时,也会丢失部分有用信号的能量;此外,尚缺少明确的截断阶数的判别准测.
对于GNSS监测信号中的随机噪声,通常采用高斯白噪声模型进行简化.白噪声模型零点处自相关函数最大,其他位置处虽不为零,但相对于零点处的自相关函数值很小,衰减速度快,相关性很小.针对高斯白噪声模型的特点,本文通过自相关函数[15]判断IMF截断数目,将所有经过处理及未处理的分量进行重构得到降噪后的GNSS信号x′(n),可表示为
| $ x'\left( n \right) = \sum\limits_{i = 1}^k {{\rm{IM}}{{\rm{F}}_i}} + \sum\limits_{j = k + 1}^N {{\rm{IM}}{{\rm{F}}_j}} . $ | (3) |
式中k为通过自相关函数判断的噪声主导模态阶数, 低于k阶的IMFi需通过小波软阈值进行滤波处理.
2 卫星监测的基础沉降提取方法大型桥梁结构的基础设施变形不可避免,采用常规人工测量方法监测工作量大、存在累积误差、观测周期长,难以达到快速准确实时监测位移变形和沉降的目的.针对上述不足,基于GNSS卫星观测系统,建立桥塔基础沉降变形监测系统可实现施工和运营阶段的基础变位连续观测.由于实测数据无法避免地存在采集误差,需要对采样数据进行实时降噪.在桥梁施工阶段,施工人员通过全站仪等测量设备对基础变位进行人工测量,因此可根据施工阶段的精密水准测量数据,对GNSS卫星观测数据进行纠偏处理,为运营阶段的基础沉降连续观测和最终沉降量的预测提供依据.
桥塔基础变位卫星监测信号的误差通常包含多径误差和随机噪声两部分,本文分别采用SWT和改进EMD分解对其进行降噪,消除GNSS信号采集的误差.由于电离层、对流层的折射与延迟误差以及多路径误差等无法完全消除,降噪后的GNSS数据仍与施工过程中采用精密水准测量得到的基础变位存在一定误差.同时,由于桥梁结构在施工过程中,基础变位的测量是按照施工工况同步进行的,且对施工过程中的临时荷载和桥塔结构质量等过程数据掌握全面.因此,可根据施工过程中的测量数据,对GNSS信号的基础变位数据进行修正,并依据准确的修正数据对沉降过程量和最终沉降量进行预测.
目前,采用实测数据预测地基沉降的方法通常是选用特定的模型,通过参数拟合确定沉降模型中的参数,对阶段/最终沉降量进行预测.应用较为普遍的沉降预测模型包括双曲线模型、指数曲线模型、星野法模型、Gompertz模型和Weibull模型.其中,双曲线模型、指数曲线模型和星野法模型是两参数模型,应用较为简便,可统一表示成
| $ {\mathit{S}_t}\mathit{ = }{\mathit{S}_0} + \Delta S\left( {a, b, t, {t_0}} \right). $ | (4) |
式中:St为随时间t变化的总沉降量;S0和ΔS分别表示初始沉降量和沉降量;t0和t分别表示沉降的初始和经过时间;a和b为待定系数.在选定沉降模型条件下,根据式(4)对观测沉降结果进行参数拟合表示桥塔的基础沉降.
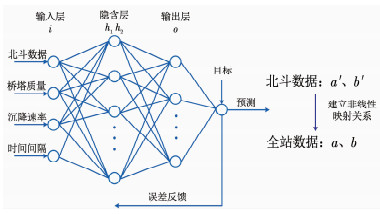
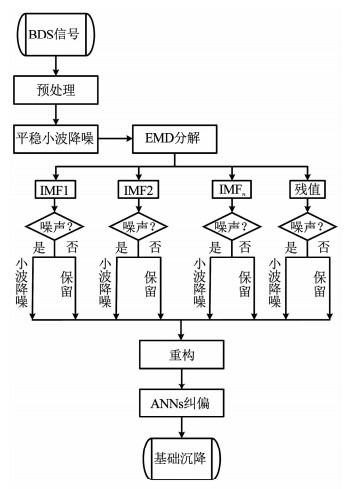
对于施工过程中的桥塔结构,本文通过BP神经网络将施工过程中基础荷载数值、GNSS测量数据、精密水准测量结果和观测间隔时间作为输入层,建立GNSS数据拟合得到的模型参数a′和b′与精密水准测量模型参数a和b间的非线性映射关系(图 1所示).对于运营过程中的桥塔基础,通常无需对桥塔进行定时的精密水准测量,因此可根据GNSS测量数据和建造过程中训练得到的非线性映射关系,将测量数据映射成修正后的基础沉降数据,并根据选择的沉降模型对最终沉降量进行预测.本文方法的流程见图 2.
|
图 1 GNSS数据纠偏与预测 Fig. 1 Correction and prediction of GNSS data |
|
图 2 本文方法流程 Fig. 2 Flow chart of the proposed method |
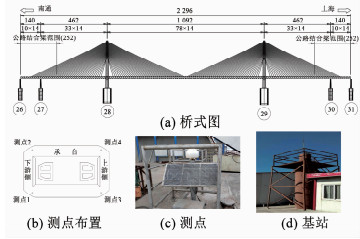
为验证本文算法的准确性,在某在建主跨1 092米公铁两用双塔斜拉桥建立BDS测点.承台4个角点各布置一台HWA-BM-300型双频接收机,可同时采集GPS卫星和BDS卫星信号.需要说明的是,本文仅采用BDS信号监测承台基础沉降.为提高BDS信号的准确性,基准站设置在与测点2 km范围内的南岸营地,营地内已设有测量放样时使用的GNSS基准点.采用无线传输和太阳能供电建设独立的承台变形监测基准站,测点与基准站如图 3所示.
|
图 3 监测点布置和测点、基站安装 Fig. 3 Layout of BDS monitoring points and installation of base station |
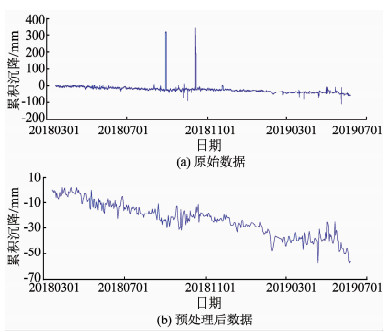
本试验数据采集的时间范围为2018年3月14日至2019年6月27日,分别对应精密水准测量工况塔柱第6节浇筑后和第54节塔柱浇筑后(主塔封顶)及Z18~19、Z67~68节段钢梁双悬臂架设工况,共计63次人工测量.其中,BDS监测点接收机根据基准站的差分修正信息,采用实时动态差分算法获取实时动态坐标,每5 s发送一次数据.由于基础沉降是一个缓慢变化的过程,针对原始数据的离散性,按照3倍绝对中位差剔除采集数据中的坏点,并采用线形插值插补由于信号遮蔽等原因引起的数据丢失,得到预处理后的信号.图 4(a)和(b)分别表示测点1的原始沉降数据和预处理后信号.如图所示,数据预处理消除了原始信号中的坏点和丢失点.
|
图 4 BDS采集数据 Fig. 4 Data from BDS |
在小波降噪中,小波基函数的选择直接关系到信号降噪的效果.为了更加精确及量化评价降噪效果,定义信噪比(SNR)和均方差(RMSE)两个参数如下:
| $ \begin{array}{l} SNR = 10lg\left[ {\frac{{\sum\limits_i^N {x_i^2} }}{{\sum\limits_i^N {{{\left[ {{x_i} - {{x'}_i}} \right]}^2}} }}} \right], \\ {\rm{RMSE = }}\sqrt {\frac{1}{N}\sum\limits_i^N {{{\left[ {{x_i} - {{x'}_i}} \right]}^2}} } . \end{array} $ | (5) |
式中,xi和x′i分别表示原始信号和去噪后的信号.
通常认为信噪比越高,均方根误差越小,降噪信号就越接近原始信号,降噪效果就越好.表 1比较了5种不同symmlets簇小波基函数的信噪比和均方根误差.如表 1所示,小波基函数sym2在硬阈值条件下的信噪比最大且均方根误差最小,可认为该种小波基函数适合用于消除BDS信号的多径误差.
| 表 1 不同小波基函数的信噪比和均方根误差 Tab. 1 Errors of SNR and RMSE of different wavelet basic functions |
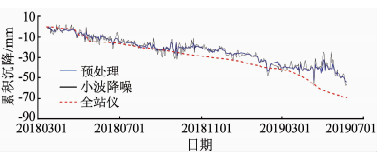
图 5为经sym2小波基函数降噪后的BDS沉降信号与全站仪人工测量结果的比较.如图所示,经过SWT降噪后BDS沉降累积曲线提取的多路径模型差值序列基本上在零水平线上,表明该方法能够更有效地提取多路径误差的系统性部分.
|
图 5 平稳小波降噪消除信号的多径误差 Fig. 5 Elimination of multipath errors by stationary wavelet transform |
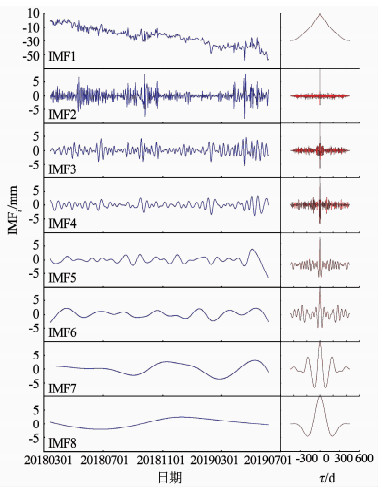
对小波降噪消除多径误差后的BDS信号采用EMD分解,并计算其自相关函数.基于EMD的降噪算法通常认为大多数被噪声污染的信号,其主要能量集中在低频段,高频段含有较多噪声.图 6为测点1经EMD分解得到的本征模态和其自相关函数.如图所示,自第1阶至第7阶本征模量均为噪声主导项,可认为是信号的噪声项,而第8阶为实测信号,需要保留.
|
图 6 EMD分解BDS信号 Fig. 6 EMD decomposition of BDS data |
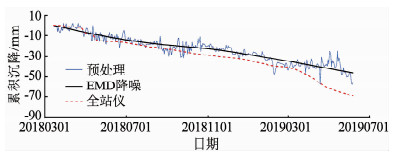
图 7为经EMD降噪的BDS信号.如图所示,相较于仅通过小波降噪的BDS信号,EMD方法大幅降低了实测信号的噪声,且与全站仪通过精密水准测量得到的测点高程具有一致的趋势.
|
图 7 经EMD降噪的BDS信号 Fig. 7 Denoising BDS data by EMD method |
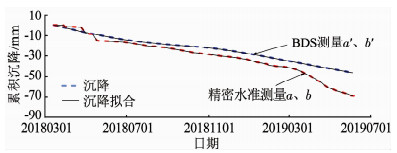
图 7所示的BDS降噪信号虽与精密水准测量的结果具有相同的趋势,但仍有较大误差,误差的均方差是3.5 mm.对于一般性工程,通过EMD降噪后的BDS数据足以满足工程需要.但是对于特大跨度桥梁等控制性工程,还需要对经降噪后的数据进行纠偏,才能满足基础沉降实时观测和最终沉降预测的需要.本文方法采用双曲线模型,分别对BDS信号降噪和精密水准测量的沉降数据进行参数拟合,得到两组数据的拟合参数,分别表示为a、b和a′、b′,拟合结果见图 8.
|
图 8 沉降曲线拟合 Fig. 8 Fitting of foundation settlement |
基于沉降曲线拟合得到的两组参数a、b,通过BP神经网络方法,由学习、验证过程建立两组数据间的非线性映射关系,对实时测量的BDS信号得到的沉降数据进行修正.
需要说明的是,BP神经网络的隐含层数、节点数和传递函数等参数通常需要试算确定.本文先将测点1的63组精密水准测量数据分成33和30两组,分别用于神经网络参数训练和结果评价.分别采用3种不同隐含节点数和传递函数,训练次数、速率和精度分别为200次、0.01和0.000 1.表 2为3种不同隐含节点和传递函数条件下,BP神经网络关于BDS沉降数据修正的计算精度.由误差分析可知,不同节点网络和传递函数对计算结果有一定影响,但差别不大.本文传递函数选择logsig函数,并采用4-8-1构建节点网格.表中MAE和MAPE可分别表示为[16]
| 表 2 不同参数的计算误差 Tab. 2 Error indexes of results obtained by proposed method |
| $ \begin{array}{*{20}{l}} {{\rm{MAE}} = \frac{1}{N}\sum\limits_{i = 1}^N {\left| {{x_i} - {{x'}_i}} \right|} ,}\\ {{\rm{MAPE}} = \frac{1}{N}\sum\limits_{i = 1}^N {\left| {\frac{{{x_i} - {{x'}_i}}}{{{{x'}_i}}}} \right|} .} \end{array} $ | (6) |
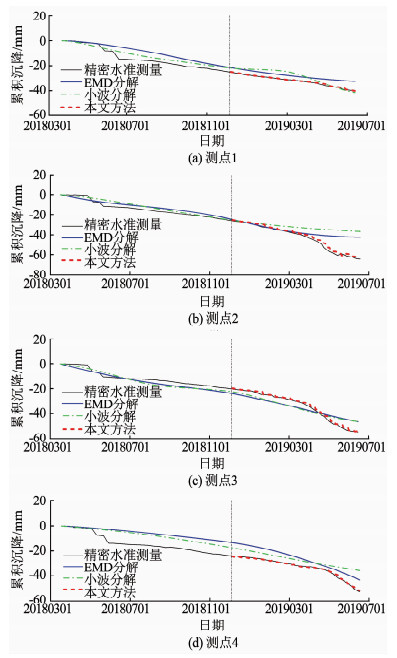
图 9和表 3比较了本文方法与EMD分解、小波分解提取的承台4测点处的基础沉降实时采集数据.图中黑色实线表示精密水准测量结果,绿色虚线和蓝色实线分别表示EMD分解和小波分解的处理结果,红色虚线表示本文方法通过平稳小波降噪和EMD分解消除多径误差和随机噪声并纠偏的实时采集测点沉降数据.需要说明的是,表中信噪比和均方差分别表示3种不同方法与精密水准测量结果间的误差.由图 9和表 3中数据可知,经本文算法修正后的实时采集BDS信号与精密水准测量间的误差均小于1 mm,较好地修正了BDS信号的误差,具有较高的精度.
|
图 9 不同测点本文方法处理后的基础沉降 Fig. 9 Foundation settlements of different measuring points processed by proposed method |
| 表 3 本文方法与传统方法的比较 Tab. 3 Comparison of proposed method with traditional methods |
为实现大跨度桥梁基础变位的实时监测,在基础承台上建立北斗卫星观测点采集基础变位数据.基于小波分解和EMD分解方法对BDS基础沉降卫星监测信号中的多径误差和随机噪声进行降噪.针对降噪后的BDS沉降数据与精密水准数据间的偏差,提出由BP神经网络算法结合施工过程信息,建立BDS数据与精密水准数据间的非线性映射关系,对BDS数据进行实时修正.经实例验证本文提出的算法可满足大跨度桥梁基础变位实时监测要求,并得到以下结论:
1) 平稳小波降噪可较好消除BDS信号中的多径误差;
2) 基于自相关函数的EMD降噪算法可有效处理含随机噪声的BDS信号;
3) 根据施工过程数据,通过BP神经网络可建立精密水准测量数据与BDS沉降数据间的非线性映射关系;
4) 本文提出的BDS信号处理算法实现了大跨度桥梁基础沉降的亚毫米精度监测.
| [1] |
吴楠, 肖军华, 陈建国, 等. 高速铁路无砟轨道桥梁基础变形对行车的影响[J]. 铁道工程学报, 2017, 34(9): 58. WU Nan, XIAO Junhua, CHEN Jianguo, et al. Effect of bridge pier deformation for high speed railway with ballastless track on train running safety and comfort[J]. Journal of Railway Engineering Society, 2017, 34(9): 58. DOI:10.3969/j.issn.1006-2106.2017.09.011 |
| [2] |
BROWNJOHN J M W, KOO K Y, SCULLION A, et al. Operational deformations in long-span bridges[J]. Structure and Infrastructure Engineering, 2015, 11(4): 556. DOI:10.1080/15732479.2014.951857 |
| [3] |
QUESADA-OLMO N, JIMENEZ-MARTINEZ M, FARJAS-ABADIA M. Real-time high-rise building monitoring system using global navigation satellite system technology[J]. Measurement, 2018, 123: 115. DOI:10.1016/j.measurement.2018.03.054 |
| [4] |
XI Ruijie, JIANG Weiping, MENG Xiaolin, et al. Bridge monitoring using BDS-RTK and GPS-RTK techniques[J]. Measurement, 2018, 120: 128. DOI:10.1016/j.measurement.2018.02.001 |
| [5] |
王翔, 王波, 汪正兴. 高速铁路运营期基础沉降长期监测技术研究[J]. 铁道工程学报, 2017, 34(5): 11. WANG Xiang, WANG Bo, WANG Zhengxing. Research on the long-term monitoring technology of subgrade settlement for high-speed railway in operation period[J]. Journal of Railway Engineering Society, 2017, 34(5): 11. |
| [6] |
李征航, 张小红. 卫星导航定位新技术及高精度数据处理方法[M]. 武汉: 武汉大学出版社, 2009. LI Zhenghang, ZHANG Xiaohong. New techniques and precise data processing methods of satellite navigation and positioning[M]. Wuhan: Wuhan University Press, 2009. |
| [7] |
余腾, 胡伍生, 吴杰, 等. 基于小波阈值去噪与EMD分解方法提取润扬大桥振动信息[J]. 振动与冲击, 2019, 38(12): 264. YU Teng, HU Wusheng, WU Jie, et al. Extraction of Runyang bridge vibration information based on a fusion method of wavelet threshold denoising and EMD decomposition[J]. Journal of Vibration and Shock, 2019, 38(12): 264. DOI:10.13465/j.cnki.jvs.2019.12.038 |
| [8] |
吴杰, 胡夏闽, 乔燕, 等. 基于交叉证认的EMD小波滤波在大桥动态监测去噪中的应用[J]. 振动与冲击, 2017, 36(22): 212. WU Jie, HU Xiamin, QIAO Yan, et al. EMD-wavelet filtering based on cross-validation and its application in bridge dynamic monitoring[J]. Journal of Vibration and Shock, 2017, 36(22): 212. DOI:10.13465/j.cnki.jvs.2017.22.033 |
| [9] |
XU Yan, BROWNJOHN J M W, HESTER D, et al. Long-span bridges: enhanced data fusion of GPS displacement and deck accelerations[J]. Engineering Structures, 2017, 147: 639. DOI:10.1016/j.engstruct.2017.06.018 |
| [10] |
熊春宝, 路华丽, 朱劲松, 等. 基于GPS-RTK和加速度计的桥梁动态变形监测试验[J]. 振动与冲击, 2019, 38(12): 69. XIONG Chunbao, LU Huali, ZHU Jinsong, et al. Dynamic deformation monitoring of bridge structures based on GPS-RTK and accelerometers[J]. Journal of Vibration and Shock, 2019, 38(12): 69. DOI:10.13465/j.cnki.jvs.2019.12.010 |
| [11] |
NASON G P, SILVERMAN B W. The stationary wavelet transform and some statistical applications[M]// ANTONIADIS A, OPPENHEIM G. Wavelets and Statistics. New York: Springer, 1995: 281. DOI: 10.1007/978-1-4612-2544-7_17
|
| [12] |
AZARBAD M R, MOSAVI M R. A new method to mitigate multipath error in single-frequency GPS receiver with wavelet transform[J]. GPS Solutions, 2014, 18(2): 189. DOI:10.1007/s10291-013-0320-1 |
| [13] |
WU Zhaohua, HUANG N E. Ensemble empirical mode decomposition: a noise-assisted data analysis method[J]. Advances in Adaptive Data Analysis, 2009, 1(1): 1. DOI:10.1142/S1793536909000047 |
| [14] |
HUANG N E, SHEN Zheng, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences, 1998, 454(1971): 903. DOI:10.1098/rspa.1998.0193 |
| [15] |
王婷. EMD算法研究及其在信号去噪中的应用[D].哈尔滨: 哈尔滨工程大学, 2010 WANG Ting. Research on EMD algorithm and its application in signal denoising[D]. Harbin: Harbin Engineering University, 2010 |
| [16] |
LIU Hui, TIAN Hongqi, LIANG Xifeng, et al. Wind speed forecasting approach using secondary decomposition algorithm and Elman neural networks[J]. Applied Energy, 2015, 157: 183. DOI:10.1016/j.apenergy.2015.08.014 |
 2021, Vol. 53
2021, Vol. 53


