弹药协调器作为大口径自行火炮弹药自动装填系统中的重要组成部分,安装在火炮车体内弹药仓与炮尾之间,负责将弹药传输到炮尾待装填位置,是一类特殊的机械臂[1].实现弹药协调器的快速精确定位控制对于提高火炮武器系统的射速从而提升其性能具有重要意义.
现有的火炮武器装备中,弹药自动装填系统包括弹药协调器大多仍采用传统的PD/PID控制方法.然而,弹药协调器是一种复杂的机电一体化系统,在其运动过程中存在负载变化、摩擦、环境外干扰等非线性因素的影响,这些都给协调器的精确稳定控制带来了困难,使得传统的PD/PID控制方法很难达到控制要求,为解决这一问题,实际系统中只能采用机械抱闸的方式进行辅助定位.这种控制和定位方式虽然保证了运动精度要求,但同时也对弹药协调器的机械结构造成了较大的冲击磨损,缩短了其使用寿命,更严重降低了整个自动装填系统的可靠性.因此,实现各部件的精确鲁棒控制成为弹药自动装填系统研究中的重点和难点问题之一.
类似于弹药协调器这类的机械臂系统在其他领域也有很广泛的应用,例如航天上的自由漂浮空间机械手[2]、工业机器人[3]、医疗机器人[4]等等.对于包含弹药协调器在内的这类机器人来说,运动精度要求都是非常高的,为提高这类机器人的控制性能及可实现性,基于模型的运动控制方法是一种很好的选择,这种方法可以同时将摩擦、扰动等非线性因素纳入考虑,得到真实的控制结果,具有重要的实际意义[5].
常用的刚性机械系统动力学模型通常由Newton-Euler方法、Lagrange方程法、Kane方法等来建立.本文基于Lagrange方法建立系统的动力学方程,经建模发现影响系统性能的主要非线性因素有两种:系统摩擦和用于平衡弹药协调器重力矩的小平衡机的支反力矩.
摩擦是一个复杂的力学现象,且普遍存在于机械系统中,对机械系统动力学有重要影响,具有非线性、时变性等特点,会导致系统出现稳态误差、极限环振荡、滞滑运动、低速爬行等问题,严重影响着系统的性能,因此,对系统的摩擦进行建模和补偿成为机器人控制领域的热点研究问题之一[6-9].实现摩擦补偿的关键问题和核心步骤是建立合适的摩擦模型.迄今为止,广泛应用的摩擦模型多达数十种,这些模型主要可以分为两大类[10-11]:静态摩擦模型和动态摩擦模型.前者将摩擦力描述为速度的相对函数,如Coulomb模型、Stribeck模型等;后者将摩擦力描述为相对速度和位移的函数,如LuGre模型、Dahl模型等.相对于静态摩擦模型而言,动态摩擦模型不仅包含了摩擦的静态特性,同时还描述了摩擦的动态特性,能够更为真实地反应摩擦状态.
区别于一般机器人动力学以及运动控制问题,本文研究的弹药协调器系统中存在的另一项特殊的而且具有重要影响的非线性因素是小平衡机的支反力矩.文献[12]用ADAMS软件建立了协调器的多体动力学仿真模型,将协调过程中小平衡机的气体变化考虑为绝热过程,将其平衡力简化为一个等效力函数来分析小平衡机气压变化对模型的影响.文献[13]在RecurDyn中建立了协调器的仿真模型,并以小平衡机的支反力和减速器的齿轮齿面磨损作为故障因素研究了其对协调器协调性能的影响.文献[14]在Simulink中建立了协调器的动力学和仿真模型,根据协调器协调过程的测试数据,采用区间辨识的方法辨识了包含小平衡机的气体初压和多变指数在内的多个不确定参数.
针对类似弹药协调器这种存在强非线性因素干扰的机器人系统,滑模变结构方法利用控制作用的不连续特性,设计与系统状态相关的滑动模态,并迫使系统按照所设计滑动模态的状态轨迹运动[15].这种方法中,滑动模态与系统无直接关联,则不受对象参数及扰动变化影响,从理论上来讲是一类有效的控制方法[16-19].除了滑模控制方法,现代鲁棒控制[20]、自适应控制[21]、神经网络方法[22]、模糊控制[23]等方法也被广泛关注.为更好地处理非线性和不确定性问题,这些方法通常会被结合使用[24-26]以取得更好的控制效果.本文采用一种基于系统Lyapunov函数的非线性控制策略[27-29]对弹药协调器的定位控制进行研究,这种方法与系统模型及动力学过程密切相关,其从形式上表现为一种连续时变的PD控制,其中的比列和微分系数决定于系统的Lyapunov函数,是系统误差变量的可微函数,随着系统趋向于控制目标,即误差变量趋近于零,控制增益会趋向于无穷大,但控制力可以始终保持给定的有界约束,可以有效解决系统的不确定性和非线性问题.
本文对某弹药协调器动力学过程进行了深入的分析,并采用Lagrange方法详细地建立了其动力学方程.结合实验和理论模型,对于协调器运动过程中对系统性能产生重要影响的摩擦和小平衡机支反力矩这两个非线性项进行了辨识.基于辨识后的摩擦模型和小平衡机支反力矩模型,在控制中引入前馈补偿项.实验结果表明,本文的控制方案在保证了定位精度的前提下,显著缩短了协调器的运动定位时间,验证了算法的有效性和正确性.
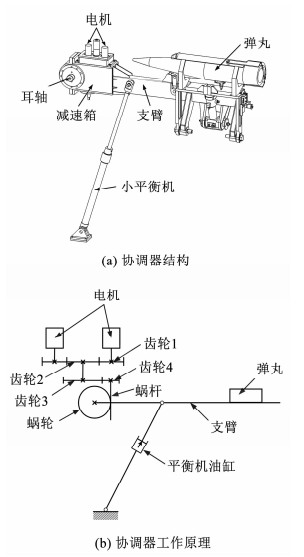
1 弹药协调器建模 1.1 协调器动力学模型弹药协调器用于接收弹仓内被推弹器推送出来的弹丸,在控制器的作用下进行弹药协调,使得弹丸轴线与待发射状态下的炮管轴线相平行,再将该弹丸传输到输弹线上,由输弹机输弹入膛,其结构图如图 1(a)所示.协调器的工作原理图如图 1(b)所示,它由两个串励式直流电机并联驱动,减速箱由两级直齿轮传动和一级蜗轮蜗杆传动组成,其中蜗轮与耳轴固联;小平衡机的作用是平衡协调器在协调过程中的重力矩,以实现减小电机负载和支撑平稳运动的目的,其结构上主要由平衡油缸和蓄能器组成.
|
图 1 弹药协调器 Fig. 1 Ammunition coordinator |
通过第2类Lagrange方法,建立协调器的动力学方程为
| $ {\mathit{J}_{\rm{e}}}\ddot \theta = {M_{\rm{d}}}i\eta + {M_{\rm{G}}} - {M_{\rm{R}}} - {M_{\rm{f}}}. $ | (1) |
式中:θ为协调器支臂转角,相应的,
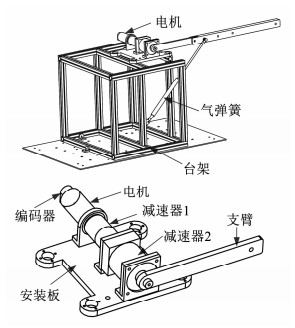
为方便实验研究,根据协调器的工作原理,实验室搭建了协调器的原理样机,如图 2所示.
|
图 2 协调器原理样机结构 Fig. 2 Structure of ammunition coordinator principle prototype |
在原理样机中,支臂通过两个减速器由自带编码器的直流电机驱动,选用的电机型号为Maxon-RE50,减速器1选用Maxon公司的GP52C行星齿轮减速器,减速比为230,减速器2选用上海寅通减速器厂生产的PF90-3行星齿轮减速器,减速比为3,编码器选用Maxon公司的HEDL5540光电编码器.另外,原理样机中采用气弹簧代替协调器的小平衡机给支臂提供支反力矩,采用在支臂末端加负载的方式代替协调器中的弹丸.
1.2 协调器摩擦建模及参数辨识本文采用LuGre模型对弹药协调器进行摩擦建模,该模型从微观的角度研究摩擦产生的机理,在建模中不仅考虑了粘性摩擦和库伦摩擦,同时还考虑了静态摩擦和Stribeck负斜率效应,是目前较为完善的一种模型.具体表达式如下:
| $ \mathit{\dot z = }\omega \mathit{ - }\frac{{{\sigma _0}}}{{g\left( \omega \right)}}z\left| \omega \right|, $ | (2) |
| $ g\left( \omega \right) = {M_{{\rm{fc}}}} + \left( {{M_{{\rm{fs}}}} - {M_{{\rm{fc}}}}} \right){{\rm{e}}^{ - {{\left| {\omega /{\omega _{\rm{s}}}} \right|}^{{n_{\rm{s}}}}}}}, $ | (3) |
| $ {M_{\rm{f}}} = {\sigma _0}\mathit{z} + {\sigma _1}\mathit{\dot z} + {\sigma _2}\omega \mathit{.} $ | (4) |
式中:z为鬃毛的平均变形;Mf为系统所受摩擦力矩;σ0为鬃毛的刚度;σ1为微观阻尼系数;σ2为粘性摩擦系数;ω为支臂角速度;g(ω)为描述Stribeck效应;Mfc为库伦摩擦力矩;Mfs为静摩擦力矩;ωs为Stribeck特征速度;ns为形状修正系数.
选取模型中待辨识参数为χ=(Mfc, Mfs, vs, σ0, σ1, σ2, ns),采用遗传算法对这些参数进行辨识.
辨识时,先断开协调器原理样机中减速输出轴和支臂之间的连接,则协调器的动力学方程(1)转化为
| $ {\mathit{J}_{\rm{e}}}\ddot \theta = {M_{\rm{d}}}i\eta - {M_{\rm{f}}}. $ | (5) |
由式(5)可知,当
电机的转速范围为[-5 950, 5 950]r/min,在该转速范围内,令电机以38 r/min为间距的一组恒定转速ωjN, N=300运动,并记录对应的不同速度下的平均电流值IjN, N=300.定义辨识误差errj(χ, ωj)=iηkTI(ωj)-
| $ \begin{array}{l} \;\;\;\;\;\;\mathop {\min }\limits_\chi g\left( {\chi , \omega } \right), \\ {\rm{s}}{\rm{.t}}{\rm{.}}\;\chi \in {\chi ^I} = \left[ {{\chi ^L}, {\chi ^R}} \right], \\ \;\;\;\;\;\;\omega \in {\omega ^I} = \left[ {{\omega ^L}, {\omega ^R}} \right]. \end{array} $ |
选择个体适应度函数f(χ, ω)=1/g(χ, ω), 取种群大小M=100,最大迭代步数Genmax=5 000,设定交叉概率pc=0.9,变异概率pm=0.01,进行辨识计算.
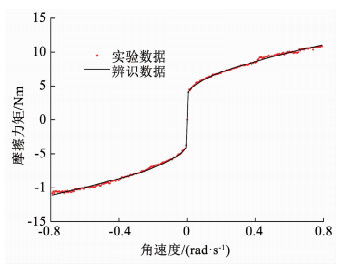
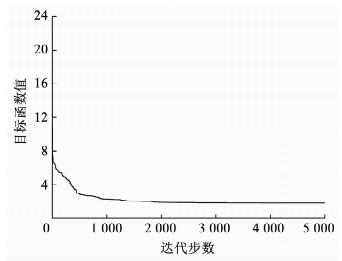
图 3给出了摩擦力矩实验结果和辨识结果的对比图,图 4为目标函数在辨识时的收敛过程,表 1为参数的具体辨识结果.由图 3可以看出辨识结果和实验结果是高度吻合的,辨识结果合理.
|
图 3 摩擦力矩辨识和实验结果对比 Fig. 3 Comparison between identification results and experimental data of friction torque |
|
图 4 目标函数收敛过程 Fig. 4 Convergence process of object function |
| 表 1 LuGre摩擦模型参数辨识结果 Tab. 1 Identificationresults of parameters in LuGre friction model |
在弹药协调器的工作过程中,存在带弹和不带弹两种工况,且同样在带弹这种工况下还存在弹丸种类不同的情形.由图 1可知,这些不同的工作状态和工作模式下,协调器支臂和弹丸相对回转中心的重力矩区别很大.为使驱动电机的负载在各工况下能够保持相对恒定,从而提高协调器工作的平稳性,采用小平衡机在协调器的协调过程中对协调器支臂产生合适的平衡力矩显得尤为重要.
分别对带弹和不带弹两种工况下,对协调器绕耳轴的重力矩进行建模,即
| $ {\mathit{M}_{{\rm{G1}}}} = {m_1}g{L_1}\cos \left( {\theta + {\theta _1}} \right) + {m_2}g{L_2}\cos \left( {\theta + {\theta _2}} \right), $ | (6) |
| $ {\mathit{M}_{{\rm{G2}}}} = {m_1}g{L_1}\cos \left( {\theta + {\theta _1}} \right). $ | (7) |
式中:m1为协调器支臂质量;m2为弹丸质量;L1为协调器支臂质心到耳轴中心的距离;L2为位于协调器上的弹丸质心到耳轴中心的距离;θ1、θ2分别为协调器协调角度在0°时支臂质心和弹丸质心与耳轴中心连线和水平线之间的夹角.
由式(6)、(7)可知,在带弹和不带弹两种情况下的重力矩差异较大,若没有小平衡机提供一定的平衡力矩,则会导致电机负载的较大差异,这就会提高电机的负载性能要求.基于平衡性考虑,小平衡机提供的平衡力矩应介于式(6)、(7)两种工况下的重力矩之间.
小平衡机由差动液压活塞缸和气囊式蓄能器组成,在原理样机中,使用气弹簧代替真实协调器中的小平衡机给支臂提供平衡力矩,采用在支臂末端加负载的方式模拟协调器带弹和不带弹两种工况.小平衡机的支反力矩取决于平衡油缸的压力以及协调器的协调角度,具体表达式为
| $ {\mathit{M}_{\rm{R}}} = {\mathit{L}_{\rm{R}}}{p_0}S{\left[ {{V_0}/\left( {{V_0} - \Delta LS} \right)} \right]^n}. $ | (8) |
式中:LR为小平衡机支反力矩的力臂,即耳轴中心到小平衡机的距离;p0为蓄能器的初始压强;S为平衡油缸活塞的面积;V0为气体的初始容积;ΔL为活塞移动距离;n为气体多变指数.其中,S、V0为已知量,LR, ΔL与支臂的角位移相关,可以根据协调器的基本几何尺寸以及支臂在运动过程中的位置角度关系求得.
模型中,p0, n为待辨识参数,和摩擦一样,这里采用遗传算法对该参数进行辨识.连接上原理样机中之前断开的支臂,则系统的运动过程由动力学方程(1)描述,由式(1)可知,当
| $ {\mathit{M}_{\rm{R}}} = {M_{\rm{d}}}i\eta + {M_{\rm{G}}} - {M_{\rm{f}}}. $ |
则,在匀速状态下,根据电机电流,式(6)、(7)重力矩MG,再带入协调器摩擦模型及参数辨识中辨识出的摩擦力矩Mf,就可以求出小平衡机的支反力矩.
同协调器摩擦建模及参数辨识中所述,令电机在转速范围内以一组恒定转速ωjN做匀速运动,并记录不同速度下的平均电流值IjN.定义辨识参数χ=[p0, n],辨识误差
| $ \begin{array}{l} \;\;\;\;\;\;\mathop {\min }\limits_\chi g\left( {\chi , \omega , \theta } \right), \\ {\rm{s}}{\rm{.t}}{\rm{.}}\;\chi \in {\chi ^I} = \left[ {{\chi ^L}, {\chi ^R}} \right], \\ \;\;\;\;\;\;\omega \in {\omega ^I} = \left[ {{\omega ^L}, {\omega ^R}} \right], \theta \in {\theta ^I} = \left[ {{\theta ^L}, {\theta ^R}} \right]. \end{array} $ |
设定种群大小为M=50,最大迭代步数为Genmax=100进行辨识计算.
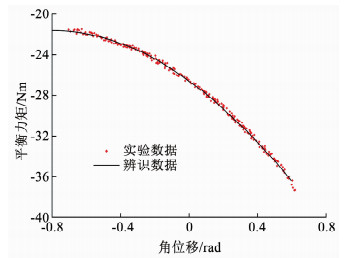
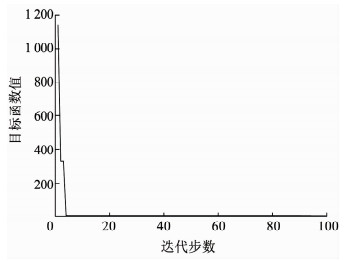
气弹簧初压辨识结果为p0=1.800 7×106 Pa,气体多变指数辨识结果为n=1.008 1,图 5给出了小平衡机支反力矩实验结果和辨识结果的对比图,图 6为目标函数在辨识时的收敛过程.由图 5、6可以看出,辨识结果和实验结果高度吻合,说明辨识后的小平衡机支反力矩项可以有效反映小平衡机在协调过程中的真实情况.
|
图 5 小平衡机支反力矩辨识和实验结果对比 Fig. 5 Comparison between identification results and experimental data of balance torque |
|
图 6 目标函数收敛过程 Fig. 6 Convergence process of object function |
为方便控制器设计以及稳定性证明,记U=Mdiη,S=MG-MR-Mf,记广义坐标q=θ,则动力学方程(1)重新整理成如下形式:
| $ {\mathit{J}_{\rm{e}}}\ddot q = U + S. $ | (9) |
方程(9)存在如下性质:
1) 等效转动惯量Je有界,即:
| $ {\lambda _1} \le {\mathit{J}_{\rm{e}}} \le {\lambda _2}, 0 < {\lambda _1} < {\lambda _2}. $ | (10) |
2) 重力矩、平衡力矩、摩擦力矩组成的复合项大小有界,即
| $ \left| S \right| \le {S_0}, $ | (11) |
其中,S0>0.
此外,基于实际工程应用的考虑,本文假设式(9)中的控制力矩也是大小有界的,即:|U|≤U0,其中,U0>0.
记系统的期望位置为qd,期望速度为
| $ U = - {k_{\rm{d}}}\dot e - {k_{\rm{p}}}\dot e, $ | (12) |
其中:
| $ {k_{\rm{d}}} = {\mathit{J}_{\rm{e}}}\alpha , \alpha \left( {e, \dot e} \right) = \frac{{{U_0}}}{4}\sqrt {\frac{6}{{{\lambda _2}V\left( {e, \dot e} \right)}}} , $ | (13) |
| $ {k_{\rm{p}}} = \beta , \beta \left( {e, \dot e} \right) = {\alpha ^2}{\lambda _2}. $ | (14) |
V(e, ė)为系统Lyapunov函数,其表达式为
| $ V\left( {e, \dot e} \right) = \frac{1}{2}{\mathit{J}_{\rm{e}}}{{\dot e}^2} + \frac{1}{2}{k_{\rm{p}}}{e^2} + \frac{1}{2}{k_{\rm{d}}}\dot ee. $ | (15) |
控制律增益kd、kp和系统Lyapunov函数V由式(13)~(15)明确定义,三者之间的关系是隐式的.随着系统误差趋向于0,即V(e, ė)趋近于0,控制增益kp和kd将趋于无穷大,尽管如此,控制力也可以满足以上提出的有界假设.
证明过程如下.
首先,引入如下变量:
| $ \begin{array}{l} \mathit{x = }{\mathit{V}^{1/2}}\left( {e, \dot e} \right), \xi = 2\sqrt {2{\mathit{J}_{\rm{e}}}{{\dot e}^2}} , \\ \eta = \frac{{2\sqrt 6 {U_0}}}{{\sqrt {{\lambda _2}} }}{\mathit{J}_{\rm{e}}}\dot ee, \gamma = \sqrt 3 {U_0}\left| e \right|. \end{array} $ | (16) |
显然,对于式(16),当(e, ė)≠0时,有
| $ {\xi ^2} + {\gamma ^2} > 0. $ | (17) |
此外,根据柯西不等式,有
| $ {\eta ^2} = \frac{{24U_0^2}}{{{\lambda _2}}}{\left( {{\mathit{J}_{\rm{e}}}\dot ee} \right)^2} \le 24U_0^2{\mathit{J}_{\rm{e}}}{{\dot e}^2}{e^2} = {\xi ^2}{\gamma ^2}, $ | (18) |
即
| $ \left| \eta \right| \le \xi \gamma . $ | (19) |
将式(13)、(14)和式(16)代入式(15),可以得到方程:
| $ 16{\mathit{x}^4} - {\xi ^2}{\gamma ^2} - \eta x - {y^2} = 0. $ | (20) |
对于一元四次方程式(20),有如下定理:
定理1 满足式(17)和式(19)的方程f(x)=16x4-ξ2x2-ηx-γ2总存在一个重数为一的正实根.
接下来证明Lyapunov函数V(e, ė)的正定性,及其导数的负定性.
根据柯西不等式,Lyapunov函数表达式的最后一项中kdėe均满足:
| $ \begin{array}{l} \left| {\alpha {\mathit{J}_{\rm{e}}}\dot ee} \right| = \left| \alpha \right|\sqrt {\left( {{\mathit{J}_{\rm{e}}}{e^2}} \right)\left( {{\mathit{J}_{\rm{e}}}{{\dot e}^2}} \right)} \le \\ \;\;\;\;\;\;\;\;\;\;\;\;\frac{1}{2}{\mathit{J}_{\rm{e}}}{{\dot e}^2} + \frac{1}{2}{\alpha ^2}{\mathit{J}_{\rm{e}}}{e^2} \le \\ \;\;\;\;\;\;\;\;\;\;\;\;\frac{1}{2}{\mathit{J}_{\rm{e}}}{{\dot e}^2} + \frac{1}{2}\beta {e^2}. \end{array} $ | (21) |
联立式(15)和式(21),可得:
| $ \frac{1}{4}\left( {{\mathit{J}_{\rm{e}}}{{\dot e}^2} + \beta {e^2}} \right) \le V \le \frac{3}{4}\left( {{\mathit{J}_{\rm{e}}}{{\dot e}^2} + \beta {e^2}} \right). $ | (22) |
由式(22)可知,对于任意(e, ė)≠0,V(e, ė)全局正定.
对V(e, ė)求导,可得:
| $ \begin{array}{l} \mathit{\dot V = }{\mathit{J}_{\rm{e}}}\dot e\ddot e + \frac{1}{2}\dot \beta {e^2} + \beta \dot ee + \\ \;\;\;\;\;\;\;\;\frac{1}{2}\dot \alpha {\mathit{J}_{\rm{e}}}\dot ee + \frac{1}{2}\alpha {\mathit{J}_{\rm{e}}}\ddot ee + \frac{1}{2}\alpha {\mathit{J}_{\rm{e}}}{{\dot e}^2}, \end{array} $ | (23) |
其中:
| $ \dot \alpha = - \frac{1}{2}\frac{{{U_0}}}{4}\sqrt {\frac{6}{{{\lambda _2}}}} {\mathit{J}_{\rm{e}}}{V^{ - 3/2}}\mathit{\dot V} = - \frac{\alpha }{2}\frac{1}{V}\mathit{\dot V}, $ | (24) |
| $ \dot \beta = - \frac{{3U_0^2}}{8}{V^{ - 2}}\mathit{\dot V} = - \frac{\beta }{V}\mathit{\dot V}, $ | (25) |
| $ \ddot e = \ddot q - {{\ddot q}_{\rm{d}}} = \frac{1}{{{J_{\rm{e}}}}}\left( {U + S} \right). $ | (26) |
将式(12)、式(24)~(26)代入式(23),可得:
| $ \begin{array}{l} \mathit{\dot V} = - \alpha \left( {\frac{1}{2}{\mathit{J}_{\rm{e}}}{{\dot e}^2} + \frac{1}{2}{\mathit{J}_{\rm{e}}}\alpha \dot ee + \frac{1}{2}\beta {e^2}} \right) - \\ \frac{{\mathit{\dot V}}}{{2V}}\left( {\beta {e^2} + \frac{1}{2}{\mathit{J}_{\rm{e}}}\alpha \dot ee} \right) + S\left( {\dot e + \frac{1}{2}\alpha e} \right), \end{array} $ | (27) |
进一步化解式(27),可得:
| $ \mathit{B}\left( {e, \dot e} \right)\mathit{\dot V} = - \alpha V + S\left( {\dot e + \frac{1}{2}\alpha e} \right), $ | (28) |
其中
| $ \mathit{B}\left( {e, \dot e} \right) = \frac{1}{V}\left( {\frac{1}{2}{\mathit{J}_{\rm{e}}}{{\dot e}^2} + \beta {e^2} + \frac{3}{4}{\mathit{J}_{\rm{e}}}\alpha \dot ee} \right). $ | (29) |
根据柯西不等式与式(10),可得:
| $ \begin{array}{l} {\left( {\dot e + \frac{1}{2}\alpha e} \right)^2} = {\left( {\frac{{{U_0}}}{8}\sqrt {\frac{6}{{{\lambda _2}V}}} e + \dot e} \right)^2} \le \\ \;\;\;\;\;\;\;\;\;\;\;{{\dot e}^2} + \frac{{{U_0}}}{4}\sqrt {\frac{6}{{{\lambda _2}V}}} e\dot e + \frac{{3U_0^2}}{{32{\mathit{J}_{\rm{e}}}V}}{e^2} = \\ \;\;\;\;\;\;\;\;\;\;\;\frac{2}{{{\mathit{J}_{\rm{e}}}}}\left( {{\mathit{J}_{\rm{e}}}{{\dot e}^2} + \frac{{{U_0}}}{8}\sqrt {\frac{6}{{{\lambda _2}V}}} {\mathit{J}_{\rm{e}}}e + \frac{{3U_0^2}}{{16V}}{e^2}} \right) = \\ \;\;\;\;\;\;\;\;\;\;\;\frac{2}{{{\mathit{J}_{\rm{e}}}}}V \le \frac{2}{{{\lambda _1}}}V. \end{array} $ | (30) |
根据式(11)与式(30),可得:
| $ \left| {S\left( {\dot e + \frac{1}{2}\alpha e} \right)} \right| \le {S_0}\sqrt {\frac{2}{{{\lambda _1}}}} {V^{1/2}}, $ | (31) |
将式(31)代入式(28),可得:
| $ \mathit{B}\left( {e, \dot e} \right)\dot V \le - \alpha V + {S_0}\sqrt {\frac{2}{{{\lambda _1}}}} {V^{1/2}}. $ | (32) |
接下来求B(e, ė)的上、下界.根据式(21)和式(29)上、下界分别可得:
| $ \begin{array}{l} \mathit{B}{\left( {e, \dot e} \right)_{{\rm{下}}}} = \frac{1}{V}\left( {\frac{1}{2}{\mathit{J}_{\rm{e}}}{{\dot e}^2} + \beta {e^2} + \frac{3}{4}\alpha {\mathit{J}_{\rm{e}}}e\dot e} \right) \ge \\ \;\;\;\;\;\;\;\frac{1}{V}\left( {\frac{1}{2}{\mathit{J}_{\rm{e}}}{{\dot e}^2} + \beta {e^2} - \frac{3}{4}\left( {\frac{1}{2}{\mathit{J}_{\rm{e}}}{{\dot e}^2} + \frac{1}{2}\beta {e^2}} \right)} \right) = \\ \;\;\;\;\;\;\;\frac{1}{{8V}}\left( {{\mathit{J}_{\rm{e}}}{{\dot e}^2} + 5\beta {e^2}} \right) > 0, \end{array} $ |
| $ \begin{array}{l} \mathit{B}{\left( {e, \dot e} \right)_{{\rm{上}}}} = \frac{1}{V}\left( {\frac{1}{2}{\mathit{J}_{\rm{e}}}{{\dot e}^2} + \beta {e^2} + \frac{3}{4}\alpha {\mathit{J}_{\rm{e}}}e\dot e} \right) \ge \\ \;\;\;\;\;\;\;\frac{1}{V}\left( {\frac{1}{2}{\mathit{J}_{\rm{e}}}{{\dot e}^2} + \beta {e^2} + \frac{3}{4}\left( {\frac{1}{2}{\mathit{J}_{\rm{e}}}{{\dot e}^2} + \frac{1}{2}\beta {e^2}} \right)} \right) = \\ \;\;\;\;\;\;\;\frac{1}{V}\left( {\frac{7}{8}{\mathit{J}_{\rm{e}}}{{\dot e}^2} + \frac{{11}}{8}\beta {e^2}} \right) \le \frac{{11}}{{8V}}\left( {{\mathit{J}_{\rm{e}}}{{\dot e}^2} + \beta {e^2}} \right). \end{array} $ |
可见,B(e, ė)始终为正,且大小有界.进一步改写式(32),可得:
| $ \dot V \le - \frac{1}{{\mathit{B}\left( {e, \dot e} \right)}}\left( {\frac{{{U_0}}}{4}\sqrt {\frac{6}{{{\lambda _2}}} - } {S_0}\sqrt {\frac{2}{{{\lambda _1}}}} } \right){V^{1/2}} $ | (33) |
由式(33)可知,若想使
| $ {U_0} > \frac{4}{3}{S_0}\sqrt {\frac{{3{\lambda _2}}}{{{\lambda _1}}}} . $ |
由此,Lyapunov函数V(e, ė)的正定性及其导数的负定性证明完毕,系统在点(e, ė)=(0, 0)处全局渐近稳定.
3 实验验证为验证上述控制算法的有效性以及摩擦和平衡力矩补偿对控制算法性能的提升和改善,采用实验室协调器原理样机进行实验研究,如图 7所示.控制器选用与Maxon电机配套的EPOS2数字位置控制器,该控制器通过USB连接到上位机(PC),以此传输通讯数据并执行控制指令.

|
图 7 协调器原理样机实验平台 Fig. 7 Experiment platform of ammunition coordinator principle prototype |
采用上文辨识出的基于模型的摩擦和气弹簧支反力矩设计补偿环节,补偿后的控制系统描述为
| $ {\mathit{J}_{\rm{e}}}\ddot \theta = U + {M_{\rm{G}}} - {M_{\rm{R}}} - {M_{\rm{f}}} + {{\dot M}_{\rm{R}}} + {{\dot M}_{\rm{f}}}. $ |
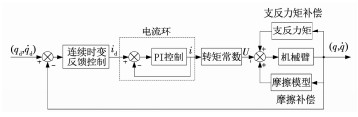
控制流程图如图 8所示,采用的Maxon电机自身带有位置控制模式、速度控制模式、电流控制模式等一系列模块化控制策略,其基本原理为三环控制.其中,电流环采用PI控制,可以单独使用.本实验采用电机的电流控制模式,即采用系统内嵌的PI控制作为电流环,同时采用本文的控制方法作为位置控制环.
|
图 8 基于模型的摩擦和支反力矩前馈补偿控制流程 Fig. 8 Flow chart of model-based friction and balance torque feedforward compensation control |
实验分为两组,第1组考虑基于模型的摩擦力矩和气弹簧支反力矩补偿对控制性能的影响,即做无补偿和加补偿情况下的对比实验;第2组在加补偿的情况下,考虑负载变化对控制性能的影响,施加负载情况为:1)无负载; 2)支臂端加一个负载质量块,质量为0.44 kg; 3)支臂末端加两个负载质量块,质量为0.88 kg.
其他系统参数以及控制参数取值见表 2.
| 表 2 系统参数及控制参数 Tab. 2 Values of system parameters and control parameters |
系统初始状态为:
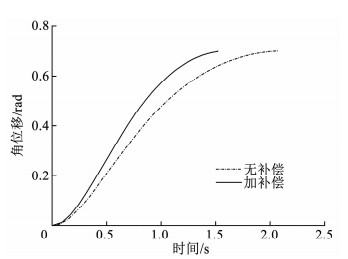
第1组实验以机械臂末端施加一个配重块为例,给出对比结果图,如图 9~12所示.
|
图 9 支臂角位移 Fig. 9 Angular displacement of transfer arm |
|
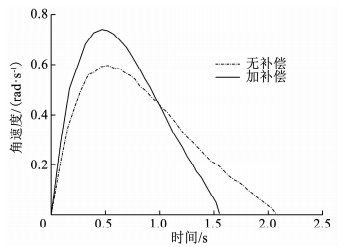
图 10 支臂角速度 Fig. 10 Angular velocity of transfer arm |
|
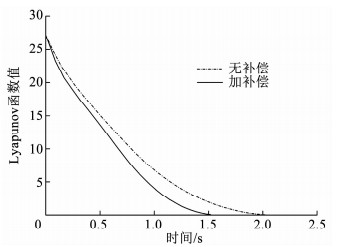
图 11 系统Lyapunov函数值 Fig. 11 Values of system Lyapunov function |
|
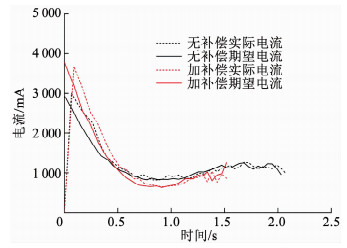
图 12 控制电流 Fig. 12 Control current |
图 9~12分别给出了支臂角位移、角速度、系统Lyapunov函数、控制电流的有无补偿对比曲线,其中,红色曲线是加摩擦和支反力矩补偿情况下的响应曲线,蓝色曲线是未加补偿情况下的响应曲线.从图中可以看出,在有补偿情况下,系统在1.55 s的时间内收敛到目标状态,而相应的未补偿状态下则需要2.07 s才能收敛到目标状态,说明补偿有效提高了控制系统的动态响应速度,缩短了协调器的定位时间,这对于提升协调器的协调效率以至于提升整个弹药装填系统的装填效率具有工程实践意义.
|
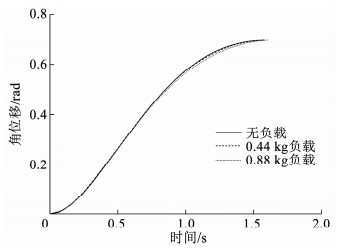
图 13 支臂角位移 Fig. 13 Angular displacement of transfer arm |
|
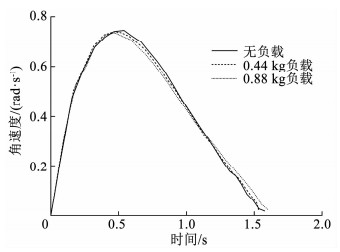
图 14 支臂角速度 Fig. 14 Angular velocity of transfer arm |
|
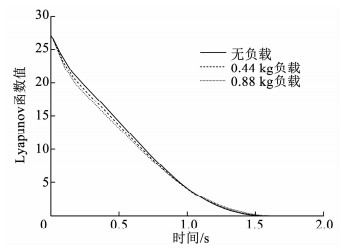
图 15 系统Lyapunov函数值 Fig. 15 Values of system Lyapunov function |
|
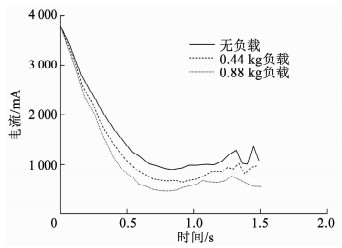
图 16 期望电流 Fig. 16 Desired current |
|
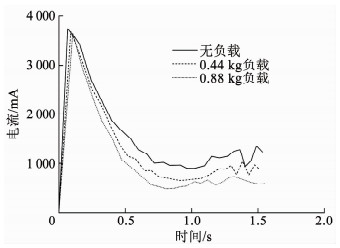
图 17 实际电流 Fig. 17 Actual current |
图 13~17给出的是不同负载情况下机械臂的运动响应,分别为支臂角位移曲线、支臂角速度曲线、系统Lyapunov函数曲线、期望电流曲线和实际电流曲线.可以看出,在负载发生变化的情况下,系统收敛到目标状态所需要的时间基本没有差别,由此说明了本文中的控制方法对系统惯量变化的鲁棒性.此外,图中,唯一有明显差别的是控制电流,负载质量越大,控制过程中所需要的控制电流反而越小,这是因为在系统的运动过程中,重力做正功,这一点在系统的动力学方程式(1)中体现为重力矩项和电机驱动力矩项符号相同,也即力矩方向相同.
以上两组实验分别说明了本文中基于模型和辨识的摩擦和支反力矩的补偿可以有效提高控制系统的性能以及控制系统对系统负载变化的鲁棒性.相应的,对于实际弹药协调器系统来说,这就意味着本文的方法可以有效解决协调器提高协调速度的问题以及不同带弹情况下的精确定位控制问题,具有工程上的现实指导意义.
4 结论1) 针对复杂非线性弹药协调器的快速精确位置控制问题,采用一种基于隐式Lyapunov函数的连续时变反馈控制算法设计了位置控制器,实现了其协调定位.
2) 过第2类Lagrange方法建立了系统的动力学方程,考虑到系统摩擦力矩以及小平衡机支反力矩会对协调器的运动过程产生影响,对这两项进行了精细建模,其中,摩擦力矩项采用的是LuGre模型.
3) 根据动力学方程结构设计实验,根据实验数据采用遗传算法对摩擦模型和小平衡机支反力矩模型中的关键参数进行了辨识,基于辨识后的模型在控制中引入了前馈补偿项.
4) 控制方案从控制律的形式上来看类似于PD控制方法,但其中的比例和微分系数取决于系统的Lyapunov函数,是时变连续的.
5) 实验结果表明,设计的控制方案可以保证系统在不同负载条件下几乎以同样的时间和运动性能达到控制目标,具有良好的鲁棒性.此外,基于模型的摩擦和支反力矩补偿显著缩短了系统的定位时间,提高了协调器系统的协调性能.
| [1] |
侯保林, 樵军谋, 刘琮敏. 火炮自动装填[M]. 北京: 兵器工业出版社, 2010: 36. HOU Baolin, QIAO Junmou, LIU Congmin. Ammunition automatic loading system of howitzer[M]. Beijing: Publishing House of Ordnance Industry, 2010: 36. |
| [2] |
RYBUS T, SEWERYN K, SASIADEK J Z. Control system for free-floating space manipulator based on nonlinear model predictive control[J]. Journal of Intelligent & Robotic Systems, 2017, 85(3/4): 491. DOI:10.1007/s10846-016-0396-2 |
| [3] |
FAULWASSER T, WEBER T, ZOMETA P, et al. Implementation of nonlinear model predictive path-following control for an industrial robot[J]. IEEE Transactions on Control Systems Technology, 2017, 25(4): 1505. DOI:10.1109/TCST.2016.2601624 |
| [4] |
DO T N, TJAHJOWIDODO T, LAU M W S, et al. Nonlinear friction modelling and compensation control of hysteresis phenomena for a pair of tendon-sheath actuated surgical robots[J]. Mechanical Systems and Signal Processing, 2015, 60. DOI:10.1016/j.ymssp.2015.01.001 |
| [5] |
JARZEBOWSKA E. Model-based tracking control of nonlinear systems[M]. New York: CRC Press, 2016: 2. DOI:10.1201/b12262
|
| [6] |
GUO Kai, PAN Yongping, YU Haoyong. Composite learning robot control with friction compensation: a neural network-based approach[J]. IEEE Transactions on Industrial Electronics, 2019, 66(10): 7841. DOI:10.1109/TIE.2018.2886763 |
| [7] |
CHEN Qiang, TAO Liang, NAN Yurong, et al. Adaptive nonlinear sliding mode control of mechanical servo system with LuGre friction compensation[J]. Journal of Dynamic Systems, Measurement, and Control, 2016, 138(2): 021003. DOI:10.1115/1.4032068 |
| [8] |
吴晓敏, 刘暾东, 贺苗, 等. 机器人关节摩擦建模与补偿研究[J]. 仪器仪表学报, 2018, 39(10): 44. WU Xiaomin, LIU Tundong, HE Miao, et al. Research on friction modeling and compensation of robot manipulator[J]. Chinese Journal of Scientific Instrument, 2018, 39(10): 44. DOI:10.19650/j.cnki.cjsi.J1803247 |
| [9] |
PAN Yongping, WANG Huiming, LI Xiang, et al. Adaptive command-filtered back-stepping control of robot arms with compliant actuators[J]. IEEE Transactions on Control Systems Technology, 2018, 26(3): 1149. DOI:10.1109/TCST.2017.2695600 |
| [10] |
丁千, 翟红梅. 机械系统摩擦动力学研究进展[J]. 力学进展, 2013, 43(1): 112. DING Qian, ZHAI Hongmei. Research progress on frictional dynamics in mechanical systems[J]. Advances in Mechanics, 2013, 43(1): 112. DOI:10.6052/1000-0992-12-039 |
| [11] |
PENNESTRI E, ROSSI V, SALVINI P, et al. Review and comparison of dry friction force models[J]. Nonlinear Dynamics, 2016, 83(4): 1785. DOI:10.1007/s11071-015-2485-3 |
| [12] |
李伟, 马吉胜, 马杨, 等. 协调器故障仿真及应用研究[J]. 火炮发射与控制学报, 2009(3): 36. LI Wei, MA Jisheng, MA Yang, et al. Study on fault simulation and application of coordinator[J]. Journal of Gun Launch & Control, 2009(3): 36. DOI:10.19323/j.issn.1673-6524.2009.03.010 |
| [13] |
王浩亦, 冯广斌, 孙华刚, 等. 协调器动力学分析及故障仿真研究[J]. 火炮发射与控制学报, 2013(1): 59. WANG Haoyi, FENG Guangbin, SUN Huagang, et al. Dynamics analysis and fault simulation study on coordinator[J]. Journal of Gun Launch & Control, 2013(1): 59. DOI:10.3969/j.issn.1673-6524.2013.01.015 |
| [14] |
赵抢抢, 侯保林. 火炮弹药协调器区间不确定参数辨识[J]. 兵工学报, 2017, 38(1): 35. ZHAO Qiangqiang, HOU Baolin. Identification of interval uncertainty parameters of a howitzer shell transfer arm[J]. Acta Armamentarii, 2017, 38(1): 35. DOI:10.3969/j.issn.1000-1093.2017.01.005 |
| [15] |
刘金琨. 滑模变结构控制MATLAB仿真[M]. 3版. 北京: 清华大学出版社, 2015. LIU Jinkun. Sliding mode control design and MATLAB simulation[M]. 3rd ed. Beijing: Tsinghua University Press, 2015. |
| [16] |
BAEK J, JIN Maolin, SOOHEE H. A new adaptive sliding-mode control scheme for application to robot manipulators[J]. IEEE Transactions on Industrial Electronics, 2016, 63(6): 3628. DOI:10.1109/TIE.2016.2522386 |
| [17] |
CUI Rongxin, CHEN Lepeng, YANG Chenguang, et al. Extended state observer-based integral sliding mode control for an underwater robot with unknown disturbances and uncertain nonlinearities[J]. IEEE Transactions on Industrial Electronics, 2017, 64(8): 6785. DOI:10.1109/TIE.2017.2694410 |
| [18] |
王尧尧, 顾临怡, 陈柏, 等. 水下机器人-机械手系统非奇异终端滑模控制[J]. 浙江大学学报(工学版), 2018, 52(5): 934. WANG Yaoyao, GU Linyi, CHEN Bai, et al. Nonsingular terminal sliding mode control of underwater vehicle-manipulator system[J]. Journal of Zhejiang University (Engineering Science), 2018, 52(5): 934. DOI:10.3785/j.issn.1008-973X.2018.05.013 |
| [19] |
WANG Yaoyao, GU Linyi, XU Yihong, et al. Practical tracking control of robot manipulators with continuous fractional-order nonsingular terminal sliding mode[J]. IEEE Transactions on Industrial Electronics, 2016, 63(10): 6194. DOI:10.1109/TIE.2016.2569454 |
| [20] |
梅生伟, 申铁龙, 刘康志. 现代鲁棒控制理论与应用[M]. 2版. 北京: 清华大学出版社, 2008: 120. MEI Shengwei, SHEN Tielong, LIU Kangzhi. Modern robust control theory and application[M]. 2nd ed. Beijing: Tsing University Press, 2008: 120. |
| [21] |
AROM K J, WITTENMARK B. Adaptive control[M]. Second edition. New York: Courier Corporation, 2013.
|
| [22] |
尹曌.非线性系统的神经网络控制算法研究及其应用[D].成都: 电子科技大学, 2016 YIN Zhao. Adaptive neural network control of a class of unknown nonlinear systems and their Applications[D]. Chengdu: University of Electronic Science and Technology of China, 2016. DOI: 10.7666/d.D00990887 |
| [23] |
DE SILVA C W. Intelligent control: Fuzzy logic applications[M]. Boca Raton: CRC press, 2018. DOI:10.1201/9780203750513
|
| [24] |
葛媛媛, 张宏基. 基于自适应模糊滑模控制的机器人轨迹跟踪算法[J]. 电子测量与仪器学报, 2017, 31(5): 746. GE Yuanyuan, ZHANG Hongji. Trajectory tracking algorithm for robot based on adaptive fuzzy sliding mode control[J]. Journal of Electronic Measurement and Instrumentation, 2017, 31(5): 746. DOI:10.13382/j.jemi.2017.05.014 |
| [25] |
VEYSI M, SOLTANPOUR M R, KHOOBAN M H. A novel self-adaptive modified bat fuzzy sliding mode control of robot manipulator in presence of uncertainties in task space[J]. Robotica, 2015, 33(10): 2045. DOI:10.1017/S0263574714001258 |
| [26] |
YANG Yueneng, YAN Ye. Neural network approximation-based nonsingular terminal sliding mode control for trajectory tracking of robotic airships[J]. Aerospace Science and Technology, 2016, 54: 192. DOI:10.1016/j.ast.2016.04.021 |
| [27] |
GUO Yufei, HOU Baolin. Implicit Lyapunov function-based tracking control of a novel ammunition autoloader with base oscillation and payload uncertainty[J]. Nonlinear Dynamics, 2017, 87(2): 741. DOI:10.1007/s11071-016-3072-y |
| [28] |
WANG Xi, HOU Baolin. Trajectory tracking control of a 2-DOF manipulator using computed torque control combined with an implicit Lyapunov function method[J]. Journal of Mechanical Science and Technology, 2018, 32(6): 2803. DOI:10.1007/s12206-018-0537-6 |
| [29] |
CHERNOUSKO F L, ANANIEVSKI I M, RESHMIN S A. Control of nonlinear dynamical systems: methods and applications[M]. Berlin: Springer-Verlag, 2008: 213. DOI:10.1007/978-3-540-70784-4
|
 2021, Vol. 53
2021, Vol. 53


