干线交通信号协调控制是解决城市道路交通堵塞的有效途径之一. 传统的研究方法主要围绕基于延误最小的优化模型和基于带宽最大的优化模型两方面展开. 在传统的干线协调控制中,绿波设计速度与运行速度往往固定,干线信号协调控制难以取得令人满意的绿波带宽. 为此,文献[1]根据检测到的交通数据,提出了一种能够实时动态调整绿波带宽的干线信号协调控制方法;文献[2]建立了一种不均匀双循环模型,能够有效减少干线上小交叉口的过度延误等问题,对提高干线信号协调效果起到了积极作用. 而更多的学者则提出了车速诱导策略,引导驾驶员调整其驾驶行为,通过车速的动态引导来减少车辆的延误和排队、减少燃油消耗与环境污染物的排放并提高干线交通的安全性[3-5]. 近年来,干道协调车速诱导模型的研究主要包括:考虑车辆平均延误和停车时间的模型[6]、基于公交优先策略的模型[7]和减少出行时间的模型[8]. 文献[9]以公交车的延误与停车次数加权最小为目标,以周期时长和相位饱和度为约束条件,建立了公交车速引导和交叉口信号配时集成优化的整数线性规划模型. 文献[10]提出了一种基于动态速度引导和动态信号配时的交通管理方法,在路段中以必要的速度动态引导车辆通过交叉口,并根据车辆检测数据,调整前一交叉口的信号配时,该策略使车辆尽量在不停车的情况下通过交叉口. 然而,这些研究的车速引导方案往往基于车辆检测或预测数据得到,面向群体发布而非针对个体车辆的定制车速引导,控制成效仍有待于进一步提高. 在车联网环境下,利用车辆和路侧设施之间双向信息交互,可实时建立单车的定制速度引导方案,为提高干线协调的绿波带宽奠定了技术基础. 如文献[11]将速度诱导策略引入到车辆跟驰模型中,有效降低了单车道多信号交叉口的油耗和停车次数; 文献[12]提出了一种城市道路网动态速度协调的非线性数学模型,通过速度协调来减少行程时间、速度方差和停车次数;文献[13]进一步提出了分布式协调优化算法,用于路网中网联车辆的动态速度优化,来保证系统的可扩展性和实时性; 文献[14]基于速度引导和交叉口信号调整,提出了一种在V2I环境下的高频公交专用道动态车头时距控制方法,用来提高车辆的运行效率; 文献[15]将被引导车辆及其后的普通车辆视为一个车队,通过分析车辆位置和速度等信息确定诱导速度,使得车辆能够不停车通过交叉口; 文献[16]提出了一种动态速度引导与动态信号配时的集成优化控制模型,对进行车速诱导后仍不能在绿灯相位通过交叉口的车辆给予绿灯时间补偿; 文献[17]提出了车联网环境下信号交叉口车速控制策略,在提高交叉口通行效率的基础上兼顾了驾驶舒适性与环境友好性; 文献[18]基于车联网技术提出了一种针对混合车流通过信号交叉口的车速诱导控制方法,能够降低车辆的燃油消耗并提高驾驶舒适性. 然而,这些研究大多着眼于单个交叉口的速度引导控制,协调控制优化模型仍为非全局的、完全动态的优化模型. 基于此,本文考虑车速引导与信号控制方案的双向调整,提出一种新的车联网环境下干线交通信号协调控制方法,期望能对上述问题的解决提供一些思路.
1 问题描述与模型假设城市主干道上的车辆以平均行驶速度行驶到下游交叉口时,会遇到3种情况:信号灯为绿灯,入口无排队;信号灯为绿灯,入口有排队车辆;信号灯为红灯. 为了实现车辆尽可能多地通过交叉口的目标,现有的控制策略通过引导车辆的行驶速度来改变车队到达下游交叉口的时间. 一般的控制方法是设置可变速度引导标,根据信号灯的状态判断进入路段的车辆是否需要速度引导. 此时,将遇到以下问题: 1)主干道上的车辆被动地根据信号灯的状态来进行速度引导,车辆在交叉口不能形成饱和车队;因引导路段长度的限制,调节效果相对有限,优化效果不理想. 2)当大多数可引导的车辆通过交叉口时,绿灯相位仍未结束,导致绿灯利用率低. 3)绿灯结束时,车辆未完全通过下游交叉口,导致车辆延误增加.
在车联网环境下,如果能根据交通流状态进行实时的交叉口信号控制方案调整和车速诱导控制,则能最大程度地提高绿灯时间的利用效率,并可以减少车辆排队,提高交叉口的交通效率. 为了量化本文所建立的车联网环境下的干线协调控制模型的潜在效益,以干线直行车流作为关键车流进行车速诱导控制,并进行交叉口的信号控制方案调整,提出如下假设:1)道路上的车辆为网联车辆,装备有车联网通信设备,具备车辆定位、实时通信和信息显示等功能. 2)所有车辆都按照交叉口交通控制系统提供的车速诱导策略信息行驶并通过信号交叉口. 3)各个交叉口信号相位方案不变,干线方向直行相位为第1相位. 4)所有车辆进入路段后及时完成车道变换. 5)暂不考虑非机动车和行人对机动车的影响.
2 干线协调交通信号控制优化模型 2.1 优化目标交叉口停车是造成交叉口运行效率和能耗低下的重要原因. 与其他方法相比,当采用车速诱导控制时,交叉口的停车次数和延误都会发生变化. 为全面反映本文建立优化模型的性能,将车均延误和平均停车次数加权形成一个综合性能评价指标(PI),来优化干线协调信号控制参数. 一般来说,PI越大,延误也就越大,停止次数也越多,PI的计算公式为
| $ \min p_{i, k}=\frac{\sum\limits_{p} \sum\limits_{k}{\rm{ P I}}_{i, k}^{(p)}}{\sum\limits_{p} \sum\limits_{k} \sum\limits_{r} q_{i, k}^{(p, r)}}. $ | (1) |
式中:d为车均延误,s/pcu;n为停车次数;w1、w2分别为延误和停车的权重.
信号控制参数优化目标为
| $ $ | (2) |
以i交叉口为例,第k周期可能成功被诱导通过交叉口的车辆进入路段的最晚时间为
| $ q_{i, k}^{(p, r)}=q_{i, k-1, 0}^{(p, r)}+q_{i, k, \text { arrive }}^{(p, r)}. $ | (3) |
式中:pi, k为i交叉口第k周期的车均PI值;PIi, k(p)为i号交叉口第k周期第p相位的总PI值;ti, k(p)′为i号交叉口第k周期第p相位信号方案调整后的绿灯开启时间,s;gi, k(p)、gi, k(p)′分别为i号交叉口第k周期第p相位信号方案调整前后的绿灯时长,s;qi, k(p, r)、qi, k-1, 0(p, r)、qi, k, arrive(p, r)分别为i号交叉口第k周期第p相位r方向的处理车辆数、上周期滞留车辆数和到达车辆数,pcu;vi, max(p, r)、vi, min(p, r)分别为i号交叉口第k周期第p相位r方向的车辆最大和最小诱导速度,km/h;li(p, r)为i号交叉口第k周期第p相位r方向路段长度,m.
诱导车速区间的最大值一般取城市道路最高限速值. 国内相关规范中并无城市道路最低限速的规定,诱导车速区间的最小值可从车辆行驶的舒适性、经济性等考虑,参照文献[19]中的方法予以确立.
2.2 约束条件 2.2.1 一般约束相位绿灯时长应满足条件:
| $ g_{i, \min }^{(p)} \leqslant g_{i, k}^{(p) \prime} \leqslant g_{i, \max }^{(p)}. $ | (4) |
式中gi, min(p)、gi, max(p)分别为i交叉口第p相位的最小绿灯时长和最大绿灯时长,s.
最小绿灯时长应满足行人过街的需要,即
| $ g_{i, \min }^{(p)} \geqslant 7+\frac{\bar{L}_{i}^{(p)}}{v_{\mathrm{w}}}-I . $ | (5) |
式中:Li(p)为i交叉口第p相位的人行横道长度,m;vw为行人平均步行速度,m/s;I为绿灯间隔时间,s.
2.2.2 相位差策略首先以关键交叉口周期时长作为公共周期时长C,以i-1和i交叉口为例,设i-1至i交叉口方向为下行方向,根据以下3种情况分别进行讨论.
1) 若要实现双向关键车流的成功诱导,理想的相位差
| $ v_{i, d}^{(1, 1)}=v_{i-1, d}^{(1, 2)}=\frac{3.6 l_{i}^{(1, 1)}}{O_{i-1, i}}=\frac{7.2 l_{i}^{(1, 1)}}{n \cdot C}, n=1, 2, 3, \cdots. $ | (6) |
式中:C为公共周期时长,s;Oi-1, i为i-1至i交叉口的相位差,s;vi, d(p, r)为i交叉口第p相位r方向的绿波带设计速度,km/h.
使得带速满足vi, d(1, 1)∈ vi, min(1, 1), vi, max (1, 1),若存在多个解,则进行每个解的信号控制方案并比选效果;若无解,以平均行程车速为基础,根据图解法或数解法计算上下行的相位差,使得两个方向的相位差接近理想相位差,并满足Oi-1, i+Oi, i-1=n·C.
2) 当交叉口间距相当短时,将相邻交叉口视为一个交叉口,进行同步式协调控制. 为使控制效果最佳,应使双向车流一半以上的车辆能成功在绿灯相位不停车通过交叉口,否则仅诱导其中一股车流时效果更好,交叉口间距应满足:
| $ $ | (7) |
式中vi(p, r)为i交叉口第p相位r方向进行干线协调控制前的平均行程车速,km/h.
3) 当交叉口间距满足:
| $ \frac{g_{i, k}^{(1)} \cdot v_{i, \max }^{(1, 1)}}{7.2}<l_{i}^{(1, 1)}<\frac{C \cdot v_{i, \min }^{(1, 1)}}{7.2}, $ | (8) |
此时难以控制双向的关键车流不停车地通过交叉口,进行关键车流交通量较大的方向的干线协调控制,如取下行相位差Oi-1, i=3.6li(1, 1)/vi(1, 1),上行相位差Oi, i-1=C-3.6li(1, 1)/vi(1, 1).
2.2.3 信号控制方案调整策略根据诱导车辆进入路段的时间确定其诱导方案及下游交叉口信号调整方案,在统计时间区间内i号交叉口第k周期第1相位r方向的第j辆车进入路段的时间为ti, k, j(1, r),其中第x辆车为上游关键诱导车队首车,为使该相位绿灯时间能被充分利用,以诱导车流形成饱和车队为目标进行信号方案调整. 进行诱导后第j辆车通过i号交叉口的时间为
| $ t_{i, k, j, 1}^{(1, r)}=\left\{\begin{array}{l} t_{i, k}^{(1)}+\left\lceil\frac{q_{i, k-1, 0}^{(1, r)}+j-1}{m_{i}^{(1, r)}}\right\rceil \cdot \bar{h}_{i}^{(1, r)}+\delta, t_{i, k, j}^{(1, r)}+\frac{3.6 l_{i}^{(1, r)}}{v_{i, \max }^{(1, r)}} \leqslant t_{i, k}^{(1)}+\left\lceil\frac{q_{i, k-1, 0}^{(1, r)}+j-1}{m_{i}^{(1, r)}}\right\rceil \cdot \bar{h}_{i}^{(1, r)}+\delta ;\\ t_{i, k, j}^{(1, r)}+\frac{3.6 l_{i}^{(1, r)}}{v_{i, \max }^{(1, r)}}, t_{i, k, j}^{(1, r)}+\frac{3.6 l_{i}^{(1, r)}}{v_{i, \max }^{(1, r)}}>t_{i, k}^{(1)}+\left\lceil\frac{q_{i, k-1, 0}^{(1, r)}+j-1}{m_{i}^{(1, r)}}\right\rceil \cdot \bar{h}_{i}^{(1, r)}+\delta . \end{array}\right. $ | (9) |
式中:ti, k, j, 1(p, r)为i号交叉口第k周期第p相位r方向的第j辆车预期通过交叉口的时间,s;ti, k(p)为i号交叉口第k周期第p相位信号方案调整前的绿灯开启时间,s; hi(p, r)为i号交叉口第p相位r方向的车流饱和车头时距,s/pcu;δ为启动损失时间,s.
当存在j≥x且第j辆车通过i号交叉口的时间满足:
| $ \begin{array}{c} t_{i, k, (j-1), 1}^{(1, r)}-t_{i, k, (j-2), 1}^{(1, r)} \leqslant t_{0}, \text { 且 } t_{i, k, j, 1}^{(1, r)}- \\ t_{i, k, (j-1), 1}^{(1, r)}>t_{0}, j \geqslant x. \end{array} $ | (10) |
则i号交叉口第k周期第1相位绿灯结束时间为ti, k, (j-1), 1(1, r),其中t0为单位绿灯时长,s. 综合考虑该相位双向关键车流形成饱和车队,取gi, k(1)′=max(ti, k, (j-1), 1(1, 1), ti, k, (j-1), 1(1, 2))-ti, k(1),为保证公共周期时长C保持不变,将第1相位时长调整值按比例在其他3个相位中调整回来,gi, k(p)′根据计算结果进行取整,并满足绿灯时间约束条件,且保持周期时长不变,即
| $ g_{i, k}^{(p) \prime}=g_{i, k}^{(p)}-\frac{g_{i, k}^{(p)} \cdot\left(g_{i, k}^{(1) \prime}-g_{i, k}^{(1)}\right)}{\sum\limits_{p=2}^{4} g_{i, k}^{(p)}}. $ | (11) |
信号控制方案调整后i号交叉口第k周期第p相位绿灯开启时间为
| $ t_{i, k}^{(p) \prime}=t_{i, k}^{(1)}+\sum\limits_{p=2}^{p} g_{i, k}^{(p-1)} {}^\prime. $ | (12) |
则在时间区间
| $ \left\{\begin{array}{l} t_{i, k, n}^{(p, r)}+\frac{3.6 l_{i}^{(p, r)}}{v_{i, \min }^{(p, r)}} \geqslant_{i, k}^{(p) \prime}+\frac{q_{i, k-1, 0}^{(p, r)}+n_{i, k}^{(p, r)}-1}{m_{i}^{(p, r)} \cdot v_{i, s}^{(p, r)}}, \\ t_{i, k, n-1}^{(p, r)}+\frac{3.6 l_{i}^{(p, r)}}{v_{i, \min }^{(p, r)}}<t_{i, k}^{(p)}{}^{ \prime}+\frac{q_{i, k-1, 0}^{(p, r)}+n_{i, k}^{(p, r)}-2}{m_{i}^{(p, r)} \cdot v_{i, s}^{(p, r)}}. \end{array}\right. $ | (13) |
式中: ni, k(p, r)≥2; mi(p, r)、vi, s(p, r)分别为i号交叉口第p相位r方向的放行车道数和排队车辆启动波传播速度,km/h.
第p相位r方向绿灯时间内最多可通行的车辆数为
| $ W_{i, k}^{(p, r)}=\left\{\begin{array}{l} \left\lfloor \frac{g_{i, k}^{(p) \prime}}{m_{i}^{(p, r)} \cdot v_{i, s}^{(p, r)}}\right\rfloor, n_{i, k}^{(p, r)}=\emptyset; \\ \left(g_{i, k}^{(p)\prime}-\left\lceil\frac{q_{i, k-1, 0}^{(p, r)}+n_{i, k}^{(p, r)}-1}{m_{i}^{(p, r)} \cdot v_{i, s}^{(p, r)}}\right\rceil\right) \cdot \frac{m_{i}^{(p, r)}}{\bar{h}_{i}^{(p, r)}}+ \\ \ \ \ \ \ q_{i, k-1, 0}^{(p, r)}+n_{i, k}^{(p, r)}-1, n_{i, k}^{(p, r)} \neq \emptyset. \end{array}\right. $ | (14) |
式中Wi, k(p, r)为i号交叉口第k周期第p相位r方向的最大放行车辆数,pcu.
第j辆车到达交叉口时的排队长度为
| $ H_{i, k, j}^{(p, r)}=\left\{\begin{array}{l} q_{i, k-1, 0}^{(p, r)}+j-1, j<n_{i, k}^{(p, r)} \text { 或 } n_{i, k}^{(p, r)}=\emptyset; \\ 0, j \geqslant n_{i, k}^{(p, r)} \text { 且 } j \leqslant W_{i, k}^{(p, r)}-q_{i, k-1, 0}^{(p, r)} ;\\ j-\left(W_{i, k}^{(p, r)}-q_{i, k-1, 0}^{(p, r)}\right)-1, j>W_{i, k}^{(p, r)}-q_{i, k-1, 0}^{(p, r)}. \end{array}\right. $ | (15) |
式中Hi, k, j(p, r)为i号交叉口第k周期第p相位r方向的第j辆车到达交叉口时的预期排队车辆数,pcu.
i号交叉口第k周期第p相位r方向的第j辆车到达交叉口时的诱导速度为
| $ v_{i, k, j}^{(p, r)} = \left\{ \begin{array}{l} \begin{array}{*{20}{l}} {v_i^{(p, r)}, j < n_{i, k}^{(p, r)};}\\ {\min \left[ {\begin{array}{*{20}{l}} {v_{i, \max }^{(p, r)}, \frac{{3.6l_i^{(p, r)}}}{{t_{i, k}^{(p)\prime } + \left\lceil {\frac{{q_{i, k - 1, 0}^{(p, r)} + n_{i, k}^{(p, r)} - 1}}{{m_i^{(p, r)} \cdot v_{i, s}^{(p, r)}}}} \right\rceil + \left\lfloor {\frac{{j - n_{i, k}^{(p, r)}}}{{m_i^{(p, r)}}}} \right\rfloor \cdot h_i^{(p, r)} - t_{i, k, j}^{(p, r)}}}} \end{array}} \right], } \end{array}\\ j \ge n_{i, k}^{(p, r)}{\rm{且 }}j \le W_{i, k}^{(p, r)} - q_{i, k - 1, 0}^{(p, r)};\\ v_i^{(p, r)}, j > W_{i, k}^{(p, r)} - q_{i, k - 1, 0}^{(p, r)}{\rm{ 或 }}n_{i, k}^{(p, r)} = \emptyset . \end{array} \right. $ | (16) |
式中vi, k, j(p, r)为i号交叉口第k周期第p相位r方向的第j辆车到达交叉口时的诱导速度,km/h.
i号交叉口第k周期第p相位r方向的第j辆车到达交叉口时的PI值为
| $ \mathrm{PI}_{i, k, j}^{(p, r)}=\left\{\begin{array}{l} w_{1} \cdot\left(t_{i, k}^{(p)}++\frac{H_{i, k, j}^{(p, r)}}{m_{i}^{(p, r)} \cdot v_{i, s}^{(p, r)}}-t_{i, k, j}^{(p, r)}-\frac{3.6 l_{i}^{(p, r)}}{v_{i}^{(p, r)}}\right)+w_{2}, j<n_{i, k}^{(p, r)} ;\\ \max \left[0, w_{1} \cdot\left(\frac{3.6 l_{i}^{(p, r)}}{v_{i, k, j}^{(p, r)}}-\frac{3.6 l_{i}^{(p, r)}}{v_{i}^{(p, r)}}\right)\right], j \geqslant n_{i, k}^{(p, r)} \text { 且 } j \leqslant W_{i, k}^{(p, r)}-q_{i, k-1, 0}^{(p, r)};\\ w_{1} \cdot\left(t_{i, k+1}^{(p)}{ }^{\prime}+\frac{H_{i, k, j}^{(p, r)}}{m_{i}^{(p, r)} \cdot v_{i, s}^{(p, r)}}-t_{i, k, j}^{(p, r)}-\frac{3.6 l_{i}^{(p, r)}}{v_{i}^{(p, r)}}\right)+2 w_{2}, j>W_{i, k}^{(p, r)}-q_{i, k-1, 0}^{(p, r)}. \end{array}\right. $ | (17) |
i号交叉口第k周期第p相位车辆的总PI值为
| $ \mathrm{P} \mathrm{I}_{i, k}^{(p)}=\sum\limits_{j} \sum\limits_{r} \mathrm{PI}_{i, k, j}^{(p, r)}. $ | (18) |
w1、w2根据一次停车过程的损失时间与延误的等效换算关系进行折算. 车辆从原车速减速—停止—加速到原车速这一过程所需的时间为
| $ t_{1}=\frac{v_{i}^{(p, r)}}{3.6 a_{1}}+\frac{v_{i}^{(p, r)}}{3.6 a_{2}}+\lambda . $ | (19) |
式中:t1为一次停车过程所需的时间,s;a1为期望减速度,m/s2;a2为期望加速度,m/s2;λ为驾驶员平均反应时间,s.
停车过程的损失时间为
| $ t_{2}=t_{1}-\frac{v_{i}^{(p, r)}}{7.2 a_{1}}-\frac{v_{i}^{(p, r)}}{7.2 a_{2}}. $ | (20) |
式中t2为车辆停车过程损失时间,s.
w1为交叉口车辆延误的权重,一般取1,根据等效换算关系,则有
| $ {w_2} = {w_1} \cdot {t_2}. $ | (21) |
本文信号控制参数优化模型待优化变量为各个相位的绿灯显示时间,优化目标为车均综合性能指标(PI)最小,属于典型的非线性整数优化模型,为解决这一问题,可采用遗传算法求解. 然而遗传算法涉及交叉、变异、终止条件判断等,运算规模大、耗时长. 鉴于各个相位的绿灯时间均有最大、最小值限制,通过有限穷举就能快速得到优化结果,较遗传算法能节省大量的运算时间. 因此,本文优化模型的求解算法采取穷举法,优化算法步骤如下.
步骤1 在满足约束条件下,确定交叉口可能的信号控制方案数m与优化结束时间,令i=1、j=1、PI0=1 000.
步骤2 根据上游交叉口的信号控制方案和交通状况确定车辆进入路段的时间分布.
步骤3 计算交叉口第i周期第j方案的车均PI值,若PI < PI0则令PI0=PI、存储当前各个相位的绿灯时间;令j=j+1.
步骤4 判断j是否小于m+1,若是,返回步骤3;否则,进入步骤5.
步骤5 以当前存储的信号控制参数作为第i周期的信号输出方案,并令i=i+1、j=1、PI0=1 000,进入下一步,开始下一周期的信号控制方案优化.
步骤6 是否已到结束时间,若否,进入步骤2;若是,结束优化流程.
3 算例分析与仿真验证 3.1 仿真交叉口以哈尔滨市祥安北大街(龙轩路—龙盛路)为例,将其从南到北的3个交叉口分别命名为A、B、C,均为4相位控制方案,南北直行相位为协调相位. 以B交叉口为研究对象,该交叉口次要道路方向相邻交叉口为D、E,干线道路进口道设置有3条直行车道(含直右)、1条左转车道,其余道路均为两条直行车道(含直右)、1条左转车道,车道宽度均为3.5 m;LAB=380 m,LBC=360 m,LBD=640 m,LBE=750 m. 各交叉口调查的平峰流量(2019年6月11日9:00—10:00)见表 1.
| 表 1 交叉口流量 Tab. 1 Traffic flow at intersections |
计算各交叉口初始信号配时方案,确定公共周期时长为100 s,并以公共周期时长为基础对干线各交叉口现状信号方案进行调整. 根据式(19)~(21) 及交通调查结果,按期望加速度(减速度)为3 m/s2、车辆启动反应时间为1.4 s[20]计算,则停车过程损失时间为5.5 s,由此确定w1=1、w2=5.5.
3.2 仿真环境构建本文借助VISSIM进行交通仿真. 首先,在VISSIM中建立5个交叉口的布局模型. 然后,根据哈尔滨市的实际调查结果,对VISSIM中的仿真参数进行标定,结果是:直行车道和左转车道的饱和流率分别为1 450 pcu/h和1 350 pcu/h,启动损失时间为3 s,平均行程速度暂定为45 km/h,最大加速度(减速度)为5 m/s2,期望加速度(减速度)为3 m/s2,静止状态平均停车距离为1.5 m,行驶状态最小距离为1.2 m. 最后,在VISSIM中建立了两种信号协调控制方案进行对比分析. 方案1为仅实施速度引导的协调信号控制方案[17],方案2为本研究提出的协调信号控制方案.
方案1和方案2使用动态链接库(DLL)进行编程. 通过VISSIM中的API接口,将定制的信号控制方案连接到VISSIM红绿灯控制器上. 在每条车道的两端分别设置交通流检测器,记录每辆车的到达时间,动态采集到达交通量. 在仿真过程中,每0.5 s对每个检测器的状态进行检测,得到到达和驶离的交通量,以此为基础来优化协调相位的信号控制参数.
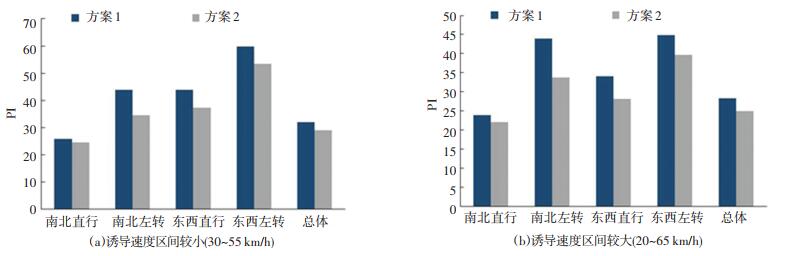
3.3 仿真结果分析在仿真参数和各方向输入交通量不变的情况下,以PI为评价指标,根据不同的诱导速度范围进行仿真,仿真时长均为1 h,仿真结果如图 1所示.
|
图 1 不同的诱导车速范围下的仿真结果对比 Fig. 1 Comparison of simulation results under different guidance speed ranges |
由图 1可以看出,当诱导速度范围较大时,交叉口的平均PI相对较低. 与仅实施速度引导策略的方案相比,本文提出的干线道路协调控制方法实施后,交叉口车均PI值有一定程度的降低. 分析交叉口不同相位车均PI值的差异后发现,由于本文根据干道直行方向的车流状态进行下游信号方案的调整,并进行车速诱导控制,干道直行相位车均PI值较小,而其他相位车辆是被动的根据交叉口信号方案进行车速诱导控制,且次要道路方向相邻交叉口的周期时长存在差异,导致车均PI值较大.
本文案例路段为城市主干路,限速60 km/h,因此诱导车速的最大值为60 km/h;诱导车速的最小值从车辆行驶的舒适性、经济性等考虑,根据文献[19]中的方法设定为25 km/h;调查得到该道路的平均行程车速为45 km/h. 综上,以诱导速度为25~60 km/h、平均行程车速为45 km/h进行仿真,仿真结果见表 2、3.
| 表 2 平均PI值对比分析 Tab. 2 Comparative analysis of average PI |
| 表 3 性能指标变化情况 Tab. 3 Variation of simulation performance indexes |
对比表 2、3中的仿真结果,本研究提出的优化方法将每辆车的平均PI值从28.72降低到25.51,与仅在相同交通条件下实施速度引导策略的方案相比降低了11.2%. 同时,车均延误和平均停车次数两个仿真性能指标的变化与每辆车PI值的变化相一致,说明PI能总体反映车均延误和平均停车次数的变化趋势. 南北直行关键车流形成车队,绿灯时间的利用效率提高,当个别周期到达车辆数较大时,延长绿灯时间能使车均PI值减少. 多数情况下,由于南北直行相位绿灯时间利用效率提高,绿灯时长缩短,其他相位绿灯时间增加且开启时间提前,从而其他相位车均PI值也有一定程度的下降. 结果表明:本文提出的干线交通信号协调控制方法是可行和有效的.
3.4 敏感性分析 3.4.1 速度诱导区间的影响车辆诱导速度的范围直接影响到车辆诱导的效果,一般来说,车辆的速度引导范围越大,车辆越有可能通过速度调节来改变到达下游交叉口的时间,从而增加诱导车辆数和减少停车次数. 依次控制道路上车辆的最小诱导速度和最大诱导速度,使最大诱导速度为50、52、54、…、66 km/h,最小诱导速度为18、20、22、…、34 km/h,步长为2 km/h,得到交叉口的平均PI值变化情况,如图 2所示.

|
图 2 车辆诱导速度范围的影响 Fig. 2 Influence of guidance speed range |
由图 2可以看出,当路段最小诱导速度降低时,车辆有更大的到达时间调整区间,特别是当车辆以较高速度行驶至下游交叉口而相位绿灯仍未开启时,可以引导车辆以低速行驶,并在排队消散时通过交叉口,交叉口的平均PI值逐渐减小.
当车辆以原平均行程车速行驶而不能在排队车辆消散时到达交叉口,可以诱导车辆以更大的速度行驶,避免绿灯时间的损失,因此当车辆的最大诱导速度增加时,车辆的速度调整范围更大且车速更高,平均PI值明显降低. 因此,在满足安全性和经济性的前提下,车辆的速度诱导区间越大,对主干道实施协调控制的效果就越好.
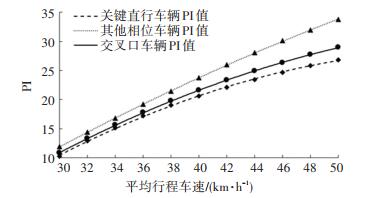
3.4.2 平均行程车速的影响本文所述的平均行程车速为进行干线协调控制之前道路上车辆的实际行驶速度,反映了进行优化控制之前道路上的交通运行状态. 从式(17)可以看出,平均行程车速对车辆PI值的计算结果有一定的影响. 当平均行程车速较低时,车辆以较高的诱导速度行驶可显著缩短路段行驶时间,从而减少车辆延误. 当平均行程车速较高时,一些以该速度行驶的车辆会在排队车辆消散之前到达下游交叉口并排队,当其以较低的诱导速度行驶时,路段上的行驶时间增加,但减少了在交叉口的停车排队,车辆延误基本不变,当PI值为负时,将其赋值为零,应避免计算车辆的PI值为负. 依次控制道路上平均行程车速为30、32、34、…、50 km/h,步长为2 km/h,得到交叉口各相位的平均PI值,如图 3所示.
|
图 3 车辆平均行程车速的影响 Fig. 3 Influence of average running speed |
当平均行程车速较低时,车辆在路段上的行驶时间较长,车辆被诱导的机会增大,停车次数能显著减少. 从仿真结果可以看出,当实施车辆速度诱导控制时,随着平均行程车速的增加,交叉口各相位的平均PI逐渐增大. 因此,当平均行程车速较低时,本文提出的干线协调控制方案效果更好.
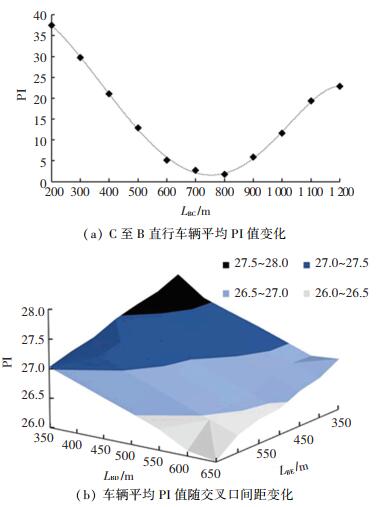
3.4.3 交叉口间距的影响交叉口间距制约了车辆到达下游交叉口时的时间区间范围的大小,对车速诱导效果的影响明显. 为研究交叉口间距对交叉口平均PI值的影响,令LBC=300、400、500、…、1 200 m,LBD=350、400、450、…、650 m,LBE=350、400、450、…、650 m,得到交叉口各相位的平均PI值,如图 4所示.
|
图 4 交叉口间距对干线协调效果的影响 Fig. 4 Influence of intersection spacing |
由2.2.2节可知,当干线交叉口间距不足时,仅能实现部分车流或某一方向车流的成功诱导,交叉口平均PI值较高. 当双向车流均能诱导时,交叉口间距会影响到下一周期各相位要处理交通量的时间区间大小(即式(3)中的到达交通量)和绿波带设计速度大小,当交叉口间距较短时,确立的时间区间较小,绿波带设计速度较小,后续进入路段的连续车流不能得到及时处理,导致协调相位绿灯时间不足,使得停车次数和延误增长;而当交叉口间距过大时,确立的时间区间过长,又会导致绿灯时间过长等待不必要协调的交通量,也会使得车均延误增长. 因此,交叉口间距与PI之间存在波动性,在LBC=750 m时,二者之间能取得最佳效果,如图 4(a)所示.
由图 4(b)可以得知,当次要道路方向交叉口间距增加时,车辆以诱导车速行驶时到达下游交叉口的时间区间更大,因此可以更好地通过调整车速实现在排队车辆消散时到达下游交叉口的目标,交叉口平均PI值逐渐减小. 而当交叉口间距较短时,通过车速引导改变车辆到达下游交叉口时间的能力有限,往往导致诱导失败,造成车辆平均PI值较大.
4 结论1) 提出了一种车联网环境下基于车速诱导的干线信号协调控制方法,相比于常规的车速诱导方案,可以根据干线道路上关键车流的实时到达情况,确定合理的车辆诱导速度和下游交叉口的信号调整方案. 同时,根据调整后的信号控制方案,进行非关键相位车辆的车速诱导控制,使得车辆能够形成饱和车队,并尽可能不停车通过交叉口,从而提高了交叉口绿灯时间的利用效率,减少了车辆延误和停车次数.
2) 建立了车联网环境下的干线协调控制相位差方案,为干线交叉口的双向协调控制奠定了基础;以形成饱和车队为目标制定了车辆速度诱导控制策略,并确定了交叉口信号控制方案调整策略;综合车辆延误和停车情况,建立了交叉口运行的评价指标模型,以交叉口车均PI最小为优化目标,建立了干线协调交叉口信号控制参数优化模型,并给出了求解算法.
3) 案例分析表明,与仅进行车速诱导的信号控制方案相比,所提出的干线协调信号控制方法能使交叉口车均PI降低11.2%. 进一步分析表明,速度诱导区间、平均行程车速、交叉口间距等因素对信号控制方案优化结果能产生显著影响.
| [1] |
KIM S, HAJBABAIE A, WILLIAMS B M, et al. Dynamic bandwidth analysis for coordinated arterial streets[J]. Journal of Intelligent Transportation Systems, 2016, 20(3): 294. DOI:10.1080/15472450.2015.1074575 |
| [2] |
ZHOU H, HAWKINS H G, ZHANG Y. Arterial signal coordination with uneven double cycling[J]. Transportation Research Part A: Policy and Practice, 2017, 103(9): 409. |
| [3] |
WU W, LI P K, ZHANG Y. Modelling and simulation of vehicle speed guidance in connected vehicle environment[J]. International Journal of Simulation Modelling, 2015, 14(1): 145. |
| [4] |
WAN N F, VAHIDI A, LUCKOW A. Optimal speed advisory for connected vehicles in arterial roads and the impact on mixed traffic[J]. Transportation Research Part C: Emerging Technologies, 2016, 69(8): 548. |
| [5] |
WANG Z, CHEN X M, OUYANG Y, et al. Emission mitigation via longitudinal control of intelligent vehicles in a congested platoon[J]. Computer-Aided Civil and Infrastructure Engineering, 2015, 30(6): 490. DOI:10.1111/mice.12130 |
| [6] |
YANG Y D, CHEN S Y, SUN J. Modeling and evaluation of speed guidance strategy in Ⅶ system[C]//13th International IEEE Annual Conference on Intelligent Transportation Systems. Madeira Island: IEEE, 2010: 1045
|
| [7] |
SHEN J, WU Z, SU B. BRT space speed guidance method within a Ⅶ environment[C]//14th COTA International Conference of Transportation Professionals. Changsha: [s.n.], 2014: 359
|
| [8] |
YANG B W, WANG Y Z, HU J M, et al. A traffic efficiency promotion algorithm for urban arterial roads based on speed guidance[C]//2013 International Conference on Connected Vehicles and Expo. Las Vegas, NV: IEEE Computer Society, 2013: 869
|
| [9] |
张鹏, 李文权, 常玉林, 等. 基于车速引导的交叉口公交优先多申请优化控制模型[J]. 中国公路学报, 2017, 30(9): 109. ZHANG Peng, LI Wenquan, CHANG Yulin, et al. Optimal control model of multiple bus signal priority requests for isolated intersection based on speed guidance[J]. China Journal of Highway and Transport, 2017, 30(9): 109. DOI:10.3969/j.issn.1001-7372.2017.09.014 |
| [10] |
CHEN S, SUN J, YAO J. Development and simulation application of a dynamic speed dynamic signal strategy for arterial traffic management[C]//14th International IEEE Conference on Intelligent Transportation Systems (ITSC). Washington DC: IEEE, 2011: 1349
|
| [11] |
TANG T Q, YI Z Y, ZHANG J, et al. A speed guidance strategy for multiple signalized intersections based on car-following model[J]. Physica A: Statistical Mechanics and its Applications, 2018, 496: 399. DOI:10.1016/j.physa.2018.01.005 |
| [12] |
TAJALLI M, HAJBABAIE A. Dynamic speed harmonization in connected urban street networks[J]. Computer-Aided Civil and Infrastructure Engineering, 2018, 33(6): 510. DOI:10.1111/mice.12360 |
| [13] |
TAJALLI M, HAJBABAIE A. Distributed optimization and coordination algorithms for dynamic speed optimization of connected and autonomous vehicles in urban street networks[J]. Transportation Research Part C, 2018, 95(10): 497. |
| [14] |
BIE Y M, XIONG X Y, YAN Y D, et al. Dynamic headway control for high-frequency bus line based on speed guidance and intersection signal adjustment[J]. Computer-Aided Civil and Infrastructure Engineering, 2020, 35: 4. DOI:10.1111/mice.12446 |
| [15] |
刘欢, 杨雷, 邵社刚, 等. 车路协同环境下信号交叉口速度引导策略[J]. 重庆交通大学学报(自然科学版), 2019, 38(12): 8. LIU Huan, YANG Lei, SHAO Shegang, et al. Speed guidance strategies at signalized intersections in a vehicle infrastructure cooperative environment[J]. Journal of Chongqing Jiaotong University (Natural Science), 2019, 38(12): 8. |
| [16] |
高志波. 基于车路协同环境的干线信号控制方法研究[D]. 长沙: 长沙理工大学, 2018 GAO Zhibo. The research on arterial signal control method based on cooperative vehicle infrastructure environment[D]. Changsha: Changsha University of Science & Technology, 2018 |
| [17] |
鹿应荣, 许晓彤, 丁川, 等. 车联网环境下信号交叉口车速控制策略[J]. 交通运输系统工程与信息, 2018, 44(11): 2257. LU Yingrong, XU Xiaotong, DING Chuan, et al. Connected autonomous vehicle speed control at successive signalized intersections[J]. Journal of Transportation Systems Engineering and Information Technology, 2018, 44(11): 2257. |
| [18] |
杨楠. 车联网环境下的信号交叉口多车协同车速引导策略及方法[D]. 西安: 长安大学, 2018 YANG Nan. Strategy andmethod of multi-vehicle cooperative speed guidance at signalized intersection based on environment of connected vehicle[D]. Xi'an: Chang'an University, 2018 |
| [19] |
李明慧. 城市快速路合理限速区间研究[D]. 哈尔滨: 哈尔滨工业大学, 2015 LI Minghui. Research on reasonable speed limit of urban expressway[D]. Harbin: Harbin Institute of Technology, 2015 |
| [20] |
李振龙, 张剑坤. 交通信号倒计时对驾驶员启动反应时间的影响[J]. 交通信息与安全, 2013, 31(5): 77. LI Zhenlong, ZHANG Jiankun. The influence of traffic signal countdown on driver's response time[J]. Journal of Transport Information and Safety, 2013, 31(5): 77. DOI:10.3963/j.issn.1674-4861.2013.05.015 |
 2021, Vol. 53
2021, Vol. 53


