2. 浙江温州沈海高速公路有限公司,浙江 温州 325000
2. Zhejiang Wenzhou Shenhai Expressway Co., Ltd., Wenzhou 325000, Zhejiang, China
随着中国公路、铁路隧道的交通建设蓬勃发展,山岭隧洞穿越富水环境的工况急剧增加[1-3],此环境中的深埋山岭隧洞主要采取“堵水限排”支护设计准则[4-5],一般通过“注浆圈+衬砌”的堵水方式实现. 现阶段,地下水在围岩中的渗流特征尚不明朗,设计人员不能准确把握水压隧洞支护设计[6]. 文献[7]指出:要在堵水限排情况下进行衬砌结构设计研究,必须从理论上研究水作用下围岩和衬砌结构的力学特征,弄清二者相互作用的机制,才能合理提供隧洞支护设计参数. 关于隧洞在渗流条件下围岩与支护结构的作用理论解析国内外诸多学者进行了研究,如文献[8]基于广义有效应力原理,提出了水压隧洞不同类型衬砌与围岩作用的解析解;文献[9]将数值试验与解析解相结合,为深埋隧道在地下水包围下初期支护与二次衬砌的初步设计提供了合理的途径;文献[10]研究了考虑衬砌和渗流场作用下海底隧道的弹塑性位移和应力解析解;文献[11]推导了围岩、注浆圈、衬砌和地下水共同作用下隧洞的弹塑性解,并提出了最优注浆圈厚度的确定方法;文献[12]基于统一强度理论,给出隧洞渗流压力、衬砌、注浆与岩体的相互作用的弹塑性解;以上支护设计研究均是基于达西定律基础上进行的,部分试验[13-14]表明:致密砂岩、破碎岩石等介质中的渗流呈现明显的非达西流特征. 为了得到合理的支护设计,必须分析岩土材料的渗流属于线性还是非线性,部分学者对非线性渗流进行了研究,如文献[15]建立二次型高速非达西本构模型,预测了深埋隧洞的涌水量;文献[16]开展了不同颗粒粒径多孔介质在高水力梯度条件下的高速非线性渗流规律试验研究,并确定了非线性渗流模型参数与颗粒粒径之间的关系;文献[17]建立岩体破坏突水非达西渗流模型,模拟了突水瞬态流动全过程,并认为岩体破坏突水问题采用非达西流模型计算十分必要;文献[18]进行了切向位移作用下粗糙单裂隙的高速非达西渗流数值模拟分析,并给出了非线性渗流模型的经验公式;文献[19]建立了粗糙岩石裂隙低速非线性渗流模型并通过试验验证;文献[20]建立了低渗透岩石非线性渗流的运动方程,并通过实验数值验证了所建立运动方程的正确性.
综上所述,岩石渗流可能是低速非线性的、线性的,或是高速非线性的,这取决于地下水在围岩中的分布和隧洞开挖岩体破坏程度. 目前,关于隧洞围岩非线性渗流理论分析鲜少被关注,因此,亟待给出隧洞处于低速非线性渗流或是高速非线性渗流状态下的弹塑性解析解,以便精确地指导隧洞支护设计. 本文将Izbash非线性渗流模型引入隧洞渗流理论,基于统一强度理论,推导深埋隧洞在注浆、衬砌作用下的应力场和位移场解析公式,并讨论了非线性渗流对隧洞围岩应力、位移和塑性区半径的影响.
1 理论基础 1.1 力学模型及基本假定建立如图 1所示的圆形隧洞力学模型,并作出如下假定:1)深埋隧洞处于地下水包围中;2)围岩为均质﹑各向同性的连续介质;3)水流经围岩和支护材料时流向以径向为主;4)初始地应力为p0,rp、r3、r2和r1分别为塑性区半径、衬砌内半径、衬砌外半径和注浆圈外半径,rw为远场水头半径,文献[21]认为隧洞远场水头半径rw一般大于30倍r1时,可保证工程精度,因此,可将隧洞在rw处的径向应力视为p0,围岩远场、弹塑性区边界、注浆圈外边界、衬砌外边界、衬砌内边界的水头分别为hw、hp、h1、h2和h3,围岩、注浆圈和衬砌的渗透系数分别为k1、k2和k3,围岩与注浆圈、注浆圈与衬砌、衬砌内边界和塑性区边界处的压力分别为p1、p2、p3和pp.

|
图 1 力学模型 Fig. 1 Mechanical model |
本文考虑的非线性渗流即围岩(或注浆圈、衬砌)的水力梯度呈非线性变化,因围岩远场水压与衬砌内水压可确定,则在边界处水头[22]有
| $ {h_s} = \left\{ {\begin{array}{*{20}{l}} {{h_{\rm{w}}}, r = {r_{\rm{w}}};}\\ {{h_1}, r = {r_1};}\\ {{h_2}, r = {r_2};}\\ {{h_3}, r = {r_3}.} \end{array}} \right. $ | (1) |
式中:hs为不同位置处的水头,hs=ps/γ,其中ps为不同位置处的水压力,γ为地下水重度. 水头一般通过监测水压并根据水头、水压的关系式获得.
幂函数型Izbash方程因其公式简单明了被广泛应用于研究岩土材料的非线性渗流特征,Izbash方程的水力梯度公式[23]为
| $ {J_s} = {A_s}{v_s}^{{m_s}}. $ | (2) |
式中:s=1、2、3,分别代表围岩、注浆圈和衬砌材料;J1、J2、J3分别为围岩、注浆圈和衬砌内某点水力梯度;A1、m1为围岩的水力梯度待定系数,A2、m2为注浆圈的水力梯度待定系数,A3、m3为衬砌的水力梯度待定系数,其中1<m1<2时,式(2)反映了显著的惯性效应而导致的非线性渗流特征,当0<m1(或m2、m3)<1时,式(2)反映了低渗透岩石介质中固液界面效应导致的非线性渗流特征,而当m1(或m2、m3)=1时,式(2)服从达西定律;v1、v2、v3分别为围岩、注浆圈、衬砌内某点渗流速度.
根据文献[24],平面径向渗流速度方程有
| $ \frac{\partial v_{s}}{\partial r}+\frac{v_{s}}{r}=0 . $ | (3) |
式中r为任意一点距离洞心的距离.
求解式(3),代入式(2)后等式两边积分,并根据Js=∂hs/∂r,可得
| $ h_{s}=\frac{A_{s} {c_{1}}^{m_{s}}}{1-m_{s}} r^{1-m_{s}}+c_{2}. $ | (4) |
式中c1、c2均为待定系数.
当r1 < r < rw时,由式(1)中边界条件hs|r=rw =hw,hs|r=r1 =h2,有
| $ \left\{\begin{array}{l} \frac{A_{s} c_{1}{ }^{m_{s}}}{1-m_{s}} r_{\mathrm{w}}^{1-m_{s}}+c_{2}=h_{\mathrm{w}}, \\ \frac{A_{s} c_{1}{ }^{m_{s}}}{1-m_{s}} r_{1}^{1-m_{s}}+c_{2}=h_{2}. \end{array}\right. $ | (5) |
式(5)为二元一次方程,可解出Asc1ms和c2,代入式(4)继而求出hs. 同理,r2 < r < r1和r3 < r < r2时的hs解法参照上述方法. 则有
| $ h_{s}=\left\{\begin{array}{l} \frac{h_{1}\left(r_{\mathrm{w}}^{1-m_{1}}-r^{1-m_{1}}\right)+h_{\mathrm{w}}\left(r^{1-m_{1}}-r_{1}^{1-m_{1}}\right)}{r_{\mathrm{w}}^{1-m_{1}}-r_{1}^{1-m_{1}}}, r_{1}<r<r_{w}; \\ \frac{h_{2}\left(r_{1}^{1-m_{2}}-r^{1-m_{2}}\right)+h_{1}\left(r^{1-m_{2}}-r_{2}^{1-m_{1}}\right)}{r_{1}^{1-m_{2}}-r_{2}^{1-m_{2}}}, r_{2}<r<r_{1}; \\ \frac{h_{3}\left(r_{2}^{1-m_{1}}-r^{1-m_{2}}\right)+h_{2}\left(r^{1-m_{3}}-r_{3}^{1-m_{3}}\right)}{r_{2}^{1-m_{3}}-r_{3}^{1-m_{3}}}, r_{3}<r<r_{2}. \end{array}\right. $ | (6) |
统一强度理论自俞茂宏创立以来,广泛应用于岩石、混凝土等拉压特性不同的材料,弥补了Mohr-Coulomb准则未能考虑中间主应力致使计算结果偏于保守的遗憾. 统一强度理论在平面应变状态下的表达式为
| $ \left\{\begin{array}{l} \frac{\sigma_{1}-\sigma_{3}}{2}=\frac{\sigma_{1}+\sigma_{3}}{2} \sin \varphi_{t}+c_{t} \cos \varphi_{t}, \\ \sin \varphi_{t}=\frac{2(1+b) \sin \varphi}{1+b(1+\sin \varphi)}, \\ c_{t}=\frac{2(1+b) c \cos \varphi}{2+b(1+\sin \varphi)} \frac{1}{\cos \varphi_{t}}. \end{array}\right. $ | (7) |
式中:σ1、σ3为第一主应力、第三主应力;c、φ为材料粘聚力、内摩擦角,ct、φt为材料统一粘聚力、内摩擦角,将围岩、注浆圈和衬砌的粘聚力分别设为c1、c2和c3及内摩擦角分别设为φ1、φ2和φ3,则材料统一粘聚力可对应为ct1、ct2和ct3,材料统一内摩擦角对应为φt1、φt2和φt3;b为参数,反映中间主应力对材料强度的影响程度,取值为0≤b≤1, b的具体值可根据材料的力学试验确定.
假设σθ(径向有效应力) > σr(切向有效应力),令σ1=σθ、σ3=σr,则式(7)中第1式可改写为
| $ \frac{{{\sigma _\theta } - {\sigma _r}}}{2} = \frac{{{\sigma _\theta } + {\sigma _r}}}{2}\sin {\varphi _{\rm{t}}} + {c_{\rm{t}}}\cos {\varphi _{\rm{t}}}. $ | (8) |
根据弹性力学理论,材料考虑渗透力时的平衡微分方程为
| $ \frac{\mathrm{d} \sigma_{r}}{\mathrm{~d} r}+\frac{\sigma_{r}-\sigma_{\theta}}{r}+F_{\mathrm{w}}=0. $ | (9) |
式中:σr、σθ分别为材料径向与切向有效应力;Fw为渗透力,
几何方程为
| $ \left\{\begin{array}{l} \varepsilon_{\theta}=\frac{u}{r}, \\ \varepsilon_{r}=\frac{\mathrm{d} u}{\mathrm{~d} r}. \end{array}\right. $ | (10) |
式中u为材料的径向位移.
弹性区服从虎克定律的平面应力应变方程为
| $ \left\{\begin{array}{l} \sigma_{r}=\frac{E_{j}\left(1-\mu_{j}\right)}{\left(1+\mu_{j}\right)\left(1-2 \mu_{j}\right)}\left(\frac{\mathrm{d} u}{\mathrm{~d} r}+\frac{\mu_{j}}{1-\mu_{j}} \frac{u}{r}\right), \\ \sigma_{\theta}=\frac{E_{j}\left(1-\mu_{j}\right)}{\left(1+\mu_{j}\right)\left(1-2 \mu_{j}\right)}\left(\frac{u}{r}+\frac{\mu_{j}}{1-\mu_{j}} \frac{\mathrm{d} u}{\mathrm{~d} r}\right). \end{array}\right. $ | (11) |
式中:Ej、μj分别为弹性模量和泊松比,且围岩、注浆圈和衬砌的弹性模量分别为E1、E2、E3,围岩、注浆圈和衬砌的泊松比分别为μ1、μ2、μ3.
2.1 弹塑性交界处位于衬砌内将式(9)与式(11)联立,并根据边界条件
| $ u_{11}=\frac{\left(1+\mu_{1}\right)\left(1-2 \mu_{1}\right)}{E_{1}}\left(a_{11} r+\frac{b_{11}}{r}+\lambda_{11} r^{2-m_{1}}\right), $ | (12) |
| $ u_{12}=\frac{\left(1+\mu_{2}\right)\left(1-2 \mu_{2}\right)}{E_{2}}\left(a_{12} r+\frac{b_{12}}{r}+\lambda_{12} r^{2-m_{2}}\right), $ | (13) |
| $ u_{13}=\frac{\left(1+\mu_{3}\right)\left(1-2 \mu_{3}\right)}{E_{3}}\left(a_{13} r+\frac{b_{13}}{r}+\lambda_{13} r^{2-m_{3}}\right) . $ | (14) |
式中:
| $ b_{11}=\lambda_{11}\left(2-m_{1}+\frac{\mu_{1}}{1-\mu_{1}}\right)\left(r_{1}^{1-m_{1}}-r_{\mathrm{w}}^{1-m_{1}}\right) , $ |
| $ \lambda_{11}=\frac{\alpha r_{\mathrm{w}}\left(h_{1}-h_{\mathrm{w}}\right)}{\left(1-\mu_{1}\right)\left(m_{1}-3\right)\left[\left(r_{\mathrm{w}}^{1-m_{1}}-r_{1}^{1-m_{1}}\right)\right]}, $ |
| $ a_{12}=-p_{1}-\lambda_{12}\left(2-m_{2}+\frac{\mu_{2}}{1-\mu_{2}}\right) r_{1}^{1-m_{2}}, $ |
| $ b_{12}=\lambda_{12}\left(2-m_{2}+\frac{\mu_{2}}{1-\mu_{2}}\right)\left(r_{2}^{1-m_{2}}-r_{1}^{1-m_{2}}\right), $ |
| $ \lambda_{12}=\frac{\alpha r_{\mathrm{w}}\left(h_{2}-h_{1}\right)}{\left(1-\mu_{2}\right)\left(m_{2}-3\right)\left[\left(r_{1}^{1-m_{2}}-r_{2}^{1-m_{2}}\right)\right]}, $ |
| $ a_{13}=-p_{2}-\lambda_{13}\left(2-m_{3}+\frac{\mu_{3}}{1-\mu_{3}}\right) r_{2}^{1-m_{3}}, $ |
| $ b_{13}=\lambda_{13}\left(2-m_{3}+\frac{\mu_{3}}{1-\mu_{3}}\right)\left(r_{\mathrm{p}}^{1-m_{3}}-r_{2}^{1-m_{3}}\right), $ |
| $ \lambda_{13}=\frac{\alpha r_{\mathrm{w}}\left(h_{\mathrm{p}}-h_{2}\right)}{\left(1-\mu_{3}\right)\left(m_{3}-3\right)\left[\left(r_{2}^{1-m_{3}}-r_{\mathrm{p}}^{1-m_{3}}\right)\right]} . $ |
其中hp在所处材料中按照差值法计算.
将式(12)~(14)代入式(11),则围岩、注浆圈和衬砌径向、切向应力分别为
| $ \left\{\begin{array}{l} \sigma_{r 11}=a_{11}+b_{11}\left(\frac{r_{1}}{r}\right)^{2}+\lambda_{11} r^{1-m_{1}}\left[\left(2-m_{1}\right)\left(1-\mu_{1}\right)+\mu_{1}\right], \\ \sigma_{\theta 11}=a_{12}-b_{12}\left(\frac{r_{1}}{r}\right)^{2}+\lambda_{11} r^{1-m_{1}}\left[1+\mu_{1}\left(1-m_{1}\right)\right] . \end{array}\right. $ | (15) |
| $ \left\{\begin{array}{l} \sigma_{r \mathrm{12}}=a_{\mathrm{12}}+b_{\mathrm{12}}\left(\frac{r_{2}}{r}\right)^{2}+\lambda_{\mathrm{12}} r^{1-m_{2}}\left[\left(2-m_{2}\right)\left(1-\mu_{2}\right)+\mu_{2}\right], \\ \sigma_{\theta 12}=a_{12}-b_{12}\left(\frac{r_{2}}{r}\right)^{2}+\lambda_{12} r^{1-m_{2}}\left[1+\mu_{2}\left(1-m_{2}\right)\right]. \end{array}\right. $ | (16) |
| $ \left\{\begin{array}{l} \sigma_{r 13}=a_{13}+b_{13}\left(\frac{r_{\mathrm{p}}}{r}\right)^{2}+\lambda_{13} r^{1-m_{3}}\left[\left(2-m_{3}\right)\left(1-\mu_{3}\right)+\mu_{3}\right], \\ \sigma_{\theta 13}=a_{13}-b_{13}\left(\frac{r_{\mathrm{p}}}{r}\right)^{2}+\lambda_{13} r^{1-m_{3}}\left[1+\mu_{3}\left(1-m_{3}\right)\right]. \end{array}\right. $ | (17) |
将式(8)与式(9)联立,并根据边界条件σr|r=r3 =-p3,则衬砌内塑性径向、切向应力分别为
| $ \left\{\begin{array}{l} \sigma_{r \mathrm{p} 14}=c_{\mathrm{t} 3} \cot \varphi_{\mathrm{t} 3}+B_{1} r^{1-m_{3}}-\left(p_{3}+c_{\mathrm{t} 3} \cot \varphi_{\mathrm{t} 3}+\right. \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \left.B_{1} r_{3}^{1-m_{3}}\right)\left(\frac{r}{r_{3}}\right)^{-\frac{2 \sin \varphi_{\mathrm{t} 3}}{1-\sin \varphi_{\mathrm{t} 3}}}, \\ \sigma_{\theta \mathrm{p} 14}=-\frac{1+\sin \varphi_{\mathrm{t} 3}}{1-\sin \varphi_{\mathrm{t} 3}}\left[\left(p_{3}+c_{\mathrm{t} 3} \cot \varphi_{\mathrm{t} 3}+B_{1} r_{3}^{1-m_{3}}\right)\right. \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \left.\left(\frac{r}{r_{3}}\right)^{-\frac{2 \sin \varphi_{\mathrm{t} 3}}{1-\sin \varphi_{\mathrm{t} 3}}}-B_{1} r^{1-m_{3}}\right]+c_{\mathrm{t} 3} \cot \varphi_{\mathrm{t} 3} . \end{array}\right. $ | (18) |
式中
| $ {B_1} = \frac{{{k_3}{r_{\rm{w}}}\left( {1 + \sin {\varphi _{{\rm{t3}}}}} \right)\left( {1 - {m_3}} \right)\left( {{h_3} - {h_2}} \right)}}{{\left[ {3\sin {\varphi _{{\rm{t3}}}} + 1 - {m_3}\left( {1 + \sin {\varphi _{{\rm{t3}}}}} \right)} \right]\left( {r_2^{1 - {m_3}} - {r_3}} \right)}}. $ |
假定材料塑性阶段体积应变为0,根据几何方程式(10),则衬砌塑性区位移为
| $ u_{14}=\left.\frac{r_{\mathrm{p}}}{r} u_{13}\right|_{r=r_{\mathrm{p}}} . $ | (19) |
联立式(12)~(14),并根据位移在边界处连续:
| $ \left.u_{11}\right|_{r=r_{1}}=\left.u_{12}\right|_{r=r_{2}}. $ | (20) |
可求得p1和p2. 将衬砌内压p3视为0,由径向应力连续:
| $ \left.\sigma_{r 3}\right|_{r=r_{\mathrm{p}}}=\left.\sigma_{r \mathrm{p} 4}\right|_{r=r_{\mathrm{p}}}. $ | (21) |
可求得rp,从而获得围岩应力,下文参照此法求p1、p2和rp.
2.2 弹塑性交界处位于注浆圈内围岩仍处于弹性状态,则围岩位移u21=u11,围岩径向、切向应力σr21=σr11、σθ21=σθ11. 将式(9)代入式(11),根据边界条件σr|r=r1=-p1,σr|r=rp=-pp, 注浆圈弹性部分位移为
| $ u_{22}=\frac{\left(1+\mu_{2}\right)\left(1-2 \mu_{2}\right)}{E_{2}}\left(a_{22} r+\frac{b_{22}}{r}+\lambda_{22} r^{2-m_{2}}\right) . $ | (22) |
式中:
| $ b_{22}=\lambda_{22}\left(2-m_{2}+\frac{\mu_{2}}{1-\mu_{2}}\right)\left(r_{\mathrm{p}}^{1-m_{2}}-r_{1}^{1-m_{2}}\right), $ |
| $ \lambda_{22}=\frac{\alpha r_{\mathrm{w}}\left(h_{\mathrm{p}}-h_{1}\right)}{\left(1-\mu_{2}\right)\left(m_{2}-3\right)\left[\left(r_{1}^{1-m_{2}}-r_{\mathrm{p}}^{1-m_{2}}\right)\right]} . $ |
材料塑性阶段位移参照式(19), 则注浆圈、衬砌塑性部分位移分别为
| $ u_{23}=\left.\frac{r_{\mathrm{p}}}{r} u_{22}\right|_{r=r_{\mathrm{p}}}, $ | (23) |
| $ u_{24}=\left.\frac{r_{2}}{r} u_{23}\right|_{r=r_{2}}. $ | (24) |
将式(22)代入式(11),将式(8)代入式(9),并根据边界条件σr|r=r2 =-p2、σr|r=r3 =-p3,注浆圈弹性部分、注浆圈塑性部分和衬砌的径向、切向应力分别为
| $ \left\{\begin{array}{l} \sigma_{r 22}=a_{22}+b_{22}\left(\frac{r_{2}}{r}\right)^{2}+\lambda_{22} r^{1-m_{2}}\left[\left(2-m_{2}\right)\left(1-\mu_{2}\right)+\mu_{2}\right], \\ \sigma_{\theta 22}=a_{22}-b_{22}\left(\frac{r_{2}}{r}\right)^{2}+\lambda_{22} r^{1-m_{2}}\left[1+\mu_{2}\left(1-m_{2}\right)\right] . \end{array}\right. $ | (25) |
| $ \left\{ {\begin{array}{*{20}{l}} {{\sigma _{r{\rm{p}}23}} = {c_{{\rm{t2}}}}\cot {\varphi _{{\rm{t2}}}} + {B_2}{r^{1 - {m_2}}} - \left( {{p_2} + {c_{{\rm{t2}}}}\cot {\varphi _{{\rm{t2}}}} + {B_2}r_2^{1 - {m_2}}} \right){{\left( {\frac{r}{{{r_2}}}} \right)}^{ - \frac{{2\sin {\varphi _{{\rm{t2}}}}}}{{1 - \sin {\varphi _{{\rm{t2}}}}}}}}, }\\ {{\sigma _{{\theta _{{\rm{p}}23}}}} = - \frac{{1 + \sin {\varphi _{{\rm{t2}}}}}}{{1 - \sin {\varphi _{{\rm{t2}}}}}}\left[ {\left( {{p_2} + {c_{{\rm{t2}}}}\cot {\varphi _{{\rm{t2}}}} + {B_2}r_2^{1 - {m_2}}} \right){{\left( {\frac{r}{{{r_3}}}} \right)}^{ - \frac{{2\sin {\varphi _{{\rm{t2}}}}}}{{1 - \sin {\varphi _{{\rm{t2}}}}}}}} - {B_2}{r^{1 - {m_2}}}} \right] + {c_{{\rm{t2}}}}\cot {\varphi _{{\rm{t2}}}}.} \end{array}} \right. $ | (26) |
| $ \left\{ {\begin{array}{*{20}{l}} {{\sigma _{r{\rm{p}}24}} = {c_{{\rm{t}}3}}\cot {\varphi _{{\rm{t}}3}} + {B_3}{r^{1 - {m_3}}} - \left( {{p_3} + {c_{{\rm{t}}3}}\cot {\varphi _{{\rm{t}}3}} + {B_3}r_3^{1 - {m_3}}} \right){{\left( {\frac{r}{{{r_3}}}} \right)}^{ - \frac{{2\sin {\varphi _{{\rm{t}}3}}}}{{1 - \sin {\varphi _{{\rm{t}}3}}}}}}, }\\ {{\sigma _{\theta {\rm{p}}24}} = - \frac{{1 + \sin {\varphi _{{\rm{t}}3}}}}{{1 - \sin {\varphi _{{\rm{t}}3}}}}\left[ {\left( {{p_3} + {c_{{\rm{t}}3}}\cot {\varphi _{{\rm{t}}3}} + {B_3}r_3^{1 - {m_3}}} \right){{\left( {\frac{r}{{{r_3}}}} \right)}^{ - \frac{{2\sin {\varphi _{{\rm{t}}3}}}}{{1 - \sin {\varphi _{{\rm{t}}3}}}}}} - {B_3}{r^{1 - {m_3}}}} \right] + {c_{{\rm{t}}3}}\cot {\varphi _{{\rm{t}}3}}.} \end{array}} \right. $ | (27) |
式中:
| $ {{B_2} = \frac{{{k_2}{r_{\rm{w}}}\left( {1 + \sin {\varphi _{{\rm{t2}}}}} \right)\left( {1 - {m_2}} \right)\left( {{h_2} - {h_1}} \right)}}{{\left[ {3\sin {\varphi _{{\rm{t2}}}} + 1 - {m_2}\left( {1 + \sin {\varphi _{12}}} \right)} \right]\left( {r_1^{1 - {m_2}} - {r_2}} \right)}}, } $ |
| $ {{B_3} = \frac{{{k_3}{r_{\rm{w}}}\left( {1 + \sin {\varphi _{{\rm{t3}}}}} \right)\left( {1 - {m_3}} \right)\left( {{h_3} - {h_2}} \right)}}{{\left[ {3\sin {\varphi _{{\rm{t3}}}} + 1 - {m_3}\left( {1 + \sin {\varphi _{{\rm{t3}}}}} \right)} \right]\left( {r_2^{1 - {m_3}} - {r_3}} \right)}}.} $ |
将式(9)与式(11)联立,并根据边界条件σr|r=rw =-p0,σr|r=rp =-pp,围岩弹性位移有
| $ {u_{31}} = \frac{{\left( {1 + {\mu _1}} \right)\left( {1 - 2{\mu _1}} \right)}}{{{E_1}}}\left( {{a_{31}}r + \frac{{{b_{31}}}}{r} + {\lambda _{31}}{r^{2 - {m_1}}}} \right). $ | (28) |
式中:
| $ {{a_{31}} = - {p_0} - {\lambda _{31}}\left( {2 - {m_1} + \frac{{{\mu _1}}}{{1 - {\mu _1}}}} \right)r_{\rm{w}}^{1 - {m_1}}, } $ |
| $ {{b_{31}} = {\lambda _{31}}\left( {2 - {m_1} + \frac{{{\mu _1}}}{{1 - {\mu _1}}}} \right)\left( {r_{\rm{p}}^{1 - {m_1}} - r_{\rm{w}}^{1 - {m_1}}} \right), } $ |
| $ {{\lambda _{31}} = \frac{{\alpha {r_{\rm{w}}}\left( {{h_{\rm{p}}} - {h_{\rm{w}}}} \right)}}{{\left( {1 - {\mu _1}} \right)\left( {{m_1} - 3} \right)\left[ {\left( {r_{\rm{w}}^{1 - {m_1}} - r_{\rm{p}}^{1 - {m_1}}} \right)} \right]}}.} $ |
材料塑性阶段位移参照式(19), 则围岩、注浆圈和衬砌塑性部分位移分别为
| $ {{u_{32}} = {{\left. {\frac{{{r_{\rm{p}}}}}{r}{u_{31}}} \right|}_{r = {r_{\rm{p}}}}}, } $ | (29) |
| $ {{u_{33}} = {{\left. {\frac{{{r_1}}}{r}{u_{32}}} \right|}_{r = {r_1}}}, } $ | (30) |
| $ {{u_{34}} = {{\left. {\frac{{{r_2}}}{r}{u_{33}}} \right|}_{r = {r_2}}}.} $ | (31) |
将式(28)代入式(11),围岩弹性部分径向、切向应力分别为
| $ \left\{ {\begin{array}{*{20}{l}} {{\sigma _{r31}} = {a_{31}} + {b_{31}}{{\left( {\frac{{{r_{\rm{p}}}}}{r}} \right)}^2} + {\lambda _{31}}{r^{1 - {m_1}}}\left[ {\left( {2 - {m_1}} \right)\left( {1 - {\mu _1}} \right) + {\mu _1}} \right], }\\ {{\sigma _{\theta 31}} = {a_{31}} - {b_{31}}{{\left( {\frac{{{r_{\rm{p}}}}}{r}} \right)}^2} + {\lambda _{31}}{r^{1 - {m_1}}}\left[ {1 + {\mu _1}\left( {1 - {m_1}} \right)} \right].} \end{array}} \right. $ | (32) |
将式(8)代入式(9),并根据边界条件σr|r=r2 =-p2、σr|r=r3 =-p3,围岩塑性部分和注浆圈的径向、切向应力分别为
| $ \left\{ {\begin{array}{*{20}{l}} {{\sigma _{r{\rm{p}}32}} = {c_{{\rm{t1}}}}\cot {\varphi _{{\rm{t1}}}} + {B_4}{r^{1 - {m_1}}} - \left( {{p_1} + {c_{{\rm{t1}}}}\cot {\varphi _{{\rm{t1}}}} + {B_4}r_1^{1 - {m_1}}} \right){{\left( {\frac{r}{{{r_1}}}} \right)}^{ - \frac{{2\sin {\varphi _{{\rm{t1}}}}}}{{1 - \sin {\varphi _{{\rm{t1}}}}}}}}, }\\ {{\sigma _{\theta {\rm{p}}32}} = - \frac{{1 + \sin {\varphi _{{\rm{t1}}}}}}{{1 - \sin {\varphi _{{\rm{t1}}}}}}\left[ {\left( {{p_1} + {c_{{\rm{t1}}}}\cot {\varphi _{{\rm{t1}}}} + {B_4}r_1^{1 - {m_1}}} \right){{\left( {\frac{r}{{{r_1}}}} \right)}^{ - \frac{{2\sin {\varphi _{{\rm{t1}}}}}}{{1 - \sin {\varphi _{{\rm{t1}}}}}}}} - {B_4}{r^{1 - {m_1}}}} \right] + {c_{{\rm{t1}}}}\cot {\varphi _{{\rm{t1}}}};} \end{array}} \right. $ | (33) |
| $ \left\{ {\begin{array}{*{20}{l}} {{\sigma _{r{\rm{p}}33}} = {c_{{\rm{t}}2}}\cot {\varphi _{{\rm{t}}2}} + {B_5}{r^{1 - {m_2}}} - \left( {{p_2} + {c_{{\rm{t}}2}}\cot {\varphi _{{\rm{t}}2}} + {B_5}r_2^{1 - {m_2}}} \right){{\left( {\frac{r}{{{r_2}}}} \right)}^{ - \frac{{2\sin {\varphi _{{\rm{t}}2}}}}{{1 - \sin {\varphi _{{\rm{t}}2}}}}}}, }\\ {{\sigma _{\theta {\rm{p}}33}} = - \frac{{1 + \sin {\varphi _{{\rm{t}}2}}}}{{1 - \sin {\varphi _{{\rm{t}}2}}}}\left[ {\left( {{p_2} + {c_{{\rm{t}}2}}\cot {\varphi _{{\rm{t}}2}} + {B_5}r_2^{1 - {m_2}}} \right){{\left( {\frac{r}{{{r_2}}}} \right)}^{ - \frac{{2\sin {\varphi _{{\rm{t}}2}}}}{{1 - \sin {\varphi _{{\rm{t}}2}}}}}} - {B_5}{r^{1 - {m_2}}}} \right] + {c_{{\rm{t}}2}}\cot {\varphi _{{\rm{t}}2}}.} \end{array}} \right. $ | (34) |
式中:
| $ {{B_4} = \frac{{{k_1}{r_{\rm{w}}}\left( {1 + \sin {\varphi _{{\rm{t}}1}}} \right)\left( {1 - {m_1}} \right)\left( {{h_1} - {h_{\rm{p}}}} \right)}}{{\left[ {3\sin {\varphi _{{\rm{t}}1}} + 1 - {m_1}\left( {1 + \sin {\varphi _{{\rm{t}}1}}} \right)} \right]\left( {r_{\rm{p}}^{1 - {m_1}} - {r_1}} \right)}}, } $ |
| $ {{B_5} = \frac{{{k_2}{r_{\rm{w}}}\left( {1 + \sin {\varphi _{{\rm{t2}}}}} \right)\left( {1 - {m_2}} \right)\left( {{h_2} - {h_1}} \right)}}{{\left[ {3\sin {\varphi _{{\rm{t2}}}} + 1 - {m_2}\left( {1 + \sin {\varphi _{{\rm{t2}}}}} \right)} \right]\left( {r_1^{1 - {m_2}} - {r_2}} \right)}}.} $ |
衬砌的径向、切向应力与式(27)相同,即σrp34= σrp24、σθp34=σθp24.
3 实例验证为了验证本文的理论解答,借助文献[15]实例参数, 隧洞衬砌内半径r1=4 m、外半径r2=5 m,注浆圈外半径r3=5.2 m, 初始地应力p0=10 MPa, 远场水头半径rw=200 m,α=1,远场水压力pw=1 MPa, 地下水重度γ=10 kN/m3,h1=50 m,h2=h3=0 m,围岩、注浆圈和衬砌参数见表 1.
| 表 1 围岩、注浆圈和衬砌参数 Tab. 1 Parameters of surrounding rock, grouting ring, and lining |
理论计算时,将隧道已知参数代入上述公式,当求得塑性区半径rp与某一种弹塑性边界情况一致时,则位移场与应力场按照该情况计算.
利用ABAQUS有限元软件模拟文献[15]工况,为了减少模型边界效应,建立模型如图 3所示,模型为210 m×210 m监测断面为隧洞纵向中心断面. 为模拟隧洞的非线性渗流,根据地下水流速公式:

|
图 2 隧道模型图 Fig. 2 Diagram of tunnel model |
|
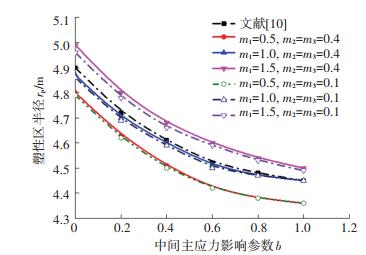
图 3 本文方法得到的塑性区半径与Li解对比图 Fig. 3 Comparison between radius of plastic zone obtained by proposed method and Li's solution |
| $ {k_s}{J_s} = {v_s}, $ | (35) |
式中ks为材料的渗透系数,并结合式(2)可得
| $ {k_s}{A_s} = v_s^{1 - {m_s}}. $ | (36) |
假设在隧洞远端的渗流速度vs和水力梯度参数As一定,且取vs为1×10-4 m/s,根据式(36),可得m1=0.5、m1=1.5的围岩等效渗透系数分别为5×10-6 m/s、0.05 m/s,则隧洞监测断面洞壁的位移、切向应力的数值解与本文理论解对比见表 2、3.
| 表 2 隧洞洞壁位移对比 Tab. 2 Contrast of tunnel top displacement |
| 表 3 隧洞切向应力对比 Tab. 3 Contrast of tunnel tangential stress |
从表 2可以看出,本文理论解较数值解略大,随着m1增大,洞壁位移误差在8.8%以内,隧洞切向应力误差最大为14.1%,理论解与数值解吻合性较好,验证了理论解的可靠性.
4 非线性渗流对隧洞塑性区半径、围岩应力和位移的影响一般来说,材料的渗透系数越小,水流穿过材料裂隙的难度越大,水力梯度待定系数越小,由于表 1中注浆圈和衬砌的渗透系数远小于围岩,不难判断,m1值大于m2和m3,假设m2=m3,分析非线性渗流对隧洞塑性区半径、围岩应力和位移的影响,如图 3、4、5所示.

|
图 4 考虑非线性渗流的隧洞应力分布 Fig. 4 Stress distribution of tunnel considering non-linear seepage |
|
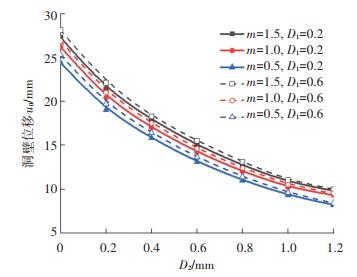
图 5 隧洞位移与支护厚度曲线 Fig. 5 Curves of tunnel displacement and support thickness |
从图 3可以看出,随着b值增大,塑性区半径rp逐渐减小且最大减小幅度为13.2%,而工程实践中rp的精确性直接影响支护结构设计,说明考虑中间主应力是必要的,否则误差较大;m1对rp值的影响远大于m2和m3,且m1越大rp越大. 根据上述分析,图 4仅探讨m1对围岩应力的影响,因此假定m2=m3=0.4. 当b=0.4时,随着m1越大,围岩径向、切向应力越小. 结合图 3和图 4,当m1=1.0、m2=m3=0.4时,围岩渗流服从达西定律,塑性区半径、围岩应力与文献[15]较为接近,从而进一步验证了本文理论方法的可行性. 综上所述,当围岩渗流为高渗透性非线性渗流时,若采用达西定律则低估塑性区半径、高估实际围岩应力,不利于支护设计;围岩渗流为低渗透性非线性渗流时,达西定律计算得到塑性区半径偏大、围岩应力偏保守.
图 5显示了b=0.4时隧洞位移与支护厚度的关系,D1、D2分别为注浆圈、衬砌厚度,当支护厚度一定时,围岩渗流从低渗透性非线性渗流向高渗透性非线性渗流转变时,隧洞位移逐渐增大,因此,当隧洞围岩处于高水压、突水严重地层时,传统的达西定律计算的洞壁位移偏于保守,不利于隧洞施工安全. 另外,随着注浆圈和衬砌厚度的增大,洞壁位移能够得到有效控制,但衬砌厚度超过1 m时,洞壁位移的控制并不显著,则支护设计时应合理设定支护材料厚度,以免造成较大浪费.
5 结论1) 在注浆、衬砌支护条件下,基于Izbash非线性渗流模型,求得围岩及支护材料的水头分布,并运用统一强度理论,推导了塑性区在不同材料位置时的应力和位移弹塑性解.
2) 考虑非线性渗流的理论位移解较等效后的ABAQUS解略大,切向应力误差在允许范围之内,吻合性较好;中间主应力和围岩的水力梯度系数m1对隧洞塑性区半径的影响显著,而对围岩应力的影响较塑性区半径略小.
3) 围岩水力梯度系数m1对隧洞位移的影响不容忽视,当隧洞围岩处于高速非线性渗流时,达西定律计算的隧洞位移偏保守,体现了研究非线性渗流作用下隧洞弹塑性分析的重要意义;另外,不能盲目追求安全性而增加支护材料厚度,否则导致支护不经济.
| [1] |
BOBET A. Effect of pore water pressure on tunnel support during static and seismic loading[J]. Tunnelling and Underground Space Technology, 2003, 18: 377. DOI:10.1016/S0886-7798(03)00008-7 |
| [2] |
DONG Xiangjian, KARRECH A, QI Chongchong, et al. Analytical solution for stress distribution around deep lined pressure tunnels under the water table[J]. International Journal of Rock Mechanics and Mining Sciences, 2019, 123: 104124. DOI:10.1016/j.ijrmms.2019.104124 |
| [3] |
ZAREIFAR M R. An analytical solution for design of pressure tunnels considering seepage loads[J]. Applied Mathematical Modelling, 2018, 62: 62. DOI:10.1016/j.apm.2018.05.032 |
| [4] |
王秀英, 谭忠盛, 王梦恕, 等. 山岭隧道堵水限排围岩力学特性分析[J]. 岩土力学, 2008, 29(1): 75. WANG Xiuying, TAN Zhongsheng, WANG Mengshu, et al. Analysis of mechanical character of surrounding rock with controlled drainage in mountain tunnels[J]. Rock and Soil Mechanics, 2008, 29(1): 75. |
| [5] |
刘新荣, 刘坤, 钟祖良, 等. 深埋隧道排水系统非对称堵塞后渗流场的解析研究[J]. 岩石力学与工程学报, 2017, 36(5): 1088. LIU Xinrong, LIU Kun, ZHONG Zuliang, et al. Analytical study on seepage field of the deep tunnel with asymmetric blocked drainage system[J]. Chinese Journal of Rock Mechanics and Engineering, 2017, 36(5): 1088. DOI:10.13722/j.cnki.jrme.2016.0955 |
| [6] |
LEE I M, NAM S W. The study of seepage forcesacting on the tunnel lining and tunnel face in shallow tunnels[J]. Tunneling and Underground Space Technology, 2001, 16: 31. DOI:10.1016/S0886-7798(01)00028-1 |
| [7] |
王秀英, 谭忠盛, 王梦恕, 等. 高水位隧道堵水限排围岩与支护相互作用分析[J]. 岩土力学, 2008, 29(6): 1623. WANG Xiuying, TAN Zhongsheng, WANG Mengshu, et al. Analysis of interaction between surrounding rock and lining in high water-level tunnels with controlled drainage[J]. Rock and Soil Mechanics, 2008, 29(6): 1623. DOI:10.16285/j.rsm.2008.06.014 |
| [8] |
ZAREIFAR M R, FAHIMIFAR A. A simplified solution for stresses around lined pressure tunnels considering non-radial symmetrical seepage flow[J]. KSCE Journal of Civil Engineering, 2016, 20(7): 2640. DOI:10.1007/s12205-016-0105-5 |
| [9] |
NAM S W, BOBET A. Radial deformations induced by groundwater flow on deep circular tunnels[J]. Rock Mechanics and Rock Engineering, 2007, 40(1): 23. DOI:10.1007/s00603-006-0097-4 |
| [10] |
吕晓聪, 许金余. 海底圆形隧道在渗流场影响下的弹塑性解[J]. 工程力学, 2009, 26(2): 216. LV Xiaocong, XU Jinyu. Elastic-plastic solution for subsea circular tunnel under the influence of seepage field[J]. Engineering Mechanics, 2009, 26(2): 216. |
| [11] |
胡力绳, 王建秀, 卢耀如. 考虑地下水、注浆及衬砌影响的深埋隧洞弹塑性解[J]. 岩土力学, 2012, 33(3): 757. HU Lisheng, WANG Jianxiu, LU Yaoru. Elastoplastic solution for deep tunnel considering influences of groundwater, grouting and lining[J]. Rock and Soil Mechanics, 2012, 33(3): 757. DOI:10.16285/j.rsm.2012.03.037 |
| [12] |
LI Xuefeng, DU Shouji, CHEN Bing. Unified analytical solution for deep circular tunnel with consideration of seepage pressure, grouting and lining[J]. Journal of Central South University, 2017, 24(6): 1483. DOI:10.1007/s11771-017-3552-3 |
| [13] |
PRADA A, CICAN F. Modification of Darcy's law for the threshold pressure gradient[J]. Journal of Petroleum Science and Engineering, 1999, 22(4): 237. DOI:10.1016/S0920-4105(98)00083-7 |
| [14] |
HANSBO S. Aspects of vertical drain design: Darcian or non-Darcian flow[J]. Geotechnique, 1997, 47(5): 983. DOI:10.1680/geot.1997.47.5.983 |
| [15] |
王媛, 秦峰, 夏志皓, 等. 深埋隧洞涌水预测非达西流模型及数值模拟[J]. 岩石力学与工程学报, 2012, 31(9): 1862. WANG Yuan, QIN Feng, XIA Zhihao, et al. Non-Darcy flow model and numerical simulation for predicting water inflow deep tunnel[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(9): 1862. DOI:10.3969/j.issn.1000-6915.2012.09.018 |
| [16] |
杨斌, 徐曾和, 杨天鸿, 等. 高水力梯度条件下颗粒堆积型多孔介质渗流规律试验研究[J]. 岩土力学, 2018, 39(11): 4017. YANG Bin, XU Zenghe, YANG Tianhong, et al. Experimental study of non-linear water flow through unconsolidated porous media under condition of high hydraulic gradient[J]. Rock and Soil Mechanics, 2018, 39(11): 4017. DOI:10.16285/j.rsm.2017.0643 |
| [17] |
陈力, 王媛, 陈晓静. 切向位移作用下粗糙单裂隙高速非达西渗流特性研究[J]. 水电能源科学, 2019, 37(2): 110. CHEN Li, WANG Yuan, CHEN Xiaojing. Study on high speed Non-Darcy seepage characteristics of rough single fissure under tangential displacement[J]. Water Resources and Power, 2019, 37(2): 110. |
| [18] |
师文豪, 杨天鸿, 刘洪磊, 等. 矿山岩体破坏突水非达西流模型及数值求解[J]. 岩石力学与工程学报, 2016, 35(3): 446. SHI Wenhao, YANG Tianhong, LIU Honglei, et al. Non-Darcy flow model and numerical simulation for water-inrush in fractured rock mass[J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(3): 446. DOI:10.13722/j.cnki.jrme.2015.0389 |
| [19] |
熊峰, 孙昊, 姜清辉, 等. 粗糙岩石裂隙低速非线性渗流模型及试验验证[J]. 岩土力学, 2018, 39(9): 3294. XIONG Feng, SUN Hao, JIANG Qinghui, et al. Theoretical model and experimental verification on non-linear flow at low velocity through rough-walled rock fracture[J]. Rock and Soil Mechanics, 2018, 39(9): 3294. DOI:10.16285/j.rsm.2016.2623 |
| [20] |
刘建军, 刘先贵, 胡雅衽. 低渗透岩石非线性渗流规律研究[J]. 岩石力学与工程学报, 2003, 22(4): 556. LIU Jianjun, LIU Xiangui, HU Yaren. Study on nonlinear seepage of rock of low permeability[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(4): 556. DOI:10.3321/j.issn:1000-6915.2003.04.009 |
| [21] |
李宗利, 任青文, 王亚红. 考虑渗流场影响深埋圆形隧洞的弹塑性解[J]. 岩石力学与工程学报, 2004, 23(8): 1291. LI Zongli, REN Qingwen, WANG Yahong. Elasto-plastic analytical solution of deep-buried circle tunnel considering fluid flow field[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(8): 1291. |
| [22] |
刘福胜, 徐国元, 黄文通. 山岭隧道地下水渗流及加固参数的解析研究[J]. 华南理工大学学报(自然科学版), 2012, 40(2): 112. LIU Fusheng, XU Guoyuan, HUANG Wentong. Analytical research on groundwater seepage and reinforcement paramenters of mountain tunnels[J]. Journal of South China University of Technology(Natural Science Edition), 2012, 40(2): 112. |
| [23] |
李文亮. 饱和花岗岩力学特性及峰后非线性渗流试验研究[D]. 南昌: 南昌大学, 2017 LI Wenliang. Experimental studies on mechanical properties and post-peak non-linear flow of saturated granite rock[D]. Nanchang: Nanchang University, 2017 |
| [24] |
翟云芳. 渗流力学[M]. 北京: 石油工业出版社, 2003. ZHAI Yunfang. Seepage mechanics[M]. Beijing: Petroleum Industry Press, 2003. |
| [25] |
李俊亭, 王愈吉. 地下水动力学[M]. 北京: 地质出版社, 1987. LI Junting, WANG Yuji. Groundwater dynamics[M]. Beijing: Geological Publishing House, 1987. |
 2021, Vol. 53
2021, Vol. 53


