2. 河北省交通规划设计院, 石家庄 050011;
3. 河北科技大学 建筑工程学院, 石家庄 050011
2. Hebei Provincial Communications Planning and Design Institute, Shijiazhuang 050011, China;
3. School of Civil Engineering, Hebei University of Science and Technology, Shijiazhuang 050011, China
桥梁结构中混凝土板裂缝的发展不但影响结构美观,而且会造成开裂截面附近的钢筋锈蚀,从而直接影响到结构的正常使用和耐久性能. 自钢筋混凝土结构问世100多年来,国内外学者针对其裂缝宽度的研究较多,对于裂缝发展的诸多影响因素已有统一的看法,但将所有因素统一概括到一个计算模式中难以实现[1-2]. 对于钢-混凝土连续组合梁的负弯矩区,同样存在着这样的问题. 现有的设计规范均按照钢筋混凝土结构的设计方法来验算和控制负弯矩区混凝土板的裂缝宽度. 但由于在钢梁与混凝土板交界面存在抗剪连接件以及界面粘结作用,混凝土板受到钢梁轴向和弯曲刚度的约束,开裂机理与钢筋混凝土构件有所区别,这样的计算方法往往会造成一定的误差.
目前,各国规范对允许开裂的钢筋混凝土构件在使用荷载下的裂缝宽度提出了多种计算方法,如依据滑移理论的欧洲模式规范CEB-FIP 2010[3],依据无滑移理论的美国规范ACI318-11[4],以及依据综合理论的中国《混凝土结构设计规范》[5]. 其中,黏结-滑移理论的应用最为广泛. 然而,由黏结-滑移理论很难得到裂缝宽度的解析解. 此时,采用数值计算方法进行裂缝宽度的计算将是一种行之有效的途径. 此外,近几十年来国内外学者对组合梁负弯矩区力学性能进行了大量的试验研究[6-7]、理论解析[8-9]和数值模拟[10-11],迄今计算和分析方法已趋于成熟,且能够较好地为设计服务[12],但针对组合梁负弯矩区裂缝宽度进行较为精确地数值分析方面鲜有文献报道. 裂缝宽度作为组合梁负弯矩区一项重要的力学性能评价指标,有必要针对其计算方法展开研究.
鉴于此,本文结合合理的本构关系并综合考虑多项影响因素,建立了基于黏结-滑移理论的组合梁负弯矩区裂缝宽度数值计算模型,通过相关文献数据验证了模型的准确性,并与国内外规范公式计算结果进行了对比分析,以期寻求具有一定可靠性的计算模式为钢-混凝土组合结构桥梁的设计提供参考.
1 模型本构关系 1.1 材料本构模型当荷载等级进入裂缝稳定阶段时,裂缝间距将保持不变,结构仍处于正常使用状态下,此时受拉钢筋未达到屈服荷载,因此可以假设组合梁负弯矩区两条裂缝间的材料处于线弹性受力阶段[1]. 那么可以给出受拉钢材和混凝土的应力-应变关系为
| $ \left\{\begin{array}{l} \sigma_{\mathrm{ct}}=E_{\mathrm{c}} \varepsilon_{\mathrm{ct}}, \\ \sigma_{\mathrm{s}}=E_{\mathrm{s}} \varepsilon_{\mathrm{s}}. \end{array}\right. $ | (1) |
式中:σct、σs分别为混凝土和钢材的应力,εct、εs分别为混凝土和钢材的应变,Ec、Es分别为混凝土和钢材的弹性模量.
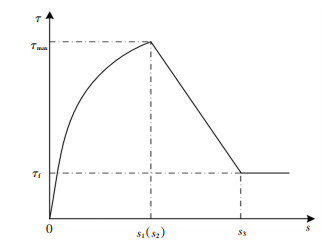
1.2 钢筋与混凝土间的黏结-滑移本构关系钢筋与混凝土之间粘结滑移关系十分复杂,其对结构开裂后的使用性能起着至关重要的作用,本文采用CEB-FIP 2010[3]给出的黏结-滑移模型,如图 1所示,具体形式为
| $ \left\{\begin{array}{l} \tau=\tau_{\max } \cdot\left(\frac{s}{s_{1}}\right)^{\alpha^{\prime}}, \quad 0 \leqslant s \leqslant s_{1}; \\ \tau=\tau_{\max }, \quad s_{1} \leqslant s \leqslant s_{2}; \\ \tau=\tau_{\max }-\left(\tau_{\max }-\tau_{\mathrm{f}}\right) \cdot\left(\frac{s-s_{2}}{s_{3}-s_{2}}\right), s_{2} \leqslant s \leqslant s_{3}; \\ \tau=\tau_{\mathrm{f}}, \quad s \geqslant s_{3}. \end{array}\right. $ | (2) |
|
图 1 静载作用下钢筋与混凝土间的黏结-滑移关系 Fig. 1 Bond-slip relationship between reniforcement and concrete under static loading |
式中:τ为黏结应力;s为钢筋与混凝土间的滑移;τmax为极限黏结强度,对于无约束、黏结性能良好的混凝土构件,τmax=2.0
当钢梁与混凝土板界面剪力与相对滑移成正比,且抗剪连接件所承受的界面剪力沿梁长度方向连续分布时,则有
| $ \upsilon = \frac{{K \cdot {s_{\rm{s}}}}}{p}. $ | (3) |
式中:υ为钢梁与混凝土板界面单位长度剪力;ss为界面相对滑移;p为栓钉纵向间距;K为界面抗滑移刚度,K=nsKs,其中ns为每排栓钉个数,Ks为单个栓钉抗剪刚度.
研究表明,对于集中或均布荷载作用下的组合梁负弯矩区的滑移大小及分布规律基本一致,因此本文采用集中荷载下的滑移和滑移应变来作为代表工况. 对于跨中单点加载,界面滑移表达式[13]可表示为
| $ s_{\mathrm{s}}=\frac{\mathrm{e}^{-\alpha x}\left(\mathrm{e}^{\alpha x}-1\right)\left(\mathrm{e}^{\alpha L}-\mathrm{e}^{\alpha x}\right) \beta P}{\left(\mathrm{e}^{\alpha L}+1\right) \alpha^{2}}. $ | (4) |
式中:x为计算截面至跨中的距离,
目前,国内外相关标准及研究文献所采用的方法得到的栓钉连接件抗剪刚度差异较大. 当滑移值小于0.2 mm时,荷载-滑移曲线近似呈线性,对应的剪力均值约为0.45倍的栓钉抗剪承载力,基本位于近似线性与非线性分界处[14]. 本文采用文献[15]的方法,即定义滑移量为0.2 mm时的割线模量为栓钉的抗剪刚度,计算式为
| $ {K_{\rm{s}}} = 0.32{d_{\rm{s}}}E_{\rm{s}}^{1/4}E_{\rm{c}}^{3/4}. $ | (5) |
式中ds为栓钉直径.
2 数值计算模型的建立钢筋混凝土梁的裂缝宽度取决于多种因素,其中钢筋和混凝土之间的粘结质量以及粘结作用的有效区域影响最为显著[16]. 对于钢-混凝土组合梁,钢梁与混凝土板间的界面剪力和滑移是负弯矩区开裂截面分析的重要因素[17],而现阶段负弯矩区裂缝宽度的计算模型往往采用钢筋混凝土结构中的方法. 本文将结合上节给出的本构关系,并综合考虑上述因素建立组合梁负弯矩区裂缝宽度的数值分析模型.
2.1 裂缝截面处钢筋应力钢梁与混凝土板间的界面滑移效应对连续组合梁负弯矩区力学性能影响较大,但在裂缝截面处的钢筋应力分析中往往直接采用材料力学方法来计算受拉钢筋应力[18],即
| $ {\sigma_{\mathrm{s}}}^{\prime}=\frac{M y_{0 \mathrm{r}}}{I_{\mathrm{cr}}}. $ | (6) |
式中:M为开裂截面处的弯矩;Icr为开裂位置的截面惯性矩,即钢梁和钢筋所形成的组合截面惯性矩;y0r为钢筋形心至组合截面中性轴的距离.
当考虑组合梁界面滑移效应时,本文根据文献[18]中的计算方法,计算裂缝截面处钢筋应力计算公式为
| $ \sigma_{\mathrm{s}}=\frac{E_{\mathrm{s}} A_{\mathrm{s}}\left(\varepsilon_{\mathrm{r} 0} I_{\mathrm{cr}} y_{0}-\varepsilon_{\mathrm{s}} I_{\mathrm{s}} y_{0 \mathrm{r}}\right)}{\left[\left(A_{\mathrm{r}}+A_{\mathrm{s}}\right) I_{\mathrm{s}}+A_{\mathrm{r}} A_{\mathrm{s}} y_{0}^{2}\right] y_{0 \mathrm{r}}}, $ | (7) |
| $ \varepsilon_{\mathrm{r} 0}=\frac{M y_{0 \mathrm{r}}}{E_{\mathrm{s}} I_{\mathrm{cr}}}, $ | (8) |
| $ \varepsilon_{\mathrm{s}}=\frac{4 \mathrm{e}^{-\alpha x}\left(\mathrm{e}^{\alpha L}-\mathrm{e}^{2 \alpha x}\right) \beta M}{\alpha\left(\mathrm{e}^{\alpha L}+1\right) L}. $ | (9) |
式中:εr0为完全组合截面的钢筋应变,εs为滑移应变.
2.2 裂缝间距计算在近些年的国内外试验研究中发现,混凝土板内横向钢筋的间距对组合梁负弯矩区的裂缝间距影响较大[16, 19],文献[12]认为横向钢筋的间距和组合梁综合力比是影响负弯矩区裂缝间距的最主要因素,并给出了经试验验证的计算模型,表达式为
| $ {l_{{\rm{cr}}}} = {l_{\rm{a}}}(1 - R_{\rm{p}}^3). $ | (10) |
式中:la为横向钢筋间距;Rp为综合力比,Rp=Arfry/Asfsy,其中fry、fsy分别为钢筋和钢梁的屈服强度. 本文根据该模型进行分析.
2.3 结构的单元划分及平衡关系组合梁负弯矩区混凝土板裂缝宽度数值模型的建立基于裂缝的稳定阶段,即裂缝间距不再变化[16]. 此外,由于裂缝出现的随机性与复杂性,在理论分析前有必要对所求解问题进行适当的简化. 因此,作如下假定:1) 混凝土板主裂缝发生在负弯矩最大位置处,即跨中截面;2) 混凝土板裂缝具有线性三角轮廓.
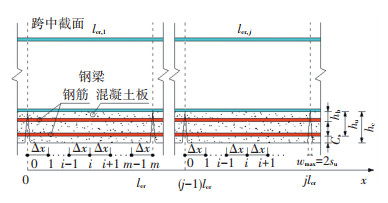
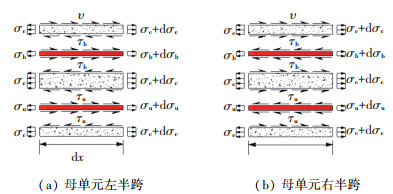
将一个母单元定义为两条相邻裂缝之间的部分,长度为平均裂缝间距lcr,可将半跨组合梁划分为k个母单元,基于有限差分法将任意母单元lcr, j离散为m+1个节点,即等分为m个子单元Δx,结构的单元划分如图 2所示. 根据钢筋混凝土结构裂缝宽度的数值计算方法[20],当混凝土板子单元的划分长度足够精细时,可按照图 3所示微分段dx的受力情况进行分析,其中钢筋与混凝土间的黏结- 滑移关系、钢梁与混凝土板间的界面剪力- 滑移关系以及单元边界条件均在图中示出,则根据力的平衡条件得到如下关系式:
| $ A_{\mathrm{u}} \mathrm{d} \sigma_{\mathrm{u}}=\mp \ {\rm{ \mathsf{ π}}} \tau_{\mathrm{u}} d_{\mathrm{u}} \mathrm{d} x , $ | (11) |
| $ A_{\mathrm{b}} \mathrm{d} \sigma_{\mathrm{b}}=\mp \ {\rm{ \mathsf{ π}}} \tau_{\mathrm{b}} d_{\mathrm{b}} \mathrm{d} x , $ | (12) |
| $ A_{\mathrm{eff}} \mathrm{d} \sigma_{\mathrm{c}}=\mp \ n_{\mathrm{u}} A_{\mathrm{u}} \mathrm{d} \sigma_{\mathrm{u}} \mp\ n_{\mathrm{b}} A_{\mathrm{b}} \mathrm{d} \sigma_{\mathrm{b}}-v \mathrm{~d} x . $ | (13) |
|
图 2 结构单元划分 Fig. 2 Structural unit division |
|
图 3 微分段应力平衡关系 Fig. 3 Equilibrium relationship of stress at differential section |
式中:dσu、dσb分别为混凝土板内上、下层钢筋的应力增量,τu、τb分别为上、下层钢筋黏结应力,Au、Ab分别为上、下层钢筋的面积,du、db分别为上、下层钢筋直径,nu、nb分别为上、下层钢筋数量,dσc为受拉区混凝土应力增量,Aeff为有效受拉区混凝土面积,dx为混凝土板子单元长度,∓或±取决于图 3所示的子单元位置.
由式(11)和式(12)可得到上、下层钢筋的应力分配系数ξ为
| $ \xi=\frac{\mathrm{d} \sigma_{\mathrm{b}}}{\mathrm{d} \sigma_{\mathrm{u}}}=\frac{\tau_{\mathrm{b}} d_{\mathrm{u}}}{\tau_{\mathrm{u}} d_{\mathrm{b}}}. $ | (14) |
当裂缝位置处上、下层钢筋的滑移量分别为su和sb时,根据混凝土板裂缝具有线性三角轮廓的假设,有
| $ s_{\mathrm{u}}=\frac{h_{\mathrm{u}}}{h_{\mathrm{b}}} s_{\mathrm{b}} . $ | (15) |
式中hu、hb分别为上、下层钢筋上表面至钢梁与混凝土界面的距离.
结合式(2)和式(15),可得到应力分配系数的新形式为
| $ \xi=\left(\frac{h_{\mathrm{b}}}{h_{\mathrm{u}}}\right)^{\alpha^{\prime}} \frac{d_{\mathrm{u}}}{d_{\mathrm{b}}}. $ | (16) |
因此,受拉混凝土的应力增量可表示为
| $ \mathrm{d} \sigma_{\mathrm{c}}=\frac{\mp\ n_{\mathrm{u}} A_{\mathrm{u}} \mathrm{d} \sigma_{\mathrm{u}} \mp \ n_{\mathrm{b}} \xi A_{\mathrm{b}} \mathrm{d} \sigma_{\mathrm{u}}-v \mathrm{~d} x}{A_{\mathrm{eff}}}. $ | (17) |
在混凝土板产生裂缝后,纵向钢筋和混凝土之间存在着应变差,从而产生相对滑移ds(x)/dx,可表示为
| $ \begin{aligned} \frac{\mathrm{d} s(x)}{\mathrm{d} x} &=\frac{\mathrm{d}\left[u_{\mathrm{s}}(x)-u_{\mathrm{c}}(x)\right]}{\mathrm{d} x}+\varepsilon_{\mathrm{sh}}=\\ & \varepsilon_{\mathrm{s}}(x)-\varepsilon_{\mathrm{c}}(x)+\varepsilon_{\mathrm{sh}}. \end{aligned} $ | (18) |
式中:us(x)、uc(x)分别为纵向钢筋与受拉混凝土的变形,εs(x)、εc(x)分别为纵向钢筋与受拉混凝土的应变,εsh为混凝土收缩应变.
当裂缝之间受拉钢筋和混凝土均处于弹性阶段,且子单元长度Δx内的黏结应力均匀分布时,对于第j个母单元,可基于有限差分法通过i截面的应力、滑移条件得到i+1截面上的应力、滑移值[21],即存在如下等式:
| $ \sigma_{\mathrm{su}, i+1}^{(j)}=\sigma_{\mathrm{su}, i}^{(j)} \mp \frac{4}{d_{\mathrm{u}}} \tau_{\mathrm{su}, i}^{(j)} \Delta x, $ | (19) |
| $ \sigma_{\mathrm{c}, i+1}^{(j)}=\sigma_{\mathrm{c}, i}^{(j)}+\frac{\pm\left(n_{\mathrm{u}} d_{\mathrm{u}}+n_{\mathrm{b}} \xi d_{\mathrm{b}}\right) {\rm{ \mathsf{ π}}} \tau_{\mathrm{su}, i}^{(j)}-\boldsymbol{v}_{i}^{(j)}}{A_{\mathrm{eff}}} \Delta x, $ | (20) |
| $ \begin{array}{l} s_{{\rm{su}},i + 1}^{(j)} = s_{{\rm{su}},i}^{(j)} \mp \left( {\frac{{\sigma _{{\rm{su}},i + 1}^{(j)} + \sigma _{{\rm{su}},i}^{(j)}}}{{2{E_{\rm{s}}}}} - \frac{{\sigma _{{\rm{c}},i + 1}^{(j)} + \sigma _{{\rm{c}},i}^{(j)}}}{{2{E_{\rm{c}}}}} + } \right.\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {{\varepsilon _{{\rm{sh }}}}} \right)\Delta x. \end{array} $ | (21) |
根据黏结-滑移理论,混凝土板裂缝的开展宽度等于该裂缝左右两侧钢筋与混凝土的相对滑移量之和,则负弯矩作用下组合梁混凝土板的裂缝宽度可表示为
| $ w_{i}^{(j)}=\left\{\begin{array}{l} 2 s_{\mathrm{su}, 0}^{(j)}, j=1, i=0 ;\\ s_{\mathrm{su}, 0}^{(j-1)}+s_{\mathrm{su}, m}^{(j)}, j>1, i=0 ;\\ 2 s_{\mathrm{su}, m}^{(j)}, j=k, i=m. \end{array}\right. $ | (22) |
以第j个母单元x=(j-1)lcr端的边界条件作为初始迭代条件,可表示为
| $ \left\{\begin{array}{l} \sigma_{\mathrm{s}, 0}^{(j)} \neq 0, \\ \sigma_{\mathrm{c}, 0}^{(j)}=0. \end{array}\right. $ | (23) |
以x=jlcr端的边界条件作为迭代收敛控制条件,即
| $ \sigma_{\mathrm{c}, m}^{(j)}=0. $ | (24) |
此外,将母单元中钢筋与混凝土相对滑移为0时作为迭代过程中母单元左右两跨的过渡条件,即
| $ s_{\mathrm{su}, i}^{(j)}=0. $ | (25) |
迭代过程及裂缝宽度计算流程如图 4所示. 通过给出开裂截面的初始滑移值ssu, 0并不断调试,即可预测在一定载荷水平下,组合梁负弯矩的裂缝宽度. 具体步骤如下:

|
图 4 裂缝宽度迭代计算流程图 Fig. 4 Flow chart for iterative calculation of crack width |
1) 输入基本信息和数据. 根据式(10)计算平均裂缝间距lcr,选取半跨结构根据裂缝间距划分k个母单元和m个子单元;以第j个母单元为研究对象,根据式(7)计算开裂截面处钢筋应力σs, 0,并按照式(23)取开裂截面处混凝土应力σc, 0=0.
2) 初设开裂截面位置即第i=0号节点处钢筋和混凝土之间的滑移值ssu, 0. 根据式(2)计算第i+1号子单元上钢筋与混凝土之间的黏结应力τsu, i;根据式(3)计算第i+1号子单元上钢梁与混凝土板界面的单位长度剪力υi.
3) 分别根据式(19)~(21)计算i+1号节点处的钢筋应力σsu, i+1、混凝土应力σcu, i+1以及钢筋和混凝土之间的滑移值ssu, i+1.
4) 设置i=i+1,并重复步骤3,直到i=m时停止初设滑移值ssu, 0的第t=1次迭代运算. 根据控制条件式(24),如果得到的混凝土应力σc, m=0或者在容许误差范围内,则直接根据式(22)给出裂缝宽度计算值;如果σc, m≠0或者超过容许误差,则根据图 4中的修正方法来修正初始滑移值ssu, 0,并继续第t=t+1次迭代运算,即重复步骤2~4,直到得出合适值.
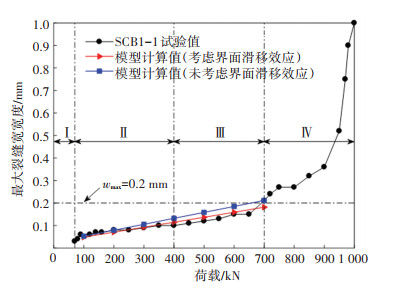
3 计算模型试验验证为验证本文数值模型的准确性,选取文献[8]中试验梁SCB1-1的静载测试数据进行对比分析,并通过MATLAB软件对图 4所示的裂缝宽度迭代计算流程进行编程实现. 采用本文模型得到的最大裂缝宽度与试验值对比情况如图 5所示. 由图 5可知,随着荷载等级的增加,裂缝宽度不断增长,并且在达到试验梁屈服荷载(70%Fu,即700 kN)之前,本文模型得到的裂缝宽度与试验结果吻合较好. 此外,图 5给出了不考虑钢梁与混凝土板之间界面滑移效应时的模型计算值,可以看出此时计算得到的最大裂缝宽度将比考虑界面滑移效应时增大10%左右,且该比例随荷载等级的提高而有所增长,因此在组合梁负弯矩区的实际设计中,对裂缝宽度进行验算时不应忽略界面滑移效应的影响.
|
图 5 裂缝宽度计算值与试验值对比 Fig. 5 Comparison of calculated crack widths with experimental values |
目前国内外钢-混凝土组合梁桥的相关规范均建议采用轴心受拉构件对连续梁中支点处的混凝土裂缝宽度进行验算. 为进一步验证本文数值计算模型的正确性及国内外设计规范所建议公式的适用性,本文将模型计算值及相关文献试验数据与各规范中最大裂缝宽度计算公式所得结果进行了对比,包括美国公路桥梁设计规范AASHTO-LRFD[22]、欧洲混凝土结构模式规范CEB-FIP-2010 [3]、欧洲钢和混凝土复合结构设计规范EN 1994-1-1[23]、日本钢结构和复合结构设计规范JSCE[24]、中国公路钢筋混凝土及预应力混凝土桥涵设计规范JTG 3362—2018[25]以及中国混凝土结构设计规范GB 50010—2010 (2010)[5].
本文采用文献[8]中试验梁SCB1-1及文献[26]中试验梁SCB1、SCB3的构造参数及裂缝宽度实测数据进行分析,将通过不同方法得到的组合梁负弯矩区最大裂缝宽度计算结果列于表 1,各模型计算结果与实测值对比情况列于表 2,并将统计分析结果列于表 3. 由表中数据分析可知,按照各国行业标准中的轴心受拉构件计算方法得到的结果与试验数据存在的偏差较大. 采用本文数值计算模型所得结果与实测值吻合度较高,离散系数极小,可为设计过程中组合梁负弯矩区裂缝宽度的验算提供参考.
| 表 1 采用不同方法得到的裂缝宽度计算结果 Tab. 1 Crack width calculation resultsobtained by different methods |
| 表 2 缝宽度计算结果与实测值对比 Tab. 2 Comparison between crack width calculation results and measured values |
| 表 3 裂缝宽度计算结果统计分析 Tab. 3 Statistical analysis of crack width calculation results |
1) 综合考虑钢筋和混凝土间的黏结应力-滑移关系、钢梁与混凝土界面的滑移效应、混凝土收缩应变以及拉伸硬化效应等因素,基于黏结-滑移理论建立了静力荷载作用下钢-混凝土组合梁负弯矩区裂缝宽度数值计算模型.
2) 采用MATLAB软件编程实现裂缝宽度的迭代计算,通过与相关文献数据进行对比分析可知,在组合梁达到屈服荷载前,本文模型得到的结果能够较好地模拟裂缝宽度的发展过程,与试验结果吻合较好;不考虑钢梁与混凝土板间界面滑移效应时计算得到的裂缝宽度比考虑界面滑移效应时增大10%左右.
3) 通过与各国规范中按照轴心受拉构件计算方法得到的结果进行对比分析可知,按照规范推荐公式得到的结果与试验值偏差较大,采用本文数值计算模型所得结果与实测值吻合度较高,离散系数极小,进一步验证了模型的准确性和适用性.
| [1] |
韩基刚, 宋玉普, 常继峰. 疲劳荷载作用下部分预应力混凝土梁裂缝宽度计算模型[J]. 中南大学学报(自然科学版), 2014, 45(11): 3977. HAN Jigang, SONG Yupu, CHANG Jifeng. Analysis model of crack width of partially prestressed concrete beams under fatigue loading[J]. Journal of Central South University (Science and Technology), 2014, 45(11): 3977. |
| [2] |
汪炳, 黄侨, 刘小玲. 疲劳荷载作用下栓钉连接件的抗剪承载力退化规律[J]. 哈尔滨工业大学学报, 2016, 48(9): 76. WANG Bing, HUANG Qiao, LIU Xiaoling. Shear capacity degradation law of stud connectors under fatigue loading[J]. Journal of Harbin Institute of Technology, 2016, 48(9): 76. |
| [3] |
Comite Euro-International du Beton.Model code for concrete structures: CEB-FIP Model Code 2010[S]. London: CEB, 2013
|
| [4] |
American Concrete Institute.Building code requirements for structural concrete and commentary: ACI 318-11[S]. Michigan: ACI, 2011
|
| [5] |
中华人民共和国住房和城乡建设部. 混凝土结构设计规范: GB 50010—2010[S]. 北京: 中国建筑工业出版社, 2010 Ministry of Housing and Urban-Rural Development of the People's Republic of China. Code for design of concrete structures: GB 50010—2010[S]. Beijing: China Architecture & Building Press, 2010 |
| [6] |
万世成, 黄侨, 关健. 预应力CFRP板加固钢-混凝土组合梁受弯性能试验[J]. 哈尔滨工业大学学报, 2019, 51(3): 80. WAN Shicheng, HUANG Qiao, GUAN Jian. Test on flexural behavior of steel-concrete composite beams strengthened with prestressed carbon fiber-reinforced polymer plates[J]. Journal of Harbin Institute of Technology, 2019, 51(3): 80. |
| [7] |
HAMODA A, HOSSAIN K M A, SENNAH K, et al. Behaviour of composite high performance concrete slab on steel Ⅰ-beams subjected to static hogging moment[J]. Engineering Structures, 2017, 140: 51. DOI:10.1016/j.engstruct.2017.02.030 |
| [8] |
SONG Aiming, WAN Shui, JIANG Zhengwen, et al. Residual deflection analysis in negative moment regions of steel-concrete composite beams under fatigue loading[J]. Construction & Building Materials, 2018, 158: 50. |
| [9] |
CHIOREAN C G, BURU S M. Practical nonlinear inelastic analysis method of composite steel-concrete beams with partial composite action[J]. Engineering Structures, 2017, 134: 74. DOI:10.1016/j.engstruct.2016.12.017 |
| [10] |
LIN Weiwei, YODA T. Numerical study on horizontally curved steel-concrete composite beams subjected to hogging moment[J]. International Journal of Steel Structures, 2014, 14(3): 557. DOI:10.1007/s13296-014-3013-x |
| [11] |
LIU Xinpei, BRADFORD M A, CHEN Qingjun, et al. Finite element modelling of steel-concrete composite beams with high-strength friction-grip bolt shear connectors[J]. Finite Elements in Analysis & Design, 2016, 108: 54. |
| [12] |
张彦玲. 钢-混凝土组合梁负弯矩区受力性能及开裂控制的试验及理论研究[D]. 北京: 北京交通大学, 2009 ZHANG Yanling.Theoretical analysis and experimental research on behavior and crack control of negative moment zone in steel-concrete composite beams[D]. Beijing: Beijing Jiaotong University, 2009 |
| [13] |
NIE Jianguo, FAN Jiansheng, CAI C S. Stiffness and deflection of steel-concrete composite beams under negative bending[J]. Journal of Structural Engineering, 2004, 130(11): 1842. DOI:10.1061/(ASCE)0733-9445(2004)130:11(1842) |
| [14] |
蔺钊飞, 刘玉擎. 焊钉连接件峰值滑移及剪力-滑移本构关系[J]. 同济大学学报(自然科学版), 2014, 42(7): 1006. LIN Zhaofei, LIU Yuqing. Peak slip and load-slip relationship of headed stud connectors[J]. Journal of Tongji University (Natural Science), 2014, 42(7): 1006. |
| [15] |
蔺钊飞, 刘玉擎, 贺君. 焊钉连接件抗剪刚度计算方法研究[J]. 工程力学, 2014, 31(7): 85. LIN Zhaofei, LIU Yuqing, HE Jun. Research on calculation method of shear stiffness for headed stud connectors[J]. Engineering Mechanics, 2014, 31(7): 85. |
| [16] |
FABBROCINO G, VERDERAME G M, POLESE M. Probabilistic steel stress-crack width relationship in R.C. frames with smooth rebars[J]. Engineering Structures, 2007, 29(1): 1. DOI:10.1016/j.engstruct.2006.04.002 |
| [17] |
MANFREDI G, FABBROCINO G, COSENZA E. Modeling of steel-concrete composite beams under negative bending[J]. Journal of Engineering Mechanics, 1999, 125(6): 654. DOI:10.1061/(ASCE)0733-9399(1999)125:6(654) |
| [18] |
樊健生, 聂建国. 负弯矩作用下考虑滑移效应的组合梁承载力分析[J]. 工程力学, 2005, 22(3): 177. FAN Jiansheng, NIE Jianguo. Effects of slips on load-carrying capacity of composite beams under negative bending[J]. Engineering Mechanics, 2005, 22(3): 177. |
| [19] |
HE Jun, LIU Yuqing, CHEN Airong, et al. Experimental study on inelastic mechanical behaviour of composite girders under hogging moment[J]. Journal of Constructional Steel Research, 2010, 66(1): 37. DOI:10.1016/j.jcsr.2009.07.005 |
| [20] |
OLIVEIRA R S, RAMALHO M A, CORRÊA M R S. A layered finite element for reinforced concrete beams with bond-slip effects[J]. Cement & Concrete Composites, 2008, 30(3): 245. |
| [21] |
CASTEL A, VIDAL T, FRANCOIS R. Finite-element modeling to calculate the overall stiffness of cracked reinforced concrete beams[J]. Journal of Structural Engineering, 2012, 138(7): 889. DOI:10.1061/(ASCE)ST.1943-541X.0000520 |
| [22] |
American Association of State Highway and Transportation Officials.Bridge design specifications: AASHTO LRFD[S]. 8th ed. Washington DC: AASHTO, 2017
|
| [23] |
CEN-European Committee for Standardization. Design of composite steel and concrete structures part 1.1 general rules and rules for buildings: Eurocode 4, EN 1994-1-1[S]. Brussels: CEN, 2005
|
| [24] |
Japan Society of Civil Engineers. Committee of steel structure: JSCE standard specifications for steel and composite structure[S]. Tokyo: JSCE, 2009
|
| [25] |
中华人民共和国交通运输部. 公路钢筋混凝土及预应力混凝土桥涵设计规范: JTG 3362—2018[S]. 北京: 人民交通出版社, 2018 Ministry of Transport of the People's Republic of China. Specifications for design of highway reinforced concrete and prestressed concrete bridges and culverts: JTG 3362—2018[S]. Beijing: China Communications Press, 2018 |
| [26] |
张彦玲, 樊健生, 李运生. 连续组合梁桥裂缝发展规律分析及裂缝宽度计算[J]. 工程力学, 2011, 28(7): 84. ZHANG Yanling, FAN Jiansheng, LI Yunsheng. Law of crack development and calculation of crack width of continuous composite beams[J]. Engineering Mechanics, 2011, 28(7): 84. |
 2021, Vol. 53
2021, Vol. 53


