2. 西南交通大学 土木工程学院,成都 610031;
3. 水利部岩土力学与工程重点实验室(长江科学院),武汉 430010
2. School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, China;
3. Key Laboratory of Geotechnical Mechanics and Engineering of Ministry of Water Resources (Changjiang River Scientific Research Institute), Wuhan 430010, China
中国膨胀土分布广泛,其中以广西、云南、四川、河北、湖北、安徽等地最为突出[1]. 因其富含强亲水性的蒙脱石、伊利石等黏土矿物,较一般黏性土具有显著的浸水体积膨胀、失水收缩开裂等特性,使得暴露于自然环境的膨胀土边坡,在雨水浸润与大气蒸发反复交替作用下极易发生溜坍破坏,给途径膨胀土地区的水利、公路和铁路工程建设带来了严重的安全隐患[1]. 诸多实例表明,降雨诱发的膨胀土路堤边坡失稳,以浅层溜坍最为典型,大多破坏形态如图 1所示,破裂滑体具有明显的三段组合式失稳破坏特征[2].

|
图 1 膨胀土边坡典型破坏形态[2]及失稳概化模式 Fig. 1 Typical failure pattern of expansive soil slope[2] and its conceptual failure mode |
目前,关于膨胀土边坡破坏机理及失稳特征的研究已取得不少成果[3-5]. 文献[6]分析了降雨入渗下的膨胀变形对膨胀土边坡渐进破坏的影响. 文献[7]开展风干和烘干膨胀土的水槽浸水试验,结果显示膨胀土有效黏聚力为零,进而说明低应力下抗剪强度包线具有的非线性特征是引起降雨诱发膨胀土边坡浅层溜坍破坏的重要原因;文献[8]开展了膨胀土饱和慢剪试验,得出抗剪强度均随法向应力的减小呈现幂函数型降低规律,再次验证了文献[7]的合理性,同时采用低应力下强度参数分析了膨胀土边坡的稳定性[9],但稳定分析时文献[7]直接采用了圆弧滑动模式,其与图 1中膨胀土边坡典型失稳模式有较大差异. 同时,文献[7-9]对较低应力下的非线性强度,均采用了分段线性化处理的方式,然而分段界限值尚不明确. 另外,文献[10]认为降雨入渗膨胀土边坡导致浅层土体顺坡向应力大幅增加,也是促使其发生浅层顺坡向平面滑动的原因之一. 文献[11]将边坡浅层溜坍模式视为无限长斜坡“顺坡平面”滑动模式. 文献[12]认为“顺坡平面”滑动模式忽略了滑体端部抗滑效应,提出了降雨诱发的路堤土质边坡浅层失稳呈现三段组合式“顺坡曲面”破坏模式,但该研究并未考虑低应力下强度非线性特点.
可见,合理评估膨胀土路堤边坡浅层稳定性的关键因素在于:一是明确膨胀土强度线性段与非线区段的应力界限值,二是采用与浅层失稳破坏形态相一致的滑动模式. 为此,通过分析膨胀土强度低应力下非线性和常规应力下线性变化的基本规律,提出膨胀土不同应力区段强度差异性变化的界限值确定方法;将膨胀土路堤边坡典型破坏形态概化为能反映其上缘张拉、中段剪切和下缘挤压效应的“顺坡曲面”失稳模式(见图 1). 据此构建反映渗流作用及低应力下抗剪强度非线性特征的膨胀土路堤边坡浅层稳定分析方法,本文研究丰富了对膨胀土路堤边坡浅层稳定性的认识.
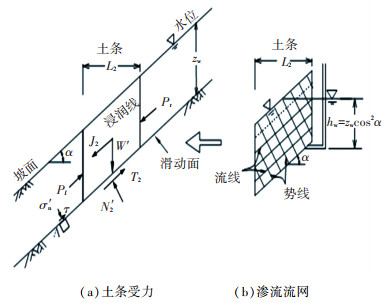
1 无限长斜坡浅层稳定分析方法 1.1 基于库伦线性强度模型的无限长斜坡法在强降雨入渗斜坡浅层形成饱和顺坡向渗流情况下,对斜坡倾角为α、入渗深度为zw、长度为L2的土条进行如图 2(a)所示的力学分析. 图 2(b)给出了无限长斜坡饱和顺坡渗流下的流网示意图及用于计算水力梯度的测压管水头hw=zwcos2α计算式,故深度zw处的孔隙水压力u=γwzwcos2α,其中γw为水的容重.
|
图 2 土条受力及渗流流网 Fig. 2 Force on soil slice and seepage flow net |
将土条整体进行隔离体受力分析,其重力W2=γsatzwL2, 其中γsat为土体饱和重度. 因此,土条底部反力N′计算公式为
| $ N^{\prime}=W_{2} \cos \alpha-u L_{2} / \cos \alpha. $ | (1) |
抗剪强度库伦模型,用有效应力表达为
| $ \tau_{\mathrm{f0}}=c^{\prime}+{\sigma_{\mathrm{n}}}^{\prime} \tan \varphi^{\prime}. $ | (2) |
式中:c′为有效黏聚力;φ′为有效内摩擦角;σn′为土体破裂面上的有效法向应力;为了区分幂函数非线性强度模型,将抗剪强度τf符号记为τf0.
土条抗滑力T与下滑力S之比即为安全系数Fs0,其方程为
| $ F_{\mathrm{s} 0}=\frac{T}{S}=\frac{\frac{c^{\prime} L_{2}}{\cos \alpha}+N^{\prime} \tan \varphi^{\prime}}{W_{2} \sin \alpha}. $ | (3) |
将式(1)代入式(3)化简后,可得无限长斜坡饱和顺坡渗流下的浅层稳定安全系数表达式[7]为
| $ F_{\mathrm{s} 0}=\frac{c^{\prime}+\gamma^{\prime} z_{\mathrm{w}} \cos ^{2} \alpha \tan \varphi^{\prime}}{\gamma_{\mathrm{sat}} z_{\mathrm{w}} \cos \alpha \sin \alpha}. $ | (4) |
已有试验表明,膨胀土抗剪强度在低应力下呈现出较明显的非线性变化特征,可采用如式(5)所示的基于应力水平的三参数幂函数模型[7, 11]进行描述. 当Ts=0时,式(5)变为式(6),即
| $ \tau_{\mathrm{f1}} =a P_{\mathrm{a}}\left(T_{\mathrm{s}}+\frac{{\sigma_{\mathrm{n}}}^{\prime}}{P_{\mathrm{a}}}\right)^{b} , $ | (5) |
| $ \tau_{\mathrm{f1}} =a P_{\mathrm{a}}\left({\sigma_{\mathrm{n}}}^{\prime} / P_{\mathrm{a}}\right)^{b}. $ | (6) |
式中:Pa为1标准大气压力,取101 kPa;a、b、Ts为无量纲参数,其中Ts与土体抗拉强度相关,-PaTs为土的抗拉强度;抗剪强度τf符号记为τf1.
当式(5)中b=1、a=tan φ′、Ts=c′/(Patan φ′)时幂函数方程可退化为库伦模型. 因此,在饱和顺坡向渗流条下,结合式(6)可导出基于幂函数非线性强度模型的无限长斜坡安全系数Fs1表达式[7]为
| $ F_{\mathrm{s} 1}=a P_{\mathrm{a}}\left(\frac{\gamma^{\prime} z_{\mathrm{w}} \cos ^{2} \alpha}{P_{\mathrm{a}}}\right)^{b} \frac{1}{\gamma_{\mathrm{sat}} z_{\mathrm{w}} \cos \alpha \sin \alpha}. $ | (7) |
可见,安全系数计算式(4)和式(7)与土条长度L2无关,故单位长度土条的安全系数即反映了无限长斜坡的稳定性. 但是,该方法假定“斜坡无限长”与实际有几何边界的膨胀土路堤边坡情况不符,忽略了滑体下缘剪出口和上缘切入口的抗滑效应,且基于低应力下强度非线性模型的安全系数方程式(7),所指低应力区段也不是十分明确.
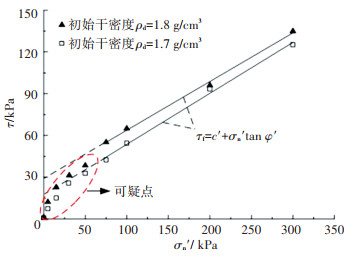
2 抗剪强度非线性与线性区段界定图 3给出了两种初始干密度ρd=1.7 g/cm3和ρd=1.8 g/cm3下饱和状态重塑膨胀土的慢剪试验结果,相应膨胀土基本物性参数见文献[9]. 由图 3可知,σn′与τ在常规应力段(75~300 kPa)符合库伦线性强度模型. 土工试验规程[13]中指出,抗剪强度实测点与拟合直线上对应抗剪强度之差,不得超过直线上对应抗剪强度±5%,否则认为试验误差太大. 但是,重塑膨胀土低应力下抗剪强度试验结果与常规应力段存在较大差异(见图 3中可疑点),且σn′→0时,有效黏聚力c′近乎为0,即Ts=0. 这并非误差所致,而是抗剪强度低应力段具有的非线性特性.
|
图 3 试样σn′与τ的关系 Fig. 3 Relation between σn′ and τ of specimen |
为明确低应力所指的应力范围,需对常规应力下的强度线性区段与低应力下强度非线性区段进行界定. 误差理论[14]中指出,试验点是否属于线性关系,须采用基于统计原理的判别方法进行判定,以避免对分析结果产生偏差.
为此,通过可疑点识别与粗差点判别两个环节确定抗剪强度线性段与非线性段界限值,具体步骤如下:
1) 可疑点识别. 在n组样本点中,任取n-1组数据进行线性回归,获得n个相关系数R2,将R2最接近1的回归方程定义为可信方程,相应数据之外的隔离点为可疑点. 因强度曲线较高应力区段基本为直线,且线性回归中拟合数据应至少包含3个点,故对σn′由高到低逐个进行可疑点识别. 以图 3中,ρd=1.8 g/cm3下的σn′-τ关系为例. 首次选取横坐标为σ1′=300 kPa、σ2′=200 kPa、σ3′=100 kPa、σ4′=75 kPa的4个点进行逐点隔离,对剩余3个点进行线性回归,结果见表 1. 可见,相关系数R2最大为0.999,对应的隔离点(σ3′,τ3)=(100,65)为可疑点.
| 表 1 相关系数R2计算结果 Tab. 1 Calculation results of correlation coefficient R2 |
2) 粗差点判别. 通常判别可疑点(σi′,τi)是否为线性回归中粗大误差的方法有Chauvenet准则[15]、“3σ”准则[14]等. 其中,样本数较多时(通常几十个样本以上)选用“3σ”准则,样本数少时推荐采用Chauvenet准则,其判别式为
| $ \varDelta=\left|c^{\prime}+{\sigma_{i}}^{\prime} \tan \varphi^{\prime}-\tau_{i}\right|-\omega S>0. $ | (8) |
式中:ω为Chauvenet系数,通过查标准正态分布表确定;当ω=3时,Chauvenet准则退化为“3σ”准则;S为样本标准差,表示为
| $ S=\sqrt{\frac{1}{n-2} \sum\limits_{i=1}^{n-1}\left(\tau_{i}-c^{\prime}-{\sigma_{i}}^{\prime} \tan \varphi^{\prime}\right)^{2}}. $ | (9) |
式(8)的含义:可疑点的残差超过ω倍标准差S,即Δ>0时,该可疑点为粗大误差. 因抗剪强度常规应力区段样本点n通常为4~6个,故采用Chauvenet准则. 当可疑点(σi′,τi)满足式(8)时,可疑点即为粗差点,不满足时为正常点. 若可疑点为粗差点,则回归直线剔除此点,仅有n-1组数据构成;若可疑点为正常点,则回归直线由包含此点的n组数据确定.
按照式(8)对可疑点(100,65)进行判别,计算结果显示Δ=-0.6 < 0,因此该可疑点为正常点. 说明σn′-τ在σn′为75~300 kPa之间满足线性关系,则新的线性回归方程由n=4个点构成可信方程,其回归参数c′=28.7、tan φ′=0.345. 基于最新线性回归方程,对横坐标σ5′=50 kPa的第5个数据点,按照式(8)进行粗差点判别,计算结果Δ=6.0>0,即第5个点为粗差点,回归直线排除此点. 同理,可以判别低于σ5′=50 kPa的其余点均为粗差点. 可知,低应力区段强度非线性变化与常规应力强度线性变化的界限值σcr′,应介于粗差点中应力最大的试验点σCmax′=50 kPa与回归直线段应力最小的试验点σLmin′=75 kPa之间,取其平均值得
| $ {\sigma_{\mathrm{cr}}}^{\prime}=\frac{{\sigma_{L \min }}^{\prime}+{\sigma_{C \max }}^{\prime}}{2}. $ | (10) |
由式(10)得σcr′=63 kPa. 因此,浸水饱和后膨胀土在σn′为0~63 kPa时属于低应力范围,该区段抗剪强度曲线向坐标原点弯曲,可采用幂函数拟合. 因此,当σn′≥σcr′时,抗剪强度随σn′增加呈库伦线性增大的规律;当σn′ < σcr′时,抗剪强度随σn′的降低呈幂函数型非线性减小的趋势,如图 4所示. 同理,ρd=1.7 g/cm3的膨胀土强度非线性与线性变化的界限值σcr′=23 kPa. 通常膨胀土路堤边坡浅层滑动深度zw=0~1.5 m时,考虑渗流条件下,按式(1)计算得剪切面上σn′约为0~11 kPa,均处于低应力区段. 且低应力段强度曲线随σn′降低斜率增加,截距减小,即有效黏聚力c′随σn′的降低逐渐减小,当σn′→0时,c′→0;而随σn′的减小,φ′逐渐增大. 即低应力下,膨胀土强度低的原因是小黏聚力和大内摩擦角. 内摩擦角大但应力水平低,故强度也低.

|
图 4 强度非线性与线性区段划分(ρd=1.8 g/cm3) Fig. 4 Strength discrimination between linear and nonlinear sections (ρd=1.8 g/cm3) |
膨胀土或黏土饱和慢剪试验结果[7-9]表明,法向应力σn′接近于零时,实测c′趋于零. 排水剪切过程中,对于正常固结黏土,有效抗剪强度包线通过坐标原点,即c′为零[16],该结果可以通过开展“土膏”试验加以验证[17],在土体正常固结尚未形成结构强度时,土体无黏聚力;而另有试验结果[8]表明,对于超固结土或压实土,即便饱和后,在法向压力等于零时,仍有一定的强度,即超固结土或压实土因曾经承受一定固结压力或外荷载,卸载后仅部分回弹,土体内部产生了内应力或留有残余应力,使得土体强度得到提高,表现出了黏聚力.
因此,直剪试验中应该区分法向“应力”和“压力(荷载)”,应力是指土体内部单元体的受力状态,而压力对应于土体外部荷载作用. 当施加高于试样初始内应力的法向压力后,土体产生屈服,即压密变形,稳定后土体的内应力才与法向压力相近;当施加低于试样初始内应力的法向压力后,土体的内应力将与外荷载无关,表现为超固结性,抗剪强度线在正常固结土的抗剪强度线上方. 当假定土体是各向同性材料时,可得
| $ \left\{\begin{array}{l} {\sigma_{\mathrm{n}}}^{\prime}=p, p>\sigma_{\mathrm{c}} ;\\ {\sigma_{\mathrm{n}}}^{\prime} \approx \sigma_{\mathrm{c}}, p \leqslant \sigma_{\mathrm{c}}. \end{array}\right. $ | (11) |
式中:p为直剪试样表面均布荷载,σc为单元土体的内应力.
对于膨胀土失水收缩后表现出裂隙性、超固结性,浸水后表现出膨胀性,文献[3, 8]分别开展膨胀土试样在有荷和无荷条件下干湿循环后的慢剪试验,无荷干湿循环后试样在低法向压力下测得黏聚力趋于零,而有荷干湿循环后试样在法向压力为零时仍然具有一定的强度,充分说明了无荷干湿循环试验,膨胀土浸水后体积可以在无约束下充分膨胀,内应力得到极大释放,最终密度大幅降低,表现出非超固结土的性质,而有荷干湿循环试样,膨胀土始终受到约束,内应力得不到充分释放,仍然表现出超固结土的性质,故而有一定的黏聚力. 膨胀土边坡常年受季节性降雨和大气蒸发反复作用,裂隙发育,而且靠近坡面的浅层土体处于近似无约束状态,在长期干旱后,遭遇强降雨,边坡浅层膨胀土遇水变化情况与无荷干湿循环试验结果相近,故有效应力σn′→0时c′→0.
综上所述,强降雨诱发的膨胀土路堤边坡浅层失稳土体处于低应力非线性区段,边坡浅层稳定分析宜采用:1)与低应力区段相匹配的非线性强度模型;2)与破坏形态吻合的组合滑面失稳模式.
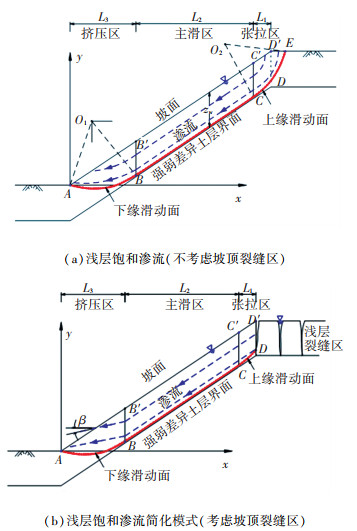
3 低应力下膨胀土路堤边坡浅层稳定性 3.1 膨胀土路堤边坡浅层失稳模式文献[18]基于资料统计得出膨胀土边坡浅层为1.0~1.5 m时受气候环境影响较为显著,浅层裂隙的开展将原本均质土层划分成了强度显著差异的不同土层,滑动面难以穿越强度高的下部区域,一般处于有裂隙的浅层内. 膨胀土边坡现场降雨试验结果显示[19],边坡浅层失稳具有如图 5所示的以中段顺坡平面滑动为主导的“顺坡曲面”破坏模式. 因此,将膨胀土边坡失稳概化为以强弱差异土层界面为顺坡平面即主滑面,上缘张拉区和下缘挤压区为圆弧滑面的三段组合式“顺坡曲面”失稳模式,且上下缘圆弧面与顺坡平面相切.
|
图 5 边坡浅层“顺坡曲面”失稳破坏及渗流简化模式 Fig. 5 "Parallel slope-curve" failure mode and simplified seepage mode |
文献[2]指出,膨胀土边坡通常处于非饱和状态,若要分析特定状态下的边坡稳定性,可考虑用非饱和土强度指标,但设计都是考虑最不利情况,不能保证强降雨时边坡不会达到饱和状态,尤其是浅层多裂隙的膨胀土,为雨水入渗提供了良好的通道. 调查显示,膨胀土边坡深层土体密度高、渗透性弱,雨水很难向深部入渗[20]. 因此,强降雨导致边坡浅层土体达到饱和后,雨水将沿着浅层强度差异土层界面,以顺坡向下渗流为主导,为简化分析,假定为饱和顺坡渗流.
3.2 膨胀土路堤边坡典型界面几何方程为便于求解滑面方程,建立直角坐标系原点于坡趾A点处. 令边坡坡比为1∶n、坡高为H,上下缘滑体滑动圆心分别为O1(xdo, ydo)和O2(xuo, yuo),中段主滑区滑动深度为zw,则可得膨胀土路堤边坡边界方程:
| $ y_{1}=\left\{\begin{array}{ll} 0, & x \leqslant 0 ; \\ \frac{x}{n}, & 0<x<n H ;\\ H, & x \geqslant n H . \end{array}\right. $ | (12) |
则强弱差异土层界面方程为y2=y1-zw. 由此,不难获得三段式组合滑体的滑面y3方程:
| $ y_{3}=\left\{\begin{array}{l} y_{\mathrm{do}}-\sqrt{R^{2}-\left(x-x_{\mathrm{do}}\right)^{2}}, x_{A}<x \leqslant x_{B}; \\ \frac{x}{n}-z_{\mathrm{w}}, x_{B}<x \leqslant x_{C}; \\ y_{\mathrm{uo}}-\sqrt{R^{2}-\left(x-x_{\mathrm{uo}}\right)^{2}}, x_{C}<x \leqslant x_{E}. \end{array}\right. $ | (13) |
式中x的下标代表图 5中相应点的横坐标.
3.3 “顺坡曲面”组合滑体静力平衡方程 3.3.1 “顺坡曲面”组合滑体受力分析根据“顺坡曲面”失稳模式,将各段滑体进行受力分析. 滑体在滑面底部受抗滑力T和法向力N′,下标代表该力作用在的滑体段上(见图 6). 如N1′为上缘张拉区滑体底部的法向力,其余类似. 下缘挤压区受中段主滑区剩余下滑力挤压作用,属被动破坏,故条间力合力采用Ep′表示;上缘张拉区受中段主滑区滑体张拉作用,属主动破坏,故条间力合力采用Ea′表示,假定合力作用点位于距土条底部1/3高度处[21],如图 6所示.

|
图 6 组合滑体受力 Fig. 6 Force analysis for three parts of composite sliding body |
“顺坡曲面”失稳模式与无限长斜坡的“顺坡平面”失稳模式不同,上下缘滑面为两段圆弧,以至于滑体底部法向力N′与坐标相关. 常用条分法通过静力平衡方程确定每个土条底部的法向反力,其计算精度除了与条间力假设相关外,还受土条划分个数影响. 因此,滑体上下缘圆弧滑面处采用微分土条处理,严格意义上,微分土条所受全部作用力,如图 7所示. 其中dW′为有效重力,dJ为渗透力,dN′为土条底部法向力,dT为土条底部切向阻力,E′+dE′为土条条间力合力.

|
图 7 上下缘滑体土条受力 Fig. 7 Force analysis for sliding body at upper and lower edges of soil slice |
目前,为了获得整个滑体稳定问题的解答,对土条两侧条间力大小、方向进行的系列假设,形成了一整套较为完善的极限平衡法,如:Fellenius法[22]、Bishop法[23]、Morgenstern-Price法[24]等. 针对三段式“顺坡曲面”组合滑面,可借鉴上述任意一种对条间力的处理方法. 但随着考虑条间力数目的增多,迭代计算过程越趋于复杂. 为简化分析,上下缘滑体微分土条条间力假设同Fellenius法. 在稳定渗流下,将土骨架作为隔离体,渗透水流作为土骨架孔隙中的连续介质独立作用于土骨架. 土条底部水压力dUs,通过图 7(a)中流线和等势线的关系确定,为dUs=hwγwdl. 当渗透力方向与滑面方向差别不大时,只考虑渗透力引起的滑动作用[25].
由图 7中几何关系,可得dθ=dx/(Rcos θ)、sin θ=(x-x0)/R.利用幂函数方程(6),结合极限平衡条件得出微分土体底部剪切抗力方程:
| $ \mathrm{d} T=\frac{1}{F_{\mathrm{a}}}\left[a P_{\mathrm{a}}\left(\sigma_{\mathrm{n}}^{\prime} / P_{\mathrm{a}}\right)\right] \mathrm{d} l. $ | (14) |
式中dl=dx/cos θ. 当xB < x < xC时,θ=α.
将σn′=γ′hscos2α代入式(14),得
| $ \mathrm{d} T=\frac{1}{F_{\mathrm{s}}}\left[a P_{\mathrm{a}}\left(\gamma^{\prime} h_{\mathrm{s}} \cos ^{2} \theta / P_{\mathrm{a}}\right)^{b}\right] / \cos \theta \mathrm{d} x. $ | (15) |
此时,
| $ \left\{\begin{array}{l} \mathrm{d} W^{\prime}=\gamma^{\prime} h_{\mathrm{s}} \mathrm{d} x ,\\ \mathrm{~d} J=\gamma_{\mathrm{w}} h_{\mathrm{s}} \mathrm{i} \mathrm{d} x. \end{array}\right. $ | (16) |
式中:ih=sin α/cos(α-β),当顺坡向渗流即β=α时ih=sin α,竖直下渗β=90°时ih=1;hs为土条高度,按式(17)计算:
| $ h_{\mathrm{s}}=\left\{\begin{array}{l} \frac{x}{n}-\left[y_{\mathrm{do}}-\sqrt{R^{2}-\left(x-x_{\mathrm{do}}\right)^{2}}\right], x_{A}<x \leqslant x_{B} ;\\ z_{w}, x_{B}<x \leqslant x_{C}; \\ \frac{x}{n}-\left[y_{\mathrm{uo}}-\sqrt{R^{2}-\left(x-x_{\mathrm{uo}}\right)^{2}}\right], x_{C}<x \leqslant x_{D}; \\ H-\left[y_{\mathrm{uo}}-\sqrt{R^{2}-\left(x-x_{\mathrm{uo}}\right)^{2}}\right], x_{D}<x \leqslant x_{E}. \end{array}\right. $ | (17) |
上缘滑体力矩平衡方程MS1=MT1,其中下滑力矩MS1和抗滑力矩MT1分别为
| $ M_{\mathrm{S} 1}=\int_{x_{C}}^{x_{E}}\left(x+\frac{\mathrm{d} x}{2}-x_{0}\right) \mathrm{d} W^{\prime}+\int_{x_{C}}^{x_{E}} R_{1} \mathrm{~d} J, $ | (18) |
| $ M_{\mathrm{T} 1}=\int_{x_{\mathrm{C}}}^{x_{E}} R_{\mathrm{u}} \mathrm{d} T+{E_{\mathrm{a}}}^{\prime} R_{2}. $ | (19) |
式中:Ru为上缘圆弧半径;R1、R2分别为J和Ea′对上缘滑面圆心的力臂;体积力J作用点位于土条中部(见图 7),满足R1=Rucos(θ-α)-0.5hscos α.
下缘滑体力矩平衡方程MT3=MS3,其中下滑力矩MS3和抗滑力矩MT3分别为
| $ M_{\mathrm{S} 3}=\int_{x_{A}}^{x_{B}}\left(x+\frac{\mathrm{d} x}{2}-x_{0}\right) \mathrm{d} W^{\prime}+{E_{\mathrm{p}}}^{\prime} R_{4}+\int_{x_{A}}^{x_{B}} R_{3} \mathrm{~d} J, $ | (20) |
| $ M_{\mathrm{T} 3}=\int_{x_{A}}^{x_{B}} R_{\mathrm{d}} \mathrm{d} T. $ | (21) |
式中:Rd为下缘圆弧半径;R3、R4分别为J和Ep′对下缘滑面圆心的力臂,由图 7(a)中几何关系得R3=Rd cos(θ-β)-0.5hscos β.
中段滑体静力平衡方程为
| $ \begin{array}{l} \int_{x_{B}}^{x_{C}} \frac{a P_{\mathrm{a}}\left(\gamma^{\prime} h_{\mathrm{s}} \cos ^{2} \theta / P_{\mathrm{a}}\right)^{b}}{F_{\mathrm{s}} \cos \alpha} \mathrm{d} x+{E_{\mathrm{p}}}^{\prime}= \\ \int_{x_{B}}^{x_{C}} \gamma_{\mathrm{sat}} z_{\mathrm{w}} \sin \alpha \mathrm{d} x+{E_{\mathrm{a}}}^{\prime} \end{array} $ | (22) |
由式(18)~(21)得
| $ {E_{\mathrm{p}}}^{\prime}=\frac{\int_{x_{A}}^{x_{B}} R_{\mathrm{d}} \mathrm{d} T-\int_{x_{A}}^{x_{B}}\left(x+x_{0}-\frac{\mathrm{d} x}{2}\right) \mathrm{d} W^{\prime}-\int_{x_{A}}^{x_{B}} R_{3} \mathrm{~d} J}{R_{4}}, $ | (23) |
| $ {E_{\mathrm{a}}}^{\prime}=\frac{\int_{x_{C}}^{x_{E}}\left(x+x_{0}-\frac{\mathrm{d} x}{2}\right) \mathrm{d} W^{\prime}+\int_{x_{C}}^{x_{E}} R_{2} \mathrm{~d} J-\int_{x_{C}}^{x_{E}} R_{\mathrm{u}} \mathrm{d} T}{R_{2}}. $ | (24) |
将式(23)和式(24)代入式(22)中,得出满足上下缘力矩平衡和中段滑体静力平衡的三段式“顺坡曲面”组合滑面稳定安全系数积分方程:
| $ F_{\mathrm{s}}=\frac{R_{1}\left[a P_{\mathrm{a}}\left(\gamma^{\prime} z_{\mathrm{w}} \cos ^{2} \alpha P_{\mathrm{a}}^{-1}\right)^{b}\right] L_{2} \cos ^{-1} \alpha+{M^{\prime}}_{\mathrm{T} 1}+M_{\mathrm{T} 3}^{\prime}}{R_{1} \gamma_{\mathrm{sat}} \sin \alpha L_{2}+{M^{\prime}}_{\mathrm{S} 1}+{M^{\prime}}_{\mathrm{S} 3}+{M^{\prime}}_{\mathrm{J} 1}+{M^{\prime}}_{\mathrm{J} 3}}. $ | (25) |
式中:MS1′、MT1′、MJ1′、MS3′、MT3′和MJ3′按式(26)计算,x-x0+dx/2略去微分小量dx/2后变为x-x0.
| $ \left\{ \begin{array}{l} \begin{array}{*{20}{l}} {M_{{\rm{T}}1}^\prime = \frac{{{R_4}}}{{{R_2}}}\int_{{x_C}}^{{x_E}} {{R_{\rm{u}}}} \left[ {a{P_{\rm{a}}}{{\left( {{\gamma ^\prime }{h_{\rm{s}}}{{\cos }^2}\theta /{P_{\rm{a}}}} \right)}^b}} \right]/\cos \theta {\rm{d}}x,}\\ {M_{{\rm{S}}1}^\prime = \frac{{{R_4}}}{{{R_2}}}\int_{{x_C}}^{{x_E}} {\left( {x - {x_0}} \right)} {\rm{d}}{W^\prime },}\\ {M_{{\rm{J}}1}^\prime = \frac{{{R_4}}}{{{R_2}}}\int_{{x_C}}^{{x_E}} {{R_3}} {\gamma _{\rm{w}}}{h_{\rm{s}}}{i_{\rm{h}}}{\rm{d}}x,}\\ {M_{{\rm{T3}}}^\prime = \frac{{{R_2}}}{{{R_4}}}\int_{{x_A}}^{{x_B}} {{R_{\rm{d}}}} \left[ {a{P_{\rm{a}}}{{\left( {{\gamma ^\prime }{h_{\rm{s}}}{{\cos }^2}\theta /{P_{\rm{a}}}} \right)}^b}} \right]/\cos \theta {\rm{d}}x,} \end{array}\\ \begin{array}{*{20}{l}} {M_{{\rm{S}}3}^\prime = \frac{{{R_2}}}{{{R_4}}}\int_{{x_A}}^{{x_B}} {\left( {x - {x_0}} \right)} {\rm{d}}{W^\prime },}\\ {M_{{\rm{J}}3}^\prime = \frac{{{R_2}}}{{{R_4}}}\int_{{x_A}}^{{x_B}} {{R_3}} {\gamma _{\rm{w}}}{h_{\rm{s}}}{i_{\rm{h}}}{\rm{d}}x.} \end{array} \end{array} \right. $ | (26) |
当L2减小至零时,且上下缘圆弧半径相等,即Ru=Rd,得滑动土体仅由上缘张拉区和下缘挤压区组成的整体圆弧滑动模式,式(25)退化为
| $ F_{\mathrm{s}}=\frac{\int_{x_{A}}^{x_{E}} R\left[a P_{\mathrm{a}}\left(\gamma^{\prime} h_{\mathrm{s}} \cos ^{2} \theta P_{\mathrm{a}}^{-1}\right)^{b}\right] \cos ^{-1} \theta \mathrm{d} x}{\int_{x_{A}}^{x_{E}}\left(x-x_{0}\right) \mathrm{d} W^{\prime}+\int_{x_{A}}^{x_{E}} R_{1} \gamma_{\mathrm{w}} h_{\mathrm{s}} i_{\mathrm{h}} \mathrm{d} x}. $ | (27) |
不考虑渗透力时,式(27)变为
| $ F_{\mathrm{s}}=\frac{\int_{x_{A}}^{x_{E}} R\left[a P_{\mathrm{a}}\left(\gamma^{\prime} h_{\mathrm{s}} \cos ^{2} \theta P_{\mathrm{a}}^{-1}\right)^{b}\right] \cos ^{-1} \theta \mathrm{d} x}{\int_{x_{A}}^{x_{E}}\left(x-x_{0}\right) \mathrm{d} W^{\prime}}. $ | (28) |
当L2增大至无穷大时,滑动土体仅由中段主滑区“顺坡平面”土条构成的“顺坡平面”滑动模式,此时,式(22)分子和分母通除以L2后,还原成无限长斜坡安全系数式(7),即为
| $ \lim \limits_{L_{2} \rightarrow \infty} F_{\mathrm{s}}=\frac{a P_{\mathrm{a}}\left(\gamma^{\prime} z_{\mathrm{w}} \cos ^{2} \theta P_{\mathrm{a}}^{-1}\right)^{b}}{\gamma_{\mathrm{sat}} z_{\mathrm{w}} \cos \alpha \sin \alpha}=F_{\mathrm{s} 1}. $ | (29) |
综上可知,该方法是在基于“顺坡曲面”失稳模式基础之上,考虑了膨胀土低应力下强度非线性特征,故称为基于幂函数非线性强度模型的“顺坡曲面”组合滑面法;当中段主滑区长度L2增大至无穷大时,还原为无限长斜坡稳定分析方法,当L2减小至零且幂函数非线性强度模型参数a=tan φ′、b=1时,可退化为基于库伦线性模型的圆弧滑面法.
3.5 基于三段式组合滑面的两参数搜索策略“顺坡曲面”组合滑面法与传统圆弧滑面法同属于刚体极限平衡法范畴,最危险滑面均需要搜索确定. 但滑面搜索是稳定分析中一项较为繁杂的工作,应该要有搜索策略.
3.5.1 建立三段组合式滑体参数与滑面圆心关系在坡长确定情况下,组合式滑体3个参数(L1、L2、L3)中仅有两个自由变量,通过建立上、下缘滑动范围L1和L3两参数与滑面圆心坐标的关系,确定“顺坡曲面”组合滑面的位置. 为简化搜索维数,假设下缘滑面过坡脚A点,且上下缘为“异心同径”圆弧,即上缘圆弧与下缘圆弧半径相等,Ru=Rd=R. 由此,可建立下式:
| $ \left\{ \begin{array}{l} \begin{array}{*{20}{l}} {{{\left( {{x_{{\rm{do}}}}} \right)}^2} + {{\left( {{y_{{\rm{do}}}}} \right)}^2} = {R^2},}\\ {{{\left( {{x_{{\rm{do}}}} - {x_B}} \right)}^2} + {{\left( {{y_{{\rm{do}}}} - {y_B}} \right)}^2} = {R^2},}\\ {\left( {{y_{{\rm{do}}}} - {y_B}} \right)/\left( {{x_{{\rm{do}}}} - {L_3}} \right) = - n,} \end{array}\\ \begin{array}{*{20}{l}} {{y_B} = {L_3}/n - {z_{\rm{w}}},}\\ {{x_C} = L - {L_1},}\\ {{x_{{\rm{uo}}}} = {x_{{\rm{do}}}} + {L_2},}\\ {{y_{{\rm{uo}}}} = {y_{{\rm{do}}}} + {L_2}\tan \alpha ,}\\ {L = {L_1} + {L_2} + {L_3}.} \end{array} \end{array} \right. $ | (30) |
由式(30)可知,8个方程中有10个未知数,只要给定任意两个未知数,方程(30)即可求解,下缘圆弧滑面和上缘圆弧滑面位置便可确定.
3.5.2 搜索策略步骤1 确定下缘挤压区起点B. 在包含强度差异土层界面与地表平面(x轴)交点位置,沿差异土层界面上下划分n1等分,每一个等分点对应的横坐标即为L3,且满足0 < L3 < L;
步骤2 确定上缘张拉区起点C. 沿差异土层界面向下划分n2等分,根据每一个等分点对应的横坐标xC便可计算出L1,且满足0 < xC≤L;同时,还要满足L1+L3≤L.
以步骤1确定的下缘挤压区起点作为搜索外循环,以步骤2确定的上缘张拉区起点为内循环,共计n1×n2搜索滑面,每次搜索滑面时即可确定三段组合式滑体的3个参数L1、L2、L3,按式(25)计算安全系数Fs.
可见,通过调整下缘滑体长度L3和上缘滑体L1两个参数,便可获得最危险滑面,这与传统圆弧滑面法搜索维数相同. 因此,上述搜索过程即为三段组合式滑体的两参数搜索策略.
4 算例分析文献[9]给出了南宁外环公路边坡膨胀土初始干密度ρd=1.7 g/cm3和ρd=1.8 g/cm3下(饱和重度分别为20.7 kN/m3和21.3 kN/m3)重塑膨胀土常规应力段强度参数c′分别为17 kPa和28.7 kPa,φ′分别为20.1°和19.3°,采用幂函数模型得出低应力段参数(a,b)分别为(0.56,0.72)和(0.64,0.65).
4.1 “顺坡平面”与“顺坡曲面”失稳模式对比图 8给出了膨胀土路堤“顺坡曲面”和“顺坡平面”失稳模式下,边坡浅层稳定安全系数Fs随坡高H的变化规律. 可见,前者Fs随高度H的增加呈现逐渐降低的规律,并以后者恒定不变的安全系数为渐近线,由方程式(29)可知,二者只有在边坡高度无穷大(即坡长无限长)时才获得一致的结果. 同时,初始干密度越小,安全系数也越低. 结果表明,ρd=1.7 g/cm3的膨胀土路堤边坡,在Fs=1.0时对应的膨胀土路堤临界高度为5.2 m,即超过该高度,路堤边坡将处于失稳状态,这与现场观察到的大量膨胀土边坡浅层破坏实例吻合.

|
图 8 Fs与H的关系(zw=1.0 m、n =1∶1.5) Fig. 8 Relation between Fs and H (zw=1.0 m, n=1∶1.5) |
基于膨胀土路堤边坡浅层“顺坡曲面”组合滑面法,给出了不同强度模型下Fs计算结果,如表 2所列. 可见,采用幂函数强度模型得出的Fs较库伦模型下的更低,原因是库伦模型采用的是常规应力段的抗剪强度参数(见图 4),有较高的c′和较低的φ′;幂函数模型获得的低应力下,c′小,而φ′大. 值得注意的是,φ′大不意味着摩擦强度高,因为边坡浅层浸水饱和后,体积膨胀致使密度减小,有效应力降低,且考虑饱和顺坡渗流时,坡面往下1.5 m深度内破裂面上σn′ < σcr′,即φ′大,但摩擦强度低.
| 表 2 Fs与zw的关系(H= 6.0 m、n =1∶1.5) Tab. 2 Relation between Fs and zw (H=6.0 m, n=1∶1.5) |
同时,随着入渗深度的增加,安全系数均呈现降低的规律.zw=1.5 m,ρd=1.8 g/cm3下的膨胀土路堤边坡稳定分析结果显示,库伦强度模型下获得的Fs=2.661高于幂函数模型下安全系数两倍以上,如表 2所列. 对于ρd=1.7 g/cm3,入渗深度zw超过1 m时,Fs < 1. 因此,对膨胀土边坡前期设计而言,可通过提高初始密实度、降低坡高或采取防渗措施等提高膨胀土边坡的浅层稳定性.
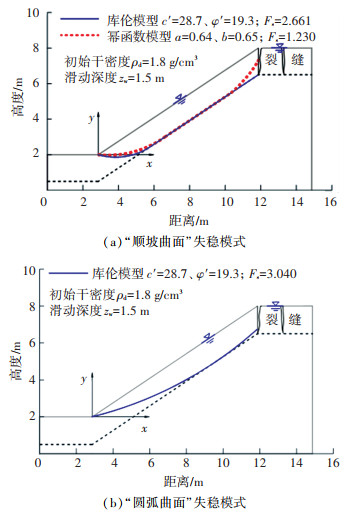
图 9(a)为计算所得危险滑面. 由图可知,“顺坡曲面”失稳模式下,库伦模型下最危险滑面基本位于幂函数模型对应最危险滑面的下方(除中段主滑区滑体部分重合外). 原因是采用常规应力段的库伦模型计算得出的c′值较大,边坡浅层稳定表现为以c′值控制为主,靠近表面土体的强度高,危险滑面尽可能向边坡内部远离坡面的位置延伸;幂函数模型重点反映低应力下强度非线性特征,边坡浅层黏聚强度和摩擦强度均较低. 因此,库伦模型上下缘滑动面整体位置略低于幂函数模型相应滑面位置.
|
图 9 失稳模式对比 Fig. 9 Comparison of failure modes |
为了与传统整体圆弧滑动面对比,利用方程(27),计算出了膨胀土路堤边坡库伦模型下的安全系数,如图 9(b)所示. 可知,传统稳定分析方法中,基于圆弧滑动破坏模式的瑞典法计算的Fs最低已成共识. 但计算结果显示,采用圆弧滑面破坏模式获得的Fs为3.040,高于幂函数强度模型下的“顺坡曲面”破坏模式,若采用常规应力下强度线性库伦模型的圆弧滑面法分析膨胀土路堤边坡浅层稳定安全系数,将严重高估边坡稳定性. 由此可见,采用与低应力状态相匹配的强度非线性幂函数模型的“顺坡曲面”失稳模式,是合理评价膨胀土路堤边坡浅层稳定性的关键要素.
5 结论针对膨胀土路堤边坡浅层溜坍破坏模式,探讨了膨胀土强度不同应力区段的差异性变化特征,分析了低应力水平及失稳模式对膨胀土路堤边坡浅层稳定性的影响,得出以下结论:
1) 基于数理统计原理的Chauvenet判别准则,提出了膨胀土低应力下强度非线性与常规应力下强度线性变化界限值σs′的确定方法. 当破裂面上法向应力σn′≥σcr′时,抗剪强度随σn′增加呈库伦线性增大的规律;当σn′ < σcr′时,抗剪强度随σn′的降低呈幂函数型非线性减小的规律. 据此,明确了膨胀土边坡浅层溜坍土体的强度处于低应力非线性段.
2) 基于“顺坡曲面”失稳破坏模式,考虑了降雨入渗引起的渗流作用,提出了能反映低应力下膨胀土强度非线性的膨胀土路堤边坡浅层稳定分析方法. 该方法在浅层滑体中段主滑区范围L2=0,且幂函数非线性强度模型参数a=tan φ′、b=1时,可退化为传统的基于库伦线性模型的圆弧滑面法.
3) 基于“顺坡曲面”组合滑面法分析表明,低应力下具有小黏聚力、大内摩擦角的幂函数模型所得滑动面相对较浅,符合因雨水入渗体积膨胀强度大幅衰减后的膨胀土边坡浅层失稳特征;膨胀土路堤边坡“顺坡曲面”失稳模式下,若采用常规应力下库伦线性模型的圆弧滑面法所得安全系数将明显偏大.
| [1] |
郑健龙. 公路膨胀土工程理论与技术[M]. 北京: 人民交通出版社, 2013. ZHENG Jianlong. Theory and technology for highway expansive soil engineering[M]. Beijing: China Communications Press, 2013. |
| [2] |
刘华强, 殷宗泽. 膨胀土边坡稳定分析方法研究[J]. 岩土力学, 2010, 31(5): 1545. LIU Huaqiang, YIN Zongze. Research on analytical method of stability of expansive soil slope[J]. Soil and Mechanics, 2010, 31(5): 1545. DOI:10.3969/j.issn.1000-7598.2010.05.033 |
| [3] |
武科, 赵闯, 张文, 等. 干湿循环作用下膨胀土表观胀缩变形特性[J]. 哈尔滨工业大学学报, 2016, 48(12): 121. WU Ke, ZHAO Chuang, ZHANG Wen, et al. Swelling-shrinking characteristics and irreversible deformation of expansive soil during wetting-drying cycles[J]. Journal of Harbin Institute of Technology, 2016, 48(12): 121. DOI:10.11918/j.issn.0367-6234.2016.12.017 |
| [4] |
杨和平, 唐咸远, 王兴正, 等. 有荷干湿循环条件下不同膨胀土抗剪强度基本特性[J]. 岩土力学, 2018, 39(7): 2311. YANG Heping, TANG Xianyuan, WANG Xingzheng, et al. Shear strength of expansive soils under wet-dry cycles with loading[J]. Soil and Mechanics, 2018, 39(7): 2311. |
| [5] |
周炳生, 王保田, 张海霞, 等. 基于整体刚体平衡法的膨胀土边坡稳定分析[J]. 岩土力学, 2016, 37(增刊2): 525. ZHOU Bingsheng, WANG Baotian, ZHANG Haixia, et al. Analysis of expansive soil slope stability based on whole rigid body equilibrium method[J]. Soil and Mechanics, 2016, 37(S2): 525. |
| [6] |
张良以, 陈铁林, 张顶立. 降雨诱发膨胀土边坡渐进破坏研究[J]. 岩土工程学报, 2019, 41(1): 70. ZHANG Liangyi, CHEN Tielin, ZHANG Dingli. Progressive failure of expansive soil slopes under rainfall[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(1): 70. |
| [7] |
LADE P V. The mechanics of surficial failure in soil slopes[J]. Engineering Geology, 2010, 114(1/2): 57. |
| [8] |
肖杰, 杨和平, 李晗峰, 等. 低应力条件下不同密度的南宁膨胀土抗剪强度试验[J]. 中国公路学报, 2013, 26(6): 15. XIAO Jie, YANG Heping, LI Hanfeng. Shear strength test of Nanning expansive soil with various dry densities and low stresses[J]. China Journal of Highway and Transport, 2013, 26(6): 15. DOI:10.3969/j.issn.1001-7372.2013.06.003 |
| [9] |
肖杰, 杨和平, 李晗峰, 等. 膨胀土边坡浅层破坏稳定性分析[J]. 交通运输工程学报, 2014, 14(2): 21. XIAO Jie, YANG Heping, LI Hanfeng, et al. Shallow failure stability analysis of expansive soil slope[J]. Journal of Traffic and Transportation Engineering, 2014, 14(2): 21. DOI:10.3969/j.issn.1671-1637.2014.02.005 |
| [10] |
包承纲. 南水北调中线工程膨胀土渠坡稳定问题及对策[J]. 人民长江, 2003, 34(5): 4. BAO Chenggang. Research on supervision and management of sewage outlet to the river in the Yangtze valley[J]. Yangtze River, 2003, 34(5): 4. DOI:10.3969/j.issn.1001-4179.2003.05.003 |
| [11] |
DAY R W, AXTEN G W. Surficial stability of compacted clay slopes[J]. Journal of Geotechnical Engineering, 1989, 115(4): 577. DOI:10.1061/(ASCE)0733-9410(1989)115:4(577) |
| [12] |
连继峰, 罗强, 蒋良潍, 等. 雨水软化下路基土质边坡失稳模式及判别阈值[J]. 岩石力学与工程学报, 2016, 35(8): 1638. LIAN Jifeng, LUO Qiang, JIANG Liangwei, et al. Failure modes and discriminating thresholds of soil subgrade slope due to rain softening[J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(8): 1638. |
| [13] |
中华人民共和国铁道部. 铁路工程土工试验规程: TB 10102—2010[S]. 北京: 中国铁道出版社, 2011 Ministry of Railways of the People's Republic of China. Code for soil test of railway engineering: TB 10102—2010[S]. Beijing: China Railway Press, 2011 |
| [14] |
盛骤, 谢式千, 潘承毅. 概率论与数理统计[M]. 4版. 北京: 高等教育出版社, 2008. SHENG Zhou, XIE Shiqian, PAN Chengyi. Probability and statistics[M]. 4th ed. Beijing: Higher Education Press, 2008. |
| [15] |
林丽芬, 肖化, 吴先球. 肖维勒准则和格拉布斯准则的比较[J]. 大学物理实验, 2012, 25(6): 86. LIN Lifen, XIAO Hua, WU Xianqiu. Comparison between Chauvenet's criterion and Grubbs criterion[J]. Physical Experiment of College, 2012, 25(6): 86. DOI:10.3969/j.issn.1007-2934.2012.06.028 |
| [16] |
李广信. 高等土力学[M]. 2版. 北京: 清华大学出版社, 2004. LI Guangxin. Advanced soil mechanics[M]. 2nd ed. Beijing: Tsinghua University Press, 2004. |
| [17] |
BURLAND J B. On the compressibility and shear strength of natural clays[J]. Geotechnique, 1990, 40(3): 329. DOI:10.1680/geot.1990.40.3.329 |
| [18] |
胡明鉴, 孔令伟, 郭爱国, 等. 基于强度分区的膨胀土路堤稳定性及土工格栅处治效果分析[J]. 岩土力学, 2007, 28(9): 1861. HU Mingjian, KONG Lingwei, GUO Aiguo, et al. Expansive soil embankment stability and geogrid treatment effect analysis with strength zoning method[J]. Soil and Mechanics, 2007, 28(9): 1861. DOI:10.3969/j.issn.1000-7598.2007.09.017 |
| [19] |
邱宽红, 林绍中, 黄斌. 基于DDA的膨胀土边坡破坏过程模拟[J]. 长江科学院院报, 2009, 26(11): 581. QIU Kuanhong, LIN Shaozhong, HUANG bin. Failure simulation of expansive soil slopes based on DDA[J]. Journal of Yangtze River Scientific Research Institute, 2009, 26(11): 581. |
| [20] |
姚海林, 郑少河, 李文斌, 等. 降雨入渗对非饱和膨胀土边坡稳定性影响的参数研究[J]. 岩石力学与工程学报, 2002, 21(7): 1034. YAO Hailin, ZHENG Shaohe, LI Wenbin, et al. Parametric study on the effect of rain infiltration on stability of unsaturated expansive soil slope[J]. Chinese Journal of Rock Mechanics and Engineering, 2002, 21(7): 1034. DOI:10.3321/j.issn:1000-6915.2002.07.019 |
| [21] |
JANBU N. Application of composite slip surfaces for stability analysis[C]// Proceedings of European Conference on Stability of Earth Slopes. Stockholm: [s.n.], 1954, 3: 43
|
| [22] |
FELLENIUS W. Calculation of the stability of earth dams[C]// Transactions of the 2nd Congress on Large Dams. Washington DC: [s.n.], 1936, 4: 445
|
| [23] |
BISHOP A W. Theuse of the slip circle in the stability analysis of earth slopes[J]. Geotechnique, 1955, 5(1): 5. |
| [24] |
MORGENSTERN N R, PRICE V E. The analysis of the stability of general slip surfaces[J]. Geotechnique, 1965, 5(1): 79. |
| [25] |
李广信, 张丙印, 于玉贞. 土力学[M]. 2版. 北京: 清华大学出版社, 2010. LI Guangxin, ZHANG Bingyin, YU Yuzhen. Soil mechanics[M]. 2nd ed. Beijing: Tsinghua University Press, 2010. |
 2021, Vol. 53
2021, Vol. 53


