2. 郑州大学 土木工程学院, 郑州 470001
2. School of Civil Engineering, Zhengzhou University, Zhengzhou 470001, China
智能网联车辆(connected and autonomous vehicles, CAV)可从微观车辆层面降低驾驶行为差异性,改善交通流特性,进而为相关交通问题的有效解决提供新途径[1]. 就目前来看,大规模CAV车辆实地真车测试的实施条件尚不成熟[2]. 因此,现阶段对CAV车辆交通流特性的研究已经成为交通流理论以及智能交通系统的研究热点[3-5],交通流稳定性是交通运营质量的内在属性,本文针对CAV混合交通流稳定性开展研究. 纵观国内外针对交通流稳定性分析的研究成果,跟驰模型稳定性解析方法众多,并已形成较为明确的结论[6],但是针对混合交通流稳定性解析的研究工作进展缓慢. Ward[7]应用李亚普诺夫稳定性方法推导了传统混合交通流稳定性解析方法,该稳定性分析方法逐渐被国内外研究学者推广至智能车辆混合交通流稳定性分析中[8-11],CAV可实时获取前车加速度信息,而该方法并不能用于基于前车加速度反馈的CAV混合交通流稳定性分析. 因此,针对基于前车加速度反馈的CAV混合交通流稳定性解析研究显得十分必要,但鲜有文献对该混合交通流稳定性解析方法开展研究. 因此,本文针对基于前车加速度反馈的CAV车辆与人工驾驶车辆构成的混合交通流,从跟驰模型的角度出发,从CAV比例与交通流平衡态速度两个方面建立该混合交通流稳定性的解析方法.
1 跟驰模型 1.1 人工驾驶模型对于人工驾驶跟驰模型而言,学者们提出了众多不同类型的模型,模型之间各有优劣,智能驾驶模型(intelligent driver model,IDM)模型[12]可较好反应智能网联环境下人工驾驶车辆的智能驾驶特性,是目前比较认可的智能网联环境下人工驾驶跟驰模型. 因此,选择IDM作为人工驾驶车辆跟驰模型,模型公式为
| $ \left\{\begin{array}{l} \dot{v}_{n}(t)=a\left[1-\left(\frac{v_{n}(t)}{v_{0}}\right)^{4}-\left(\frac{s_{1}}{h_{n}(t)-l}\right)^{2}\right], \\ s_{1}=s_{0}+v_{n}(t) T-\frac{v_{n}(t)\left(v_{n-1}(t)-v_{n}(t)\right)}{2 \sqrt{a b}} . \end{array}\right. $ | (1) |
式中:
目前针对CAV跟驰建模工作而言,不同的学者提出了不同的建模方式,然而尚没有形成统一明确的结论[4]. 相关研究表明[13],CAV跟驰模型可在IDM模型基础之上,通过前车反馈信息构成,而加速度反馈是目前普遍认为的前车反馈的基本必要信息. 因此,本文的CAV跟驰模型为
| $ \dot{v}_{n}(t)=a\left[1-\left(\frac{v_{n}(t)}{v_{0}}\right)^{4}-\left(\frac{s_{1}}{h_{n}(t)-l}\right)^{2}\right]+\dot{r} v_{n-1}(t). $ | (2) |
式中:r为前车加速度反馈系数,
基于传统驾驶车辆跟驰模型与CAV跟驰模型,应用控制领域的传递函数理论推导不同CAV比例下的混合交通流稳定性判别条件.
首先定义交通流速度扰动与车头间距扰动为
| $ \left\{\begin{array}{l} \tilde{v}_{n}(t)=v_{n}(t)-v_{\mathrm{e}}, \\ \tilde{h}_{n}(t)=h_{n}(t)-h_{\mathrm{e}}. \end{array}\right. $ | (3) |
式中:
应用一阶泰勒公式对人工驾驶车辆跟驰模型在交通流平衡态展开,并计算扰动传播传递函数,计算结果为
| $ F_{1}(s)=\frac{\sqrt{\frac{a}{b}} \frac{v_{\mathrm{e}}\left[1-\left(v_{\mathrm{e}} / v_{0}\right)^{4}\right]}{s_{0}+v_{\mathrm{e}} T} s+2 a \frac{\left[1-\left(v_{\mathrm{e}} / v_{0}\right)^{4}\right] \sqrt{1-\left(v_{\mathrm{e}} / v_{0}\right)^{4}}}{s_{0}+v_{\mathrm{e}} T}}{s^{2}+\left(\sqrt{\frac{a}{b}} \frac{v_{\mathrm{e}}\left[1-\left(v_{\mathrm{e}} / v_{0}\right)^{4}\right]}{s_{0}+v_{\mathrm{e}} T}+\frac{4 a {v_{\mathrm{e}}}^{3}}{v_{0}{ }^{4}}+\frac{2 a T\left[1-\left(v_{\mathrm{e}} / v_{0}\right)^{4}\right]}{s_{0}+v_{\mathrm{e}} T}\right) s+2 a \frac{\left[1-\left(v_{\mathrm{e}} / v_{0}\right)^{4}\right] \sqrt{1-\left(v_{\mathrm{e}} / v_{0}\right)^{4}}}{s_{0}+v_{\mathrm{e}} T}}. $ | (4) |
式中:F1(s)为人工驾驶扰动传递函数,s表示拉普拉斯域.
同理,计算CAV扰动传递函数,计算结果为
| $ F_{2}(s)=\frac{r s^{2}+\sqrt{\frac{a}{b}} \frac{v_{\mathrm{e}}\left[1-\left(v_{\mathrm{e}} / v_{0}\right)^{4}\right]}{s_{0}+v_{\mathrm{e}} T} s+2 a \frac{\left[1-\left(v_{\mathrm{e}} / v_{0}\right)^{4}\right] \sqrt{1-\left(v_{\mathrm{e}} / v_{0}\right)^{4}}}{s_{0}+v_{\mathrm{e}} T}}{s^{2}+\left(\sqrt{\frac{a}{b}} \frac{v_{\mathrm{e}}\left[1-\left(v_{\mathrm{e}} / v_{0}\right)^{4}\right]}{s_{0}+v_{\mathrm{e}} T}+\frac{4 a {v_{\mathrm{e}}}^{3}}{{v_{0}}^{4}}+\frac{2 a T\left[1-\left(v_{\mathrm{e}} / v_{0}\right)^{4}\right]}{s_{0}+v_{\mathrm{e}} T}\right) s+2 a \frac{\left[1-\left(v_{\mathrm{e}} / v_{0}\right)^{4}\right] \sqrt{1-\left(v_{\mathrm{e}} / v_{0}\right)^{4}}}{s_{0}+v_{\mathrm{e}} T}}. $ | (5) |
式中F2(s)为CAV扰动传递函数.
在混合车队中,假设共有N辆车,扰动在车队中的传播具有相邻车辆两两传播的特性,这可由各车辆扰动项传递函数的乘积进行表达,即
| $ G(s) = {({F_1}(s))^{Np}}{({F_2}(s))^{N(1 - p)}}. $ | (6) |
式中:G(s)为整体混合交通流扰动传递函数,p为CAV比例,1-p为人工驾驶比例.
令s=jω,将式(6)传递函数由拉普拉斯域转变至频率域,根据传递函数理论,得到不同CAV比例p时的混合交通流稳定性判别条件为
| $ \begin{array}{l} \|G(\mathrm{j} \omega)\|_{\infty}=\left\|\left(F_{1}(\mathrm{j} \omega)\right)^{p}\left(F_{2}(\mathrm{j} \omega)\right)^{(1-p)}\right\|_{\infty} \leqslant 1, \\ \forall \omega \geqslant 0 . \end{array} $ | (7) |
式中:‖·‖∞为传递函数幅频特性最大幅值,ω为角频率.
因此,当满足式(7)的判别条件时,混合交通流稳定,否则不稳定. 由式(4)、(5)与式(7)可以看出,不同CAV比例下的混合交通流稳定性由CAV比例p与交通流平衡态速度ve共同确定. 同时,当CAV比例p分别取值0或1时,式(7)中的混合交通流稳定性判别条件分别转化为同质人工驾驶交通流稳定性判别条件与同质CAV交通流稳定性判别条件.
3 稳定性解析结果 3.1 同质交通流稳定性将p=0或p=1分别代入式(7)计算同质人工驾驶交通流与CAV交通流稳定性解析判别条件,计算结果分别为
| $ \begin{array}{l} \frac{1}{2}\left(\frac{4 a {v_{\mathrm{e}}}^{3}}{v_{0}^{4}}+\frac{2 a T\left[1-\left(v_{\mathrm{e}} / v_{0}\right)^{4}\right]}{s_{0}+v_{\mathrm{e}} T}\right)^{2}+\left(\frac{4 a {v_{\mathrm{e}}}^{3}}{v_{0}^{4}}+\frac{2 a T\left[1-\left(v_{\mathrm{e}} / v_{0}\right)^{4}\right]}{s_{0}+v_{\mathrm{e}} T}\right) \sqrt{\frac{a}{b}} \frac{v_{\mathrm{e}}\left[1-\left(v_{\mathrm{e}} / v_{0}\right)^{4}\right]}{s_{0}+v_{\mathrm{e}} T}- \\ \ \ \ \ \ \ \ \ 2 a \frac{\left[1-\left(v_{\mathrm{e}} / v_{0}\right)^{4}\right] \sqrt{1-\left(v_{\mathrm{e}} / v_{0}\right)^{4}}}{s_{0}+v_{\mathrm{e}} T} \geqslant 0, \end{array} $ | (8) |
| $ \begin{array}{l} \frac{1}{2}\left(\frac{4 a {v_{\mathrm{e}}}^{3}}{{v_{0}}^{4}}+\frac{2 a T\left[1-\left(v_{\mathrm{e}} / v_{0}\right)^{4}\right]}{s_{0}+v_{\mathrm{e}} T}\right)^{2}+\left(\frac{4 a {v_{\mathrm{e}}}^{3}}{{v_{0}}^{4}}+\frac{2 a T\left[1-\left(v_{\mathrm{e}} / v_{0}\right)^{4}\right]}{s_{0}+v_{\mathrm{e}} T}\right) \sqrt{\frac{a}{b}} \frac{v_{\mathrm{e}}\left[1-\left(v_{\mathrm{e}} / v_{0}\right)^{4}\right]}{s_{0}+v_{\mathrm{e}} T}- \\ \ \ \ \ \ \ \ \ (1-r) 2 a \frac{\left[1-\left(v_{\mathrm{e}} / v_{0}\right)^{4}\right] \sqrt{1-\left(v_{\mathrm{e}} / v_{0}\right)^{4}}}{s_{0}+v_{\mathrm{e}} T} \geqslant 0. \end{array} $ | (9) |
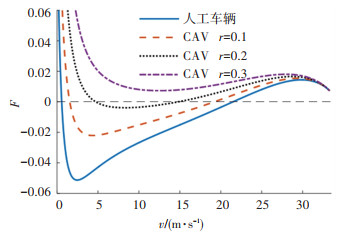
式(8)为同质人工驾驶交通流稳定性判别条件,式(9)为同质CAV交通流稳定性判别条件,可以看出,同质交通流稳定性仅与交通流平衡态速度ve相关. 用F统一表示人工驾驶与CAV交通流稳定性判别式(8)、(9)中的不等式左边项. 即F大于0,表示稳定,否则不稳定. 在自由流速度为0~33.3 m/s时,通过式(8)、(9)分别计算得到不同平衡态速度下人工车辆和CAV车辆的稳定性情况,如图 1所示.
|
图 1 同质交通流稳定性 Fig. 1 Stability of homogeneous traffic flow |
在图 1中,对CAV加速度反馈系数r进行参数敏感性分析,显示了r=0.1、r=0.2与r=0.3时的稳定性情况,为了便于观察曲线的稳定性情况,在平衡态速度为0 m/s附近限制了较大的纵坐标显示范围. 计算可知,人工车辆在0.6~21.4 m/s较大速度时不稳定,而CAV随着r的增大,不稳定的速度范围逐渐缩小. 当r=0.1时,CAV在1.6~19.2 m/s时不稳定;当r=0.2时,CAV在4.8~14.7 m/s时不稳定;当r增大至0.3时,可在自由流速度范围内均稳定.
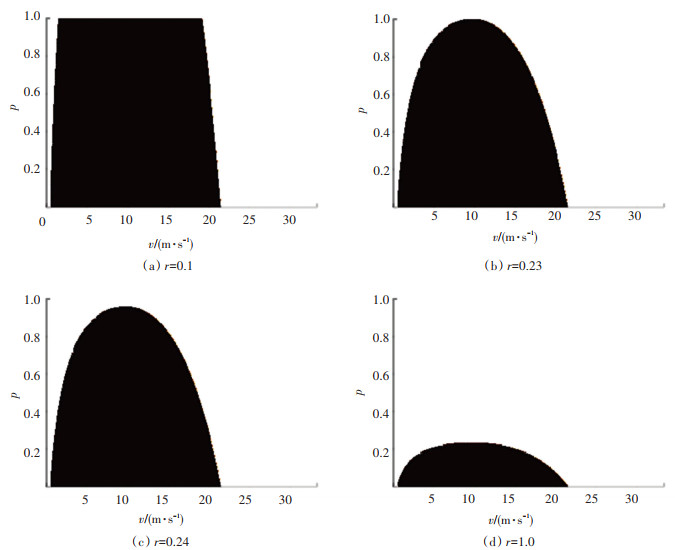
3.2 混合交通流稳定性依据混合交通流稳定性判别式(7),计算不同CAV比例、不同平衡态速度下的混合交通流稳定域,如图 2所示. 图 2给出了4种r特定取值时的稳定域情况,图中黑色包围的区域为不稳定区域,黑色外部的白色区域为稳定区域. 图 2中CAV比例为0时,黑色不稳定区域与白色稳定区域的速度边界值为人工车辆稳定与不稳定的速度边界值,由上述图 1的分析计算可知,该速度边界值分别为0.6、21.4 m/s. 图 2(a)中,CAV比例为1时对应的速度边界值为CAV在r=0.1时稳定与不稳定的速度边界值,该边界值分别为1.6、19.2 m/s. r取值越大,CAV不稳定的速度范围越小,当r取值增大至0.23时,CAV仅在9.7 m/s的平衡态速度处不稳定,如图 2(b)所示. 当r取值继续增大时,CAV可在自由流速度范围内稳定,如图 2(c)所示. 当r取最大值1时,最有利于稳定性,如图 2(d)所示.
|
图 2 混合交通流稳定域 Fig. 2 Stability regions of mixed traffic flow |
由图 2可以看出,CAV车辆不稳定时的速度范围在人工车辆不稳定速度范围以内,因此,在人工车辆稳定的速度范围,任意CAV比例时,混合交通流均稳定. 在人工车辆不稳定的速度范围,CAV比例越大,越有利于混合交通流转变为稳定状态. 此外,随着加速度反馈系数r的增大,混合交通流不稳定的区域逐渐缩小,在r=1时,可计算得到CAV比例达到0.23以上时,混合交通流在自由流速度范围内均稳定.
4 数值仿真 4.1 实验设计应用人工车辆和CAV车辆跟驰模型,基于数值仿真实验分析小扰动在不同CAV比例混合交通流中的传播情况. 依据上述稳定性解析结果,CAV跟驰模型的前车加速度反馈系数r在0~1之间取值越大,稳定性越好,为不失一般性,在仿真实验中取其中间值r=0.5. 相关研究[14]表明,交通流稳定性与车辆加减速过程中的驾驶舒适性存在定性的相关关系,因此,基于数值仿真实验,分析CAV对混合交通流驾驶舒适性的影响.
在仿真实验中,100辆车随机地分布在单车道道路上,人工车辆和CAV车辆的相对数量、位置均由事先设定的CAV比例随机确定. 混合车队在初始时刻以平衡态速度行驶,然后由头车产生小扰动打破车队平衡态,在扰动向车队上游传播的过程中,获得各车辆的速度变化情况以及驾驶舒适性. 根据上述稳定性解析结果,人工车辆在0.6~21.4 m/s时不稳定,为了仿真CAV对传统交通流不稳定的影响,选取车队初始平衡态速度为11 m/s进行数值仿真,并且头车以-0.5 m/s2的加速度减速2 s,形成小扰动[10]. 数值仿真实验基于MATLAB软件,仿真步长为0.01 s. 同时,选取文献[15]中基于国际ISO2631-1标准的驾驶舒适性指标评价小扰动传播过程中的驾驶舒适性. 舒适性指标计算公式为
| $ {\rm{CI}} = {\left[ {\frac{1}{m}\sum\limits_{i = 0}^m {a_i^2} } \right]^{1/2}}. $ | (10) |
式中:CI为舒适性指标,ai为统计得到的各车辆加速度值,m为加速度仿真值统计总量.
舒适性指标CI值越小,舒适性越好,具体详见文献[15]. 考虑到数值仿真中的随机性,各条件下的舒适性仿真实验均独立重复10次,并取均值作为该条件下的舒适性仿真结果.
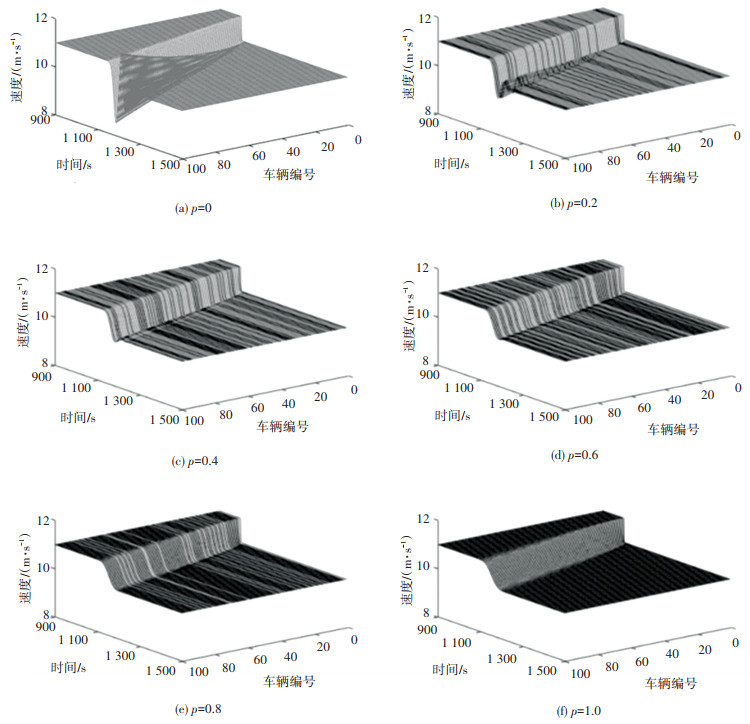
4.2 仿真结果基于上述数值仿真实验设计,小扰动传播过程中混合交通流稳定性仿真结果如图 3所示,舒适性仿真结果见表 1.
|
图 3 稳定性仿真结果 Fig. 3 Simulation results of stability |
| 表 1 驾驶舒适性仿真结果 Tab. 1 Simulation results of driving comfort |
在图 3中,灰色曲线和黑色曲线分别表示人工车辆和CAV车辆在小扰动传播过程中的速度变化曲线. 从图 3可以看出,全部人工驾驶车辆交通流(图 3(a))时,头车的小扰动会随着时间的推移,从头车向上游车辆逐渐传播,并且得到放大,即上游车辆将该扰动放大造成交通流不稳定.而随着CAV比例的增加(图 3(b)、3(c)、3(d)),头车产生的小扰动在向上游车辆传播时,仍然会被逐渐放大,形成不稳定车流,但扰动被放大的幅值明显小于全部人工驾驶车辆情况(图 3(a)). 当CAV比例增大到一定程度时(图 3(e)、3(f)),头车产生的小扰动在向上游车辆传播时,并没有被放大,而得到有效抑制,即交通流变为稳定状态. 因此,CAV比例的增加可有效提升交通流的不稳定性,最终使得混合交通流转变为稳定状态,这与上述稳定性解析结果相一致.
在表 1的舒适性仿真结果中,CI指标降低率是指不同CAV比例时的CI仿真结果相对于CAV比例为0时仿真结果的降低百分比. 如前所述,CI指标值越小,舒适性越好,因此由表 1可知,CAV比例的增加可逐步提升驾驶舒适性,基于上述小扰动数值仿真实验,100%CAV交通流相比于100%人工驾驶交通流的舒适性指标值可降低约74.76%. 此外,在仿真实验中通过改变小扰动类型、大小以及初始平衡态速度进行多次仿真实验,发现CAV车辆有利于混合交通流稳定性与驾驶舒适性提升的定性化结论不受影响.
5 结论1) 针对基于前车加速度反馈的CAV车辆与人工车辆混合交通流,建立了CAV混合交通流稳定性解析方法,理论推导得到不同CAV比例、不同平衡态速度下混合交通流稳定性判别条件,可理论计算关于CAV比例与交通流平衡态速度的混合交通流稳定域.
2) 理论解析计算结果表明,关于CAV比例与平衡态速度的混合交通流稳定域可分析CAV混合交通流稳定性情况;在人工车辆稳定的速度范围,不同CAV比例时的混合交通流均稳定;人工车辆不稳定的速度范围,CAV比例的增加有利于稳定性的提升;CAV跟驰模型前车加速度反馈系数越大,混合交通流稳定域越大,加速度反馈系数取值为1,且CAV比例达到0.23以上时,混合交通流在自由流速度范围内均稳定. 数值仿真结果表明,CAV车辆有利于抑制小扰动向车队上游传播过程中逐渐被放大的趋势,且CAV比例的增加可定性地逐步提升驾驶舒适性.
3) 建立的CAV混合交通流稳定性解析方法可同样扩展至其他跟驰模型,可为混有前车加速度反馈的CAV混合交通流稳定解析提供直接的理论依据,同时为未来大规模CAV车辆实地测试的实施提供理论参考. 智能网联环境下车联网技术的进一步发展将最终实现多车互联、协同行驶,因此多车协作下的混合交通流稳定性解析是下一步的研究内容.
| [1] |
秦严严, 王昊, 王炜, 等. 自适应巡航控制车辆跟驰模型综述[J]. 交通运输工程学报, 2017, 17(3): 121. QIN Yanyan, WANG Hao, WANG Wei, et al. Review of car-following models of adaptive cruise control[J]. Journal of Traffic and Transportation Engineering, 2017, 17(3): 121. DOI:10.3969/j.issn.1671-1637.2017.03.013 |
| [2] |
MAHMASSANI H S. 50th anniversary invited article—autonomous vehicles and connected vehicle systems: flow and operations considerations[J]. Transportation Science, 2016, 50(4): 1140. DOI:10.1287/trsc.2016.0712 |
| [3] |
MILANES V, SHLADOVER S E, SPRING J, et al. Cooperative adaptive cruise control in real traffic situations[J]. IEEE Transactions on Intelligent Transportation Systems, 2014, 15(1): 296. DOI:10.1109/TITS.2013.2278494 |
| [4] |
MILANES V, SHLADOVER S E. Modeling cooperative and autonomous adaptive cruise control dynamic responses using experimental data[J]. Transportation Research Part C: Emerging Technologies, 2014, 48: 285. DOI:10.1016/j.trc.2014.09.001 |
| [5] |
CHEN D, AHN S, CHITTURI M, et al. Truck platooning on uphill grades under cooperative adaptive cruise control (CACC)[J]. Transportation Research Part C: Emerging Technologies, 2018, 94: 50. DOI:10.1016/j.trc.2017.08.025 |
| [6] |
SAU J, MONTEIL J, BILLOT R, et al. The root locus method: application to linear stability analysis and design of cooperative car-following models[J]. Transportmetrica B: Transport Dynamics, 2014, 2(1): 60. DOI:10.1080/21680566.2014.893416 |
| [7] |
WARD J A. Heterogeneity, lane-changing and instability in traffic: a mathematical approach[D]. Bristol: University of Bristol, 2009
|
| [8] |
TALEBPOUR A, MAHMASSANI H S. Influence of connected and autonomous vehicles on traffic flow stability and throughput[J]. Transportation Research Part C: Emerging Technologies, 2016, 71: 143. DOI:10.1016/j.trc.2016.07.007 |
| [9] |
秦严严, 张健, 陈凌志, 等. 手动-自动驾驶混合交通流元胞传输模型[J]. 交通运输工程学报, 2020, 20(2): 229. QIN Yanyan, ZHANG Jian, CHEN Lingzhi, et al. Cell transportation model of mixed traffic flow of manual-automated driving[J]. Journal of Traffic and Transportation Engineering, 2020, 20(2): 229. |
| [10] |
WANG H, QIN Y, WANG W, et al. Stability of CACC-manual heterogeneous vehicular flow with partial CACC performance degrading[J]. Transportmetrica B: Transport Dynamics, 2019, 7(1): 788. DOI:10.1080/21680566.2018.1517058 |
| [11] |
NGODUY D. Analytical studies on the instabilities of heterogeneous intelligent traffic flow[J]. Communications in Nonlinear Science and Numerical Simulation, 2013, 18(10): 2699. DOI:10.1016/j.cnsns.2013.02.018 |
| [12] |
TREIBER M, HENNECKE A, HELBING D. Congested traffic states in empirical observations and microscopic simulations[J]. Physical Review E, 2000, 62(2): 1805. DOI:10.1103/PhysRevE.62.1805 |
| [13] |
QIN Y, WANG H. Analytical framework of string stability of connected and autonomous platoons with electronic throttle angle feedback[J]. Transportmetrica A: Transport Science, 2021, 17(1): 59. DOI:10.1080/23249935.2018.1518964 |
| [14] |
秦严严, 王昊, 王炜, 等. 混有CACC车辆和ACC车辆的混合交通流驾驶舒适性[J]. 哈尔滨工业大学学报, 2017, 49(9): 103. QIN Yanyan, WANG Hao, WANG Wei, et al. Driving comfort of traffic flow mixed with cooperative adaptive cruise control vehicles and adaptive cruise control vehicles[J]. Journal of Harbin Institute of Technology, 2017, 49(9): 103. |
| [15] |
PADDAN G S, GRIFFIN M J. Evaluation of whole-body vibration in vehicles[J]. Journal of Sound and Vibration, 2002, 253(1): 195. DOI:10.1006/jsvi.2001.4256 |
 2021, Vol. 53
2021, Vol. 53


