自锚式悬索桥由于其独特的造型、不需要庞大的重力式锚或复杂的隧道锚,对地质地形条件的适应性强,在一般跨径悬索桥中应用越来越广泛[1]. 自锚式悬索桥吊索张拉过程即为体系转换过程. 目前通常采用吊索的无应力状态控制法建立有限元模型对其进行分析、计算. 此方法在目标成桥状态已确定的情况下,计算较为简便、精度较高. 但在结构体系的设计阶段,目标成桥状态尚未完全确定,须根据其受力、施工等多方面综合进行优化、调整. 此时,若采用无应力状态法计算,则需要建立大量有限元模型,分别对各假定目标成桥状态进行体系转换分析,降低了计算效率.
自锚式悬索桥主要受力结构依然是主缆,主缆的受力与线型变化是主缆、吊索、加劲梁三者综合作用的体现. 因此,在体系转换过程中可通过对主缆进行计算得到其各工况下的内力情况,再根据主缆内力状态与全桥内力状态的一一对应关系,转而计算出各工况下相应吊索内力状态,得到吊索张拉力.
为此,本文将自锚式悬索桥整体结构简化为其主缆结构进行近似分析、计算,建立一种以主缆内力状态控制为主的方法计算自锚式悬索桥的体系转换过程. 如此简化,可反映出结构状态的变化情况,得到满足精度要求的计算结果,同时提高了计算效率.
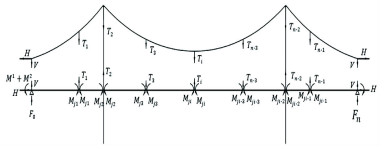
1 结构状态分析自锚式悬索桥作为高次超静定结构,直接计算存在一定困难. 考虑缆-梁联合作用的恒载状态计算方法,将自锚式悬索桥拆开为主缆和加劲梁两部分,对两者进行独立分析. 将自锚式悬索桥简化为图 1所示力学模型[2].
|
图 1 计算模型简化图 Fig. 1 Simplified diagram of calculation model |
自锚式悬索桥一般采用“先梁后缆”的方式进行施工,对于一般跨径自锚式悬索桥,通常需要搭设支架对已施工完成的加劲梁进行支撑.
在体系转换过程中,尤其对于混凝土自锚式悬索桥,由于其加劲梁刚度较大,受到支架的支撑作用(支架预压充分,变形很小),加劲梁的竖向变形较小. 因此,在近似计算中,可假定在自锚式悬索桥体系转换过程中加劲梁不发生变形.
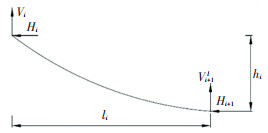
1.2 主缆受力分析如图 2所示,取主缆吊索间一段悬索,单位缆长重为q. 由于实际中,自锚式悬索桥主缆缆长变化量非常小,较主缆全长可忽略不计. 吊索间任一索段都必须满足[3]:
|
图 2 索形力学模型简化图 Fig. 2 Simplified diagram of cable-shaped mechanical model |
| $ l_{i}=\frac{H_{i}}{q}\left(\operatorname{sh}^{-1} \frac{V_{i}}{H_{i}}-\operatorname{sh}^{-1} \frac{V_{i}-q\ s_{i}}{H_{i}}\right) , $ | (1) |
| $ h_{i}=\frac{H_{i}}{q}\left(\sqrt{1+\left(\frac{V_{i}}{H_{i}}\right)^{2}}-\sqrt{1+\left(\frac{V_{i}-q\ s_{i}}{H_{i}}\right)^{2}}\right) . $ | (2) |
式中:li为i号梁段吊索间距,hi为i号梁段主缆吊点高差,si为号梁段主缆无应力长度.
对仅有垂直吊杆的情况时,
| $ \left\{\begin{array}{l} V_{i+1}{ }^{l}=V_{i}-q\ s_{i} ,\\ V_{i+1}{ }^{r}=V_{i}-q\ s_{i}-T_{i+1}. \end{array}\right. $ | (3) |
式中Ti+1为i+1号吊索索力.
结合自锚式悬索桥
对于图 2所示主缆节段有
| $ {V_i} = \frac{{q{\kern 1pt} {s_i}}}{2} + H\sqrt {{{\left( {\frac{{{s_i}}}{{{l_i}}}} \right)}^2} - 1} . $ | (4) |
将主缆在其各吊点处划分为多个主缆节段,各节段间通过其水平及竖向分力相互联系. 如此划分,各主缆节段均分别满足
上述方法,即采用多个直杆单元来模拟主缆,确定好主缆线型以及主缆节段的数量,确保计算精度满足要求.
2 基于主缆状态的分析方法自锚式悬索桥吊索张拉一次到位最为理想,但在实际施工过程中,受诸多因素限制,某些吊索需要分多次才能将其张拉到位[4-5].
对于每个施工阶段,吊索张拉存在以下4种情况:1)未张拉(吊索索力Ti=0);2)一次性张拉到位;3)加接长杆,张拉到指定索力;4)加接长杆,张拉到位.
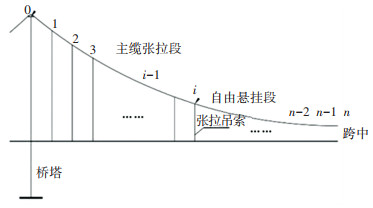
以主跨吊索张拉为例,取如图 3所示结构,并规定吊索张拉顺序从桥塔至跨中依次进行.
|
图 3 主跨吊索张拉过程示意图 Fig. 3 Schematic of main span cable tension process |
假设,1至i-1号吊索均已张拉到位,现对i号吊索进行张拉,计算张拉力.
2.1 求解思路根据结构对称性,取主跨一半结构进行分析. 如图 3所示,由于自锚式悬索桥各主缆节段可通过相应的水平分力及竖向分力相互联系起来,因此,在桥塔塔顶以及主缆吊点i处添加约束使i处的水平及竖向分力与目标状态相同,则吊点i之前的所有主缆节段内力状态均与目标状态相同(不考虑加劲梁影响)[6-8]:1)0~i节段,由于塔顶以及吊点i处约束的存在,可使此部分已张拉完成的主缆节段处于其相应的目标状态,称之为主缆张拉完成段. 2)i~n节段,此部分主缆节段相应吊索尚未张拉,处于自由悬挂状态,称之为主缆自由悬挂段.
将塔顶与吊点i处约束释放,主缆张拉完成段及自由悬挂段将会自由变形,达到新的平衡,其主缆内力状态分别从相应的目标状态、自由悬挂状态转换至平衡状态,该平衡状态即为体系转换完成后的主缆所对应的内力状态.
通过计算平衡状态下各主缆节段的竖向分力,由式(3)计算可得体系转换完成后各吊索的索力.
2.2 求解关键步骤分析根据结构对称性,将主缆分为半主跨及边跨两部分,分别进行讨论(仅释放图 3中吊点i处约束).
令i号吊索进行张拉完成后主缆水平分力为H′、竖向分力为Vj′. 由式(4),对任意主缆节段j~j+1,有
| $ {l_{j}}^{\prime}=\frac{H^{\prime} \ s_{j}}{\sqrt{\left({V_{j}}^{\prime}-\frac{q s_{j}}{2}\right)^{2}+H^{\prime 2}}} . $ | (5) |
对式(5)中主缆节段竖向分力Vj′的讨论:
1) j∈[i, n](即主缆j节段处于主缆自由悬挂段),根据对称性可得,Vn′=0, 故有
| $ {V_j}^\prime = q{\kern 1pt} {s_{j - n}}. $ |
2) j∈[0, i](即主缆j节段处于主缆张拉段),该主缆节段是由相应主缆目标状态转换而来,其水平分力、竖向分力分别由初始目标状态的H、Vj转换为H′、Vj′.
各主缆节段通过直杆单元模拟,根据能量原理,各主缆节段在外力作用下发生变形,同时外力作用点亦随之产生相应的位移,不考虑变形过程中伴随产生的能量损失,外力所作的功全部被主缆节段吸收. 因此,外力所做的功应等于该主缆节段应变能,即
| $ {V_\varepsilon } = W, $ | (6) |
假设一个主缆水平分力H′.
以i-1~i节段为例,如图 4所示,释放i号吊点处的强迫位移约束,在此过程中,

|
图 4 约束释放前后主缆节段变化 Fig. 4 Change of main cable segments before and after restraint release |
| $ W = {W_V} + {W_H} + {W_G}. $ | (7) |
式中:WV为竖向分力作功,WH为水平分力作功,WG为重力作功.
从而可求得该节段中水平分力H′所对应的竖向分力Vj′. 通过式(5)求得H′、Vj′对应的各段主缆节段吊点间距lj′.
主缆的变形协调条件为
| $ L = \sum {{l_j}^\prime } , $ | (8) |
式中L为主跨半跨径.
若H′满足变形协调条件式(8),则假设的H′即为所求,为主缆节段转换后的水平分力. 将上述所求各主缆节段H′、Vj′代入式(3),即可求得各吊索索力:
| $ {T_i} = {V_{i - 1}} - {V_i} - q{\kern 1pt} {s_{i - 1}}, $ | (9) |
边跨吊索的张拉参照主跨进行,在此不再赘述.
2.3 塔顶水平位移计算为了防止桥塔受到过大不平衡水平分力的作用,需根据具体边、中跨主缆水平分力的大小对主缆鞍座进行顶推,得到合理的鞍座顶推量[9-10].
假定目标状态主缆的主跨半跨径、边跨跨径分别为LZ、LB.在计算中,预设体系转换完成后主缆鞍座偏位值a,此时主缆主跨半跨径、边跨跨径分别为LZ+a、LB-a,代入式(5)~(7),可分别求得考虑鞍座偏位后的主跨与边跨主缆水平分力,并求得主缆鞍座处不平衡水平分力,此部分不平衡水平力应由桥塔承受,因此将主缆鞍座处计算所得的不平衡水平分力以及相应竖向分力提取出来施加于桥塔结构上,计算得到主缆鞍座偏位值a所对应的桥塔内力状态及桥塔水平偏位b. 若桥塔内力符合设计要求,则鞍座预偏值a满足要求,根据鞍座与桥塔的变形协调条件鞍座顶推值a-b.
2.4 二次张拉当2.2节中计算所得的吊索张拉力过大,超出了吊索可以承受的范围时,很难将其一次性张拉到位,需先将该吊索张拉至一指定索力,待后面吊索张拉后进行二次张拉,使之张拉到位[11-12]. 求解方法与2.2节中所述方法类似,但在计算中由于存在某些主缆节段尚未张拉到位,对于这些主缆节段在用能量法求解时,不能利用其最终目标状态进行计算,须以前一工况为基础,对计算结果进行修正.
2.5 计算流程图具体流程图见图 5. 上述求解思路亦可直接与有限元方法结合,建立相应工况的主缆模型,对计算结果进行迭代修正,提高计算精度与计算效率.

|
图 5 计算流程图 Fig. 5 Calculation flow chart |
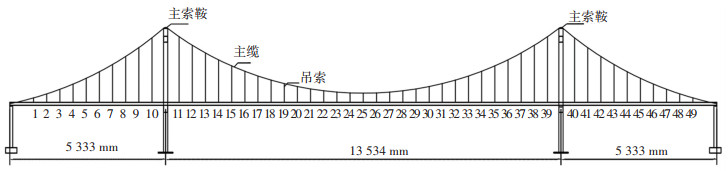
本工程实例数据源于桃花峪黄河大桥全桥模型试验,如图 6所示[13-14]. 试验模型由两根主缆、58根吊索、加劲梁、加劲梁锚固端、索塔和临时墩以及静动力测试系统构成. 全桥模型总长为24.2 m,宽为1.3 m,北索塔高为4.52 m,南索塔高为4.6 m,主缆横向间距为1.2 m,吊索纵向间为距0.45 m. 全桥模型的几何缩尺比为1∶30,模型各部分(除桥塔外)均采用与实桥相同弹性模量和泊松比的材料. 在综合考虑了模型承载力和试验条件等因素的情况下,拟定力的缩尺比例为1∶1. 吊索张拉顺序是从桥塔向两侧开始逐根对称张拉. 吊索编号如图 7所示.

|
图 6 桃花峪黄河大桥全桥模型试验示意 Fig. 6 Model test of Taohuayu Yellow River Bridge |
|
图 7 吊索编号示意图 Fig. 7 Numbering of cables |
本试验自锚式悬索桥模型,跨径布置:5 333.5 mm+13 533 mm+5 333.5 mm. 主缆选用16根直径为3 mm的钢丝,截面面积为117.78 mm2,弹性模量E=1.95×105 MPa. 吊索选用1根直径为4 mm细钢丝,保证与原桥抗拉刚度一致. 主梁采用Q345D钢材,截面积为0.002 51 m2,竖弯惯性矩为4.631×10-6 m4,扭转惯性矩为1.214×10-5 m4.
一期恒载的配重包括主梁的配重和主缆的配重,经计算,模型非锚固段主梁一期配重约为703.4 kg/m,试验中采用集中力模拟均布力的方式均匀作用于主梁分段的节点上. 单根主缆需配重6.993 kN,约为26.96 kg/m;索夹的配重约为2.0 kg,通过在主缆上穿挂圆柱块施加荷载.
二期恒载的配重采用在模型梁顶面摊铺混凝土块的方式. 经计算,模型主梁二期恒载配重约为175.33 kg/m.
3.3 目标成桥状态确定以主跨为例,由于主跨对称,故取主跨一半结构进行分析. 目标成桥状态主缆水平分力H=32 867.8 N,吊索索力及分布情况见表 1.
| 表 1 目标成桥状态吊索索力及分布情况 Tab. 1 Cableforce and distribution of suspension cables in target completion state |
令主跨吊索张拉顺序为11→25. 按如图 5所示计算流程中所述步骤计算,即可得到该工况吊索张拉完成后主缆的状态.
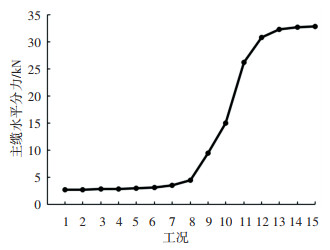
3.4.1 主缆受力状态在自锚式悬索桥整个吊索张拉的过程中,主缆水平分力变化如图 8所示.
|
图 8 主缆水平分力变化示意图 Fig. 8 Horizontal component change of main cable |
由图 8可得,主缆水平分力会随着各吊索的张拉而逐渐增大. 在吊索张拉的初期变化均较为平缓. 从工况8开始,主缆水平分力随着之后吊索的张拉迅速增大,直至13号吊索张拉完成后,主缆水平分力趋于稳定. 这是由于主缆在体系转换过程中从分别经历了松弛状态(工况1~8)、过度状态(工况8~12)、紧绷状态(工况12~15).
松弛状态(工况1~8):主缆应力水平较低、刚度小、柔性大,对内力的变化不敏感. 过度状态(工况8~12):此状态下主缆水平分力随吊索张拉几乎呈线型增大(类似弹性阶段). 紧绷状态(工况12~15):当吊索张拉到一定程度后,主缆内力维持在较高水平,此时主缆水平分力增加速度明显放缓趋于平衡状态(类似屈服阶段).
3.4.2 吊索索力根据主缆水平分力的变化情况,取12号、19号吊索索力值变化情况进行分析. 通过计算值与试验值的对比,发现两者趋势一致,说明上述计算方法准确、有效. 张拉较早的吊索(如12号吊索),索力主要受主缆水平分力的影响,其变化趋势与主缆水平分力变化一致,如图 9(a)所示. 随着体系转换的进行,吊索张拉力逐根增大.

|
图 9 12、19号吊索索力变化 Fig. 9 Cable force changes of cables No.12 and No.19 |
当吊索张拉至主跨跨径的1/4至3/8这一区域时(如19号吊索),其所需的吊索初始张拉力较大,如图 9(b)所示. 这是由于主缆由松弛状态逐步过渡到紧绷状态,这一过程中需要吸收大量能量,其内力迅速增大,需要较大的吊索初始张拉力. 随着后续各吊索的张拉,该吊索逐渐变化至成桥索力.
随着体系转换的进一步进行, 对于张拉较晚的吊索,其初始张拉力与成桥索力基本一致,此时,主缆处于紧绷状态,主缆内力状态趋于稳定,吊索张拉力亦随之趋于成桥状态.
各吊索张拉力见表 2,其中由于工况10~13吊索分两次张拉到位,在吊索第1次张拉时的吊索力是根据实际情况预设的,可假设试验预设值与计算预设值相等. 通过对比计算结果满足精度要求.
| 表 2 吊索初拉力 Tab. 2 Preliminary tension of cable |
综上所述,此方法以分析吊索张拉过程中主缆的内力状态变化为核心,计算得到各主缆节段在吊索张拉过程中的内力、线型情况,通过各主缆节段竖向不平衡分力计算得到相应吊索索力,计算精度满足要求.
4 结论1) 自锚式悬索桥基于主缆状态的吊索力转换分析方法,以分析、研究主缆在吊索张拉过程中的状态为核心,可对自锚式悬索桥体系转换过程进行近似计算、求解.
2) 所述方法无需依赖于上一阶段的效应状态,可方便、快捷的分析吊索张拉中任意指定工况的各种效应.
3) 通过工程实例将所述方法的计算结果与试验结果进行对比,结果表明本文计算精度满足要求.
4) 此方法计算方便简洁,适用于一般跨径自锚式悬索桥的体系转换分析以及结构设计分析,对结构设计、优化具有一定的指导作用.
| [1] |
张哲. 混凝土自锚式悬索桥[M]. 北京: 人民交通出版社, 2003. ZHANG Zhe. Concrete self-anchored suspension bridge[M]. Beijing: China Communications Press, 2003. |
| [2] |
王邵锐, 周志祥, 高艳梅, 等. 考虑缆-梁联合作用的自锚式悬索桥恒载状态计算方法研究[J]. 土木工程学报, 2015, 48(8): 70. WANG Shaorui, ZHOU Zhixiang, GAO Yanmei, et al. Study on the calculation method of the dead load state for the self-anchored suspension bridge considering the joint action of cable-stiffening girder[J]. China Civil Engineering Journal, 2015, 48(8): 70. |
| [3] |
项海帆, 张士铎, 杜国华, 等. 高等桥梁结构理论[M]. 2版. 北京: 人民交通出版社, 2013. XIANG Haifan, ZHANG Shiduo, DU Guohua, et al. Structural theory of higher bridges[M]. 2nd ed. Beijing: China Communications Press, 2013. |
| [4] |
李传习, 刘光栋, 柯红军. 悬索桥主缆系统数值解析法计算的一种收敛算法[J]. 工程力学, 2008, 25(7): 66. LI Chuanxi, LIU Guangdong, KE Hongjun. A convergent algorithm for numerical-analytic method of calculating main cable system of suspension bridge[J]. Engineering Mechanics, 2008, 25(7): 66. |
| [5] |
唐茂林, 强士中, 沈锐利. 悬索桥成桥主缆线形计算的悬链线法[J]. 铁道学报, 2003, 25(1): 87. TANG Maolin, QIANG Shizhong, SHEN Ruili. Segmental catenary method of calculating the cable curve of suspension bridge[J]. Journal of the China Railway Society, 2003, 25(1): 87. DOI:10.3321/j.issn:1001-8360.2003.01.018 |
| [6] |
黄振. 自锚式悬索桥斜拉扣挂施工法体系转换关键技术研究[D]. 成都: 西南交通大学, 2017 HUANG Zhen. Key technologies for system conversion of cable-stayed and buckling construction method for self-anchored suspension bridge[D]. Chengdu: Southwest Jiaotong University, 2017 |
| [7] |
OCHSENDORF J A, BILLINGTON D P. Self-anchored suspension bridges[J]. Journal of Bridge Engineering, 1999, 4(3): 151. DOI:10.1061/(ASCE)1084-0702(1999)4:3(151) |
| [8] |
刘厚军, 刘钊. 自锚式悬索桥吊索张力及主缆线形的设计研究[J]. 土木工程学报, 2008, 41(3): 79. LIU Houjun, LIU Zhao. Design of hanger tension and cable configuration for self-anchored suspension bridges[J]. China Civil Engineering Journal, 2008, 41(3): 79. DOI:10.3321/j.issn:1000-131X.2008.03.013 |
| [9] |
SUN J, MANZANAREZ R, NADER M. Suspension cable design of the New San Francisco-Oakland Bay Bridge[J]. Journal of Bridge Engineering, 2004, 9(1): 101. DOI:10.1061/(ASCE)1084-0702(2004)9:1(101) |
| [10] |
FORSBERG T. Multi-span suspension bridges[J]. International Journal of Steel Structures, 2001, 11(1): 63. |
| [11] |
HARICHANDRAN R S, HAWWARI A, SWEIDAN B N. Response of long-span bridges to spatially varying ground motion[J]. Journal of Structural Engineering, 1996, 122(5): 476. DOI:10.1061/(ASCE)0733-9445(1996)122:5(476) |
| [12] |
YAMAMURA N, TANAKA H. Response analysis of flexible MDF systems for multiple support Seismic excitations[J]. Earthquake Engineering & Structural (Dynamics), 1990, 19(3): 345. |
| [13] |
王桢. 超大跨径自锚式悬索桥几何非线性行为理论与试验性能研究[D]. 重庆: 重庆交通大学, 2013 WANG Zhen. Theoretical and experimental study on geometric nonlinear behavior of super-long span self-anchored suspension bridge[D]. Chongqing: Chongqing Jiaotong University, 2013 |
| [14] |
牛登辉, 周志祥, 吴海军, 等. 自锚式悬索桥体系转换过程的无应力状态控制法[J]. 重庆交通大学学报(自然科学版), 2014, 33(1): 21. NIU Denghui, ZHOU Zhixiang, WU Haijun, et al. Control method of stress-free status in transition process of structural system for self-anchored suspension bridge[J]. Journal of Chongqing Jiaotong University (Natural Science), 2014, 33(1): 21. |
 2021, Vol. 53
2021, Vol. 53


