2. 内蒙古自治区桥梁检测与维修加固工程技术研究中心,呼和浩特 010070;
3. 青岛理工大学 土木工程学院, 山东 青岛 266033
2. Inner Mongolia Engineering Research Center of Testing and Strengthening for Bridges, Hohhot 010070, China;
3. School of Civil Engineering, Qingdao University of Technology, Qingdao 266033, Shandong, China
CFRP具有重量轻、强度高、易于加工成形、便于施工、耐腐蚀等优点,广泛用于混凝土结构及钢结构的加固补强工程中[1-2]. 黏贴CFRP加固钢结构技术通过胶粘剂将CFRP片材与钢材连接成一体共同受力.该技术钢材不需要开孔或焊接,避免了焊接连接引起的焊接残余应力或栓接连接导致的截面削弱[3]. CFRP与钢材之间的黏结界面是整个加固体系的薄弱环节,其黏结性能是加固成功的关键,这方面学者们已经开展了大量卓有成效的试验研究[4-6]和理论分析[7-8],包括界面黏结失效形式、黏结滑移本构关系、极限承载力计算方法和数值模拟分析等.在长期荷载作用下,结构加固工程中常用的胶粘剂表现出黏弹性特性[9],既有固体的弹性又有流体的黏性. 胶粘剂随时间而变化的变形过程,主要表现为蠕变和应力松弛. 胶粘剂的蠕变变形会导致加固结构界面发生内力重分布[10],致使黏结界面发生蠕变损伤,这种损伤会影响黏结界面的黏结性能[3, 11]. 在CFRP加固体系中若要明确胶粘剂的黏弹性特性对加固结构影响,关键在于得到准确表征胶粘剂剪切蠕变行为的黏弹性本构方程.
近年来研究者们对CFRP-混凝土单面搭接试件或双面搭接试件进行长期加载试验,并考虑多种因素影响以获得表征胶粘剂蠕变变形的本构模型.文献[12]认为界面剪应力水平和胶层厚度对胶粘剂蠕变行为有显著影响. 文献[13]在文献[12]研究基础上引入了胶粘剂养护龄期的影响,采用改进的Maxwell模型和Findley幂律方程预测界面的蠕变变形.文献[14]采用广义的Maxwell模型预测界面的蠕变变形以及界面的蠕变断裂发展. 文献[15]和文献[16]应用时间-温度等效原理(TTSP),通过短时间高温条件下双剪试件拉伸蠕变试验获得界面的黏弹性特性,并用串联的标准线性固体模型模拟界面的蠕变变形. 文献[17]利用TTSP原理进行了短期胶体拉伸蠕变试验得到了Burgers本构模型,基于此模型对持续拉伸荷载作用下CFRP-混凝土双剪试件进行了试验验证和有限元分析.
在CFRP加固钢结构方面,文献[10]采用有限元分析方法研究了胶粘剂黏弹性对CFRP-钢界面应力的影响,考虑胶粘剂黏弹性后,界面剪应力和剥离应力随时间增加而减小.本文对CFRP-钢双剪试件进行了长期蠕变试验,采用Burgers模型和Findley幂律方程表征CFRP-钢界面胶粘剂的剪切蠕变行为,基于Burgers模型特性及胶层剪应变-时间曲线推导了各参数的求解方法,结合试验结果进行了拟合分析,得到了本构模型中考虑剪应力影响的各参数表达式,并对模型的预测结果进行了对比和验证.
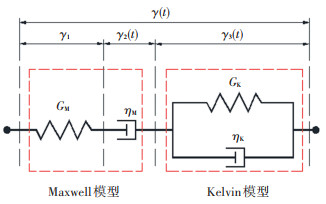
1 黏弹性本构模型 1.1 Burgers模型图 1所示为典型的Burgers模型,该模型属于流变力学模型的一种,具有概念清晰以及物理意义明确的特点.Burgers模型由Maxwell模型和Kelvin模型串联而成.Maxwell模型由“弹簧”元件和“黏壶”元件串联而成,GM为剪切弹性模量,ηM为黏度系数.Kelvin模型由“弹簧”元件和“黏壶”元件并联而成,GK为剪切弹性模量,ηK为黏度系数.
|
图 1 Burgers模型 Fig. 1 Burgers model |
在恒定的剪应力τ0作用下,任意t时刻Burgers模型的总应变γ(t)可表示成3部分:Maxwell模型中“弹簧”元件的剪切弹性应变γ1和“黏壶”元件的黏性应变γ2(t),Kelvin模型的延迟弹性应变γ3(t).根据流变力学理论γ1、γ2(t)、γ3(t)的表达式分别为
| $ \gamma_{1}=\tau_{0} / G_{\mathrm{M}} , $ | (1) |
| $ \gamma_{2}(t)=\frac{\tau_{0} \cdot t}{\eta_{\mathrm{M}}} , $ | (2) |
| $ \gamma_{3}(t)=\frac{\tau_{0}}{G_{\mathrm{K}}}\left(1-\mathrm{e}^{-\frac{G_{\mathrm{K}} \cdot t}{\eta_{\mathrm{K}}}}\right) . $ | (3) |
式中:γ1为瞬时弹性应变,γ2(t)和γ3(t)的和为蠕变应变.
t时刻的总应变γ(t)为
| $ \gamma(t)=\gamma_{1}+\gamma_{2}(t)+\gamma_{3}(t). $ | (4) |
将式(1)~(3)代入式(4)得
| $ \gamma(t)=\tau_{0}\left[\frac{1}{G_{\mathrm{M}}}+\frac{t}{\eta_{\mathrm{M}}}+\frac{1}{G_{\mathrm{K}}}\left(1-\mathrm{e}^{-\frac{G_{\mathrm{K}} \cdot t}{\eta_{\mathrm{K}}}}\right)\right] . $ | (5) |
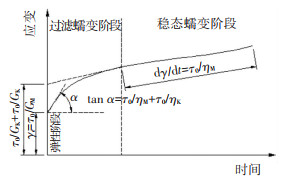
在正常使用阶段的荷载作用下,黏弹性材料的应变-时间关系如图 2所示.在加载瞬间黏弹性材料产生瞬时弹性应变,此时为弹性阶段.随后加载大小不变而应变随时间逐渐增加,增加的应变即为蠕变应变,大致可分为两个阶段:一个是过渡蠕变阶段,在此阶段黏弹性材料的应变速率(曲线的斜率)随加载时间的增加而不断降低;一个是稳态蠕变阶段,在此阶段曲线基本为一条直线,即曲线的斜率保持不变,也就是说蠕变应变与加载时间成正比例关系.
|
图 2 应变-时间关系 Fig. 2 Strain-time relationship |
根据Burgers模型特性以及黏弹性材料的应变-时间关系曲线特点,可通过下列步骤逐步求解Burgers模型的各参数.
步骤1 将加载时间t=0,代入式(5)中得,瞬时弹性应变γe为
| $ \gamma_{\mathrm{e}}=\tau_{0} / G_{\mathrm{M}}. $ | (6) |
对应于图 2中的弹性阶段,式(6)变换后可得参数GM=τ0/γe.
步骤2 在式(5)中取t = ∞,则
| $ \gamma(t)=\frac{\tau_{0} \cdot t}{\eta_{\mathrm{M}}}+\left(\frac{\tau_{0}}{G_{\mathrm{M}}}+\frac{\tau_{0}}{G_{\mathrm{K}}}\right). $ | (7) |
在式(7)中取t = 0,有γ(0)=τ0/GM+τ0/GK,表示稳态蠕变阶段曲线的延长线与应变轴的交点到原点的距离,如图 2所示.在步骤1中求得参数GM后,继而可求参数GK.
步骤3 对式(5)求导,得
| $ \frac{\mathrm{d} \gamma(t)}{\mathrm{d} t}=\frac{\tau_{0}}{\eta_{\mathrm{M}}}+\frac{\tau_{0}}{\eta_{\mathrm{K}}} \mathrm{e}^{-\frac{G_{\mathrm{K}} \cdot t}{\eta_{\mathrm{K}}}}. $ | (8) |
当式(8)中取t = ∞,则
| $ \left.\frac{\mathrm{d} \gamma(t)}{\mathrm{d} t}\right|_{t=\infty}=\frac{\tau_{0}}{\eta_{\mathrm{M}}}. $ | (9) |
式(9)表示稳态蠕变阶段曲线的斜率k=τ0/ηM,如图 2所示.根据曲线斜率k,可求参数ηM=τ0/k.
步骤4 当t = 0时,式(8)简化为
| $ \left.\frac{\mathrm{d} \gamma(t)}{\mathrm{d} t}\right|_{t=0}=\frac{\tau_{0}}{\eta_{\mathrm{M}}}+\frac{\tau_{0}}{\eta_{\mathrm{K}}}. $ | (10) |
式(10)表示过渡蠕变阶段曲线的初始应变速率为tan α=(τ0/ηK+τ0/ηM),如图 2所示.在步骤3中求得参数ηM后,继而可求参数ηK.
1.2 Findley幂律方程Findley幂律方程最早是由Findley[18]提出的.因其公式简单,参数较少,在表征高分子聚合物的黏弹性方面应用广泛.Findley幂律方程的剪切应变γ(t)形式为
| $ \gamma(t)=\gamma_{0}+m \cdot t^{n}. $ | (11) |
式中: γ(t)为时间为t时的总剪应变; γ0为初始弹性剪应变; m和n为相关系数,由试验结果确定.
2 长期加载试验 2.1 试件设计及制作试验采用的钢板为热轧Q235B,宽度为50 mm,长度为300 mm,厚度为6 mm,抗拉强度为309 MPa,弹性模量为190 GPa. CFRP布采用密度为300 g/mm2的东丽UT70-30型,宽度为30 mm,长度为420 mm,厚度为0.167 mm,抗拉强度为3 920 MPa,弹性模量为237 GPa,伸长率为1.71%. 胶粘剂采用爱牢达XH 180型,抗拉强度为47 MPa,弹性模量为2.86 GPa钢-钢拉伸抗剪强度为16 MPa,伸长率为1.90%.
为方便试验加载及有效采集试验数据,试验中采用双剪试件. 试件制作时首先用电砂轮打磨钢板除去表面锈迹和油污,并用800目砂纸磨掉表面毛刺,用丙酮擦拭钢板,待干燥后用毛刷均匀地涂抹胶粘剂,利用刮板均匀挤压CFRP布赶出气泡. 制作好一面后,24 h后再黏贴另一面. 待试件制作完成后,在实验室条件下养护7 d.
试件尺寸及应变片布置如图 3所示.试件每面各布置12个应变片,每个试件黏贴24个应变片.为方便试验结果表达,将测试面分别定义为Q面和H面,应变片编号从加载端到固定端依次定义为Q0#~Q11#及H0#~H11#.其中编号Q0#和H0#两个应变片位于两块钢板空隙处的CFRP布上.

|
图 3 CFRP-钢板双剪试件及应变片布置(mm) Fig. 3 CFRP-steel plate double-lap specimen and layout of strain gauges (mm) |
试验共设计并制作27个CFRP-钢双剪试件. A组3个试件,待养护完成后进行静力破坏试验,得到极限承载力Pu分别为27.4、28.8、31.6 kN,Pu平均值为29.3 kN,标准差为2.1. 平均极限剪切强度τu=Pu/(2bclc),其中bc为CFRP宽度30 mm,lc为CFRP黏结长度200 mm,可计算得到τu=2.44 MPa. B、C、D、E组每组6个试件,持续施加的界面名义剪应力τ0分别取0.22τu、0.44τu、0.60τu和0.73τu,即分别为0.54、1.07、1.46、1.78 MPa.试验的分组情况、黏结界面上长期施加的界面名义剪应力τ0和加载时间见表 1.
| 表 1 试件分组 Tab. 1 Arrangement of specimens |
长期加载采用自制的加载装置,与文献[19]一样.该装置根据杠杆原理制作,整个装置由底梁、立柱、横梁组成,底梁与立柱通过焊接连接,立柱与横梁通过螺栓连接.横梁一端加载重物,一端连接试件,为减小重物的重量,两力臂的比值为10∶1. 重物为浇筑的立方体混凝土块. 一个底梁对称分布两套加载装置,两套装置之间通过与立柱焊接的连接杆进行连接以保证结构的稳定性. 不同重量的混凝土块进行组合后,通过丝杆串联,丝杆顶部采用花篮螺栓与加载横梁相连. 通过调节旋紧花篮螺栓的速度,可以控制加载重物的提升速度,以保证匀速加载.
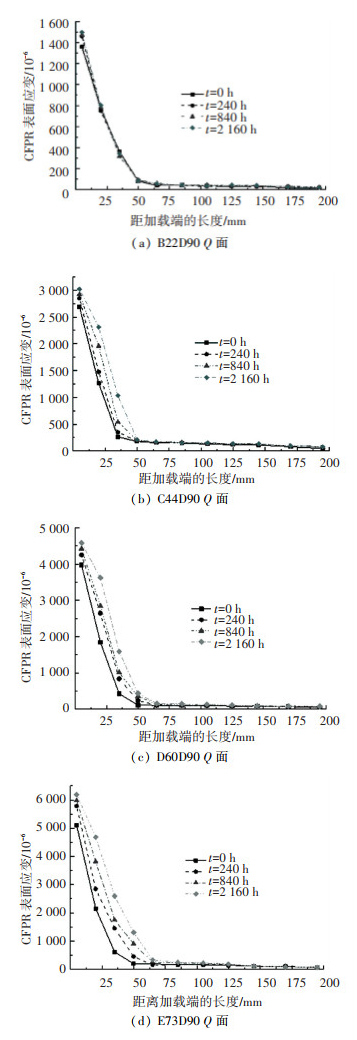
2.3 试验结果 2.3.1 CFRP表面应变分布试件B22D90、C44D90、D60D90、E73D90的CFRP表面应变分布(每组仅示出一个试件)如图 4所示. 观察各图中CFRP应变分布曲线可知,在荷载作用下仅在测点Q1#~Q5#范围内CFRP布应变响应较大,测点Q1#(加载端部)应变值最大,距测点Q1#越远,应变值急剧减小,测点Q5#后各测点应变较小.表明荷载仅在CFRP-钢界面端部一部分区域内传递,且CFRP应变呈现非线性减小.对比图中同一测点在不同加载时间的应变数值,可知随着加载时间的增加,测点Q1#~Q5#范围应变数值逐渐增大.
|
图 4 CFRP应变分布 Fig. 4 Strain distribution of CFRP |
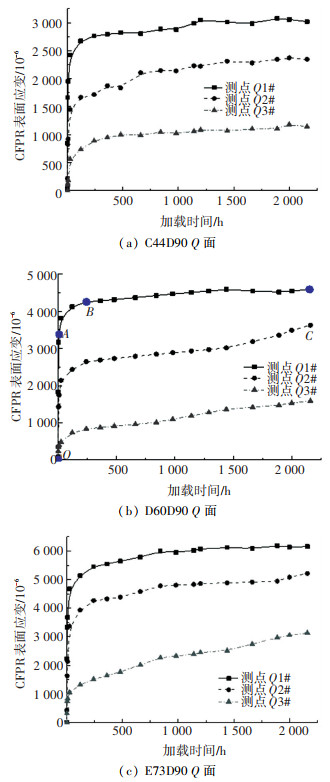
为更直观表达各测点应变随加载时间的变化情况,将图 4中试件C44D90、D60D90、E73D90(试件B22D90应变变化较小)测点Q1#、Q2#、Q3#在整个试验周期内的应变数值进行整理如图 5所示.由图 5可知,测点Q1#、Q2#、Q3#的应变值均随着加载时间的增加而增大.各组曲线具有相似的特点,由3个阶段组成,以图 5中(b)图中测点Q1#为例,第1阶段,图中OA段,荷载施加瞬时CFRP发生弹性变形,应变与荷载大小成正比;第2阶段,图中AB段,弹性变形完成后,CFRP应变随着时间的增加逐渐增大,但增大速率不断减小,即曲线斜率变小;第3阶段,图中BC段,应变增大速率减小到一定值后,在剩余试验周期内基本不发生变化或变化很小.图 5中CFRP应变随时间变化关系与图 7中胶粘剂的剪应变-时间关系曲线具有相似特性,即应变在前期增大较快,后期增大逐渐减缓,最后应变增加速率保持不变.这是因为在持续荷载作用下胶粘剂层发生了蠕变变形,致使试件发生了内力重分布,表现为CFRP应变增加,为保持受力平衡与胶粘剂层临近的钢板表面应变应减小.
|
图 5 CFRP应变随时间变化 Fig. 5 Strain distribution of CFRP varying with time |
另外,经过2 160 h后,试件C44D90、D60D90和E73D90测点Q1#的蠕变应变(总应变减去第1阶段弹性应变)与弹性应变比值的分别为0.122、0.153和0.206,表明在测试周期内CFRP应变分别增加了12.2%、15.3%和20.6%.说明界面名义剪应力τ越大,胶粘剂蠕变变形就越大,CFRP应变增加的就越多.
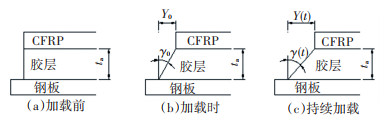
3 胶粘剂层的剪切变形CFRP-钢双面搭接试件在受到拉伸荷载作用后,胶层的变形如图 6所示.
|
图 6 胶层剪切荷载作用 Fig. 6 Adhesive layer under shear load |
由图 6中的几何关系可知,加载瞬时γ0为
| $ {\gamma _0} = {Y_0}/{t_{\rm{a}}}. $ | (12) |
式中:ta为胶层的厚度,γ0为加载瞬时胶层的剪应变,Y0为胶层上、下表面的之间相对变形.
随着加载时间的增加胶粘剂将发生蠕变,则γ(t)为
| $ \gamma (t) = Y(t)/{t_{\rm{a}}}, $ | (13) |
式中:γ(t)为t时刻胶层总的剪应变,Y(t)为胶层上、下表面的总的相对变形.
假设CFRP-胶粘剂界面不发生相对滑动且CFRP全截面上应变不变,对CFRP表面应变进行积分可得Y(t)为
| $ Y(t) = \int\limits_0^x \varepsilon (x){\rm{d}}x, $ | (14) |
式中ε(x)为CFRP表面应变.
本试验中测得的CFRP表面应变是不连续的,可通过数值积分的方法近似计算Y(t)[20]为
| $ \begin{aligned} Y(t)=& \frac{\left(\varepsilon_{\mathrm{c}, i+1}+\varepsilon_{\mathrm{c}, i}\right)}{4}\left(L_{i+1}-L_{i}\right)+\\ & \sum\limits_{j=i}^{n} \frac{\left(\varepsilon_{\mathrm{c}, j+1}+\varepsilon_{\mathrm{c}, j+2}\right)}{2}\left(L_{i+2}-L_{i+1}\right), \end{aligned} $ | (15) |
式中:εc, i为第i个CFRP表面应变测点的数值,Li为第i个CFRP表面应变测点到加载端的距离.
结合式(13)和式(15),可以得到任意t时刻γ(t)为
| $ \begin{aligned} \gamma(t)=& \frac{\left(\varepsilon_{\mathrm{c}, i+1}+\varepsilon_{\mathrm{c}, i}\right)}{4 t_{\mathrm{a}}}\left(L_{i+1}-L_{i}\right)+\\ & \frac{1}{t_{\mathrm{a}}} \sum\limits_{j=i}^{n} \frac{\left(\varepsilon_{\mathrm{c}, j+1}+\varepsilon_{\mathrm{c}, j+2}\right)}{2}\left(L_{i+2}-L_{i+1}\right). \end{aligned} $ | (16) |
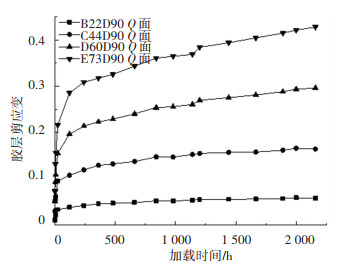
根据长期加载试验实测数据,可通过式(16)得到胶层剪应变与加载时间的关系.试件B22D90、C44D90、D60D90、E73D90的胶层剪应变随时间变化(每组仅示出1个试件)如图 7所示.观察图 7中各条曲线可知,曲线特征与图 2类似,可分为3个阶段:弹性阶段、过渡蠕变阶段和稳态蠕变阶段.
|
图 7 胶层剪应变与加载时间关系 Fig. 7 Relationship between shear strain of adhesive layer and loading time |
根据第2节的试验结果及式(16),可得各组试件胶层剪应变随时间变化曲线,结合第1节中Burgers模型中各参数的求解方法,可得到Burgers模型中各参数的数值.GM通过式(6)计算得25.44 MPa,其他参数见表 2. 表 2中各参数求解时以各组试件的Q面应变数据为依据.
| 表 2 Burgers模型计算结果 Tab. 2 Calculation results of Burgers model |
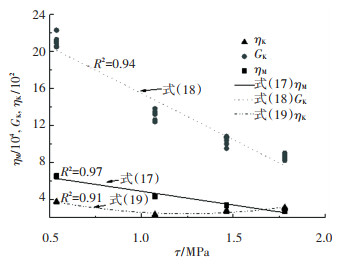
以表 2中参数ηM、GK和ηK的数值为纵坐标,各组试件的界面名义剪应力τ为横坐标绘制Burgers模型参数与名义剪应力关系曲线,如图 8所示.由图 8可看出,各组试件参数ηM、GK和ηK的数值的大小与界面名义剪应力有一定关系.根据最小二乘法原理,采用MATLAB实现曲线拟合得到参数ηM、GK和ηK与界面名义剪应力τ的函数关系分别为
|
图 8 Burgers模型参数与名义剪应力关系 Fig. 8 Relationship between parameters of Burgers model and nominal shear stress |
| $ \eta_{\mathrm{M}}(\tau)=-29\;728 \tau+783\;379, $ | (17) |
| $ G_{\mathrm{K}}(\tau)=-10 \tau+25.5 , $ | (18) |
| $ \eta_{\mathrm{K}}(\tau)=254.3 \tau^{2}-633.4 \tau+637.2. $ | (19) |
则Burgers模型的表达式为
| $ \gamma(\tau, t)=\tau\left[\frac{1}{G_{\mathrm{M}}}+\frac{t}{\eta_{\mathrm{M}}(\tau)}+\frac{1}{G_{\mathrm{K}}(\tau)}\left(1-\mathrm{e}^{\left.-\frac{G_{\mathrm{K}}(\tau) \cdot t}{\eta_{\mathrm{K}}(\tau)}\right)}\right]\right.. $ | (20) |
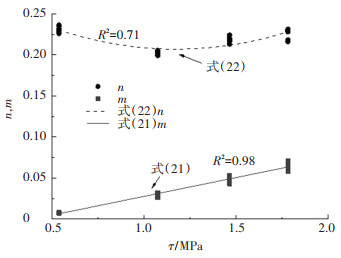
根据各组试件胶层剪应变随时间变化曲线,同样可采用最小二乘法回归分析得到Findley幂律方程中的参数,结果见表 3. 从表 3中可知,各组试件的m与n大小不同,说明界面名义剪应力的大小对参数有影响.参数m、n与界面名义剪应力τ的关系如图 9所示.采用MATLAB对数据进行拟合分析,可得到参数m与n为因变量,剪应力τ为自变量的函数方程为
| 表 3 Findley幂律方程计算结果 Tab. 3 Calculation results of Findley power law equation |
|
图 9 Findley幂律方程参数与名义剪应力关系 Fig. 9 Relationship between parameters of Findley power law equation and nominal shear stress |
| $ m(\tau)=0.045\;5 \tau-0.017\;6, $ | (21) |
| $ n(\tau)=0.059\;9 \tau^{2}-0.14 \tau+0.287\;8 . $ | (22) |
在得到Burgers模型和Findley幂律方程各参数表达式后,为检验两类模型的预测能力,采用H面的试验结果进行验证.通过均方根误差(RMSE)的大小反映预测值与试验值的偏离程度,RMSE越小表示模型的预测精度越高.RMSE的表达式为
| $ \mathrm{RMSE}=\sqrt{\sum\limits_{i=1}^{n} \frac{\left(\gamma_{i}^{\exp }-\gamma_{i}^{\text {pred }}\right)^{2}}{N}}, $ | (23) |
式中:γiexp为H面的试验数据计算的胶层剪应变,γipred为由模型预测的胶层剪应变,N为试验数据点的数量.
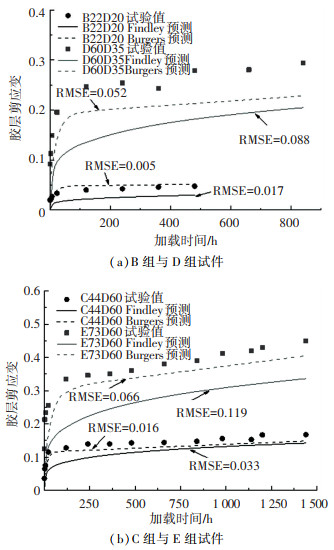
选取试件B22D20、C44D60、D60D35和E73D60作为每组的代表,将胶层剪应变的试验值、Burgers模型的预测曲线及Findley幂律方程的预测曲线绘制于图 10中.由图 10可知,两类模型的RMSE均较小,表明模型预测值与试验值偏离较小,两类模型都可以很好地预测CFRP-钢界面的剪切蠕变变形.
|
图 10 胶层剪应变的试验值与预测值 Fig. 10 Experimental and predicted values of shear strain in adhesive layer |
各组试件胶层剪应变Burgers模型的预测值与H面试验值之间的RMSE见表 2,Findley幂律方程的预测值与H面试验值之间的RMSE见表 3.对比表 2与表 3中的RMSE大小可知,Burgers模型得到的RMSE普遍小于Findley幂律方程得到的RMSE,尤其对于D组和E组试件表现更为明显.这可能是因为Findley幂律方程中参数m拟合方程的R2较小,即拟合曲线对观测值的拟合程度一般,D组和E组试件的界面名义剪应力较高,这种影响就会越大.说明对于CFRP-钢界面胶粘剂的剪切蠕变变形的表征上Burgers模型要优于Findley幂律方程.这点也可从图 10中直观看出,Burgers模型的预测曲线更接近于试验值.
5 结论1) 在长期界面剪切应力作用下CFRP-钢界面胶粘剂发生了蠕变变形.胶层蠕变导致黏结界面发生了内力重分布,直观表现为同一位置处CFRP应变随加载时间增加而增大,CFRP应变前期增大较快,后期增大较慢.另外,不同组试件之间对比发现界面名义剪应力τ越大,胶粘剂蠕变变形就越大,CFRP应变增加的就越多.
2) 可采用Burgers模型和Findley幂律方程表征剪应力作用下CFRP-钢界面胶粘剂的蠕变变形.两类本构模型中参数与界面剪应力τ的大小有一定关系. Burgers模型中参数ηM和GK均与剪应力τ具有线性关系,参数ηK是剪应力τ的二次函数. Findley幂律方程中参数m是剪应力τ的一次函数,参数n是剪应力τ的二次函数.
3) Burgers模型和Findley幂律方程的RMSE均较小,即预测值与试验值偏离较小,说明两类模型都可以很好地预测CFRP-钢界面的剪切蠕变变形.相对而言,Burgers模型的RMSE要小于Findley幂律方程的RMSE,尤其是当界面剪应力较高时更为明显,说明Burgers模型预测的CFRP-钢界面胶粘剂蠕变变形与试验结果吻合更好.
| [1] |
AL-SAADI N T K, MOHAMMED A, AL-MAHAIDI R, et al. A state-of-the-art review: near-surface mounted FRP composites for reinforced concrete structures[J]. Construction and Building Materials, 2019, 209: 748. DOI:10.1016/j.conbuildmat.2019.03.121 |
| [2] |
ZHAO X L, ZHANG L. State-of-the-art review on FRP strengthened steel structures[J]. Engineering Structures, 2007, 29(8): 1808. DOI:10.1016/j.engstruct.2006.10.006 |
| [3] |
徐佰顺. CFRP-钢复合结构界面时变力学行为研究[D]. 成都: 西南交通大学, 2017 XU Baishun. Research on time-dependent mechanical behavior of CFRP-steel composite structure interface [D]. Chengdu: Southwest Jiaotong University, 2017 |
| [4] |
李传习, 柯璐, 陈卓异, 等. CFRP-钢界面粘结性能试验与数值模拟[J]. 复合材料学报, 2018, 35(12): 3534. LI Chuanxi, KE Lu, CHEN Zhuoyi, et al. Experimental study and numerical simulation for bond behavior of interface between CFRP and steel[J]. Acta Materiae Compositae Sinica, 2018, 35(12): 3534. DOI:10.13801/j.cnki.fhclxb.20180316.001 |
| [5] |
薛耀, 张龙, 曹双寅, 等. 低龄期下CFRP-钢界面黏结性能试验研究[J]. 东南大学学报(自然科学版), 2015, 45(2): 360. XUE Yao, ZHANG Long, CAO Shuangyin, et al. Experimental study on bonding behavior of CFRP-to-steel interface under early curing age[J]. Journal of Southeast University (Natural Science Edition), 2015, 45(2): 360. DOI:10.3969/j.issn.1001-0505.2015.02.028 |
| [6] |
TENG J G, YU T, FERNANDO D. Strengthening of steel structures with fiber-reinforced polymer composites[J]. Journal of Constructional Steel Research, 2012, 78: 131. DOI:10.1016/j.jcsr.2012.06.011 |
| [7] |
李春良, 李凯, 张立辉, 等. CFRP端部被锚固后加固钢结构的界面粘结行为[J]. 哈尔滨工业大学学报, 2016, 48(9): 113. LI Chunliang, LI Kai, ZHANG Lihui, et al. Interfacial bond behavior of CFRP reinforced steel structures with end anchorage[J]. Journal of Harbin Institute of Technology, 2016, 48(9): 113. DOI:10.11918/j.issn.0367-6234.2016.09.020 |
| [8] |
FERNANDO D, YU T, TENG J G. Behavior of CFRP laminates bonded to a steel substrate using a ductile adhesive[J]. Journal of Composites for Construction, 2013, 18(2): 04013040. DOI:10.1061/(ASCE)CC.1943-5614.0000439 |
| [9] |
COSTA I, BARROS J. Tensile creep of a structural epoxy adhesive: experimental and analytical characterization[J]. International Journal of Adhesion and Adhesives, 2015, 59: 115. DOI:10.1016/j.ijadhadh.2015.02.006 |
| [10] |
徐佰顺, 钱永久, 唐继舜, 等. 基于黏弹性本构的CFRP-钢界面应力参数敏感性分析[J]. 公路交通科技, 2017, 34(11): 57. XU Baishun, QIAN Yongjiu, TANG Jishun, et al. Analysis on CFRP-to-steel interfacial stress parameter sensitivity based on viscoelastic constitution[J]. Journal of Highway and Transportation Research and Development, 2017, 34(11): 57. DOI:10.3969/j.issn.1002-0268.2017.11.009 |
| [11] |
马明, 徐佰顺, 张方, 等. 持续荷载下CFRP-混凝土界面黏结性能试验与分析[J]. 哈尔滨工业大学学报, 2018, 50(3): 128. MA Ming, XU Baishun, ZHANG Fang, et al. Experiment and performance analysis on bonding behavior of CFRP-concrete interface under sustained load[J]. Journal of Harbin Institute of Technology, 2018, 50(3): 128. DOI:10.11918/j.issn.0367-6234.201703086 |
| [12] |
CHOI K K, MESHGIN P, TAHA M M R. Shear creep of epoxy at the concrete-FRP interfaces[J]. Composites Part B: Engineering, 2007, 38(5/6): 772. DOI:10.1016/j.compositesb.2006.10.003 |
| [13] |
MESHGIN P, CHOI K K, TAHA M M R. Experimental and analytical investigations of creep of epoxy adhesive at the concrete-FRP interfaces[J]. International Journal of Adhesion and Adhesives, 2009, 29(1): 56. DOI:10.1016/j.ijadhadh.2008.01.003 |
| [14] |
DIAB H, WU Z. A linear viscoelastic model for interfacial long-term behavior of FRP-concrete interface[J]. Composites Part B: Engineering, 2008, 39(4): 722. DOI:10.1016/j.compositesb.2007.05.007 |
| [15] |
FERRIER E, MICHEL L, JURKIEWIEZ B, et al. Creep behavior of adhesives used for external FRP strengthening of RC structures[J]. Construction and Building Materials, 2011, 25(2): 461. DOI:10.1016/j.conbuildmat.2010.01.002 |
| [16] |
MEAUD C, JURKIEWIEZ B, FERRIER E. Investigation of creep effects in strengthened RC structures through double lap shear testing[J]. Composites Part B: Engineering, 2011, 42(3): 359. DOI:10.1016/j.compositesb.2010.12.024 |
| [17] |
HOUHOU N, BENZARTI K, QUIERTANT M, et al. Analysis of the nonlinear creep behavior of concrete/FRP-bonded assemblies[J]. Journal of Adhesion Science and Technology, 2014, 28(14/15): 1345. DOI:10.1080/01694243.2012.697387 |
| [18] |
FINDLEY W N. Mechanism and mechanics of creep of plastics[J]. Society of Plastic Engineering, 1960, 16(1): 57. |
| [19] |
徐佰顺, 姚亚东, 钱永久, 等. 具有荷载作用历史的CFRP-钢界面粘结性能试验[J]. 哈尔滨工业大学学报, 2020, 52(9): 167. XU Baishun, YAO Yadong, QIAN Yongjiu, et al. Experiment on bonding behavior of CFRP-steel interface with load history[J]. Journal of Harbin Institute of Technology, 2020, 52(9): 167. |
| [20] |
FERNANDO N D. Bond behaviour and debonding failures in CFRP-strengthened steel members [D]. Hong Kong: The Hong Kong Polytechnic University, 2010
|
 2021, Vol. 53
2021, Vol. 53


