2. 海军工程大学 基础部,武汉 430033
2. Department of Basic Courses, Naval University of Engineering, Wuhan 430033, China
舰船腐蚀及防腐电流在其附近产生的电流场称为舰船腐蚀电场[1],随着水下电场探测技术的不断发展,舰船腐蚀电场已成为一种新型的水下信号源[2-3]. 目前,舰船腐蚀电场主要有实船测量、物理缩比模型等实验研究方法和等效电偶极子模型、边界元等仿真研究方法,实验研究不仅成本高、周期长,且难以测得舰船周围全空间的电场分布. 边界元法是一种非常适合求解开域问题的高精度数值计算方法[4],已被广泛应用于石油钻井平台、舰船等海洋结构件的腐蚀防护技术的仿真[5-6],近年来,已有学者将其应用于舰船腐蚀电场的仿真研究[7-9]. 学者们研究了海床电导率、海水电导率、温度、流速、深度等海洋环境因素对舰船腐蚀电场的影响[2, 10-11],建立了舰船腐蚀电场等效电偶极子模型,并分析了水平和垂直电偶极子在多层介质中产生的电磁场[12-14].
船舶和海洋工程结构的复杂性及其服役环境的特殊性,使得结构产生复杂的应力应变,如肋骨与船体的焊接处和船体表面的腐蚀缺陷处等都会产生应力集中[15-17],另外,潜艇在下潜与上浮的过程中,结构应力会随着静水压力的变化而发生显著的改变[18]. 载荷和腐蚀介质的交互作用被定义为金属腐蚀的力学化学效应,它主要包括在载荷和腐蚀介质的协同作用下金属腐蚀电位的降低和腐蚀速率的增大[19-20]. 已有研究[21]表明,在结构应力接近160 MPa时,Q235B钢在质量分数为3.5%的NaCl溶液中的腐蚀速率增大了约44%,因此,金属在海水中腐蚀的力学化学效应不容忽视. 然而,这些研究并没有考虑力学因素对腐蚀电场的影响,而载荷与腐蚀介质协同作用下的腐蚀电场的研究具有重要的工程意义和实用价值,因此,本文旨在研究舰船在服役过程中产生的复杂应力应变对其腐蚀电场的影响规律.
随着服役时间的增加,船壳的防腐涂层不可避免地会遭到破损,涂层破损处发生严重的腐蚀而形成腐蚀缺陷,在外界作用力下,腐蚀缺陷处会产生应力集中. 因此,本文基于腐蚀缺陷,将结构应力应变耦合到电极反应的平衡电位和交换电流密度表达式以建立腐蚀电场的力学化学耦合模型,得到了拉伸位移对力学化学耦合效应下腐蚀电位、电流密度以及腐蚀电场的影响规律.
1 数值仿真模型采用COMSOL Multiphysics仿真软件建立基于腐蚀缺陷的力学化学耦合模型,仿真模型主要分析以下3个方面内容:一是船体钢的弹塑性固体应力分布;二是在固体应力和腐蚀介质协同作用下溶液中的电位分布以及金属/溶液界面的腐蚀电位分布;三是在力学化学效应下溶液中的腐蚀电场分布,前者采用固体力学模块求解,后两者采用二次电流分布模块求解.
1.1 结构应力仿真由于圆柱壳体的对称性,将船体结构的三维模型简化为二维模型,如图 1所示,取船体钢的长度为两肋骨间的单跨长度(0.6 m),壳体厚度为28 mm,腐蚀缺陷为椭球型,其长度为200 mm,深度为12 mm. 考虑到船体结构腐蚀缺陷处的应力集中可能会导致局部的塑性变形,因此,使用小塑性应变模型和von Mises屈服准则来实现船体结构的弹塑性应力仿真,并采用各向同性硬化模型,相应的硬化函数(σyhard)定义[20]为

|
图 1 基于腐蚀缺陷的力学化学耦合模型示意图 Fig. 1 Schematic diagram of mechanochemical coupling model based on corrosion defect |
| $ \sigma_{\text {yhard }}=\sigma_{\exp }\left(\varepsilon_{\text {eff }}\right)-\sigma_{\mathrm{ys}}=\sigma_{\exp }\left(\varepsilon_{\mathrm{p}}+\sigma_{\mathrm{e}} / E\right)-\sigma_{\mathrm{ys}}. $ | (1) |
式中:σexp为由船体钢应力应变曲线得到的实验应力函数,εeff为弹塑性应变,σys为船体钢的屈服强度,εp为塑性应变,σe为弹性应力,E为弹性模量,σe/E为弹性应变.
由拉伸实验得到船体钢的应力-应变曲线如图 2所示,采用控制位移的方式对试样进行加载,加载速度为1 mm/min,拉伸过程中并没有出现明显的屈服现象,故取塑性应变为0.2%所对应的应力值为船体钢的屈服强度,因此,船体钢的屈服强度和抗拉强度分别为708、754 MPa,弹性模量为200 GPa,泊松比为0.3. 边界条件:考虑到船体结构的受力较为复杂,将船体钢右端简化为沿X方向的拉伸位移d,在Y方向为自由移动,利用COMSOL软件中参数化扫描功能实现拉伸位移的变化,位移取值分别为0、0.4、0.8、1.2、1.6、1.8 mm;船体钢的左端为固定约束;船体钢的内壁在Y方向的位移为0,在X方向为自由移动. 网格类型为自由三角形网格,且在腐蚀缺陷处进行了细分处理,最大和最小单元尺寸分别为2.00、0.18 mm,三角形单元总数为22 538个.

|
图 2 船体钢应力应变曲线 Fig. 2 Stress-strain curve of hull steel |
考虑到实际情况,对模型进行以下假设:1)船体钢的主要成分为铁,故认为阳极溶解反应只有铁的氧化反应而忽略其他杂质元素的溶解;2)船体钢在自腐蚀电位下,氧还原和铁氧化反应均属于高过电位下的电极反应,因此,电极过程动力学由Butler-Volmer方程简化为Tafel方程;3)钢/溶液界面同时发生铁的氧化与氧的还原两个共轭反应,而溶液的其他边界为电绝缘.
铁阳极氧化溶解的局部电流为
| $ j_{\mathrm{a}}=j_{\mathrm{a}, \mathrm{ref}}^{0} 10^{\eta_{\mathrm{a}} / b_{\mathrm{a}}}. $ | (2) |
式中:ja, ref0为无应力作用时阳极反应的交换电流密度,ba为阳极塔菲尔斜率,ηa为阳极反应的过电位,且
| $ \eta_{\mathrm{a}}=\varphi-\varphi_{\mathrm{a}, \mathrm{eq}}, $ | (3) |
其中φ为钢/溶液界面的电极电位,φa, eq为应力状态下阳极反应的平衡电位,并由下式[15]计算
| $ \varphi_{\mathrm{a}, \mathrm{eq}}=\varphi_{\mathrm{a}, \mathrm{eq}}^{0}-\frac{\Delta P V_{\mathrm{m}}}{z F}-\frac{R T}{z F} \ln \left(\frac{v \alpha}{N_{0}} \varepsilon_{\mathrm{p}}+1\right). $ | (4) |
式(4)右边第2项为由弹性应力引起的阳极平衡电位负移量,第3项为由塑性应变引起的阳极平衡电位负移量,φa, eq0为无应力时阳极反应的平衡电位,其值由Nernst方程得到;ΔP为应力张量中水静压部分的绝对值,本模型将ΔP设置为2.1节中求得的von Mises应力;Vm为金属的摩尔分子体积,对于碳钢,Vm=7.13×10-6 m3/mol;z为阳极溶解反应转移的电荷数;F为法拉第常数;R、T分别为气体常数和绝对温度;υ为方向因子;α为系数;N0为塑性变形前的初始位错密度;εp为塑性应变. 氧阴极还原反应的局部电流为
| $ j_{\mathrm{c}}=j_{\mathrm{c}}^{0} 10^{\eta_{\mathrm{c}} / b_{\mathrm{c}}}. $ | (5) |
式中:jc0为应力状态下阴极反应的交换电流密度;bc、ηc分别为阴极反应的塔菲尔斜率和过电位,且
| $ \eta_{\mathrm{c}}=\varphi-\varphi_{\mathrm{c}, \mathrm{eq}}^{0}, $ | (6) |
其中φc, eq0为无应力时阴极反应的平衡电位,其值由Nernst方程得到.
研究表明,应力的存在会加速阴极反应的交换电流密度,描述力学化学效应对阴极反应交换电流密度影响的半经验公式[20]为
| $ j_{\mathrm{c}}^{0}=j_{\mathrm{c}, \mathrm{ref}}^{0} \times 10^{\frac{\sigma_{\mathrm{Mises}} \mathrm{Vm}}{6 \mathrm{~F}(-b\mathrm{c})}}. $ | (7) |
式中:jc, ref0为无应力作用时阴极反应的交换电流密度,σMises为2.1节中求得的von Mises应力.
采用三电极体系在CS310电化学工作站上测试船体钢的动电位极化曲线,实验介质为质量分数为3.5%的NaCl溶液. 工作电极为采用环氧树脂封装的圆柱形船体钢,其直径为1.1 cm,高度为1 cm,金属暴露面积为1 cm2,用SiC湿砂纸逐级打磨至1 000目,丙酮脱脂,并依次用乙醇和蒸馏水冲洗,然后置于干燥箱中烘干;参比电极为Ag/AgCl电极;辅助电极为铂片电极. 工作电极先在待测溶液中浸泡一段时间,等到开路电位基本稳定后开始测试,极化曲线的扫描电位为-1.1~-0.1 V(相对参比电极),扫描速率为1.0 mV/s. 图 3为船体钢在质量分数为3.5%的NaCl溶液中的极化曲线,由极化曲线得到船体钢的腐蚀电化学参数见表 1.

|
图 3 船体钢在质量分数为3.5%的NaCl溶液中的极化曲线 Fig. 3 Polarization curve of hull steel in 3.5% NaCl solution |
| 表 1 船体钢的腐蚀电化学参数 Tab. 1 Electrochemical corrosion parameters of hull steel |
对于二维腐蚀电场问题,电极/溶液界面的电极电位和溶液中的电位分布符合拉普拉斯方程[8]:
| $ \nabla^{2} \varphi=\frac{\partial^{2} \varphi}{\partial^{2} x}+\frac{\partial^{2} \varphi}{\partial^{2} y}=0. $ | (8) |
根据电场与电位的关系式E=-▽φ,则
| $ \left\{\begin{array}{l} E_{x}=-\partial \varphi / \partial x ,\\ E_{y}=-\partial \varphi / \partial y ,\\ |\boldsymbol{E}|=\left[\left(E_{x}\right)^{2}+\left(E_{y}\right)^{2}\right]^{1 / 2}. \end{array}\right. $ | (9) |
式中:EX、EY分别为溶液中电场的X和Y分量,|E|为电场模量.
2 结果与讨论 2.1 腐蚀缺陷处的应力分布图 4为由力学化学耦合模型计算得到的不同拉伸位移下腐蚀缺陷处的von Mises应力分布,由图可知,应力对称分布于腐蚀缺陷中心两侧,且最大应力出现在腐蚀缺陷中心,而腐蚀缺陷的两端点则出现应力最小值. 结构的von Mises应力水平随着拉伸位移的增大而增大,当拉伸位移为1.6 mm和1.8 mm时,腐蚀缺陷中心区域的局部应力值超过了船体钢的屈服强度(708 MPa),此时,腐蚀缺陷中心区域发生了一定程度的塑性变形,而其他区域则仍处于弹性应力阶段.

|
图 4 不同拉伸位移下腐蚀缺陷处的应力分布 Fig. 4 Stress distribution of corrosion defect under different tensile displacements |
图 5为不同拉伸位移下溶液中的电位分布和船体钢中的应力分布,由图可知,船体钢中的腐蚀缺陷处发生了明显的应力集中,且拉伸位移越大应力集中效应也越明显,缺陷的其他区域的应力分布则较为均匀. 溶液中的电位随着拉伸位移的增大而负移,由于船体钢中腐蚀缺陷处的应力集中,导致了溶液中电位分布的不均匀性,且拉伸位移越大,溶液中电位分布的不均匀性越明显. 当拉伸位移为1.6 mm和1.8 mm时,腐蚀缺陷附近的溶液与其他区域的溶液形成了明显的电位差,这与2.1节中分析的腐蚀缺陷中心区域发生的塑性变形有关.

|
图 5 不同拉伸位移下溶液中的电位分布和船体钢中的应力分布 Fig. 5 Potential distribution in solution and stress distribution in hull steel under different tensile displacements |
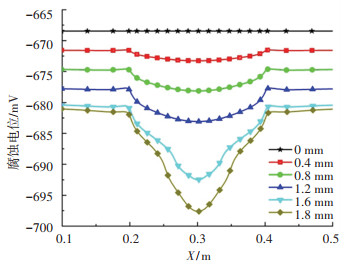
图 6为由力学化学耦合模型计算得到的不同拉伸位移下金属/溶液界面的腐蚀电位分布,当拉伸位移为0 mm时,电极表面的腐蚀电位处处相等,当拉伸位移不为零时,缺陷两边的腐蚀电位随着拉伸位移的增大均匀地负移,而缺陷处腐蚀电位的负移量大于两边,尤其是拉伸位移为1.6 mm和1.8 mm时,缺陷中心区域的腐蚀电位负移量远远大于两边,这是因为此时缺陷中心区域发生了塑性变形. 根据电化学理论推导,可得由于应力引起的金属腐蚀电位的变化值[21]为
|
图 6 不同拉伸位移下金属/溶液界面的腐蚀电位分布 Fig. 6 Corrosion potential distribution of metal/solution interface under different tensile displacements |
| $ \Delta \varphi_{\text {corr }}=\frac{b_{c}}{b_{\mathrm{a}}+b_{\mathrm{c}}} \Delta \varphi_{\mathrm{a}, \mathrm{eq}}. $ | (10) |
式中Δφa, eq为力学化学效应所引起的阳极氧化反应平衡电位的负移量,即
| $ \Delta \varphi_{\mathrm{a}, \mathrm{eq}}=-\frac{\Delta P \mathrm{~V}_{\mathrm{m}}}{z F}-\frac{R T}{z F} \ln \left(\frac{v \alpha}{N_{0}} \varepsilon_{\mathrm{p}}+1\right). $ | (11) |
由式(10)、(11)可知,当金属结构不发生塑性变形(εp=0)时,由于力学化学效应引起的金属腐蚀电位的负移量与Von Mises应力存在线性关系,当结构发生塑性变形时,式(11)中的ΔP为屈服强度,且腐蚀电位负移量与塑性应变之间存在对数关系,因此,腐蚀电位负移量明显增大,文献[22]也证实了弹塑性应变所引起的力学化学效应明显大于弹性应力. 在弹性变形范围内,当原子由晶格节点的平衡位置做较小的位移时,受激的金属原子将增加其位能,该位能使受激的金属原子的电化学位增加,电化学位的改变将引起平衡电位的改变. 金属在塑性变形范围内,产生新的位错并形成位错平面塞积群,从而引起电化学位的增大,在塑性滑移条件下,单位体积内完成的机械变形功等于系统在单位体积中形成位错时热力势的增加,由此可以得到位错密度与因位错产生的电化学位之间的关系. 因此,不论是弹性变形还是塑性变形都会导致金属的电化学电位增大,从而使得金属的平衡电位降低,由式(10)可知,金属的腐蚀电位相应降低.
2.3 力学化学效应对电流密度及腐蚀电场的影响图 7为由力学化学耦合模型计算得到的不同拉伸位移下腐蚀缺陷处的阴阳极电流密度分布以及净电流密度分布. 当拉伸位移为0 mm时,船体钢表面的铁阳极氧化溶解反应电流密度处处相等,都为85 mA/m2,当拉伸位移从0.4 mm增大到1.2 mm时,铁阳极氧化电流密度也随之增大,且电流密度在整个腐蚀缺陷的长度上分布较为均匀,当拉伸位移进一步增大到1.6 mm和1.8 mm时,腐蚀缺陷中心的阳极氧化电流密度急剧增大,分别为130 mA/m2和142 mA/m2,由于腐蚀缺陷两端点的应力值最小,因此,这两点的阳极氧化电流密度也最小. 当不存在拉伸位移时,船体钢表面的氧阴极还原的电流密度都为-85 mA/m2,这与阳极氧化电流密度的大小相等,阴极电流密度大小随着拉伸位移的增大而增大,塑性变形对阴极还原反应力学化学效应的影响也大于弹性变形. 当腐蚀缺陷处发生弹性变形时,缺陷长度上的净电流密度均小于5 mA/m2,而发生塑性变形时,缺陷中心的净电流密度急剧增大,分别为21、28 mA/m2,而缺陷两边的净电流密度为负,说明由于缺陷附近应力分布的不均匀引起了局部的应力腐蚀电偶.

|
图 7 不同拉伸位移下腐蚀缺陷处的电流密度分布 Fig. 7 Current density distribution at corrosion defect under different tensile displacements |
图 8为不同拉伸位移下溶液中的腐蚀电场模量和船体钢中的应力分布,图中箭头方向为溶液中的电流流向,箭头大小正比于电流大小. 由图可知,随着拉伸位移的增大,腐蚀缺陷处的应力增大,导致溶液中的腐蚀电场明显增大,且电流由腐蚀缺陷中心流向两边,这是因为缺陷中心的应力集中使得溶液中的电位负移,溶液中电位梯度的存在为溶液中的电流流动提供了驱动力,从而形成应力腐蚀电偶,且缺陷中心为阳极而缺陷两边为阴极. 另外,腐蚀缺陷的面积远远小于非缺陷区域,形成了小阳极大阴极的现象,这使得应力腐蚀电偶效应进一步增强,因此产生的腐蚀电场也越大.

|
图 8 不同拉伸位移下溶液中的腐蚀电场模量分布 Fig. 8 Distribution of corrosion electric field modulus in solution under different tensile displacements |
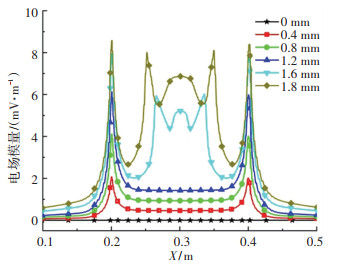
图 9为由力学化学耦合模型计算得到的不同拉伸位移下腐蚀缺陷处的电场模量分布,当拉伸位移为零时,船体钢不存在应力,其表面发生均匀腐蚀,阳极电流密度与阴极电流密度大小相等符号相反,因此不产生腐蚀电场. 当拉伸位移不为零时,腐蚀缺陷处的应力集中导致了应力腐蚀电偶的形成,从而产生腐蚀电场,弹性变形范围内,腐蚀电场在缺陷长度上均匀分布,电场模量随着应力的增大而均匀增大,且电场模量值均较小,发生塑性变形时,腐蚀电场显著增大,这是因为金属在塑性变形的易滑移阶段和形变强化阶段产生新的位错并形成位错平面塞积群,导致力学化学效应急剧增大[23].
|
图 9 不同拉伸位移下腐蚀缺陷处的电场模量分布 Fig. 9 Distribution of electric field modulus at corrosion defect under different tensile displacements |
1) 应力对称分布于腐蚀缺陷中心两侧,缺陷中心存在应力集中,当拉伸位移为1.6 mm和1.8 mm时,缺陷中心区域发生了一定程度的塑性变形.
2) 力学化学效应使得金属腐蚀电位负移,缺陷处的应力集中导致了溶液中电位分布的不均匀性,当发生塑性变形时,腐蚀缺陷附近的溶液与其他区域的溶液形成了明显的电位差.
3) 溶液中电位梯度的存在为电流流动提供了驱动力,从而形成应力腐蚀电偶,且缺陷中心为阳极而缺陷两边为阴极,由于腐蚀缺陷的面积远远小于非缺陷区域,因此形成了小阳极大阴极的现象,这使得应力腐蚀电偶效应进一步增强.
4) 塑性范围内的力学化学效应明显大于弹性阶段.
| [1] |
王向军, 嵇斗. 舰船电场防护原理[M]. 武汉: 海军工程大学出版社, 2016: 123. WANG Xiangjun, JI Dou. Electric field elimination principle of ship[M]. Wuhan: Naval University of Engineering Press, 2016: 123. |
| [2] |
KIM Y S, LEE S K, CHUNG H J, et al. Influence of a simulated deep sea condition on the cathodic protection and electric field of an underwater vehicle[J]. Ocean Engineering, 2018, 148: 223. DOI:10.1016/j.oceaneng.2017.11.027 |
| [3] |
WANG Jinhong, LI Bin, CHEN Lianping. A novel detection method for underwater moving targets by measuring their ELF emissions with inductive sensors[J]. Sensors, 2017, 17: 56. DOI:10.3390/s17081734 |
| [4] |
王泽忠, 石雨鑫. 三维电场多极子曲面边界元方法研究[J]. 电工技术学报, 2018, 33(24): 5797. WANG Zezhong, SHI Yuxin. Fast multipole curved boundary element method for 3D electrostatic field[J]. Transactions of China Electrotechnical Society, 2018, 33(24): 5797. DOI:10.19595/j.cnki.1000-6753.tces.171636 |
| [5] |
KIM Y S, KIM J, CHOI D, et al. Optimizing the sacrificial anode cathodic protection of the rail canal structure in seawater using the boundary element method[J]. Engineering Analysis with Boundary Elements, 2017, 77: 36. DOI:10.1016/j.enganabound.2017.01.003 |
| [6] |
XING S H, LI Y, SONG H Q, et al. Optimization the quantity, locations and output currents of anodes to improve cathodic protection effect of semi-submersible crane vessel[J]. Ocean Engineering, 2016, 113: 144. DOI:10.1016/j.oceaneng.2015.12.047 |
| [7] |
XU Qinglin, WANG Xiangjun, XU Chong. Frumkin correction of corrosion electric field generated by 921A-B10 galvanic couple[J]. Journal of Electroanalytical Chemistry, 2019, 855: 113599. DOI:10.1016/j.jelechem.2019.113599 |
| [8] |
WANG Xiangjun, XU Qinglin, ZHANG Jianchun, et al. Simulating underwater electric field signal of ship using the boundary element method[J]. Progress in Electromagnetics Research M, 2018, 76: 43. DOI:10.2528/PIERM18092706 |
| [9] |
KIM Y S, SEOL S, LEE J S, et al. Optimizing anode location in impressed current cathodic protection system to minimize underwater electric field using multiple linear regression analysis and artificial neural network methods[J]. Engineering Analysis with Boundary Elements, 2018, 96: 84. DOI:10.1016/j.enganabound.2018.08.012 |
| [10] |
徐庆林, 王向军, 张建春, 等. 温度对舰船阴极保护和腐蚀静电场的影响[J]. 国防科技大学学报, 2019, 41(4): 182. XU Qinglin, WANG Xiangjun, ZHANG Jianchun, et al. Influence of temperature on the cathodic protection and corrosion electrostatic field of ships[J]. Journal of National University of Defense Techno-logy, 2019, 41(4): 182. DOI:10.11887/j.cn.201904026 |
| [11] |
SCHAEFER D, DOOSE J, PICHLMAIER M, et al. Conversion of UEP signatures between different environmental conditions using shaft currents[J]. IEEE Journal of Oceanic Engineering, 2014, 42: 1. DOI:10.1109/JOE.2015.2401991 |
| [12] |
陈聪, 龚沈光, 李定国. 基于混合模型的舰船腐蚀相关静态电、磁场[J]. 哈尔滨工业大学学报, 2010, 42(3): 495. CHEN Cong, GONG Shenguang, LI Dingguo. Corrosion related static electric and magnetic field of ships based on mixed modeling[J]. Journal of Harbin Institute of Technology, 2010, 42(3): 495. |
| [13] |
毛伟. 浅海环境下运动舰船轴频电磁场建模方法及传播规律研究[D]. 武汉: 海军工程大学, 2009 MAO Wei. Research on modeling method of the moving ship SREM field and its propagation in shallow sea[D]. Wuhan: Naval University of Engineering, 2009 |
| [14] |
陈聪. 舰船电磁场的模型研究和深度换算[D]. 武汉: 海军工程大学, 2008 CHEN Cong. Research on the modeling and the extrapolation of electromagnetic field of a ship [D]. Wuhan: Naval University of Engineering, 2008 |
| [15] |
XU L, CHENG Y F. A finite element based model for prediction of corrosion defect growth on pipelines[J]. International Journal of Pressure Vessels and Piping, 2017, 153: 70. DOI:10.1016/j.ijpvp.2017.05.002 |
| [16] |
WANG Y, WHARTON J A, SHENOI R A. Mechano-electrochemical modelling of corroded steel structures[J]. Engineering Structures, 2016, 128: 1. DOI:10.1016/j.engstruct.2016.09.015 |
| [17] |
WANG Haitao, HAN Enhou. Computational simulation of corrosion pit interactions under mechanochemical effects using a cellular automaton/finite element model[J]. Corrosion Science, 2016, 103: 305. DOI:10.1016/j.corsci.2015.11.034 |
| [18] |
马荣耀, 赵林, 王长罡, 等. 静水压力对金属腐蚀热力学及动力学的影响[J]. 金属学报, 2019, 55(2): 281. MA Rongyao, ZHAO Lin, WANG Changgang, et al. Influence of hydrostatic pressure on the thermodynamics and kinetics of metal corrosion[J]. Acta Metallurgica Sinica, 2019, 55(2): 281. |
| [19] |
YANG Hongqi, ZHANG Qi, TU Sanshan, et al. Effects of inhomogeneous elastic stress on corrosion behaviour of Q235 steel in 3.5% NaCl solution using a novel multi-channel electrode technique[J]. Corrosion Science, 2016, 110: 1. DOI:10.1016/j.corsci.2016.04.017 |
| [20] |
XU L Y, CHENG Y F. Development of a finite element model for simulation and prediction of mechanoelectrochemical effect of pipeline corrosion[J]. Corrosion Science, 2013, 73: 150. DOI:10.1016/j.corsci.2013.04.004 |
| [21] |
杨宏启, 张崎, 李一民, 等. 弹性应力对碳钢在海水环境中腐蚀速率的影响[J]. 华中科技大学学报, 2016, 44(10): 16. YANG Hongqi, ZHANG Qi, LI Yimin, et al. Effects of elastic stress on corrosion rate of carbon steel in seawater[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2016, 44(10): 16. |
| [22] |
XU L Y, CHENG Y F. Corrosion of X100 pipeline steel under plastic strain in a neutral pH bicarbonate solution[J]. Corrosion Science, 2012, 64: 145. DOI:10.1016/j.corsci.2012.07.012 |
| [23] |
WANG Yongxing, ZHAO Weimin, AI Hua, et al. Effects of strain on the corrosion behaviour of X80 steel[J]. Corrosion Science, 2011, 53(9): 2761. DOI:10.1016/j.corsci.2011.05.011 |
 2021, Vol. 53
2021, Vol. 53


