2. 空间智能控制技术重点实验室(北京控制工程研究所), 北京100190
2. Science and Technology on Space Intelligent Control Laboratory (Beijing Institute of Control Engineering), Beijing 100190, China
随着现代化技术的迅猛发展及航天任务需求的不断增加,以卫星为核心的相关技术得到了广泛的应用[1-3]. 单一卫星由于自身的局限性,越来越难以满足空间任务的需要. 卫星编队技术可以突破卫星自身载荷支持能力限制,通过将多个载荷分散至多颗卫星,不仅可以实现星间备份,提高系统的可靠性,同时空间中的卫星通过星间链路相互协作,具有单颗卫星无可比拟的优势,被广泛应用于干涉合成孔径雷达、空间攻防、电子侦察等方面,在军用和民用方面都发挥着极其重要的作用,是世界各航天大国空间技术发展的主流方向. 对卫星编队来说,姿态同步控制至关重要.
近年来,多卫星编队协同控制完成复杂的航天任务受到国内外研究机构越来越广泛的关注. 在卫星编队姿态协同控制中,其控制目标是编队姿态及角速度分别跟踪上期望的参考指令信息,同时每个卫星与邻居卫星保持相对的姿态指向及姿态稳定度,分散式编队是一种常用的编队方式. 文献[4]针对刚体航天器编队姿态协调控制问题,提出一种基于行为控制器,在保证航天器对期望姿态跟踪的同时,实现了与其通信航天器间的姿态同步. 文献[5]基于行为法,将控制率分为位置保持部分和编队保持部分,应用PD以及姿态跟踪控制算法保证了闭环系统的稳定性. 文献[6]采用线性滑模方法对位置保持部分和编队保持部分进行设计,进一步提升了控制器鲁棒性. 文献[7]综合考虑线性滑模与行为控制方法,开创性提出在线性滑模面进行位置保持项和编队保持项设计策略,基于线性滑模面的控制器实现了航天器在有向及无向通信拓扑下的分散式编队控制. 文献[8]利用非奇异快速终端滑模取代线性滑模,进行了编队加权滑模面的重新设计,并结合自适应技术,实现了外界干扰以及系统不确定性作用下航天器编队跟踪误差在原点附近小邻域范围内的有限时间收敛. 由此可见,卫星编队控制目前是研究的热点问题,而在编队过程中,由于受所携带的低速陀螺或特定的航天任务影响,卫星的机动角速度不能过大,必须保持在某一范围内,以保证载荷的有效正常工作,否则错误的姿态测量信息会对卫星安全飞行带来不利影响. 因此,国内外学者对卫星角速度约束进行了深入的研究[9-12]. 文献[13]针对角速度约束下的刚柔卫星姿态跟踪控制,提出了一种输入输出饱和转化的方法,有效解决了角速度约束,实现姿态稳定跟踪. 文献[14]综合考虑卫星执行器故障及角速度约束,设计了指令滤波方法,保证对期望姿态的渐近收敛. 文献[15]同时考虑了卫星角速度及输入约束,提出一种新型控制器设计方法,实现了姿态的大范围渐近稳定控制. 通过调研可知,角速度约束下的卫星编队有限时间姿态同步控制目前研究较少,也是本文的研究重点.
传统的Simulink均为离线仿真,只适用于卫星控制算法的初步验证工作,算法在实时情况下的性能无法得到保证. 此外,传统分析手段依赖于抽象的数据与图表,如何以更为直观的方式进行控制算法评估成为当前的热点问题. 文献[16]提出了一种硬件在环仿真架构TMO-HILS,并基于该架构开发了无人机控制仿真系统. 在嵌入式控制器中运行控制算法,在PC机上运行无人机动力学模型,并基于FlightGear开发了视景显示模块,用于多无人机协同控制的分布式实时仿真. 文献[17]针对无人驾驶飞行器UAV设计了一种硬件在环实时仿真框架,该设计已成功应用于多种飞行测试的模拟. 文献[18]基于xPC实时仿真技术开发了一套卫星电磁编队控制实时仿真系统,可用于离线模型实时性能的评估工作. 文献[19]基于MATLAB与STK间的数据通信,实现了仿真过程的可视化显示. 由此可见,在控制算法的实时仿真验证及控制过程的视景演示方面,相关学者对平台硬件及软件的架构设计与选型开展了一系列工作,但在分布式实时仿真、定制化视景演示方面还存在较大空白.
本文考虑角速度约束下卫星编队的姿态同步控制与实时演示验证问题,将角速度约束转换为角速度跟踪误差约束,基于新型附加系统动态设计姿态同步控制器,实现约束下编队姿态的有限时间同步控制. 通过搭建分布式实时仿真验证平台,在验证控制算法实时可靠性的同时对姿态同步控制过程进行真实模拟.
1 卫星编队模型及问题描述本文考虑由N个刚体卫星组成的编队系统,FBi(i=1, 2,…,N)为第i个卫星的本体坐标系,FI及FD分别为惯性系及期望坐标系. 那么第i个卫星的姿态运动学及动力学模型表达为
| $ \left\{\begin{array}{l} \dot{\boldsymbol{q}}_{v i}=\frac{1}{2}\left(q_{0 i} \boldsymbol{I}_{3}+{\boldsymbol{q}_{v i}}^{\times}\right) \boldsymbol{\omega}_{i}, \\ \dot{q}_{0 i}=-\frac{1}{2} \boldsymbol{q}_{v i}^{\mathrm{T}} \boldsymbol{\omega}_{i}. \end{array}\right. $ | (1) |
| $ \boldsymbol{\dot J}_{i} {\boldsymbol{\omega}_{i}=-} \boldsymbol{\omega}_{i}^{\times} \boldsymbol{J}_{i} \boldsymbol{\omega}_{i}+\boldsymbol{u}_{i}(t), i=1,2, \cdots, N $ | (2) |
其中:I3∈R3×3为单位矩阵,ωi=[ωi1 ωi2 ωi3]T表示第i个卫星的角速度,Ji为转动惯量,q0i为四元数标量部分,qvi=[q1i q2i q3i]T为四元数矢量部分,ui(t)为控制力矩. qvi×为斜对称矩阵,表示为qvi×=
考虑卫星运行过程中低速陀螺等卫星要求影响,需要对角速度进行一定的限制,表示为
| $ \boldsymbol{\omega}_{i}=\left\{\boldsymbol{\omega}_{i j}(t) \| \boldsymbol{\omega}_{i j}(t) \mid \leqslant \omega_{\max }, j=1,2,3\right\}. $ | (3) |
其中ωmax为允许的最大角速度.
假设领航者的姿态四元数ql及角速度ωl由以下动态系统获得[20]:
| $ \left\{\begin{array}{l} \dot{\boldsymbol{q}}_{v l} =\frac{1}{2}\left(q_{0 l} \boldsymbol{I}_{3}+{\boldsymbol{q}_{v l}}^{\times}\right) \boldsymbol{\omega}_{l}, \\ \dot{q}_{0 l} =-\frac{1}{2} \boldsymbol{q}_{v l}^{\mathrm{T}} \boldsymbol{\omega}_{l}; \end{array}\right. $ | (4) |
| $ \dot{\boldsymbol{\omega}}_{l}=\boldsymbol{S} \boldsymbol{\omega}_{l}. $ | (5) |
其中:ql=[q0l q1l q2l q3l]T=[q0l qvlT]T为领航者在本体系FB0相对惯性系FI下的姿态四元数,满足q0l2+qvlTqvl=1. ωl∈R3为领航者在本体系FB0相对惯性系FI的角速度,S∈R 3×3为常数矩阵.
假设1 Gn是连通的.
假设2 系统
假设3 领航者的角速度及其导数是范数有界的,即满足
引理1 [21]针对系统ẋ=f(t, x),如果存在连续可微的正定函数V(x): D→Rn,正常数λ及0 < τ < 1,使得
| $ \boldsymbol{T}_{\text {reach }} \leqslant \frac{\boldsymbol{V}^{1-\tau}\left(x_{0}\right)}{\lambda(1-\tau)}, $ | (6) |
其中V(x0)为V(x)的初值.
本文控制目标为:基于第i个卫星的运动学及动力学模型(1)、(2),考虑角速度约束(3),设计编队控制器ui(i=1, 2,…,N),使得编队中所有跟随者卫星能够在有限时间实现对领航者姿态四元数方程(4)及角速度方程(5)的跟踪控制,且保证满足角速度约束限制.
2 姿态同步控制器设计基于领航者姿态方程(4)、(5),考虑分散式编队特点,第i个卫星的跟踪误差可表示为
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{q}}_{evi}} = {q_{0l}}{\mathit{\boldsymbol{q}}_{vi}} - \mathit{\boldsymbol{q}}_{vl}^ \times {\mathit{\boldsymbol{q}}_{vi}} - {q_{0i}}{\mathit{\boldsymbol{q}}_{vl}},}\\ {{q_{e0i}} = \mathit{\boldsymbol{q}}_{vl}^{\rm{T}}{\mathit{\boldsymbol{q}}_{vi}} + {q_{0i}}{q_{0l}},}\\ {{\mathit{\boldsymbol{\omega }}_{ei}} = {\mathit{\boldsymbol{\omega }}_i} - {\mathit{\boldsymbol{R}}_i}{\mathit{\boldsymbol{\omega }}_l},} \end{array}} \right. $ | (7) |
其中Ri为期望坐标系FD到本体坐标系FBi的旋转矩阵,其表达式为Ri=2qeviqeviT+(qe0i2-qeviTqevi)I3-2qe0iqevi×. 因此,基于方程(1)、(2)、(7),可得姿态跟踪误差动态为
| $ \left\{\begin{array}{l} \dot{\boldsymbol{q}}_{e v i}=\frac{1}{2}\left(q_{e 0 i} \boldsymbol{I}_{3}+\boldsymbol{q}_{e v i}^{\times}\right) \boldsymbol{\omega}_{e i} ,\\ \dot{q}_{e 0 i}=-\frac{1}{2} \boldsymbol{q}_{e v i}^{\mathrm{T}} \boldsymbol{\omega}_{e i}, \\ \boldsymbol{J}_{i} \boldsymbol{\dot \omega}_{e i}=-{\boldsymbol{\omega}_{i}}^{\times} \boldsymbol{J}_{i} \boldsymbol{\omega}_{i}+\boldsymbol{J}_{i}\left(\boldsymbol{\omega}_{e i}^{\times} \boldsymbol{R}_{i} \boldsymbol{v}_{i}-\boldsymbol{R}_{i} \boldsymbol{\dot v}_{i}\right)+\boldsymbol{u}_{i} . \end{array}\right. $ | (8) |
其中角速度ωi必须满足约束(3).
考虑到控制器设计时所使用的状态变量为姿态角速度跟踪误差,而非姿态角速度本身,故首先将姿态角速度约束(3)转化为角速度跟踪误差约束,以便在后续的控制器设计中保证满足约束要求.
基于‖Ri‖=1及式(7),角速度跟踪误差约束设置为
| $ \boldsymbol{\omega}_{e i}=\left\{\boldsymbol{\omega}_{e i j}|| \boldsymbol{\omega}_{e i j} \mid \leqslant \omega_{e, \max }, j=1,2,3\right\}. $ | (9) |
其中ωe, max=ωmax-ωl, max为姿态角速度误差约束,ωmax>ωl, max. 由式(9)可以看出,如果ωei满足约束(9),那么角速度约束ωi就会满足约束(3). 因此,在后续控制器设计过程中,只需保证约束(9)成立即可.
下面将采用分环控制思想,通过将系统(8)分为姿态角子系统与角速度子系统,分别基于各子系统进行卫星编队姿态同步控制器设计.
2.1 姿态角子系统控制器设计本小节针对姿态角子系统,通过将角速度跟踪误差视为控制量,设计虚拟控制输入,并保证满足姿态角速度跟踪误差约束(9).
姿态角子系统为
| $ \left\{\begin{array}{l} \dot{\boldsymbol{q}}_{e v i}=\boldsymbol{\varXi}_{i}\left(\boldsymbol{q}_{e i}\right) \boldsymbol{\omega}_{e i} ,\\ \dot{q}_{e 0 i}=-\frac{1}{2} \boldsymbol{q}_{e v i}^{\mathrm{T}} \boldsymbol{\omega}_{e i}. \end{array}\right. $ | (10) |
其中Ξ(qei)=
考虑到姿态四元数的性能,如果qevi收敛到0,那么qe0i也会收敛到0. 因此,当前控制目标为:在满足姿态角速度跟踪误差约束(9)条件下设计虚拟控制输入,保证qevi的有限时间收敛.
定义虚拟角速度跟踪误差输入ωdi∈R3,考虑约束(9),真正的虚拟角速度跟踪误差ωai∈R3, 则
| $ \omega_{a i, j}=\left\{\begin{array}{l} \omega_{e, \max }, \omega_{d i, j}>\alpha \omega_{e, \max }, \\ \omega_{d i, j},\left|\omega_{d i, j}\right| \leqslant \alpha \omega_{e, \max } ,\\ -\omega_{e, \max }, \omega_{d i, j}<-\alpha \omega_{e, \max }. \end{array}\right. $ | (11) |
其中:0 < α < 1,ωdi=[ωdi, 1 ωdi, 2 ωdi, 3]T,ωai=[ωai, 1 ωai, 2 ωai, 3]T.
定义超出姿态角速度约束的变量为ωei, Δ=ωai-ωdi. 为保证满足角速度跟踪误差约束影响,设计如下有限时间附加系统来调整虚拟控制输入:
| $ \begin{aligned} \boldsymbol{\xi}_{1 i}=&-k_{1 i} \boldsymbol{\xi}_{1 i}+\varXi_{i}\left(\boldsymbol{q}_{e i}\right) \boldsymbol{\omega}_{e i, \Delta}+\\ & \varXi_{i}\left(\boldsymbol{q}_{e i}\right) \boldsymbol{\xi}_{2 i}-\lambda_{3 i}\left|\boldsymbol{\xi}_{1 i}\right|^{r_{1}} \operatorname{sgn} \boldsymbol{\xi}_{1 i}. \end{aligned} $ | (12) |
其中:ξ1i为姿态角子系统附加信号,ξ2i为角速度子系统附加信号,k1i>0, λ3i>0, 0 < r1 < 1. Ξi(qei)ξ2i项用于后续稳定性证明,Ξi(qei)ωei, Δ项用来补偿超出角速度误差约束值. 当未超过约束时,ξ1i会在有限时间收敛到0,即不再起作用;当超过约束时,ξ1i的值会发生变化,进而改变所设计的虚拟控制输入的值,补偿因超过约束对系统带来的影响.
基于姿态四元数跟踪误差系统(10),设计虚拟控制输入ωdi:
| $ \begin{aligned} \boldsymbol{\omega}_{d i}=& \varXi_{i}\left(\boldsymbol{q}_{e i}\right)^{-1}\left[-k_{1 i} \boldsymbol{q}_{e i}-\right.\\ &\left.\lambda_{1 i} \boldsymbol{v}_{1 i}^{\varepsilon_{1}}-\lambda_{3 i}\left|\boldsymbol{\xi}_{1 i}\right|^{r_{1}} \operatorname{sgn} \boldsymbol{\xi}_{1 i}\right]. \end{aligned} $ | (13) |
其中:qei=[qevi qe0i]为第i个航天器姿态四元数跟踪误差,v1i=qevi-ξ1i,λ1i>0, 0 < ε1 < 0.
2.2 角速度子系统控制器设计针对角速度子系统,设计控制输入ui,需要在有限时间实现对ωai的稳定跟踪.
考虑角速度子系统:
| $ \boldsymbol{J}_{i} \dot{\boldsymbol{\omega}}_{e i}=-{\boldsymbol{\omega}_{i}}^{\times} \boldsymbol{J}_{i} \boldsymbol{\omega}_{i}+\boldsymbol{J}_{i}\left(\boldsymbol{\omega}_{e i}^{\times} \boldsymbol{R}_{i} \boldsymbol{v}_{i}-\boldsymbol{R}_{i} \dot{\boldsymbol{v}}_{i}\right)+\boldsymbol{u}_{i}, $ | (14) |
那么,ωei的动态跟踪误差为
| $ \begin{aligned} \boldsymbol{J}_{i} \dot{\boldsymbol{e}}_{\omega i}=& \boldsymbol{J}_{i} \dot{\boldsymbol{\omega}}_{e i}-\boldsymbol{J}_{i} \dot{\boldsymbol{\omega}}_{a i}=-{\boldsymbol{\omega}_{i}}^{\times} \boldsymbol{J}_{i} \boldsymbol{\omega}_{i}+\\ & \boldsymbol{J}_{i}\left(\boldsymbol{\omega}_{e i}^{\times} \boldsymbol{R}_{i} \boldsymbol{v}_{i}-\boldsymbol{R}_{i} \dot{\boldsymbol{v}}_{i}\right)+\boldsymbol{u}_{i}-\boldsymbol{J}_{i} \dot{\boldsymbol{\omega}}_{a i}. \end{aligned} $ | (15) |
设计如下附加系统:
| $ \boldsymbol{\xi}_{2 i}=-k_{2 i} \boldsymbol{\xi}_{2 i}-\lambda_{4 i}\left|\boldsymbol{\xi}_{2 i}\right|^{r_{2}} \operatorname{sgn}\left(\boldsymbol{\xi}_{2 i}\right)-\varXi_{i}^{\mathrm{T}}\left(\boldsymbol{q}_{e i}\right) \boldsymbol{\xi}_{1 i}. $ | (16) |
其中:k2i, λ4i>0, 0 < r2 < 1,v2i=eωi-ξ2i.
基于角速度误差动态(15),设计真实控制输入:
| $ \begin{aligned} \boldsymbol{u}_{i}=& \boldsymbol{J}_{i}^{-1}\left[-k_{2 i} \boldsymbol{e}_{\omega i}+{\boldsymbol{\omega}_{i}}^{\times} \boldsymbol{J} \hat{\boldsymbol{\omega}}_{i}+\boldsymbol{J}_{i} \dot{\boldsymbol{\omega}}_{a i}-\right.\\ & \boldsymbol{J}_{i}\left(\boldsymbol{\omega}_{e i}^{\times} \boldsymbol{R}_{i} \boldsymbol{v}_{i}-\boldsymbol{R}_{i} \dot{\boldsymbol{v}}_{i}\right)-\lambda_{2 i} \boldsymbol{v}_{2 i}^{\varepsilon_{2}}-\\ &\left.\lambda_{4 i}\left|\boldsymbol{\xi}_{2 i}\right|^{r_{2}} \operatorname{sgn}\left(\boldsymbol{\xi}_{2 i}\right)-\varXi_{i}^{\mathrm{T}}\left(\boldsymbol{q}_{e i}\right) \boldsymbol{q}_{e v i}\right]. \end{aligned} $ | (17) |
其中:λ2i>0, 0 < ε2 < 1.
定理1 针对i卫星的运动学及动力学模型(1)、(2),考虑角速度约束(3). 若设计如式(17)所示的控制器,如式(12)、(16)所示的附加系统,那么存在一系列常数k1i、k2i、λ1i、λ2i、λ3i、λ4i>0,0 < ε1、ε2、r1、r2 < 1使得姿态跟踪误差qevi及ωei将会在有限时间收敛到平衡点附近的小邻域.
证明 定义Lyapunov函数:
| $ {\mathit{\boldsymbol{V}}_V} = {\mathit{\boldsymbol{V}}_{v1}} + {\mathit{\boldsymbol{V}}_{v2}}, $ | (18) |
其中
| $ \begin{aligned} \dot{\boldsymbol{V}}_{v 1}=& \sum\limits_{i=1}^{N} \boldsymbol{v}_{1 i}^{\mathrm{T}} \dot{\boldsymbol{v}}_{1 i}=\sum\limits_{i=1}^{N} \boldsymbol{v}_{1 i}^{\mathrm{T}}\left(\dot{\boldsymbol{q}}_{e v i}-\dot{\boldsymbol{\xi}}_{1 i}\right)=\\ & \sum\limits_{i=1}^{N} \boldsymbol{v}_{1 i}^{\mathrm{T}}\left(\varXi_{e i}\left(\boldsymbol{q}_{e i}\right)\left(\boldsymbol{\omega}_{d i}+\boldsymbol{e}_{\omega i}+\boldsymbol{\omega}_{e i, \Delta}\right)\right)-\\ & \sum\limits_{i=1}^{N} \boldsymbol{v}_{1 i}^{\mathrm{T}} \boldsymbol{\xi}_{1 i}=\sum\limits_{i=1}^{N} \boldsymbol{v}_{1 i}^{\mathrm{T}}\left(-k_{1 i} \boldsymbol{v}_{1 i}-\lambda_{1 i} \boldsymbol{v}_{1 i}^{\varepsilon_{1}}+\right.\\ &\left.\varXi_{i}\left(\boldsymbol{q}_{e i}\right) \boldsymbol{v}_{2 i}\right). \end{aligned} $ | (19) |
其中:eωi=ωei-ωai为ωei的跟踪误差,v2i=eωi-ξ2i.
基于式(15)~(17)及式(19),对VV求导可得
| $ \begin{aligned} \dot{\boldsymbol{V}}_{V}=& \dot{\boldsymbol{V}}_{v 1}+\sum\limits_{i=1}^{N} \boldsymbol{v}_{2 i}^{\mathrm{T}} \dot{\boldsymbol{v}}_{2 i}=\\ & \dot{\boldsymbol{V}}_{v 1}+\sum\limits_{i=1}^{N} \boldsymbol{v}_{2 i}^{\mathrm{T}}\left(\boldsymbol{J}_{i} \dot{\boldsymbol{e}}_{\omega i}-\dot{\boldsymbol{\xi}}_{2 i}\right)=\\ & \dot{\boldsymbol{V}}_{v 1}+\sum\limits_{i=1}^{N} \boldsymbol{v}_{2 i}^{\mathrm{T}}\left(-k_{2 i} \boldsymbol{v}_{2 i}-\lambda_{2 i} \boldsymbol{v}_{2 i}^{\varepsilon_{2}}-\varXi_{i}^{\mathrm{T}}\left(\boldsymbol{q}_{e i}\right) \boldsymbol{v}_{1 i}\right)=\\ & \sum\limits_{j=1}^{2} \sum\limits_{i=1}^{N}\left(-k_{j i} \boldsymbol{v}_{j i}^{\mathrm{T}} \boldsymbol{v}_{j i}-\lambda_{j i} \boldsymbol{v}_{j i}^{\varepsilon_{j}+1}\right) \leqslant \\ &-2 K_{1} \boldsymbol{V}_{V}-\sqrt{2} \gamma_{1} \boldsymbol{V}^{(\varepsilon+1)} / 2. \end{aligned} $ | (20) |
其中:K1=min{k1i, k2i, i=1, …, N},ε=min{ε1, ε2},γ1=min{λ1i, λ2i, i=1, …, N}.
由式(20)可知,Lyapunov函数VV,即v1i及v2i是有界的. 因此,针对姿态角子系统(10)及角速度子系统(14),qevi、ωei是有界的. 此外,由引理1及式(20)可知,v1i和v2i将会在有限时间收敛到0. 下面将进行附加系统ξ1i、ξ2i的有限时间收敛证明.
定义Lyapunov函数:
| $ {\mathit{\boldsymbol{V}}_\xi } = {\mathit{\boldsymbol{V}}_{\xi 1}} + {\mathit{\boldsymbol{V}}_{\xi 2}}, $ | (21) |
其中
基于式(12)首先对Vξ1求导,可得
| $ \begin{aligned} \dot{\boldsymbol{V}}_{\xi 1}=& \sum\limits_{i=1}^{N} \boldsymbol{\xi}_{1}^{\mathrm{T}} \dot{\boldsymbol{\xi}}_{1 i}=\sum\limits_{i=1}^{N}-k_{1 i} \boldsymbol{\xi}_{1 i}^{\mathrm{T}} \boldsymbol{\xi}_{1 i}+\boldsymbol{\xi}_{1 i}^{\mathrm{T}} \varXi_{i}\left(\boldsymbol{q}_{e i}\right) \boldsymbol{\omega}_{e i, \Delta}+\\ & \sum\limits_{i=1}^{N} \boldsymbol{\xi}_{1 i}^{\mathrm{T}} \varXi_{i}\left(\boldsymbol{q}_{e i}\right) \boldsymbol{\xi}_{2 i}-\lambda_{3 i}\left|\boldsymbol{\xi}_{1 i}\right|^{r_{1}+1}. \end{aligned} $ | (22) |
对Lyapunov函数Vξ求导,代入式(16)、(22),可得
| $ \begin{array}{c} \dot{\boldsymbol{V}}_{\xi}=\dot{\boldsymbol{V}}_{\xi 1}+\sum\limits_{i=1}^{N} \boldsymbol{\xi}_{2 i}^{\mathrm{T}} \boldsymbol{\xi}_{2 i}=\dot{\boldsymbol{V}}_{\xi 1}+\sum\limits_{i=1}^{N} \boldsymbol{\xi}_{2 i}^{\mathrm{T}}\left(-k_{2 i} \boldsymbol{\xi}_{2 i}-\right. \\ \left.\lambda_{4 i}\left|\boldsymbol{\xi}_{2 i}\right|^{r_{2}} \operatorname{sgn}\left(\boldsymbol{\xi}_{2 i}\right)\right)+\sum\limits_{i=1}^{N} \boldsymbol{\xi}_{2 i}^{\mathrm{T}}\left(-\varXi_{i}^{\mathrm{T}}\left(\boldsymbol{q}_{e}\right) \boldsymbol{\xi}_{1 i}\right) \leqslant \\ -K_{1} \sum\limits_{j=1}^{2} \sum\limits_{i=1}^{N}\left(\boldsymbol{\xi}_{j i}^{\mathrm{T}} \boldsymbol{\xi}_{j i}\right)-\lambda \sum\limits_{j=3}^{4} \sum\limits_{i=1}^{N}\left(\left|\boldsymbol{\xi}_{j i}\right|^{r+1}\right)+ \\ \sum\limits_{i=1}^{N} \frac{\gamma}{2} \boldsymbol{\xi}_{2 i}^{\mathrm{T}} \boldsymbol{\xi}_{2 i}+\sum\limits_{i=1}^{N} \frac{\gamma}{2} \boldsymbol{\xi}_{1 i}^{\mathrm{T}} \boldsymbol{\xi}_{1 i}+\sum\limits_{i=1}^{N} \frac{1}{2 \gamma}\left\|\boldsymbol{\omega}_{e i, \Delta}\right\|^{2} \leqslant \\ \left(-K_{1}+\frac{\gamma}{2}\right) \boldsymbol{V}_{\xi}-\lambda \boldsymbol{V}_{\xi}^{(r+1) / 2}+\sum\limits_{i=1}^{N} \frac{1}{2 \gamma}\left\|\boldsymbol{\omega}_{e i, \Delta}\right\|^{2}. \end{array} $ | (23) |
其中:λ=min{λ3i, λ4i, i=1, …, N},γ>0.
选择参数K1>γ/2,则上式转换为
| $ {\mathit{\boldsymbol{\dot V}}_\xi } \le - {K_3}{\mathit{\boldsymbol{V}}_\xi } - \lambda \mathit{\boldsymbol{V}}_\xi ^{(r + 1)/2} + \zeta . $ | (24) |
其中:0≤K3≤K2-
基于对式(20)的描述,‖ωei, Δ‖是有界的,根据引理1可得,附加系统状态ξ1i、ξ2i会在有限时间收敛到平衡点附近小邻域内. 以上分别证明了v1i、v2i、ξ1i和ξ2i的有限时间收敛特性,考虑到v1i、v2i的定义,可得跟踪误差qevi,ωei也是有限时间收敛的. 证毕.
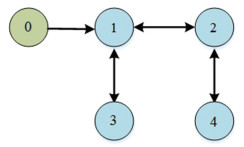
2.3 离线仿真验证 2.3.1 仿真参数设置仿真过程中,考虑4个跟随者,1个领航者组成的卫星编队系统. 其中,跟随者姿态四元数及角速度由式(1)、(2)确定,领航者姿态四元数及角速度由式(4)、(5)确定. 卫星间的通信形式如图 1所示,从图中可以确定,星间相连的权值系数为a10=a12=a21=a13=a31=a24=a42=1.
|
图 1 卫星编队拓扑图 Fig. 1 Topology of satellite formation |
领航者卫星常数矩阵S=
基于上述设计的姿态同步控制器以及给定的仿真参数,仿真结果如图 2~5所示.

|
图 2 姿态角子系统附加信号变化曲线 Fig. 2 Additional signal curves of attitude angle subsystem |
|
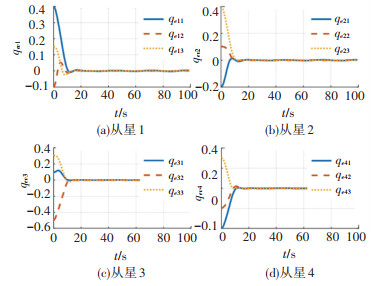
图 3 姿态四元数跟踪误差曲线 Fig. 3 Tracking error curves of quaternion |
|
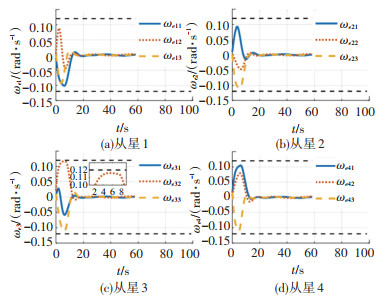
图 4 角速度跟踪误差曲线 Fig. 4 Tracking error curves of angular velocity |
|
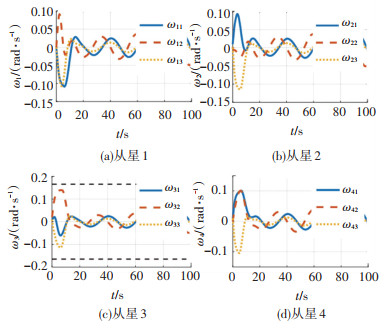
图 5 实际角速度曲线 Fig. 5 True angular velocity curves |
图 2为第i个跟随者姿态角子系统中附加信号ξ1i的变化曲线. 从仿真图中可以看出,在姿态机动的初始阶段,为了补偿角速度超出的约束值,附加信号ξ1i的值会相应增大,当角速度在约束值范围之内时,附加系统将不再发挥作用,且会保持稳定,不会对系统控制产生影响,从而验证了所设计有限时间附加系统的有效性. 图 3、4分别为第i个跟随者姿态四元数及角速度的跟踪误差变化曲线. 从仿真图中可以看出,每个跟随者的跟踪误差均会在20 s内收敛,即达到姿态同步,且满足角速度误差约束±0.12 rad/s,从而验证了所设计姿态同步控制器的有效性. 图 5为考虑约束下的实际角速度变化曲线. 图中两条黑色虚线分别为本节所设置的角速度约束±0.17 rad/s. 可以看出,卫星实际角速度的大小在整个机动过程中均未超过约束,从而证明本文所设计的时间附加系统确实能解决角速度约束问题.
3 分布式实时仿真虚拟平台搭建与三维视景演示本节搭建分布式实时仿真虚拟平台,在验证控制算法实时有效性的同时,以一种更为直观的形式演示卫星编队的控制过程.
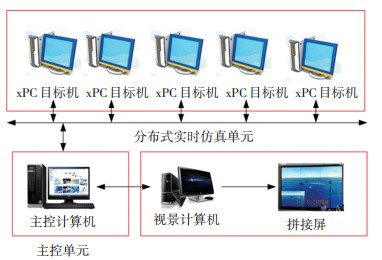
3.1 仿真平台架构仿真平台的总体结构及硬件组成如图 6、7所示. 平台主要分为3个部分,即实时仿真单元、主控单元和视景演示单元.
|
图 6 实时仿真平台总体结构图 Fig. 6 Architecture of real-time simulation platform |

|
图 7 平台硬件设备图 Fig. 7 Platform hardware devices |
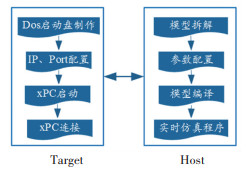
分布式实时仿真单元是基于xPC[23]技术搭建的快速原型仿真环境,通过装载卫星编队的仿真模型与控制算法,对其在实时状态下的性能进行测试,从而完成算法实时有效性的验证. xPC是MATLAB提供的一种用于产品原型测试、开发和实时系统配置的PC机解决方案. xPC目标机可采用常见的PC机进行配置,通过DOS系统下运行的实时内核构建一个实时环境. 主要操作流程如图 8所示.
|
图 8 分布式实时仿真流程 Fig. 8 Distributed real-time simulation procedure |
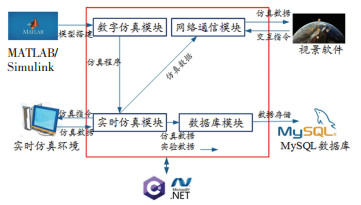
主控单元负责卫星编队控制实时仿真的进程控制、模型下载和数据管理. 在连接xPC之后,将编译好的实时仿真程序下载进目标机中进行实时仿真,同时利用MATLAB提供的xPC API—xPCFramework提取卫星的实时仿真数据,在主控面板进行曲线绘制的同时,通过网络通信将数据发送至视景演示单元,驱动视景软件进行三维可视化演示. 仿真实验结束后,将仿真数据存储到数据库,以便对模型及控制算法实时性能的进一步分析与评估. 本单元基于WPF[24](windows presentation foundation)进行开发. 主控单元结构图如图 9所示.
|
图 9 主控单元结构图 Fig. 9 Structure of main control unit |
视景演示单元基于Unity3D[25]搭建卫星任务场景,通过数据驱动的方式进行编队过程的三维可视化模拟. Unity3D是Unity Technologies开发的一个着力于创建诸如三维视频游戏、建筑可视化、实时三维动画等类型互动内容的多平台综合型游戏开发工具. 针对卫星编队控制的视景演示需求,场景搭建主要涉及太空背景的模拟、地球模型和卫星模型的制作以及光照的渲染. 其中,太空背景可由Unity提供的天空盒(Skybox)技术进行实现;专业的3D建模软件3ds Max为模型制作及格式转换提供了支持;Unity官方所提供的Effect特效中涉及了太阳耀斑的模拟;最后,编写数据接收脚本以获取主控单元传来的实时仿真数据.
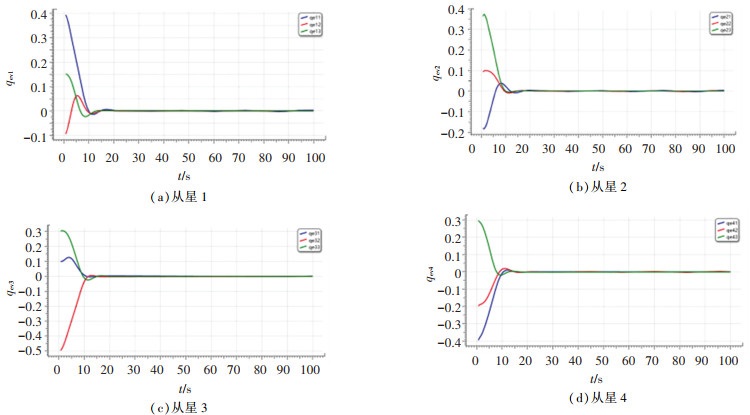
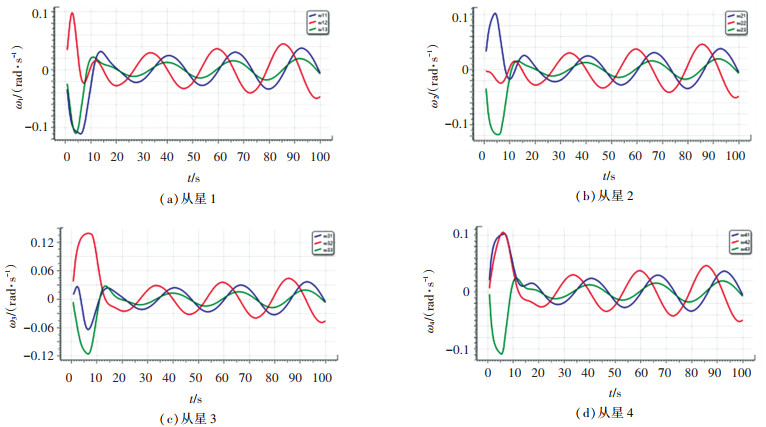
3.2 实时仿真验证及视景演示以2.3节一主四从卫星为例,对上述提出的角速度约束下卫星编队姿态同步控制算法进行实时仿真验证与视景演示. 实时仿真曲线如图 10、11所示. 可以看出,实时状态下的仿真曲线与离线仿真图吻合,在满足角速度误差约束和角速度约束的前提下,实现了跟随者对领航者姿态及角速度的快速同步,且满足角速度约束,从而验证了本文所提控制算法在实时环境下的有效性.
|
图 10 姿态四元数实时跟踪误差曲线 Fig. 10 Real-time tracking error curves of quaternion |
|
图 11 实际角速度实时曲线 Fig. 11 Real-time curves of actual angular velocity |
最终基于实时仿真数据驱动的卫星编队视景如图 12所示,可以看到,从星完成了对领航者的姿态同步跟随.

|
图 12 视景演示图 Fig. 12 Visual presentation |
1) 针对角速度约束问题,建立了卫星编队控制模型. 考虑控制器设计中所用变量为姿态角速度误差,而非角速度本身,故通过设计安全阈值实现两者的转换.
2) 通过设计新型附加系统状态,在有限时间内消除了超过约束部分对系统的影响,并在此基础上基于分环思想设计控制器,进行了整体闭环系统的稳定性证明,实现了满足角速度约束下的卫星编队有限时间姿态同步,仿真结果验证了算法的可靠性.
3) 基于分布式实时环境搭建了卫星编队仿真平台,完成了对所提算法实时有效性的验证. 进一步利用实时仿真数据驱动基于Unity3D搭建的卫星三维虚拟任务场景,实现了编队姿态同步控制过程的可视化演示.
| [1] |
FENG Jiajia, WANG Zuowei. GEO satellite thruster configuration and optimization[J]. Journal of Harbin Institute of Technology (New Series), 2020, 27(1): 52. |
| [2] |
WU Yunhua, HAN Feng, HUA Bing, et al. Review: a survey of single gimbal control moment gyroscope for agile spacecraft attitude control[J]. Journal of Harbin Institute of Technology (New Series), 2018, 25(6): 22. |
| [3] |
HUANG Jie, YOU Chaolan, HOU Peng, et al. Study on thermal deformation measurement of optical remote sensing satellite platform based on machine vision[J]. Journal of Harbin Institute of Technology (New Series), 2019, 26(5): 72. |
| [4] |
LAWTON J R, BEARD R W. Synchronized multiple spacecraft rotations[J]. Automatica, 2002, 38(8): 1359. DOI:10.1016/S0005-1098(02)00025-0 |
| [5] |
VANDYKE M C, HALL C D. Decentralized coordinated attitude control within a formation of spacecraft[J]. Journal of Guidance, Control, and Dynamics, 2006, 29(5): 1101. DOI:10.2514/1.17857 |
| [6] |
LIANG Haizhao, SUN Zhaowei, WANG Jianying. Robust decentralized attitude control of spacecraft formations under time-varying topologies, model uncertainties and disturbances[J]. Acta Astronautica, 2012, 81(2): 445. DOI:10.1016/j.actaastro.2012.08.017 |
| [7] |
WU Baolin, WANG Danwei, POH E K. Decentralized sliding-mode control for attitude synchronization in spacecraft formation[J]. International Journal of Robust and Nonlinear Control, 2013, 23(11): 1183. DOI:10.1002/rnc.2812 |
| [8] |
ZHOU Ning, XIA Yuanqing, LU Kunfeng, et al. Decentralised finite-time attitude synchronisation and tracking control for rigid spacecraft[J]. International Journal of Systems Science, 2015, 46(14): 2493. DOI:10.1080/00207721.2013.868949 |
| [9] |
SHAHROOEI A, KAZEMI M H. Multiple model adaptive attitude control of LEO satellite with angular velocity constraints[J]. International Journal of Aeronautical and Space Sciences, 2018, 19(1): 153. DOI:10.1007/s42405-018-0013-7 |
| [10] |
LI Dongyu, MA Guangfu, LI Chuanjiang, et al. Distributed attitude coordinated control of multiple spacecraft with attitude constraints[J]. IEEE Transactions on Aerospace and Electronic Systems, 2018, 54(5): 2233. DOI:10.1109/TAES.2018.2812438 |
| [11] |
HU Qinglei. Robust adaptive backstepping attitude and vibration control with L2-gain performance for flexible spacecraft under angular velocity constraint[J]. Journal of Sound and Vibration, 2009, 327(3): 285. |
| [12] |
MARSHALL A, TSIOTRAS P. Spacecraft angular velocity stabilization using a single-gimbal variable speed control moment gyro[C]//AIAA Guidance, Navigation and Control Conference and Exhibit. Austin: AIAA, 2003: 5654
|
| [13] |
BURLION L, BIANNIC J M, AHMED A T. Attitude tracking control of a flexible spacecraft under angular velocity constraints[J]. International Journal of Control, 2017, 92(7): 1524. |
| [14] |
SHEN Qiang, YUE Chengfei, GOH C H, et al. Rigid-body attitude tracking control under actuator faults and angular velocity constraints[J]. IEEE/ASME Transactions on Mechatronics, 2018, 23(3): 1338. DOI:10.1109/TMECH.2018.2812871 |
| [15] |
HU Qinglei, TAN X. Unified attitude control for spacecraft under velocity and control constraints[J]. Aerospace Science and Technology, 2017, 67: 257. DOI:10.1016/j.ast.2017.04.009 |
| [16] |
XU J, PARK H, JEONG K, et al. TMO-HILS architecture for real-time control system[C]// 2007 International Conference on Control, Automation and Systems. Seoul: IEEE, 2007: 1855
|
| [17] |
CAI Guowei, CHEN B M, LEE T H, et al. Design and implementation of a hardware-in-the-loop simulation system for small-scale UAV helicopters[J]. Mechatronics, 2009, 19(7): 1057. DOI:10.1016/j.mechatronics.2009.06.001 |
| [18] |
姚红, 汤亚锋, 胡敏. 基于xPC的航天器电磁编队控制系统实时仿真研究[C]// 第14届中国系统仿真技术及其应用学术年会. 三亚: 中国自动化学会, 2012: 692 YAO Hong, TANG Yafeng, HU Min. Research on real-time simulation of spacecraft electromagnetic formation control system based on xPC[C]// Proceedings of 14th Chinese Conference on System Simulation Technology & Application. Sanya: CAA, 2012: 692 |
| [19] |
FANG Xiang, GENG Yunhai. Simulations of spacecraft attitude control for tracking maneuvers with MATLAB and STK[C]// 2014 IEEE International Conference on Information and Automation. Hailar: IEEE, 2014: 1160
|
| [20] |
CAI He, HUANG Jie. The leader-following attitude control of multiple rigid spacecraft systems[J]. Automatica, 2014, 50(4): 1109. DOI:10.1016/j.automatica.2014.01.003 |
| [21] |
BHAT S P, BERNSTEIN D S. Continuous finite-time stabilization of the translational and rotational double integrators[J]. IEEE Transactions on Automatic Control, 1998, 43(5): 678. DOI:10.1109/9.668834 |
| [22] |
ZONG Qun, SHAO Shikai. Decentralized finite-time attitude synchronization for multiple rigid spacecraft via a novel disturbance observer[J]. ISA Transactions, 2016, 65: 150. DOI:10.1016/j.isatra.2016.08.009 |
| [23] |
王超, 王仕成, 刘志国. 基于MATLAB/xPC Target的实时仿真系统研究[J]. 控制工程, 2007(增刊2): 165. WANG Chao, WANG Shicheng, LIU Zhiguo. Research on real time simulation system based on MATLAB/xPC target[J]. Control Engineering of China, 2007(S2): 165. |
| [24] |
TROELSEN A, JAPIKSE P. WPF controls, layouts, events, and data binding[M]. Berkeley: Apress, 2020: 915.
|
| [25] |
XIE Jingming. Research on key technologies base Unity3D game engine[C]// 20127th International Conference on Computer Science & Education (ICCSE). Melbourne: IEEE, 2012: 695
|
 2021, Vol. 53
2021, Vol. 53


