2. 土木工程智能防灾减灾工业和信息化部重点实验室(哈尔滨工业大学), 哈尔滨 150090
2. Key Lab of Smart Prevention and Mitigation of Civil Engineering Disasters(Harbin Institute of Technology), Ministry of Industry and Information Technology, Harbin 150090, China
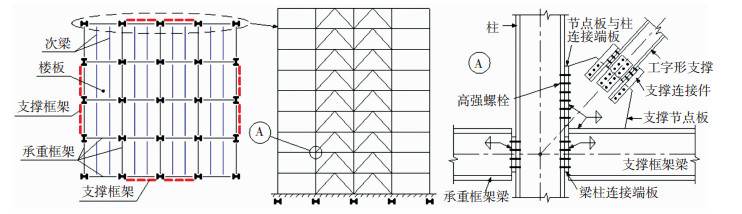
对于中心支撑-钢框架结构(以下称CBF),水平荷载作用下梁、柱、支撑等均以承受轴力为主,不考虑抗弯框架的刚度贡献。因此,梁柱节点可采用铰接,也可采用刚接,仅对节点转动能力提出要求,而不对其抗弯能力进行验算,本质上属于单重抗侧力体系结构。这种单重体系的CBF在国内外多高层工业与民用建筑中得到了广泛的应用。图 1给出了单重体系的装配式CBF的相关做法。
|
图 1 装配式CBF示意 Fig. 1 Diagram of fabricated steel concentrically braced frames |
然而,GB 50011—2010[1]和JGJ 99—2015[2]都倾向于推荐使用钢框架-中心支撑双重体系结构,未对这种单重体系结构给出明确规定,仅在CECS 160[3]中,依据抗震设计类别给出了CBF的高度和高宽比的限值。钢框架-中心支撑双重体系需要对支撑、梁、柱及其节点进行严格的抗震计算和构造设计,才能形成支撑和钢框架的双重抗震防线,显然存在施工难度高、经济性差的弊端。
可喜的是,新修订的GB 50017—2017[4]终于将支撑结构纳入到常用多高层结构体系,但在构件、节点及整个结构体系的抗震性能、低周疲劳寿命、大震抗倒塌能力、抗震设计方法及推广应用等方面仍有大量亟待进行的研究工作。
1 不同延性的CBF 1.1 不同延性的CBF的抗震性能差别CBF通过支撑的轴向刚度来抵抗侧向力,支撑的屈服和屈曲是弹塑性层间变形的主要来源。同层支撑或其节点断裂失效的数量越多,结构的承载力丧失越快,越容易产生薄弱楼层和倒塌机制。可以通过两种途径确保结构的大震不倒,一是增加单重体系中支撑系统的承载力来抵抗罕遇地震力;二是允许通过支撑的大量屈曲和屈服发展塑性,在往复弹塑性层间变形作用下,支撑及其节点不发生断裂而退出工作,结构维持大震不倒。依据上述两种抗震思想,形成了所谓低延性-高承载力的结构和高延性-适度承载力的结构,这正对应于AISC 341—16[5]中所谓的普通中心支撑-钢框架结构(OCBF)和特殊中心支撑-钢框架结构(SCBF)、EC8[6]中的中等延性中心支撑-钢框架结构(DCM)和高延性中心支撑-钢框架结构(DCH)。
1.2 不同延性的CBF的构造要求CBF单重体系的延性主要取决于支撑及其节点连接的设计方法和构造措施。支撑及其连接经常会出现低周疲劳寿命不足的情况,如:未对抗震设防做出严格的构造要求,其结果是大震情况下某些楼层的支撑及其连接可能发生劣化、甚至出现断裂[7]。若对CBF单重体系的支撑及其节点进行严格的抗震设计,确保构件具有足够的延性、节点具有足够的承载力或变形能力,结构体系将具有良好延性和抗震耗能能力。
各国规范中有关H形截面的支撑构件构造要求[1, 4-6]见表 1。尽管各国规范对支撑的长细比要求不尽相同,但对高延性结构中支撑构件的高厚比和宽厚比的要求相对于非抗震要求更为严格。通过对比欧美规范[5-6]和中国规范[1, 4]中的规定,可以发现:满足GB 50017—2017[1]抗震性能化设计中BS1和BS2等级(或者GB 50011—2010[1]的一级和二级)构造要求的支撑为延性支撑构件,满足BS3等级(或者抗震规范的三级和四级)而不满足前两个等级的为低延性的构件(比欧美规范构造要求更为严格)。虽然中国规范通过构造要求提高了中心支撑的延性,却没有配套其他部分的高延性设计要求,例如:AISC 341—16[5]中对高延性的中心支撑结构体系依据弹塑性阶段的能力设计法,给出了更严格的梁、柱及相关节点设计要求;支撑跨的柱子和梁需要设计成高延性构件,梁柱节点转动能力不得小于0.025 rad等。可见,对于高延性CBF,不但需要满足支撑为高延性构件,还需结合结构强震作用下的弹塑性反应,对梁、柱构件及相关节点提出更严格的构造及承载力要求,对于不满足这些要求的CBF可认定为低延性CBF。
| 表 1 各国规范人字形支撑构件(H型截面)的构造要求 Tab. 1 Construction requirements of inverted chevron braces (H-shaped) in different codes |
低延性CBF在地震中预期发生的非弹性变形很小,设计时需使用更高的地震力水平,形成更大的截面尺寸,使支撑系统更少的发展塑性。虽然结构延性较差,但不期望支撑构件充分发展塑性,也同时降低了对构件及连接节点的抗震构造要求,便于设计和施工质量控制。因此,低延性中心支撑结构体系更适用于中低烈度区的多层及高层建筑物和构筑物。其抗震耗能及变形能力远不如高延性的结构体系,如果实际地震强度高于预期地震,构件及连接可能会破坏。
高延性CBF体系有许多细节的抗震构造要求,以确保更高的延性,更适合于在中高烈度地区使用,能够更好地依靠塑性变形进行滞回耗能。但其对设计工程师、钢结构加工厂以及施工队伍也提出了更高的要求。钢结构建筑在中国过去几十年的高速发展中得到了广泛应用,使得现在高延性钢结构对设计、加工、施工各方面严格的要求也可以得到满足。
2 高延性CBF的抗震设计方法进展美国北岭地震和日本阪神大地震后,工程师们开始关注支撑体系的延性和耗能能力,通过提高对支撑体系延性(特别是往复荷载作用下的塑性变形能力)的要求,来降低对承载力的要求,从而建立更经济合理、抗震效果更好的支撑体系,这类支撑体系可视为高延性CBF体系[8]。对于高延性CBF体系而言,在罕遇地震作用下,支撑将反复受压屈曲和受拉屈服,如何保证支撑斜杆和连接节点在经历强震下较大的塑性变形而不过早破坏,是高延性CBF设计的关键。
2.1 支撑及其连接的低周疲劳寿命是CBF倒塌的控制因素大量试验及震后调研表明,CBF经历强震后的破坏主要是支撑及节点的低周疲劳断裂,钢柱、钢梁端板也会产生一定变形,见图 2。因此,需要严格限制高延性CBF的构造要求,使其节点及构件具有较高的低周疲劳寿命,国内已进行的试验都验证了高延性CBF体系在多层钢结构电厂厂房中的抗震可靠性[9-10],为确保大震发生时支撑及其连接具有足够的低周疲劳寿命,不因发生断裂而退出工作,应至少从以下几个方面入手:

|
图 2 CBF构件及连接屈曲或破坏形态 Fig. 2 Buckling or failure modes of members or connections of steel concentrically braced frames |
1) 提高支撑自身的低周疲劳寿命,包括使用宽厚比较小的紧凑截面、适当放宽支撑的长细比、简化支撑两端的约束条件等[11],很多学者进行的支撑滞回性能试验[12-13]和理论分析[14-15]均验证了这些内容。
2) 使节点连接具有高于支撑的低周疲劳寿命,包括使支撑节点连接具有高于考虑超强系数后的支撑全截面受拉屈服承载力,支撑节点在支撑往复受压失稳过程中具有良好的塑性转动能力等。例如使用支撑板式节点时,要求支撑端板的节点板上具有2t净距(t为节点板厚度)或椭圆净距的要求[16-18],2t净距可保证节点板面外有良好的转动能力,同时塑性损伤发展集中在2t板带范围内,节点板与梁柱连接边不会过早撕裂使节点板提前退出工作。
3) 强化人字形支撑横梁的设计,使其在能够承受自身竖向荷载的同时,还能承受人字形支撑拉、压杆件屈服和屈曲后引起的竖向不平衡力[19],这是从结构整体刚度和承载力不至于过早劣化的角度上保证中心支撑具有充分滞回耗能能力的关键。GB 50017—2017则考虑了上下层支撑引起梁的轴力,要求对梁按照压弯构件计算。AISC 341—16还规定,在与人字形支撑相交处的横梁上应设置侧向支承点,来防止横梁的整体扭转。
4) 强化支撑体系中钢柱的设计,不仅要使其在弹性设计阶段具有足够的承载力,也要使其在各层支撑均进入受拉屈服和受压屈曲的最不利塑性发展机制下具有充足的稳定性[5]。各国规范对CBF中钢柱的设计均采用了能力设计的方法,AISC 341—16要求柱能够抵抗结构充分发展塑性对应的力(即所有受拉支撑均屈服且所有受压支撑均屈曲),而EC8和GB 50017—2017则对钢柱的设计采用了地震内力乘以超强系数的能力设计方法。
5) 保证梁柱节点有足够的转动能力,不至过早破坏[5]。
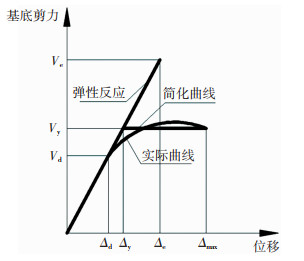
2.2 高延性CBF抗震计算方法 2.2.1 基于承载力的抗震设计如图 3所示,强震下延性结构进入弹塑性,基底剪力明显小于单质点弹性体系,地震力折减系数R[5, 20-24](又称结构影响系数)是基本烈度下按弹性计算的最大基底剪力与结构的设计基底剪力的比值:
| $ R=\frac{V_{\mathrm{e}}}{V_{\mathrm{d}}}=\frac{V_{\mathrm{e}}}{V_{\mathrm{y}}} \times \frac{V_{\mathrm{y}}}{V_{\mathrm{d}}}=R_\mathtt{μ} \times R_{\Omega} $ | (1) |
|
图 3 结构的性能曲线 Fig. 3 Performance curve of structure |
式中:Ve为结构按弹性计算的最大基底剪力,Vy为结构明显屈服时基底剪力,Vd为结构设计基底剪力,Rμ为结构延性折减系数,RΩ为结构的超强折减系数。
结构的延性是地震力折减的关键因素,而GB 50011—2010[1]对高延性结构与低延性结构采用了相同的地震力折减系数(结构影响系数),制约了中国高延性结构的发展,这也引发了国内关于钢结构地震力折减系数的大讨论[20-24],并推动中国新修订的GB 50017—2017[4]中引入了钢结构体系抗震性能设计的相关内容。
国内外学者用等效静力Pushover分析法和增量动力时程分析法(IDA),对CBF的影响系数进行了研究,这使得结构影响系数的取值更加科学合理,而不再是最初的概念性的粗放取值。例如:Salem等[25]通过Pushover方法分析了应用于工业建筑中普通的CBF,以塑性铰法考虑梁柱的塑性发展,并考虑了支撑屈曲刚度和承载力的退化,结果认为美国规范中的建议取值偏小;张文元等[26]通过推覆实验,得到了板式连接的SCBF的影响系数在9左右;Hsiao等[27]通过弹簧单元模拟支撑节点板、引入支撑断裂模型,较为精确地分析了不同层数下特殊的中心支撑-钢框架(SCBF)的结构影响系数,也证实了建筑物层数(高度)将影响结构影响系数的取值;杨俊芬等[28]通过增量动力时程分析法,得到了不同层数、跨度、高跨比的人字形CBF的影响系数普遍在3~4。
2.2.2 规范对延性结构的倒塌判定的不合理因素限于GB 50011—2010[1]对大震下的变形限制要求过于严格,国内学者计算得到的结构影响系数普遍要小于国外的值[25-28],从某种程度上看,过于严格的变形要求也限制了高延性结构对于其延性的利用。GB 50017—2017[4]中抗震性能化设计一章给出了不同结构构件的最低延性等级,并规定了相应延性等级的塑性耗能区的性能系数以及设防地震下构件的验算方法,对于延性的CBF,塑性耗能区性能系数最小值为0.35,即使考虑到中美规范中的反应谱和构件设计方法的差别,也与AISC 341—16规定的R=6(相当于性能系数为1/6≈0.167)有很大的差距,这可能与GB 50011—2010中要求的罕遇烈度下的位移限制为1/50,而AISC 341—16则要求2/3最大地震的设计地震下的层间位移角限值为1/50有关,EC8只对10年超越概率为10%的层间位移角做1/200~1/100的限值要求。
以位移作为大震不倒的控制因素从原理上更适用于延性较差的钢筋混凝土结构、砌体结构和低延性的钢结构,这些结构在强震作用下,当位移超过某一极限数值可能会直接发生倒塌;而对于一些延性比较好的结构,在经历数次强震甚至经历远超过预期强度的地震作用时,即使最大位移超过GB 50011—2010中的限值,也并不会发生倒塌,如麦浩[29]对按照8度设计的高延性CBF进行了振动台试验,结构经历多次8度小震及中震地震作用后,结构各构件及节点均保持完好,仅在最后几次9度大震作用后,支撑产生了较大不可恢复的残余变形(见图 4),但从整体结构层面看依然表现良好,没有出现明显的塑性发展。

|
图 4 震后支撑的残余变形 Fig. 4 Residual deformation of braces after earthquake |
尽管用位移来判定结构的极限倒塌状态更加便于工程师使用,但对于高延性的结构,大震作用下位移很难达到其极限倒塌位移。而在经历数次地震作用后,结构损伤不断累积,可能发生构件或节点的低周疲劳破坏,从而导致结构倒塌。因此,位移可能并不是判定延性结构倒塌最好的方法。
有些学者提倡使用损伤指数(结构参数化损伤程度与损伤极限的比值)来判定结构的倒塌状态,例如,欧进萍等[30]根据钢筋混凝土结构的损伤程度,结合三水准设防的概念提出了损伤的性能目标(见表 2)。对于高延性的CBF,相应的损伤程度和损伤性能目标尚待验证及完善。
| 表 2 三水准抗震设防与损伤指标 Tab. 2 Damage indexes and three-level seismic fortification |
基于承载力的设计方法并未考虑地震持时对结构造成的累积损伤效应,有些学者提出了基于损伤和能量的抗震设计方法,通过建立不同滞回模型单质点体系的能量谱以及耗能构件的累积滞回耗能比谱,得到耗能构件的累积滞回耗能情况,从而进行设计[31-34]。而通过耗能构件的累积滞回耗能和其极限耗能能力又可以得到其损伤状态。即
| $ E_{\mathrm{H}} =E_{1} \times \alpha_{\mathrm{E}} $ | (2) |
| $ D =E_{\mathrm{H}} / E_{\mathrm{U}} $ | (3) |
式中:EH为耗能构件的累积滞回耗能,E1为结构的总输入能量,由能量谱得到,αE为耗能构件的累积滞回耗能占结构总输入能量的比例系数,由累积滞回耗能比谱得到,EU为耗能构件的极限滞回耗能能力,D为耗能构件的损伤因子。
在日本,能量设计法被称为“一般化特别验算法”,通过将地震时输入的能量与结构自身能够消耗的能量进行比较,来验证结构安全[35],这种方法比较适用于能够明确定义结构各部分的累积塑性变形能力的钢结构以及消能减震结构。
McCabe等[36]从低周疲劳角度,提出了如下损伤模型:
| $ $$ D=\left(\frac{E^{+}+E^{-}}{E_{\mathrm{U}}}\right)^{2}+\left(\frac{E^{+}-E^{-}}{E_{\mathrm{U}}}\right)^{2} $$ $ | (4) |
式中:E+为结构正向总滞回耗能,E-为结构负向总滞回耗能。
CBF单重体系的受力简单,耗能原理明确,非常适用于采用能量法进行设计。但显然,若想对CBF进行一般化设计,则需要利用支撑的长细比、宽厚比等对上述公式进行进一步的参数修正,还需要结合特有的滞回模型开发针对CBF单重体系的能量谱。
对于CBF单重体系,严格限制构造要求的中心支撑为主要耗能构件,可以利用地震力折减的方法进行初步设计并利用能量法结合其在大震的作用下的损伤状态进行验算[37],而对于梁、柱构件,则可采用能力设计的方法保证CBF体系具有良好的延性性能。
2.3 小结对于高延性CBF,有必要研究其大震屈服机制和倒塌机理,提出构件及节点构造要求,建立支撑节点与支撑构件之间的低周疲劳寿命匹配准则,提出基于支撑和节点低周疲劳寿命的构造要求。
由于梁、柱及节点采用了能力设计,高延性CBF罕遇地震破坏本质是中心支撑的低周疲劳破坏,但各国规范及学者对其地震力折减系数R的取值更多的是根据结构在强震作用下的弹塑性承载力得到的,控制结构反应的因素多采用层间位移,支撑低周疲劳损伤对R的取值的影响没有被重视。事实上,R的取值越大,支撑构件的疲劳损伤会越大,若对结构采用现行规范或学者得到的R值进行设计,经历大震后,其损伤是否接近结构的损伤极限还有待商榷。
有必要从保证生命安全出发,建立基于可靠度的“大震不倒”控制指标,结合结构的损伤程度确定高延性CBF结构的位移限值和损伤限值,同时确定与之相配套的同时考虑承载力和耗能的构件抗震设计方法。
3 低延性CBF抗倒塌储备能力 3.1 低延性CBF的储备能力低延性CBF结构,大震作用下某些支撑破坏后,整体并非一触即溃,结构仍然具有一定的抗倒塌储备能力。例如1994年美国Northridge地震中发现了大量钢框架在梁柱节点和支撑节点处的开裂破坏,但没有一栋这样的钢结构建筑物发生倒塌。用今天的眼光看这些钢结构建筑并未严格满足抗震构造要求,但这些钢结构建筑仍然具有很强的抗倒塌能力。支撑破坏后,潜在的剩余抗倒塌储备能力如果能够得到适当利用,将极大提高结构经济性,这也促进了ASCE 7—10[38]的更新与进步,增加了OCBF可在低烈度区酌情使用的建议。
3.2 储备能力的来源如果把CBF视为理想铰接桁架,则当支撑或其节点破坏后,结构变为了机构,会马上倒塌。但实际的情况是,即使支撑破坏,剩余的结构仍具有一定的抗倒塌储备能力,包括刚度、承载力和延性等,具有一定的继续维持结构大震不倒的能力。这种剩余的抗倒塌储备能力来源于:
1) 梁截面较大时,梁与柱的连接端板或连接角钢上的高强螺栓群的半刚性抗弯能力[39];2)梁柱节点处有支撑节点板时,节点板使节点抗弯能力的进一步增强作用[40],能够达到半刚接、甚至刚接;3)楼板与钢梁形成组合作用时,在梁端能够形成分别抵抗正负弯矩的能力[41];4)柱子通常是竖向连续构件,即使某一层的支撑退出工作,柱子的竖向连续性仍使结构在这一层上存在冗余度,能够类似于抗弯钢框架一样工作[42];5)支撑或其连接在受拉开裂时失去刚度,但受压时裂缝恢复接触而又重新产生一定的受压刚度[43];6)柱脚配置的锚栓数量较多时,形成具有一定抗弯刚度的半刚接或刚接柱脚,从而形成了排架柱的抗弯能力[43-44];等等。
3.3 储备能力的有效利用对于低延性CBF,大震情况下某些楼层的支撑及其连接可能发生劣化、甚至出现断裂,此时低延性CBF的抗倒塌储备能力将可能发挥重要作用,能够在一定程度上继续维持结构的大震不倒[42],这种能力将对确保生命安全具有重要意义。
例如,张文元等[40]的数值模拟分析证实了支撑节点板会使正常使用状态下的梁端次弯矩(在发生层间变形时,因支撑节点板对梁柱节点转动刚度的增强作用而引起的附加弯矩)达到梁塑性铰弯矩的10%以上,而弹塑性层间侧移角达到1/50时的次弯矩甚至会达到梁端塑性铰弯矩;Stoakes等[45-46]通过试验和理论分析,证实了支撑节点板能够提高角钢连接的梁柱节点抵抗正负弯矩的能力,可以达到梁全截面塑性弯矩的30%~99%,而最大弹塑性层间侧移角普遍都可以达到0.015~0.04 rad;Liu等[47-48]通过试验证明了典型的梁柱端板连接的抗弯能力只能达到梁端塑性铰弯矩的20%,如果考虑失去组合前的楼板的贡献时节点抗弯能力将达到梁端塑性铰弯矩的50%,如果再同时使用角钢加强梁下翼缘与柱的连接,则梁柱抗弯能力可以达到梁端塑性铰弯矩的80%;Judd等[49]指出一栋建筑物中承重框架端板连接的半刚性节点数量众多,尽管每个节点的刚度和承载有限,仅为完全刚性节点的10%~30%,但其总量是惊人的,是结构剩余抗倒塌储备能力的重要来源;Flores等[50]则在大量不同结构算例分析的基础上得出承重框架柱子的连续性和梁柱半刚性连接对结构剩余抗倒塌储备能力具有重要贡献,连续的柱子可以使结构第一阶振型更加均匀,避免出现薄弱楼层破坏机制。
FEMA P695[51]定义了倒塌储备系数RCM作为评价结构抗倒塌能力的评价指标:
| $ R_{\mathrm{CM}}=I_{50 \%} / I_{\mathrm{MCE}} $ | (5) |
式中:I50%为倒塌概率达到50%时对应的地震强度,IMCE为美国规范考虑的最大地震强度,其值为设计地震强度的1.5倍。
对于极限状态(倒塌点)的判定,有DM准则和IM准则。DM准则是以损伤指标的阈值来定义结构的倒塌点,而IM准则是以强度参数的阈值来定义结构的倒塌点。王伟等[52]结合FEMA相关规范,综合考虑了DM准则和IM准则,对极限状态的判定给出了定义,见表 3。对于CBF,是否可采用低周疲劳损伤相关指标进行倒塌点的判定,值得进行深入的研究。
| 表 3 极限状态定义 Tab. 3 Definition for limit states |
虽然一些学者认识到了结构的剩余抗倒塌能力,但基础研究工作刚刚起步,在结构倒塌之前能否充分激活剩余抗倒塌能力的基本物理概念尚待验证,剩余抗倒塌储备能力尤其是梁柱节点半刚接、柱子的竖向连续性以及柱脚螺栓群的半刚接的潜能尚待开发。有必要从模型试验、数值模拟到理论分析等方面展开全方位的工作,包括评估低延性CBF的易损性和极限状态、量化抗倒塌储备能力的潜在来源、确定抗倒塌储备能力对地震响应的影响、开发考虑抗倒塌储备能力的设计方法等。
4 结论本文介绍了不同延性的CBF的国内外研究进展,为进一步推广应用,有必要从以下方面对CBF体系进行研究:
1) 节点及支撑低周疲劳寿命是CBF倒塌的控制因素,有必要针对构件的几何参数、连接节点的构造形式等关键影响因素,提出高延性CBF的节点及构件的设计要求。
2) 对设计地震作用进行折减是充分发挥高延性CBF良好变形能力的关键方法,有必要结合IDA及推覆分析等方法,研究高延性CBF的能力曲线、损伤机制及倒塌机理,总结出地震力折减水平和耗能构件(支撑)的低周疲劳累积滞回耗能需求规律,提出承载力和能量设计相结合的抗震设计方法。
3) 梁柱节点半刚接、柱子的竖向连续性以及柱脚螺栓群的半刚接等因素对低延性CBF的抗倒塌储备能力的贡献不可忽视,有必要进行深入的研究,提出利用抗倒塌储备能力的设计方法,扩展低延性CBF的使用范围。
| [1] |
中华人民共和国住房和城乡建设部. 建筑抗震设计规范: GB 50011—2010[S]. 北京: 中国建筑工业出版社, 2010 Ministry of Housing and Urban-Rural Development of the People's Republic of China. Code for seismic design of buildings: GB 50011—2010[S]. Beijing: China Architecture & Building Press, 2010 |
| [2] |
中华人民共和国住房和城乡建设部. 高层民用建筑钢结构技术规程: JGJ 99—2015[S]. 北京: 中国建筑工业出版社, 2015 Ministry of Housing and Urban-Rural Development of the People's Republic of China. Technical specification for steel structure of tall building: JGJ 99—2015[S]. Beijing: China Architecture & Building Press, 2015 |
| [3] |
中国地震局工程力学研究所. 建筑工程抗震性态设计通则: CECS 160: 2004[S]. 北京: 中国计划出版社, 2004 Institute of Engineering Mechanics. General rule for performance-based seismic design of buildings: CECS 160: 2004[S]. Beijing: China Planning Press, 2004 |
| [4] |
中华人民共和国住房和城乡建设部. 钢结构设计标准: GB 50017—2017[S]. 北京: 中国建筑工业出版社, 2017 Ministry of Housing and Urban-Rural Development of the People's Republic of China. Standard for design of steel structures: GB 50017—2017[S]. Beijing: China Architecture & Building Press, 2017 |
| [5] |
American Institute of Steel Construction. Seismic provisions for structural steel buildings. ANSI/AISC 341—16[S]. Chicago: American Institute of Steel Construction, 2016
|
| [6] |
European Committee for Standardization. Eurocode 8: design of structures for earthquake resistance: BS EN 1998-1: 2004[S]. Brussels: CEN, 2004
|
| [7] |
FAHNESTOCK L A, HINES E M, TREMBLAY R, et al. Reserve capacity and implications for seismic collapse prevention for low-ductility braced frames in moderate seismic regions[C]// Proceedings of the 10th National Conference in Earthquake Engineering. Anchorage: Earthquake Engineering Research Institute, 2014: 6. DOI: 10.4231/D3V698C70
|
| [8] |
罗桂发. 钢支撑和框架的弹塑性抗侧性能及其协同工作[D]. 杭州: 浙江大学, 2011 LUO Guifa. Elastic-plastic resistances of steel brace moment-resisting frame and their cooperation in dual system[D]. Hangzhou: Zhejiang University, 2011 |
| [9] |
张文元, 麦浩, 于海丰. 特殊铰接中心支撑框架结构振动台试验[J]. 哈尔滨工业大学学报, 2016, 48(6): 23. ZHANG Wenyuan, MAI Hao, YU Haifeng. Shaking table test of special concentrically braced steel frame with pinned connections[J]. Journal of Harbin Institute of Technology, 2016, 48(6): 23. DOI:10.11918/j.issn.0367-6234.2016.06.003 |
| [10] |
沈祖炎, 黄奎生, 陈以一, 等. 大型火电厂房钢支撑-框架结构振动台试验模型[J]. 建筑科学与工程学报, 2006, 23(4): 1. SHEN Zuyan, HUANG Kuisheng, CHEN Yiyi, et al. Shaking table test model with steel braced frame structure about main plant of large thermal power plant[J]. Journal of Architecture and Civil Engineering, 2006, 23(4): 1. DOI:10.3321/j.issn:1673-2049.2006.04.001 |
| [11] |
ZHANG Yaochun, LIAN Weian, ZHANG Wenyuan. Factors affecting the low cycle fatigue behavior around the weak axis of welded Ⅰ-section bracing members[J]. Key Engineering Materials, 2006, 324(2): 959. DOI:10.4028/www.scientific.net/KEM.324-325.959 |
| [12] |
张耀春, 连尉安, 张文元. 焊接工字形截面钢支撑低周疲劳性能试验研究[J]. 建筑结构学报, 2005, 26(6): 114. ZHANG Yaochun, LIAN Weian, ZHANG Wenyuan. The low-cycle fatigue tests of welded Ⅰ-section bracing members[J]. Journal of Building Structures, 2005, 26(6): 114. DOI:10.14006/j.jzjgxb.2005.06.016 |
| [13] |
ZENG Lijing, ZHANG Wenyuan, DING Yukun. Representative strain-based fatigue and fracture evaluation of Ⅰ-shaped steel bracing members using the fiber model[J]. Journal of Constructional Steel Research, 2019, 160: 476. DOI:10.1016/j.jcsr.2019.05.051 |
| [14] |
WIJESUNDARA K K, NASCIMBEBE R, SULLIVAN T J. Equivalent viscous damping for steel concentrically braced frame structures[J]. Bulletin of Earthquake Engineering, 2011, 9(5): 1535. DOI:10.1007/s10518-011-9272-4 |
| [15] |
SANTAGATI S, BOLOGNINI D, NASCIMBENE R. Strain life analysis at low-cycle fatigue on concentrically braced steel structures with RHS shape braces[J]. Journal of Earthquake Engineering, 2012, 16(S): 107. DOI:10.1080/13632469.2012.675840 |
| [16] |
LEHMAN D E, ROEDER C W, HERMAN D. Improved seismic performance of gusset plate connections[J]. Journal of Structural Engineering (ASCE), 2008, 134(6): 890. DOI:10.1061/(ASCE)0733-9445(2008)134:6(890) |
| [17] |
GOGGINS J, BRODERICK B M, ELGHAZOULI A Y, et al. Shake table testing of concentrically braced steel structures with realistic connection details subjected to earthquakes[J]. Structures, 2018, 13(3): 102. DOI:10.1016/j.istruc.2017.12.003 |
| [18] |
建築物の構造関係技術基準解説書編集委員会. 建築物の構造關係技術基準解說書[S]. 東京: 日本国土交通省住宅局建築指導课, 2007
|
| [19] |
KIM J, CHOI H. Response modification factors of chevron-braced frames[J]. Engineering Structures, 2005, 27(2): 285. DOI:10.1016/j.engstruct.2004.10.009 |
| [20] |
翟长海, 谢礼立. 抗震规范应用强度折减系数的现状及分析[J]. 地震工程与工程振动, 2006, 26(2): 1. ZHAI Changhai, XIE Lili. State of art of applications of strength reduction factors in seismic design codes[J]. Earthquake Engineering and Engineering Dynamics, 2006, 26(2): 1. DOI:10.13197/j.eeev.2006.02.001 |
| [21] |
马琳琳, 李钢, 董志骞, 等. 钢框架-中心支撑结构强度折减系数谱研究[J]. 建筑结构, 2017, 47(增刊): 766. MA Linlin, LI Gang, DONG Zhiqian, et al. Strength reduction factor spectrum of the steel concentrically braced frames[J]. Building Structure, 2017, 47(S): 766. |
| [22] |
于海丰, 张耀春, 张文元. 有关钢结构地震作用的讨论[J]. 地震工程与工程振动, 2006, 26(1): 96. YU Haifeng, ZHANG Yaochun, ZHANG Wenyuan. Discussion on earthquake action on steel structures[J]. Earthquake Engineering and Engineering Dynamics, 2006, 26(1): 96. |
| [23] |
童根树. 与抗震设计有关的结构和构件的分类及结构影响系数[J]. 建筑科学与工程学报, 2007, 24(3): 65. TONG Genshu. Classification of structures and components related to seismic design and structural influence coefficient[J]. Journal of Architecture and Civil Engineering, 2007, 24(3): 65. DOI:10.3321/j.issn:1673-2049.2007.03.013 |
| [24] |
顾强, 申永康, 李成. 钢结构的地震反应修正系数[J]. 苏州科技学院学报(工程技术版), 2011, 24(4): 18. GU Qiang, SHEN Yongkang, LI Cheng. The seismic response modification factors of steel structures[J]. Journal of Suzhou University of Science and Technology (Engineering and Technology), 2011, 24(4): 18. |
| [25] |
SALEM Y S, NASR M A M. Evaluating response modification factors of open-frames steel platforms[C]// Proceedings of the 10th National Conference in Earthquake Engineering. Anchorage: Earthquake Engineering Research Institute, 2014: 21
|
| [26] |
张文元, 麦浩, 于海丰. 板式连接中心支撑钢框架结构推覆试验研究[J]. 工程力学, 2017, 34(10): 135. ZHANG Wenyuan, MAI Hao, YU Haifeng. Pushover tests of steel concentrically braced frames with gusset plate connections[J]. Engineering Mechanics, 2017, 34(10): 135. |
| [27] |
HSIAO P C, LEHMAN D E, ROEDER C W. Evaluation of the response modification coefficient and collapse potential of special concentrically braced frames[J]. Earthquake Engineering & Structural Dynamics, 2013, 42(10): 1547. DOI:10.1002/eqe.2286 |
| [28] |
杨俊芬, 张凡, 顾强. 人字形中心支撑钢框架的结构影响系数研究[J]. 建筑结构, 2007, 37(10): 51. YANG Junfen, ZHANG Fan, GU Qiang. Study on response modification factors of inverted V CBF[J]. Building Structure, 2007, 37(10): 51. |
| [29] |
麦浩. 板式连接中心支撑钢框架结构的抗震性能研究[D]. 哈尔滨: 哈尔滨工业大学, 2015 MAI Hao. Seismic performance of special concentrically braced steel frame with pinned connections[D]. Harbin: Harbin Institute of Technology, 2015 |
| [30] |
欧进萍, 何政, 吴斌, 等. 钢筋混凝土结构基于地震损伤性能的设计[J]. 地震工程与工程振动, 1999, 19(1): 21. OU Jinping, HE Zheng, WU Bin, et al. Design of reinforced concrete structure based on seismic damage performance[J]. Earthquake Engineering and Engineering Dynamics, 1999, 19(1): 21. DOI:10.13197/j.eeev.1999.01.004 |
| [31] |
FAJFAR P. Equivalent ductility factors, taking into account low-cycle fatigue[J]. Earthquake Engineering & Structural Dynamics, 1992, 21(10): 837. DOI:10.1002/eqe.4290211001 |
| [32] |
叶列平, 程光煜, 曲哲, 等. 基于能量抗震设计方法研究及其在钢支撑框架结构中的应用[J]. 建筑结构学报, 2012, 33(11): 36. YE Lieping, CHENG Guangyu, QU Zhe, et al. Study on energy-based seismic design method and application on steel braced frame structures[J]. Journal of Building Structures, 2012, 33(11): 36. DOI:10.14006/j.jzjgxb.2012.11.005 |
| [33] |
周知, 钱江, 黄维. 基于修正的Park-Ang损伤模型在钢构件中的应用[J]. 建筑结构学报, 2016, 37(增刊1): 448. ZHOU Zhi, QIAN Jiang, HUANG Wei. Application of modified Park-Ang damage model to steel members[J]. Journal of Building Structures, 2016, 37(S1): 448. DOI:10.14006/j.jzjgxb.2016.S1.064 |
| [34] |
何浩祥, 陈奎, 范少勇. 基于弹塑性耗能差率的地震损伤评估模型及分析方法[J]. 振动工程学报, 2018, 31(3): 382. HE Haoxiang, CHEN Kui, FAN Shaoyong. Seismic damage assessment model and analysis method based on elastic-plastic energy dissipation ratio[J]. Journal of Vibration Engineering, 2018, 31(3): 382. DOI:10.16385/j.cnki.issn.1004-4523.2018.03.003 |
| [35] |
日本建筑结构技术者协会. 日本建筑钢结构设计[M]. 亚洲建设技术交流促进会, 译. 北京: 中国建筑工业出版社, 2019: 30 Japan Association of Building Structure Technologists. Steel structure design of Japanese architecture[M]. Asia Association for the Promotion of Construction Technology Exchange, translate. Beijing: China Architecture & Building Press, 2019: 30 |
| [36] |
MCCABE S L, HALL J. Assessment of seismic structural damage[J]. Journal of Structural Engineering, 1989, 115(9): 2166. DOI:10.1061/(ASCE)0733-9445(1989)115:9(2166) |
| [37] |
叶列平, 缪志伟, 程光煜, 等. 建筑结构基于能量抗震设计方法研究[J]. 工程力学, 2014, 31(6): 5. YE Lieping, MIAO Zhiwei, CHENG Guangyu, et al. Study on the energy-based seismic design method of building structures[J]. Engineering Mechanics, 2014, 31(6): 5. DOI:10.6052/j.issn.1000-4750.2013.05.0388 |
| [38] |
American Society of Civil Engineers. Minimum design loads for buildings and other structures: ASCE/SEI 7—10[S]. Reston, Virginia: ASCE, 2010
|
| [39] |
YANG Bo, TAN Kanghai. Robustness of bolted-angle connections against progressive collapse: mechanical modelling of bolted-angle connections under tension[J]. Engineering Structures, 2013, 57(4): 153. DOI:10.1016/j.engstruct.2013.08.041 |
| [40] |
张文元, 周宇, 张耀春. 支撑节点板对铰接框架梁柱附加弯矩的影响[J]. 哈尔滨工业大学学报, 2013, 45(6): 7. ZHANG Wenyuan, ZHOU Yu, ZHANG Yaochun. Influence of gusset plate connections on the secondary moments in beams and columns of braced frames[J]. Journal of Harbin Institute of Technology, 2013, 45(6): 7. |
| [41] |
WEN Rou, AKBAS B, SHEN J. Practical moment-rotation relations of steel shear tab connections[J]. Journal of Constructional Steel Research, 2013, 88: 296. DOI:10.1016/j.jcsr.2013.05.018 |
| [42] |
BRADLEY C, SIZEMORE J, NELSON J, et al. Large-scale testing of low-ductility, concentrically braced frames[C]// Proceedings of Structures Congress 2014. Boston: American Society of Civil Engineers, 2014: 2417. DOI: 10.1061/9780784413357.212
|
| [43] |
崔瑶, 王枫智, 于贵书. 强震作用下柱脚连接刚度对钢框架性能的影响[J]. 地震工程与工程振动, 2016, 36(3): 162. CUI Yao, WANG Fengzhi, YU Guishu. Effect of column base stiffness on seismic behavior of steel frame under severe earthquake[J]. Earthquake Engineering and Engineering Dynamics, 2016, 36(3): 162. |
| [44] |
KANVINDE A M, GRILLI D A, ZAREIAN F. Rotational stiffness of exposed column base connections: experiments and analytical models[J]. Journal of Structural Engineering, 2012, 8(5): 549. DOI:10.1061/(ASCE)ST.1943-541X.0000495 |
| [45] |
STOAKES C D, FAHNESTOCK L A. Cyclic flexural testing of concentrically braced frame beam-column connections[J]. Journal of Structural Engineering, 2011, 137(7): 739. DOI:10.1061/(ASCE)ST.1943-541X.0000326 |
| [46] |
STOAKES C D, FAHNESTOCK L A. Cyclic flexural analysis and behavior of beam-column connections with gusset plates[J]. Journal of Constructional Steel Research, 2012, 72: 227. DOI:10.1016/j.jcsr.2011.12.008 |
| [47] |
LIU J, ASTANEH A. Cyclic behavior of steel shear connections with floor slab[C]// Proceedings of 6th ASCCS International Conference on Steel-Concrete Composite Structures. Los Angeles: [s. n. ], 2000: 32
|
| [48] |
LIU J, ASTANEHASL A. Cyclic testing of simple connections including effects of slab[J]. Journal of Structural Engineering, 2000, 126(1): 32. DOI:10.1061/(ASCE)0733-9445(2000)126:1(32) |
| [49] |
JUDD J P, CHARNEY F A. Seismic performance of buildings designed for wind[C]// Proceedings of Structures Congress 2014. Boston: American Society of Civil Engineers, 2014: 2342. DOI: 10.1061/9780784413357.206
|
| [50] |
FLORES F X, CHARNEY F A, LOPEZ G D. Influence of the gravity framing system on the collapse performance of special steel moment frames[J]. Journal of Constructional Steel Research, 2014, 101: 351. DOI:10.1016/j.jcsr.2014.05.020 |
| [51] |
CHARLES K, MICHAEL C, GREGORY D, et al. Quantification of building seismic performance factors: FEMA P695[R]. Washington DC: Federal Emergency Management Agency, 2009
|
| [52] |
王伟, 胡书领, 邹超. 基于增量动力分析的梁贯通式支撑钢框架地震易损性研究[J]. 建筑结构学报, 2021, 42(4): 44. WANG Wei, HU Shuling, ZOU Chao. Seismic fragility analysis of beam-through steel braced frames based on IDA method[J]. Journal of Building Structures, 2021, 42(4): 44. DOI:10.14006/j.jzjgxb.2019.0268 |
 2021, Vol. 53
2021, Vol. 53


