2. 西安建筑科技大学土木工程学院, 西安 710055;
3. 亚热带建筑科学国家重点实验室(华南理工大学), 广州 510640
2. School of Civil Engineering, Xi'an University of Architecture and Technology, Xi'an 710055, China;
3. State Key Lab of Subtropical Building Science(South China University of Technology), Guangzhou 510640, China
钢筋锈蚀及其导致的混凝土胀裂是影响钢筋混凝土(RC)结构耐久性的重要因素之一[1],造成混凝土及钢筋性能的退化[2]。在材料尺度,胡志坚等[3]、Otieno等[4]对锈蚀钢筋锈蚀量及锈胀裂缝宽度进行了研究,根据试验数据总结了锈蚀累积和锈胀开裂的一般规律,但模型不能体现混凝土保护层厚度以及钢筋所在位置等因素的影响。Du等[5-6]、Ou等[7]研究了纵筋锈蚀后的等效应力、应变的变化,但是未考虑钢筋的纵向不均匀锈蚀。Vu等[8]研究了箍筋锈蚀对约束混凝土性能的影响,并分析约束混凝土侧向约束力和极限压应变的变化;在结构尺度,邢国华等[9]推导了锈蚀RC柱的修正压-剪-弯理论分析模型;Vu等[10]建立了锈蚀RC柱3D模型,但是未能考虑锈蚀产物不均匀分布的影响。
目前关于截面材料性能劣化的研究较为充分,但对结构尺度的研究仍较少。在数值模型方面,基于细观三维有限元的模拟较多,但是细观有限元方法对于混凝土结构非线性阶段的能力预测较差,且结果往往难以收敛[11]。在宏观模型尺度,关于锈蚀RC柱性能劣化的数值研究更是匮乏。随着性能化地震工程的不断发展,对结构非线性分析模型提出了更高的需求,兼具精度的宏观模型近年来一直是研究的热点领域之一,且已被多国规范采纳[12-13]。
另一方面,现有试验研究中,大多依赖加速锈蚀的试验方法,与真实环境中的锈蚀规律有一定差别,加速锈蚀后RC柱中钢筋基本都为均匀锈蚀。而自然环境下RC柱的锈蚀是复杂和不均匀的,不同部位钢筋的锈蚀对RC柱的影响也不同,需要区别对待。因此,在数值建模时有必要尽可能考虑真实非均匀锈蚀的影响。
本文的目标是在已有研究的基础上,进一步提出非均匀锈蚀情况下从截面材料到整体结构的数值模型,并基于已有试验结果检验模型的预测性能,为相关领域的研究和应用提供参考。
1 锈胀裂缝宽度模型钢筋锈蚀程度的评估指标主要有质量锈蚀率、锈蚀深度、锈胀裂缝宽度等。质量锈蚀率可以较为准确地描述钢筋的锈蚀程度,被广泛应用于研究工作中。质量锈蚀率的测量较为复杂,相关研究中对质量锈蚀率的测定大多是在试件加载结束后将锈蚀钢筋从试件中分离,然后进行测定。相较于无法直接观测的质量锈蚀率,锈胀裂缝宽度更加易于测定,常在实际评估中作为主要评估指标。建立锈胀裂缝宽度与质量锈蚀率的计算模型,有助于研究成果向实际工程应用的转化。
对于既有RC柱,其内部钢筋的锈蚀往往是不均匀的,Yuan等[14]利用数字显微技术对钢筋锈蚀产物的分布进行了观测,结果表明锈蚀产物沿钢筋环向的分布呈现明显的不均匀性,靠近侵蚀界面一侧的锈蚀程度明显大于背离侵蚀界面的一侧。
钢筋锈蚀后,锈蚀产物产生体积膨胀并挤压周围混凝土,当混凝土的应力超过其抗拉强度时便会产生内部微裂缝。若锈蚀产物继续增加,则内部微裂缝逐渐扩展直至形成宏观裂缝。靠近侵蚀界面一侧的钢筋截面锈蚀产物最多,因此最早产生裂缝,并最终贯通形成构件表面的锈胀裂缝,混凝土锈胀裂缝的发展见图 1(a),图中R为纵筋半径。由于应力在裂缝处集中,减少了裂缝以外范围的应力,在锈蚀前期和中期产生的裂缝大多为一条主裂缝,同时,背离侵蚀界面一侧锈蚀产物产生的挤压应力方向与靠近侵蚀界面一侧的应力方向相反,对主裂缝宽度影响较小,但会引起附近区域产生微裂缝。基于前述分析,本文假定同一钢筋中靠近侵蚀界面一侧的锈蚀产物决定了裂缝宽度。

|
图 1 钢筋的锈蚀开裂过程和锈胀裂缝模型 Fig. 1 Corrosion induced cracking process and its model |
锈蚀产物膨胀过程中钢筋及锈蚀产物的总面积增大,而混凝土由于挤压应力产生形变和开裂。主裂缝形成后,钢筋锈胀导致的挤压应力将大幅降低,处于较低的水平。此外,混凝土弹性变形引起的形状改变占比较低,因此在锈胀开裂极限状态混凝土的弹性变形可以忽略,进而可认为靠近侵蚀界面一侧的锈蚀产物膨胀面积Acor等于锈胀裂缝面积Acra。靠近侵蚀界面一侧的钢筋外边界变化见图 1(b)。在小变形情况下,裂缝面积可近似以矩形计算
| $ {A_{{\rm{cor}}}} = {A_{{\rm{cra}}}} = w(c + 2r) $ | (1) |
式中:Acor为靠近侵蚀界面一侧锈蚀产物总膨胀面积,Acra为裂缝面积,w为锈胀裂缝宽度,c为混凝土保护层厚度,r为箍筋半径。
Zhao等[15]对锈蚀产物边界进行了拟合研究,发现锈蚀产物厚度沿圆周服从高斯分布,表达式为:
| $ {{p_\theta } = \frac{{{a_1}}}{{{a_2}\sqrt {2{\rm{ \mathsf{ π} }}} }}{{\rm{e}}^{ - {{\left( {\frac{{\theta - {\rm{ \mathsf{ π} }}}}{{\sqrt 2 {a_2}}}} \right)}^2}}}} $ | (2) |
| $ {{a_1} = \frac{{A_{{\rm{cor}}}^{{\rm{tot}}}}}{R}} $ | (3) |
| $ {{a_2} = \frac{{{a_1}}}{{{p_{\max }} + {p_{{\rm{pit}}}}}}\sqrt {2{\rm{ \mathsf{ π} }}} } $ | (4) |
式中:pθ为锈蚀产物的厚度,pmax为锈蚀产物表面到钢筋原表面的最大距离,ppit为锈蚀钢筋最大半径损失,θ=π处表示锈蚀产物最大厚度处,Acortot为锈蚀产物总膨胀面积。
以上是针对单向侵蚀的情况,混凝土结构中角部钢筋往往是双向侵蚀。根据Zhao等[15]的研究,双向侵蚀情况下锈蚀产物的厚度分布可视为单向侵蚀时的叠加。因此对角部的钢筋锈蚀模型,只需将单向侵蚀的分析结果进行叠加即可。锈蚀钢筋的体积膨胀系数为2.45[16],因此锈蚀产物总膨胀面积为
| $ A_{{\rm{cor}}}^{{\rm{tot}}} = 2.45{\eta _{\rm{s}}}{\rm{ \mathsf{ π} }}{R^2} $ | (5) |
式中ηs为钢筋的截面锈蚀率(%)。
图 1(c)为钢筋锈蚀后的几何形状模型。由于锈蚀的影响,钢筋截面的有效半径减少,钢筋在微段Δ内削减的有效面积为ΔApit;钢筋锈蚀过程会产生体积膨胀,在微段Δ内膨胀净面积为ΔAmax。膨胀后微段Δ内锈蚀产物的总面积为ΔApit+ΔAmax。Δ为局部计算单元的弧长,基于小变形假定并忽略高阶微量的影响,则有
| $ \Delta A_{\mathrm{pit}}+\Delta A_{\max }=2.45 \Delta A_{\mathrm{pit}} $ | (6) |
其中ΔApit=Δ·ppit,ΔAmax=Δ·pmax,因此上式可写成
| $ \Delta\left(p_{\mathrm{pit}}+p_{\max }\right)=2.45 \Delta \cdot p_{\mathrm{pit}} $ | (7) |
可得到锈蚀产物最大厚度ppit+pmax与最大半径损失ppit的关系为
| $ p_{\mathrm{pit}}+p_{\max }=2.45 p_{\mathrm{pit}} $ | (8) |
根据Yuan等[14]的研究结论,钢筋锈蚀最严重处的半径损失ppit表示为
| $ p_{\mathrm{pit}}=\frac{5 \eta_{\mathrm{s}} R}{3} $ | (9) |
将式(5)、(8)~(9)代入式(2)~(4)并消元,可得
| $ {p_\theta } = 0.65{\eta _{\rm{s}}}{{\mathop{\rm Re}\nolimits} ^{ - {{\left( {\frac{{\theta - {\rm{ \mathsf{ π} }}}}{{6.682}}} \right)}^2}}} $ | (10) |
故靠近保护层一侧的锈蚀产物面积为
| $ {A_{{\rm{cor }}}} = A_{{\rm{cor }}}^{{\rm{tot }}}\frac{{\int_{0.5{\rm{ \mathsf{ π} }}}^{1.5{\rm{ \mathsf{ π} }}} {{p_\theta }} {\rm{d}}\theta }}{{\int_0^{2{\rm{ \mathsf{ π} }}} {{p_\theta }} {\rm{d}}\theta }} = 0.646A_{{\rm{cor}}}^{{\rm{tot }}} $ | (11) |
将其代入式(1),可以得锈胀裂缝宽度的计算公式为
| $ w = \frac{{0.646A_{{\rm{cor }}}^{{\rm{tot }}}}}{{c + 2r}} $ | (12) |
把式(5)代入式(12)可以得到锈胀裂缝宽度近似计算公式为
| $ w = \frac{{4.97{\eta _{\rm{s}}}{R^2}}}{{c + 2r}} $ | (13) |
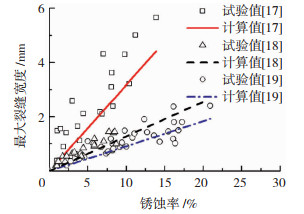
为验证本公式可广泛适用于不同钢筋直径、不同保护层厚度的钢筋混凝土构件,将本文计算结果与Zhang等[17]、Apostolopoulos等[18]、Lin等[19]的试验研究中各种不同设计参数的试验数据进行对比,三组试验中构件长度分别为3 000、310、300 mm,钢筋直径分别为8、8、10 mm,保护层厚度分别为10、25、40 mm,对比结果见图 2。根据对比结果可以看出,本文模型与不同学者的试验结果总体规律一致,尽管各试验参数有所差别但总体吻合较好。需要指出Zhang等[17]的试验测试值大多数高于本文模型结果。式(13)所用的锈蚀率指标为截面锈蚀率,然而在试验中往往只能测得平均锈蚀率。试件长度越小平均锈蚀率越接近于截面锈蚀率。而Zhang等[17]的试验中,试件长度较长,沿钢筋纵向锈蚀产物的分布可能并不均匀,平均锈蚀率要低于截面锈蚀率的最大值,因此用平均锈蚀率代替截面锈蚀率时,模型结果较试验值低。对于纵向不均匀锈蚀较为明显的构件,应根据不同的裂缝宽度计算不同位置处的钢筋截面锈蚀率以更为准确的评价锈蚀钢筋的力学性能。
|
图 2 裂缝宽度对比 Fig. 2 Comparison of crack widths |
钢筋锈蚀后由于锈坑的出现导致的截面削弱以及应力集中是钢筋力学性能降低的主要原因。现有的锈蚀钢筋模型大多以平均锈蚀率作为钢筋力学性能退化的评估指标。在实际工程中,由于锈蚀环境的差异,纵筋的锈蚀不仅沿环向呈现不均匀分布,沿纵向也呈现出不均匀分布的特征,因此纵筋不同部位的力学性能劣化呈现出一定的差异。结构的性能往往对塑性铰区的材料性能改变最为敏感,因此在锈蚀钢筋的力学性能模型中应能够体现纵向锈蚀不均匀性的影响,从而使得结构分析模型更加准确。目前锈蚀钢筋的力学模型中通常是假定钢筋截面不变,通过改变钢筋的等效强度以体现锈蚀的影响。在锈蚀钢筋拉拔试验中,剩余截面较小处应力较大,先进入屈服状态。因此锈蚀钢筋的屈服应力应与钢筋的最小剩余截面即截面锈蚀率的最大值有关。罗小勇等[20]通过试验给出锈蚀钢筋等效屈服应力与钢筋截面锈蚀率最大值的拟合关系式
| $ \frac{f_{\mathrm{y}}^{\mathrm{c}}}{f_{\mathrm{y}}}=1-0.948 \eta_{\max } $ | (14) |
式中fyc、fy分别为锈蚀钢筋和未锈蚀钢筋屈服应力,ηmax为钢筋截面锈蚀率最大值。
Zhang等[21]的锈蚀钢筋模型中屈服应力与锈蚀率的关系为
| $ \frac{f_{\mathrm{y}}^{\mathrm{c}}}{f_{\mathrm{y}}}=1-1.12 \bar{\eta} $ | (15) |
式中η为钢筋纵向的平均锈蚀率。
Zhang等[21]的模型未考虑钢筋的不均匀锈蚀,但平均锈蚀率要小于截面锈蚀率的最大值,因此以上两个模型虽然关键系数不同,但对于拉拔试验预测结果相差不大。必须指出的是,在锈蚀钢筋的拉拔试验中,钢筋沿纵向的拉力是相等的,最大锈蚀截面的位置并不影响钢筋性能,因此上述基于平均锈蚀率或最大锈蚀率的锈蚀钢筋模型均和试验结果吻合较好;然而在侧向荷载作用下RC柱中钢筋沿纵向的拉力分布是变化的,钢筋锈蚀发生在塑性铰区与发生在反弯点附近对结构性能的影响截然不同。因此在钢筋模型中有必要考虑钢筋的纵向不均匀锈蚀与最大锈蚀率出现的位置。
2.2 锈胀裂缝类型及锈蚀影响系数钢筋纵向不均匀锈蚀导致的几种常见裂缝形态见图 3,其中wmax为最大裂缝宽度;ηa、ηb分别为裂缝两端处锈蚀率,裂缝宽度一旦被观测到就已经具有一定宽度,故ηa、ηb接近0但不为0。

|
图 3 裂缝及钢筋锈蚀形态示意 Fig. 3 Schematic of cracks and steel corrosion |
对侧向荷载作用下的框架柱而言,柱底受到的弯矩最大,反弯点处为零。因此反弯点处钢筋锈蚀对性能几乎无影响,而柱底或柱顶的锈蚀则会最大限度影响框架柱的抗侧移能力。本文提出锈蚀影响系数αη用以描述钢筋锈蚀对结构性能的影响。对受侧向荷载作用的RC柱,锈蚀影响系数表达式为
| $ {\alpha _\eta } = \frac{{L - {L_x}}}{L} $ | (16) |
式中:Lx为计算截面到柱底部的高度,L为柱底至反弯点的高度,当Lx=0时,即柱底处锈蚀影响系数为1,Lx=L时,即反弯点处锈蚀影响系数为0。
对于其他受力形式,锈蚀影响系数需结合其内力分布特点。孔航挺[22]通过试验测量了不均匀锈蚀RC梁的钢筋剩余截面分布与钢筋断裂位置,荷载作用形式为双对称集中荷载,其锈蚀影响系数αη在弯剪区段线性分布,在纯弯区段均匀分布,将试验中涉及的η、αη与ηαη沿梁长度方向绘制,见图 4。图中L为梁总长度,Lx为截面距梁起点的长度。结果显示梁内纵筋断裂处既不在截面锈蚀率最大处也不在锈蚀影响系数或弯矩最大处,而是在锈蚀影响系数与锈蚀率乘积的最大处。可以看出,锈蚀影响系数的引入可完善锈蚀钢筋的力学模型。

|
图 4 锈蚀纵筋断裂位置 Fig. 4 Fracture position of corroded longitudinal reinforcement |
基于前文所述,本文认为钢筋截面锈蚀率与锈蚀影响系数共同决定RC柱中锈蚀钢筋的力学性能,考虑钢筋纵向不均匀锈蚀的计算模型为
| $ f_{\mathrm{y}}^{\mathrm{e}}=f_{\mathrm{y}}\left[1-\max \left(\alpha_{\eta} \eta_{\mathrm{s}}\right)\right] $ | (17) |
式中max(αηηs)为截面锈蚀率与锈蚀影响系数乘积的最大值。
对锈蚀裂缝为菱形的情况,其计算模型见图 5。各截面锈蚀率为ηa、ηb、ηmax,到柱基础的距离分别为La、Lb、Lmax。

|
图 5 模型计算示意 Fig. 5 Schematic of calculation model |
根据锈蚀影响系数的分布,max(αηηs)处于La与Lmax之间。计算步骤:
1) 测量裂缝两端以及最大处宽度,由式(13)计算对应锈蚀率ηa、ηb、ηmax。
2) 简化锈蚀率变化为线性变化,得到La与Lmax区段内锈蚀率表达式为
| $ \eta=\eta_{\mathrm{a}}+\frac{\eta_{\max }-\eta_{\mathrm{a}}}{L_{\max }-L_{\mathrm{a}}}\left(L_{x}-L_{\mathrm{a}}\right) $ | (18) |
3) 测量柱高以得到锈蚀影响系数表达式为
| $ \alpha_{\eta}=\frac{L-L_{x}}{L} $ | (19) |
4) 计算使得
5) 将max(ηsαη)代入式(17)得到钢筋应力。
对于其他锈蚀类型,三角形锈蚀可分为正三角形与倒三角形,倒三角形计算过程与菱形锈蚀流程相同;正三角形锈蚀情况下,锈蚀率与锈蚀影响系数均随柱高递减,因此ηs与αη即为最大裂缝宽度处对应的纵筋锈蚀率和锈蚀影响系数;对均匀锈蚀,ηs沿柱高不变,可沿柱高多次测量取裂缝平均值计算其截面锈蚀率,αη取1。
由于现有的锈蚀钢筋性能试验研究以拉拔试验为主,考虑纵筋纵向不均匀锈蚀的RC柱试验也较为缺乏。为验证本文改进的锈蚀钢筋力学模型的合理性,本文基于OPENSEES平台设计了含有四根锈蚀钢筋的RC柱构件,每根钢筋锈蚀区段均处于不同位置,模拟RC柱参数以及分段模型见图 6。混凝土强度为30 MPa,纵筋与箍筋屈服强度分别为400、335 MPa,锈蚀区段局部锈蚀率为20%。保护层混凝土与约束区混凝土分别使用Concrete01与Concrete04材料模拟,钢筋使用Steel02材料模拟。宏观有限元模型中杆件单元采用基于位移法的非线性梁柱单元,截面采用纤维截面,分别沿柱截面长宽方向划分40个计算单元。分别使用三种模拟方法对设计构件进行建模。

|
图 6 有限元宏观模型示意 Fig. 6 Macro-scale finite element model |
1) 将RC柱分为四段,每段柱单元内锈蚀钢筋不同。此方法可真实反应钢筋锈蚀情况,但是面对复杂的实际工程,数值模型可能需要更为复杂的区段划分,不便于使用,且可能导致计算无法收敛。
2) 使用本文改进的锈蚀钢筋力学模型分别计算每根钢筋的等效强度,应用于钢筋全长,不再对RC柱进行区段划分,可大大简化建模过程且便于计算。
3) 在现场评估中,简便起见常常将整根钢筋的锈蚀率都按最大锈蚀率计算,而不考虑不均匀锈蚀的影响。因此用最大锈蚀率代表整根钢筋的锈蚀率,将此方法作为对比模型,与上述两种方法进行对比。
三种方法计算的RC柱骨架曲线见图 7,可看出使用本文所提模型计算的RC柱荷载-位移曲线与分段模型吻合的更好,而对比模型对RC柱峰值荷载的低估较为严重。因此本文所提锈蚀钢筋模型是可靠的,且计算简单,便于工程实际使用。

|
图 7 锈蚀钢筋模型对比 Fig. 7 Comparison of models |
已有研究在计算锈蚀对RC柱核心区混凝土影响时,常以箍筋锈蚀率为判断依据。而计算箍筋锈蚀率需要将箍筋取出进行测量。此外,由于旧版《混凝土结构设计规范》中对混凝土保护层的定义是指混凝土外边缘到纵向受力钢筋外边缘的距离,因此遵循旧版规范设计的既有混凝土结构(服役超过20 a)普遍存在箍筋保护不足的问题。这一问题导致既有混凝土结构箍筋部位的混凝土更加容易剥落,即使是在纵筋的锈胀裂缝较小的阶段。因此对于箍筋锈蚀程度的评估,不宜以箍筋的锈胀裂缝宽度作为评价指标。
同立向[23]对十组共120根混凝土构件进行了干湿交替的锈蚀试验,并测试了箍筋平均锈蚀率与纵筋的平均锈蚀率。试验中的变化参数为箍筋直径与保护层厚度,纵筋直径保持不变。对其试验结果进行重新整理分析,见图 8,可以看出箍筋锈蚀率和纵筋锈蚀率呈现出线性变化关系,但在相同保护层厚度的情况下,箍筋锈蚀率与纵筋锈蚀率之比随着箍筋直径的增大而减小。在相同的服役环境中,截面纵筋和箍筋的锈蚀程度与其在截面上的位置有关。经反复试算,发现该比例关系与箍筋和纵筋直径、及其到侵蚀界面的净距离有关,见表 1。

|
图 8 箍筋和纵筋锈蚀率的关系 Fig. 8 Relation between corrosion rates of stirrup and longitudinal reinforcement |
| 表 1 箍筋锈蚀率拟合 Tab. 1 Fitting of stirrup corrosion rate |
可以看出试验值与拟合方程的系数具有良好的对应关系,因此本文提出箍筋和纵筋的锈蚀关系模型,表达式为
| $ \eta_{\mathrm{sv}}=\frac{c+2 r}{c} \cdot \frac{R^{2}}{r^{2}} \cdot \eta_{\mathrm{s}} $ | (20) |
式中ηsv为箍筋平均锈蚀率。
整体误差指数IAE被普遍用于评价模型的整体精度[24-25],表达式为
| $ I_{\mathrm{AE}}=\sum \frac{\mid \text { Expe }-\text { Theo } \mid}{\sum \mid \text { Expe } \mid} $ | (21) |
式中Expe、Theo分别为试验值和模型值。
用式(21)对同立向[23]论文中的120个试验数据进行计算,IAE值为0.158。IAE值越接近0,表明模型精度越高,可看出本文模型具有较好的精度。
3.2 箍筋锈蚀对核心区混凝土性能的影响箍筋锈蚀导致的箍筋对核心区混凝土约束能力的降低是影响核心区混凝土性能的主要因素。本文基于Mander模型[26],通过研究箍筋锈蚀对约束区混凝土侧向抗压强度f′l、有效约束系数ke、形状系数rc等主要指标的影响。建立锈蚀箍筋约束的混凝土应力应变模型。
箍筋锈蚀后其对约束混凝土的侧向约束能力由最薄弱部位箍筋的能力所决定,即箍筋的最大锈蚀率决定了约束混凝土的侧向抗压强度,因此有
| $ f_{1}^{\prime \mathrm{c}}=\frac{1}{2} k_{\mathrm{e}}^{\mathrm{c}} \rho_{\mathrm{sv}} f_{\mathrm{yh}}^{\mathrm{c}} $ | (22) |
式中: fl′c为锈蚀箍筋约束区混凝土侧向抗压强度,kec为箍筋锈蚀后的有效约束系数,ρsv为配箍率,fyhc为锈蚀箍筋的等效屈服强度。
根据裂缝宽度分布,按本文2.3节方法评估出纵筋等效强度后,再结合式(20)得出相应位置的锈蚀箍筋等效屈服强度为
| $ f_{\mathrm{yh}}^{\mathrm{c}}=\eta_{\mathrm{s}}\left(\frac{c+2 r}{c} \cdot \frac{R^{2}}{r^{2}}\right) f_{\mathrm{yh}} $ | (23) |
式中ηs为本文2.2节计算得到的纵筋截面锈蚀率,fyh为未锈蚀箍筋的屈服强度。
Mander模型[26]中有效约束系数体现了箍筋的约束范围,计算发现锈蚀箍筋的有效约束系数对箍筋锈蚀率的变化不敏感,见图 9。即使锈蚀程度较高,有效约束系数也未出现显著降低,在锈蚀率达到75%时,有效约束系数仅降低了约4%。同时发现有效约束系数的变化与锈蚀率呈明显的线性关系,因此在建模过程中仍将其考虑在内。需要强调的是有效约束系数仅体现箍筋的约束范围,约束效果则由混凝土侧向抗压强度体现,因此当锈蚀程度较高时,虽然约束范围没有显著变化,但箍筋的约束效果大幅降低。

|
图 9 有效约束系数变化 Fig. 9 Variation of effective constraint coefficient |
将式(22)与式(23)的计算结果代入Mander模型[26]中,即可计算得到锈蚀箍筋约束区混凝土的峰值应力、峰值应变与极限应变。然而模型计算曲线与Vu等[8]和刘磊等[27]的试验数据进行对比发现计算的极限应力均高于试验极限应力,试验试件设计参数见表 2。由于Mander模型[26]中极限应力值是将峰值应力,峰值应变,极限应变与形状系数等参数代入模型的曲线方程中得到的(式(24)),而此方程仅适用于未锈蚀构件,因此模型对锈蚀后约束区混凝土下降段的强度有所高估。因此需对模型的峰值应力进行修正。
| $ {f_{{\rm{cu}}}} = \frac{{{f_{{\rm{co}}}}{r^{\rm{c}}}x}}{{{r^{\rm{c}}} - 1 + {x^{{r^{\rm{c}}}}}}} $ | (24) |
| 表 2 约束混凝土材性试验试件设计参数 Tab. 2 Specimen parameters of constrained concrete property test |
式中:fcu、fco分别为约束区混凝土极限应力与峰值应力,rc为形状系数,x为核心区混凝土极限应变与峰值应变的比值。
由式24可知,在不改变峰值应力、峰值应变与极限应变的情况下,对形状系数进行修正可有效降低极限应力。
| $ {r_{{\rm{cc}}}} = {\chi _{\rm{c}}}{r_{\rm{c}}} $ | (25) |
式中: rcc为锈蚀后约束区混凝土形状系数,χc为锈蚀箍筋约束混凝土模型形状系数的修正系数。
分别计算Vu等[8]和刘磊等[27]试验中各个试块的修正系数,见图 10。可见各试块的修正系数窄幅变动,其平均值为1.34。因此可取修正系数为1.34,使得极限应力的计算值与实验值吻合。
| $ r_{\mathrm{cc}}=1.34 r_{\mathrm{c}} $ | (26) |
式中rcc为锈蚀后约束区混凝土形状系数。

|
图 10 形状系数拟合 Fig. 10 Fitting of shape factor |
将本文计算结果与Vu等[8]和刘磊等[27]的试验数据进行对比,结果见图 11,本文模型与实验结果吻合良好。

|
图 11 试验与计算应力-应变曲线对比 Fig. 11 Comparison of test and calculated stress-strain curves |
OPENSEES有限元平台是地震工程相关科研领域广泛使用的数值仿真平台之一,本文基于OPENSEES有限元平台,基于所提出的材料模型对锈蚀RC柱的性能劣化进行数值仿真。
4.1 试验概况本文选取王学民[28]、Goksu等[29]、Meda等[30]论文中以弯曲破坏为主的锈蚀RC长柱进行对比验证。试验RC柱的主要参数见表 3,截面及配筋见图 12。试验均采用了悬臂柱的加载方式,其中柱的计算长度取柱底到反弯点(加载中点)的距离。表中所列锈蚀率均为裂缝区段内所对应的截面锈蚀率,而非整根钢筋的平均锈蚀率。其中XZ-2和XZ-7构件存在纵向不均匀锈蚀现象,其锈蚀裂缝集中分布于试件的下半段,钢筋等效强度按本文2.3节模型计算。除XZ-2和XZ-7外其余试件的锈胀裂缝均沿钢筋全长均匀分布,其截面锈蚀率与平均锈蚀率相等且沿柱高不变,锈蚀影响系数取1。

|
图 12 试验柱详细构造 Fig. 12 Details of test column |
| 表 3 试验RC柱设计参数 Tab. 3 Design parameters of RC columns |
宏观有限元模型中杆件单元采用基于位移法的非线性梁柱单元,截面采用纤维截面。沿柱高度设置5个节点,4个计算单元,截面分别沿长宽方向划分40根纤维,以保证截面的计算效率与精度,有限元划分与图 6划分形式一致。保护层与核心区混凝土材料采用OPENSEES中的Concrete02材料模拟。保护层混凝土本构关系使用Kent-Scott-Park混凝土模型[31],核心区混凝土本构关系中峰值点与极限点应力应变值根据本文所提模型计算结果输入。钢筋本构关系采用OPENSEES中的Steel02材料模拟,钢筋等效屈服应力由本文2.3节模型计算。各试件所涉及截面材料的模型计算值见表 3。
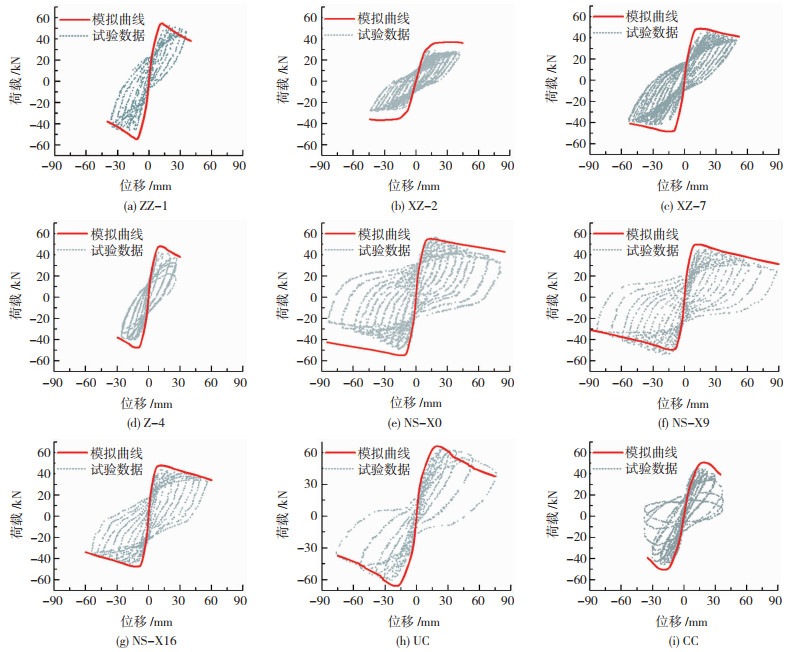
4.3 荷载-位移反应图 13为各试件的柱顶水平荷载-位移的模型预测结果和试验测试结果。其中ZZ-1,NS-X0,和UC为无锈蚀情况,作为参照对象。无锈蚀情况的计算结果与试验结果高度吻合,基础的数值模型有较高的准确度。对于具有不同锈蚀率且混凝土强度,配箍率和轴压比等参数各不相同的RC柱,模型计算结果与试验结果总体吻合较好。
|
图 13 模拟结果与试验结果对比 Fig. 13 Comparison of simulation and test results |
根据试验曲线可以看到构件Z-4与CC均出现了等幅加载时承载力突然下降的现象。根据本文所提纵筋箍筋锈蚀率关系模型计算得到的构件Z-4与CC的箍筋锈蚀率均接近于100%,很有可能是在试验过程中发生了箍筋突然拉断的现象。构件CC的预测曲线略高于试验曲线。在箍筋锈蚀率较高情况下,构件的抗剪能力和混凝土与纵筋粘结强度均有所下降,剪切变形与滑移变形所占柱顶总位移比重增加。锈蚀程度相当的Z-4构件,由于在构件制作过程中采取了在纵筋端部加焊短钢筋的措施以减少滑移变形,因此试验曲线与模拟曲线的误差低于CC构件的误差。部分试验的滞回曲线呈现一定的不对称性,可能是RC柱两侧纵筋的锈蚀程度不一致所导致,然而由于文献本身未对钢筋锈蚀的情况作更加详尽的描述,因此建模时无法作出更细致的匹配。
5 结论1) 本文建立的锈胀裂缝宽度模型符合已有试验结果中探明的一般规律,可反映混凝土保护层厚度,钢筋尺寸及其所在位置,纵筋截面锈蚀率的影响。模型计算结果与已有试验结果吻合度较好,可以较好地评估既有混凝土结构钢筋锈蚀程度。
2) 本文基于已有试验数据提出的纵筋与箍筋锈蚀率的关联模型可体现纵筋和箍筋直径以及其距侵蚀界面净距离的影响。模型计算结果的整体误差较小,可以根据纵筋锈蚀率计算箍筋的锈蚀率。
3) 箍筋锈蚀后,核心区混凝土的侧向抗压强度降低,但箍筋锈蚀程度对有效约束系数几乎没有影响。箍筋锈蚀是影响核心区混凝土侧向抗压强度的主要因素。
4) 本文基于OPENSEES平台建立的锈蚀RC柱的整体数值模型与试验结果吻合较好,说明本文提出的相关模型具有较好的适用性。
| [1] |
DAI Kuangyu, LIU Chang, LU Dagang, et al. Experimental investigation on seismic behavior of corroded RC columns under artificial climate environment and electrochemical chloride extraction: A comparative study[J]. Construction and Building Materials, 2020, 242: 118014. DOI:10.1016/j.conbuildmat.2020.118014 |
| [2] |
DAI Kuangyu, YU Xiaohui, LU Dagang, et al. Phenomenological hysteretic model for corroded RC columns[J]. Engineering Structures, 2020, 210: 110315. DOI:10.1016/j.engstruct.2020.110315 |
| [3] |
胡志坚, 夏雷雷, 程晨, 等. 钢筋混凝土构件锈蚀开裂与锈胀力分析[J]. 哈尔滨工业大学学报, 2020, 52(3): 99. HU Zhijian, XIA Leilei, CHENG Chen, et al. Investigation on corrosion-induced cracking and corrosion expansive pressure in reinforced concrete members[J]. Journal of Harbin Institute of Technology, 2020, 52(3): 99. DOI:10.11918/201812061 |
| [4] |
OTIENO M, IKOTUN J, BALLIM Y. Experimental investigations on the influence of cover depth and concrete quality on time to cover cracking due to carbonation-induced corrosion of steel in RC structures in an urban, inland environment[J]. Construction and Building Materials, 2019, 198(20): 172. DOI:10.1016/j.conbuildmat.2018.11.215 |
| [5] |
DU Y G, CLARK L A, CHAN A H C. Residual capacity of corroded reinforcing bars[J]. Magazine of Concrete Research, 2005, 57(3): 135. DOI:10.1680/macr.2005.57.3.135 |
| [6] |
DU Y G, CLARK L A, CHAN A H C. Effect of corrosion on ductility of reinforcing bars[J]. Magazine of Concrete Research, 2005, 57(7): 407. DOI:10.1680/macr.2005.57.7.407 |
| [7] |
OU Yuchen, SUSANTO Y T T, ROH H. Tensile behavior of naturally and artificially corroded steel bars[J]. Construction and Building Materials, 2016, 103: 93. DOI:10.1016/j.conbuildmat.2015.10.075 |
| [8] |
VU N S, YU Bo, LI Bing. Stress-strain model for confined concrete with corroded transverse reinforcement[J]. Engineering Structures, 2017, 151: 472. DOI:10.1016/j.engstruct.2017.08.049 |
| [9] |
邢国华, 杨成雨, 常召群, 等. 锈蚀钢筋混凝土柱的修正压-剪-弯分析模型研究[J]. 工程力学, 2019, 36(8): 87. XING Guohua, YANG Chengyu, CHANG Zhaoqun, et al. Study on modified axial-shear-flexure interaction model for corroded reinforced concrete columns[J]. Engineering Mechanics, 2019, 36(8): 87. DOI:10.6052/j.issn.1000-4750.2018.07.0376 |
| [10] |
VU N S, YU Bo, LI Bing. Prediction of strength and drift capacity of corroded reinforced concrete columns[J]. Construction and Building Materials, 2016, 115: 304. DOI:10.1016/j.conbuildmat.2016.04.048 |
| [11] |
李磊, 罗光喜, 王卓涵, 等. 震损钢筋混凝土柱剩余能力的数值模型[J]. 工程力学, 2020, 37(12): 52. LI Lei, LUO Guangxi, WANG Zhuohan, et al. Numerical model for residual seismic capacity of the seismic damaged reinforced concrete columns[J]. Engineering Mechanics, 2020, 37(12): 52. DOI:10.6052/j.issn.1000-4750.2019.12.0789 |
| [12] |
ACI Committee. Building code requirements for structural concrete (ACI 318-08) and commentary (ACI 318R-08)[S]. Farmington Hills: American Concrete Institute, 2008
|
| [13] |
混凝土结构设计规范: GB 50010—2002[S]. 北京: 中国建筑工业出版社, 2002 Code for design of concrete structures: GB 50010—2002[S]. Beijing: China Architecture & Building Press, 2002 |
| [14] |
YUAN Yingshu, JI Yongsheng. Modeling corroded section configuration of steel bar in concrete structure[J]. Construction and Building Materials, 2009, 23(6): 2461. DOI:10.1016/j.conbuildmat.2008.09.026 |
| [15] |
ZHAO Yuxi, ZHANG Xiaowen, DING Hangjie, et al. Non-uniform distribution of a corrosion layer at a steel/concrete interface described by a Gaussian model[J]. Corrosion Science, 2016, 112: 8. DOI:10.1016/j.corsci.2016.06.021 |
| [16] |
姬永生, 袁迎曙, 宋萌, 等. 不同锈蚀条件下混凝土内钢筋锈蚀物膨胀性能比较和机理分析[J]. 北京工业大学学报, 2011, 37(11): 1677. JI Yongsheng, YUAN Yingshu, SONG Meng, et al. Volume expansion characteristic and mechanism of rebar corrosion products in concrete with different corrosion approaches[J]. Journal of Beijing University of Technology, 2011, 37(11): 1677. DOI:10.11936/bjutxb2011111677 |
| [17] |
ZHANG Ruijin, CASTEL A, FRANCOIS R. Concrete cover cracking with reinforcement corrosion of RC beam during chloride-induced corrosion process[J]. Cement and Concrete Research, 2010, 40(3): 415. DOI:10.1016/j.cemconres.2009.09.026 |
| [18] |
APOSTOLOPOULOS C A, KOULOURIS K F, APOSTOLOPOULOS A C. Correlation of surface cracks of concrete due to corrosion and bond strength (between steel bar and concrete)[J]. Advances in Civil Engineering, 2019, 2019: 3438743. DOI:10.1155/2019/3438743 |
| [19] |
LIN Hongwei, ZHAO Yuxi. Effects of confinements on the bond strength between concrete and corroded steel bars[J]. Construction and Building Materials, 2016, 118: 127. DOI:10.1016/j.conbuildmat.2016.05.040 |
| [20] |
罗小勇, 刘晋宏, 聂经纶. 锈蚀钢筋截面分布特征及轴向拉伸力学性能[J]. 建筑材料学报, 2019, 22(5): 730. LUO Xiaoyong, LIU Jinhong, NIE Jinglun. Cross-section distribution characteristics and tensile behavior of corroded reinforcing steel bars[J]. Journal of Building Materials, 2019, 22(5): 730. DOI:10.3969/j.issn.1007-9629.2019.05.009 |
| [21] |
ZHANG Weiping, SONG Xiaobin, GU Xianglin, et al. Tensile and fatigue behavior of corroded rebars[J]. Construction and Building Materials, 2012, 34: 409. DOI:10.1016/j.conbuildmat.2012.02.071 |
| [22] |
孔航挺. 非均匀锈蚀下钢筋砼耐久性退化机理及剩余承载力分析[D]. 杭州: 浙江大学, 2018 KONG Hangting. Durability deterioration mechanism and residual bearing capacity of reinforced concrete under non-uniform corrosion[D]. Hangzhou: Zhejiang University, 2018 |
| [23] |
同立向. 箍筋锈蚀引起的混凝土保护层损伤及对纵筋锈蚀的影响研究[D]. 西安: 西安建筑科技大学, 2013 TONG Lixiang. Research on the damage of concrete and the influence for the longitudinal reinforcement corrosion by stirrup corrosion[D]. Xi'an: Xi'an University of Architecture and Technology, 2013 |
| [24] |
WANG Zhuohan, LI Lei, ZHANG Yixin, et al. Bond-slip model considering freeze-thaw damage effect of concrete and its application[J]. Engineering Structures, 2019, 201: 109831. DOI:10.1016/j.engstruct.2019.109831 |
| [25] |
李磊, 王卓涵, 张艺欣, 等. 冻融损伤钢筋混凝土构件黏结滑移本构模型研究[J/OL]. 建筑结构学报, (2020-01-19). DOI: 10.14006/j.jzjgxb.2019.0415 LI Lei, WANG Zhuohan, ZHANG Yixin, et al. Bond-slip model considering freeze-thaw damage effect of concrete and its application[J/OL]. Journal of Building Structures, (2020-01-19). DOI: 10.14006/j.jzjgxb.2019.0415 |
| [26] |
MANDER J B, PRIESTLEY M J N, PARK R. Theoretical stress-strain model for confined concrete[J]. Journal of Structural Engineering, 1988, 114(8): 1804. DOI:10.1061/(ASCE)0733-9445(1988)114:8(1804) |
| [27] |
刘磊, 牛荻涛, 李强, 等. 锈蚀箍筋约束混凝土应力-应变本构关系模型[J]. 建筑材料学报, 2018, 21(5): 811. LIU Lei, NIU Ditao, LI Qiang, et al. Stress-strain constitutive relation model of corroded stirrups confined concrete[J]. Journal of Building Materials, 2018, 21(5): 811. DOI:10.3969/j.issn.1007-9629.2018.05.018 |
| [28] |
王学民. 锈蚀钢筋混凝土构件抗震性能试验与恢复力模型研究[D]. 西安: 西安建筑科技大学, 2003 WANG Xuemin. Research of seismic performance and hysteretic mode of corroded reinforced concrete members[D]. Xi'an: Xi'an University of Architecture and Technology, 2003 |
| [29] |
GOKSU C, ILKI A. Seismic behavior of RC columns with corroded plain and deformed reinforcing bars[J]. ACI Structural Journal, 2016, 113(5): 1053. |
| [30] |
MEDA A, MOSTOSI S, RINALDI Z, et al. Experimental evaluation of the corrosion influence on the cyclic behaviour of RC columns[J]. Engineering Structures, 2014, 76: 112. DOI:10.1016/j.engstruct.2014.06.043 |
| [31] |
MOHD Y M H. Nonlinear analysis of prestressed concrete structures under monotonic and cyclic loads[D]. Berkeley: University of California, 1994
|
 2021, Vol. 53
2021, Vol. 53


