超高性能混凝土(ultra-high performance concrete, UHPC)是一种新型水泥基复合材料,具有超高强、高抗拉强度、高耐久、高韧性等特点。研究表明[1],提高混凝土强度可以有效减少钢筋用量和截面尺寸,有效降低试件轴压比,进而提高构件的延性和耗能能力。UHPC为结构向轻质高强、高延性方向发展提供了材料支撑,在特殊建筑工程、结构修复及改造等方面应用前景广阔。
国内外对UHPC及其构件性能研究已有长足进展。Voo等[2-3]对预应力UHPC无腹筋工字形梁进行了抗剪试验和理论分析,研究得出提高UHPC中的钢纤维掺量可提高试件抗剪承载力,增大试件剪跨比将降低承载力。陈彬[4]对配置CRB550箍筋的预应力UHPC梁进行了抗剪试验,研究表明掺杂钢纤维可以影响试件的破坏形态,腹筋能明显改善斜裂缝的分布。邓宗才等[5-6]对配置HRB500级箍筋的UHPC梁进行了抗剪试验,结果表明HRB500级箍筋强度能得到充分发挥,混杂纤维和提高配箍率可以提高试件的抗剪承载力。金凌志等[7]研究了高强钢筋UHPC简支梁的受剪性能,研究证实高强钢筋与UHPC协同工作效果良好,在一定剪跨比范围内,适当配置箍筋可以改善试件的受剪延性。此外,一些学者[8-10]对UHPC试件进行了弯曲性能试验研究,结果表明UHPC试件具有良好的弯曲韧性,其开裂应变远高于普通混凝土试件。
赵冠远等[11]对4根剪跨比为8.3的配筋UHPC柱进行了无轴压的低周往复试验,研究表明UHPC柱具有较好的抗震性能;在保证不发生纵筋屈曲及剪切破坏的前提下,可以大幅度减小箍筋的数量及间距。郝文秀等[12]对5个剪跨比为4.3的UHPC空心桥墩进行了低周往复试验和有限元模拟,研究表明UHPC试件具有良好的抗震性能;变形能力和延性随配箍率的增加而改善。鞠彦忠等[13]对18根剪跨比为7.5的普通钢筋UHPC柱进行了低周往复试验,研究表明UHPC柱的延性随轴压比的增大而下降,提高配箍率一定程度上改善了滞回特性。徐慎春[14]进行了12根剪跨比为3.3和5.3的高强纵筋UHPC柱抗震性能试验,试验表明增大轴压比会降低水平承载力和延性,影响试件破坏形态。
然而,以往对UHPC柱抗震性能的研究均为大剪跨比工况,而对剪跨比小于3的UHPC柱破坏规律的研究鲜见报道。为此,本文对5个配筋UHPC柱进行了低周往复试验和理论分析,研究了CFRP布缠绕、配筋强度和剪跨比对UHPC柱抗震性能的影响,为工程设计与应用提供参考。
1 试验概况 1.1 试件材料 1.1.1 UHPC制备UHPC的原材料有P·Ⅱ52.5R硅酸盐水泥、硅灰、粉煤灰、矿粉、水、石英砂和钢纤维,各组分配比见表 1。P·Ⅱ52.5R硅酸盐水泥实测3 d抗折强度7.2 MPa,实测3 d抗压强度34.8 MPa。硅灰的指标:比面积20.2 m2/kg,SiO2含量95 %,烧失量1.3 %,需水量比124 %。粉煤灰为一级粉煤灰,其主要指标:细度(45 μm方孔筛筛余量)6.3 %,需水量比91 %,烧失量1.61 %,含水量1.0 %。矿粉的等级为S95,其主要指标:比表面积418 m2/kg,密度2.88 g/cm3,烧失量0.97 %,7 d活性指数84 %,流动度比99 %。石英砂粒径为10~40目(0.85~2.05 mm)。钢纤维长度为13 mm,直径0.3 mm,长径比43,抗拉强度2 800 MPa。
| 表 1 UHPC材料组成与配合比 Tab. 1 Composition and mix proportion of UHPC |
浇筑试件时预留18个边长150 mm的UHPC立方体试块,与UHPC柱在同条件下养护,试验前测得其立方体抗压强度fcu的平均值为125.6 MPa和劈裂强度ft, s的平均值为19.8 MPa,根据文献[15],取UHPC轴心抗压强度平均值fck=0.88fcu,计算得UHPC的轴心抗压强度平均值为110.53 MPa。预留100 mm×100 mm×300 mm UHPC试块3个,试验前测得弹性模量为56.04 GPa。
1.1.2 碳纤维布碳纤维增强树脂基(carbon fiber reinforced polymer, CFRP)布为单向编织,编织方向见图 1。CFRP布的抗拉强度为3 602 MPa,弹性模量为233 GPa。CFRP布及缠绕效果见图 1。

|
图 1 CFRP约束 Fig. 1 CFRP confinement |
试验使用了两种不同强度等级的钢筋,分别为Ⅲ级普通钢筋和Ⅳ级高强钢筋。普通钢筋UHPC柱的纵筋和箍筋分别采用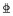
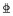
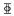
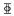
| 表 2 钢筋表 Tab. 2 Details of reinforcement |
试验共设计了5个试件,柱截面尺寸均为250 mm×250 mm,柱高700 mm或1 200 mm,保护层厚度为25 mm。利用UHPC轴心抗压强度,求得试验轴压比为0.2。试验共设置了3种不同约束形式的UHPC柱:LC-2.0为普通钢筋UHPC柱,HC-1.5、HC-2.0和HC-4.0为高强钢筋UHPC柱,为了对比箍筋与CFRP的横向约束效果,设置了一个CFRP布缠绕的普通钢筋UHPC柱LC-2.0F。各试件的参数见表 3。
| 表 3 试件参数设置 Tab. 3 Parameters setting of specimens |
试件的详细配筋和尺寸见图 2。

|
图 2 试件详图(mm) Fig. 2 Details of specimen (mm) |
柱顶部施加轴向荷载大小根据轴压比确定,在整个试验过程中保持轴力恒定。根据JGJ 101—96《建筑抗震试验方法规程》,正式加载前先预加载至估算开裂荷载的25 %,检查加载装置是否与试件充分接触、各测量仪器是否正常工作。正式加载时,采用力-位移混合控制的加载方式,试件屈服前采用力控制,依次加载预估屈服荷载的25 %、50 %、75 %、100 %,每级循环一次;试件屈服之后采用位移控制,每级位移为Δy、2Δy、3Δy、4Δy,其中Δy为试件屈服位移,每级循环2次,各级加载后均持荷5 min。当加载承载力下降到最大荷载值的85 %时,试件达到极限荷载,即认为试件丧失承载力,试验结束。加载装置见图 3。

|
图 3 加载装置 Fig. 3 Diagram of loading equipment |
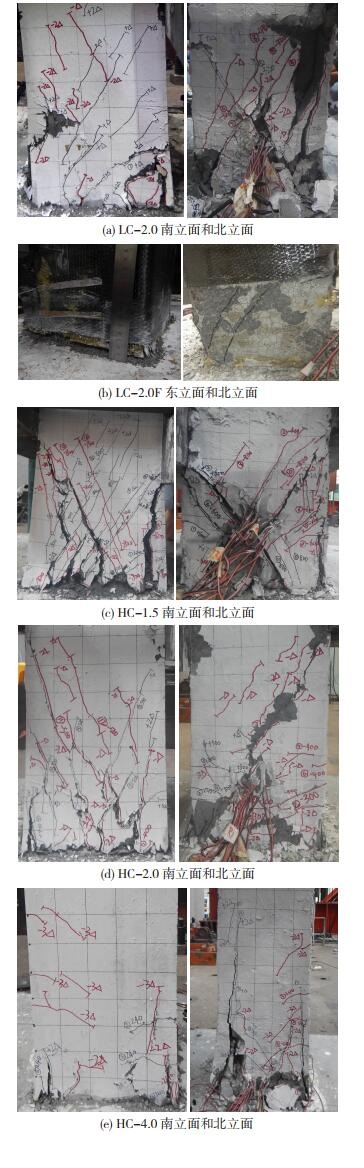
5个试件的破坏模式分为两类:剪压破坏和弯剪破坏。当剪跨比较小时,试件发生剪压破坏,如试件LC-2.0、HC-1.5和HC-2.0;当CFRP布缠绕或剪跨比较大时,试件发生弯剪破坏,如试件LC-2.0F和HC-4.0。试件最终破坏形态见图 4。
|
图 4 试件最终破坏形态 Fig. 4 Final failure modes of specimens |
LC-2.0:当加载至±320 kN时,试件东西两立面出现横向裂缝,最大裂缝长度12 cm;北立面出现斜裂缝,裂缝长度20 cm。当荷载达到±400 kN时,东立面有横向裂缝贯通立面,裂缝呈斜向发展趋势。当加载至±550 kN时,箍筋率先屈服,并有少量纵筋屈服。
HC-1.5:当加载至400 kN时,西立面和北立面分别出现长15 cm和29 cm的斜裂缝。加载至600 kN时,西立面和北立面新增多条斜裂缝,东侧柱底横向裂缝贯通立面,部分箍筋率先屈服。当加载至750 kN时,斜裂缝继续发展,相继有箍筋和纵筋屈服。
HC-2.0:当加载至±200 kN时,出现一条连接东立面和北立面的横向裂缝,裂缝长度10 cm。当加载至400 kN时,西立面出现长7 cm的斜裂缝。当加载至±500 kN时,部分箍筋屈服,卸载时轴力掉载明显。当荷载达到550 kN时,柱底横向裂缝贯通立面,部分纵筋屈服。
2.2 弯剪破坏LC-2.0F:当加载至400 kN时,西立面出现长6 cm横向裂缝。加载至550 kN时,东西两侧底部的横向裂缝贯通,纵筋受拉屈服,卸载时轴力掉载明显。
HC-4.0:当加载至±200 kN时,东立面和北立面分别出现长14 cm和8 cm的横向裂缝,西立面出现两条通长裂缝和一条长20 cm横向裂缝。当加载至±220 kN时,西立面底部横向裂缝贯通,西侧受拉纵筋屈服。当荷载达到240 kN时,东立面底部横向裂缝贯通,东侧受拉纵筋屈服。加载过程中,裂缝不断扩展,并在位移加载时出现UHPC剥落。
由试件破坏过程看出,对于剪跨比最小的试件HC-1.5,斜裂缝首先出现,并迅速扩展形成临界斜裂缝。而试件LC-2.0和HC-2.0首先在东西立面上出现横向裂缝,接着向其相邻两个立面斜向扩展,最终形成临界斜裂缝,箍筋屈服,横向裂缝贯通试件底部,部分纵筋受拉屈服。对于CFRP布缠绕的试件LC-2.0F,斜裂缝发展受到抑制,箍筋应变增长较慢,在柱底横向裂缝贯通立面后,纵筋先于箍筋受拉屈服,LC-2.0F发生弯剪破坏。剪跨比较大的试件HC-4.0,以横向裂缝发展为主,仅南北立面有少量斜裂缝,且最终未形成临界斜裂缝。
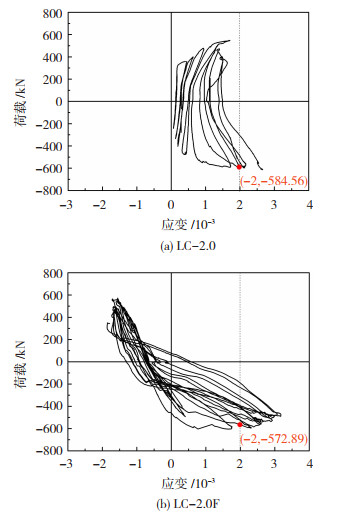
3 试验结果及分析 3.1 钢筋应变为了说明纵筋、箍筋应力与荷载的关系,部分典型试件的纵筋和箍筋的应力-水平荷载曲线见图 5、6。可知,剪切破坏试件(如LC-2.0)的纵筋在位移加载时屈服,而箍筋屈服点与峰值荷载相近。弯剪破坏试件(如LC-2.0F)的箍筋在峰值荷载后屈服,与纵筋屈服时刻相近。剪切破坏和弯剪破坏试件的纵筋和箍筋屈服时,水平荷载均达到或接近峰值荷载,说明配筋UHPC短柱中的钢筋与UHPC变形协调良好,钢筋强度均得到充分发挥。峰值荷载前,LC-2.0和LC-2.0F的塑性变形较小,纵筋和箍筋的应变增长缓慢。峰值荷载后,LC-2.0的纵筋和箍筋应变增幅较大,应变片很快失效,而LC-2.0F在CFRP布约束下,纵筋和箍筋的应变增幅较小,应变片可继续工作。
|
图 5 纵筋应力-水平荷载曲线 Fig. 5 Longitudinal steel stress-horizontal load curves |

|
图 6 箍筋应力-水平荷载曲线 Fig. 6 Stirrup stress-horizontal load curves |
各试件的特征荷载和特征位移见表 4。极限位移取水平荷载下降至峰值荷载的85 %时所对应的水平位移,试件屈服点由通用屈服弯矩法确定。表 4中,Fy和Δy表示屈服荷载和屈服位移,Fp和Δp表示峰值荷载和峰值位移,Δu表示极限位移。试件延性系数μ由式(1)确定。文献[16]指出,对于剪跨比小于2的结构构件,用极限位移角θp来评价构件延性更为合适。
| $ \mu=\varDelta_{\mathrm{u}} / \varDelta_{\mathrm{y}} $ | (1) |
| $ \theta_{\mathrm{p}}=\varDelta_{\mathrm{u}} / H $ | (2) |
| 表 4 试件的特征荷载和特征位移 Tab. 4 Characteristic load and displacement of specimens |
式中H为加载点到柱基础顶面的垂直高度。
试件LC-2.0和LC-2.0F相比,LC-2.0F的屈服位移和峰值位移较LC-2.0分别减小了25.2 %和47.4 %,而其水平承载力相近,证明CFRP布可以有效提高UHPC柱刚度,延缓试件裂缝的扩展。试件LC-2.0F的延性系数较LC-2.0提高了71.2 %,说明CFRP布可以显著减缓UHPC柱水平承载力衰减,提高试件延性。
试件LC-2.0和HC-2.0相比,当提高试件纵筋和箍筋的强度后,UHPC柱屈服荷载和峰值荷载有所提高。相较于LC-2.0,HC-2.0的屈服位移有所增加,峰值位移略有降低,极限位移提高显著,延性系数提高了5.7 %。试件进入塑性变形阶段后,高强钢筋可以有效减缓UHPC柱水平承载力衰减,改善试件延性。
试件HC-1.5、HC-2.0和HC-4.0相比,可知试件的水平承载力随着剪跨比的增大而降低,当剪跨比超过一定限值后,UHPC柱发生弯剪破坏。由表 4可以看出,无论剪压破坏还是弯剪破坏,UHPC柱均具有良好的延性。
3.3 水平荷载-加载点位移滞回曲线图 7为试件的水平荷载-加载点位移滞回曲线。在加载初期,试件处于弹性工作阶段,滞回环窄小;随着水平荷载的增加,裂缝出现并扩展,曲线由弹性阶段进入弹塑性阶段,箍筋和纵筋逐渐屈服,滞回环趋于饱满,试件耗能增加,滞回曲线无明显捏拢效应,UHPC柱表现出良好的耗能能力。

|
图 7 试件加载点位移-水平荷载滞回曲线 Fig. 7 Displacement-horizontal load hysteresis loops of specimens |
不同横向约束方式对比。相较于LC-2.0,CFRP布缠绕试件LC-2.0F的承载力衰减和卸载刚度衰减变缓,滞回环更加饱满。提高钢筋强度后,HC-2.0的承载力衰减较LC-2.0有所缓解,而卸载刚度衰减没有明显改善。
不同剪跨比对比。由试件HC-1.5、HC-2.0和HC-4.0的滞回曲线可知,随着剪跨比的增加,试件的延性和滞回性能显著改善,极限位移提高明显。
3.4 骨架曲线由于部分试件的剪跨比不同,不能直观地从其骨架曲线比较试件之间性能差异。因此取每个加载循环的最大荷载及其对应的位移作为参考点,将各试件的骨架曲线进行归一化处理,各试件归一化后的骨架曲线见图 8。由图 8可知,各试件的峰前响应基本一致。而在峰值点后,各试件的延性和刚度退化差异明显。

|
图 8 归一化后的骨架曲线 Fig. 8 Skeleton curves after normalization processing |
CFRP布缠绕和箍筋是对UHPC的不同横向约束方式。反向加载时,LC-2.0在水平承载力在峰值点后衰减迅速,脆性特征明显。试件LC-2.0F和HC-2.0的延性分别在CFRP布和高强箍筋的约束下明显改善,刚度退化有效减缓。普通箍筋UHPC短柱的延性相对较差,提高箍筋强度或CFRP缠绕可以改善UHPC受剪构件的延性和刚度退化。
不同剪跨比对比。由HC-1.5、HC-2.0和HC-4.0可知,当剪跨比为1.5时,试件HC-1.5在反向加载时出现明显的荷载突减,脆性特征明显;随着剪跨比的增大,试件的特征位移增大,延性改善。
3.5 耗能能力用耗能和等效黏滞阻尼系数来表征试件的耗能能力,其计算方法见式(3)、(4)和图 9。试件的耗能以滞回环包围的面积来计算,计算耗能值为两次加载循环的耗能平均值。
| $ {E = {S_{ABC}} + {S_{ACD}}} $ | (3) |
| $ {{\xi _{{\rm{hyst }}}} = \frac{1}{{{\rm{2 \mathsf{ π} }}}} \cdot \frac{{{S_{ABC}} + {S_{ACD}}}}{{{S_{OBE}} + {S_{ODF}}}}} $ | (4) |

|
图 9 耗能和等效黏滞阻尼系数计算简图 Fig. 9 Calculation for energy dissipation and equivalent viscous damping coefficient |
式中:E表示一个加卸载循环下试件的耗能,ξhyst为等效黏滞阻尼系数,SABC和SACD表示滞回曲线与横坐标轴所围成的面积,SOBE和SODF表示三角形OBE和ODF的面积。
图 10为各试件的耗能及等效黏滞阻尼系数与位移之间的关系图。所有试件的等效黏滞阻尼系数均在0.4以上,配筋UHPC柱具有良好的抗震能力。

|
图 10 耗能与等效黏滞阻尼系数 Fig. 10 Energy dissipation and equivalent viscous damping coefficient |
不同横向约束方式对比。相较于LC-2.0,试件LC-2.0F和HC-2.0的残余变形较小,等效黏滞阻尼系数有所降低。在加载后期,CFRP布和高强钢筋可有效增强试件的耗能能力。
不同剪跨比对比。由HC-1.5、HC-2.0和HC-4.0可知,随剪跨比的增大,水平荷载减小,试件的耗能也随之降低。在加载后期,随剪跨比的增大,UHPC柱的耗能和等效黏滞阻尼系数衰减加快。
3.6 影响因素分析 3.6.1 钢筋强度当箍筋屈服强度由437 MPa提高到606 MPa后,HC-2.0的抗剪承载力较LC-2.0提高了1.5 %。UHPC的开裂应力和开裂应变较大,UHPC开裂时,普通箍筋已接近屈服,未能有效抑制裂缝的发展。对于UHPC受剪构件,当箍筋屈服强度小于606 MPa时,箍筋的裂后工作能力较差,脆性特征明显。
3.6.2 CFRP布缠绕CFRP布的横向约束可以有效抑制斜裂缝的发展,减小试件的变形。CFRP布缠绕试件LC-2.0F的特征位移较LC-2.0下降了25 %~47 %,而特征荷载仅相差1.0 %~1.4 %。由试件的破坏过程可知,LC-2.0F未形成临界斜裂缝,发生弯剪破坏。因此在配筋UHPC受剪构件的设计中,应当考虑CFRP布缠绕对临界斜裂缝倾角和破坏模式的影响。
3.6.3 剪跨比当剪跨比在1.5~2.0之间时,剪应力和正应力的比值较大,UHPC裂缝以斜裂缝为主,试件发生剪切破坏,且斜裂缝与竖直方向的夹角随着剪跨比的增大而减小;当剪跨比增大至4.0时,剪应力和正应力的比值较小,UHPC裂缝以横向裂缝为主,试件发生弯剪破坏。剪跨比越小,斜裂缝发展越迅速,构件的脆性特征越明显。由试验可知,剪跨比不小于1.5的配筋UHPC柱均具有良好的延性。
4 抗剪承载力计算方法 4.1 UHPC柱抗剪机理分析的桁架-拱模型利用桁架-拱模型对发生剪切破坏的试件进行承载力分析,见图 11。假定箍筋和纵筋只受拉力,考虑混凝土的抗拉贡献,临界斜裂缝形成后,Ⅰ区为零应力区,Ⅱ区为箍筋和UHPC共同作用区域,Ⅲ区UHPC为单向受压的斜压杆。

|
图 11 试件的桁架-拱模型 Fig. 11 Truss-arch model of specimens |
图 11中:V表示试件所受剪力,θ表示UHPC斜压杆与竖直方向的夹角,a为剪力到支座边缘的距离。
试件的抗剪承载力V可以分为由桁架机构提供的抗剪贡献Vt和由拱机构提供的抗剪贡献Va,见图 12。图 12中:ca为UHPC斜压杆在水平方向的宽度,σa表示试件达到其承载力时,UHPC斜压杆的压应力,α表示临界斜裂缝的倾角,xc表示试件截面的受压区宽度,c为试件的保护层厚度。

|
图 12 桁架和拱机构示意 Fig. 12 Diagram of truss and arch mechanisms |
分别取桁架机构的Ⅰ区和Ⅱ区为隔离体,见图 13。图 13中:Vs表示箍筋在水平方向的抗拉合力;Vc表示UHPC在垂直剪切裂缝方向的抗拉合力;σc表示桁架机构中UHPC腹杆的压应力。

|
图 13 隔离体受力分析 Fig. 13 Force analysis for free body |
考虑UHPC的抗拉作用,剪切裂缝范围内箍筋在水平方向上的抗拉合力Vs和混凝土在垂直于裂缝方向上的抗拉合力Vc分别见式(5)、(6)。
| $ V_{\mathrm{s}}=\frac{f_{\mathrm{yv}} A_{\mathrm{sv}}}{s} h_{\mathrm{j}} \cot \alpha=\rho_{\mathrm{s} \mathrm{W}} f_{\mathrm{yv}} b h_{\mathrm{j}} \cot \alpha $ | (5) |
| $ V_{\mathrm{c}}=f_{\mathrm{t}} b h_{\mathrm{j}} / \cos \alpha $ | (6) |
式中:fyv为箍筋屈服强度,Asv为同一截面内箍筋各肢面积之和,s为箍筋间距,hj为截面两侧纵筋间中心距,ρsv为试件的配箍率,ft为UHPC轴心抗拉强度实测值,b为试件垂直于剪力方向的截面宽度。
由图 13(a)可得桁架机构所承担的抗剪承载力见式(7)。
| $ V_{\mathrm{t}}=V_{\mathrm{s}}+V_{\mathrm{c}} \sin \alpha=\left(\rho_{\mathrm{sv}} f_{\mathrm{yv}}+f_{\mathrm{t}}\right) b h_{\mathrm{j}} \cot \alpha $ | (7) |
根据图 13(b)中隔离体的内力平衡,结合式(5)和式(7)可得
| $ V_{\mathrm{t}}=\sigma_{\mathrm{c}} b h_{\mathrm{j}} \cos \alpha \sin \alpha $ | (8) |
由1/sin2α=1+cot2α,可得桁架机构中UHPC腹杆的压应力σc为
| $ \sigma_{\mathrm{c}}=\left(\rho_{\mathrm{sv}} f_{\mathrm{yv}}+f_{\mathrm{t}}\right)\left(1+\cot ^{2} \alpha\right) $ | (9) |
文献[17]通过摩尔圆应力分析,给出了考虑轴压影响的矩形箍筋试件临界斜裂缝倾角的计算式:
| $ \alpha=k_{\mathrm{n}} \tan ^{-1}\left(\frac{0.608 \rho_{\mathrm{sv}} \gamma_{\mathrm{E}}+\xi_{1} \frac{\rho_{\mathrm{sv}} A_{\mathrm{v}}}{\rho_{l} A_{\mathrm{g}}}}{1+4 \rho_{\mathrm{sv}} \gamma_{\mathrm{E}}}\right)^{\frac{1}{4}} $ | (10) |
式中:kn为轴压比修正系数,取kn=1.8n2-2.25n+1.54;n为试验轴压比;ρsv =Asv/(bs)为配筋率,ρl =As/(bh)为纵筋的毛配筋率,As为纵筋的配筋面积;h为试件平行于剪力方向的截面宽度;ζ1为边界条件系数,根据文献[18],本文取1.57;γE =Es/Ec,为钢筋与混凝土弹性模量比;Av=bhj为试件的有效截面面积,Ag为试件的毛截面面积。由试验可知,当CFRP布横向约束配筋UHPC柱时,临界斜裂缝倾角变大,甚至改变试件破坏模式。
4.1.2 拱机构1) 拱机构所承担的剪力。拱机构所承担抗剪贡献的计算简图见图 12(b)。文献[17]给出了考虑轴力影响的钢筋混凝土柱截面受压区宽度的计算公式:
| $ x_{\mathrm{c}}=\left(0.25+0.85 \frac{N}{f_{\mathrm{c}} A_{\mathrm{g}}}\right) \cdot h $ | (11) |
式中N为轴力,fc为UHPC圆柱体抗压强度实测值。
文献[19]给出了拱机构中UHPC的强度σa的计算公式:
| $ \sigma_{\mathrm{a}}=\gamma_{\mathrm{c}} f_{\mathrm{c}}-\cos (\theta-\alpha) \sigma_{\mathrm{c}} $ | (12) |
式中γc为UHPC的强度软化系数,取0.7;cos(θ-α) 为桁架与拱机构中混凝土斜压杆的倾角差异,取0.9[20]。
将式(9)代入式(12)中,得
| $ \sigma_{\mathrm{a}}=\left[1-\frac{0.9\left(\rho_{\mathrm{sv}} f_{\mathrm{yv}}+f_{\mathrm{t}}\right)\left(1+\cot ^{2} \alpha\right)}{\gamma_{\mathrm{c}} f_{\mathrm{c}}}\right] \cdot \gamma_{\mathrm{a}} f_{\mathrm{c}} $ | (13) |
令
| $ \eta=\frac{0.9\left(\rho_{\mathrm{sv}} f_{\mathrm{yv}}+f_{\mathrm{t}}\right)\left(1+\cot ^{2} \alpha\right)}{\gamma_{\mathrm{c}} f_{\mathrm{c}}} \leqslant 1.0 $ | (14) |
则
| $ \sigma_{\mathrm{a}}=(1-\eta) \gamma_{\mathrm{a}} f_{\mathrm{c}} $ | (15) |
UHPC斜压杆所承担的抗剪承载力可由式(16)确定。
| $ V_{\mathrm{a}}=\sigma_{\mathrm{a}} b\left(x_{\mathrm{c}}-c\right) \tan \theta $ | (16) |
2) 引入剪跨比的影响。剪跨比对抗剪承载力的影响体现在拱机构中斜压杆与竖直方向夹角θ上,由图 12(b)的几何关系可得
| $ \tan \theta=\frac{h-x_{c}}{\left(x_{c}-c\right) \tan \theta+a} $ | (17) |
把剪跨比λ=a/h和式(11)代入式(17),近似取c/h=0,可得
| $ \tan \theta=\frac{\sqrt{\lambda^{2}+4 \sin ^{2} \alpha \cos ^{2} \alpha}-\lambda}{2 \cos ^{2} \alpha} $ | (18) |
研究表明[21-22],UHPC中无序排列的钢纤维可以明显改善混凝土构件的抗剪承载力。文献[23-25]把UHPC的抗拉贡献Vcf视为混凝土基体的抗拉贡献Vc和钢纤维的抗拉贡献Vf之和,钢纤维承担的剪力与钢纤维含量特征值成正比。
| $ {{V_{{\rm{cf}}}} = {V_{\rm{c}}} + {V_{\rm{f}}}} $ | (19) |
| $ {{V_{\rm{f}}} = k \cdot {\lambda _{\rm{f}}}{f_{\rm{t}}}b{h_{\rm{j}}}/\cos \alpha } $ | (20) |
式中:k为考虑钢纤维形状黏结系数,对剪切平直形钢纤维,取0.45[25];λf为钢纤维含量特征值,取λf=ρflf/df;ρf、lf和df分别为钢纤维的体积掺率、长度和直径。
综上,用式(19)中的Vcf替代式(7)中的Vc,则配筋UHPC柱抗剪承载力公式:
| $ \begin{aligned} V=& V_{\mathrm{t}}+V_{\mathrm{a}}=\left[\rho_{\mathrm{sv}} f_{\mathrm{yv}}+f_{\mathrm{t}}\left(1+k \lambda_{\mathrm{f}}\right)\right] b h_{\mathrm{j}} \cot \alpha+\\ &(1-\eta) \gamma_{\mathrm{c}} f_{\mathrm{c}} b\left(x_{\mathrm{c}}-c\right) \tan \theta \end{aligned} $ | (21) |
运用式(21)及GB 50010—2010《混凝土结构设计规范》中的抗剪承载力公式(22)分别对试验中的试件进行计算,并与试验值作对比,见表 5。
| $ V=\frac{1.75}{1+\lambda} f_{\mathrm{t}} b h_{0}+f_{\mathrm{yv}} \frac{A_{\mathrm{sv}}}{s} h_{0}+0.07 N $ | (22) |
| 表 5 抗剪承载力公式对比 Tab. 5 Comparison of formulas for shear capacity |
表 5中,Vc表示混凝土受压腹杆的抗剪贡献,Vs表示箍筋的抗剪贡献,Va表示拱机构的抗剪贡献,Vcal为承载力计算值,Vcal=Vc+Vs+Va或Vcal=Vc+Vs+0.07N,Vtest表示承载力试验值。VFRP表示CFRP布的抗剪贡献,参考文献[26],由式(23)计算。
| $ {V_{{\rm{FRP}}}} = 2{f_{{\rm{FRP}},e}}{t_{{\rm{FRP}}}}{h_{{\rm{FRP}},e}}{\rm{cot}}{\kern 1pt} {\kern 1pt} \alpha $ | (23) |
式中:fFRP, e为CFRP布的有效抗拉强度,取0.5fFRP;fFRP表示CFRP布的受拉强度,tFRP表示CFRP布的厚度;hFRP, e表示试件上粘贴的CFRP布的有效高度,取0.9 h;h为试件平行于剪力方向的截面宽度。
由表 5可看出,试件LC-2.0F和LC-4.0的抗剪承载力计算值远大于实测水平承载力,进一步说明LC-2.0F和LC-4.0发生弯剪破坏而非剪切破坏。对于其余发生剪切破坏的试件,式(21)、(22)的剪切承载力计算值与试验值之比(Vcal/Vtest)的平均值分别为1.01和1.15,变异系数分别为2.1%和10.5%,说明式(21)对钢纤维UHPC配筋构件的抗剪承载力的预测精度较高。由表 5可以看出,式(21)、(22)计算值的主要差异在箍筋的抗剪贡献Vs和UHPC的拉抗贡献Vc上,这是因为式(21)考虑了钢纤维的抗拉贡献、轴压比和配筋对临界斜裂缝的倾角的影响,因此式(21)的计算精度高于式(22)。
4.2.2 适用性验算为了验证式(21)适用性,从文献[27-29]中选取了15根钢纤维混凝土受剪试件,钢纤维混凝土受压强度为65~134 MPa,钢纤维体积掺率为0.8 %~2.0 %,剪跨比为1.5~2.2。试件的详细参数见表 6。
| 表 6 文献[27-29]中受剪试件的承载力计算 Tab. 6 Calculation of bearing capacity of shear specimens in previous studies[27-29] |
利用式(21)对表 6中的试件进行验算,计算值与试验值见表 6。Vcal/Vtest的平均值为0.99,变异系数为7.6 %,理论计算值与试验值吻合良好。
5 结论通过对5个配筋UHPC柱的抗震性能试验和理论分析,得出主要结论:
1) 通过合理配筋,剪跨比在1.5~4.0之间的配筋UHPC柱均具表现出良好的抗震性能。试件的延性系数均在3以上,具有良好的延性。试件的滞回环饱满,无明显捏拢效应,等效黏滞阻尼系数均在0.4以上,具有良好的耗能能力。
2) 剪跨比对UHPC柱的破坏模式影响明显:试件LC-2.0、HC-1.5和HC-2.0等较小剪跨比试件发生剪压破坏,试件以斜裂缝为主,斜裂缝发展较快,脆性相对明显;较大剪跨比试件HC-4.0发生了延性较好的弯剪破坏,试件以横向裂缝为主。
3) 在CFRP约束下,试件LC-2.0F的屈服位移和峰值位移较LC-2.0分别提高了25.2 %和47.4 %,延性系数提高了71.2 %。CFRP布有效约束了斜裂缝的发展,LC-2.0F发生弯剪破坏,延性明显改善。
4) 提高纵筋和箍筋的强度后,试件HC-2.0的承载力和延性系数较LC-2.0有所提高,峰值荷载后水平力的降低速率减缓,抗震性能得到改善。普通箍筋的裂后工作能力较差,UHPC受剪构件的箍筋屈服强度应不小于600 MPa。
5) 基于桁架-拱模型,给出了考虑UHPC抗拉贡献、轴压比和剪跨比影响的抗剪承载力计算公式,计算值与试验值吻合良好。
| [1] |
孙治国, 司炳君, 王东升, 等. 高强箍筋高强混凝土柱抗震性能研究[J]. 工程力学, 2010, 27(5): 135. SUN Zhiguo, SI Bingjun, WANG Dongsheng, et al. Research on the seismic performance of high-strength concrete columns with high-strength stirrups[J]. Engineering Mechanics, 2010, 27(5): 135. |
| [2] |
VOO Y L, FOSTER S J, GILBERT R I. Shear strength of fiber reinforced reactive powder concrete prestressed girders without stirrups[J]. Journal of Advanced Concrete Technology, 2006, 4(1): 128. DOI:10.3151/jact.4.123 |
| [3] |
VOO Y L, POON W K, FOSTER S J. Shear strength of steel fiber-reinforced ultrahigh-performance concrete beams without stirrups[J]. Journal of Structural Engineering, 2010, 136(11): 1395. DOI:10.1061/(asce)st.1943-541x.0000234 |
| [4] |
陈彬. 预应力RPC梁抗剪性能研究[D]. 长沙: 湖南大学, 2007 CHEN Bin. Study on the shear strength of prestressed RPC girders[D]. Changsha: Hunan University, 2007 |
| [5] |
徐海宾, 邓宗才, 陈春生, 等. 超高性能纤维混凝土梁抗剪性能试验研究[J]. 土木工程学报, 2014, 47(12): 97. XU Haibin, DENG Zongcai, CHEN Chunsheng, et al. Experimental study on shear strength of ultra-high performance fiber reinforced concrete beams[J]. China Civil Engineering Journal, 2014, 47(12): 97. DOI:10.15951/j.tmgcxb.2014.12.011 |
| [6] |
邓宗才, 陈春生, 陈兴伟. 混杂纤维活性粉末混凝土梁抗剪性能试验研究[J]. 土木工程学报, 2015, 48(5): 60. DENG Zongcai, CHEN Chunsheng, CHEN Xingwei. Experimental research on the shear behaviors of hybrid fiber reinforced RPC beams[J]. China Civil Engineering Journal, 2015, 48(5): 60. DOI:10.15951/j.tmgcxb.2015.05.006 |
| [7] |
金凌志, 祁凯能, 曹霞. 高强钢筋活性粉末混凝土简支梁受剪性能试验研究[J]. 武汉理工大学学报, 2013, 35(8): 112. JIN Lingzhi, QI Kaineng, CAO Xia. Experimental study on shear behavior of high strength reinforced reactive powder concrete beam[J]. Journal of Wuhan University of Technology, 2013, 35(8): 112. |
| [8] |
曹霞, 彭金成, 金凌志. 预应力活性粉末混凝土简支梁受力性能试验研究[J]. 武汉理工大学学报, 2014, 36(1): 121. CAO Xia, PENG Jincheng, JIN Lingzhi. Experimental research on mechanical performance of prestressed RPC beam[J]. Journal of Wuhan University of Technology, 2014, 36(1): 121. DOI:10.3963/j.issn.1671-4431.2014.01.023 |
| [9] |
郑文忠, 卢姗姗, 李莉. GFRP筋活性粉末混凝土梁受力性能试验研究[J]. 建筑结构学报, 2011, 32(6): 123. ZHENG Wenzhong, LU Shanshan, LI Li. Experimental research on mechanical performance of reactive powder concrete beams reinforced with GFRP bars[J]. Journal of Building Structures, 2011, 32(6): 123. DOI:10.14006/j.jzjgxb.2011.06.004 |
| [10] |
李庆华, 徐世烺. 钢筋增强超高韧性水泥基复合材料弯曲性能计算分析与试验研究[J]. 建筑结构学报, 2010, 31(3): 60. LI Qinghua, XU Shilang. Analysis and experiment of reinforced ultra-high toughness cementitious composite flexural members[J]. Journal of Building Structures, 2010, 31(3): 60. DOI:10.14006/j.jzjgxb.2010.03.008 |
| [11] |
赵冠远, 阎贵平. 活性粉末混凝土柱的抗震性能试验研究[J]. 中国安全科学学报, 2004, 14(7): 97. ZHAO Guanyuan, YAN Guiping. Experimental study on seismic performance of reactive powder concrete columns[J]. China Safety Science Journal, 2004, 14(7): 97. DOI:10.16265/j.cnki.issn1003-3033.2004.07.024 |
| [12] |
郝文秀, 钟铁毅. 活性粉末混凝土桥墩延性试验研究与数值分析[J]. 土木工程学报, 2010, 43(6): 85. HAO Wenxiu, ZHONG Tieyi. Experimental study and numerical analysis of the ductility of reactive powder concrete piers[J]. China Civil Engineering Journal, 2010, 43(6): 85. DOI:10.15951/j.tmgcxb.2010.06.004 |
| [13] |
鞠彦忠, 王德弘, 白俊峰. 活性粉末混凝土柱抗震性能试验[J]. 哈尔滨工业大学学报, 2013, 45(8): 116. JU Yanzhong, WANG Dehong, BAI Junfeng. Seismic performance of reactive powder concrete columns[J]. Journal of Harbin Institute of Technology, 2013, 45(8): 116. |
| [14] |
徐慎春. 高强钢筋及薄壁钢管超高性能混凝土柱抗震性能试验研究与数值模拟[D]. 天津: 天津大学, 2018 XU Shenchun. Seismic behavior of high strength reinforced UHPC columns and UHPC filled thin-walled steel tubular columns: experimental study and numerical simulation[D]. Tianjin: Tianjin University, 2018 |
| [15] |
屈文俊, 邬生吉, 秦宇航. 活性粉末混凝土力学性能试验[J]. 建筑科学与工程学报, 2008, 25(4): 16. QU Wenjun, WU Shengji, QIN Yuhang. Mechanical property tests of reactive powder concrete[J]. Journal of Architecture and Civil Engineering, 2008, 25(4): 16. |
| [16] |
翁义军, 沈聚敏, 马宝民. 复合箍对钢筋混凝土柱延性的改善[J]. 建筑结构学报, 1985(1): 47. WENG Yijun, SHEN Jumin, MA Baomin. Improvement of ductility of reinforced concrete columns with different types of stirrups[J]. Journal of Building Structures, 1985(1): 47. DOI:10.14006/j.jzjgxb.1985.01.004 |
| [17] |
余波, 陈冰, 吴然立. 剪切型钢筋混凝土柱抗剪承载力计算的概率模型[J]. 工程力学, 2017, 34(7): 138. YU Bo, CHEN Bing, WU Ranli. Probabilistic model for shear strength of shear-critical reinforced concrete columns[J]. Engineering Mechanics, 2017, 34(7): 138. |
| [18] |
KIM J H, MANDER J B. Truss modeling of reinforced concrete shear-flexural behavior: technical report MCEER-99-0005[R]. Buffalo, NY: Multidisciplinary Center for Earthquake Engineering Research, 1990
|
| [19] |
马熙伦, 陈宝春, 杨艳, 等. R-UHPC梁的抗剪承载力计算方法[J]. 交通运输工程学报, 2017, 17(5): 23. MA Xilun, CHEN Baochun, YANG Yan, et al. Calculation method of shear bearing capacity of R-UHPC beam[J]. Journal of Traffic and Transportation Engineering, 2017, 17(5): 23. |
| [20] |
管品武. 钢筋混凝土框架柱塑性铰区抗剪承载力试验研究及机理分析[D]. 长沙: 湖南大学, 2001 GUAN Pinwu. Research on seismic shear capacity of columns within yield hinge regions[D]. Changsha: Hunan University, 2001 |
| [21] |
崔发, 田水, 柯杨. 无腹筋钢纤维混凝土梁抗剪承载力的研究[J]. 建筑科学, 2019, 35(3): 24. CUI Fa, TIAN Shui, KE Yang. Study on shear capacity of steel fiber reinforced concrete beams without web reinforcement[J]. Building Science, 2019, 35(3): 24. DOI:10.13614/j.cnki.11-1962/tu.2019.03.004 |
| [22] |
王尚艳. 钢纤维混凝土无腹筋梁抗剪承载力研究[D]. 郑州: 华北水利水电大学, 2019 WANG Shangyan. Study on shear capacity of steel fiber reinforced concrete beams without web reinforcement[D]. Zhengzhou: North China University of Water Resources and Electric Power, 2019 |
| [23] |
MANSUR M A, ONG K C G, PARAMASIVAM P. Shear strength of fibrous concrete beams without stirrups[J]. Journal of Structure Engineering, 1986, 112(9): 2076. DOI:10.1061/(asce)0733-9445(1986)112:9(2066) |
| [24] |
NARAYANAN R, DARWISH I Y S. Use of steel fibers as shear reinforcement[J]. ACI Structural Journal, 1987, 84(3): 223. DOI:10.14359/2654 |
| [25] |
钢纤维混凝土结构设计标准: JGJ/T 465—2019[S]. 北京: 中国建筑工程出版社, 2019 Standard for design of steel fiber reinforced concrete structures: JGJ/T 465—2019[S]. Beijing: China Architecture and Building Press, 2019 |
| [26] |
CHEN J F, TENG J G. Shear capacity of fiber-reinforced polymer-strengthened reinforced concrete beams: fiber reinforced polymer rupture[J]. Journal of Structural Engineering, 2003, 129(5): 623. DOI:10.1061/(ASCE)0733-9445(2003)129:5(615) |
| [27] |
曹霞, 陈逸聪, 唐婷, 等. 不同剪跨比下纵筋率对RPC梁受剪性能的影响[J]. 武汉理工大学学报, 2017, 39(4): 54. CAO Xia, CHEN Yicong, TANG Ting, et al. Influence of longitudinal reinforcement ratio on shear behavior of RPC beam under different shear span ratio[J]. Journal of Wuhan University of Technology, 2017, 39(4): 54. DOI:10.3963/j.issn.1671-4431.2017.04.009 |
| [28] |
王强, 金凌志, 曹霞, 等. 活性粉末混凝土梁抗剪性能试验研究[J]. 浙江大学学报(工学版), 2017, 51(5): 928. WANG Qiang, JIN Lingzhi, CAO Xia, et al. Experimental study on shear performance of reactive powder concrete beam[J]. Journal of Zhejiang University (Engineering Science), 2017, 51(5): 928. DOI:10.3785/j.issn.1008-973X.2017.05.011 |
| [29] |
卞祝. 钢纤维高强钢筋混凝土梁受剪性能试验研究[D]. 马鞍山: 安徽工业大学, 2013 BIAN Zhu. Experimental study on shear resistance properties of steel fiber high-strength reinforced concrete beam[D]. Maanshan: Anhui University of Technology, 2013 |
 2021, Vol. 53
2021, Vol. 53


