目前,外贴CFRP加固技术已经广泛应用于混凝土结构加固工程中[1-2]。在外贴CFRP加固构件中,加固区端部CFRP与混凝土黏结界面剥离是一种常见的破坏模式[3]。各国学者对剥离破坏及控制方法进行了大量的界面和试件试验研究[4-5],并且形成了许多理论成果,如界面剥离行为模型[6]和加固设计方法[7]。然而,上述工作均为常温环境下的界面或构件性能研究,并未考虑温度作用。对于服役于强日照辐射、昼夜温差大等环境下的加固构件,虽然实际温度值不高,但由于线膨胀系数的差异,CFRP和混凝土黏结界面均会产生较大的温度应力,因此会对界面黏结行为带来显著影响[8]。Gao等[9]采用理论方法分析了温度作用对纯外贴CFRP-混凝土界面黏结行为的影响,首次提出了预测界面剥离全过程的解析解,指出温度作用会加快自由端界面滑移发展。因此,温度作用下的界面剥离控制是进行CFRP加固设计的关键。
端部锚固措施可以很好地提高黏结界面的承载能力。李春良等[10]、周英武等[11]、张峰等[12]给出了基于强度理论的端锚界面剥离承载力计算公式;王珍珍等[13]结合四线性界面黏结-滑移本构,给出了端锚CFRP加固混凝土梁IC剥离全过程的计算模型。上述研究体现了端锚措施控制剥离的良好效果,但并未涉及温度应力的分析。Firmo等[14]和Correia等[15]先后进行了温度作用下端部锚固CFRP-混凝土的界面拉伸剪切试验,结果表明,温度作用下的黏结界面在进行端锚后会具备更高的承载性能,但两位学者仅从试验角度对界面黏结强度进行了研究,并未给出表征界面黏结行为的理论模型。
本文基于双线性黏结-滑移本构,建立了温度作用下端锚CFRP-混凝土界面黏结行为解析模型,并与试验数据和有限元结果进行了对比验证。利用解析模型,分析了端锚对界面荷载-滑移响应、界面滑移、界面剪应力及CFRP正应力的影响,分析了温度变化、CFRP厚度和弹模变化对端锚界面的剥离承载力的影响。
1 界面黏结行为的解析模型 1.1 基本假定在界面黏结行为解析分析过程中,做如下的基本假定:1)在拉伸剪切分析时,黏结界面层仅承受剪应力,不承受法向正应力,界面剥离为Ⅱ型破坏;2)解析模型中忽略黏结层的厚度,胶黏剂的性质均体现在界面黏结-滑移本构的参数中;3)CFRP-混凝土界面剥离以内聚破坏为主,与CFRP和混凝土材料破坏的关系较小,因此假定CFRP、混凝土材料均为理想弹性体;4)CFRP材料所受正应力沿厚度方向均匀分布,且不考虑宽度方向的应力变化;5)整个CFRP加固混凝土构件处于均匀的温度场中,不考虑温度变化过程中材料的蠕变;6)锚固端为完全锚固,CFRP片材在该位置处无滑动。
1.2 界面微分方程的建立图 1给出了温度作用下端锚CFRP-混凝土结点单剪试验示意图。

|
图 1 端锚CFRP-混凝土单剪试验 Fig. 1 Single-lap shear test of CFRP-to-concrete bonded joints with end anchorage |
结合前述基本假定,对图 1微元体进行受力分析,可建立力学平衡方程:
| $ \frac{\mathrm{d} \sigma_{\mathrm{f}}}{\mathrm{d} x}-\frac{\tau}{t_{\mathrm{f}}}=0 $ | (1) |
| $ \sigma_{\mathrm{f}} b_{\mathrm{f}} t_{\mathrm{f}}+\sigma_{\mathrm{c}} b_{\mathrm{c}} t_{\mathrm{c}}=0 $ | (2) |
式中:σf、tf、bf分别为CFRP应力、厚度和宽度,σc、tc、bc分别为混凝土应力、厚度和宽度,τ为界面剪应力。
温度作用下CFRP和混凝土材料以及黏结界面的本构关系:
| $ \sigma_{\mathrm{f}}=E_{\mathrm{f}}\left(\frac{\mathrm{d} u_{\mathrm{f}}}{\mathrm{d} x}-\alpha_{\mathrm{f}} \Delta T\right) $ | (3) |
| $ \sigma_{\mathrm{c}}=E_{\mathrm{c}}\left(\frac{\mathrm{d} u_{\mathrm{c}}}{\mathrm{d} x}-\alpha_{\mathrm{c}} \Delta T\right) $ | (4) |
| $ \tau=f(s) $ | (5) |
| $ s=u_{\mathrm{f}}-u_{\mathrm{c}} $ | (6) |
式中:αf和αc分别为CFRP和混凝土的线膨胀系数,Ef和Ec分别为CFRP和混凝土的弹性模量,ΔT为界面温度差值,s为界面滑移,uf和uc分别为CFRP和混凝土的轴向变形。
联立式(1)~(6),得界面微分方程为
| $ \frac{\mathrm{d}^{2} s}{\mathrm{~d} x^{2}}-\lambda^{2} f(s)=0 $ | (7) |
式中
联立式(2)~(4)、(6)可得CFRP正应力的表达式为
| $ \sigma_{\mathrm{f}}=\frac{1}{t_{\mathrm{f}} \lambda^{2}}\left[\frac{\mathrm{d} s}{\mathrm{~d} x}-\left(\alpha_{\mathrm{f}}-\alpha_{\mathrm{c}}\right) \Delta T\right] $ | (8) |
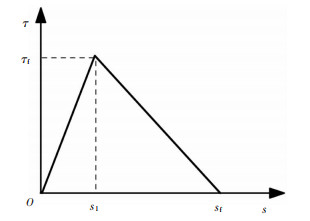
界面黏结-滑移本构是CFRP-混凝土界面荷载传递分析的关键。选取双线性的界面黏结-滑移本构进行界面剥离全过程的非线性求解,该模型可较为真实地模拟界面的黏结-滑移行为,并且双线性的界面黏结-滑移本构广泛的应用于CFRP-混凝土界面黏结剥离行为的解析推导中[3, 6]。因此,本文选取双线性本构模型进行解析推导。见图 2,该本构模型具有一个线性上升分支(弹性段),在达到剪应力峰值后,是一个线性下降分支(软化段),直至剪应力降为0而进入脱黏段,其表达式见式(9)。
| $ \boldsymbol{\tau}=f(s)=\left\{\begin{array}{ll} \frac{\boldsymbol{\tau}_{\mathrm{f}}}{s_{1}} s, & 0<s \leqslant s_{1} \\ \frac{\tau_{\mathrm{f}}}{s_{\mathrm{f}}-s_{1}}\left(s_{\mathrm{f}}-s\right), & s_{1}<s \leqslant s_{\mathrm{f}} \\ 0, & s>s_{\mathrm{f}} \end{array}\right. $ | (9) |
|
图 2 双线性黏结-滑移模型 Fig. 2 Bi-linear bond-slip model |
式中:τf为剪应力峰值,s1为剪应力峰值对应的滑移量,sf为剪应力下降为0时对应的滑移量。
与纯外贴CFRP-混凝土界面剥离全过程[9]不同的是,端部锚固后,端点处的滑移量始终为0。因此,在剥离全过程中只会出现弹性阶段、弹性-软化阶段和弹性-软化-脱黏阶段,而不存在软化-脱黏阶段和脱黏阶段。剥离全过程中的剪应力分布见图 3。图 3中a为界面软化长度、ad为界面脱黏出现时的软化长度、d为界面脱黏长度。

|
图 3 剥离过程及剪应力分布 Fig. 3 Debonding process and shear stress distribution |
当荷载较小,整个黏结界面处于弹性阶段时,见图 3(a),将黏结-滑移本构中的第一分支公式代入界面微分方程式(7)可得
| $ \frac{\mathrm{d}^{2} s}{\mathrm{~d} x^{2}}-\lambda_{1}^{2} s=0 $ | (10) |
式中
由锚固端和加载端的受力分析可确定边界条件为
| $ \left\{\begin{array}{l} x=0, s=0 \\ x=L, \sigma_{\mathrm{f}}=\frac{P}{b_{\mathrm{f}} t_{\mathrm{f}}} \end{array}\right. $ | (11) |
利用边界条件式(11)对界面微分方程式(10)进行求解,可得弹性阶段的界面滑移、剪应力和CFRP正应力分布的解析式:
| $ s=\left[\frac{s_{1} \lambda_{1}}{b_{\mathrm{f}} \tau_{\mathrm{f}}} \frac{P}{\cosh \left(\lambda_{1} L\right)}+\frac{\left(\alpha_{\mathrm{f}}-\alpha_{\mathrm{c}}\right) \Delta T}{\lambda_{1} \cosh \left(\lambda_{1} L\right)}\right] \sinh \left(\lambda_{1} x\right) $ | (12) |
| $ \tau=\frac{\tau_{\mathrm{f}}}{s_{1}}\left[\frac{s_{1} \lambda_{1}}{b_{\mathrm{f}} \tau_{\mathrm{f}}} \frac{P}{\cosh \left(\lambda_{1} L\right)}+\frac{\left(\alpha_{\mathrm{f}}-\alpha_{\mathrm{c}}\right) \Delta T}{\lambda_{1} \cosh \left(\lambda_{1} L\right)}\right] \sinh \left(\lambda_{1} x\right) $ | (13) |
| $ \sigma_{\mathrm{f}}=\frac{P}{b_{\mathrm{f}} t_{\mathrm{f}}} \frac{\cosh \left(\lambda_{1} x\right)}{\cosh \left(\lambda_{1} L\right)}+\frac{\left(\alpha_{\mathrm{f}}-\alpha_{\mathrm{c}}\right) \Delta T}{t_{\mathrm{f}} \lambda^{2}}\left[\frac{\cosh \left(\lambda_{1} x\right)}{\cosh \left(\lambda_{1} L\right)}-1\right] $ | (14) |
定义加载端(x=L)滑移为CFRP-混凝土黏结界面的整体滑移,用Δ表示。根据定义,黏结界面的荷载-滑移关系(P-Δ)表达式为
| $ P=\frac{b_{\mathrm{f}} \tau_{\mathrm{f}}}{s_{1} \lambda_{1}}\left[-\frac{\left(\alpha_{\mathrm{f}}-\alpha_{\mathrm{c}}\right) \Delta T}{\lambda_{1}}+\frac{\Delta}{\tanh \left(\lambda_{1} L\right)}\right] $ | (15) |
在弹性阶段的终点,加载端界面剪应力将达到其峰值τf,见图 3(b),此时界面滑移量为s1,将Δ=s1代入式(15)可得黏结界面在弹性阶段所能承受的最大荷载Pe。
| $ P_{\mathrm{e}}=\frac{b_{\mathrm{f}} \tau_{\mathrm{f}}}{\lambda_{1}} \frac{1}{\tanh \left(\lambda_{1} L\right)}-\frac{b_{\mathrm{f}} \tau_{\mathrm{f}}}{s_{1} \lambda_{1}^{2}}\left(\alpha_{\mathrm{f}}-\alpha_{\mathrm{c}}\right) \Delta T $ | (16) |
随着黏结界面所承受的荷载作用的增大,在靠近加载端区域内会出现软化现象,而靠近锚固端区域仍旧处于弹性状态,即黏结界面进入弹性-软化阶段,见图 3(c)。将黏结-滑移关系中的第一、第二分支公式分别代入微分方程式(7),可对弹性区域和软化区域进行分别求解。令软化区域的长度为a,则弹性区域的长度为L-a。
1) 弹性区域
在0≤x≤L-a的区域内,黏结界面处于弹性状态,其界面微分方程同弹性阶段的方程式(10)。在x=L-a处,剪应力达到峰值,所对应的界面滑移量为s1。故边界条件可改写为
| $ \left\{\begin{array}{l} x=0, s=0 \\ x=L-a, s=s_{1} \end{array}\right. $ | (17) |
将式(17)代入式(10)可得弹性区域的界面物理量及CFRP正应力分布的解析式:
| $ s=s_{1} \frac{\sinh \left(\lambda_{1} x\right)}{\sinh \left[\lambda_{1}(L-a)\right]} $ | (18) |
| $ \tau=\tau_{\mathrm{f}} \frac{\sinh \left(\lambda_{1} x\right)}{\sinh \left[\lambda_{1}(L-a)\right]} $ | (19) |
| $ \sigma_{\mathrm{f}}=\frac{\tau_{\mathrm{f}}}{t_{\mathrm{f}}}\left\{\frac{1}{\lambda_{1}} \frac{\cosh \left(\lambda_{1} x\right)}{\sinh \left[\lambda_{1}(L-a)\right]}-\frac{\left(\alpha_{\mathrm{f}}-\alpha_{\mathrm{c}}\right) \Delta T}{\lambda^{2} \tau_{\mathrm{f}}}\right\} $ | (20) |
2) 软化区域
在L-a<x≤L的区域内,黏结界面处于软化状态。将黏结-滑移本构中第二分支公式代入界面微分方程式(7)可得:
| $ \frac{\mathrm{d}^{2} s}{\mathrm{~d} x^{2}}+\lambda_{2}^{2} s=\lambda_{2}^{2} s_{\mathrm{f}} $ | (21) |
式中
依据弹性区域与软化区域的连续性,边界条件可改写为
| $ \left\{\begin{array}{l} x=L-a, s=s_{1} \\ x=L-a, \sigma_{\mathrm{f}} \text { 连续 } \end{array}\right. $ | (22) |
同理,可求解得软化区域的界面各物理量和CFRP正应力分布的解析公式为:
| $ \begin{array}{c} s=s_{\mathrm{f}}+\left(s_{\mathrm{f}}-s_{1}\right)\left\{\frac{\lambda_{2}}{\lambda_{1}} \frac{\sin \left[\lambda_{2}(x-L+a)\right]}{\tanh \left[\lambda_{1}(L-a)\right]}-\right. \\ \left.\cos \left[\lambda_{2}(x-L+a)\right]\right\} \end{array} $ | (23) |
| $ \begin{array}{c} \tau=-\tau_{\mathrm{f}}\left\{\frac{\lambda_{2}}{\lambda_{1}} \frac{1}{\tanh \left[\lambda_{1}(L-a)\right]} \sin \left[\lambda_{2}(x-L+a)\right]-\right. \\ \left.\cos \left[\lambda_{2}(x-L+a)\right]\right\} \end{array} $ | (24) |
| $ \begin{array}{c} \sigma_{\mathrm{f}}=\frac{\tau_{\mathrm{f}}}{t_{\mathrm{f}}}\left\{\frac{1}{\lambda_{1}} \frac{\cos \left[\lambda_{2}(x-L+a)\right]}{\tanh \left[\lambda_{1}(L-a)\right]}-\frac{\left(\alpha_{\mathrm{f}}-\alpha_{\mathrm{c}}\right) \Delta T}{\lambda^{2} \tau_{\mathrm{f}}}\right. \\ \left.\frac{1}{\lambda_{2}} \sin \left[\lambda_{2}(x-L+a)\right]\right\} \end{array} $ | (25) |
在加载端(x=L)处,将
| $ \begin{array}{c} P=\tau_{\mathrm{f}} b_{\mathrm{f}}\left\{\frac{1}{\lambda_{1}} \frac{\cos \left(\lambda_{2} a\right)}{\tanh \left[\lambda_{1}(L-a)\right]}+\frac{1}{\lambda_{2}} \sin \left(\lambda_{2} a\right)-\right. \\ \left.\frac{1}{\lambda^{2} \tau_{\mathrm{f}}}\left(\alpha_{\mathrm{f}}-\alpha_{\mathrm{c}}\right) \Delta T\right\} \end{array} $ | (26) |
同时,可得加载端滑移Δ:
| $ \varDelta=\left(s_{\mathrm{f}}-s_{1}\right)\left\{\frac{\lambda_{2}}{\lambda_{1}} \frac{\sin \left(\lambda_{2} a\right)}{\tanh \left[\lambda_{1}(L-a)\right]}-\cos \left(\lambda_{2} a\right)\right\}+s_{\mathrm{f}} $ | (27) |
随着荷载继续增加,加载端首先开始进入脱黏状态,此时加载端τ=0,s=sf,见图 3(d)。定义脱黏现象出现时的软化长度为ad,将s=sf代入式(27)可得ad的计算方法,见式(28)。
| $ \frac{\lambda_{2}}{\lambda_{1}} \frac{\sin \left(\lambda_{2} a_{\mathrm{d}}\right)}{\tanh \left[\lambda_{1}\left(L-a_{\mathrm{d}}\right)\right]}-\cos \left(\lambda_{2} a_{\mathrm{d}}\right)=0 $ | (28) |
将脱黏出现时的软化长度ad代入式(26),可建立界面剥离承载力的解析公式:
| $ \begin{array}{c} P_{\mathrm{deb}}=\tau_{\mathrm{f}} b_{\mathrm{f}}\left\{\frac{1}{\lambda_{1}} \frac{\cos \left(\lambda_{2} a_{\mathrm{d}}\right)}{\tanh \left[\lambda_{1}\left(L-a_{\mathrm{d}}\right)\right]}+\frac{\sin \left(\lambda_{2} a_{\mathrm{d}}\right)}{\lambda_{2}}-\right. \\ \left.\frac{\left(\alpha_{\mathrm{f}}-\alpha_{c}\right) \Delta T}{\lambda^{2} \tau_{\mathrm{f}}}\right\} \end{array} $ | (29) |
随着脱黏的发展,界面剪应力分布见图 3(e)。令界面脱黏长度为d,用L-d代替L,则式(18)~(20)和式(23)~(25)依旧成立,可得弹性-软化-脱黏阶段的各物理量分布。荷载-滑移关系则改写为:
| $ \begin{array}{c} P=\tau_{\mathrm{f}} b_{\mathrm{f}}\left\{\frac{1}{\lambda_{1}} \frac{\cos \left(\lambda_{2} a\right)}{\tanh \left[\lambda_{1}(L-d-a)\right]}+\frac{\sin \left(\lambda_{2} a\right)}{\lambda_{2}}\right.\\ \left.\frac{\left(\alpha_{\mathrm{f}}-\alpha_{\mathrm{c}}\right) \Delta T}{\lambda^{2} \tau_{\mathrm{f}}}\right\} \end{array} $ | (30) |
| $ \varDelta=s_{\mathrm{f}}+\frac{P}{b_{\mathrm{f}}}\left(\frac{1}{E_{\mathrm{f}} t_{\mathrm{f}}}+\frac{b_{\mathrm{f}}}{E_{\mathrm{c}} b_{\mathrm{c}} t_{\mathrm{c}}}\right) d+\left(\alpha_{\mathrm{f}}-\alpha_{\mathrm{c}}\right) \Delta T d $ | (31) |
利用在x=L-d处,界面剪应力τ=0的边界条件,代入替换后的式(24)中,可以求得脱黏过程中软化长度a。
2 解析模型的验证为了验证本文所建立解析模型的正确性,利用Mazzotti等[16]进行的端部锚固CFRP加固混凝土的常温荷载试验,并对其试验过程进行了数值模拟分析,对比了解析模型与数值模型、试验的结果。由于现有文献[14-15]中端锚CFRP加固界面试验数据不足,缺少材料线膨胀系数这一关键数据,无法完成解析模型的建立。因此,为了验证解析模型在温度作用下的适用性和准确性,仅选用数值模拟试验手段对解析模型做了对比验证。其中,数值模拟通过有限元软件ABAQUS进行分析,完整的二维有限元模型见图 4。

|
图 4 有限元模型 Fig. 4 Finite element model |
有限元模型的材料和几何参数均来源文献[16]的试验:Ec=30.4 GPa、Ef =195.7 GPa、tc=200 mm、tf =1.2 mm、bc=150 mm、bf =80 mm、L=300 mm、s1=0.044 mm、sf =0.121 3 mm、τf =6.43 MPa。CFRP和混凝土材料分别采用T2D2桁架单元和CPS4R实体单元进行表示;端锚的体现则是通过将端部位置的CFRP节点与混凝土节点之间利用Tie进行节点的绑定,即图 4中的节点A、B,以此来保证CFRP片材不会出现滑动,实现与解析模型相一致的完全锚固;在CFRP与混凝土之间采用Connector连接单元进行界面黏结-滑移行为的模拟;混凝土棱柱体底面各节点均受垂直运动约束,右下角节点受水平位移约束。
图 5给出了常温下荷载-滑移曲线的解析解、数值解和试验数据的对比。

|
图 5 常温下的荷载-滑移曲线对比 Fig. 5 Comparison of load-slip curves at room temperature |
通过对比可看出,在弹性阶段、弹性-软化阶段、弹性-软化-脱黏阶段的“平台期”时,三者之间具备良好的吻合。而在渡过“平台期”之后,试验中荷载的增长幅度小于解析解和数值解。这是因为试验中所采取的端部锚固无法达到完全锚固,锚固区域的CFRP片材在界面出现剥离后的加载过程中会产生滑动,从而延缓了极限荷载的上升趋势;而解析解和数值解则是基于完全锚固的边界假定,这是造成试验值与解析解、数值解之间产生偏差的原因。
在进行温度作用下的模型验证时,根据文献[17]中给出的材料数据,参与有限元模型的CFRP和混凝土材料的线膨胀系数分别取为0.3×10-6/℃和10.2×10-6/℃,其余参数均同文献[16]试验一致。因加固中使用的胶黏剂玻璃化温度大多高于服役温度,此处暂不考虑胶黏剂软化的影响,仅反映温差变化对界面性能的影响。通过图 6所示的荷载-滑移曲线和CFRP正应力分布图的对比,说明解析解与数值解之间吻合良好,进一步验证了解析模型在温度作用下的适用性。因此,该解析模型可以良好反映端部锚固CFRP-混凝土界面的受力状态。

|
图 6 温度作用下的解析模型验证 Fig. 6 Validation of analytical model with temperature variation |
为明确端部锚固对温度作用下CFRP-混凝土界面黏结行为的影响,利用本文解析模型,与文献[9]中纯外贴下界面黏结行为的解析模型进行对比。解析计算的工况参数为:Ec=26.8 GPa、Ef =165 GPa、tc=75 mm、tf =1.2 mm、bc=150 mm、bf =100 mm、L=300 mm、s1=0.09 mm、sf =0.41 mm、τf =2.77 MPa。一般情况下,服役环境温度值始终低于胶黏剂的玻璃化转变温度(Tg), 胶黏剂不会出现软化现象。因此,在分析过程中不考虑胶黏剂性质变化,即界面黏结-滑移本构中参数保持不变[18]。
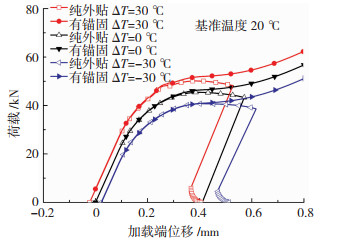
3.1 荷载-滑移曲线利用解析模型,图 7给出了在温度作用下,有端锚和纯外贴的界面剥离全过程的荷载-滑移响应。
|
图 7 荷载-滑移曲线对比 Fig. 7 Comparison of load-slip curves |
由图 7看出,在施加端部锚固后,加载端荷载在弹性阶段和弹性-软化阶段一直处于上升状态,这和纯外贴的加载端荷载表现是相同的;在脱黏出现后,进入弹性-软化-脱黏阶段,在这一阶段中,加载端荷载在经历一段“平台期”后,继续保持持续上升的状态,直至CFRP片材达到抗拉强度而破坏,这与纯外贴的加载端荷载表现是不同的,体现了端锚附加的机械作用,大幅度提高了界面的极限承载能力,充分利用CFRP片材的高强特点。其次,正向温差(温升)可以提高界面的承载能力,负向温差(温降)会降低界面承载能力。同时,在相同的外力荷载下,正向温差(温升)下的位移较小,负向温差(温降)下的位移较大,这是由材料的自由膨胀所导致的。
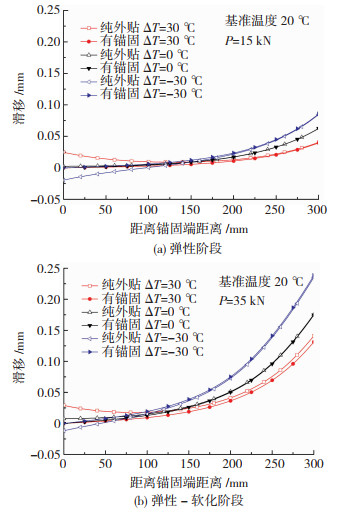
3.2 界面滑移及剪应力分布图 8给出了正向温差(ΔT=30 ℃)和负向温差(ΔT=-30 ℃)的界面滑移量对比。
|
图 8 界面滑移分布 Fig. 8 Interfacial slip distribution |
由图 8看出,施加端锚后,界面滑移量呈现单调递增的趋势,相比于纯外贴的黏结界面的滑移分布,端锚对界面滑移的影响主要集中在靠近锚固位置的区域内,而对靠近加载端范围内界面滑移量的影响较小。同时,在温升的情况下,界面滑移量降低,这是因为在外力荷载作用下的滑移方向与温度荷载作用下的滑移相反,导致了这部分滑移量的相互抵消,也就是说,在温升时,作用于黏结界面的一部分外力荷载受到了温度应力的抵消。而在温降时,外力荷载引起的界面滑移和温度荷载产生的界面滑移方向相同,导致了界面滑移量的增大;相比于纯外贴的界面黏结行为,温降时,端锚的黏结界面不会出现负向滑移量,滑移量都是正向单调发展。
图 9给出了界面剪应力在不同工况下的对比。在弹性阶段,施加端锚后,界面剪应力呈现非线性弹性增长;温升降低了界面剪应力,温降则会造成界面剪应力的增大。在进入弹性-软化区域后,温升会减小界面软化区域的长度,而温降则会导致软化区域的增长。相比于纯外贴黏结界面,端锚的引入对靠近锚固范围的剪应力发展抑制明显;减小了温升时的界面软化长度,但对温降时的界面软化长度影响较小。

|
图 9 界面剪应力分布 Fig. 9 Interfacial shear stress distribution |
由图 10中的CFRP正应力分布的对比可知,当施加了端锚后,CFRP在锚固处产生了一定的CFRP正应力,而在无锚固措施的情况下,自由端的CFRP正应力为0。并且,随着温差的产生,端部锚固处的CFRP正应力变大,温升产生更大的拉应力,温降导致CFRP片材承受更大的压应力。

|
图 10 QCFRP正应力分布 Fig. 10 CFRP axial stress distribution |
这是因为在黏结端部,首先由于端锚措施的引入,当CFRP片材受到荷载作用时,受到了锚固措施的约束反力,产生了相应的CFRP约束应力;其次,在温度作用下时,端锚手段限制了CFRP片材自由膨胀的发展,同样产生了相应的CFRP约束应力。因此,在温度作用下,端锚后CFRP片材承担的正应力增长,意味着在温度作用下的界面剥离过程中,充分利用了CFRP片材高强的特点,提高了CFRP片材的强度利用效率。
3.4 界面剥离承载力 3.4.1 温度变化图 11给出了界面剥离承载力的对比,其中纵坐标为各工况下的界面剥离承载力均除以纯外贴T=0 ℃时的界面剥离承载力做归一化处理得到的。

|
图 11 温度变化对有锚固和纯外贴的界面剥离承载力影响 Fig. 11 Effect of temperature on debonding load of interface with or without anchorage |
由图 11看出,在T≥0 ℃时,相同的温升,施加端锚的黏结界面具有更高的界面剥离承载力(Pdeb),并且温升可以提高界面剥离承载力;在T<0 ℃时,是否采取端锚措施对界面剥离承载力的影响较小,但温降会降低界面剥离承载力。因此,在施加锚固的CFRP加固设计中,需要充分考虑温度降低对界面承载能力产生的不利影响。
3.4.2 CFRP厚度和弹模变化在明确了温度变化对界面剥离承载力的影响后,利用解析模型,分析了端部锚固后不同的CFRP厚度和弹模对温度作用下界面剥离承载力的影响,如图 12所示。

|
图 12 CFRP厚度和弹模变化对界面剥离承载力的影响 Fig. 12 Effect of CFRP thickness and modulus on interfacial debonding load |
图 12中,纵坐标为以T=0 ℃的界面剥离承载力为标准进行归一化处理。对于相同的温升,当使用较厚或较大弹模的CFRP片材时,界面剥离荷载的增加幅度明显增大;而对于相同的温降,当CFRP厚度或弹模较大时,界面剥离承载力同样具有较大的下降幅度。因此,对于施加端部锚固的加固构件,在保证常温工况下加固效果的基础上,可以采取厚度和弹模较小的CFRP片材来减小温度应力的影响。
3.5 剥离后的界面黏结行为图 13给出了剥离时刻和剥离后的界面剪应力以及CFRP正应力分布。

|
图 13 剥离时和剥离后界面应力分布 Fig. 13 Distribution of interfacial stress at and after debonding moment |
由图 13(a)分析可得,当外荷载达到界面剥离承载力(Pdeb)时,即界面剥离出现的时刻,加载端的剪应力强度丧失,黏结界面将进入弹性-软化-脱黏阶段;并且,在弹性区域和软化区域内,剪应力呈现非线性的增长和下降。随着外荷载的增大,意味着界面剥离程度的加深,脱黏长度逐渐增大,黏结界面的弹性区域和软化区域的范围逐渐变短;同时,在剥离发展的过程中,界面剪应力的峰值点向锚固端移动;并且,剪应力在弹性区域和软化区域内呈现近似线性状态的增长和下降。
由图 13(b)分析可得,在界面剥离后,CFRP片材所承担的拉应力逐渐增大;其中,在锚固端的CFRP正应力增长幅度大于加载端,这意味着端部锚固件逐渐提供了更大的机械作用;同时,在脱黏长度的范围内,CFRP片材与混凝土界面间无剪应力的存在,相当于这段长度内CFRP片材仅受外荷载的拉力作用,因此,CFRP正应力分布呈现“平段”。
4 结论本文采用双线性界面黏结-滑移本构,建立了端锚CFRP-混凝土界面在温度作用下界面剥离全过程解析模型。该模型可较好的反映端锚措施对温度作用下CFRP-混凝土界面黏结行为的影响,主要结论如下:
1) 本文解析模型给出了界面滑移量、界面剪应力和CFRP正应力分布的计算公式,建立了可用于性能评估的荷载-滑移响应和界面剥离承载力的计算方法,并与试验和数值模拟结果吻合良好。该解析模型可为温度作用下CFRP加固的端锚设计提供理论手段。
2) 相比于纯外贴情况,在温度到达胶黏剂的玻璃化温度前,端锚措施可提高温升下界面剥离承载力,但对于温降环境下界面剥离承载力的影响不明显。
3) 相比于纯外贴情况,端部锚固的存在,可使CFRP片材在界面失效前承受更大的正应力,且应力分布较为均匀,大大提高了温度作用下CFRP片材强度利用率。
4) 参数分析表明,对于施加端部锚固的加固构件,在保证常温加固效果的基础上,可采取选用厚度和弹模较小的CFRP片材来减小温度应力的影响。
| [1] |
叶列平, 冯鹏. FRP在工程结构中的应用与发展[J]. 土木工程学报, 2006, 39(3): 24. YE Lieping, FENG Peng. Applications and development of fiber-reinforced polymer in engineering structures[J]. China Civil Engineering Journal, 2006, 39(3): 24. DOI:10.15951/j.tmgcxb.2006.03.004 |
| [2] |
纤维增强复合材料建设工程应用技术规范: GB 50608—2016[M]. 北京: 中国计划出版社, 2010 Technical code for FRP composites in construction: GB 50608—2016[M]. Beijing: Planning Press of China, 2010 |
| [3] |
YUAN Hong, TENG Jinguang, SERACINO R, et al. Full-range behavior of FRP-to-concrete bonded joints[J]. Engineering Structures, 2004, 26(5): 553. DOI:10.1016/j.engstruct.2003.11.006 |
| [4] |
高磊, 张峰, 刘佳琪, 等. HB-FRP布加固混凝土对其界面粘结性能的影响[J]. 华南理工大学学报(自然科学版), 2018, 46(9): 51. GAO Lei, ZHANG Feng, LIU Jiaqi, et al. Characterization of interfacial bonding for HB-FRP strengthened concrete beams[J]. Journal of South China University of Technology (Natural Science Edition), 2018, 46(9): 51. DOI:10.3969/j.issn.1000-565x.2018.09.008 |
| [5] |
胡克旭, 侯梦君, 高皖扬, 等. 不同保护措施下CFRP加固混凝土梁耐火性能试验[J]. 哈尔滨工业大学学报, 2018, 50(6): 138. HU Kexu, HOU Mengjun, GAO Wanyang, et al. Experimental study on fire performance of CFRP-strengthened reinforced concrete beams with different protection schemes[J]. Journal of Harbin Institute of Technology, 2018, 50(6): 138. DOI:10.11918/j.issn.0367-6234.201709047 |
| [6] |
STURM A B, VISINTIN P, VACULIK J, et al. Analytical approach for global load-slip behaviour of FRP plates externally bonded to brittle substrates with anchors[J]. Composites Part B: Engineering, 2019, 160: 177. DOI:10.1016/j.compositesb.2018.10.024 |
| [7] |
CHEN Cheng, CHENG Lijuan, SUI Lili, et al. Design method of end anchored FRP strengthened concrete structures[J]. Engineering Structures, 2018, 176: 143. DOI:10.1016/j.engstruct.2018.08.081 |
| [8] |
胡克旭, 董坤, 杨耀武. 温度作用对碳纤维—混凝土界面黏结性能的影响[J]. 同济大学学报(自然科学版), 2016, 44(6): 845. HU Kexu, DONG Kun, YANG Yaowu. Temperature effect on bond behavior of carbon fiber reinforced polymer to concrete interface[J]. Journal of Tongji University, 2016, 44(6): 845. DOI:10.11908/j.issn.0253-374x.2016.06.005 |
| [9] |
GAO Wanyang, TENG Jinguang, DAI Jianguo. Effect of temperature variation on the full-range behavior of FRP-to-concrete bonded joints[J]. Journal of Composites for Construction, 2012, 16(6): 671. DOI:10.1061/(ASCE)CC.1943-5614.0000296 |
| [10] |
李春良, 李凯, 张立辉, 等. CFRP端部被锚固后加固钢结构的界面粘结行为[J]. 哈尔滨工业大学学报, 2016, 48(9): 113. LI Chunliang, LI Kai, ZHANG Lihui, et al. Interfacial bond behavior of CFRP reinforced steel structures with end anchorage[J]. Journal of Harbin Institute of Technology, 2016, 48(9): 113. DOI:10.11918/j.issn.0367-6234.2016.09.020 |
| [11] |
ZHOU Yingwu, WANG Xiaowei, SUI Lili, et al. Effect of mechanical fastening pressure on the bond behaviors of hybrid-bonded FRP to concrete interface[J]. Composite Structures, 2018, 204: 731. DOI:10.1016/j.compstruct.2018.08.008 |
| [12] |
张峰, 徐向锋, 李术才. HB-FRP加固RC梁的精细有限元分析[J]. 哈尔滨工业大学学报, 2015, 47(8): 125. ZHANG Feng, XU Xiangfeng, LI Shucai. Meso-scale element analysis of HB-FRP strengthened reinforced concrete beams[J]. Journal of Harbin Institute of Technology, 2015, 47(8): 125. DOI:10.11918/j.issn.0367-6234.2015.08.025 |
| [13] |
王珍珍, 周智, 白石, 等. 端部锚固CFRP板加固RC梁IC剥离过程非线性分析[J]. 土木工程学报, 2020, 53(1): 1. WANG Zhenzhen, ZHOU Zhi, BAI Shi, et al. Nonlinear analysis of IC debonding progress for the RC beams strengthened with end-anchored CFRP plates[J]. China Civil Engineering Journal, 2020, 53(1): 1. DOI:10.15951/j.tmgcxb.2020.01.001 |
| [14] |
FIRMO J P, CORREIA J R, PITTA D, et al. Experimental characterization of the bond between externally bonded reinforcement (EBR) CFRP strips and concrete at elevated temperatures[J]. Cement and Concrete Composites, 2015, 60: 44. DOI:10.1016/j.cemconcomp.2015.02.008 |
| [15] |
CORREIA L, BARRIS C, FRANCA P, et al. Effect of temperature on bond behavior of externally bonded FRP laminates with mechanical end anchorage[J]. Journal of Composites for Construction, 2019, 23(5): 04019036. DOI:10.1061/(ASCE)CC.1943-5614.0000961 |
| [16] |
MAZZOTTI C, SAVOIA M, FERRACUTI B. A new single-shear set-up for stable debonding of FRP-concrete joints[J]. Construction and Building Materials, 2009, 23(4): 1529. DOI:10.1016/j.conbuildmat.2008.04.003 |
| [17] |
KLAMER E L, HORDIJK D A, JANSSEN H J M. The influence of temperature on the debonding of externally bonded CFRP[J]. ACI Special Publication, 2005(230): 1551. |
| [18] |
DONG Kun, HU Kexu. Development of bond strength model for CFRP-to-concrete joints at high temperatures[J]. Composites Part B: Engineering, 2016, 95: 264. DOI:10.1016/j.compositesb.2016.03.088 |
 2021, Vol. 53
2021, Vol. 53


