2. 土木工程智能防灾减灾工业和信息化部重点实验室(哈尔滨工业大学),哈尔滨 150090
2. Key Lab of Smart Prevention and Mitigation of Civil Engineering Disasters (Harbin Institute of Technology), Ministry of Industry and Information Technology, Harbin 150090, China
近年来,恐怖袭击及意外事故频发,建筑结构在冲击、爆炸等极端荷载下的响应受到广泛关注。将薄壁金属构件作为耗能构件,通过其自身的变形以及屈曲耗散能量,可以有效地保护受到冲击、爆炸等荷载作用的结构。铝合金具有自重轻、比强度高、耐腐蚀、抗疲劳、无低温脆性等优势[1],常应用于飞行器设计[2]以及车辆工程[3]中作为吸能构件。针对建筑用铝合金构件的吸能能力,国内外学者也开展了相关研究。Marzbanrad等[4]对6060-T5和6060-T4薄壁圆形铝管在轴向冲击荷载下的行为进行了数值研究,并采用加权求和法对轴向压缩荷载下的铝合金圆管进行了多目标优化分析。孙宏图等[5]分析了铝合金薄壁方管轴向冲击载荷下的吸能特性,发现随着构件的壁厚、长度和冲击速度的增加,铝合金方管容易出现混合变形模式,且吸能能力有所降低。
泡沫铝具有低密度、高孔隙率、高比强度、高比刚度等特性[6],将其作为芯体填充到薄壁金属构件形成复合耗能构件是近年来研究的热点方向[7-8]。Reyes等[9]针对有无泡沫铝填充方管构件在斜向压缩荷载下的变形模式和耗能性能开展试验研究,结果表明当泡沫铝密度高于一定值后,构件的比吸能减小。Rajendran等[10]利用落锤冲击试验研究了泡沫铝填充管构件的能量吸收效率,发现当初始的冲击能量相同时,相比于芯材与薄壁钢管,泡沫铝填充管的吸能效果最优。Duarte等[11]将泡沫铝填充到6060-T6铝合金圆管中,采用三点弯曲冲击试验研究其在动态弯曲下的力学性能,结果表明侧向冲击荷载下,填充的泡沫材料通过变形吸收大量能量,并提高构件的耗能性能。
已有研究结果表明泡沫铝填充薄壁金属构件具有优良的耗能性能,而目前泡沫铝填充铝合金圆管的研究多使用低标号的铝合金,针对6082-T6高强铝合金圆管的耗能能力及其与泡沫铝共同工作的性能研究有待补充。基于上述背景,本文采用泡沫铝填充6082-T6铝合金圆管作为耗能构件,通过轴向压缩试验得到构件的全过程响应、破坏模式以及耗能特性,并对构件的破坏机理进行探究。同时建立了6082-T6铝合金与闭孔泡沫铝的本构方程,通过数值方法得到不同管径、壁厚以及高度对构件破坏模式、耗能能力的影响规律,为构件在实际工程中的应用提供理论依据。
1 材性试验由于泡沫铝强度较低,物理切割会造成表面扭曲变形或内部孔穴坍塌,因此在试件制作过程中使用电火花线切割法加工铝合金管和泡沫铝,得到的铝合金构件切割表面光滑并具有较高的尺寸精度,泡沫铝芯体表面平整,泡孔结构完整无坍塌,试件的加工过程见图 1。

|
图 1 试件加工过程 Fig. 1 Fabrication process of specimens |
为得到6082-T6铝合金的力学性能指标,对不同截面尺寸的铝合金圆管进行材性试件取样,根据规范GB/T 228—2010[12]制作了15个材性试件(5组,每组3个)并进行单轴拉伸试验,加载方式为位移控制,加载速度为2 mm/min。铝合金圆管的截面尺寸及力学性能指标见表 1,表中D、t分别表示圆管的外径以及厚度;E表示弹性模量;σy、σu分别为屈服强度(卸载后残余应变为0.2%的名义屈服强度)和极限强度;e表示伸长率(e=(Lk-L0)/L0,其中L0、Lk分别为试件拉断前、后的标距长度)。
| 表 1 6082-T6铝合金材料参数 Tab. 1 Mechanical properties of 6082-T6 aluminum alloy |
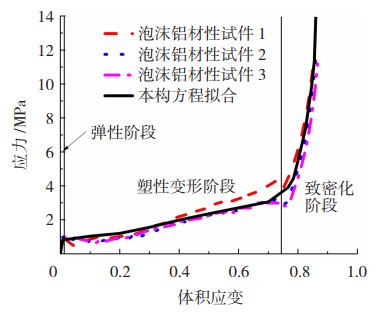
本文采用的泡沫铝孔洞形式为闭孔,孔隙率为68%~91%,利用电子万能试验机对三组泡沫铝材性试块(边长150 mm的立方体)进行单轴压缩试验,得到应力-体积应变曲线见图 2。可以看出泡沫铝在压缩过程中经历3个阶段:1)弹性阶段:在压缩前期力随位移线性增大;2)塑性变形阶段:泡沫铝孔隙不断被压溃,力值相对稳定;3)致密化阶段:构件内部孔隙完全压实,孔壁相互接触,压力随位移增大迅速增加直至试件压溃。根据试验结果得到泡沫铝的材料密度为245.7 kg/m3,弹性模量为114 MPa,平台应力为0.81 MPa。
|
图 2 泡沫铝轴压应力-应变曲线 Fig. 2 Stress-strain curves of aluminum foam under axial compression |
为研究泡沫铝填充6082-T6铝合金圆管以及铝合金空管的轴压力学性能及耗能能力,考虑到不同径厚比、高径比对构件性能的影响,分别进行了10根空管和10根填充管的轴压试验,试件的尺寸见表 2。试件编号中的首字母E/F表示空管(empty)构件/泡沫铝填充(foam-filled)构件;编号中的数字依次表示试件的截面外径、壁厚和计算高度。表格中试件尺寸均为实际测量数据。
| 表 2 试件参数及试验结果 Tab. 2 Parameters of specimens and experiment results |
本文采用哈尔滨工业大学结构试验室的1 000 kN电液微机伺服试验机进行轴压试验,试验装置见图 3。试验机底部平台与加载钢板仅能竖向平动,底部通过夹具进行固定,实现构件底部的完全固支约束。底部夹具高度为50 mm,针对不同截面尺寸的构件,分别使用相匹配的套环作为底部约束对试件进行固定,见图 3(c)。试验采用位移加载,加载速度为2 mm/min,压缩至构件计算高度的80%时停止加载。

|
图 3 试验装置 Fig. 3 Axial compression experiment setup |
试件在轴向压缩荷载下的变形过程见图 4,d表示压缩位移。根据试件的变形过程总结出3种破坏模式:劈裂破坏(F)、叠缩劈裂破坏(R+F)和叠缩劈裂+不规则变形破坏(R+F+I)。发生劈裂破坏时(见图 4(a)),构件首先在其上部产生塑性铰,形成圆环形褶皱(d=5 mm),在压缩过程中构件的塑性铰点处出现竖向裂纹,这些裂纹随着位移增大逐渐扩展(d=10 mm),当圆环形褶皱被挤压完全时,构件塑性铰点处出现横向裂缝,褶皱上部基本脱落(d=20 mm),构件发生劈裂破坏,随着位移增大铝合金构件劈裂处形成多瓣且向外翻转并逐渐脱落(d=50 mm),构件剩余部分不断发生劈裂破坏直至最后。对于发生叠缩劈裂破坏的构件(见图 4(b)),在形成塑性铰后首先发生轴对称叠缩变形(d=4 mm),在完全叠缩后形成新的塑性铰(d=15 mm)并发生进一步叠缩(d=34 mm),但在第二次叠缩过程中塑性铰点处形成竖向裂纹(d=42 mm),随后试件发生劈裂破坏。当构件发生叠缩劈裂+不规则变形破坏时(见图 4(c)),在加载初期出现塑性铰并发生对称叠缩变形(d=10 mm),在叠缩完全后产生裂纹并发生劈裂破坏(d=30 mm),随着位移的增大,构件的剩余部分没有继续发生劈裂破坏,而是产生不规则变形(d=60 mm)。

|
图 4 不同破坏模式变形过程 Fig. 4 Deformation process of different failure modes |
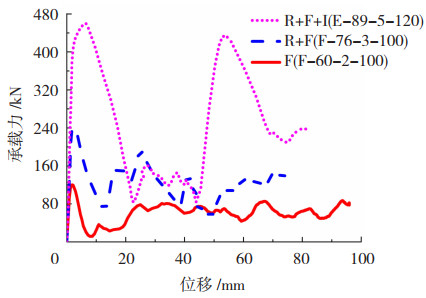
图 5给出了不同破坏模式构件的力-位移曲线,从图中可以看出所有构件在压缩初期均发生弹性变形,荷载随位移线性增大。在塑性铰开始形成时(出现第一个圆环形褶皱),承载力达到峰值点,随后荷载随着位移的增加而明显下降,当出现裂缝后试件发生劈裂破坏,承载力逐渐达到最低点,而后上部破坏部分被压实,承载力有所提高且随着裂缝的扩展在一定范围内抖动。发生叠缩劈裂破坏的构件其力-位移曲线具有多个峰值点,分别对应不同叠缩过程中形成塑性铰时的构件承载力,当试件产生裂缝后发生劈裂破坏,承载力不再明显提高。当构件发生叠缩劈裂+不规则变形破坏时,荷载在达到峰值点后迅速下降,此时构件开始叠缩并在叠缩完成后产生裂缝,随后构件发生不规则变形,荷载随着位移的增大明显增大,在到达峰值点后由于构件顶部裂缝发展,承载力逐渐降低。
|
图 5 不同破坏模式力-位移曲线 Fig. 5 Load-displacement curves of different failure modes |
试件的破坏模式总结见表 2,主要受管壁厚度以及有无泡沫铝填充影响。总结铝合金圆管及泡沫铝填充管在轴压荷载下的失效机理如下:壁厚较小的铝合金圆管韧性较差,在叠缩过程中圆环褶皱处横向受拉致使管壁出现竖向裂缝,各竖向裂缝将圆环褶皱分为数瓣,随着位移增大各瓣褶皱出现横向裂缝发生弯折破坏。裂缝的扩展使构件剩余部分的截面不再保持平整,从而导致构件无法再形成圆环形褶皱,而是发生劈裂破坏直至构件被压缩完全。当铝合金圆管内填充泡沫铝时,由于在压缩前期即出现劈裂破坏,泡沫铝未被压缩密实因而对此破坏模式影响不大。发生叠缩劈裂破坏时,构件在前期叠缩并依次形成圆环形褶皱,但压缩过程中圆环褶皱处因横向受拉产生裂缝,导致在加载后期叠缩形成的圆环因应力不均匀而破碎脱落,剩余部分因裂缝扩展而发生劈裂破坏。叠缩劈裂+不规则变形破坏模式发生在壁厚较大的空管构件中,圆环形褶皱在叠缩完成后破碎,而在压缩中后期,构件顶部存在缺陷,形成塑性铰的位置随机,因此发生不规则变形,当构件填充泡沫铝后,泡沫铝在压缩中后期被压实在铝管内部,对管壁起到良好的支撑作用,构件发生叠缩劈裂破坏。
2.3 耗能能力分析对于耗能构件的耗能能力常用如下指标进行评价:总吸能Eabs(energy absorption),平均压缩力FMCL(mean crush load)及压缩效率ηCLE(crush load efficiency)。其定义分别为:
总吸能表示构件在变形过程中通过自身材料的叠缩、屈曲以及断裂等形式所吸收的全部能量,计算公式如下,其中P为压缩力,d为试件的压缩位移。
| $ {E_{{\rm{abs}}}} = \int_0^d P {\rm{d}}\delta $ | (1) |
平均压缩力FMCL是吸能与位移的比值,见式(2),其意义为构件发生单位位移时所能吸收的能量,能直接反映构件耗能能力大小。
| $ {F_{{\rm{MCL}}}} = \frac{{{E_{{\rm{abs}}}}}}{d} $ | (2) |
压缩力效率为构件平均压缩力与峰值压缩力的比值,见式(3)。压缩力效率越大说明平均压缩力越接近峰值压缩力,材料的有效利用率越高。
| $ {\eta _{{\rm{CLE}}}} = \frac{{{F_{{\rm{MCL}}}}}}{{{F_{{\rm{PCL}}}}}} $ | (3) |
各试件的吸能指标见表 2。填充泡沫铝后构件峰值压缩力FPCL(peak crush load)提升较小,其中F-76-4-120相较于E-76-4-120其FPCL提升幅度最大,仅为4.5%。这一方面是当荷载达到峰值时,构件的竖向位移较小,此时泡沫铝尚处于弹性阶段,对荷载贡献较小。另一方面因为本文所用泡沫铝密度较低,抗压强度远小于6082-T6铝合金,因此其对构件的FPCL提升不大。从表 2可以看到,填充泡沫铝后构件的FMCL得到了明显的提高,其中F-76-4-120相较于E-76-4-120其FMCL提升幅度达到19.26%。
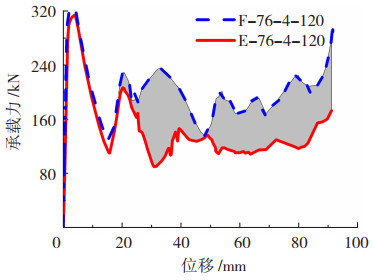
图 6给出了铝合金空管与泡沫铝填充管的力-位移曲线对比。其中阴影区域为构件填充泡沫铝之后其总吸能增加部分,且耗能能力的提高主要发生在轴压过程的中后段,此时泡沫铝也达到了平台段和上升段,能为构件抵抗荷载的能力提供较大贡献。此外泡沫铝的填充也使构件的变形模式得到了改善,避免了不规则变形模式的产生,有利于构件的能量吸收。综上,填充泡沫铝有效提高了构件的总吸能和平均压缩力,其提高主要来源于以下3个部分:泡沫铝自身强度贡献、构件变形模式得到改善、泡沫铝与管壁之间的摩擦作用。
|
图 6 填充管与空管力-位移曲线对比 Fig. 6 Comparison of load-displacement curves of foam-filled tube and empty tube |
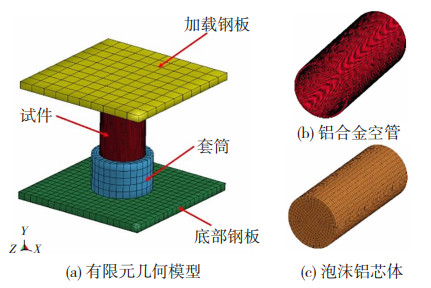
基于ANSYS/LS-DYNA进行泡沫铝填充6082-T6铝合金圆管的轴压试验有限元模拟,有限元模型见图 7,该模型分为4个部分:轴压试件、顶部加载钢板、约束套筒以及底部约束钢板。为保证与试验条件一致,将底部钢板设置为固定约束,同时约束加载钢板的侧向位移以及全部转角位移。考虑到模型在加载过程中发生叠缩以及劈裂破坏,选取solid164实体单元进行铝管的有限元模拟,同时使用全积分算法以消除沙漏影响。对于泡沫铝芯体同样使用solid164实体单元计算。为使有限元模拟具有较高的计算效率,将加载钢板、约束套筒以及底部约束钢板设置为刚体。铝合金圆管的单元尺寸为1 mm×1 mm×1 mm,泡沫铝的网格采用4 mm×4 mm×4 mm。
|
图 7 有限元模型 Fig. 7 FE model |
由于试验过程中铝管发生劈裂破坏后管与加载钢板之间的接触界面结点发生了改变,因此选用自动面面接触对铝管与各约束之间的接触进行模拟。而泡沫铝芯体结点过多,采用上述接触设置会消耗大量运算资源,因此对泡沫铝芯体与各部分之间的接触设置为自动点面接触,该接触只需定义泡沫铝表面的结点与各部分之间的接触。在轴压试验过程中,铝管发生叠缩以及劈裂破坏时,自身结点发生接触,故而对铝管自身采用自动单面接触。在接触算法中使用罚函数法进行计算,控制接触界面穿透的罚函数参数定义为1.1[13]。
3.2 材料模型铝合金的材料模型选用Mat_Modified_Johnson_Cook材料模型,该模型可以较好地模拟无明显屈服点的材料,其本构关系为[14]
| $ \begin{array}{l} {\sigma _{\rm{y}}} = \left( {A + B{r^n} + \sum\limits_{i = 1}^2 {{Q_i}} \left( {1 - \exp \left( { - {C_i}r} \right)} \right)} \right) \times \\ \;\;\;\;\;\;\;\;\;{\left( {1 + {{\dot r}^*}} \right)^c}\left( {1 - {T^m}} \right) \end{array} $ | (4) |
式中: A为材料的屈服极限,B、n为材料参数,c为应变率效应参数,m为温度参数。该本构方程由3个部分组成:一般情况下的应力应变关系、应变率效应的影响和温度的影响。本文中仅考虑常温下材料的静态力学行为,因此忽略本构方程后两部分的影响。A、B、n通过对铝合金单轴拉伸试验数据进行线性回归拟合得到,取值见表 3。
| 表 3 铝合金本构模型参数 Tab. 3 Parameters of constitutive model for aluminum alloy |
为了模拟铝合金管的劈裂破坏,在有限元模拟中考虑了材料的失效,使用Cockcroft-Latham韧性断裂准则作为判定材料失效的方法。该准则将等效塑性应变能作为判断材料发生失效的临界参数。该临界参数以及失效判定准则如下[14]:
| $ {\dot D = \frac{{{D_{\rm{c}}}}}{{{W_{{\rm{cr}}}}}}\max \left( {{\sigma _1}, 0} \right)\dot p} $ | (5) |
| $ {W = \int_0^{{\varepsilon ^p}} {\max } \left( {{\sigma _1}, 0} \right){\rm{d}}{{\bar \varepsilon }^p} \ge {W_{{\rm{cr}}}}} $ | (6) |
式中: σ1表示第一主应力;Wcr表示应变能积分量W的临界值;εp表示等效塑性应变。其中第一主应力与等效塑性应变均通过对铝合金单向拉伸试验进行有限元模拟得到,不同壁厚的铝合金临界失效塑性应变能见表 3。
泡沫铝材料采用Mat_Crushable_Foam进行数值模拟,该模型需要输入泡沫铝应力-体积应变曲线,该曲线通过对试验应力应变曲线进行本构方程的拟合得到(见图 2)。泡沫铝本构方程为[15]
| $ \sigma = {\sigma _{\rm{p}}} + \gamma \frac{{{\xi _{\rm{v}}}}}{{{\xi _{\rm{D}}}}} + {\alpha _2}\ln \left( {\frac{1}{{1 - {{\left( {{\xi _{\rm{v}}}/{\xi _{\rm{D}}}} \right)}^\beta }}}} \right) $ | (7) |
式中:ξV为体积应变,σp为平台应力,γ为屈服强度,ξD为致密化应变,α2为形状系数,β为拟合参数。拟合后泡沫铝的参数取值见表 4。
| 表 4 泡沫铝本构模型参数 Tab. 4 Parameters of constitutive model for aluminum foam |
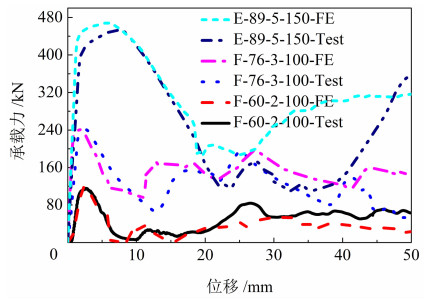
有限元模拟和试验得到的力-位移曲线以及变形模式对比见图 8、9。在变形后期力-位移曲线相差较大,产生误差的主要原因为:铝管发生断裂后,试验中上部损坏的部分被压实在试件与顶部加载钢板之间,而在有限元模拟中上部损坏的部分发生脱落。对峰值荷载和首个折叠单元内的平均压缩力进行对比,试验结果与模拟结果对比见表 5,可以看出有限元方法得到的结果误差较小。
|
图 8 仿真与试验力-位移曲线对比 Fig. 8 Load-displacement curves of experiment and simulation |

|
图 9 仿真与试验变形模式对比 Fig. 9 Failure modes of experiment and simulation |
| 表 5 仿真与试验峰值压缩力和平均压缩力对比 Tab. 5 Comparison of experiment and simulation results of FPCL and FMCL |
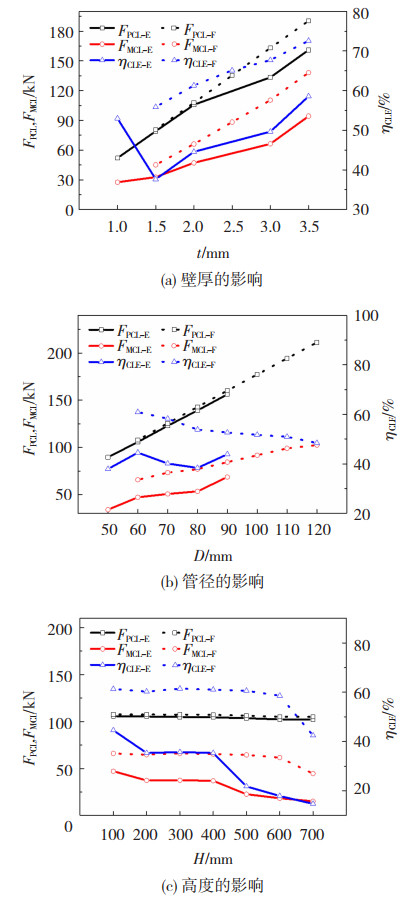
首先考虑管壁厚对轴压力学性能的影响。保持铝合金管外径60 mm、高度100 mm以及填充的泡沫铝密度不变,对不同壁厚的铝合金空管和泡沫铝填充管构件进行了轴压数值模拟研究,得到各试件的峰值压缩力FPCL、平均压缩力FMCL及压缩力效率ηCLE,见图 10(a)。当铝合金管壁厚度由1 mm增大到3.5 mm时,铝合金空管的FPCL和FMCL分别增大209.7%和242.2%,当厚度为1.5 mm时空管的ηCLE最小,为37.6%,当厚度由1.5 mm增大到3.5 mm时,ηCLE随之提高55.5%。当厚度由1.5 mm增大到3.5 mm时,复合构件的FPCL、FMCL和ηCLE分别增大135.9%、206.6%和29.9%。对于内部填充泡沫铝的复合构件,其各项吸能指标均高于同尺寸的铝合金圆管构件,且当厚度增大时(1.5 mm增大到3.5 mm),泡沫铝填充管与相同壁厚的空管的压缩力效率比值由1.48减小到1.24。可以发现,填充泡沫铝后,增大管壁厚度对复合构件吸能能力的提升作用有所减小。
|
图 10 几何参数对构件吸能特性的影响 Fig. 10 Influence of geometric parameters on energy absorbing characteristics |
管径的不同将导致填充的泡沫铝的体积不同,保持铝合金管壁厚2 mm和高度100 mm不变,对管径在50 mm至120 mm间的5组铝合金圆管构件和泡沫铝填充铝合金管短柱构件进行了轴压数值模拟研究,图 10(b)为各构件的峰值荷载、平均压缩荷载及平均压缩力效率与管径的关系曲线。铝合金空管与泡沫铝填充复合管的FPCL均随管径的增加而线性增大:当管外径由60 mm增大到90 mm时,空管与复合管的FPCL分别提高47.7%和48.7%,同时构件的FMCL也随之增大,铝合金空管与泡沫铝填充管的FMCL分别增大45.5%和28.5%。对于铝合金空管构件,构件的FPCL与FMCL随管径的增大提升比率较为接近,因而管径改变时,构件的ηCLE在37.9%~44.6%范围内变化。当构件的管径由60 mm增大到120 mm时,泡沫铝填充铝合金圆管构件的ηCLE减小20.5%,但当管径增大时,泡沫铝填充管与同尺寸的空管压缩力效率ηCLE的比值由1.37减小到1.2。说明当管径增大时,泡沫铝填充对构件耗能能力提升的效率有所减小。
4.3 高度的影响保持管径60 mm和铝管壁厚2 mm不变,对14组不同高度的铝合金圆管构件和泡沫铝填充铝合金管短柱构件进行了轴压数值模拟研究,各试件的峰值荷载、平均压缩荷载及压缩力效率见图 10(c)。当构件的高度由100 mm增大到700 mm时,空管与填充管的FPCL分别减小了3.2%和2.5%,而FMCL分别减小68%和32.5%。结果表明填充泡沫铝后,构件在压缩过程后期的吸能能力优于铝合金空管,且随着构件高度增大泡沫铝的贡献也随之增大。当空管构件的H/D>8和泡沫铝填充构件的H/D>10时,试件在轴压荷载作用下发生失稳破坏,填充泡沫铝后构件发生失稳破坏的临界高径比提高。
5 结论本文开展了泡沫铝填充6082-T6铝合金圆管短柱构件的静力轴压试验,建立了6082-T6高强铝合金的材料本构模型及失效准则,提出了较为准确的有限元仿真建模方法并对影响复合构件轴压力学性能的参数进行了分析,主要结论如下:
1) 泡沫铝填充6082-T6铝合金圆管及空管在轴向压缩荷载下表现出三种破坏模式:劈裂破坏、叠缩劈裂破坏、叠缩劈裂+不规则变形破坏。填充泡沫铝可以改善构件在轴压荷载下的变形模式,平均压缩力和压缩力效率均得到提升,具有更高的耗能能力。
2) 构件在轴压荷载下形成塑性铰而发生叠缩,随后产生裂缝发生叠缩劈裂破坏;壁厚较小的圆管在塑性铰开始形成时产生裂缝直接发生劈裂破坏;壁厚较大的构件由于存在缺陷,塑性铰出现位置随机,叠缩劈裂后发生不规则变形。
3) 当泡沫铝填充复合管壁厚由1.5 mm增大到3.5 mm时,构件的峰值压缩力和平均压缩力分别提高135.9%和206.6%;当管径由60 mm增大到90 mm时,构件的峰值压缩力和平均压缩力分别提高48.7%和28.5%。
4) 构件壁厚分别为1.5 mm和3.5 mm时,等壁厚的泡沫铝填充管与空管的压缩力效率比值分别为1.48和1.24;当管径由60 mm增大到90 mm时,同一管径下泡沫铝填充管与空管的压缩力效率的比值由1.37减小到1.2。因此,填充泡沫铝对管径与壁厚较小的铝合金圆管吸能能力的提升作用更明显。
5) 当构件高度由100 mm增大到700 mm时,构件的峰值压缩力基本不变;空管和复合管的平均压缩力分别减小68%和32.5%。当铝合金空管高径比超过8、泡沫铝填充管高径比超过10时,构件发生失稳破坏。
| [1] |
张其林. 铝合金结构在我国的应用研究与发展[J]. 施工技术, 2018, 47(15): 13. ZHANG Qilin. Applications researches and developments of aluminum alloy structures in China[J]. Construction Technology, 2018, 47(15): 13. DOI:10.7672/sgjs2018150013 |
| [2] |
YANG Xianfeng, MA Jingxuan, WEN Dongsheng, et al. Crashworthy design and energy absorption mechanisms for helicopter structures: A systematic literature review[J]. Progress in Aerospace Sciences, 2020, 114: 100618. DOI:10.1016/j.paerosci.2020.100618 |
| [3] |
ACAR E, ALTIN M, GULER M A. Evaluation of various multi-cell design concepts for crashworthiness design of thin-walled aluminum tubes[J]. Thin-Walled Structures, 2019, 142: 227. DOI:10.1016/j.tws.2019.05.012 |
| [4] |
MARZBANRAD J, EBRAHIMI M R. Multi-objective optimization of aluminum hollow tubes for vehicle crash energy absorption using a genetic algorithm and neural networks[J]. Thin-Walled Structures, 2011, 49(12): 1605. DOI:10.1016/j.tws.2011.08.009 |
| [5] |
孙宏图, 王健, 何士龙, 等. 铝合金薄壁方管轴向冲击变形及断裂行为研究[J]. 机械强度, 2016, 38(2): 364. SUN Hongtu, WANG Jian, HE Shilong, et al. Deformation and fracture behavior of aluminum alloy thin-walled square tubes under axial impact[J]. Journal of Mechanical Strength, 2016, 38(2): 364. DOI:10.16579/j.issn.1001.9669.2016.02.026 |
| [6] |
康建功, 石少卿, 陈进. 泡沫铝衰减冲击波压力的理论分析[J]. 振动与冲击, 2010, 29(12): 128. KANG Jiangong, SHI Shaoqing, CHEN Jin. Analysis of cladding aluminum foam attenuating blasting pressure[J]. Journal of Vibration and Shock, 2010, 29(12): 128. DOI:10.3969/j.issn.1000-3835.2010.12.029 |
| [7] |
WANG Yonghui, ZHAI Ximei, WANG Wei. Numerical studies of aluminum foam filled energy absorption connectors under quasi-static compression loading[J]. Thin Walled Structures, 2017, 116: 225. DOI:10.1016/j.tws.2017.03.032 |
| [8] |
WANG Yonghui, ZHAI Ximei, YAN Jiachuan, et al. Experimental, numerical and analytical studies on the aluminum foam filled energy absorption connectors under impact loading[J]. Thin-Walled Structures, 2018, 131: 566. DOI:10.1016/j.tws.2018.07.056 |
| [9] |
REYES A, HOPPERSTAD O S, LANGSETH M. Aluminum foam-filled extrusions subjected to oblique loading: experimental and numerical study[J]. International Journal of Solids and Structures, 2004, 41(5/6): 1645. DOI:10.1016/j.ijsolstr.2003.09.053 |
| [10] |
RAJENDRAN R, PREM SAI K, CHANDRASEKAR B, et al. Impact energy absorption of aluminium foam fitted AISI 304L stainless steel tube[J]. Materials and Design, 2009, 30(5): 1777. DOI:10.1016/j.matdes.2008.07.021 |
| [11] |
DUARTE I, VESENJAK M, KRSTULOVIĆ-OPARA L. Dynamic and quasi-static bending behaviour of thin-walled aluminum tubes filled with aluminum foam[J]. Composite Structures, 2014, 109: 48. DOI:10.1016/j.compstruct.2013.10.040 |
| [12] |
金属材料. 拉伸试验. 第1部分: 室温试验方法: GB/T 228.1—2010[S]. 北京: 中国标准出版社, 2010: 37 Metallic materials—Tensile testing—Part 1: Method of test at room temperature: GB/T 228.1—2010[S]. Beijing: China Standards Press, 2010: 37 |
| [13] |
丁珂. 冲击作用下铝基复合泡沫填充管动态力学及吸能性能研究[D]. 哈尔滨: 哈尔滨工业大学, 2017: 60 DING Ke. Study on dynamic mechanical properties and energy absorption performance of aluminum matrix composite foam-filled circular tube under impact[D]. Harbin: Harbin Institute of Technology, 2017: 60 |
| [14] |
LS TC. LS-DYNA® keyword user's manual volume Ⅱ: material models[M]. Livermore, California: Livermore Software Technology Corporation, 2013: 438.
|
| [15] |
HANSSEN A G, HOPPERSTAD O S, LANGSETH M, et al. Validation of constitutive models applicable to aluminium foams[J]. International Journal of Mechanical Sciences, 2002, 44(2): 376. DOI:10.1016/S0020-7403(01)00091-1 |
 2021, Vol. 53
2021, Vol. 53


