文献[1-2]指出中国作为一个地震多发国家,大量震害实例表明,存在非对称结构和薄弱区域的建筑在地震作用下容易产生扭转、局部变形集中等现象,加重了建筑的损坏,严重的甚至会引发倒塌,极大危害了人们生命财产安全。一方面,文献3]说明非对称结构是由于结构平面布置、使用功能及建筑外观等传统影响因素,使得结构形式与受力变得复杂,在地震作用下易出现局部应力、变形集中;另一方面,文献[4]提出了由于近年来预制装配式结构的大力推广,许多装配式建筑可能由于设计或者施工不当,使得预制装配部件的拼装区成为薄弱区域,易使该区域产生较大的集中变形。为了解决这些问题,开展地震作用下非对称框架-装配式剪力墙结构不利变形的控制机理与加固技术研究,具有重要的理论和现实指导意义。
传统加固方法主要有增大截面加固、预应力加固、碳纤维布加固等,这些方法主要专注于提高结构的局部承载力或延性,对结构整体的损伤变形模式如扭转、层间位移集中等控制力度有限,且容易因施工问题而受到住户的抵制。为此文献[5-7]提出外附摇摆结构加固的方式,利用摇摆加固方式在降低自身地震反应的同时,增加结构薄弱层的层抗侧刚度,实现结构损伤变形模式的控制;另外,加固是在建筑物外部进行加固施工,不影响建筑的正常使用,可以大幅度缩短工期、降低造价。文献[8-9]研究发现外附摇摆结构底部与建筑基础之间采用不同连接方式(如铰接、固结、结合摩擦或阻尼器的铰接等),会对结构的抗震性能产生不同的影响。文献[10-11]提出了摇摆-框架结构控制损伤机制并用于实际建筑加固中,经受住了地震的考验。由于摇摆墙自重大、混凝土易开裂、地震下不易发生摇摆,文献[12-13]采用自重较轻的摇摆架作为外附加固的子结构来改善结构的失效模式,实现损伤变形的控制。文献[14-15]说明了虽然外附摇摆架加固应用前景广阔,但目前的研究对象主要集中在框架结构,并通过二维平面模型进行加固研究,而其他结构体系如框剪结构体系、剪力墙结构体系以及带有装配式构件的结构体系,采用外附摇摆架加固方法及其设计方式是否适用,仍需进一步研究;文献[16]提出虽然装配混凝土结构近来研究比较多但主要集中在新型装配构件/结构的研发,缺少对震损结构的加固研究。总的来说,目前外附摇摆结构加固的研究对象较少,实际工程可能面临多样化的三维整体结构及装配结构可能带来的更复杂、不利的变形模式,给加固带来更加严峻的考验,外附加固的相关研究还不够系统和充分,以及已有的设计计算方法是否适用,需要进一步深入研究。
为了更加贴合实际工程的加固需求,本文选取了三层AFPSW作为加固对象,分析了其存在的问题,并利用动力学方程推导揭示了外附摇摆架变形控制机理并提出相应的设计方法,在三层AFPSW振动台试验基础上,通过非线性动力时程分析,对比研究了外附摇摆架加固前后结构的性能提升,以期为类似工程加固提供参考。
1 AFPSW结构存在的问题 1.1 试验概况装配式剪力墙的应用以及实际工程中常因功能、场地等需要,导致建筑产生非对称布置,易使结构产生不利变形,会极大地影响结构的抗震性能,为此进行了三层非对称框架-装配式剪力墙结构振动台试验。结构长为1.8 m,宽为0.9 m,层高均为1.0 m,剪力墙厚度均为75 mm,梁截面为70 mm×135 mm,柱截面为100 mm×100 mm,楼板厚为60 mm。梁、柱、剪力墙和楼板的受力钢筋均为A6,梁箍筋为A3@50,框架柱箍筋为A3@60,剪力墙采用双排双向受力分布筋A6@100,楼板的配筋为双层双向A3@60,保护层为5 mm,混凝土强度等级取为C30,钢筋为HPB300。选用Ⅱ类场地,抗震设防烈度为7度,按照GB 50011—2010《建筑抗震设计规范》[17]要求,地震波选用El-Centro波、Taft波及上海波,沿图 1(a)y向单向输入,图 1(c)所示为3条波在7度频遇地震(峰值加速度为0.15 g)作用下谱加速度反应谱与规范谱的对比,表 1为结构的相似比。

|
图 1 振动台试验概况 Fig. 1 Overview of shaking table test |
| 表 1 模型相似比 Tab. 1 Similarity ratio of model system |
通过图 1(a)平面图可发现,由于剪力墙为左右非对称布置,会使平面的质心与刚心产生偏离。根据平面法计算其质心:
| $ {x_{\rm{m}}} = \sum {{x_i}{m_i}} /\sum {{m_i}} $ | (1) |
| $ {y_{\rm{m}}} = \sum {{y_i}} {m_i}/\sum {{m_i}} $ | (2) |
式中:xm、ym为质心坐标,xi、yi为到x、y轴的距离,mi为构件质量。
刚心计算方法与质心计算方法类似。建立以o为原点的平面坐标系,计算得到质心与刚心之间偏心较大,距离为288 mm,见图 2(a);同时对结构进行有限元模态分析,得到其二阶模态以平面扭转为主,见图 2(b)。由于扭转易造成结构附加地震损伤,因此对结构的扭转效应进行控制,显得尤为重要。
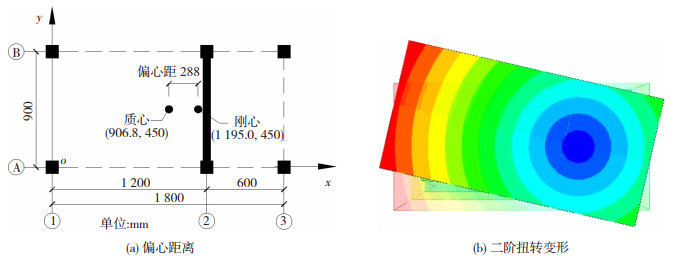
|
图 2 结构的扭转 Fig. 2 Torsion of the structure |
规范[17]规定当楼层的最大侧向位移大于同层两端的侧向位移平均值的1.2倍时,认为该结构属于扭转不规则。根据本文结构平面形式和规范计算方法,可换算成δ2>1.5δ1,其中δ2、δ1分为图 1(a)中的①、③轴水平位移,将其换算成扭转角其限值为5.02×10-4,当超过限值时,结构视为扭转不规则。从图 3可得,3种波作用下结构的扭转角均大于规范限值,且随着峰值加速度的提升,扭转角大幅度增加;当峰值加速度为0.62 g时,结构的扭转角达到0.022,远大于现行规程扭转限值5.02×10-4,属于严重的平面不规则。通过前述研究可知[1-2],严重的平面不规则易引起结构局部应力、变形集中而造成局部破坏,极大降低了结构的抗震性能,因此改善AFPSW结构的不规则性显得尤为迫切。
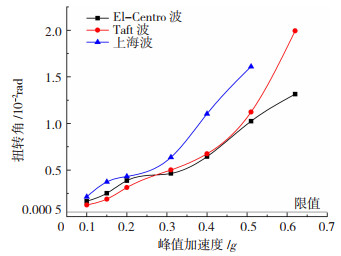
|
图 3 不同峰值加速度下的结构扭转角 Fig. 3 Torsion angle of the structure under different peak ground acceleration |
改善结构的变形模式能够发挥其整体抗震性能,然而由于结构的设计或使用问题往往导致结构出现层间位移集中现象,为了更好地评价结构的竖向变形效果,采用了层间位移集中系数NDCF判断结构是否出现薄弱层。
| $ {N_{{\rm{DCF}}}} = \frac{{{\theta _{{\rm{max}}}}}}{{{\mu _{\rm{t}}}/H}} $ | (3) |
式中θmax为结构所有楼层中的最大层间位移,ut为结构顶层位移,H为结构总高度。通过公式可知,NDCF越接近于1时,结构的竖向变形越均匀,反之则结构的局部变形越集中,可能产生薄弱层破坏。
由表 2看出,峰值加速度为0.10 g时,3条地震波作用下的NDCF分别为1.03、1.04、1.01,基本接近于1,此时结构各层的层间变形基本一致且较为均匀;当峰值加速度从0.20 g开始,NDCF与1之间差值基本呈现不断增大的趋势,说明结构的不均匀变形逐渐加重;最后,峰值加速度达到0.62 g,结构的层间位移集中系数为1.53,与1之间的差值最大,此时对应结构的最大层间位移角为1/241,产生较大的弹塑性变形,说明此时结构出现较为严重的局部变形集中现象,易引起楼层发生破坏甚至倒塌,降低其抗震性能.因此控制本结构的集中变形是改善其抗震性能的另一重要方式。
| 表 2 不同峰值加速度下结构的NDCF Tab. 2 NDCF of the structure under different peak ground acceleration |
由前述可知,结构的抗震性能与变形模式密切相关,本文基于此对结构进行抗震加固,以实现预期损伤变形机制。外附摇摆架加固对结构变形模式有较好的控制效果、且不入户加固,但目前主要基于半经验式设计,有待于进一步解释其变形控制机理,并建立相应的设计方法。
2.1 摇摆架的变形控制机理为了了解外附摇摆架的变形控制机理,结合文献[18]所提出的简化分析模型,建立了外附摇摆架-原结构体系的动力学方程,并选取其中某一楼层作为隔离体进行简化分析,见图 4。
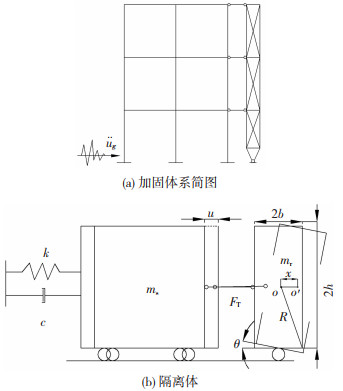
|
图 4 结构简化分析模型 Fig. 4 Simplified analysis model of the structure |
取结构某层作为隔离体分析可得到,当外附摇摆架受到原结构的作用后会发生摆动与变形,并通过连接杆提供反作用力给原结构,其动力学方程
| $ {m_{\rm{s}}}(\ddot u + {\ddot u_g}) + c\dot u + ku = {F_{\rm{T}}} $ | (4) |
式中:ms、c、k为原结构的质量、阻尼系数、体系刚度,相对地面的位移为u、速度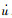
在文献[18]所提的简化分析模型及式(4)的基础上进一步推导可得,摇摆架提供的反作用力会影响原结构的地震响应,因此需要求解未知量FT。取摇摆架作为隔离体进行受力分析(图 5),可知质心点在地震力、连接杆轴力和转动力矩3种力作用下由点o移动到o′,根据达朗贝尔原理得到平衡方程
| $ {M_{\rm{ \mathit{ θ} }}} + {F_{\rm{T}}}x + {m_{\rm{r}}}{\ddot u_g}x = {m_{\rm{r}}}gx $ | (5) |

|
图 5 摇摆架的受力简图 Fig. 5 Schematic diagram of the rocking frame |
式中:Mθ为转动力矩,mr、x分别为摇摆架的质量、质心点相对地面位移,g为重力加速度,其中未知量为Mθ、x。
连接杆长度远大于原结构相对位移u时,可将原结构相对位移与摇摆架质心点相对位移视为相等,即u=x,此时摇摆架的转动角度θ与相对地面位移u的关系如式(6),并求其二阶导数,可得到其角加速度:
| $ u=x=h \sin \theta $ | (6) |
| $ \dot{u}=h \dot{\theta} \cos \theta $ | (7) |
| $ \ddot{u}=h \ddot{\theta} \cos \theta-h \dot{\theta}^{2} \sin \theta $ | (8) |
摇摆架高2h、宽为2b,绕底部中点转动,其转动惯量可通过平行轴定理计算:
| $ l=\frac{1}{3} m_{\mathrm{r}} R^{2}+m_{\mathrm{r}} h^{2} $ | (9) |
| $ R^{2}=b^{2}+h^{2} $ | (10) |
| $ M_{\theta}=I \ddot{\theta} $ | (11) |
由式(5)~(11)可得FT为
| $ F_{\mathrm{T}}=m_{\mathrm{r}} g-m_{\mathrm{r}} \ddot{u}_{g}-\left(\frac{1}{3} m_{\mathrm{r}} R^{2}+m_{\mathrm{r}} h^{2}\right) \frac{\ddot{\theta}}{h \sin \theta} $ | (12) |
式(12)说明当摇摆架的质量mr固定时,反作用力FT的大小主要取决于其转动角度θ;由于分析时采用结构某一层作为隔离体,从结构整体角度观察可以得到,θ可视为摇摆架的层间位移角,与摇摆架的刚度相关;FT可视为原结构层间剪力的反作用力,可减小结构的层间变形。
因此,外附摇摆架的变形控制机理是当原结构某一楼层相对于其上下楼层发生一定的层间变形后,会引起摇摆架产生变形而产生水平反作用力(抵抗力),从而部分抵消原结构的层间剪力,达到控制结构损伤变形的目的。所以,当结构某层的变形越集中,引起的摇摆架抵抗力就越大,对该层的控制效果就越明显。
2.2 摇摆架的设计方法综上可知,摇摆架通过抵抗力抵消原结构的层间剪力而达到控制效果,摇摆架的抵抗力与其层抗侧刚度成正比,所以通过摇摆架层抗侧刚度的合理设置,才能实现损伤变形控制的作用,为此需要通过对摇摆架的层抗侧刚度进行合理计算,保证控制效果同时提高经济性。
计算摇摆架的层抗侧刚度,需要知道其所受的水平作用力和变形值大小。由于摇摆架的变形与原结构的变形基本保持一致,所以通过设定原结构的变形目标值后,利用加速度反应谱计算出作用在结构上的水平地震作用,即可得到摇摆架的刚度需求大小。具体加固设计步骤如下:
已知原结构的尺寸、重力荷载代表值及自振周期,且以第一振型为主,则结构各楼层的水平地震作用Fi为:
| $ F_{\mathrm{ek}}=\alpha_{1} G_{\mathrm{eq}} $ | (13) |
| $ F_{i}=\frac{G_{i} h_{i}}{\sum\limits_{i=1}^{n} G_{i} h_{i}} F_{\mathrm{ek}}(i=1,2, \cdots, n) $ | (14) |
式中:Fek、α1、Geq为结构底部总剪力、地震影响系数、原结构的总重力荷载,Gi、hi为结构第i层的重量、高度。摇摆架的层抗侧刚度krock及原结构的层抗侧刚度ksw为:
| $ k_{\text {rock }} =12 E_{\mathrm{s}} I_{\mathrm{s}} / h_{i}^{3}+E_{\mathrm{s}} A_{\mathrm{s}} l^{2} / L_{\mathrm{s}}^{3} $ | (15) |
| $ k_{\mathrm{sw}} =12 n E_{\mathrm{c}} I_{\mathrm{c}} / h_{i}^{3}+G A_{\mathrm{c}} / h_{i} $ | (16) |
式中:Es、Is为摇摆架钢材的弹性模量、柱的惯性矩,As、l、Ls为摇摆架斜杆的截面积、跨度与长度;Ec、G为原结构混凝土弹性模量、剪切模量,Ic框架柱的惯性矩,Ac为剪力墙的截面积。
利用前述的各层剪力以及ksw,可得到原结构的最大顶点位移ut为
| $ {u_{\rm{t}}} = (3{F_{{\rm{ek}}}} + 2{F_2} + 3{F_3})/{k_{{\rm{sw}}}} $ | (17) |
当NDCF越接近于1时,结构层间变形的均匀性越好,一般默认为常数,因此根据结构设计需要确定ut后,可得到结构的最大层间位移角为
| $ \theta_{\max }=N_{\mathrm{DCF}} \cdot u_{\mathrm{t}} / h $ | (18) |
选取最大层间位移角θmax及对应的楼层剪力Fi,计算可得到层抗侧刚度KT:
| $ K_{\mathrm{T}}=F_{i} / \theta_{\mathrm{max}} $ | (19) |
| $ K_{\mathrm{T}}=k_{\mathrm{rock}}+k_{\mathrm{sw}} $ | (20) |
通过以上公式计算可得到外附摇摆架的层抗侧刚度,并对其尺寸进行设计可得:梁柱的型号均为H 100 mm×100 mm×6 mm×8 mm,人字形斜撑的型号为Ⅰ 64 mm×44 mm×3 mm×5 mm。通过外附摇摆架的质量和刚度对结构的偏心率进行调整后,得到e=125 mm,相对于加固前减少了57%。
3 加固AFPSW结构的性能提升为了验证外附摇摆架加固设计方法的准确性和有效性,分析了AFPSW结构加固前后的内力、扭转、层间位移角和损伤状态划分,并进行了比较。
3.1 有限元模型建立与验证 3.1.1 模型建立采用Abaqus软件建立了三层AFPSW结构有限元模型,结构尺寸参数具体见1.1节。结构材料单元选用为关键拼接区域的混凝土与钢框设置为精细化实体单元,非关键区域的梁柱构件采用纤维梁单元,采用多点约束进行连接。楼板与非装配区剪力墙采用壳单元。材料的本构模型选用方面,混凝土采用塑性损伤本构,钢框采用双折线强化模型,纤维梁单元其本构设置通过调用文献[19]提出的子程序iFiberLUT的iSteel01与iConcrete04实现钢筋与混凝土的模拟。抗剪螺栓在整个受力过程处于弹性状态,为提高计算效率,采用剪切弹簧模拟,其刚度值设为较大的数值,默认不发生变形。结构的边界条件为放松图 1(a)y方向的位移,作为地震波加速度的输入方向,其余的自由度全部约束。考虑重力荷载影响,选用隐式动力分析方式,建立非线性动力时程分析模型,如图 6(a)~(c)。摇摆架与原结构之间通过图 6(d)所示连接件进行连接,同时为避免连接部位应力集中,连接件在原结构刚性楼板部位植入钢筋形成固连。
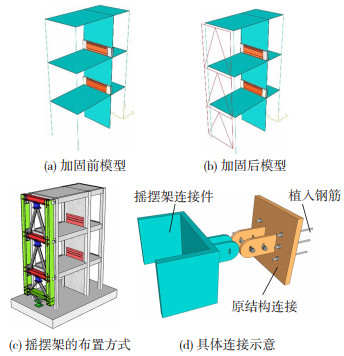
|
图 6 结构有限元模型及材料本构 Fig. 6 Finite element model and material constitutive of the structure |
运用前面建立的有限元模型分别进行模态分析及非线性动力时程分析,计算了结构的一、二阶自振频率及各楼层的质心加速度时程曲线,以峰值加速度为0.62 g El-Centro波下的计算结果为例,与1.1节振动台试验数据进行比较,见表 3和图 7。
| 表 3 模拟、实测频率对比 Tab. 3 Comparison of simulated and measured frequencies |

|
图 7 El-Centro地震作用下各个楼层加速度响应对比 Fig. 7 Comparison of acceleration responses of each floor under El-Centro earthquake |
由表 3的频率对比可以得到一二阶频率的模拟结果与实际振动台测量得到的数值基本一致,误差保持在0.5%以内,证明了有限元模型的基本物理参数基本与试验一致。
通过对模型的非线性时程分析,取结构楼层加速度时程曲线前10 s的试验值与仿真值进行对比,可以看出两者的波峰与波谷趋势基本一致且数值相差不大,误差值保持在5%精度较高的范围以内,验证了有限元动力时程分析模型的准确性。
3.2 加固后的性能提升为了研究加固后体系的性能提升,选取结构的应力状态、变形及损伤等级评估进行研究,来全面地展示外附摇摆架的变形控制与抗震性能提升效果。
3.2.1 结构体系内力分析由于加固前的结构存在较大的偏心,易在地震作用下出现平扭耦合效应和鞭梢效应,使得结构的长边梁柱结构处出现较大的应力集中现象,应力最大为93.0 MPa。而通过外附摇摆架的加固后,对比图 8(a)、(b)可看到,通过外附摇摆架对框剪结构进行加固与偏心改善后,使得结构的竖向变形变得均匀,应力最大为15.2 MPa,证明摇摆架可以有效地改善结构的局部应力集中,改善结构的内力分布,达到提升其抗震性能的效果。

|
图 8 加固前后结构的应力分布 Fig. 8 Stress distribution of the structure with or without reinforcement |
为了了解加固前后装配式拼接区混凝土与连接钢框的损伤发展情况,选取拼接区的屈服状态云图作对比分析,见图 9。

|
图 9 拼接区的损伤发展示意 Fig. 9 Diagram of damage development in connection area |
从图 9可得出,连接钢框无论是加固后还是加固前,在峰值加速度在0.1 g~0.62 g的地震作用下均未出现屈服现象,保证了其连接性能,进一步体现了该连接设计的可靠性,可作为装配区的有效连接方式。而对于装配区的混凝土可以看出,加固可以有效降低混凝土的损伤,加固前混凝土在0.2 g时开始出现屈服,对应的最大Mises应力为14.0 MPa,等效塑性应变为1.2×10-4,而加固后拼接区混凝土基本处于弹性阶段,其最大Mises应力为9.8 MPa,等效塑性应变为8.9×10-5;加速度峰值施加到0.62 g时,加固前的混凝土不仅在受拉区出现屈服现象,且损伤进一步扩展到受压区部位的混凝土,而通过加固的混凝土延缓了损伤的扩展,只在受拉区发生屈服现象。综上可见,外附结构加固可以有效降低拼接区的应力值,延缓其损伤扩展分布,提升了拼接区的力学性能。
3.2.3 结构变形:扭转角与层间位移角为了研究外附摇摆架对AFPSW结构不利变形的控制效果,选取了El-Centro波峰值加速度为0.62 g下结构加固前后结构的扭转角、层间位移角进行对比分析,见图 10。
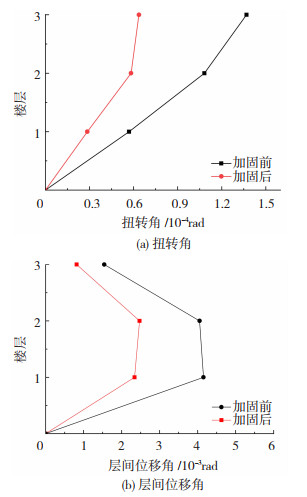
|
图 10 加固前后扭转、层间位移角对比 Fig. 10 Comparison of torsion angle and inter-story drift angle with or without reinforcement |
将结构各层平面长边方向两端端点的相对位移进行求差值,可以得到各层平面的位移差值,各层位移差值与长边的比值为各层扭转位移角。图 10(a)为加固前后结构模型的扭转角对比,可看出结构的顶层扭转角在加固后为0.637×10-4,相对于加固前的1.37×10-4减小了53%,说明采用外附摇摆架能够较好地改善偏心框剪结构的平面形状指标。
从图 10(b)可看出结构的层间位移主要集中在一、二层,采用外附摇摆架加固后框剪结构的各层层间位移角相对于未加固结构均有不同程度的减小,加固前结构最大层间位移角为1/241而加固后为1/428,降低了43.6%,说明了外附摇摆加固对层间位移的控制效果较为显著;结构的层间位移集中系数NDCF在加固前为1.53,通过加固后为1.21,下降了20.9%,加固后有效提高了结构变形的均匀性,也证实了外附加固具有较好的损伤变形控制能力。
3.2.4 不同峰值加速度下的震害评估规范[17]提出弹性层间位移角θe为1/800,弹塑性层间位移角θp为1/100,参考规范对结构的性能指标θs进行划分。选用El-Centro波从0.1 g到0.62 g对结构进行分析,得到加固后各个峰值加速度下结构各层的层间位移角,并对加固前后的层间位移角进行对比,见表 4、图 11。
| 表 4 结构地震损伤等级划分 Tab. 4 Classification of earthquake damage levels of the structure |
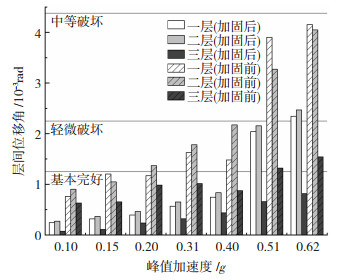
|
图 11 不同峰值加速度下结构加固前后的层间位移角对比 Fig. 11 Comparison of inter-story drift angle with or without reinforcement under different peak ground acceleration |
从图 11可看出,结构未加固前,当峰值加速度为0.1 g、0.15 g时基本处于完好状态,达到0.2 g时,结构二层开始出现轻微损伤,对应的层间位移角为1/730;此后,随着峰值加速度增加,结构的层间位移角继续增大,但仍未达到中等破坏水平;而达到0.51 g时,结构的一、二层开始进入了中等破坏状态,对应层间位移角为1/257、1/306,且三层开始出现轻微损伤。最后,峰值加速度增至0.62 g,最大层间位移角出现在一层为1/241,保持在中等破坏水准。
比较发现,加固后结构在峰值加速度为0.51 g之前基本保持完好状态,且结构扭转、层间位移集中系数都得到控制,改善了局部变形,进而降低了损伤状态等级;峰值加速度达到0.51 g时,结构一、二层开始出现轻微损伤,对应的层间位移角分别为1/490、1/462,相对于加固前的1/257、1/306减小了47.6%、33.9%,可以看出一层的层间位移角控制效果优于二层,由变形控制机理研究可知,变形越严重的楼层受到外附摇摆架的反作用力也越大,大幅度抵消了结构的层间剪力,减小其层间位移角,也说明了外附加固有效控制了集中变形,提升结构整体变形均匀性;当峰值加速度为0.62 g时,加固后结构的一、二层进入了中等破坏水平,其最大层间位移角为1/404,相对于未加固的减小了40.5%。由此可见,采用外附摇摆架加固方式能够有效减低结构的损伤状态等级,减小局部层间位移集中现象,发挥结构的整体抗震能力。
4 结论结合三层AFPSW结构振动台试验,通过外附摇摆架加固的方式,对AFPSW结构加固的损伤控制机理与设计方法进行了研究,得到以下结论:
1) 推导了外附摇摆架加固结构体系的动力学方程,揭示了外附摇摆架的变形控制机理。研究发现,外附摇摆架利用自身刚度、变形产生的反作用力来抵消结构的层间剪力,层间变形越集中反作用力越大,结构的变形愈均匀,变形控制效果越显著。
2) 基于外附摇摆架的变形控制机理,结合原结构的体系特点,以结构的最大层间位移角为加固的目标值,推导建立了外附摇摆架的设计方法,动力时程对比分析结果表明,外附摇摆架能够有效改善AFPSW结构地震作用下扭转和层间位移集中过大的问题,也验证了设计方法的准确性。
3) 通过AFPSW结构的内力、变形和损伤等级的对比分析结果表明,采用外附摇摆架的加固,使结构整体的内力峰值得到降低,扭转和层间位移集中分别减小了53%、20.9%,提升了结构的均匀性,结合相关的震害评估,进一步说明了改善AFPSW结构的不利变形问题,能够有效提升结构的抗震性能。
| [1] |
LIM H K, KANG J W, PAK H, et al. Seismic response of a three-dimensional asymmetric multi-storey reinforced concrete structure[J]. Applied Sciences, 2018, 8(4): 479. DOI:10.3390/app8040479 |
| [2] |
翟长海, 王晓敏, 孔璟常, 等. 砌体填充墙RC框架结构抗震性能研究现状及展望[J]. 哈尔滨工业大学学报, 2018, 50(6): 2. ZHAI Changhai, WANG Xiaomin, KONG Jingchang, et al. Progress and prospect of seismic performance of masonry-infilled RC frames[J]. Journal of Harbin Institute of Technology, 2018, 50(6): 2. DOI:10.11918/j.issn.0367-6234.201801073 |
| [3] |
王琛, 陶慕轩, 崔明哲, 等. 非对称复杂连体结构抗震性能与变形差控制实例研究[J]. 建筑结构学报, 2020, 41(4): 68. WANG Chen, TAO Muxuan, CUI Mingzhe, et al. Case study on seismic behavior and displacement difference control of complicated asymmetric connected structures[J]. Journal of Building Structure, 2020, 41(4): 68. DOI:10.14006/j.jzjgxb.2018.5225 |
| [4] |
张偲严, 李宏男, 李超. 装配式剪力墙高效阻尼器耗能连接的简化模型研究与数值分析[J]. 建筑结构学报, 2019, 40(10): 62. ZHANG Caiyan, LI Hongnan, LI Chao. Simplified model development and numerical simulation of a high-efficiency energy-dissipating joint for prefabricated concrete shear walls[J]. Journal of Building Structure, 2019, 40(10): 62. DOI:10.14006/j.jzjgxb.2019.0038 |
| [5] |
曲哲, 张令心. 日本钢筋混凝土结构抗震加固技术现状与发展趋势[J]. 地震工程与工程振动, 2013, 33(4): 61. QU Zhe, ZHANG Lingxin. State of the art and development tendency of seismic retrofit for reinforced concrete structures in Japan[J]. Earthquake Engineering and Engineering Dynamics, 2013, 33(4): 61. DOI:10.11810/1000-1301.20130408 |
| [6] |
FENG Yulong, ZHANG Zhi, CHONG Xun, et al. Elastic displacement spectrum-based design of damage-controlling BRBFs with rocking walls[J]. Journal of Constructional Steel Research, 2018, 148: 691. DOI:10.1016/j.jcsr.2018.06.022 |
| [7] |
吴守君, 潘鹏, 张鑫. 框架-摇摆墙结构受力特点分析及其在抗震加固中的应用[J]. 工程力学, 2016, 33(6): 54. WU Shoujun, PAN Peng, ZHANG Xin. Characteristics of frame rocking wall structure and its application in aseismic retrofit[J]. Engineering Mechanics, 2016, 33(6): 54. |
| [8] |
MOTTIER P, TREMBLAY R, ROGERS C. Seismic retrofit of low-rise steel buildings in Canada using rocking steel braced frames[J]. Earthquake Engineering & Structural Dynamics, 2017, 47(2): 353. DOI:10.1002/eqe.2953 |
| [9] |
GIOIELLA L, TUBALDI E, GARA F, et al. Stochastic seismic analysis and comparison of alternative external dissipative systems[J]. Shock and Vibration, 2018, 2018: 5403737. DOI:10.1155/2018/5403737 |
| [10] |
曲哲. 摇摆墙—框架结构抗震损伤机制控制及设计方法研究[D]. 北京: 清华大学, 2010: 64-76 QU Zhe. Study on seismic damage mechanism control and design of rocking wall-frame structures[D]. Beijing: Tsinghua University, 2010: 64-76 |
| [11] |
QU Zhe, WADA A, MOTOYUI S, et al. Pin-supported walls for enhancing the seismic performance of building structures[J]. Earthquake Engineering and Structural Dynamics, 2012, 41(14): 2075. DOI:10.1002/eqe.2175 |
| [12] |
杜永峰, 武大洋. 基于刚度需求设计的轻型消能摇摆架减震性态分析[J]. 土木工程学报, 2014, 47(1): 25. DU Yongfeng, WU Dayang. Performance analysis of light energy dissipative rocking frame designed on the basis of stiffness demand[J]. China Civil Engineering Journal, 2014, 47(1): 25. DOI:10.15951/j.tmgcxb.2014.01.006 |
| [13] |
贾明明, 周洲, 吕大刚, 等. 摇摆桁架-钢框架结构的刚度比需求及地震响应分析[J]. 工程力学, 2018, 35(10): 67. JIA Mingming, ZHOU Zhou, LÜ Dagang, et al. Demand stiffness ratio and earthquake response analysis of rocking truss-steel frame system[J]. Engineering Mechanics, 2018, 35(10): 67. DOI:10.6052/j.issn.1000-4750.2017.06.0470 |
| [14] |
GIOIELLA L, TUBALDI E, GARA F, et al. Modal properties and seismic behavior of buildings equipped with external dissipative pinned rocking braced frames[J]. Engineering Structures, 2018, 172: 810. DOI:10.1016/j.engstruct.2018.06.043 |
| [15] |
尹保江, 程绍革, 吉飞宇, 等. 外部附加带框钢支撑弱连接模式加固框架结构抗震性能试验研究[J]. 工程抗震加固与改造, 2019, 41(3): 110. YIN Baojiang, CHENG Shaoge, JI Feiyu, et al. Experimental study on seismic performance of frame structure strengthened with weak attached steel braces[J]. Earthquake Resistant Engineering and Retrofitting, 2019, 41(3): 110. DOI:10.16226/j.issn.1002-8412.2019.03.016 |
| [16] |
吴刚, 冯德成. 装配式混凝土框架节点基本性能研究进展[J]. 建筑结构学报, 2018, 39(2): 2. WU Gang, FENG Decheng. Research progress on fundamental performance of precast concrete frame beam-to-column connections[J]. Journal of Building Structure, 2018, 39(2): 2. DOI:10.14006/j.jzjgxb.2018.02.001 |
| [17] |
建筑抗震设计规范: GB 50011—2010[S]. 北京: 中国建筑工业出版社, 2010 Code for seismic design of buildings: GB 50011—2010[S]. Beijing: China Architecture & Building Press, 2010 |
| [18] |
MAKRIS N, AGHAGHOLIZADEH M. The dynamics of an elastic structure coupled with a rocking wall[J]. Earthquake Engineering and Structural Dynamics, 2017, 46(6): 948. DOI:10.1002/eqe.2838 |
| [19] |
吴星蓉, 史艳莉, 王文达. 基于纤维梁单元模型的内配工字型钢方钢管混凝土压弯构件延性分析[J]. 钢结构, 2017, 32(7): 32. WU Xingrong, SHI Yanli, WANG Wenda. Ductility analysis of concrete-filled square steel tubular member with inner-profiled steel based on fiber beam element model[J]. Steel Construction, 2017, 32(7): 32. DOI:10.13206/j.gjg201707007 |
 2021, Vol. 53
2021, Vol. 53


