2. 上海大学 风工程和气动控制研究中心,上海 200444;
3. 上海大学 力学和工程科学学院,上海 200444
2. Wind Engineering and Aerodynamic Flow Control Research Center, Shanghai University, Shanghai 200444, China;
3. School of Mechanics and Engineering Science, Shanghai University, Shanghai 200444, China
极值风压和风压非高斯特性是超高层建筑围护结构、屋盖结构和冷却塔结构等风敏感结构在设计中重点关注的问题。已有研究[1-4]表明,结构表面某些区域的风压概率统计特性会表现出明显的非高斯特性,按照传统的具有高斯特性的峰值因子法估计极值风压,会导致极值风压偏小,结构设计偏于不安全。方形截面是超高层建筑常用形式,采用角部措施的气动措施(如切角、圆角、凹角)能有效减小其风荷载和风效应[5]。然而,目前对于角部措施对方形截面超高层建筑极值风压和风压非高斯特性的作用机理尚未澄清。
研究者对矩形截面超高层建筑的风压非高斯特性进行了研究[6-8]。Gioffre等[6]通过风洞试验研究表明,高层建筑的风压非高斯特性与风压时程中的极值风压有关,建议采用风压脉动的偏度值和峰度值来判断风压的非高斯特性。庄翔等[7]基于测压风洞试验,研究了风向角对高层建筑风压非高斯区域的影响,发现在建筑迎风面边缘和角部出现小部分非高斯区域。韩宁等[8]的研究指出高层建筑风压非高斯区域受风向角影响较大,分离流和尾流作用区域会呈现风压非高斯现象。上述文献主要针对风压发生非高斯特性的区域及其影响因素进行研究,对高层建筑出现极值风压和风压非高斯特性的流场机理研究很少。
切角气动措施是降低超高层建筑风荷载的常用气动性能优化手段,可明显改善方柱的气动性能,抑制或减小柱体的气弹失稳[9]。Wang等[10]研究了切角率对方柱表面风压的影响,结果表明小切角率能明显减小方柱侧风面和背风面的负压,大切角率能有效降低角部负压。楼文娟等[11]则研究了带切角和凹槽组合的超高层建筑的风压非高斯特性。目前,角部措施对超高层建筑极值风压和风压非高斯特性的影响规律及其机理尚未澄清。
超高层建筑的表面风压特性会受到多种因素的影响,如截面形式、地面粗糙度、来流湍流度、风向角、顶部形式、临近建筑干扰等,情况非常复杂。为理解角部措施对超高层建筑表面极值风压和风压非高斯特性的影响规律及其流场机理,并为进一步的气动措施研究提供依据,本文以简化的超高层建筑模型(均匀来流作用下的标准方柱和切角方柱)为研究对象,考虑切角率和风向角的影响,采用大涡模拟方法,在雷诺数Re=2.2×104时,研究了两种方柱的气动性能、流场特性和风压非高斯特性随风向角的变化规律,探讨了流场结构与风压非高斯区域之间的内在联系,分析了角部措施对方柱表面风压非高斯特性的影响,并基于瞬时流场结构解释了角部措施对方柱极值风压和风压非高斯特性的流场作用机制。
1 计算模型和验证结果 1.1 计算模型和计算域本文计算模型见图 1,U为来流风速,B为方柱边长(0.1 m),R为切角边长长度。本文采用的切角率为R/B=1/7。风向角α在0°~45°之间变化。

|
图 1 计算模型示意 Fig. 1 Computational model |
图 2为计算域及边界条件示意,来流入口边界采用圆弧形入口,弧顶端距离方柱中心20B;出口边界距离方柱中心30B,横风向计算域为40B,最大阻塞率(α=45°)为3%。计算域采用速度入口边界条件(均匀流),自由出口边界,两侧采用对称边界,方柱展向采用周期性边界,方柱表面为无滑移壁面边界。
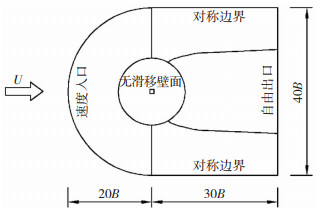
|
图 2 计算域及边界条件示意 Fig. 2 Computational domain and boundary conditions |
本文计算采用大涡模拟湍流模型和WALE亚格子尺度模型,压力求解采用SIMPLEC格式,对基本控制方程的离散采用有限体积法,空间离散采用中心差分格式,时间离散采用二阶全隐格式。切角方柱的网格模型见图 3,采用结构化网格,角部网格加密处理,近壁面网格增长率为1.04。

|
图 3 切角方柱网格模型 Fig. 3 Grid scheme of chamfered corner square cylinder |
为检验计算结果网格独立性和正确性,首先针对α=0°的标准方柱,研究了周向网格数、时间步长、展向网格数和展向长度等参数对气动性能的影响,详细验证工作见文献[12]。通过参数比选,本文计算模型的展向长度L=4B,展向布置40层网格,方柱周向网格数为200,角部网格加密,总网格数为122万,计算的无量纲时间步Δt*为0.025 (Δt*=ΔtU/B,其中Δt为有量纲时间步,U为来流风速),近壁面最小网格厚度为0.001B,近壁面y+≈1。
表 1给出本文结果与文献值的比较。可见,本文结果与文献中的数值模拟和风洞试验结果相近。本文和文献数值模拟得到的脉动升力系数较风洞试验值略微偏高,这可能是由风洞试验和数值模拟的参数(如来流湍流度、方柱长度、方柱端部条件等[12])的差异所致。图 4给出标准方柱的平均风压系数和脉动风压系数,并与试验值进行对比,其结果吻合良好。
| 表 1 α=0°标准方柱的计算结果及其验证 Tab. 1 Results of sharp corner square cylinder for α=0° and its comparison with previous data |

|
图 4 α=0°标准方柱表面风压系数:(a) 平均风压系数;(b) 脉动风压系数 Fig. 4 Pressure coefficients distributions of sharp corner square cylinders at α=0°: (a) Mean pressure coefficient; (b) RMS pressure coefficient |
根据方柱流场结构特征,两类方柱在不同风向角下均有三种流态,即:“前角分离流态”、“分离泡流态”和“附着流流态”,各流态的风向角范围见表 2。可见,切角方柱出现“分离泡流态”的风向角比标准方柱更小,而出现“附着流流态”的风向角比标准方柱更大。
| 表 2 方柱不同流场结构的风向角范围 Tab. 2 Ranges of wind angle for different flow patterns of square cylinders |
图 5给出α=0°、9°、12.6°、45°时四种典型风向角下两种方柱在展向中间截面的平均流线图。切角方柱出现分离泡的风向角更小,标准方柱为α=12.6°,切角方柱为α=9°。总体而言,切角方柱的剪切层比标准方柱更加贴近壁面。当α=0°时,两类方柱都处于“前角分离流态”;标准方柱的来流在前角a、d处发生分离,并在柱体两侧和尾部形成四个回流区;对于切角方柱来说,分离点后移,侧面回流区较小,而尾流回流区较大。标准方柱和切角方柱分别在α=9°和α=12.6°时出现“分离泡流态”,上侧剪切层开始再附形成单侧分离泡。当α=45°时,两类方柱均为“附着流流态”,来流附着在迎风面(ab和ad)流动,在角部b、d附近发生分离,切角方柱的尾流回流区相对较短。

|
图 5 标准方柱和切角方柱的平均流线图 Fig. 5 Time-averaged streamlines of sharp and chamfered corner square cylinders |
本节给出两类方柱表面风压的偏度(skewness,简写为S)和峰度(kurtosis,简写为K),其定义式[8]分别为:
| $S=\frac{1}{N} \sum\limits_{i=1}^{N}\left(C_{\mathrm{p}}(i, t)-C_{\mathrm{p}}(i)\right)^{3} \sigma_{C_{\mathrm{p}}(i, t)}^{-3} $ | (1) |
| $K=\frac{1}{N} \sum\limits_{i=1}^{N}\left(C_{\mathrm{p}}(i, t)-C_{\mathrm{p}}(i)\right)^{4} \sigma_{C_{\mathrm{p}}(i, t)}^{-4} $ | (2) |
式中N为风压系数时程的样本数。
图 6给出α=0°、9°、12.6°、45°时两类方柱风压的峰度和偏度。可见,当α=0°时,标准方柱侧风面后角点c处的峰度和偏度较高;切角方柱在角部附近的峰度骤降,而背风面风压的峰度和偏度则增大。当α=9°时,标准方柱背风面的峰度和偏度明显增大,而切角方柱背风面风压的峰度和偏度变化不大。当α=12.6°时,标准方柱下侧面后角点的峰度和偏度明显增大,切角方柱的峰度和偏度较小。当α=45°时,标准方柱在迎风面角点a处和背风面c处的风压峰度和偏度较大,而切角方柱的峰度和偏度进一步减小。

|
图 6 标准方柱和切角方柱的风压峰度K与偏度S: (a) α=0°; (b) α=9°; (c) α=12.6°; (d) α=45° Fig. 6 Kurtosis and skewness of sharp and chamfered corner square cylinders: (a) α=0°; (b) α=9°; (c) α=12.6°; (d) α=45° |
图 7给出上述四种风向角下两类方柱的风压非高斯区域,用粗条标识注明,并给出平均风压场的对比结果。不同文献对于风压非高斯特性的判定标准不同,本文参考楼文娟等[11]的判定界限,将|K|>3.5且|S|>0.2的区域定义为风压非高斯区域。

|
图 7 标准方柱和切角方柱平均风压场和风压非高斯区域 Fig. 7 Time-averaged pressure fields and non-Gaussian regions of sharp and chamfered corner square cylinders |
由图 7可见,风压非高斯区域随流态变化明显。在α=0°时,标准方柱和切角方柱的风压非高斯区域分别对称分布在侧面后角部位附近(b、c)和背风面(bc)。当α=9°时,标准方柱在背风面开始出现风压非高斯区域,而侧风面风压非高斯区域却消失;切角方柱下侧风面(cd)后角部位开始出现风压非高斯区域。当α=12.6°时,两类方柱均处于“分离泡流态”,标准方柱背风面(bc)风压非高斯区域开始减小,而下侧风面(cd)开始出现风压非高斯区域;此时切角方柱风压非高斯区域达到最小。当α=45°时,两类方柱风压非高斯区域对称分布在背风面(bc和cd),切角方柱在角部位置c附近风压非高斯区域明显减小。
此外,两类方柱上侧面(ab)和背风面(bc)的平均风压分别呈现先增大后减小和先减小后增大的趋势。切角方柱和标准方柱分别在α=9°和α=12.6°时上侧风面达到极大值,而背风面尾流区达到极小值。总体来说,在三种流态下,切角方柱表面平均风压小于标准方柱,这是由于切角方柱剪切层更加靠近方柱壁面。
2.4 极值风压的流场机理已有研究表明建筑物表面的风压时程会间歇性出现大幅脉冲(极值风压),而这种脉冲信号将会在风压概率统计上表现出非高斯特性[22],为进一步阐明标准方柱极值风压的流场机理及角部措施的影响,本文选取出现极值风压的瞬时流场作进一步分析。结果表明:两类方柱出现极值风压的机理均有两种,即方柱后角的角部附着涡机理和背风面的尾流卡门涡机理。
2.4.1 角部极值风压的作用机理图 8、9给出了典型风向角(α=0°和α=45°)标准方柱后角部的结果对比。其中,极值风压时刻及测点位置均用黑点注明。由图 8(a)、8(b)可见,在α=0°(前角分离流态)时,标准方柱A1测点的概率密度函数出现明显的“拖尾”现象,表明该测点风压时程出现较强的非高斯特性。由图 8(c)、8(d)可见,在下侧剪切层作用下,产生明显的角部附着涡,附着涡内部负压达到极值,其大小为-4.7,这种间歇性的角部附着涡会增大风压非高斯特性。同理,从图 9可见,当α=45°(附着流流态)时,在上侧卡门涡与下侧的剪切层共同作用下,在A3测点附近产生明显的角部附着涡,极值负压增至-5.9,从而导致风压非高斯区域增大。

|
图 8 标准方柱后角部位极值风压流场机理(α=0°):(a) 风压时程图; (b) 风压概率密度分布; (c) t=3 027.2 s时刻瞬态流线图; (d) t=3 027.2 s时刻局部瞬态流线和风压图 Fig. 8 Flow mechanism of extreme wind pressure at the rear corner of sharp corner square cylinder (α=0°): (a) Pressure time history of typical tap; (b) Probability density distribution; (c) Instantaneous streamlines at t=3 027.2 s; (d) Local instantaneous streamlines and wind pressure at t=3 027.2 s |

|
图 9 标准方柱后角部位极值风压流场机理(α=45°):(a) 风压时程图; (b) 风压概率密度分布; (c) t=3 497.1 s时刻瞬态流线图; (d) t=3 497.1 s时刻局部瞬态流线和风压图 Fig. 9 Flow mechanism of extreme wind pressure at the rear corner of sharp corner square cylinder (α=45°): (a) Pressure time history of typical tap; (b) Probability density distribution; (c) Instantaneous streamlines at t=3 497.1 s; (d) Local instantaneous streamlines and wind pressure at t=3 497.1 s |
典型风向角(α=0°和α=45°)切角方柱后角部的结果对比见图 10、11。与标准方柱相比,切角方柱角部测点B1(α=0°)和B2(α=45°)风压时程更为平整,其极值负压分别为-2.5和-4,概率密度函数的“拖尾”现象明显减轻甚至消失,风压非高斯特性减弱。这是由于切角方柱剪切层更加贴近壁面(见图 5),从而减弱了尾流卡门涡的强度,导致角部附着涡消失,极值负压下降,风压非高斯特性减弱。

|
图 10 切角方柱后角部位极值风压流场机理(α=0°):(a) 风压时程图; (b) 风压概率密度分布; (c) t=2 589.8 s时刻瞬态流线图; (d) t=2 589.8 s时刻局部瞬态流线和风压图 Fig. 10 Flow mechanism of extreme wind pressure at the rear corner of chamfered corner square cylinders (α=0°): (a) Pressure time history of typical tap; (b) Probability density distribution; (c) Instantaneous streamlines at t=2 589.8 s; (d) Local instantaneous streamlines and wind pressure at t=2 589.8 s |

|
图 11 切角方柱后角部位极值风压流场机理(α=45°):(a) 风压时程图; (b) 风压概率密度分布; (c) t=2 163.1 s时刻瞬态流线图; (d) t=2 163.1 s时刻局部瞬态流线和风压图 Fig. 11 Flow mechanism of extreme wind pressure at the rear corner of chamfered corner square cylinder (α=45°): (a) Pressure time history of typical tap; (b) Probability density distribution; (c) Instantaneous streamlines at t=2 163.1 s; (d) Local instantaneous streamlines and wind pressure at t=2 163.1 s |
图 12、13为α=0°和α=12.6°时标准方柱背风面的结果对比。背风面的极值负压与卡门涡的涡脱密切相关,且极值负压的位置随着卡门涡的移动而变化。在α=0°(前角分离流态)时,标准方柱A3测点在风压时程上极值负压频繁出现,概率密度函数“拖尾现象”消失,风压的峰度和偏度的绝对值分别为2.98和0.05,呈风压高斯状态。在α=12.6°(分离泡流态)时,标准方柱概率密度函数出现“拖尾现象”,其下侧风面部分气流与尾流卡门涡融合,背风面回流作用强烈,A4测点极值负压达到-2.5,背风面出现风压非高斯区域。

|
图 12 标准方柱背风面极值风压流场机理(α=0°):(a) 风压时程图; (b) 风压概率密度分布; (c) t=3 071 s时刻瞬态流线图; (d) t=3 071 s时刻局部瞬态流线和风压图 Fig. 12 Flow mechanism of extreme wind pressure at the leeward surface of sharp corner square cylinder (α=0°): (a) Pressure time history of typical tap; (b) Probability density distribution; (c) Instantaneous streamlines at t=3 071 s; (d) Local instantaneous streamlines and wind pressure at t=3 071 s |

|
图 13 标准方柱背风面极值风压流场机理(α=12.6°):(a) 风压时程图; (b) 风压概率密度分布; (c) t=3 283.3 s时刻瞬态流线图; (d) t=3 283.3 s时刻局部瞬态流线和风压图 Fig. 13 Flow mechanism of extreme wind pressure at the leeward surface of sharp corner square cylinder (α=12.6°): (a) Pressure time history of typical tap; (b) Probability density distribution; (c) Instantaneous streamlines at t=3 283.3 s; (d) Local instantaneous streamlines and wind pressure at t=3 283.3 s |
图 14、15为α=0°和α=12.6°时切角方柱背风面的结果对比。当α=0°(前角分离流态)时,切角方柱B3测点的风压时程出现明显的脉冲,此时的概率密度函数“拖尾”现象明显,表明风压非高斯特性显著。虽然其卡门涡内部极值负压接近标准方柱(-2.5),但是切角方柱剪切层卷起的涡沿切角斜面提前进入尾流区,尾流卡门涡更加靠近背风面,使得卡门涡回流作用更加强烈,造成背风面风压非高斯特性突出。当α=12.6°(分离泡流态)时,受风向角和切角措施的影响,剪切层更加靠近壁面,卡门涡脱强度减弱,背风面B4测点极值负压降至-2,使得风压非高斯特性减弱。

|
图 14 切角方柱背风面极值风压流场机理(α=0°):(a) 风压时程图; (b) 风压概率密度分布; (c) t=2 587.6 s时刻瞬态流线图; (d) t=2 587.6 s时刻局部瞬态流线和风压图 Fig. 14 Flow mechanism of extreme wind pressure at the leeward surface of chamfered corner square cylinder(α=0°): (a) Pressure time history of typical tap; (b) Probability density distribution; (c) Instantaneous streamlines at t=2 587.6 s; (d) Local instantaneous streamlines and wind pressure at t=2 587.6 s |

|
图 15 切角方柱背风面极值风压流场机理(α=12.6°):(a) 风压时程图; (b) 风压概率密度分布; (c) t=1 576.5 s时刻瞬态流线图; (d) t=1 576.5 s时刻局部瞬态流线和风压图 Fig. 15 Flow mechanism of extreme wind pressure at the leeward surface of chamfered corner square cylinder(α=12.6°): (a) Pressure time history of typical tap; (b) Probability density distribution; (c) Instantaneous streamlines at t=1 576.5 s; (d) Local instantaneous streamlines and wind pressure at t=1 576.5 s |
在雷诺数Re=2.2×104下,采用大涡模拟方法,在均匀来流下研究了标准方柱和切角方柱的风压非高斯区域的变化规律,从流场的角度分析了引起方柱极值风压和风压非高斯特性的原因及角部措施对减小其大小的作用机理,主要结论如下:
1) 相比标准方柱,切角方柱在更小的风向角下出现“分离泡流态”,柱体的风压特性受流态变化影响较大。总体来说,在三种流态下,切角措施使剪切层更加靠近方柱壁面,均不同程度地减小方柱表面平均风压。随着流态的变化,风压的非高斯区域变化显著。
2) 方柱表面风压非高斯分布区域主要集中在方柱侧面后角部位和方柱背风面,而方柱侧面的剪切层再附区域(即分离泡区域)没有明显的风压非高斯现象;总体上看,除了来流垂直于方柱表面时(即α=0°),切角措施会明显减小方柱侧面后角部位和背风面的风压非高斯区域。
3) 在不同风向角下,方柱表面出现极值风压的流场机理可分为两类,方柱侧面后角部位的角部附着涡机理和方柱背风面的卡门涡机理,即间歇性的角部附着涡和强烈的卡门涡回旋均能引起极值风压,从而导致风压非高斯特性增强。
4) 相比标准方柱,切角措施使方柱的分离剪切层更贴近于方柱壁面、方柱尾流的卡门涡强度减弱、方柱角部附着涡的强度减弱甚至消失,从而导致极值风压和风压非高斯特性的减弱。
| [1] |
HUANG M F, LOU Wenjuan, CHAN C M, et al. Peak distributions and peak factors of wind-induced pressure processes on tall buildings[J]. Journal of Engineering Mechanics, 2013, 139(12): 1750. DOI:10.1061/(asce)em.1943-7889.0000616 |
| [2] |
KUMAR K S, STATHOPOULOS T. Wind loads on low building roofs: a stochastic perspective[J]. Journal of Structural Engineering, 2000, 126(8): 947. DOI:10.1061/(asce)0733-9445(2000)126:8(944) |
| [3] |
柯世堂, 葛耀君, 赵林. 大型双曲冷却塔表面脉动风压随机特性——非高斯特性研究[J]. 实验流体力学, 2010, 24(3): 13. KE Shitang, GE Yaojun, ZHAO Lin. Feature of fluctuating wind pressure on large hyperbolic cooling tower: discuss on extreme wind pressure[J]. Journal of Experiments in Fluid Mechanics, 2010, 24(3): 13. DOI:10.3969/j.issn.1672-9897.2010.03.003 |
| [4] |
DAVENPORT A G. Note on the distribution of the largest value of a random function with application to gust loading[J]. Proceedings of the Institution of Civil Engineers, 1964, 28(2): 190. DOI:10.1680/iicep.1964.10112 |
| [5] |
顾明, 张正维, 全涌. 降低超高层建筑横风向响应的气动措施研究进展[J]. 同济大学学报(自然科学版), 2012, 41(3): 318. GU Ming, ZHANG Zhengwei, QUAN Yong. Aerodynamic measures for mitigations of across-wind responses of super tall buildings: state of art[J]. Journal of Tongji University(Natural Science), 2012, 41(3): 318. DOI:10.3969/j.issn.0253-374x.2013.03.001 |
| [6] |
GIOFFRE M, GUSELLA V, GRIGORIU M. Non-Gaussian wind pressure on prismatic buildings. I: Stochastic field[J]. Journal of Structural Engineering, 2001, 127(9): 984. DOI:10.1061/(asce)0733-9445(2001)127:9(981) |
| [7] |
庄翔, 董欣, 郑毅敏, 等. 矩形高层建筑非高斯风压时程峰值因子计算方法[J]. 工程力学, 2017, 34(7): 185. ZHUANG Xiang, DONG Xin, ZHENG Yimin, et al. Peak factor estimation methods of non-Gaussian wind pressures on a rectangular high-rise building[J]. Engineering Mechanic, 2017, 34(7): 185. DOI:10.6052/j.issn.1000-4750.2016.02.0134 |
| [8] |
韩宁, 顾明. 方形高层建筑风压脉动非高斯特性分析[J]. 同济大学学报(自然科学版), 2012, 40(7): 971. HAN Ning, GU Ming. Analysis on non-Gaussian feature of fluctuating wind pressure on square tall buildings[J]. Journal of Tongji University (Natural Science), 2012, 40(7): 971. DOI:10.3696/j.issn.0253-374x.2012.07.002 |
| [9] |
KAWAI H. Effect of corner modifications on aeroelastic instabilities of tall buildings[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1998, 74: 728. DOI:10.1016/s0167-6105(98)00065-8 |
| [10] |
WANG Xingrong, GU Ming. Experimental study on Re number effects on aerodynamic characteristics of 2D square prisms with corner modifications[J]. Wind and Structures, 2016, 22(5): 581. DOI:10.12989/was.2016.22.5.573 |
| [11] |
楼文娟, 李进晓, 沈国辉, 等. 超高层建筑脉动风压的非高斯特性[J]. 浙江大学学报(工学版), 2011, 45(4): 671. LOU Wenjuan, LI Jinxiao, SHEN Guohui, et al. Non-Gaussian feature of wind-induced pressure on super-tall building[J]. Journal of Zhejiang University (Engineering Science), 2011, 45(4): 671. DOI:10.3785/j.issn.1008-973X.2011.04.014 |
| [12] |
杜晓庆, 田新新, 马文勇, 等. 圆角化对方柱气动性能影响的流场机理[J]. 力学学报, 2018, 50(5): 1013. DU Xiaoqing, TIAN Xinxin, MA Wenyong, et al. Effects of rounded corner on aerodynamics of square cylinders and its flow mechanisms[J]. Chinese Journal of Theoretical and Applied Mechanics, 2018, 50(5): 1013. DOI:10.6052/0459-1879-18-123 |
| [13] |
LYN D A, EINAV S, RODI W, et al. A laser-Doppler velocimetry study of ensemble-averaged characteristics of the turbulent near wake of a square cylinder[J]. Journal of Fluid Mechanics, 1995, 304: 312. DOI:10.1017/s0022112095004435 |
| [14] |
BEARMAN P W, OBASAJU E D. An experimental study of pressure fluctuations on fixed and oscillating square-section cylinders[J]. Journal of Fluid Mechanics, 1982, 119: 301. DOI:10.1017/s0022112082001360 |
| [15] |
LEE B E. The effect of turbulence on the surface pressure field of a square prism[J]. Journal of Fluid Mechanics, 1975, 69(2): 266. DOI:10.1017/s0022112075001437 |
| [16] |
LUO S C, YAZDANI M G, CHEW Y T, et al. Effects of incidence and afterbody shape on flow past bluff cylinders[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1994, 53(3): 380. DOI:10.1016/0167-6105(94)90092-2 |
| [17] |
SOHANKAR A, DAVIDSON L, NORBERG C. Large eddy simulation of flow past a square cylinder: comparison of different subgrid scale models[J]. Journal of Fluids Engineering, 2000, 122(1): 41. DOI:10.1115/1.483224 |
| [18] |
RODI W. Comparison of LES and RANS calculations of the flow around bluff bodies[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1997, 69: 61. DOI:10.1016/s0167-6105(97)00147-5 |
| [19] |
CAO Yong, TAMURA T. Large-eddy simulations of flow past a square cylinder using structured and unstructured grids[J]. Computers & Fluids, 2016, 137: 41. DOI:10.1016/j.compfluid.2016.07.013 |
| [20] |
西村宏昭, 谷池義人. 二次元正方形角柱の変動風圧特性[J]. 日本建築学会構造系論文集, 2000, 65(533): 38. NISHIMURA H, TANIIKE Y. Fluctuating pressures on a two- dimensional square prism[J]. Journal of Structural and Construction Engineering, 2000, 65(533): 38. DOI:10.3130/aijs.65.37_3 |
| [21] |
TAMURA T, ONO Y. LES analysis on aeroelastic instability of prisms in turbulent flow[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2003, 91(12/13/14/15): 1838. DOI:10.1016/j.jweia.2003.09.032 |
| [22] |
KO N H, YOU K P, KIM Y M. The effect of non-Gaussian local wind pressures on a side face of a square building[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2005, 93(5): 393. DOI:10.1016/j.jweia.2005.03.001 |
 2021, Vol. 53
2021, Vol. 53


