Potential constitutive equation of unsaturated double-porosity media and its application
随着对岩土孔隙尺度分布特征的深入了解,发现许多岩土材料具有明显的双重孔隙结构特征[1-2]。岩土工程界把较小尺寸的孔隙仍称为孔隙,把较大尺寸的孔隙称为裂隙,把具有双重孔隙结构的岩土材料统称为双重孔隙介质。混合物理论是非饱和双重孔隙介质常用的建模方法之一[3-8]。Borja等[3]推导了非饱和双重孔隙介质的能量守恒方程,并根据功共轭量的力学性质提出采用Skempton型有效应力、孔隙内修正吸力和孔隙间平均修正吸力作为应力状态变量来构建非饱和双重孔隙介质的本构模型。Zhang等[4]基于Borja等[3]的建议,创建了非饱和双重孔隙土的横观各向同性线弹性方程。Li等[5-6]假定固相和吸附水之间存在质量交换,通过变形功公式中的功共轭对来选择应力和应变变量,建立非饱和双重孔隙膨胀土的弹塑性模型,较好地揭示了Alonso等[1]试验呈现出的变形和持水特性。Sanchez等[7]把土应变拆分成两个独立的固相应变之和,通过组合这两个固相应变的本构模型来建立非饱和双重孔隙土的弹塑性模型。Guo等[8]把Borja等[3]建立的能量守恒方程转化为采用两个固相应变和两个有效应力相共轭表示的形式,建立了非饱和双重孔隙土的双有效应力弹塑性模型。上述研究有力地推动了非饱和双重孔隙介质力学理论和本构模型的发展。
在非饱和多孔介质中,固液气相的赋存空间均与孔隙状态密切相关。孔隙变形同时影响固液气三相的应变量,协调、传递和制约流固之间的耦合作用,在多相耦合机制中处于举足轻重的关键纽带地位[9]。然而在以往的混合物理论研究中,却没有把孔隙变形当做一个独立的应变量来对待,从而忽略了孔隙变形与各相应变之间的内在关系,难以揭示多孔介质流固耦合作用的力学本质,限制了多孔介质力学理论的进一步深入发展。胡亚元[9]把孔隙变形作为一个独立的应变量来对待,较好地解决了非饱和单重孔隙介质流固两相本构关系之间的耦合问题。非饱和双重孔隙介质存在两种尺度的孔隙类型,需要两个反映孔隙变形的应变来度量。为了实现这一目的,本文把双重孔隙介质视为两个单重孔隙介质的嵌套叠加。如在双重孔隙土中,内含孔隙的团聚体是一个单重孔隙介质;把内含孔隙的团聚体整体视为基质,把团聚体间裂隙视为单重孔隙,又构成单重裂隙介质。双重孔隙土可视为单重裂隙介质的基质中嵌套单重孔隙介质而成。又例如,孔隙- 裂隙岩体可视为由含有单重孔隙的完整岩块作为基质,以裂隙作为单重裂隙的裂隙岩体。前一个单重孔隙介质(含孔隙的完整岩块)作为基质嵌套在后一个单重孔隙介质(裂隙岩体)之中。根据上述嵌套思路,本文首先把固相变形拆分为固相基质变形和每个孔隙率变化引起的固相骨架应变之和,然后从混合物理论出发推导非饱和双重孔隙介质的能量平衡方程,建立了非饱和双重孔隙介质的一般自由能势函数本构理论框架。
线弹性模型是岩土工程固结和波动理论中必不可少的本构模型,如陈正汉[10]、Fredlund等[11]、周万欢等[12]、胡亚元[13]和Moradi等[14]运用线弹性本构模型建立了非饱和单重孔隙土的波动和固结理论,用于建筑场地的波动和固结特性分析。Berryman等[15]、Khalili等[16]和Yang等[17]利用线弹性本构模型研究了饱和双重孔隙场地的波动和固结特性。本文的另一项研究工作是从自由能势函数本构方程出发,推导了非饱和双重孔隙介质的线弹性本构方程,并运用它建立了膨润土的固结控制方程。根据本文研究成果,能够较方便地建立非饱和双重孔隙介质波动和固结方程。
1 质量、动量和动量矩守恒方程 1.1 双重孔隙介质的组分占比指标 双重孔隙介质由固相基质(在土力学中也称为土颗粒),孔隙(或小孔隙)和裂隙(或大孔隙)组成,在孔隙和裂隙中各含有液体和气体。设固相用S表示,孔隙用P表示,裂隙用F表示,液相用L表示,气相用G表示。PL和PG分别表示孔隙中的液相和气相;而FL和FG分别表示裂隙中的液相和气相。把裂隙视为广义的孔隙,令β为孔隙类别指标,β∈{P, F},当β=P时为孔隙,而β=F时为裂隙;γ为流相类别指标,γ∈{L, G},当γ=L时为液相,而γ=G时为气相。φ表示体积分数,有:
|
$
\varphi_{\mathrm{S}}+\sum\limits_{\beta=\mathrm{P}}^{\mathrm{F}} \varphi_{\beta}=\varphi_{\mathrm{S}}+\sum\limits_{\beta=\mathrm{P}}^{\mathrm{F}} \sum\limits_{\gamma=\mathrm{L}}^{\mathrm{G}} \varphi_{\beta \gamma}=1, \varphi_{\beta}=\sum\limits_{\gamma=\mathrm{L}}^{\mathrm{G}} \varphi_{\beta \gamma}
$
|
(1) |
令SrF=φFL/φF和SrP=φPL/φP分别为裂隙和孔隙中液相饱和度。ρRS和ρRβγ分别是固相和β孔隙中γ相的真实(材料)密度,则固相和β孔隙中γ流相的平均密度分别为ρS=φSρRS和ρβγ=φβγρRβγ,混合物总密度为$\rho=\rho_{\mathrm{S}}+\sum\limits_{\beta=\mathrm{P}}^{\mathrm{F}} \sum\limits_{\gamma=\mathrm{L}}^{\mathrm{G}} \rho_{\beta \gamma}$。
从嵌套视角看,双重孔隙介质可视为先由固相基质与孔隙组成单重孔隙介质,再以单重孔隙介质整体作为基质与裂隙一起组成单重裂隙介质,即双重孔隙介质可视为把固相基质与孔隙组成的单重孔隙介质作为高一级基质嵌套在单重裂隙介质之中。非饱和孔隙介质作为非饱和裂隙介质的基质是低一级层次的单重孔隙介质,而非饱和裂隙介质是高一级层次的单重孔隙介质。用SP表示非饱和孔隙介质,它在双重孔隙介质中的体积分数为φSP=φS+φP。故当把非饱和孔隙介质视为一个单独的混合物时,非饱和孔隙介质中固相的体积分数为φSP=φS/φSP,孔隙的体积分数为φPP=φP/φSP,φSP+φPP=1。孔隙中γ流相的体积分数为φγP=φPγ/φSP。令ρSP为固相在非饱和孔隙介质中的平均密度,有ρSP=φSPρRS。
1.2 质量守恒 根据混合物理论,把混合物各组分按体积分数平均到整个混合物空间后,固相、裂隙和孔隙中液相和气相共同连续地占有非饱和双重介质混合物的空间位置。令α为组成非饱和双重孔隙介质的组分指标,α∈{S, PL, PG, FL, FG},设第α组分的初始位置为Xa,在当前t时刻的空间位置为x,则每一组分的运动方程可表示为x=xα(Xα, t),速度可表示为vα=dxα(Xα, t)/dt,加速度可表示为aα=d2xα(Xα, t)/dt2。对于定义在x和t上的标量场或矢量场Γα,基于α组分的物质导数的定义为
|
$
\left(\mathrm{d}^{\alpha} \varGamma_{\alpha} / \mathrm{d} t\right)=\left(\partial \varGamma_{\alpha} / \partial t\right)+\operatorname{grad} \varGamma_{\alpha} \cdot \boldsymbol{v}_{\alpha}
$
|
(2) |
假定固相、液相和气相之间不存在质量交换,但裂隙液相与孔隙液相以及裂隙气相与孔隙气相间存在质量交换,各组分的质量守恒方程为:
|
$
\left(\mathrm{d}^{\mathrm{S}} \rho_{\mathrm{s}} / \mathrm{d} t\right)+\rho_{\mathrm{s}} \operatorname{div} \boldsymbol{v}_{\mathrm{S}}=0
$
|
(3) |
|
$
\left(\mathrm{~d}^{\beta \gamma} \rho_{\beta \gamma} / \mathrm{d} t\right)+\rho_{\beta \gamma} \operatorname{div} \boldsymbol{v}_{\beta \gamma}=c_{\beta \gamma}
$
|
(4) |
式中β∈{P, F}和γ∈{L, G},下同;cβγ表示β孔隙中γ流相的质量交换率,有
|
$
\sum\limits_{\beta=\mathrm{P}}^{\mathrm{F}} c_{\beta \gamma}=0
$
|
(5) |
把固相作为非饱和双重孔隙介质混合物的参考构形,令β孔隙中γ流相相对固相的扩散速度为Wβγ=vβγ-vS。把它和ρβγ=φβγρRβγ代入式(4)得
|
$
\begin{array}{c}
\frac{\varphi_{\beta \gamma}}{\rho_{\mathrm{R} \beta \gamma}} \frac{\mathrm{d}^{\beta \gamma} \rho_{\mathrm{R} \beta \gamma}}{\mathrm{d} t}+\frac{\mathrm{d}^{\mathrm{S}} \varphi_{\beta \gamma}}{\mathrm{d} t}+\varphi_{\beta \gamma} \operatorname{div} \boldsymbol{v}_{\mathrm{S}}+\varphi_{\beta \gamma} \operatorname{div} \boldsymbol{W}_{\beta \gamma}+ \\
\boldsymbol{W}_{\beta \gamma} \operatorname{grad} \varphi_{\beta \gamma}-\left(c_{\beta \gamma} / \rho_{\mathrm{R} \beta \gamma}\right)=0
\end{array}
$
|
(6) |
根据嵌套思路将双重孔隙介质视为以孔隙介质为基质的裂隙介质。利用ρS=φSρRS=φSPρSP得
|
$
\left(\mathrm{d}^{\mathrm{S}} \rho_{\mathrm{S}} / \mathrm{d} t\right)=\varphi_{\mathrm{SP}}\left(\mathrm{d}^{\mathrm{S}} \rho_{\mathrm{S}}^{\mathrm{P}} / \mathrm{d} t\right)+\rho_{\mathrm{S}}^{\mathrm{P}}\left(\mathrm{d}^{S} \varphi_{\mathrm{SP}} / \mathrm{d} t\right)
$
|
(7) |
把式(7)代入式(3)并利用ρS=φSPρSP得
|
$
\left(\mathrm{d}^{\mathrm{S}} \rho_{\mathrm{S}}^{\mathrm{P}} / \mathrm{d} t\right) / \rho_{\mathrm{S}}^{\mathrm{P}}+\left(\mathrm{d}^{\mathrm{S}} \varphi_{\mathrm{SP}} / \mathrm{d} t\right) / \varphi_{\mathrm{SP}}+\operatorname{div} \boldsymbol{v}_{\mathrm{S}}=0
$
|
(8) |
式(8)等式左侧第一项dSρSP/(ρSPdt)反映的是非饱和孔隙介质中固相平均密度ρSP变化对固相总变形的贡献。设xSP为非饱和孔隙介质中固相的空间位置,vSP为其变形速率,则与式(3)的推导过程相一致,关于非饱和孔隙介质固相的质量守恒方程有
|
$
\left(\mathrm{d}^{\mathrm{S}} \rho_{\mathrm{S}}^{\mathrm{P}} / \mathrm{d} t\right) / \rho_{\mathrm{S}}^{\mathrm{P}}+\operatorname{div} \boldsymbol{v}_{\mathrm{S}}^{\mathrm{P}}=0
$
|
(9) |
把式(8)减去式(9)得
|
$
\left(\mathrm{d}^{\mathrm{S}} \varphi_{\mathrm{SP}} / \mathrm{d} t\right) / \varphi_{\mathrm{SP}}+\operatorname{div} \boldsymbol{v}_{\mathrm{S}}-\operatorname{div} \boldsymbol{v}_{\mathrm{S}}^{\mathrm{P}}=0
$
|
(10) |
1.3 动量和动量矩守恒 令σ为非饱和双重孔隙介质混合物的Cauchy总应力张量,σS为固相组分的Cauchy应力张量,σβγ为β孔隙中γ流相组分的Cauchy应力张量,有
|
$
\boldsymbol{\sigma}=\boldsymbol{\sigma}_{\mathrm{S}}+\sum\limits_{\beta=\mathrm{P}}^{\mathrm{F}} \sum\limits_{\gamma=\mathrm{L}}^{\mathrm{G}} \boldsymbol{\sigma}_{\beta \gamma}
$
|
(11) |
令I为二阶单位张量,注意到在混合物中应力以拉为正而压力以压为正,故非饱和双重孔隙介质混合物上的总压力为PT=-σ∶I/3;固相基质所受的真实压力为PS=-σS∶I/(3φS),β孔隙中γ流相的孔压为PβγI=-σβγ/φβγ,由式(11)得
|
$
P_{\mathrm{T}}=\varphi_{\mathrm{S}} P_{\mathrm{S}}+\sum\limits_{\beta=\mathrm{P}}^{\mathrm{F}} \sum\limits_{\gamma=\mathrm{L}}^{\mathrm{G}} \varphi_{\beta \gamma} P_{\beta \gamma}
$
|
(12) |
图 1给出了非饱和双重孔隙介质中孔隙和裂隙介质的结构层次关系和应力关系。图 1(a)为非饱和双重孔隙介质单元体,图 1(b)显示了非饱和双重孔隙介质总压力与各组分压力关系式(12)的力学内涵。
把作为裂隙介质基质的孔隙介质视为一个单独的混合物来进行分析。非饱和孔隙介质的应力等于组成非饱和孔隙介质的各组分应力之和:
|
$
\boldsymbol{\sigma}_{\mathrm{SP}}=\boldsymbol{\sigma}_{\mathrm{S}}+\sum\limits_{\gamma=\mathrm{L}}^{\mathrm{G}} \boldsymbol{\sigma}_{\mathrm{P} \gamma}
$
|
(13) |
假定混合物体孔隙率等于面孔隙率,则非饱和孔隙介质视为单独混合物时的总应力为σSPP=σSP/φSP,固相和孔隙中流相的应力分别为σSP=σS/φSP和σγP=σPγ/φSP。令PSP=-σSPP: I/3,有
|
$
P_{\mathrm{SP}}=\varphi_{\mathrm{S}}^{\mathrm{P}} P_{\mathrm{S}}+\sum\limits_{\gamma=\mathrm{L}}^{\mathrm{G}} \varphi_{\gamma}^{\mathrm{P}} P_{\mathrm{P} \gamma}
$
|
(14) |
图 1(c)显示了从非饱和双重孔隙介质隔离出来的非饱和孔隙介质单元体,图 1(d)图显示了非饱和孔隙介质总压力和各组分压力关系式(14)的力学内涵。
令$\hat{\boldsymbol{p}}_{\alpha}$和bα分别是第α组分的动量供给量和外体力密度,根据混合物理论,固相、裂隙和孔隙中液气两相的动量守恒方程分别为:
|
$
\rho_{\mathrm{S}} \boldsymbol{a}_{\mathrm{S}}=\operatorname{div} \boldsymbol{\sigma}_{\mathrm{S}}+\rho_{\mathrm{S}} \boldsymbol{b}_{\mathrm{S}}+\hat{\boldsymbol{p}}_{\mathrm{S}}
$
|
(15) |
|
$
\rho_{\beta \gamma} \boldsymbol{a}_{\beta \gamma}=\operatorname{div} \boldsymbol{\sigma}_{\beta \gamma}+\rho_{\beta \gamma} \boldsymbol{b}_{\beta \gamma}+\hat{\boldsymbol{p}}_{\beta \gamma}
$
|
(16) |
假定第α组分的动量矩供应量为0,则由动量矩平衡方程可得σα应力张量是对称张量。
2 能量平衡方程 令qα、rα和$\hat{\varepsilon}_{\alpha}$分别为第α组分的热流向量、外热供给量和能量供给量,ξα为第α组分的内能密度,则固相、裂隙和孔隙中液气两相的能量平衡方程为:
|
$
\rho_{\mathrm{S}}\left(\mathrm{d}^{\mathrm{S}} \xi_{\mathrm{S}} / \mathrm{d} t\right)=\boldsymbol{\sigma}_{\mathrm{S}}: \boldsymbol{D}_{\mathrm{S}}-\operatorname{div} \boldsymbol{q}_{\mathrm{S}}+\rho_{\mathrm{S}} r_{\mathrm{S}}+\hat{\varepsilon}_{\mathrm{S}}
$
|
(17) |
|
$
\rho_{\beta \gamma}\left(\mathrm{d}^{\beta \gamma} \xi_{\beta \gamma} / \mathrm{d} t\right)=\boldsymbol{\sigma}_{\beta \gamma}: \boldsymbol{D}_{\beta \gamma}-\operatorname{div} \boldsymbol{q}_{\beta \gamma}+\rho_{\beta \gamma} r_{\beta \gamma}+\hat{\varepsilon}_{\beta \gamma}
$
|
(18) |
式中DS=[grad vS+(grad vS)T]/2表示固相变形率,Dβγ=[grad vβγ+(grad vβγ)T]/2分别表示裂隙和孔隙中液气两相变形率。令DSP=[grad vSP+(grad vSP)T]/2为孔隙介质固相的变形速率,PF=SrFPFL+(1-SrF)PFG和PP=SrPPPL+(1-SrP)PPG分别为裂隙和孔隙中流相的平均孔压,sF=PFG-PFL和sP=PPG-PPL为裂隙和孔隙中的吸力,$\tilde{\boldsymbol{\sigma}}_{\mathrm{C}}=\sigma+\bar{P}_{\mathrm{F}} \boldsymbol{I}$和$\tilde{\boldsymbol{\sigma}}_{\mathrm{H}}=\boldsymbol{\sigma}_{\mathrm{SP}}^{\mathrm{P}}+\bar{P}_{\mathrm{P}} \boldsymbol{I}$为裂隙和孔隙中的有效应力。由式(1)、式(6)~(7)、式(9)~(11)及各相孔隙率之间的关系可得
|
$
\begin{array}{l}
\sum\limits_{\alpha=\mathrm{S}}^{\mathrm{FG}} \rho_{\alpha} \frac{\mathrm{d}^{\alpha} \xi_{\alpha}}{\mathrm{d} t}=\widetilde{\boldsymbol{\sigma}}_{\mathrm{C}}: \boldsymbol{D}_{\mathrm{C}}-\varphi_{\mathrm{F}} s_{\mathrm{F}} \frac{\mathrm{d}^{\mathrm{S}} S_{\mathrm{rF}}}{\mathrm{d} t}+ \\
\ \ \ \ \ \ \ \ \varphi_{\mathrm{SP}}\left(\widetilde{\boldsymbol{\sigma}}_{\mathrm{H}}: \boldsymbol{D}_{\mathrm{H}}-\varphi_{\mathrm{P}}^{\mathrm{P}} s_{\mathrm{P}} \frac{\mathrm{d}^{\mathrm{S}} S_{\mathrm{rP}}}{\mathrm{d} t}\right)+\sum\limits_{\alpha=\mathrm{S}}^{\mathrm{FG}} P_{\alpha} \varphi_{\alpha} \frac{\mathrm{d}^{\alpha} \boldsymbol{\vartheta}_{\alpha}}{\mathrm{d} t}+ \\
\ \ \ \ \ \ \ \ \sum\limits_{\beta=\mathrm{P}}^{\mathrm{F}} \sum\limits_{\gamma=\mathrm{L}}^{\mathrm{G}} P_{\beta \gamma} \boldsymbol{W}_{\beta \gamma} \cdot \operatorname{grad} \varphi_{\beta \gamma}-\sum\limits_{\beta=\mathrm{P}}^{\mathrm{F}} \sum\limits_{\gamma=\mathrm{L}}^{\mathrm{G}} P_{\beta \gamma} \frac{c_{\beta \gamma}}{\rho_{\mathrm{R} \beta \gamma}}+ \\
\ \ \ \ \ \ \ \ \sum\limits_{\alpha=\mathrm{S}}^{\mathrm{FG}}\left(-\operatorname{div} \boldsymbol{q}_{\alpha}+\rho_{\alpha} r_{\alpha}+\hat{\varepsilon}_{\alpha}\right)
\end{array}
$
|
(19) |
式中$\vartheta_{\alpha}=\ln \left(\rho_{{\mathrm{R} \alpha}} / \rho_{{\mathrm{R} \alpha 0}}\right)$为第α相基质体应变,ρRα0和ρRα为第α相的初始和现时真实密度。DH=DSP+(dSρRS/dt)I/(3ρRS)和DC=DS-DSP,有:
|
$
\boldsymbol{D}_{\mathrm{C}}: \boldsymbol{I}=\boldsymbol{D}_{\mathrm{S}}: \boldsymbol{I}-\boldsymbol{D}_{\mathrm{R}}^{\mathrm{P}}: \boldsymbol{I}=-\left(\mathrm{d}^{\mathrm{S}} \varphi^{\mathrm{SP}} / \mathrm{d} t\right) / \varphi^{\mathrm{SP}}
$
|
(20) |
|
$
\boldsymbol{D}_{\mathrm{H}}: \boldsymbol{I}=-\left(\mathrm{d}^{\mathrm{S}} \varphi_{\mathrm{S}}^{\mathrm{P}} / \mathrm{d} t\right) / \varphi_{\mathrm{S}}^{\mathrm{P}}
$
|
(21) |
式(20)~(21)表明,DC与孔隙介质在裂隙介质中的体积分数有关,孔隙介质是裂隙介质的基质,在裂隙介质中起到骨架作用,故DC称为裂隙骨架变形率。同理DH称为孔隙骨架变形率。知道DC和DH的力学内涵后,式(19)所表示的能量守恒方程的物理内涵就变得十分明显。式(19)等式右边的前两项表示的是与裂隙骨架及吸力相关的变形能,第三四项(即第一个括号内的那两项)表示的与孔隙骨架及吸力相关的变形能,第五项为各组分基质引起的变形能,第六七项是非饱和双重孔隙介质各组分内部相互作用引起的能量耗散,最后三项为热传递和热交换引起的能量变化。
从式(19)推导过程可知,固相变形率DS被分解成三部分:DC、DH和固相基质体应变率$\mathrm{d}^{\mathrm{S}} \vartheta_{\mathrm{s}} / \mathrm{d} t$。在单重裂隙介质中,裂隙介质基质的体积分数和裂隙体积分数之和等于1,故DC也与裂隙介质中裂隙体积分数的变化相关。同理DH也与孔隙介质的孔隙体积分数变化相关。这种变形分解方式有利于突出孔隙变形在多孔介质力学多场耦合机制中的纽带作用。固相应变的上述嵌套分解结果也可以采用连续介质力学变形梯度的极分解理论来解释。如图 2所示,把双重孔隙介质视为以孔隙介质为基质的裂隙介质,故固相变形梯度可分解为孔隙介质变形梯度和裂隙骨架变形梯度的乘积;再把孔隙介质视为由固相基质与孔隙组成,故孔隙介质变形梯度可分解为固相基质变形梯度与孔隙骨架变形梯度的乘积。
令JS=ρS0/ρS, FSP=∂xSP/∂XS, JSP=detFSP, FS=∂xS/∂xS,FH=(JS)-1/3FSP,EH=(FHTFH-I)/2,ESP=[(FSP)TFSP-I]/2, ES = (FSTFS-I)/2, dSEH/dt=FHT·[DSP+(d2ϑS/dt)I/3]·FH,$\tilde{\boldsymbol{T}}_{\mathrm{C}}=\boldsymbol{F}_{\mathrm{S}}^{-1} \cdot \tilde{\boldsymbol{\sigma}}_{\mathrm{C}} \cdot\boldsymbol{F}_{\mathrm{S}}^{-\mathrm{T}}$, $\tilde{\boldsymbol{T}}_{\mathrm{H}}=\boldsymbol{F}_{\mathrm{H}}^{-1} \cdot \widetilde{\boldsymbol{\sigma}}_{\mathrm{H}} \cdot \boldsymbol{F}_{\mathrm{H}}^{-\mathrm{T}}$, FC=(FSP)-1FS, JS=detFS, dSUC/dt=dSES/dt-FCT·(dSESP/dt)·FC式中:JS为固相基质的体积比,FSP为孔隙介质的变形梯度,JSP为FSP的行列式值,ESP为孔隙介质的Green应变张量,FH为孔隙骨架的变形梯度,EH为孔隙骨架的Green应变张量,$\widetilde{\boldsymbol{T}}_{\mathrm{H}}$为孔隙介质的Piola-Kirchhoff有效应力。FS为固相的变形梯度,JS为FS的行列式值,ES为固相Green应变张量,FC为裂隙骨架变形梯度,UC为裂隙骨架应变,$\tilde{\boldsymbol{T}}_{\mathrm{S}}$为裂隙介质的Piola-Kirchhoff有效应力,把它们代入到式(19)得
|
$
\begin{array}{l}
\sum\limits_{\alpha=\mathrm{S}}^{\mathrm{FG}} \rho_{\alpha} \frac{\mathrm{d}^{\alpha} \xi_{\alpha}}{\mathrm{d} t}=\tilde{\boldsymbol{T}}_{\mathrm{C}}: \frac{\mathrm{d}^{\mathrm{S}} \boldsymbol{U}_{\mathrm{C}}}{\mathrm{d} t}-\varphi_{\mathrm{F}} s_{\mathrm{F}} \frac{\mathrm{d}^{\mathrm{S}} S_{\mathrm{rF}}}{\mathrm{d} t}+ \\
\ \ \ \ \ \ \ \ \varphi_{\mathrm{SP}}\left(\tilde{\boldsymbol{T}}_{\mathrm{H}}: \frac{\mathrm{d}^{\mathrm{S}} \boldsymbol{E}_{\mathrm{H}}}{\mathrm{d} t}-\varphi_{\mathrm{P}}^{\mathrm{P}} s_{\mathrm{P}} \frac{\mathrm{d}^{\mathrm{S}} S_{\mathrm{rP}}}{\mathrm{d} t}\right)+\sum\limits_{\alpha=\mathrm{S}}^{\mathrm{FG}} P_{\alpha} \varphi_{\alpha} \frac{\mathrm{d}^{\alpha} \vartheta_{\alpha}}{\mathrm{d} t}+ \\
\ \ \ \ \ \ \ \ \sum\limits_{\beta=\mathrm{P}}^{\mathrm{F}} \sum\limits_{\gamma=\mathrm{L}}^{\mathrm{G}} P_{\beta \gamma} \boldsymbol{W}_{\beta \gamma} \cdot \operatorname{grad} \varphi_{\beta \gamma}-\sum\limits_{\beta=\mathrm{P}}^{\mathrm{F}} \sum\limits_{\gamma=\mathrm{L}}^{\mathrm{G}} P_{\beta \gamma} \frac{c_{\beta \gamma}}{\rho_{\mathrm{R} \beta \gamma}}+ \\
\ \ \ \ \ \ \ \ \sum\limits_{\alpha=\mathrm{S}}^{\mathrm{FG}}\left(-\operatorname{div} \boldsymbol{q}_{\alpha}+\rho_{\alpha} r_{\alpha}+\hat{\varepsilon}_{\alpha}\right)
\end{array}
$
|
(22) |
当忽略孔隙只考虑裂隙,非饱和双重孔隙介质变为非饱和单重多孔介质时,PPL、PPG、sP、cFL、cPL、cFG、cPG和DH为0。根据DH=0可知DSP=-I(dSρRS/dt)/(3ρRS)。把这些公式代入到式(19)后可退化到文献[9]中的非饱和单重孔隙介质能量方程。
3 小应变线弹性本构方程 在小应变条件下,令εS为固相应变张量ES的近似值,εC为裂隙骨架应变张量UC的近似值,εH为孔隙骨架应变张量EH的近似值,有:
|
$
\boldsymbol{\varepsilon}_{\mathrm{S}}=\boldsymbol{\varepsilon}_{\mathrm{C}}+\boldsymbol{\varepsilon}_{\mathrm{H}}-\left({\vartheta}_{\mathrm{S}} / 3\right) \boldsymbol{I}
$
|
(23) |
|
$
\boldsymbol{\varepsilon}_{\mathrm{C}}=\left[\left(\partial \boldsymbol{u}_{\mathrm{C}} / \partial \boldsymbol{X}_{\mathrm{S}}\right)+\left(\partial \boldsymbol{u}_{\mathrm{C}} / \partial \boldsymbol{X}_{\mathrm{S}}\right)^{\mathrm{T}}\right] / 2
$
|
(24) |
|
$
\boldsymbol{\varepsilon}_{\mathrm{H}}=\left[\left(\partial \boldsymbol{u}_{\mathrm{H}} / \partial \boldsymbol{X}_{\mathrm{S}}\right)+\left(\partial \boldsymbol{u}_{\mathrm{H}} / \partial \boldsymbol{X}_{\mathrm{S}}\right)^{\mathrm{T}}\right] / 2
$
|
(25) |
|
$
{\vartheta}_{\mathrm{S}}=\ln \left(\rho_{\mathrm{RS}} / \rho_{\mathrm{RS} 0}\right) \approx\left(\rho_{\mathrm{RS}}-\rho_{\mathrm{RS} 0}\right) / \rho_{\mathrm{RS} 0}
$
|
(26) |
式中uC=xS-xSP,uH=xSP-xM,xSP是孔隙介质变形后的位置,xM是固相基质发生体积应变ϑS后的位置。令εVS为固相体应变,εVC为裂隙骨架体应变,εVH为孔隙骨架体应变,对式(23)取迹可得
|
$
\varepsilon_{\mathrm{VS}}=\varepsilon_{\mathrm{VC}}+\varepsilon_{\mathrm{VH}}-\vartheta_{\mathrm{S}}
$
|
(27) |
注意到dεVC/dt=DC∶I,dεVH/dt=DH∶I。根据式(20)~(21)并在小应变条件下略去高次项得:
|
$
\varepsilon_{\mathrm{VC}}=-\ln \left(\varphi_{\mathrm{SP}} / \varphi_{\mathrm{SP} 0}\right) \approx\left(\varphi_{\mathrm{SP} 0}-\varphi_{\mathrm{SP}}\right) / \varphi_{\mathrm{SP} 0}
$
|
(28) |
|
$
\varepsilon_{\mathrm{VH}}=-\ln \left(\varphi_{\mathrm{S}}^{\mathrm{P}} / \varphi_{\mathrm{S} 0}^{\mathrm{P}}\right) \approx\left(\varphi_{\mathrm{S} 0}^{\mathrm{P}}-\varphi_{\mathrm{S}}^{\mathrm{P}}\right) / \varphi_{\mathrm{S} 0}^{\mathrm{P}}
$
|
(29) |
式中φSP0为孔隙介质在裂隙介质中的初始体积分数,φS0P为固相在孔隙介质中的初始体积分数。小应变条件下β孔隙中γ流相的基质体应变ϑβγ为
|
$
\vartheta_{\beta \gamma}=\ln \left(\rho_{\mathrm{R} \beta \gamma} / \rho_{\mathrm{R} \beta \gamma 0}\right) \approx\left(\rho_{\mathrm{R} \beta \gamma}-\rho_{\mathrm{R} \beta \gamma 0}\right) / \rho_{\mathrm{R} \beta \gamma 0}
$
|
(30) |
令εVβγ为小应变情况下β孔隙中γ流相的体应变。注意到$\dot{\varepsilon}_{\mathrm{V} \beta \gamma}=\operatorname{div} \boldsymbol{v}_{\beta \gamma}$,对式(4)等式两边先除以ρβγ后对时间求积分,再利用ρFL=φFSrFρRFL、ρFG=φF(1-SrF)ρRFG、ρPL=φSPφPPSrPρRPL和ρPG=φSPφPP(1-SrP)ρRPG,可得εVβγ的计算表达式为:
|
$
\begin{aligned}
\varepsilon_{\mathrm{VFL}} &=-\ln \left(\rho_{\mathrm{FL}} / \rho_{\mathrm{FL} 0}\right)+\int_{0}^{t}\left(c_{\mathrm{FL}} / \rho_{\mathrm{FL}}\right) \mathrm{d} t \approx \\
&-\frac{\varphi_{\mathrm{SP} 0}}{\varphi_{\mathrm{F} 0}} \varepsilon_{\mathrm{VC}}+\frac{S_{\mathrm{rF} 0}-S_{\mathrm{rF}}}{S_{\mathrm{rF} 0}}-\vartheta_{\mathrm{FL}}+\int_{0}^{t} \frac{c_{\mathrm{FL}}}{\rho_{\mathrm{FL} 0}} \mathrm{~d} t
\end{aligned}
$
|
(31) |
|
$
\varepsilon_{\mathrm{VFG}} \approx-\frac{\varphi_{\mathrm{SPO}}}{\varphi_{\mathrm{F} 0}} \varepsilon_{\mathrm{VC}}-\frac{S_{\mathrm{rF} 0}-S_{\mathrm{rF}}}{1-S_{\mathrm{rF} 0}}-\vartheta_{\mathrm{FG}}+\int_{0}^{t} \frac{c_{\mathrm{FG}}}{\rho_{\mathrm{FG} 0}} \mathrm{~d} t
$
|
(32) |
|
$
\varepsilon_{\mathrm{VPL}} \approx \varepsilon_{\mathrm{VC}}-\frac{\varphi_{\mathrm{S} 0}}{\varphi_{\mathrm{P} 0}} \varepsilon_{\mathrm{VH}}+\frac{S_{\mathrm{rP0}}-S_{\mathrm{rP}}}{S_{\mathrm{rP} 0}}-\vartheta_{\mathrm{PL}}+\int_{0}^{t} \frac{c_{\mathrm{PL}}}{\rho_{\mathrm{PL} 0}} \mathrm{~d} t
$
|
(33) |
|
$
\varepsilon_{\mathrm{VPG}} \approx \varepsilon_{\mathrm{VC}}-\frac{\varphi_{\mathrm{S} 0}}{\varphi_{\mathrm{P} 0}} \varepsilon_{\mathrm{VH}}-\frac{S_{\mathrm{rP} 0}-S_{\mathrm{rP}}}{1-S_{\mathrm{rP} 0}}-\vartheta_{\mathrm{PG}}+\int_{0}^{t} \frac{c_{\mathrm{PG}}}{\rho_{\mathrm{PG} 0}} \mathrm{~d} t
$
|
(34) |
式中ρβγ0和φβ0分别是β孔隙中γ流相的初始密度和初始体积分数,φSO是固相的初始体积分数,SrPO和SrFO分别是孔隙和裂隙的初始饱和度。从式(27)、式(31)~(34)可以看出,εVS和εVFL、εVFG的计算式中均含有裂隙骨架体应变εVC;εVS和εVPL、εVPG的计算式中均含有裂隙和孔隙骨架体应变εVC和εVH,故εVS与εVFL、εVFG、εVPL、εVPG之间存在耦合作用,它们是通过εVC和εVH传递的。本文选用裂隙和孔隙变形引起的εVC和εVH作为独立变量,可以把非饱和双重孔隙介质的耦合机理通过显式表达式呈现出来,这是以往的研究中从来没有揭示过的。定义β孔隙中γ流相的渗入量为ζβγ=φβγ0(εVS-εVβγ),利用式(27)和式(31)~(34)可得ζβγ的表达式为:
|
$
\zeta_{\mathrm{FL}}=\varphi_{\mathrm{FL} 0}\left(\frac{\varepsilon_{\mathrm{VC}}}{\varphi_{\mathrm{F} 0}}+\varepsilon_{\mathrm{VH}}+\frac{S_{\mathrm{rF}}-S_{\mathrm{rF} 0}}{S_{\mathrm{rF} 0}}-\vartheta_{\mathrm{S}}+\vartheta_{\mathrm{FL}}-\int_{0}^{t} \frac{c_{\mathrm{FL}}}{\rho_{\mathrm{FL} 0}} \mathrm{~d} t\right)
$
|
(35) |
|
$
\zeta_{\mathrm{FG}}=\varphi_{\mathrm{FG} 0}\left(\frac{\varepsilon_{\mathrm{VC}}}{\varphi_{\mathrm{F} 0}}+\varepsilon_{\mathrm{VH}}-\frac{S_{\mathrm{rF}}-S_{\mathrm{rF} 0}}{1-S_{\mathrm{rF} 0}}-\vartheta_{\mathrm{S}}+\vartheta_{\mathrm{FG}}-\int_{0}^{t} \frac{c_{\mathrm{FG}}}{\rho_{\mathrm{FG} 0}} \mathrm{~d} t\right)
$
|
(36) |
|
$
\zeta_{\mathrm{PL}}=\varphi_{\mathrm{PL}0}\left(\frac{\varphi_{\mathrm{SP0}}}{\varphi_{\mathrm{PL} 0}} \varepsilon_{\mathrm{VH}}+\frac{S_{\mathrm{rP}}-S_{\mathrm{rP} 0}}{S_{\mathrm{rP0}}}-\vartheta_{\mathrm{S}}+\vartheta_{\mathrm{PL}}-\int_{0}^{t} \frac{c_{\mathrm{PL}}}{\rho_{\mathrm{PL} 0}} \mathrm{~d} t\right)
$
|
(37) |
|
$
\zeta_{\mathrm{PG}}=\varphi_{\mathrm{PG} 0}\left(\frac{\varphi_{\mathrm{SP0}}}{\varphi_{\mathrm{P} 0}} \varepsilon_{\mathrm{VH}}-\frac{S_{\mathrm{rP}}-S_{\mathrm{rP} 0}}{1-S_{\mathrm{rP} 0}}-\vartheta_{\mathrm{S}}+\vartheta_{\mathrm{PG}}-\int_{0}^{t} \frac{c_{\mathrm{PG}}}{\rho_{\mathrm{PG} 0}} \mathrm{~d} t\right)
$
|
(38) |
接下来推导小应变条件下非饱和双重孔隙介质的一般自由能势函数本构方程(下文如无特殊说明均假定小应变条件)。令$\xi=\sum\limits_{\alpha=\mathrm{S}}^{\mathrm{FG}} \rho_{\alpha 0} \xi_{\alpha}$有
|
$
\sum\limits_{\alpha=\mathrm{S}}^{\mathrm{FG}} \rho_{\alpha} \frac{\mathrm{d}^{\alpha} \xi_{\alpha}}{\mathrm{d} t} \approx \sum\limits_{\alpha=\mathrm{S}}^{\mathrm{FG}} \rho_{\alpha 0} \frac{\mathrm{d} \xi_{\alpha}}{\mathrm{d} t} \approx \dot{\xi}
$
|
(39) |
能量平衡方程根据小应变条件和式(22)近似等于
|
$
\begin{aligned}
\dot{\xi}=\tilde{\boldsymbol{\sigma}}_{\mathrm{C}} &: \dot{\boldsymbol{\varepsilon}}_{\mathrm{C}}+\varphi_{\mathrm{SP0}} \tilde{\boldsymbol{\sigma}}_{\mathrm{H}}: \dot{\boldsymbol{\varepsilon}}_{\mathrm{H}}-\sum\limits_{\beta=\mathrm{P}}^{\mathrm{F}} \varphi_{\beta 0} s_{\beta} \dot{S}_{\mathrm{r} \beta}+\sum\limits_{\alpha=\mathrm{S}}^{\mathrm{FG}} \varphi_{\mathrm{\alpha} 0} P_{\alpha} \dot{\vartheta}_{\alpha}+\\
& \sum\limits_{\beta=\mathrm{P}}^{\mathrm{F}} \sum\limits_{\gamma=\mathrm{L}}^{\mathrm{G}} P_{\beta \gamma}\left(\boldsymbol{W}_{\beta \gamma} \cdot \operatorname{grad} \varphi_{\beta \gamma}-\frac{c_{\beta \gamma}}{\rho_{\mathrm{R} \beta \gamma}}\right)+\\
& \sum\limits_{\alpha=\mathrm{S}}^{\mathrm{FG}}\left(-\operatorname{div} \boldsymbol{q}_{\alpha}+\rho_{\alpha} r_{\alpha}+\hat{\varepsilon}_{\alpha}\right)
\end{aligned}
$
|
(40) |
假定受力过程满足热力学局部平衡假定,则内能可表示为ξ=ξ(η, εC, εH, Srβ, ϑα),对ξ求全微分后由式(40)和理性力学的Coleman关系可得:
|
$
\theta=\frac{\partial \xi}{\partial \eta}, \tilde{\boldsymbol{\sigma}}_{\mathrm{C}}=\frac{\partial \xi}{\partial \boldsymbol{\varepsilon}_{\mathrm{C}}}, \varphi_{\mathrm{SP0}} \tilde{\boldsymbol{\sigma}}_{\mathrm{H}}=\frac{\partial \xi}{\partial \boldsymbol{\varepsilon}_{\mathrm{H}}}
$
|
(41) |
|
$
\varphi_{\beta 0} s_{\beta}=-\frac{\partial \xi}{\partial S_{\mathrm{r} \beta}}, \varphi_{\alpha 0} P_{\alpha}=\frac{\partial \xi}{\partial {\vartheta}_{\alpha}}
$
|
(42) |
|
$
\begin{array}{l}
\theta \dot{\eta}=\sum\limits_{\beta=\mathrm{P}}^{\mathrm{F}} \sum\limits_{\gamma=\mathrm{L}}^{\mathrm{G}} P_{\beta \gamma}\left(\boldsymbol{W}_{\beta \gamma} \cdot \operatorname{grad} \varphi_{\beta \gamma}-\frac{c_{\beta \gamma}}{\rho_{\mathrm{R} \beta \gamma}}\right)+ \\
\ \ \ \ \ \ \ \ \sum\limits_{\alpha=\mathrm{S}}^{\mathrm{FG}}\left(-\operatorname{div} \boldsymbol{q}_{\alpha}+\rho_{\alpha} r_{\alpha}+\hat{\varepsilon}_{\alpha}\right)
\end{array}
$
|
(43) |
引入Helmhotlz自由能ψ=ψ(θ, εC, εH, Srβ, ϑα),它与内能之间的关系为ψ=ξ-θη,对ψ求全微分后由式(41)~(42)得:
|
$
\eta=-\frac{\partial \psi}{\partial \theta}, \tilde{\boldsymbol{\sigma}}_{\mathrm{C}}=\frac{\partial \psi}{\partial \boldsymbol{\varepsilon}_{\mathrm{C}}}, {\varphi}_{\mathrm{SP0}} \tilde{\boldsymbol{\sigma}}_{\mathrm{H}}=\frac{\partial \psi}{\partial \boldsymbol{\varepsilon}_{\mathrm{H}}}
$
|
(44) |
|
$
\varphi_{\beta 0} s_{\beta}=-\frac{\partial \psi}{\partial S_{\mathrm{r} \beta}}, \varphi_{\alpha 0} P_{\alpha}=\frac{\partial \psi}{\partial \vartheta_{\alpha}}
$
|
(45) |
式(44)~(45)中的ψ是自由能势函数,就热力学性质而言是可逆的,故式(44)~(45)是非饱和双重孔隙介质的一般弹性本构关系。非饱和双重孔隙介质的粘塑性力学特性可以根据非平衡态热力学从式(43)获得,相关研究可借鉴文献[9],受篇幅限制本文不拟展开研究。
现在来推导非饱和双重孔隙介质的线弹性本构模型。假定温度恒定,非饱和双重孔隙介质混合物初始平衡态为(θ, εC, εH, Srβ, ϑα)=(θ0, 0, 0, Srβ0, 0),在受到微小扰动后到达一个新的平衡态为(θ0, εC, εH, Srβ0+Srβ+, ϑα),式中Srβ+为β孔隙的饱和度增量。取自由能为状态变量的二次多项式有
|
$
\begin{aligned}
\psi=& \frac{1}{2} \boldsymbol{\varepsilon}_{\mathrm{C}}: \boldsymbol{K}_{\mathrm{CC}}: \boldsymbol{\varepsilon}_{\mathrm{C}}+\frac{1}{2} \boldsymbol{\varepsilon}_{\mathrm{H}}: \boldsymbol{K}_{\mathrm{HH}}: \boldsymbol{\varepsilon}_{\mathrm{H}}-\\
& \frac{1}{2} \sum\limits_{\beta=\mathrm{P}}^{\mathrm{F}} \sum\limits_{\zeta=\mathrm{P}}^{\mathrm{F}} K_{\mathrm{r} \beta \zeta} S_{\mathrm{r} \beta}^{+} S_{\mathrm{r} \zeta}^{+}+\frac{1}{2} \sum\limits_{\alpha=\mathrm{S}}^{\mathrm{FG}} \sum\limits_{\chi=\mathrm{S}}^{\mathrm{FG}} K_{\alpha \chi} \vartheta_{\alpha} \vartheta_{\chi}+\\
&\boldsymbol{\varepsilon}_{\mathrm{C}}: \boldsymbol{K}_{\mathrm{CH}}: \boldsymbol{\varepsilon}_{\mathrm{H}}+\sum\limits_{\beta=\mathrm{P}}^{\mathrm{F}} \boldsymbol{K}_{\mathrm{Cr} \beta}: \boldsymbol{\varepsilon}_{\mathrm{C}} S_{\mathrm{r} \beta}^{+}+\\
&\sum\limits_{\alpha=\mathrm{S}}^{\mathrm{FG}} \boldsymbol{K}_{\mathrm{C} \alpha}: \boldsymbol{\varepsilon}_{\mathrm{C}} \vartheta_{\alpha}+\sum\limits_{\beta=\mathrm{P}}^{\mathrm{F}} \boldsymbol{K}_{\mathrm{Hr} \beta}: \boldsymbol{\varepsilon}_{\mathrm{H}} S_{\mathrm{r} \beta}^{+}+\\
&\sum\limits_{\alpha=\mathrm{S}}^{\mathrm{FG}} \boldsymbol{K}_{\mathrm{H} \alpha}: \boldsymbol{\varepsilon}_{\mathrm{H}} \vartheta_{\alpha}+\sum\limits_{\beta=\mathrm{P}}^{\mathrm{F}} \sum\limits_{\alpha=\mathrm{S}}^{\mathrm{FG}} K_{\mathrm{J} \beta \alpha} S_{\mathrm{r} \beta}^{+} \vartheta_{\alpha}
\end{aligned}
$
|
(46) |
式中KCC、KHH、Krβζ、Kαχ、KCH、KCrβ、KCα、KHrβ、KHα和KJβα为模型的弹性参数,Kαχ=Kχα,Krβζ=Krζβ,α, χ∈{S, PL, PG, FL, FG},β, ζ∈{P, F}。把式(46)代入式(44)~(45)得:
|
$
\tilde{\boldsymbol{\sigma}}_{\mathrm{C}}=\boldsymbol{K}_{\mathrm{CC}}: \boldsymbol{\varepsilon}_{\mathrm{C}}+\boldsymbol{K}_{\mathrm{CH}}: \boldsymbol{\varepsilon}_{\mathrm{H}}+\sum\limits_{\beta=\mathrm{P}}^{\mathrm{F}} \boldsymbol{K}_{\mathrm{Cr\beta}} S_{\mathrm{r} \beta}^{+}+\sum\limits_{\alpha=\mathrm{S}}^{\mathrm{FG}} \boldsymbol{K}_{\mathrm{C} \alpha} \boldsymbol{\vartheta}_{\alpha}
$
|
(47) |
|
$
\varphi_{\mathrm{SP} 0} \tilde{\boldsymbol{\sigma}}_{\mathrm{H}}=\boldsymbol{K}_{\mathrm{CH}}: \boldsymbol{\varepsilon}_{\mathrm{C}}+\boldsymbol{K}_{\mathrm{HH}}: \boldsymbol{\varepsilon}_{\mathrm{H}}+\sum\limits_{\beta=\mathrm{P}}^{\mathrm{F}} \boldsymbol{K}_{\mathrm{Hr\beta}} S_{\mathrm{r} \beta}^{+}+\sum\limits_{\alpha=\mathrm{S}}^{\mathrm{FG}} \boldsymbol{K}_{\mathrm{H} \alpha} \boldsymbol{\vartheta}_{\alpha}
$
|
(48) |
|
$
\varphi_{\beta 0} s_{\beta}=-\boldsymbol{K}_{\mathrm{Cr\beta}}: \boldsymbol{\varepsilon}_{\mathrm{C}}-\boldsymbol{K}_{\mathrm{Hr} \beta}: \boldsymbol{\varepsilon}_{\mathrm{H}}+\sum\limits_{\zeta=\mathrm{P}}^{\mathrm{F}} K_{\mathrm{r} \beta \zeta} S_{\mathrm{r} \zeta}^{+}-\sum\limits_{\alpha=\mathrm{S}}^{\mathrm{FG}} K_{\mathrm{J} \beta \alpha} \vartheta_{\alpha}
$
|
(49) |
|
$
\varphi_{\alpha 0} P_{\alpha}=\boldsymbol{K}_{\mathrm{C}{\alpha}}: \boldsymbol{\varepsilon}_{\mathrm{C}}+\boldsymbol{K}_{\mathrm{H}{\alpha}}: \boldsymbol{\varepsilon}_{\mathrm{H}}+\sum\limits_{\beta=\mathrm{P}}^{\mathrm{F}} K_{\mathrm{J} \alpha \beta} S_{\mathrm{r} \beta}^{+}+\sum\limits_{\chi=\mathrm{S}}^{\mathrm{FG}} K_{\alpha \chi} \vartheta_{\chi}
$
|
(50) |
由于假定温度保持不变,故式(47)~(50)中不含温度变量。
在非饱和双重孔隙介质研究中,为了简化本构方程便于工程实用,通常假定裂隙和孔隙之间以及它们与各组分基质之间的力学性质相互独立。此时由式(47)~(50)可得:
|
$
\tilde{\boldsymbol{\sigma}}_{\mathrm{C}}=\boldsymbol{K}_{\mathrm{CC}}: \boldsymbol{\varepsilon}_{\mathrm{C}}+\boldsymbol{K}_{\mathrm{CrF}} S_{\mathrm{rF}}^{+}
$
|
(51) |
|
$
\varphi_{\mathrm{SP} 0} \tilde{\boldsymbol{\sigma}}_{\mathrm{H}}=\boldsymbol{K}_{\mathrm{HH}}: \boldsymbol{\varepsilon}_{\mathrm{H}}+\boldsymbol{K}_{\mathrm{HrP}} S_{\mathrm{rP}}^{+}
$
|
(52) |
|
$
\varphi_{\mathrm{F} 0} s_{\mathrm{F}}=-\boldsymbol{K}_{\mathrm{CrF}}: \boldsymbol{\varepsilon}_{\mathrm{C}}+K_{\mathrm{rF}} S_{\mathrm{rF}}^{+}
$
|
(53) |
|
$
\varphi_{\mathrm{P} 0} s_{\mathrm{P}}=-\boldsymbol{K}_{\mathrm{HrP}}: \boldsymbol{\varepsilon}_{\mathrm{H}}+K_{\mathrm{rP}} S_{\mathrm{rP}}^{+}
$
|
(54) |
|
$
P_{\alpha}=K_{\mathrm{R} \alpha} \vartheta_{\alpha}
$
|
(55) |
式中KRα=Kαα/φα0表示各组分基质的体积模量。假定非饱和双重孔隙介质为各向同性材料,则KCC、KHH、KCrF和KCrP的具体表达式为:
|
$
\boldsymbol{K}_{\mathrm{CC}}=\frac{E_{\mathrm{C}}}{1-2 {\upsilon}_{\mathrm{C}}}\left(\frac{{\upsilon}_{\mathrm{C}}}{1+{\upsilon}_{\mathrm{C}}}-\frac{\zeta_{\mathrm{F}}}{1+3 \zeta_{\mathrm{F}}}\right) \boldsymbol{I} \otimes \boldsymbol{I}+\frac{E_{\mathrm{C}}}{1+{\upsilon}_{\mathrm{C}}} \boldsymbol{I}_{4}
$
|
(56) |
|
$
\boldsymbol{K}_{\mathrm{HH}}=\frac{\varphi_{\mathrm{SP} 0} E_{\mathrm{H}}}{1-2 {\upsilon}_{\mathrm{H}}}\left(\frac{{\upsilon}_{\mathrm{H}}}{1+{\upsilon}_{\mathrm{H}}}-\frac{\zeta_{\mathrm{P}}}{1+3 \zeta_{\mathrm{P}}}\right) \boldsymbol{I} \otimes \boldsymbol{I}+\frac{{\varphi}_{\mathrm{SP} 0} E_{\mathrm{H}}}{1+{\upsilon}_{\mathrm{H}}} \boldsymbol{I}_{4}
$
|
(57) |
|
$
\boldsymbol{K}_{\mathrm{CrF}} =\frac{\zeta_{\mathrm{F}} H_{\mathrm{CF}}}{1+3 \zeta_{\mathrm{F}}} \boldsymbol{I}, K_{\mathrm{rF}}=\frac{\varphi_{\mathrm{F} 0} H_{\mathrm{rF}}}{1+3 \zeta_{\mathrm{F}}}
$
|
(58) |
|
$
\boldsymbol{K}_{\mathrm{HrP}} =\frac{\varphi_{\mathrm{SP} 0} \zeta_{\mathrm{P}} H_{\mathrm{HP}}}{1+3 \zeta_{\mathrm{P}}} \boldsymbol{I}, K_{\mathrm{rP}}=\frac{\varphi_{\mathrm{P} 0} H_{\mathrm{rP}}}{1+3 \zeta_{\mathrm{P}}}
$
|
(59) |
式中I为二阶单位张量,I4为四阶单位张量,式中υC和EC分别是裂隙骨架的泊松比和弹性模量,υH和EH分别是孔隙骨架的泊松比和弹性模量,HCF和HrF分别为裂隙有效应力和吸力对裂隙饱和度的弹性模量,HHP和HrP分别为孔隙有效应力和吸力对孔隙饱和度的弹性模量。ζF和ζP按下式计算:
|
$
\zeta_{\mathrm{F}} =\frac{\varphi_{\mathrm{F} 0} E_{\mathrm{C}} H_{\mathrm{rF}}}{\left(1-2 v_{\mathrm{C}}\right) H_{\mathrm{CF}}^{2}}, \zeta_{\mathrm{P}}=\frac{\varphi_{\mathrm{P} 0} E_{\mathrm{H}} H_{\mathrm{rP}}}{\varphi_{\mathrm{SP} 0}\left(1-2 \boldsymbol{v}_{\mathrm{H}}\right) H_{\mathrm{HP}}^{2}}
$
|
(60) |
令KC=EC/[3(1-2υC)]和KH=EH/[3(1-2υH)]分别为裂隙和孔隙骨架的体积模量,Eb和υb为:
|
$
\frac{1}{E_{\mathrm{b}}}=\frac{1}{E_{\mathrm{C}}}+\frac{1}{\varphi_{\mathrm{SP} 0} E_{\mathrm{H}}}+\frac{1}{9 \varphi_{\mathrm{S} 0} K_{\mathrm{RS}}}
$
|
(61) |
|
$
{\upsilon}_{\mathrm{b}}=\left(\frac{{\upsilon}_{\mathrm{C}}}{E_{\mathrm{C}}}+\frac{{\upsilon}_{\mathrm{H}}}{\varphi_{\mathrm{SP}} E_{\mathrm{H}}}-\frac{1}{9 \varphi_{\mathrm{S} 0} K_{\mathrm{RS}}}\right) E_{\mathrm{b}}
$
|
(62) |
令Kb=Eb/[3(1-2υb)]。把式(56)~(59)代入到式(51)~(54),对式(51)~(55)求逆后代入式(23)和式(35)~(38),并把它们转化为用σ和Pβγ表示的形式:
|
$
\begin{aligned}
\varepsilon_{\mathrm{S}} &=\left(-\frac{\boldsymbol{v}_{\mathrm{b}}}{E_{\mathrm{b}}} \boldsymbol{I} \otimes \boldsymbol{I}+\frac{1+\boldsymbol{v}_{\mathrm{b}}}{E_{\mathrm{b}}} \boldsymbol{I}_{4}\right): \boldsymbol{\sigma}+\frac{A_{12}}{3} P_{\mathrm{FL}} \boldsymbol{I}+\\
& \frac{A_{13}}{3} P_{\mathrm{FG}} \boldsymbol{I}+\frac{A_{14}}{3} P_{\mathrm{PL}} \boldsymbol{I}+\frac{A_{15}}{3} P_{\mathrm{PG}} \boldsymbol{I}
\end{aligned}
$
|
(63) |
|
$
\begin{aligned}
\zeta_{\mathrm{FL}} &=-A_{12} P_{\mathrm{T}}+\left(A_{22}+\varphi_{\mathrm{FL} 0} / K_{\mathrm{RFL}}\right) P_{\mathrm{FL}}+A_{23} P_{\mathrm{FG}}+\\
& A_{24} P_{\mathrm{PL}}+A_{25} P_{\mathrm{PG}}-\int_{0}^{t}\left(c_{\mathrm{FL}} / \rho_{\mathrm{RF} 10}\right) \mathrm{d} t
\end{aligned}
$
|
(64) |
|
$
\begin{aligned}
\zeta_{\mathrm{FG}} &=-A_{13} P_{\mathrm{T}}+A_{23} P_{\mathrm{FL}}+\left(A_{33}+\varphi_{\mathrm{FG} 0} / K_{\mathrm{RFG}}\right) P_{\mathrm{FG}}+\\
& A_{34} P_{\mathrm{PL}}+A_{35} P_{\mathrm{PG}}-\int_{0}^{t}\left(c_{\mathrm{FG}} / \rho_{\mathrm{RFG} 0}\right) \mathrm{d} t
\end{aligned}
$
|
(65) |
|
$
\begin{aligned}
\zeta_{\mathrm{PL}} &=-A_{14} P_{\mathrm{T}}+A_{24} P_{\mathrm{FL}}+A_{34} P_{\mathrm{FG}}+\left(A_{44}+\right.\\
&\left.\varphi_{\mathrm{PL} 0} / K_{\mathrm{RPL}}\right) P_{\mathrm{PL}}+A_{45} P_{\mathrm{PG}}-\int_{0}^{t}\left(c_{\mathrm{FL}} / \rho_{\mathrm{RPL} 0}\right) \mathrm{d} t
\end{aligned}
$
|
(66) |
|
$
\begin{aligned}
\zeta_{\mathrm{PG}}=&-A_{15} P_{\mathrm{T}}+A_{25} P_{\mathrm{FL}}+A_{35} P_{\mathrm{FG}}+A_{45} P_{\mathrm{PL}}+\\
&\left(A_{55}+\varphi_{\mathrm{PG} 0} / K_{\mathrm{RPG}}\right) P_{\mathrm{PG}}-\int_{0}^{t}\left(c_{\mathrm{PG}} / \rho_{\mathrm{RPG} 0}\right) \mathrm{d} t
\end{aligned}
$
|
(67) |
式中:
|
$
A_{12} =\frac{S_{\mathrm{rF} 0}}{K_{\mathrm{C}}}+\frac{3 \varphi_{\mathrm{F} 0}}{H_{\mathrm{CF}}}+\frac{\varphi_{\mathrm{FL} 0}}{\varphi_{\mathrm{SP} 0} K_{\mathrm{H}}}+\frac{\varphi_{\mathrm{FL} 0}}{\varphi_{\mathrm{S} 0} K_{\mathrm{RS}}}
$
|
(68) |
|
$
A_{13}=\frac{1-S_{\mathrm{rF} 0}}{K_{\mathrm{C}}}-\frac{3 \varphi_{\mathrm{F} 0}}{H_{\mathrm{CF}}}+\frac{\varphi_{\mathrm{FG} 0}}{\varphi_{\mathrm{SP} 0} K_{\mathrm{H}}}+\frac{\varphi_{\mathrm{FG} 0}}{\varphi_{\mathrm{S} 0} K_{\mathrm{RS}}}
$
|
(69) |
|
$
A_{14} =\frac{S_{\mathrm{rP0}}}{K_{\mathrm{H}}}+\frac{3 \varphi_{\mathrm{P} 0}}{\varphi_{\mathrm{SP} 0} H_{\mathrm{HP}}}+\frac{\varphi_{\mathrm{PL} 0}}{\varphi_{\mathrm{S} 0} K_{\mathrm{RS}}}
$
|
(70) |
|
$
A_{15} =\frac{1-S_{\mathrm{rP0}}}{3 K_{\mathrm{H}}}-\frac{\varphi_{\mathrm{P} 0}}{\varphi_{\mathrm{SP0}} H_{\mathrm{HP}}}+\frac{\varphi_{\mathrm{PL} 0}}{3 \varphi_{\mathrm{S} 0} K_{\mathrm{RS}}}
$
|
(71) |
|
$
A_{22}=\frac{\left(S_{\mathrm{rF} 0}\right)^{2}}{K_{\mathrm{C}}}+\frac{6 \varphi_{\mathrm{FL} 0}}{H_{\mathrm{CF}}}+\frac{\left(\varphi_{\mathrm{FL} 0}\right)^{2}}{\varphi_{\mathrm{SP} 0} K_{\mathrm{H}}}-\frac{\varphi_{\mathrm{F} 0}}{H_{\mathrm{rF}}}+\frac{\left(\varphi_{\mathrm{FL} 0}\right)^{2}}{\varphi_{S 0} K_{\mathrm{RS}}}
$
|
(72) |
|
$
\begin{aligned}
A_{23} &=\frac{S_{\mathrm{rF0}}\left(1-S_{\mathrm{rF} 0}\right)}{K_{\mathrm{C}}}+\frac{3\left(1-2 S_{\mathrm{rF} 0}\right) \varphi_{\mathrm{F} 0}}{H_{\mathrm{CF}}}+\frac{\varphi_{\mathrm{FL} 0} \varphi_{\mathrm{FG} 0}}{\varphi_{\mathrm{SP}} K_{\mathrm{H}}}+\\
& \frac{\varphi_{\mathrm{F} 0}}{H_{\mathrm{rF}}}+\frac{\varphi_{\mathrm{FL} 0} \varphi_{\mathrm{FG} 0}}{\varphi_{\mathrm{S} 0} K_{\mathrm{RS}}}
\end{aligned}
$
|
(73) |
|
$
A_{24} =\varphi_{\mathrm{FL} 0}\left(\frac{S_{\mathrm{rP} 0}}{K_{\mathrm{H}}}+\frac{3 \varphi_{\mathrm{P} 0}}{\varphi_{\mathrm{SP} 0} H_{\mathrm{HP}}}+\frac{\varphi_{\mathrm{PL} 0}}{\varphi_{\mathrm{S} 0} K_{\mathrm{RS}}}\right)
$
|
(74) |
|
$
A_{25} =\varphi_{\mathrm{FL} 0}\left(\frac{1-S_{\mathrm{rP} 0}}{K_{\mathrm{H}}}-\frac{3 \varphi_{\mathrm{P} 0}}{\varphi_{\mathrm{SP0}} H_{\mathrm{HP}}}+\frac{\varphi_{\mathrm{PG} 0}}{\varphi_{\mathrm{S} 0} K_{\mathrm{RS}}}\right)
$
|
(75) |
|
$
\begin{aligned}
A_{33} &=\frac{\left(1-S_{\mathrm{rF} 0}\right)^{2}}{K_{\mathrm{C}}}-\frac{6 \varphi_{\mathrm{FG} 0}}{H_{\mathrm{CF}}}+\frac{\left(\varphi_{\mathrm{FG} 0}\right)^{2}}{\varphi_{\mathrm{SP} 0} K_{\mathrm{H}}}-\frac{\varphi_{\mathrm{F} 0}}{H_{\mathrm{rF}}}+\\
& \frac{\left(\varphi_{\mathrm{FG} 0}\right)^{2}}{\varphi_{\mathrm{S} 0} K_{\mathrm{RS}}}
\end{aligned}
$
|
(76) |
|
$
A_{34}=\varphi_{\mathrm{FG} 0}\left(\frac{S_{\mathrm{rP} 0}}{K_{\mathrm{H}}}+\frac{3 \varphi_{\mathrm{P} 0}}{\varphi_{\mathrm{SP} 0} H_{\mathrm{HP}}}+\frac{\varphi_{\mathrm{PL} 0}}{\varphi_{\mathrm{S} 0} K_{\mathrm{RS}}}\right)
$
|
(77) |
|
$
A_{35}=\varphi_{\mathrm{FG} 0}\left(\frac{1-S_{\mathrm{rPO}}}{K_{\mathrm{H}}}-\frac{3 \varphi_{\mathrm{P} 0}}{\varphi_{\mathrm{SP}} H_{\mathrm{HP}}}+\frac{\varphi_{\mathrm{PG} 0}}{\varphi_{\mathrm{S} 0} K_{\mathrm{RS}}}\right)
$
|
(78) |
|
$
A_{44}=\frac{\left(S_{\mathrm{rP} 0}\right)^{2} \varphi_{\mathrm{SP}0}}{K_{\mathrm{H}}}+\frac{6 \varphi_{\mathrm{PL} 0}}{H_{\mathrm{HP}}}-\frac{\varphi_{\mathrm{P} 0}}{H_{\mathrm{rP}}}+\frac{\left(\varphi_{\mathrm{PL} 0}\right)^{2}}{\varphi_{\mathrm{S} 0} K_{\mathrm{RS}}}
$
|
(79) |
|
$
\begin{aligned}
A_{45} &=\frac{S_{\mathrm{rP0}}\left(1-S_{\mathrm{rP0}}\right) \varphi_{\mathrm{SP} 0}}{K_{\mathrm{H}}}+\frac{3\left(1-2 S_{\mathrm{rP0}}\right) \varphi_{\mathrm{P} 0}}{H_{\mathrm{HP}}}+\\
& \frac{\varphi_{\mathrm{P} 0}}{H_{\mathrm{rP}}}+\frac{\varphi_{\mathrm{PL} 0} \varphi_{\mathrm{PG} 0}}{\varphi_{\mathrm{S} 0} K_{\mathrm{RS}}}
\end{aligned}
$
|
(80) |
|
$
A_{55} =\frac{\left(1-S_{\mathrm{rP} 0}\right)^{2} \varphi_{\mathrm{SP} 0}}{K_{\mathrm{H}}}-\frac{6 \varphi_{\mathrm{PG} 0}}{H_{\mathrm{HP}}}-\frac{\varphi_{\mathrm{P0}}}{H_{\mathrm{rP}}}+\frac{\left(\varphi_{\mathrm{PG} 0}\right)^{2}}{\varphi_{\mathrm{S} 0} K_{\mathrm{RS}}}
$
|
(81) |
cFL、cFG、cPL和cPG根据文献[8]的研究可表示为:
|
$
c_{\mathrm{FL}}=-c_{\mathrm{PL}}=\xi_{\mathrm{L}}\left(P_{\mathrm{PL}}-P_{\mathrm{FL}}\right)
$
|
(82) |
|
$
c_{\mathrm{FG}}=-c_{\mathrm{PG}}=\xi_{\mathrm{G}}\left(P_{\mathrm{PG}}-P_{\mathrm{FG}}\right)
$
|
(83) |
式(63)~(67)是小应变各向同性线弹性条件下非饱和双重孔隙介质的固相本构方程、裂隙和孔隙中液气两相的渗入量本构方程。不难验证:1)当非饱和双重孔隙介质退化为饱和双重孔隙介质时,φFG0、φPG0、sF、sP、1/HCF、1/HHP、1/HrP和1/HrF均为0,SrP0和SrF0等于1,把它们代入到式(63)~(64)和式(66)后可获得Khalili线弹性方程;2)当忽略孔隙只考虑裂隙,非饱和双重孔隙介质变为非饱和单重孔隙介质时,PPL、PPG、cFL、cPL、cFG、cPG、1/EH、1/KH和1/HrP均为0,把它们代入式(63)~(65)可得到非饱和单重孔隙介质线弹性方程[13],这说明当双重孔隙退化为单重孔隙或非饱和退化为饱和时,非饱和双重孔隙介质的线弹性本构方程可退化为相应介质的线弹性本构方程。
把应力用应变表示时式(63)~(67)可变换得:
|
$
\begin{aligned}
\boldsymbol{\sigma}=& 3 K_{\mathrm{b}}\left(\frac{\upsilon_{\mathrm{b}}}{1+\upsilon_{\mathrm{b}}} \boldsymbol{I} \otimes \boldsymbol{I}+\frac{1-2 \upsilon_{\mathrm{b}}}{1+\upsilon_{\mathrm{b}}} \boldsymbol{I}_{4}\right): \boldsymbol{\varepsilon}_{\mathrm{s}}-A_{12} K_{\mathrm{b}} P_{\mathrm{FL}} \boldsymbol{I}-\\
& A_{13} K_{\mathrm{b}} P_{\mathrm{FG}} \boldsymbol{I}-A_{14} K_{\mathrm{b}} P_{\mathrm{PL}} \boldsymbol{I}-A_{15} K_{\mathrm{b}} P_{\mathrm{PG}} \boldsymbol{I}
\end{aligned}
$
|
(84) |
|
$
\begin{array}{l}
\zeta_{\mathrm{FL}}=A_{12} K_{\mathrm{b}} \boldsymbol{\varepsilon}_{\bf{S}}: \boldsymbol{I}+\left(A_{22}-A_{12}^{2} K_{\mathrm{b}}+\varphi_{\mathrm{FL0}} / K_{\mathrm{RFL}}\right) P_{\mathrm{FL}}+ \\
\ \ \ \ \ \ \ \ \ \ \left(A_{23}-A_{12} A_{13} K_{\mathrm{b}}\right) P_{\mathrm{FG}}+\left(A_{24}-A_{12} A_{14} K_{\mathrm{b}}\right) P_{\mathrm{PL}}+ \\
\ \ \ \ \ \ \ \ \ \ \left(A_{25}-A_{12} A_{15} K_{\mathrm{b}}\right) P_{\mathrm{PG}}-\int_{0}^{t}\left(c_{\mathrm{FL}} / \rho_{\mathrm{RFL0}}\right) \mathrm{d} t
\end{array}
$
|
(85) |
|
$
\begin{aligned}
\zeta_{\mathrm{FG}} &=A_{13} K_{\mathrm{b}} \boldsymbol{\varepsilon}_{\bf{S}}: \boldsymbol{I}+\left(A_{23}-A_{12} A_{13} K_{\mathrm{b}}\right) P_{\mathrm{FL}}+\\
&\left(A_{33}-A_{13}^{2} K_{\mathrm{b}}+\varphi_{\mathrm{FG} 0} / K_{\mathrm{RFG}}\right) P_{\mathrm{FG}}+\\
&\left(A_{34}-A_{13} A_{14} K_{\mathrm{b}}\right) P_{\mathrm{PL}}+\left(A_{35}-A_{13} A_{15} K_{\mathrm{b}}\right) P_{\mathrm{PG}}-\\
& \int_{0}^{t}\left(c_{\mathrm{FG}} / \rho_{\mathrm{RFL} 0}\right) \mathrm{d} t
\end{aligned}
$
|
(86) |
|
$
\begin{aligned}
\zeta_{\mathrm{PL}} &=A_{14} K_{\mathrm{b}} \boldsymbol{\varepsilon}_{\bf{s}}: \boldsymbol{I}+\left(A_{24}-A_{12} A_{14} K_{\mathrm{b}}\right) P_{\mathrm{FL}}+\\
&\left(A_{34}-A_{13} A_{14} K_{\mathrm{b}}\right) P_{\mathrm{FG}}+\left(A_{44}-A_{14}^{2} K_{\mathrm{b}}+\varphi_{\mathrm{PL} 0} / K_{\mathrm{RPL}}\right) P_{\mathrm{PL}}+\\
&\left(A_{45}-A_{14} A_{15} K_{\mathrm{b}}\right) P_{\mathrm{PG}}-\int_{0}^{t}\left(c_{\mathrm{PL}} / \rho_{\mathrm{RPL} 0}\right) \mathrm{d} t
\end{aligned}
$
|
(87) |
|
$
\begin{aligned}
\zeta_{\mathrm{PG}} &=A_{15} K_{\mathrm{b}} \boldsymbol{\varepsilon}_{\bf{S}}: \boldsymbol{I}+\left(A_{25}-A_{12} A_{15} K_{\mathrm{b}}\right) P_{\mathrm{FL}}+\\
&\left(A_{35}-A_{13} A_{15} K_{\mathrm{b}}\right) P_{\mathrm{FG}}+\left(A_{45}-A_{14} A_{15} K_{\mathrm{b}}\right) P_{\mathrm{PL}}+\\
&\left(A_{55}-A_{15}^{2} K_{\mathrm{b}}+\varphi_{\mathrm{PG} 0} / K_{\mathrm{RPG}}\right) P_{\mathrm{PG}}-\\
& \int_{0}^{t}\left(c_{\mathrm{PG}} / \rho_{\mathrm{RPG} 0}\right) \mathrm{d} t
\end{aligned}
$
|
(88) |
4 算例 4.1 基于本文理论的膨润土试验结果分析 在高放废物深埋处置库的概念设计中,需要采用膨润土作缓冲材料充填于废物罐和围岩之间,阻止核素随地下水迁移。经过研究比选,我国采用高庙子膨润土作为核废料处置库的缓冲材料。由于膨润土存在聚集体内的孔隙和颗粒间的裂隙,许多学者采用双重孔隙介质来建立膨润土的本构模型[6, 8, 18]。在这些模型中,大多根据孔隙水的性质,把孔隙视为被水饱和而裂隙被水部分饱和[6, 8, 18],本文也遵循这一性质。
Morena等[18]假定当吸力大于20 MPa时膨润土只有孔隙含水而裂隙不含水,总结了中国学者[19-20]研究高庙子膨润土的系列试验成果。笔者在Morena等[18]研究基础之上,结合本文理论模型,重新整理了高庙子膨润土的试验数据。试验时膨润土固相、裂隙和孔隙体积分数为φS0=0.642、φF0=0.179和φP0=0.179,饱和孔隙骨架应变及其有效应力的关系见图 3,饱和裂隙骨架应变及其有效应力的关系见图 4,裂隙饱和度与膨胀应变之间的关系见图 5。
裂隙土水特征曲线符合Van Genuchten模型:SrF=[1+(αSF)n]-m,式中m=0.825、n=1/(1-m)和α=2.16×10-4 kPa-1。从图 3~5可以看出,膨润土应力与应变存在较明显的非线性关系。根据图 3、4和本文理论可得饱和排水条件下膨润土应变随总应力的变化曲线见图 6。图 6也给出根据单重孔隙介质理论获得的膨润土应变随总应力曲线,从图 6可以看出本文提出的双重孔隙介质理论比较符合试验数据。
线弹性本构模型由于物理概念清楚,数学关系简单,因此常用割线模量来近似建立土体的线弹性模型。泊松比按经验值取为0.3,根据图 3~5提供的试验数据和割线模型的计算方法,利用完全侧限试验的性质,膨润土裂隙和孔隙骨架的力学参数见表 1。
表 1
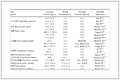
表 1 非饱和双重孔隙膨润土MX80试样的模型参数
Tab. 1 Model parameters of sample MX80 for unsaturated double-porosity bentonite
KRS/
MPa |
EC/
MPa |
υC |
HCF/
MPa |
HrF/
MPa |
EH |
υH |
| =∞ |
71.7 |
0.3 |
62 |
-6.0 |
496 |
0.3 |
|
| HHP |
HrP |
KRPL=KPFL |
KRFG/
MPa |
ξF/
(kg·m-3·s-1) |
ξP |
| =∞ |
=∞ |
=∞ |
0.14 |
1.8×10-10 |
0 |
|
表 1 非饱和双重孔隙膨润土MX80试样的模型参数
Tab. 1 Model parameters of sample MX80 for unsaturated double-porosity bentonite
|
图 4给出的是饱和条件下获得的试验数据,非饱和条件下的杨氏模量比饱和条件下的有所提高,两者可根据Alonso等[1]提出的计算公式进行换算[18]:EC(sF)=EC(0)/[0.836+0.164exp(-0.7sF)],本算例裂隙吸力平均值约为1.2 MPa,故取吸力sF=1.2 MPa时的模量作为裂隙骨架的割线模量。试验表明[21]高庙子膨润土中水的渗透系数为5×10-11 m/s,气体的渗透系数为5×10-10 m/s,由于孔隙假定饱和,无需KRPG值,故表中未给出相应值。根据表 1和式(61)~(62)可得Eb=61 MPa,υb= 0.3,Kb=50.9 MPa。
4.2 核废料缓冲材料的轴对称固结控制方程 现在应用本文的线弹性本构方程来建立膨润土作为核废料储藏罐的固结方程。把膨润土缓冲设置简化为圆柱轴对称模型来分析,由于核废料储藏罐的体积较小,为简便起见,把膨润土视为实心圆柱体。注意到固结方程不考虑加速度和体力,首先把式(15)~ (16)按所有相相加得
|
$
\operatorname{div} \boldsymbol{\sigma}=0
$
|
(89) |
在轴对称条件下,由式(89)可得
|
$
\left(\partial \sigma_{r} / \partial r\right)+\left(\sigma_{r}-\sigma_{\theta}\right) / r=0
$
|
(90) |
同时各相间的相互作用力$\hat{\boldsymbol{p}}_{\beta \gamma}=P_{\beta \gamma} \nabla n_{\beta \gamma}-n_{\beta \gamma} n_{\beta \gamma 0} \boldsymbol{W}_{\beta \gamma} \gamma_{\mathrm{w}} / K_{\beta \gamma}$[13],把它们代入到式(16)得
|
$
\left(K_{\beta \gamma} / \gamma_{\rm{w}}\right) \nabla P_{\beta \gamma}+n_{\beta \gamma 0} \boldsymbol{W}_{\beta \gamma}=0
$
|
(91) |
对式(91)求散度后应用ζβγ的定义并写成轴对称形式得
|
$
\frac{K_{\beta \gamma}}{\gamma_{\rm{w}} r} \frac{\partial}{\partial r}\left(r \frac{\partial P_{\beta \gamma}}{\partial r}\right)-\dot{\zeta}_{\beta \gamma}=0
$
|
(92) |
假定固相和水基质不可压缩,孔隙被水饱和而裂隙被水部分饱和,把这些条件代入到式(84)~(88)后利用εr=∂u/∂r、εθ=u/r、式(90)和式(92)得:
|
$
\frac{1-\upsilon _{b}}{1+\upsilon _{b}} \frac{\partial \theta}{\partial r}+\frac{A_{12}}{3} \frac{\partial P_{\mathrm{FL}}}{\partial r}+\frac{A_{13}}{3} \frac{\partial P_{\mathrm{FG}}}{\partial r}+\frac{A_{14}}{3} \frac{\partial P_{\mathrm{PL}}}{\partial r}=0
$
|
(93) |
|
$
\begin{aligned}
\frac{\partial \theta}{\partial t}=&-\frac{K_{\mathrm{FL}} / \gamma_{\mathrm{w}}}{A_{12} K_{\mathrm{b}} r} \frac{\partial}{\partial r}\left(r \frac{\partial P_{\mathrm{FL}}}{\partial r}\right)+\left(\frac{A_{22}}{A_{12} K_{\mathrm{b}}}-A_{12}\right) \frac{\partial P_{\mathrm{FL}}}{\partial t}+\\
&\left(\frac{A_{23}}{A_{12} K_{\mathrm{b}}}-A_{13}\right) \frac{\partial P_{\mathrm{FG}}}{\partial t}+\left(\frac{A_{24}}{A_{12} K_{\mathrm{b}}}-A_{14}\right) \frac{\partial P_{\mathrm{PL}}}{\partial t}-\\
&\frac{c_{\mathrm{FL}} / \rho_{\mathrm{RFL} 0}}{A_{12} K_{\mathrm{b}}}=0
\end{aligned}
$
|
(94) |
|
$
\begin{aligned}
\frac{\partial \theta}{\partial t}=&-\frac{K_{\mathrm{FG}} / \gamma_{a}}{A_{13} K_{\mathrm{b}} r} \frac{\partial}{\partial r}\left(r \frac{\partial P_{\mathrm{FG}}}{\partial r}\right)+\left(\frac{A_{23}}{A_{13} K_{\mathrm{b}}}-A_{12}\right) \frac{\partial P_{\mathrm{FL}}}{\partial t}+\\
&\left(\frac{A_{33}}{A_{13} K_{\mathrm{b}}}-A_{13}+\frac{\varphi_{\mathrm{FG} 0} / K_{\mathrm{RFG}}}{A_{13} K_{\mathrm{b}}}\right) \frac{\partial P_{\mathrm{FG}}}{\partial t}+\\
&\left(\frac{A_{34}}{A_{13} K_{\mathrm{b}}}-A_{14}\right) \frac{\partial P_{\mathrm{PL}}}{\partial t}=0
\end{aligned}
$
|
(95) |
|
$
\begin{aligned}
\frac{\partial \theta}{\partial t}=&-\frac{K_{\mathrm{PL}} / \gamma_{\mathrm{w}}}{A_{14} K_{\mathrm{b}} r} \frac{\partial}{\partial r}\left(r \frac{\partial P_{\mathrm{PL}}}{\partial r}\right)+\left(\frac{A_{24}}{A_{14} K_{\mathrm{b}}}-A_{12}\right) \frac{\partial P_{\mathrm{FL}}}{\partial t}+\\
&\left(\frac{A_{34}}{A_{14} K_{\mathrm{b}}}-A_{13}\right) \frac{\partial P_{\mathrm{FG}}}{\partial t}+\left(\frac{A_{44}}{A_{14} K_{\mathrm{b}}}-A_{14}\right) \frac{\partial P_{\mathrm{PL}}}{\partial t}- \\
&\frac{c_{\mathrm{PL}} / \rho_{\mathrm{RF} \mathrm{L} 0}}{A_{14} K_{\mathrm{b}}}=0
\end{aligned}
$
|
(96) |
式中θ=-(∂u/∂r+u/r)。设膨润土半径为R,由于线性系统的解答与土的初始应力无关,初始条件可等效地设置为:
|
$
\zeta_{\beta \gamma}=0, P_{\beta \gamma}(R, t)=0, u_{\mathrm{s}}(0, t)=0
$
|
(97) |
|
$
\frac{E_{\mathrm{b}}}{\left(1-2 \upsilon _{\mathrm{b}}\right)\left(1+\upsilon _{\mathrm{b}}\right)}\left[\left(1-\upsilon _{\mathrm{b}}\right) \frac{\partial u}{\partial r}+v_{\mathrm{b}} \frac{u}{r}\right]=p
$
|
(98) |
式中p为作用在半径R处圆柱体外侧的外荷载,式(93)~(98)即是轴对称条件下的固结控制方程和初边值条件,如在推导式(93)~(98)方程中加上加速度项,就可以获得波动控制方程。式(93)~(98)固结控制方程极其复杂,求解十分困难,但可以采用数值方法如差分法进行求解。
5 结论 1) 在考虑固相和流相基质变形的条件下,用嵌套思路推导了非饱和双重孔隙介质的能量平衡方程。根据内能表达式中功共轭对的力学内涵揭示非饱和双重孔隙介质本构模型的应变状态变量为裂隙和孔隙骨架应变,裂隙和孔隙饱和度和各组分基质体应变;相应的应力状态变量为裂隙和孔隙有效应力,裂隙和孔隙吸力和各组分基质压力。
2) 在小应变条件下,把固相应变分解为裂隙骨架应变、孔隙骨架应变和固相基质体应变之和。根据热力学局部平衡假定,获得非饱和孔隙介质的一般自由能势函数本构方程。取自由能势函数为状态变量的二次多项式,获得非饱和双重孔隙介质的线弹性本构模型。然后根据混合物均匀化响应原理获得各向同性线弹性本构方程。根据土工试验获得了非饱和膨润土线弹性本构方程的模型参数。
3) 把本文获得的非饱和双重孔隙介质的各向同性线弹性本构模型退化为饱和双重孔隙介质和非饱和单重孔隙介质情形,可以获得与前人相同的各向同性线弹性本构模型。把非饱和双重孔隙介质线弹性本构方程与平衡方程和达西定理相结合,建立了非饱和膨润土的轴对称固结控制方程,可用于非饱和膨润土防渗缓冲层的固结特性分析。






 2021, Vol. 53
2021, Vol. 53


