2. 广东粤港供水有限公司,广东 深圳 518021;
3. 深圳市拓安信计控仪表有限公司,广东 深圳 518100
2. Guangdong GDH Water Co., Ltd., Shenzhen 518021, Guangdong, China;
3. Shenzhen ANSO Measurement & Control Instrument Co., Ltd., Shenzhen 518100, Guangdong, China
供水管网漏损控制过程可分为漏损现状评估、漏损监测以及漏损控制.在我国提倡以分区计量管理作为漏损控制方法背景下,漏损现状评估是首要工作.世界卫生组织统计资料表明:欧亚大陆国家管网漏损水量中的70%为漏失水量[1].因此,将漏失水量作为漏损评估指标可在一定程度上进行管网漏损现状评估.已有研究提出的漏失量估计方法包括水量平衡法[2]、夜间最小流量法[3]、漏失模型预测法[4]、卡曼滤波法[5]、盲源分离法[6].水量平衡法依据国际水协(IWA)提出的水量平衡表划分总供水量,但免费供水量和表观漏损水量均为估计值,且仪表计量误差会产生累积效应,影响计算结果.夜间最小流量法中,最小夜间流量时刻的用户用水量由经验值估算得出,结果的精确性和可靠性不高.漏失模型预测法需要大量漏失统计历史数据作为前提,且预测模型经验参数的选取具有主观性,没有考虑气温、节假日等因素对用水量影响,难以保证预测精度.卡曼滤波法只有在以天为最小单位时,管网漏失量方差才大致相等,在更小的时间间隔下,应用前提条件不能保证.盲源分离法在源信号满足非高斯性和独立性的要求下,只需利用管网入口处的压力和流量数据便可成功分离漏失量,对时间间隔以秒计算时也能准确实现分离,具有数据需求量少、易于实测、分离结果准确的优点.综合以上方法,利用盲源分离法进行供水管网漏失量分离,并针对已有的盲源分离算法进行改进,以得到更好的分离效果.
1 盲源分离理论盲源分离是指从多个观测到的混合信号中提取、恢复(分离)出不能直接观测的原始信号过程.这里的“盲”意味着源信号是不可观测的,并且混合系统特性是未知的或只知少量先验知识.独立成分分析(ICA)是求解盲源信号分离问题的主要方法,是一种基于源信号独立性的盲源信号分离方法[7].ICA的求解步骤是:根据统计独立原则建立观测信号的目标函数,然后采用优化算法分离观测信号,使得输出分量在统计学上尽最大可能独立或者完全独立,便可以对信号进行分离[8].
盲源分离用于漏失量分离是以管网入口处的压力和流量数据作为观测信号,将管网漏失量和用水量作为源信号[9],在两个源信号满足统计独立的情况下,采用上述求解过程完成漏失量分离.
1.1 漏失量分离模型漏失量分离模型如下
| $ \left[ \begin{array}{l} {x_1}\left( t \right)\\ {x_2}\left( t \right) \end{array} \right] = \mathit{\boldsymbol{X}} = \mathit{\boldsymbol{AS}} = \left[ \begin{array}{l} {a_{11}}\;\;\;\;{a_{12}}\\ {a_{21}}\;\;\;{a_{22}} \end{array} \right] \cdot \left[ \begin{array}{l} {s_1}\left( t \right)\\ {s_2}\left( t \right) \end{array} \right]. $ | (1) |
式中:X为观测信号矩阵,x1(t)为管网入口处供水总流量,x2(t)为供水管网入口处压力值,A为混合矩阵,a11、a12、a21、a22为混合矩阵中的元素,S为源信号矩阵,s1(t)为用水量值,s2(t)为漏失量值.
1.2 求解算法选取模型求解过程中,分离算法的选取是准确快速分离漏失量的关键.高金良等[6]首次应用快速独立成分分析(FastICA)算法分离出漏失量.郑成志[10]对盲源分离算法进一步筛选,得到分离效果优于FastICA算法的约束独立成分分析(CICA)算法,但在数据处理过程中,CICA算法存在误收敛问题,影响分离效果.
米建勋[11]基于CICA算法,通过重启算法并将初始权值向量旋转90°,以作为新的权值向量方法,有效解决了CICA算法误收敛问题,得到了改进的ICA-R算法.陈莹等[12]通过进行多信号提取仿真实验,利用信噪比和相关系数作为提取性能量化指标,证明了改进的ICA-R算法相比ICA-R算法,在信号提取精度、鲁棒性和收敛速度上的优势.顾玲玲等[13]从理论上对FastICA算法分析得出,FastICA在提取弱信号方面不足,并结合弱信号分离试验证实,包含先验信息的ICA-R算法在提取弱信号精度上优于未利用先验信息的FastICA算法.以上研究间接证明改进ICA-R算法相比FastICA算法在信号提取精度上的优势,为将改进算法用于漏失量分离提供理论基础.本文将改进ICA-R算法用于供水管网漏失量分离,并与FastICA直接对比,对改进ICA-R算法的优越性进行验证.
2 独立成分分析用于漏失量分离在将独立成分分析用于漏失量分离过程中,对于漏失量和用水量两个源信号是否完全独立,李娟娟等[6]认为,两源信号相互独立且互不影响.郑成志[10]提到,两源信号存在一定相关性,相关程度与所处管网中位置和管网运行情况有关.为避免对不同情况下源信号相关性的讨论,本文在两个源信号独立性强弱不同情况下,分别采用改进ICA-R和FastICA两种算法进行漏失量分离,以验证算法分离效果.
2.1 目标函数选取ICA中常用的目标函数包括互信息最小化、似然函数极大化和非高斯性最大化3种.漏失量分离中,需要根据源信号特性和求解过程选取合适的目标函数.
漏失量分离过程如下
| $ \left[ \begin{array}{l} {y_1}\left( t \right)\\ {y_2}\left( t \right) \end{array} \right] = \mathit{\boldsymbol{Y}} = \mathit{\boldsymbol{WX}} = \mathit{\boldsymbol{WAS}} = \mathit{\boldsymbol{GS}} = \mathit{\boldsymbol{G}} \cdot \left[ \begin{array}{l} {s_1}\left( t \right)\\ {s_2}\left( t \right) \end{array} \right]. $ | (2) |
式中:y1(t)和y2(t)为所得分离信号,W为分离矩阵,G为分离矩阵与混合矩阵乘积.
根据中心极限定理[14]:两个相互独立随机变量相加形成的分布比两个源信号中任何一个都更接近于高斯分布.则在漏失量分离中,由漏失量和用水量形成的分离信号y1(t)和y2(t)的高斯性要比两源信号s1(t)和s2(t)的高斯性强.当分离信号是成功分离的一个源信号时,分离信号高斯性最弱.因此,分离信号的非高斯最大化便是分离过程求解的目标.
峭度和负熵是较为常用的非高斯性评价指标.峭度的计算简单,但对野值非常敏感并且鲁棒性很差.负熵的计算过程复杂,且由于服从高斯分布的变量熵值最大,负熵总是非负值.结合二者的优势,用高阶累积量的密度展开式估计负熵,将其中多项式替换后得到的近似负熵作为度量非高斯性的指标,选取近似负熵最大化作为分离信号求解的目标函数.
2.2 信号处理及效果评价漏失量分离过程中,为减轻模型运算压力,需要对观测得到数据进行预处理,去均值中心化、球化、单位标准正交化,之后采用改进ICA-R和FastICA两种算法分离得到漏失量和用水量的趋势,使用皮尔逊相关系数评价分离效果,得到较优分离算法.
此时得到的源信号的分离趋势不具有任何物理意义,是在真实源信号基础上进行缩放和平移得到的.为获得源信号,需要通过分离趋势得到源信号尺度[15]即进行幅值还原,近而求得每一时刻的分离漏失量和用水量还原值,对分离效果较优算法的分离趋势进行幅值还原,利用平均相对误差评价算法分离误差,评价该算法的分离精度.
3 实验平台及方案设计为比较改进ICA-R和FastICA用于漏失量分离效果,采用算例管网模型模拟在不考虑系统噪声的情况下管网漏失,验证在理想状态下算法分离效果.为更准确模拟真实管网漏失情况,搭建管网漏失实验平台模拟不同用水工况和不同漏点个数管网漏失状况,保证实验结果可靠性.
3.1 算例管网模型算例管网模型利用EPANET 2.0构建漏失模型,通过改变时变化系数,对不同漏点个数、不同漏点位置的管网漏失进行延时模拟.以1 d 24 h用水情况为一个周期,共采集168 h的用水数据.根据采集得到的入口流量和压力数据,分别利用改进ICA-R和FastICA进行无误差无噪声分析.
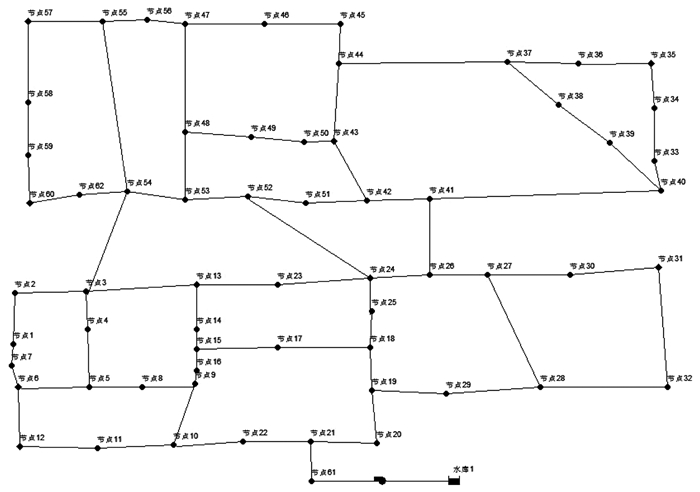
算例管网模型采用单水源供水,由水泵从高位水池取水并输送至配水管网.管网共包含62个节点,76条管段.每个管网节点处地面标高取相同值,采用海曾威廉公式计算水头损失,平差精度为1%,最大迭代次数设置为40.管网中管段管径位于150~1 000 mm.管网模型见图 1.
|
图 1 算例管网模型 Fig. 1 Example pipe network model |
算例管网模型共进行6组实验,漏点数目为2~7个,实验方案见表 1.
| 表 1 算例管网模型实验方案设计 Tab. 1 Experimental design of the example pipe network model |
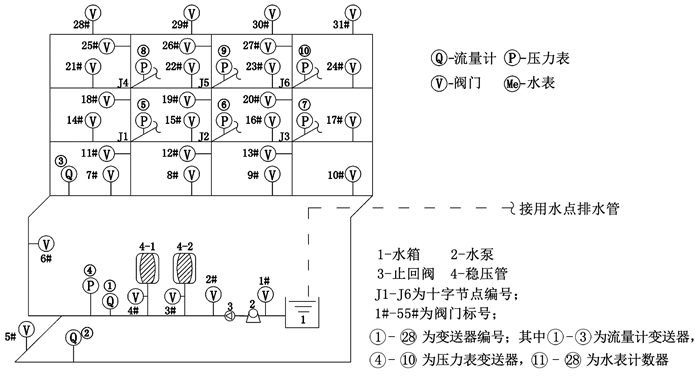
为检验漏失模型的准确度,搭建有管网漏失实验平台:主干管(DN50)与水箱相连,由一台变速泵将水压入配水管中.管网中支管(DN32)形成12个环,共有6个十字节点,每个节点处通过用户管(DN20)连接3个用水点.在管网入口处安装流量计和压力表,在节点处安装远传压力表,在用水点处安装在线水表,管网内远传数据可通过动态模拟平台实时获取.管网中共有52个节点、64条管段、18块水表、7块远传压力表、3台流量计.管网漏失实验平台示意见图 2,用户用水点详图见图 3.
|
图 2 管网漏失实验平台示意图 Fig. 2 Schematic diagram of experimental platform for pipe network leakage |

|
图 3 用户用水点详图 Fig. 3 Details of users' water consuming points |
实验平台中选择上面两排共12个用水点作为用水点,最下面一排共6个用水点作为漏失点.通过最下排开启阀门个数控制漏点数目,通过调节上面两排阀门开度控制漏失量变化,以此模拟不同漏点个数和不同漏失率下的管网运行状况.利用收集的管网入口处压力和流量数据检验改进ICA-R和FastICA漏失量分离效果.实验平台共设计8组实验,每组实验均设置用水量为0时的工况,每组实验有24个工况,每组持续120 s.实验方案设计见表 2.
| 表 2 漏失实验平台实验方案设计 Tab. 2 Experimental design for leakage experimental platform |
根据算例管网模型和漏失实验平台所得两源信号相关系数,按照0~0.3为弱相关、0.3~0.6为中等相关、0.6~1.0为强相关这一标准将各组实验分为源信号强相关、中等强度相关和不相关(弱相关)3类.比较在源信号相关强度不同的情况下两种算法漏失量分离效果.
4.1 算例管网模型以实验1为例,该组源信号的相关系数为0.78,呈现强相关关系即弱独立性.在对源信号进行预处理后,分别使用两种算法分离漏失量趋势,经幅值还原后得到漏失量值.所得分离趋势及还原漏失量见图 4.使用相关系数评价分离效果,FastICA处理得到漏失量分离趋势与源信号相关系数为10.79%,改进ICA-R处理得到漏失量分离趋势与源信号相关系数为99.99%,改进ICA-R漏失量分离效果明显优于FastICA.由此可说明,在源信号存在强相关关系的情况下,FastICA漏失量分离效果不佳,而改进ICA-R漏失量分离效果不受影响.对改进ICA-R得到分离趋势进行幅值还原,求得漏失量的平均相对误差为2.74%,表明利用改进ICA-R分离漏失量精度高.

|
图 4 FastICA算法和改进ICA-R算法分离得到的漏失量趋势及还原漏失量 Fig. 4 Leakage trend and reduction leakage obtained by FastICA and improved ICA-R |
改进ICA-R用于算例管网模型分离漏失量,显示出很好的分离效果.但由于算例管网模型中不存在仪器计量、人为读数等误差,不能保证改进ICA-R在实际管网中的适用性.因此,将改进ICA-R用于实际漏失实验平台中,进一步验证分离效果.使用两种算法获得的6组实验分离趋势的皮尔逊相关系数如表 3所示.
| 表 3 FastICA和改进ICA-R分离结果分析 Tab. 3 Analysis of separation results of FastICA and improved ICA-R |
以实验5为例,该组源信号相关系数为0.02,呈现弱相关关系,即两源信号呈现强独立性.在对源信号进行预处理后,使用两种算法分离漏失量趋势,经幅值还原后得到漏失量值.所得分离趋势及还原漏失量见图 5.采用相关系数评价分离效果,FastICA处理得到漏失量分离趋势与源信号相关系数为77.47%,改进ICA-R处理得到漏失量分离趋势与源信号相关系数为94.15%.在实验2中,两源信号呈现强相关关系,对信号处理后,由FastICA处理得到漏失量分离趋势与源信号相关系数为34.93%,由改进ICA-R处理得到漏失量分离趋势与源信号相关系数为92.19%.由此可见,无论源信号相关性如何,使用改进ICA-R分离效果均优于FastICA.

|
图 5 FastICA算法和改进ICA-R算法分离得到的漏失量趋势及还原漏失量 Fig. 5 Leakage trend and reduction leakage obtained by FastICA and improved ICA-R |
对改进ICA-R处理得到漏失量数据进行处理分析,得到漏失量平均相对误差分析,见表 4.可以看出,漏失量分离平均相对误差在15%以内.由此可说明,改进ICA-R分离精度高,可作为一种实际管网漏失量计算的参考方法.
| 表 4 改进ICA-R分离漏失量平均相对误差分析 Tab. 4 Average relative error of separation leakage by improved ICA-R |
针对传统CICA算法用于漏失量估计中存在误收敛问题,提出利用改进ICA-R算法用于漏失量计算.利用EPANET 2.0搭建的算例管网模型和实际漏失实验平台分别进行实验验证,结果表明:改进ICA-R算法得到漏失量分离信号与源信号的相关系数维持在90%附近,分离效果较CICA稳定.改进ICA-R漏失量平均相对误差维持在15%以内,能为漏失量计算提供参考.该方法可用于分区计量管理实施前管网漏损现状评估,便于各水司采取针对性漏损控制措施.
| [1] |
刘阔, 赵顺萍, 刘锁祥, 等. 《城镇供水管网漏损控制及评定标准》CJJ 92—2016重点内容解读[J]. 城镇供水, 2017(5): 39. LIU Kuo, ZHAO Shunping, LIU Suoxiang, et al. Key content interpretation: Urban water supply network leakage control and evaluation standards: CJJ 92-2016[J]. City and Town Water Supply, 2017(5): 39. DOI:10.14143/j.cnki.czgs.2017.05.008 |
| [2] |
CICHON T, KROLIOWSKA J. Reduction of water losses through metering of water supply network districts[J]. Environmental Engineerin, 2017, 59. |
| [3] |
张瑛. 供水管网漏损分析与漏水量模型建立方法的研究[D]. 天津: 天津大学, 2010 ZHANG Ying. A research on leakage analysis and establishing leakage model of water distribution system[D]. Tianjin: Tianjin University, 2010 |
| [4] |
GUPTA A, KULAT K D. A selective literature review on leak management techniques for water distribution system[J]. Water Resources Management, 2018, 32(10): 3247. DOI:10.1007/s11269-018-1985-6 |
| [5] |
简彩, 姚芳, 赵志领. 应用Kalman滤波算法计算供水管网漏失量[J]. 哈尔滨工业大学学报, 2017, 49(8): 60. JIAN Cai, YAO Fang, ZHAO Zhiling. Applying Kalman filtering algorithm to calculate leakage of water distribution system[J]. Journal of Harbin Institute of Technology, 2017, 49(8): 60. DOI:10.11918/j.issn.0367-6234.201605097 |
| [6] |
高金良, 李娟娟, 郑成志, 等. 区域供水管网盲源分离漏失量研究[J]. 哈尔滨工业大学学报, 2015, 47(6): 33. GAO Jinliang, LI Juanjuan, ZHENG Chengzhi, et al. Study on leakage of regional distribution network using blind source separation[J]. Journal of Harbin Institute of Technology, 2015, 47(6): 33. DOI:10.11918/j.issn.0367-6234.2015.06.006 |
| [7] |
李成杰. 盲源信号分离算法研究及应用[D]. 成都: 电子科技大学, 2017 LI Chengjie. Research on algorithm and application of blind source signal separation[D]. Chengdu: University of Electronic Science and Technology of China, 2017 |
| [8] |
潘子逸. 基于ICA的盲源分离频域算法研究[D]. 广州: 华南理工大学, 2018 PAN Ziyi. Research on the algorithm of frequency domain blind source separation based on ICA[D]. Guangzhou: South China University of Technology, 2018 |
| [9] |
GAO Jinliang, YAO Fang, XU Yongpeng, et al. Analysis model of physical leakage flow based on blind source separation theory[J]. Procedia Engineering, 2017, 186: 269. DOI:10.1016/j.proeng.2017.03.241 |
| [10] |
郑成志. 基于信号处理算法的供水管网物理漏损流量分析模型研究[D]. 哈尔滨: 哈尔滨工业大学, 2015 ZHENG Chengzhi. Research on leakage discharge analysis model of water distribution network based on algorithm for signal processing[D]. Harbin: Harbin Institute of Technology, 2015 |
| [11] |
米建勋. 带参考信号的独立分量分析理论及其应用研究[D]. 合肥: 中国科学技术大学, 2010 MI Jianxun. The study of independent component analysis with reference and its applications[D]. Hefei: University of Science and Technology of China, 2010 |
| [12] |
陈莹, 王法松, 王忠勇, 等. 基于改进ICA-R算法的多用户信号盲提取[J]. 通信技术, 2016, 49(3): 282. CHEN Ying, WANG Fasong, WANG Zhongyong, et al. Blind extraction of multi-user signals based on modified ICA-R algorithm[J]. Communications Technology, 2016, 49(3): 282. DOI:10.3969/j.issn.1002-0802.2016.03.007 |
| [13] |
顾玲玲, 刘国庆. 一种参考独立成分分析算法在弱信号提取中的应用[J]. 计算机科学, 2016, 43(6): 122. GU Lingling, LIU Guoqing. Application of ICA-R algorithm in weak signal extraction[J]. Computer Science, 2016, 43(6): 122. DOI:10.11896/j.issn.1002-137X.2016.6.025 |
| [14] |
李广彪, 张剑云, 毛云祥. 盲源分离中的非高斯性极大准则[J]. 舰船电子对抗, 2005, 28(5): 33. LI Guangbiao, ZHANG Jianyun, MAO Yunxiang. Nongaussian maximization criterion using in blind source separation[J]. Shipboard Electronic Countermeasure, 2005, 28(5): 33. DOI:10.16426/j.cnki.jcdzdk.2005.05.010 |
| [15] |
郑成志, 高金良, 何文杰. 基于FastICA算法的物理漏损流量分析模型[J]. 浙江大学学报(工学版), 2016, 50(6): 1031. ZHENG Chengzhi, GAO Jinliang, HE Wenjie. Leakage discharge analysis model based on FastICA algorithm[J]. Journal of Zhejiang University (Engineering Science), 2016, 50(6): 1031. DOI:10.3785/j.issn.1008-973X.2016.06.004 |
 2021, Vol. 53
2021, Vol. 53


