随着城市规模的扩张,供水管网规模渐增,结构无序性加剧,易带来运行调度不便、漏损率过高等问题.供水管网分区管理是应对这些问题的有效手段[1].管网的分区方法可分为人工经验方法和计算分区方法[2].人工经验方法主要依据自然地理边界或人为屏障作为区域边界,结合人的主观经验进行分区.计算分区方法多基于图论和复杂网络理论创建.人工经验方法适应于在建设前即有分区考虑的新建管网或边界明确的现状管网,但是对于复杂现状管网,分区方案难于制定.而计算分区方法可以有效保障分区的科学性和便捷性,对于复杂现状管网实现区块化的新型管理模式具有重要意义.
计算分区方法中,以深度优先搜索或广度优先搜索为基础,寻找管网系统中的强连接结构,并据此分区的算法[3-4]出现较早且有持续性应用;以模块度增加为评判标准,衡量区域内部连接紧密性的社区发现算法[5-6]是较为经典的方法;利用特征值和特征向量挖掘管网系统特征的谱聚类算法[7-8]是近年来的研究热点.此外,还有以能量损失最小化为核心的最短路径算法[9]、以平衡各分区信息为核心的图划分算法[10]等.然而这些方法缺乏系统性的比较,分区实践时难以选择合适的方法.现有少数比较研究[11-12]忽略了不同管网之间固有特征的差异,仅就1~2个特定案例对特定指标简单分析.而不同管网案例受拓扑结构、运行状态、模型质量等多重因素的影响差异很大,在特定案例上得出的研究结论参考价值有限.另外,选取的不同赋权形式和分区数也会对结果造成影响,分区过程中应对这两个问题予以考虑.
深度优先搜索-部分接近度算法(DFS-PCC)、快速迭代模块度的贪心算法(CNM)和遗传优化的谱聚类算法(GA-SC)分别是上述前3类算法中的一种代表性算法.本文对此3种方法在5个标准管网案例上的分区效果进行了比较,并分析了算法赋权对分区结果的影响,讨论了不同方法确定分区数的差异.对比方法性能时,考虑了管网案例的固有属性差异.
1 计算分区方法 1.1 深度优先搜索-部分接近度算法深度优先搜索-部分接近度算法先使用深度优先搜索发现网络系统中存在的若干极大强连通子图,再将极大强连通子图外的所有节点按照部分接近度最小原则,并入相应的子图.对应于实际管网,极大强连通子图是指在一段时间内存在环流现象的最大管网结构.确定出强连通分区后,使用部分接近度函数判断剩余节点到每个区域的能量损失,将剩余节点分入最合适的区域中.其具体步骤为[13]:
1) 连续模拟一段时间,将模拟结果以有向图形式表示.使用Tarjan搜索算法[14]访问所有节点,得到各极大强连通子图.在其中选择确定K个极大强连通子图,作为强连通分区.
2) 以水头差ΔHij表示供水高峰时刻从管段起点i到管段终点j的能量损失,建立以ΔHij为权重的管网邻接矩阵,使用Dijkstra算法[15]求解得到从任意节点i到另一节点j的最小能量损失.
3) 计算节点i至区域Tr的部分接近度
| $ P = \frac{{{J_T}}}{{\mathop \sum \limits_{j \in {\mathit{\boldsymbol{T}}_r}} \left| {\Delta {H_{ij}}} \right|}},i \notin {T_r}. $ | (1) |
式中:Tr为第r个区域,r=1, 2, …, K;JT为区域Tr中的节点数.若部分接近度越大,节点i与该区域特征越接近.
4) 对于不属于任何强连通分区的各个节点,计算其与K个区域Tr的部分接近度,将各个节点划入与其部分接近度最高的区域中,直至所有节点都被划分完毕为止.
1.2 快速迭代模块度的贪心算法模块度M是用来衡量网络社区结构划分质量的函数,其定义为网络中连接社区结构内部节点的边所占比例与随机网络中连接社区结构内部节点的边所占比例的期望值之差[16-17].社区定义为连接紧密的边和节点构成的子图,社区外部的边应比社区内部连接得更加稀疏[18].社区划分质量越高,社区内部连接越紧密,模块度越大.其计算公式可表示为
| $ M = \frac{1}{{2m}}\mathop \sum \limits_{vw} \left[ {{A_{vw}} - \frac{{{k_v}{k_w}}}{{2m}}} \right]\delta \left( {{C_v}, {C_w}} \right). $ | (2) |
式中:A为网络的邻接矩阵,v和w为节点,m为网络的边数,kv为节点v的度,Cv为节点v所在的社区.若节点v和节点w在同一社区,则Cv=Cw,δ=1, 否则δ=0.
| $ {A_{vw}} = \left\{ \begin{array}{l} 1, {\rm{节点}}v{\rm{和节点}}w{\rm{相连}};\\ 0, {\rm{其他}}. \end{array} \right. $ | (3) |
基于贪心算法的思想,从每个节点为一个社区开始,沿着使模块度增加最大或减少最小的方向不断合并节点,直至获得期望的社区划分结果.其具体步骤为[5]:
1) 初始化.每个节点为一个社区,初始模块度M=0.计算辅助矩阵e和辅助向量a.
| $ {e_{ij}} = \left\{ \begin{array}{l} 1/2m, {\rm{节点}}i{\rm{和节点}}j{\rm{相连}};\\ 0, {\rm{其他}}. \end{array} \right. $ | (4) |
| $ {a_i} = {k_i}/2m. $ | (5) |
式中:eij表示节点i与节点j连接的度与网络的度的比值,ai表示节点i的度与网络的度的比值.
这样,初始的模块度增量矩阵ΔM的元素构成为
| $ \Delta {M_{ij}} = \left\{ \begin{array}{l} 1/2m - {k_i}{k_j}/{\left( {2m} \right)^2}, {\rm{节点}}i{\rm{和节点}}j{\rm{相连}};\\ 0, {\rm{其他}}. \end{array} \right. $ | (6) |
2) 建立最大值堆H,储存模块度增量矩阵ΔM中每一行的最大元素.选择其中最大的ΔMij,合并相应社区i和j,合并后社区标号记为j.依次更新模块度增量矩阵ΔM、最大值堆H和辅助向量a.
更新ΔM时,删除第i行和第i列,更新第j行和第j列的元素
| $ \Delta M{\prime _{jk}} = \left\{ \begin{array}{l} \Delta {M_{ik}} + \Delta {M_{jk}}, {\rm{社区}}k{\rm{与社区}}i{\rm{和}}j{\rm{都相连}};\\ \Delta {M_{ik}} - 2{a_j}{a_k}, {\rm{社区}}k{\rm{仅与社区}}i{\rm{相连}};\\ \Delta {M_{jk}} - 2{a_i}{a_k}, {\rm{社区}}k{\rm{仅与社区}}j{\rm{相连}}. \end{array} \right. $ | (7) |
更新a时,令
| $ a{\prime _j} = {a_i} + {a_j}, $ | (8) |
| $ a{\prime _i} = 0. $ | (9) |
3) 重复步骤2),直至得到预期的分区数K.
1.3 遗传优化的谱聚类算法谱聚类算法将原始数据集映射到由K个正交向量组成的K维空间R,以此空间近似表示原始数据的内在特征,继而使用K-means算法进行聚类.由于K-means算法对初始聚类中心敏感,随机产生的不同初始聚类中心会得到不同的聚类结果.为提高方法的全局搜索能力,每次循环过程中使用遗传算法优化聚类中心,以得到更稳定的分区结果.此方法的具体步骤为[7, 19]:
1) 计算管网的拉普拉斯(Laplacian)矩阵.非规范化拉普拉斯矩阵为
| $ \mathit{\boldsymbol{L}} = \mathit{\boldsymbol{D}} - \mathit{\boldsymbol{A}}. $ | (10) |
式中:A为管网的邻接矩阵,D为对角矩阵,对角线上的值为节点的度
| $ {D_{ii}} = \mathop \sum \limits_{j = 1}^n {A_{ij}}. $ | (11) |
规范化拉普拉斯矩阵为
| $ {\mathit{\boldsymbol{L}}_{sym}} = {\mathit{\boldsymbol{D}}^{ - \frac{1}{2}}}\mathit{\boldsymbol{L}}{\mathit{\boldsymbol{D}}^{ - \frac{1}{2}}}. $ | (12) |
2) 计算Lsym的特征值.确定分区数K后,选择K个最小特征值对应的特征向量x1, x2, …, xK,构造矩阵X=[x1, x2, …, xK]∈Rn×K.将矩阵X的行向量变为单位向量,得到矩阵Y,将矩阵Y的每一行作为RK空间中的一点y.
| $ {Y_{ij}} = \frac{{{X_{ij}}}}{{\sqrt {\mathop \sum \limits_j } X_{ij}^2}}. $ | (13) |
3) 使用遗传优化的K-means算法聚类.随机选取K个聚类中心,使用K-means算法将每个空间点分配到与其最近的聚类中心对应的聚类.每次聚类后,使用遗传算法校正聚类中心,再次进行聚类.校正时,定义所有空间点到其各自所属聚类的聚类中心的欧式距离平方和为距离平方和DS,以DS最小化为目标函数度量每次迭代的聚类质量,并通过线性排序确定适应度.
| $ {D_S} = \mathop \sum \limits_{i = 1}^K \mathop \sum \limits_{y \in {C_i}} d{(\mathit{\boldsymbol{y}}, {\mathit{\boldsymbol{c}}_i})^2}. $ | (14) |
式中:Ci为第i个聚类,ci为其聚类中心,y为某个空间点,K为聚类总数,d表示y到ci的欧式距离.
2 评价指标 2.1 分区结果的评价指标影响管网分区的首要因素是分区目的,除此之外,主要影响因素还有管网属性、分区方法、赋权形式和分区数量.根据分区目的和具体需求选用评价指标对分区结果进行评判,可以从特定角度量化分区结果的优劣,继而指导分区方法的选择.选取归一化互信息、模块度、节点数均衡性、联络管数量、联络管流量和联络管流量波动性6项指标.
1) 归一化互信息[20](normalized mutual information, NMI).NMI指标可表征计算分区结果与已有的经验(或基准)分区结果的一致性,进而评价计算分区结果的合理性.若已知经验法的分区结果,可进行带基准的分区评价;NMI越接近1,计算分区与经验分区结果越接近,则计算分区结果较合理.其计算公式为
| $ NMI\left( {\mathit{\boldsymbol{V}}, \mathit{\boldsymbol{W}}} \right) = \frac{{ - 2\mathop \sum \limits_{i = 1}^{{C_V}} \mathop \sum \limits_{j = 1}^{{C_W}} {N_{ij}}{\rm{log}}\left( {\frac{{{N_{ij}}{N_t}}}{{{N_{i.}}{N_{.j}}}}} \right)}}{{\mathop \sum \limits_{i = 1}^{{C_V}} {N_{i.}}{\rm{log}}\left( {\frac{{{N_{i.}}}}{{{N_t}}}} \right) + \mathop \sum \limits_{j = 1}^{{C_W}} {N_{.j}}{\rm{log}}\left( {\frac{{{N_{.j}}}}{{{N_t}}}} \right)}}. $ | (15) |
式中:V为经验分区结果,W为计算分区结果,CV和CW分别为两结果的社区数;N为混乱矩阵,Nij为既在V的社区i中出现又在W的社区j中出现的节点数,Ni.和N.j分别为第i行和第j列之和;Nt为节点总数.
2) 模块度M.一般情况下,管网的经验分区结果未知.此时可从图论和复杂网络理论角度,遵循管网拓扑结构特征,进行不带基准的分区评价.使用模块度(式(2))评价社区的优劣,模块度越接近1,社区结构越明显,分区效果越好.
3) 节点数均衡性B.从分区管理角度,各区域间节点数量应较为接近,区域规模不应相差过大.使用节点数均衡性可以反应各区域间规模的差异.节点数均衡性用各个分区间节点数的标准差表示,标准差越小,均衡性越高,管理成本越小.其计算公式为
| $ B = \sqrt {\frac{1}{{{C_n}}}\mathop \sum \limits_{i = 1}^{{C_n}} {{\left( {{n_i} - \bar n} \right)}^2}} . $ | (16) |
式中:Cn为分区数,ni为第i个区域的节点数,n为各区域平均节点数.
4) 联络管数量、流量、流量波动性.联络管数量是指连接各分区间的管道数量.联络管所在位置需安装流量计或阀门,因而联络管数量可以间接反映分区改造所需的投资.从投资成本角度,联络管数量应相对较少.
联络管流量可以反映分区间的水量交换.选择高峰时刻的流量进行分析,若联络管的流量较大,加装流量计可监测到的水量较大,测量误差对测量结果的影响较小.若联络管的流量较小,则此管道不是供水主力路径,条件适宜时可在此处设置阀门形成物理分割.
联络管流量波动性可以反应一段时间内联络管流量的波动.基于管网延时水力模型,一段时间内联络管流量的标准差可表征联络管流量波动性.从监测和调控区域水量角度,流量计应安装在联络管流量和流量波动性均较大的管道上,以得到较好的监测效果.
2.2 管网属性的表征指标不同管网案例的固有属性可能相差很大.为量化这些差异,除使用节点数、管道数等指标表征管网基础信息外,还可使用复杂网络理论中的指标评价管网的固有属性.选取平均度、聚类系数、环状系数、标准结构熵4项指标.
1) 平均度<k>[18]可以反应管网的连接特性.其计算公式为
| $ \left\langle k \right\rangle = \frac{{2m}}{n}. $ | (17) |
式中:m为网络中的边数,n为网络中的节点数.平均度越高,各节点连接的边数越多,管网连接越复杂.
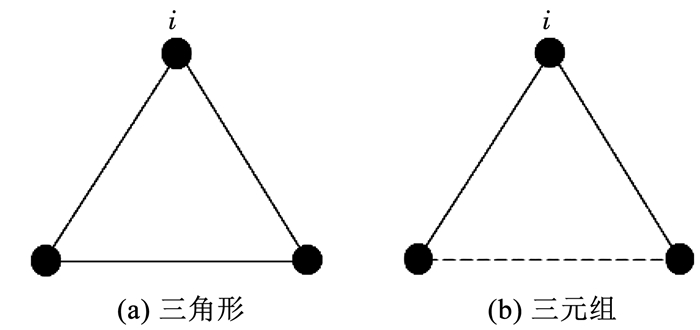
2) 聚类系数CC[18]可以反应管网的聚类特性.某一节点i的聚类系数定义为与该点相连的三角形数量和三元组数量之比.其中,三角形是指网络中存在的3个节点由3条边两两相连的结构,如图 1(a)所示;三元组是指网络中存在的3个节点中,节点i至少与其两个邻居节点相连的结构,如图 1(b)所示.图中虚线表示此边有、无均可,即三角形是三元组的一种特殊形式.全网的聚类系数为所有节点聚类系数的均值.其计算公式为
| $ {C_{\rm{C}}} = \frac{1}{n}\mathop \sum \limits_{i = 1}^n \frac{{{E_i}}}{{C_{{b_i}}^2}}. $ | (18) |
|
图 1 三角形和三元组 Fig. 1 Triangles and triples |
式中:Ei为节点i的bi个邻居节点间实际存在的边数,C2bi为节点i的bi个邻居节点间可存在的最大连接边数.聚类系数在0~1取值.聚类系数越高,管网中呈强三角形连接结构越明显.
3) 环状系数Rm[21]可以反应管网的成环特性.环状系数定义为管网中独立环网数与可能存在的最大独立环网数之比.其计算公式为
| $ {R_{\rm{m}}} = \frac{{m - n + 1}}{{2n - 5}}. $ | (19) |
环状系数越高,管网冗余度越高,成环特性越明显.
4) 标准结构熵E[22]可以反应管网"序"的状态.其计算公式为
| $ \bar E = \frac{{ - 2\mathop \sum \limits_{i = 1}^n {I_i}{\rm{ln}}\;{I_i} - {\rm{ln}}\left[ {4\left( {n - 1} \right)} \right]}}{{2{\rm{ln}}\;n - {\rm{ln}}\left[ {4\left( {n - 1} \right)} \right]}}, $ | (20) |
| $ {I_i} = \frac{{{k_i}}}{{\mathop \sum \limits_{i = 1}^n {k_i}}}. $ | (21) |
式中Ii为第i个节点的重要度.标准结构熵在0~1取值.标准结构熵越大,则各节点的重要度越均衡,网络越呈现无序状态.反之,网络中存在核心节点越少,末梢节点越多,网络越呈现有序状态.
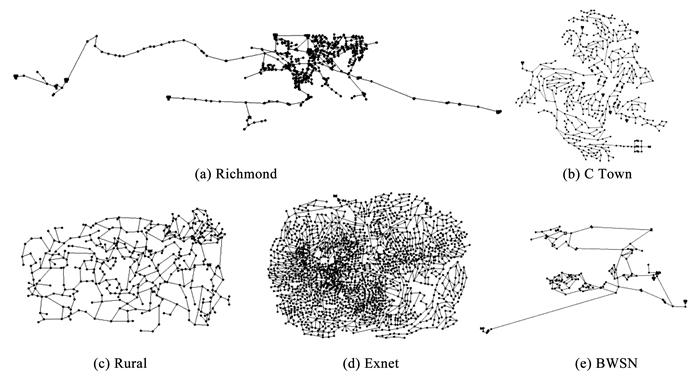
3 结果与分析 3.1 管网案例分析选取5个典型管网案例对第1节所述的3种计算方法进行比较,各管网案例的信息如表 1及图 2所示.其中,使用元件基本信息反应案例规模和管网中的控制因素;使用第2.2节提出的管网属性表征指标量化案例的拓扑差异.
| 表 1 管网案例基本信息 Tab. 1 Basic information of water network cases |
|
图 2 管网案例图示 Fig. 2 Illustration of water network cases |
由表 1可知,5个管网案例的平均度和环状系数大小排序一致,自低到高依次为Richmond、C Town、Rural、Exnet、BWSN.聚类系数仅能评价管网中三角形连接的数量,得到的结果有所局限,聚类特性可由环状系数间接表示.标准结构熵均在0.965~0.976,各管网相差很小,网络的无序程度均较高.因而,主要采用平均度和环状系数表征管网固有属性.
Richmond[23]是英国约克郡的某真实案例.其<k>=2.195,Rm=0.049,树状特性最高,树状分支多分布在管网外围,管网中心仍有部分环状管网;水池和控制元件较多,呈现一定的供水周期性;但3个水池分布在树状管网远端由外向内供水,3个水池处于管网中心,区域特性不明显.
C Town[24]是管网校核竞赛(The Battle of Water Calibration Networks)提供的研究案例.其<k>=2.242,Rm=0.062,树状特性较高;水池较多且分布均匀,供水区域特性且周期性较强;控制元件较多,最终可能形成不同水源供给不同区域的分区结构.
Rural[25]是某真实案例,年平均供水量4 546.090 m3/d.其<k>=2.499,Rm=0.127,环状特性较高,全网连接紧密;没有控制元件调控管网运行,供水区域特性和周期性不强,分区边界不易确定.
Exnet[26]是由英国Exeter大学提供的研究案例,服务人口40万人.其<k>=2.606,Rm=0.152,环状特性较高;管网规模较大,且有5个节点接收来自相邻系统的输水,但控制元件较少,调节能力不足;与Rural案例相似,供水区域特性和周期性不强.
BWSN[27]是管网传感器布设竞赛(The Battle of Water Sensor Networks)提供的研究案例.其<k>=2.760,Rm=0.198,虽环状特性最高,但输配水管较分明,两个水池能够带来一些管道周期性的流向变化;有较多控制元件调控管网运行,可为分区提供帮助.
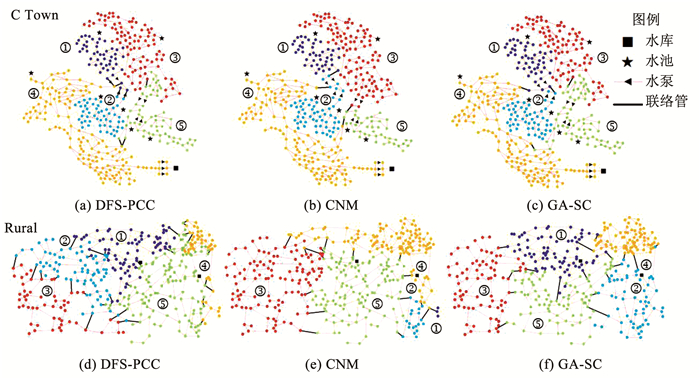
3.2 不同分区方法的比较分别使用第1节的3种方法对各案例分区.BWSN案例节点数较少,设定分区数为3,其他案例设定分区数为5.选取0~12点和0~24点两水力模拟时段分别计算分区结果,所得结果无差异,为减小计算量,后续采用0~12点进行计算.由3.1节可知,C Town案例管网树状特性较高,供水区域特性且周期性较强,有较多元件调控管网运行;与C Town不同,Rural案例管网环状特性较高,供水区域特性和周期性不强,管网中没有控制元件.并且,C Town和Rural两案例节点规模近似,C Town经验法分区结果[24]已知.故选取这两个固有属性差异较大的案例具体分析,并使用其他案例补充说明.C Town和Rural案例的分区结果见图 3,图中不同区域用序号①~⑤表示.使用NMI评价不同分区结果在两案例中的一致性,所得数据统计于表 2.各案例评价指标如表 3第3,4,7列所示(CNM、GA-SC使用无权形式).
|
图 3 C Town和Rural分区结果 Fig. 3 Partition results of C Town and Rural |
| 表 2 不同方法所得结果的一致性 Tab. 2 Consistency of results obtained by different methods |
| 表 3 评价指标比较 Tab. 3 Comparison of evaluation indicators |
由图 3(a)~(c)可知,使用3种方法对C Town分区得到的结果接近.以经验分区结果[24]为基准,DFS-PCC、CNM、GA-SC分区结果与经验分区结果的NMI分别为0.890,0.932,0.881,说明3种计算结果均与经验法结果有较高的吻合度,CNM计算结果与经验法最接近.由表 2可知,以3种计算结果互为基准,DFS-PCC与CNM的NMI为0.872,DFS-PCC与GA-SC的NMI为0.929,CNM与GA-SC的NMI为0.857,说明3种分区结果较为相似.同时,计算上述3种结果的模块度,具体数值依次为0.746,0.738,0.758,各方法连接紧密程度基本一致.由此可知,在树状特性较高且区域性供水特征明显的C Town管网中,3种方法均能得到良好结果.
由图 3(d)~(f)可知,使用3种方法对Rural分区得到的结果有显著差别.由于Rural经验分区结果未知,仅比较3种结果互为基准得到的NMI值.由表 2可知,DFS-PCC与CNM的NMI为0.458,DFS-PCC与GA-SC的NMI为0.436,CNM与GA-SC的NMI为0.506,3种结果均差异较大.由表 3可知,此案例中DFS-PCC、CNM、GA-SC 3种方法所得结果的模块度分别为0.692,0.663,0.750,GA-SC计算结果的模块度最高.由此可知,在环状特性较高且无明显区域性供水特征的管网中,不同方法分区结果差异较大,GA-SC区域内部连接更紧密.
3.2.2 节点均衡性如表 3所示,C Town案例中DFS-PCC、CNM、GA-SC 3种方法所得结果的节点数均衡性依次为33.701,39.408,31.186,Rural案例中依次为27.476,53.484,7.250.固有属性不同的两案例中,均是GA-SC结果中节点数更均衡,且其他3个案例也存在此现象.这是由于GA-SC采用的多路规范割集准则(multiway normalized cut)能够有效规避倾斜问题[28],同时考虑区域间和区域内的连接特性,从而使各区域的节点数更加均衡.
由图 3(e)可知,Rural案例中,CNM计算结果的第1区域仅用一条联络管就能将其与其他区域分开,区域间连接稀疏,对于减少联络管数量效果很好.但此区域只有3个节点,与节点数较多的第3、第5区域规模相差过大,各区域节点数非常不均衡.并且,第1区域的3个节点内部连接并不十分紧密,一定程度上影响了其模块度值.在C Town案例中所得结果与经验法最接近的CNM方法应用在Rural案例中效果不佳.由此可知,在某一特定案例应用较好的分区方法不一定能够很好地适用于其他案例.但就表 3各案例分析结果可知,GA-SC普遍适用性较好.
3.2.3 联络管数量如表 3所示,C Town案例中DFS-PCC、CNM、GA-SC 3种方法所得结果的联络管数量依次为7,4,4,Rural案例中联络管数量依次为38,17,22.固有属性不同的两案例中,DFS-PCC分区结果的联络管数量均高于另两种方法,其他3个案例也存在此现象.这是由于CNM和GA-SC仅考虑管网的拓扑结构,而DFS-PCC除考虑拓扑连通性外,还考虑了能量的变化.这会使DFS-PCC更可能将联络管位置选择在水泵、阀门等控制元件所在的管道上,但同时也会导致联络管数量的增加.C Town案例中,如图 3(a)所示的7个联络管中有3个为水泵所在管道,1个为将状态置于关闭的管道.而Rural案例中没有控制元件和水池,DFS-PCC的特点未能明显表征.且Rural案例拓扑结构复杂,DFS-PCC结果的联络管数更多.
3.2.4 联络管流量与流量波动性联络管流量和联络管流量波动性与具体管网案例有关.如表 3中5个案例所示,通常情况下DFS-PCC分区结果的上述两项指标较CNM和GA-SC更小.这是因为管网中多数管道流量及流量波动性均较小,而DFS-PCC挑选出的联络管数量较多,挑选出的联络管更可能符合多数管道的特征.
3.3 不同赋权形式的比较第1节所述3种方法中,CNM和GA-SC基于复杂网络理论创建,其赋权形式可分为无权和有权两种;而DFS-PCC是基于图论相关理论创建,该方法中没有对于权重的考虑,但考虑了能量变化,故也相当于一种有权算法.在3.2节的比较中,CNM和GA-SC采用常见的无权形式,即仅根据拓扑结构进行分区.本节讨论CNM和GA-SC赋权计算的结果.
CNM和GA-SC赋权计算,可采用管道流量、直径、能量损失等作为边权,也可采用节点需水量等作为点权[11].本节分别以流量q和1/q为边权的赋权形式对5个案例分区.具体计算方式为将第1.2和1.3节中邻接矩阵A分别改写为以q或1/q的赋权形式,即
| $ {A_{vw}} = \left\{ \begin{array}{l} {q_{vw}}{\rm{或}}1/{q_{vw}}, {\rm{节点}}v{\rm{和节点}}w{\rm{相连}};\\ 0, {\rm{其他}}. \end{array} \right. $ | (22) |
其他步骤与无权形式相同.赋权后得到的评价指标如表 3第5,6,8,9列所示.
3.3.1 联络管流量可以通过对GA-SC赋权选择流量较大或较小的管道作为联络管.例如,由表 3中C Town案例可知,对GA-SC赋1/q权,联络管流量较大,平均为91.908 L/s;赋q权,联络管流量较小,平均为32.612 L/s;无权情况下,联络管流量处于两者之间,平均为56.993 L/s.图 4以联络管流量平均值(Qcon)与管网中管道流量最大值(Qmax)之比为纵坐标作图,可以发现取不同案例不同分区数时皆可体现此规律.其原因在于,GA-SC的原理使用权重直接控制不同社区间连接的选择,这与寻求流量较大或较小的管道作为联络管的需求吻合.而CNM没有此明显规律.

|
图 4 GA-SC赋权对联络管选择的影响 Fig. 4 Influence of GA-SC with weights on the selection of feed lines |
管道流量波动性通常与管道流量值存在一定的线性关系.例如,图 5为Rural案例中各管道流量与流量波动性的散点图.可以看出,一般管道流量越大,管道流量波动性越大.对GA-SC赋q权获得的各联络管流量及其波动性多数较小,此两个评价指标的频率分布曲线波峰均最靠前;赋1/q权获得的各联络管流量及其波动性多数较大,两个指标的频率分布曲线波峰均最靠后;无权的频率分布曲线的波峰处于1/q权和q权的波峰之间.图中虚线位置表示各赋权形式联络管流量及波动性均值.表 3中Exnet和BWSN的联络管流量波动性平均值也能够反映出此特点,而C Town和Richmond略有出入是由于此两案例树状特性较高,联络管数很少,平均值受单个管道影响较大.可见,在使用GA-SC以流量为参数的赋权形式选择联络管时,也可以较好地体现所选联络管的流量波动特性.而CNM没有此明显规律.
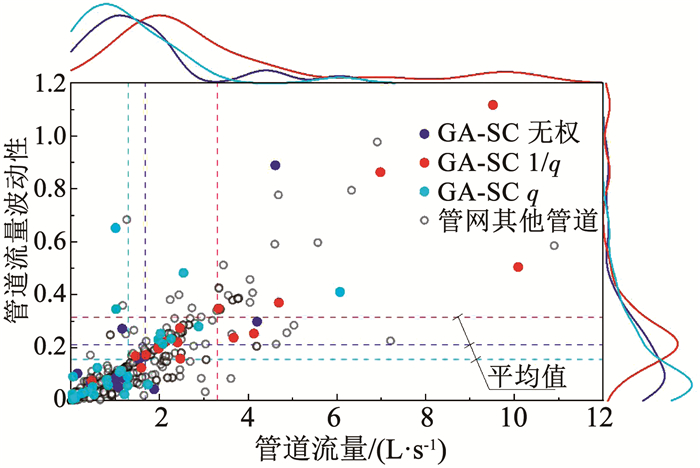
|
图 5 Rural案例中管道流量与流量波动性 Fig. 5 Flow and flow fluctuation of feed lines in Rural |
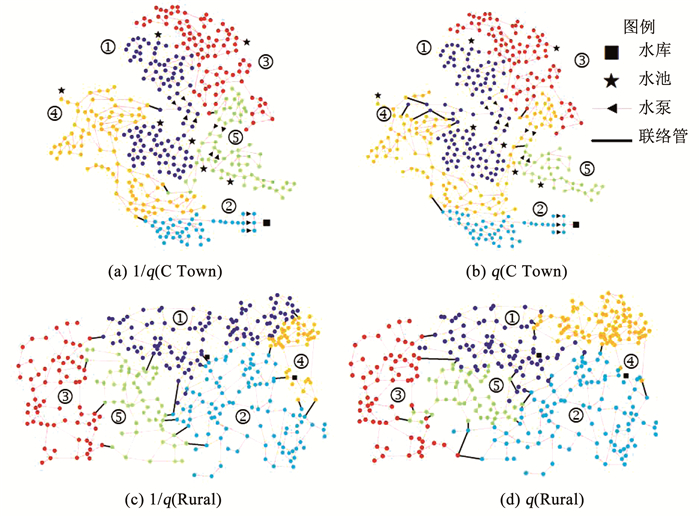
比较不同方法不同赋权形式所需的信息,如表 4所示.可以看出,无权形式的CNM和GA-SC仅需拓扑结构信息就能够进行分区,需获取的数据信息最少.由3.2节的分析可知,对区域供水特征分明的C Town案例,使用无权形式即能达到良好的分区效果.由图 6(a)、(b)赋权计算结果可知,根据管道流量选择联络管位置还会在一定程度上破坏区域特性.
| 表 4 分区所需信息比较 Tab. 4 Comparison of information required for partitioning |
|
图 6 GA-SC的赋权分区结果 Fig. 6 Weighted partition results of GA-SC |
对环状特性较高的Rural案例,拓扑结构不能反映出更多信息.鉴于GA-SC良好的使用灵活性,若模型质量较高,可使用此方法赋权分区.如图 6(c)、(d)所示,由于Rural案例没有控制元件且全网连接紧密,采用赋权分区的形式不会大幅破坏管网的区域特性.
使用DFS-PCC需获取的信息量最多,这表示DFS-PCC能够利用的管网信息更多,但也意味着此方法受管网固有属性影响更强.对于区域供水特征不明显的环状管网,DFS-PCC可能导致强连通分区节点数过少或各强连通分区的空间分布不均,最终导致分区结果不理想.
3.4 分区数的确定在上述比较中,分区数是人为指定的.但是,CNM、GA-SC两方法是可以自动确定分区数的,DFS-PCC方法也可以辅助确定分区数.选择DFS-PCC以及无权形式的CNM、GA-SC对不同案例确定分区数,结果如表 5所示.
| 表 5 分区数的自动确定 Tab. 5 Automatic determination of partition numbers |
1) DFS-PCC可通过获得的极大强连通子图作为确定分区数的参考.在1.1节步骤1)中确定出极大强连通子图数量后,最多可划分的区域数量也随即确定.对类似于Rural的案例,其水池数和控制元件较少,可按照节点数从多到少的顺序并兼顾空间分布的均匀性,选择适宜数量的极大强连通子图作为强连通分区;对类似于C Town的案例,存在较多具有规律性进出水特征的水池,每个水池各属于一个极大强连通子图,可选取位置分布适宜且具有水池的子图作为强连通分区.此方法可通过人为干预选择分区数和强连通分区所在位置,选择的数量和位置不同,会得到不同的分区结果.本节中为统一此方法对各案例确定分区数的方式,选择节点数大于2的所有极大强连通子图数量作为分区数,得到表 5中的结果.
2) CNM通过模块度增量控制迭代终止条件,从而确定分区数.在1.2节步骤3),当模块度增量ΔMij≤0时停止迭代,此时模块度达到最大值,凝聚得到的社区数即为分区数.此方法不需人为干预,获得的分区数唯一且明确.
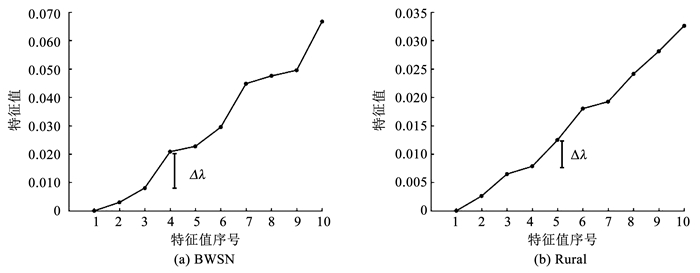
3) GA-SC通过本征间隙[29](Eigengap)确定分区数.在1.3节步骤3),将矩阵Lsym的特征值从小到大排列为λ1≤λ2≤…≤λn的形式.本征间隙是指相邻两个特征值之间的差值.根据矩阵扰动理论,若第k个和第k+1个特征值之间的差值Δλ越大,选取k个特征向量所构成的特征向量空间就越稳定[19].找出较小的k个特征值,若此k个特征值较为接近,而第k+1个特征值相对较大,则将k确定为分区数[29].此方法识别分区数的效果与管网固有特征有关.例如,对区域特征较明显的BWSN案例,如图 7(a)所示,易得出分区数为3.而Rural案例无明显区域特征,如图 7(b)所示,各间隙之间差异不大.
|
图 7 GA-SC分区数的确定 Fig. 7 Determination of partition numbers based on GA-SC |
如表 5所示,对区域特征较明显的BWSN和C Town案例,3种方法确定的分区数较为接近;而对区域特征不明显的其他案例,3种方法确定的分区数差异较大.实际应用时,应根据所需的区域规模做进一步考虑.
4 结论1) DFS-PCC从能量的角度进行分区.此方法在区域供水特征明显、树状特性较高、控制元件数较多的案例上能得到较好效果,且易于选择控制元件所在管道作为联络管;但对于区域供水特征不明显、环状特性较高、控制元件数较少的案例,会造成联络管数量过多,经济性下降.此方法较适用于设计合理、已有潜在分区结构的管网.使用此方法可得到分区数的选取范围.
2) CNM和GA-SC从拓扑结构的角度进行分区.两方法可根据收集的信息和管网特征灵活选用无权或赋权形式,对分区所需信息要求较少.CNM所得结果中联络管数量较少,对于一些区域特性明显、树状特性较高的案例分区效果很好.但对于区域特性不明显、环状特性较高的案例,可能导致区域规模严重不均.此方法时间复杂度较低,适宜快速产生大型管网分区方案.使用此方法可自动确定分区数.
3) GA-SC在连接特性和环状特性不同的5个案例中都能得到较高的模块度、较少的联络管数量,总体适用效果良好.此方法区域节点数均衡性最佳,较适用于以区块化管理为目的的分区.对GA-SC赋权有助于对区域供水特征不明显的案例进行联络管的选择.使用1/q权的赋权形式分区,可选择流量和流量波动性相对较大的管道作为联络管,以便为流量计布设提供参考.当区域特征明显时,使用此方法易于确定分区数.
分区时,应结合管网特征合理选择上述方法.实际工程中,由于受到多重条件制约,分区方案的制定更加复杂.例如,如何合理利用已有检测设备、是否对分区进行实际物理分割、分割后如何保障供水安全,都值得深入探讨.此外,从不同角度制定的多个评价指标相互制约,一般不能在同一分区方案中达到最佳.因而,工程应用单位应根据分区目的和具体需求选择合适的评价指标并对其进行优先级排序,结合管网属性选择适宜的分区方法、赋权形式和分区数量,以做出合理决策.
| [1] |
刘锁祥, 赵顺萍, 曹楠, 等. 供水管网漏损控制研究和实践[J]. 中国给水排水, 2015, 31(10): 24. LIU Suoxiang, ZHAO Shunping, CAO Nan, et al. Research and practice of water loss control of water distribution network[J]. China Water & Wastewater, 2015, 31(10): 24. |
| [2] |
李斌, 蒋浩, 聂锦旭, 等. 基于节点能量冗余差的给水管网DMA分区方法研究[J]. 给水排水, 2017, 43(3): 120. LI Bin, JIANG Hao, NIE Jinxu, et al. Study on automated creation of DMA boundaries of water supply networks based on the difference of energy redundancy of nodes[J]. Water & Wastewater Engineering, 2017, 43(3): 120. DOI:10.3969/j.issn.1002-8471.2017.03.025 |
| [3] |
TZATCHKOV V G, ALCOCER-YAMANAKA V H, ORTÍZ V B. Graph theory based algorithms for water distribution network sectorization projects[C]//Proceedings of Eighth Annual Water Distribution Systems Analysis Symposium. Cincinnati: American Society of Civil Engineers, 2006: 1. DOI: 10.1061/40941(247)172
|
| [4] |
PERELMAN L, OSTFELD A. Topological clustering for water distribution systems analysis[J]. Environmental Modelling & Software, 2011, 26(7): 969. DOI:10.1016/j.envsoft.2011.01.006 |
| [5] |
DIAO Kegong, ZHOU Yuwen, RAUCH W. Automated creation of district metered area boundaries in water distribution systems[J]. Journal of Water Resources Planning and Management, 2013, 139(2): 184. DOI:10.1061/(ASCE)WR.1943-5452.0000247 |
| [6] |
王彤, 冯雪峰, 赵明, 等. 基于快速网络算法的供水管网区块化研究[J]. 中国给水排水, 2018, 34(5): 37. WANG Tong, FENG Xuefeng, ZHAO Ming, et al. Water supply network blocks based on a fast algorithm for detecting community structure in networks[J]. China Water & Wastewater, 2018, 34(5): 37. |
| [7] |
刘俊, 周鹏. 谱聚类在给水管网分区优化中的应用[J]. 土木建筑与环境工程, 2016, 38(6): 142. LIU Jun, ZHOU Peng. Spectral clustering for optimal design of district metered areas in water distribution systems[J]. Journal of Civil Architectural and Environmental Engineering, 2016, 38(6): 142. DOI:10.11835/j.issn.1674-4764.2016.06.019 |
| [8] |
NARDO A D, GIUDICIANNI C, GRECO R, et al. Applications of graph spectral techniques to water distribution network management[J]. Water, 2018, 10(1): 45. DOI:10.3390/w10010045 |
| [9] |
NARDO A D. A heuristic design support methodology based on graph theory for district metering of water supply networks[J]. Engineering Optimization, 2011, 43(2): 193. DOI:10.1080/03052151003789858 |
| [10] |
NARDO A D, NATALE M D, SANTONASTASO G F, et al. Graph partitioning for automatic sectorization of a water distribution system[C]//Proceedings of 11th International Conference on Computing and Control for Water Industry. Exeter: [s.n.], 2011: 841
|
| [11] |
PERELMAN L S, ALLEN M, PREIS A, et al. Automated sub-zoning of water distribution systems[J]. Environmental Modelling & Software, 2015, 65: 1. DOI:10.1016/j.envsoft.2014.11.02 |
| [12] |
LIU Haixing, ZHAO Mengke, ZHANG Chi, et al. Comparing topological partitioning methods for district metered areas in the water distribution network[J]. Water, 2018, 10(4): 368. DOI:10.3390/w10040368 |
| [13] |
张正培. 基于复杂网络理论的城市供水管网的建模与分区分层[D]. 上海: 上海交通大学, 2014 ZHANG Zhengpei. Modeling, partitioning and layering of urban water supply network based on complex network theory[D]. Shanghai: Shanghai Jiao Tong University, 2014 |
| [14] |
TARJAN R. Depth-first search and linear graph algorithms[C]//Proceedings of 12th Annual Symposium on Switching and Automata Theory. East Lansing: IEEE, 1971. DOI: 10.1109/SWAT.1971.10
|
| [15] |
DIJKSTRA E W. A note on two problems in connexion with graphs[J]. Numerische Mathematik, 1959, 1(1): 269. DOI:10.1007/BF01386390 |
| [16] |
NEWMAN M E J, GIRVAN M. Finding and evaluating community structure in networks[J]. Physical Review E, 2004, 69: 026113. DOI:10.1103/PhysRevE.69.026113 |
| [17] |
CLAUSET A, NEWMAN M E J, MOORE C. Finding community structure in very large networks[J]. Physical Review E, 2004, 70: 066111. DOI:10.1103/PhysRevE.70.066111 |
| [18] |
孙玺菁, 司守奎. 复杂网络算法与应用[M]. 北京: 国防工业出版社, 2015: 22. SUN Xijing, SI Shoukui. Complex network algorithms and applications[M]. Beijing: National Defense Industry Press, 2015: 22. |
| [19] |
赵金利, 张群华, 余贻鑫, 等. 输电网网架结构的谱聚类分析算法[J]. 电力系统及其自动化学报, 2009, 21(4): 10. ZHAO Jinli, ZHANG Qunhua, YU Yixin, et al. Spectral clustering approach for structure analysis of transmission networks[J]. Proceedings of the CSU-EPSA, 2009, 21(4): 10. DOI:10.3969/j.issn.1003-8930.2009.04.002 |
| [20] |
KUNCHEVA L I, HADJITODOROV S T. Using diversity in cluster ensembles[C]//Proceedings of 2004 IEEE International Conference on Systems, Man and Cybernetics. The Hague: IEEE, 2004: 1216. DOI: 10.1109/ICSMC.2004.1399790
|
| [21] |
YAZDANI A, JEFFREY P. Applying network theory to quantify the redundancy and structural robustness of water distribution systems[J]. Journal of Water Resources Planning and Management, 2012, 138(2): 155. DOI:10.1061/(ASCE)WR.1943-5452.0000159 |
| [22] |
谭跃进, 吴俊. 网络结构熵及其在非标度网络中的应用[J]. 系统工程理论与实践, 2004, 24(6): 1. TAN Yuejin, WU Jun. Network structure entropy and its application to scale-free networks[J]. Systems Engineering: Theory & Practice, 2004, 24(6): 1. DOI:10.3321/j.issn:1000-6788.2004.06.001 |
| [23] |
VAN ZYL J E, SAVIC D A, WALTERS G A. Operational optimization of water distribution systems using a hybrid genetic algorithm[J]. Journal of Water Resources Planningand Management, 2004, 130(2): 160. DOI:10.1061/(ASCE)0733-9496(2004)130:2(160) |
| [24] |
OSTFELD A, SALOMONS E, ORMSBEE L, et al. Battle of the water calibration networks[J]. Journal of Water Resources Planning and Management, 2012, 138(5): 523. DOI:10.1061/(ASCE)WR.1943-5452.0000191 |
| [25] |
MARCHI A, DANDY G, WILKINS A, et al. Methodology for comparing evolutionary algorithms for optimization of water distribution systems[J]. Journal of Water Resources Planningand Management, 2014, 140(1): 22. DOI:10.1061/(ASCE)WR.1943-5452.0000321 |
| [26] |
FARMANI R, SAVIC D A, WALTERS G A. Evolutionary multi-objective optimization in water distribution network design[J]. Engineering Optimization, 2004, 37(2): 167. DOI:10.1080/03052150512331303436 |
| [27] |
OSTFELD A, UBER J G, SALOMONS E, et al. The battle of the water sensor networks (BWSN): A design challenge for engineers and algorithms[J]. Journal of Water Resources Planning and Management, 2008, 134(6): 556. DOI:10.1061/(asce)0733-9496(2008)134:6(556) |
| [28] |
高琰, 谷士文, 唐琎, 等. 机器学习中谱聚类方法的研究[J]. 计算机科学, 2007, 34(2): 201. GAO Yan, GU Shiwen, TANG Jin, et al. Research on spectral clustering in machine learning[J]. Computer Science, 2007, 34(2): 201. DOI:10.3969/j.issn.1002-137X.2007.02.051 |
| [29] |
VONLUXBURG U. A tutorial on spectral clustering[J]. Statistics and Computing, 2007, 17(4): 395. DOI:10.1007/s11222-007-9033-z |
 2021, Vol. 53
2021, Vol. 53


