2. 同济大学 建筑与城市规划学院, 上海 200092
2. College of Architecture and Urban Planning, Tongji University, Shanghai 200092, China
在存量规划的城市发展新模式下,对老旧城区进行可持续化的更新改造是城市规划与城市建设面临的新课题.在城市更新改造中,城市绅士化是较为彻底的一类改造方式,这一概念由西方学者在20世纪60年代提出,是指在城市中心区域的空地或拆迁空地进行住房改造和住宅建设,将原有低收入阶层居民替换为中产阶级或富有群体的过程[1-4].伴随着中国城市化进程,一些大中城市绅士化改造不可避免.目前,中国城市绅士化相关研究主要从宏观角度对绅士化现象[5-9]、城市贫困[10]、城市政策[11-12]进行了社会学、经济学研究,尚未涉及更加直观反映微观尺度——街区空间形态特征的定性或定量研究.
上海作为中国经济最为发达与开放的大城市之一,其绅士化进程给这个海派城市带来显著影响.在城市绅士化片区,不但原有的社会关系和历史文化纽带几近消失,同时反映人对城市空间、交通体系以及与周围区域相互关系认知的城市形态也发生了巨大变化.在这一背景下,对街区城市形态特征的演变分析有助于了解和认识城市绅士化改造对城市社会关系、空间结构的影响,对于可持续发展的城市改造建设与城市发展规划具有指导作用.
现有城市形态的研究可分为定性和定量研究两大类.传统图形学研究以图形分析为工具,对城市形态进行定性研究,以文献综述、实地调研、类型学等研究方法对城市形态的结构、模式、演变规律进行定性归纳[13-19].城市形态定量研究兴起于计算机软件(AutoCAD、GIS等软件)和大数据的普及.这类研究所应用的理论可分为空间结构理论和空间强度理论.以BILL HILLER为代表的空间句法研究将拓扑关系应用到对城市形态空间结构的定量研究中,并发展出一套完整的特征值定量分析模型[20],例如,连接值、集成度和可理解性等.这种定量研究理论可以深入地探究城市空间结构关系,但是不能反映城市空间的高度、密度等强度特征[21].另一种理论是以反映空间强度的各类特征值为主进行城市形态定量研究[22-26],如计算城市空间中的建筑密度、混合度、绿化率等特征值,探究城市形态对城市居民居住、行为、感受的影响,应用这种理论的研究可以直观地梳理城市空间的密度、多样性、绿地面积占比等形态特征,对城市形态的空间强度进行量化描述,但是不能反映城市空间结构上的拓扑关系.以上各项城市形态特征值均能反映城市形态的某一个客观属性,但是,对城市形态进行综合评价时,各项特征值无具体、明确的评价标准,具有一定的不确定性,例如,反映单位面积上建筑面积的密度特征值容积率(RFA),过高或过低均不利于城市可持续发展.且由于缺少一种统筹各项空间特征的量化方法,已有研究对城市形态特征分析仅限于分项特征值的定量描述或综合的定性评估,无法量化区分不同城市空间形态的优劣差异.
模糊性是指某些事物或概念的边界不清楚, 这种边界不清的模糊概念, 不是由于人的主观认识达不到客观实际造成的, 而是事物的一种客观属性[27].已有研究指出,对于评价标准没有明确界定的事物可以应用模糊数学量化处理此类模糊性问题[28-29]:以隶属函数作为桥梁,使用模糊集合描述指标性能的“亦此亦彼”特征, 将模糊性加以量化,可以得到向量形式的综合评估结果, 从而获得比较精确的定量结果,是对受多因素影响的事物做出全面评价的一种十分有效的多因素决策方法.该方法已被广泛应用于绿色建筑节能评价、住宅建筑功能性评价、城市交通系统综合评估、环境质量评价以及食品工程等各个领域[30-37],可作为解决多因素、多指标综合评价与决策问题的有效替代方法[30].模糊数学理论应用于城市问题研究较少,有学者在城市土地功能适用性、城市蔓延问题、城市生态系统评价研究中应用该理论[38-40],取得较为有效的评价结论.目前,关于模糊数学理论用于城市形态评估的研究尚未见文献报道.本文以上海中心城区两个典型绅士化片区城市形态为研究对象,基于对两个典型片区内各个街区的“空间强度特征值”——容积率和混合土地利用率、“空间结构特征值”——连接值和集成度的定量计算,定量分析绅士化街区城市形态特征,探讨不同类型街区的空间结构差异;利用模糊数学综合评估法量化街区空间形态的优劣,探索城市绅士化运动对城市形态的积极与消极影响,为可持续的城市改造、设计和规划方案制定提供技术参考.
1 研究区域与研究方法 1.1 研究区域与数据收集选取上海市两个典型的绅士化片区——虹镇老街和世博北岸片区为研究区域,见图 1.虹镇老街片区面积约1.00 km2,原多为计划经济时代的职工家属区和自建房,随着20世纪90年代后期改革开放的深入和房地产业的兴起,高档商品房、商业综合体和配套教育建筑正在逐步替换原有的工厂、棚户区、公房,同时改变了片区的居民构成,绅士化现象逐渐显现.世博北岸片区面积约1.94 km2,主要为江南造船厂、上海南市发电厂等多家工业企业用地及其配套家属区,以及以棚户、旧式里弄为主要建筑类型的居住用地.为配合2010年上海世博会的建设,片区内90%的居住用地拆迁,所有工业企业搬迁,部分厂房保留结构进行改造.至2015年底,拆迁的棚户区住户全部迁出,替换为新建中高档商品房的购房者;同时,原世博会场馆亦改建为文化观演、展览等功能建筑,大部分区域已逐步置换为绅士化社区.
|
图 1 上海市绅士化典型片区区位示意 Fig. 1 Location of the two neighbourhoods |
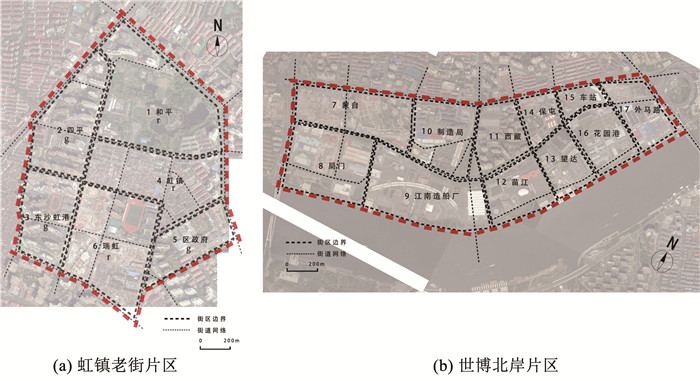
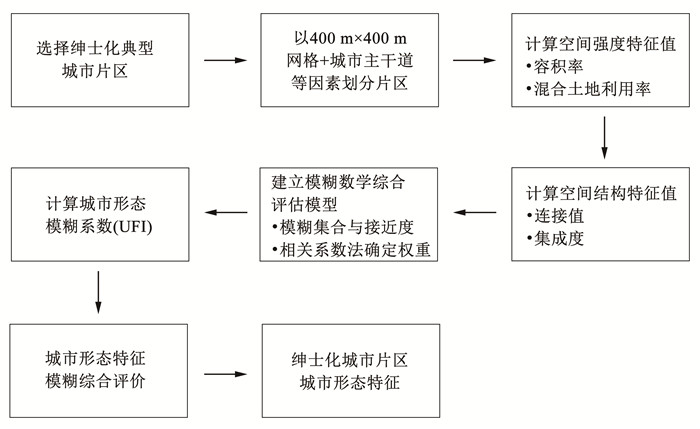
为揭示典型绅士化街区的城市形态总体特征,将两个具有不同改造背景和建设目标的绅士化片区合并进行统一分析评估.利用2015年测绘数据和同年卫星影像图,以400 m×400 m网格并结合城市主干道、空间特征等因素将两个研究片区划分为17个街区,并依据各街区改造现状划分为保留街区(r)与绅士化街区(g),见图 2.研究步骤与技术路线见图 3.
|
图 2 虹镇老街与世博北岸片区街区划分示意(来源:作者改绘) Fig. 2 Blocks division of the two neighbourhoods |
|
图 3 研究步骤与技术路线 Fig. 3 Research procedure |
容积率(floor area ratio,RFA)和混合土地利用率(mixed land use index,IM)是分析城市局部空间形态的基础参数,能够反映城市空间的体量、密度与土地利用情况,可作为反映研究区域开发强度的“空间强度特征值”;依据空间句法理论[24],空间拓扑参数连接值(connectivity,C)、集成度(integration,I)反映了城市空间连通程度、可达性或孤立程度,可作为反映研究区域空间组织结构的“空间结构特征值”.
1.2.1.1 空间强度特征值计算1) 容积率
容积率(RFA)的计算公式为
| $ {R_{{\rm{FA}}}} = \frac{{{A_{\rm{t}}}}}{{{A_{\rm{p}}}}}. $ | (1) |
式中:At为某一街区内建筑面积之和,Ap为某一街区的总面积.
容积率中的各分项指标具有比较明确的定义和量度,在密度计算和评价中,容积率是一项相对清晰的指标.
2) 混合土地利用率
混合土地利用率(IM)的计算公式[23]为
| $ {I_{\rm{M}}} = 1 - \left\{ {\frac{{\left| {\frac{r}{T} - \frac{1}{3}} \right| + \left| {\frac{c}{T} - \frac{1}{3}} \right| + \left| {\frac{o}{T} - \frac{1}{3}} \right|}}{{4/3}}} \right\}. $ | (2) |
式中,T为片区总建筑面积,T=r+c+o, 其中,r, c和o分别代表居住用地建筑面积(包括公寓和住宅),商业用地建筑面积(包括零售、办公和酒店)和其他用地建筑面积(包括工厂、政府机关、学校和医院); IM介于0和1,当值趋近于1时,表示某一城市空间区域内的不同功能用地面积平均分布,空间形式丰富,多样性较好.
基于空间地理特征的传统城市形态特征值从街区层面直观地展现局部空间形态特征,但是无法表现局部街区与整体城市空间之间联系.因此,需引入反映局部与整体拓扑关系的空间句法理论进行空间组织结构特征的分析.
1.2.1.2 空间结构特征值计算空间结构特征值主要取自基于拓扑关系描述城市结构形态的空间句法理论.该理论将城市结构简化为凸空间和轴线两种空间,城市形态均可由两种空间基础元素描述[24],由此演化出包括连接值(connectivity)和集成度(integration)等5个空间拓扑参数,用于反映城市空间的连通程度、可达性与集聚离散程度[26].
某节点(空间)i的连接值(Ci)可以表述为[24]
| $ {C_{\rm{i}}} = k. $ | (3) |
式中k为与节点(空间)i直接相连的空间数.
集成度(I)可以由相对不对称值(relative asymmetry, AR)的倒数计算得出.AR的计算公式如下[24]:
| $ {A_{{\rm{R}}i}} = \frac{{2\left( {{D_{{\rm{M}}i}} - 1} \right)}}{{n - 2}}. $ | (4) |
式中:DMi为平均深度值,
表示街区空间强度与空间结构的4项特征值参数含义不同,量级上亦有显著差异,且无统一评价标准的界限,无法实现对各个街区形态特征的量化对比分析.因此,需要一种客观地综合评估街区城市形态的定量方法.
1.2.2 城市形态模糊数学综合评估模型的建立利用表示空间开发强度的容积率和混合土地利用率,以及表示空间局部组织特征的连接值和表示全局组织特征的集成度,构建城市形态模糊数学综合评估模型,以城市形态模糊系数(urban fuzzy index,IUF)[42]统筹上述反映不同城市形态的特征值指标,按照最大隶属度原则,计算各街区的特征值参数与研究区域相对最优(或最劣)标准特征值集合的接近程度,确定各街区的IUF,由此对比分析各街区城市形态的优劣和差异.
| $ {I_{{\rm{UF}}}} = d = \mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\mathit{\boldsymbol{\omega }}^{\rm{T}}}. $ | (5) |
式中:Δ为特征值数量n=4时m个街区的模糊关系矩阵;ωj=(0.29,0.29,0.23,0.19),为依据相关系数赋权方法求得的4个特征值权重系数[42];d= {d1,d2,di,…,dm},i为某个街区,di表示街区i到标准特征值向量所表示的虚拟街区的拓扑距离,即为i街区的城市形态模糊系数(IUF),综合反映了该街区的空间形态特征与标准特征值向量之间的总体差异.若di越小则i街区距离标准特征值向量所表示的虚拟街区形态越接近,空间形态差异越小;故最小值dmin=min(d1, d2, …, dm)街区是研究区域内城市形态相对最优(或最劣)的街区.
1.2.3 城市形态模糊综合评估标准的确定确定标准特征值向量f0是城市形态模糊数学综合评估的关键步骤.标准特征值向量f0反映了研究区域城市形态相对最优(或最劣)的虚拟街区的空间形态特征.
目前,包括容积率、混合土地利用率、连接值、集成度在内的一些空间形态特征值尚无具体明确的评判优或劣的界限标准.林奇的环境行为学[13]认为,一个好的城市形态是能够让使用者感觉舒适、亲切,而决定城市形态质量的要素包括:1)活力(多样性与混合土地利用);2)感受(可识别性);3)适宜(接近人体的空间体量);4)可达性;5)管理[13].本研究依据环境行为学理论,以活力、感受、适宜和可达性作为评判空间特征值优劣标准的原则.
1) 容积率的评价标准因价值取向角度不同而异.于开发商而言,高容积率意味着高收益; 于政府角度,高容积率意味着能够解决更多人口的住房问题; 于住户而言,高容积率则意味着高大的建筑体量和封闭拥挤的空间.但是过低的容积率会降低城市多样性和城市效率,亦不一定是好的城市形态.在城市规划相关文件中,一般对容积率上限进行了规定.综上,高容积率的城市形态违背适宜原则,当其他外部环境条件相同的情况下,高容积率作为较差城市形态的评判标准更具有普遍性.
2) 混合土地利用率是衡量城市多样性的重要指标之一.单位面积内多种使用功能的空间混合分布,可以增加城市局部空间的活力,为不同社会群体相互交往提供空间.在力求城市空间资源充分利用的语境下,多样性的城市空间形式和功能无疑会有利于城市空间和居民日常生活的活力,而低混合土地利用率对于街区城市形态的影响是消极的.因此,低混合土地利用率将作为较差城市形态的评判标准.
3) 连接值与集成度均与城市空间的可达性有关.为保证城市居民使用空间资源、进行空间消费的基本权利,其中一个重要的条件是需要空间具有良好的可达性,局部空间与局部空间的隔离程度尽可能缩小.因此,低连接值与低集成度的街区是消极的城市形态.
综合考虑,与相对最优特征值标准相比,高容积率、低混合土地利用率、低连接值与低集成度作为城市形态相对最劣标准更具有普遍性与合理性.
2 街区城市形态特征值与城市形态模糊系数计算结果 2.1 街区城市形态特征值计算结果表 1为17个街区4项城市形态特征值定量计算结果.可以看出,各街区各项特征值数值差异较大,缺乏明显的规律性,难于通过各项特征值对比评估街区城市形态的优劣.
| 表 1 街区城市形态特征值计算结果汇总 Tab. 1 Urban form indexes of 17 blocks |
各街区城市形态模糊系数IUF计算结果如下:
| $ \begin{array}{*{20}{l}} {\;\;\;\;\;{I_{{\rm{UF}}}} = (0.45, 0.26, 0.26, 0.38, 0.39, 0.46}\\ {0.22, 0.41, 0.29, 0.42, 0.31, 0.39, 0.33, 0.39, }\\ {0.38, 0.37, 0.40)} \end{array} $ |
各街区IUF如表 2所示.其中,蒙自街区的IUF最小(0.22),表示与相对最劣标准特征值所表示的虚拟街区形态差异较小;瑞虹街区IUF最大(0.46),表示与相对最劣标准特征值向量所表示的虚拟街区形态差异较大;各街区IUF平均值为0.36,IUF最大差值为0.24,街区城市形态区分明显.
| 表 2 各个街区城市形态模糊系数 Tab. 2 IUF of 17 blocks |
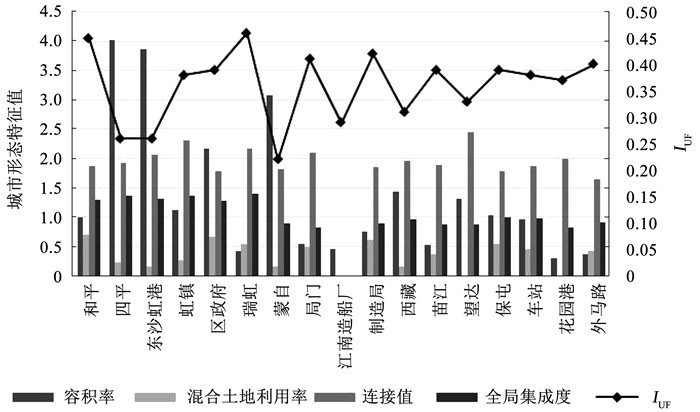
为了判断城市形态模糊综合评价方法的可行性和客观性,以及对比分析研究区域各个街区的城市形态特征,将17个街区的4项特征值与城市形态模糊系数IUF进行汇总对比,如图 4所示.可以看出,城市形态模糊系数与各项特征值具有一定的关联性,能够综合反应街区局部形态和空间整体性特征,表明基于模糊数学理论的城市形态特征综合评估结果能够客观地反映研究区域的城市形态特征,用作城市形态综合定量评估是可行的.
|
图 4 各街区城市形态特征值与城市形态模糊系数对比 Fig. 4 Contrast of IUF and urban form index of blocks |
瑞虹街区的模糊综合评价指数是17个街区中的最大值(0.46),主要因为该街区处于拆迁新建阶段,容积率较低,考虑到该街区现有城市形态的临时性和未来规划,下文不再将该街区纳入分析样本中.
在分析样本中,绅士化街区12个,保留街区4个.其中,IUF最高的街区为保留街区,IUF最低的街区为绅士化街区.总体上,绅士化街区的IUF普遍较低,亦有部分绅士化街区的IUF高于保留街区.
在保留街区中,和平街区城市形态模糊系数为0.45,是分析样本中的最大值.和平街区以街区内的和平公园命名,公园占地面积17.6万m2,占据街区的绝大部分.虽然街区内有新建的高容积率的商品房住宅与写字楼商业综合体建筑,但是便利的可达性、超大面积的开放空间、多样性的基础设施建设以及部分保留的公房住宅,使得这个街区的城市形态较为优良.
制造局街区为保留街区,城市形态模糊系数为0.42.街区西部、中部建筑保留,东部的部分高层塔楼、低层办公楼、住宅楼因道路拓宽等原因被拆除,后续建设并未跟上,土地处于空置状态,导致该街区现存建筑容积率低、使用功能单一(基本全部为居住建筑),但是原有街区的肌理仍然存在,街道巷陌相通,可达性良好,街区较为开放,与周围城市空间相融合,城市形态良好.
虹镇街区为17个街区中较少的完整保留了原有城市形态的街区,城市形态模糊系数为0.38.该街区位于虹镇老街片区的核心地带,截止2015年底,该街区尚未进行拆迁重建.街区内有3层以下自建住宅和简易房、多层公房和高层塔楼.街区容积率较低,街巷互相连通,可达性和便利性均较高,但该区域土地利用功能单一,建筑老旧,质量参差不一,街区城市形态在分析样本中处于中等水平.
在绅士化改造街区中,虹口区政府街区(IUF=0.39)原为棚户区、工厂和文化观演类建筑共存,经过拆迁改造,该街区内的用地功能改变:原工厂、棚户区和公共建筑被替换为区政府、商品房住宅和配套教育设施.虽然容积率显著增高,但因为街区内公共空间增加,街区内的可达性较高,可识别性高,是区域内少数绅士化改造比较成功的街区.
江南造船厂街区(IUF=0.29)为世博会企业展区,现有多座场馆封闭管理,出入口单一,场馆毗邻的滨水公共空间亦不对公众开放,街区较为孤立.与之情况相似的还有花园港街区(IUF=0.37),该街区整体为南市水厂办公与生产用地,仅供工作人员出入,出入口较少,空间较为孤立.上述2个街区城市形态模糊系数值较低,空间形态相对较差.
蒙自街区的城市形态模糊系数最小(IUF=0.22),表明其与研究区域相对最劣标准特征值所表示的虚拟街区城市形态最为接近,其城市形态在两个绅士化片区范围内最差.该街区位于世博北岸片区,原为工厂、棚户区,在筹建世博会和城市整体改造的运动中全部拆迁,建设有高档商品房住宅与豪华写字楼,街区的容积率较高,土地利用极为单一,可达性中等,相对孤立于周围片区.究其原因应为街区内各个地块之间互不连通,出入口较少,建筑高度较高,且缺乏配套公建.这些因素在其他城市形态相对较差的绅士化街区,如东沙虹港街区、西藏街区内亦存在.
根据17个街区的模糊综合评估结果可知,绅士化运动对城市街区形态有明显的影响.与保留街区相比,大部分绅士化改造完成后的街区(如蒙自、东沙虹港、西藏街区)呈现出消极的城市形态特征,主要表现为:建筑物高、体量大,致使街区容积率过高;街区土地利用多以居住功能为主, 相关配套设施尚不健全;各地块之间互不连通,街区整体封闭,孤立于周围城市空间.这些街区的绅士化改造不仅影响了整体城市形态,同时改变了原有片区的社会关系和历史文化纽带,以及伴随而来的高房价、社区隔离、不断攀升的服务业费用以及社会多样性缺失等社会问题.
在17个街区中,改造较为成功的绅士化街区(如虹口区政府街区)表现出了积极的城市形态特征:虽然绅士化改造后的街区建筑物高度、体量与保留街区相比有显著升高,但其建筑空间疏密有致、体量适中,容积率适宜、可识别度高;较高的混合土地利用率;良好的可达性.多功能、多形式的土地利用,良好的街区可达性、开放性,能够带来社会结构与经济结构的多样性,使得街区具有活力与生气.
4 结论1) 绅士化改造对街区空间形态有显著影响,绅士化街区的城市形态普遍低于保留街区,表现为街区封闭、用地类型单一等消极城市形态特征;少数绅士化改造比较成功的街区(如虹口区政府)表现出多样性与易达性等积极城市形态特征.
2) 积极的城市形态特征主要表现为良好的可达性、多功能的土地开发利用、尺度适宜与开放的空间形态,这种形态特征有利于活力度高、可识别性高的城市空间与多样性的社会经济结构.反之,消极的城市形态特征则表现在街区居住建筑的容积率与封闭性均较高,相对孤立于区域周围空间,土地开发利用功能较为单一,配套设施不完善,这种形态特征不利于城市街区的可持续发展,存量规划背景下的城市更新应注意避免令城市街区形成此类消极的城市形态特征.
3) 采用城市形态模糊系数(IUF)统筹各项城市形态特征值指标,用于街区城市形态的定量综合评估具有客观性和可行性,街区IUF与其各项特征值具有一定的关联性,能够综合反应街区局部形态和空间整体性特征,为城市形态特征的综合定量分析提供了一种有效途径.
上述城市绅士化改造对城市形态积极或消极影响的归纳分析对于存量规划背景下的城市更新改造具有借鉴作用.
| [1] |
SMITH N. The new urban frontier: Gentrification and the revanchist city[M]. London: Routledge, 1996.
|
| [2] |
DAVIDSON M, LEES L. New-build 'gentrification' and London's riverside renaissance[J]. Environment and Planning A: Economy and Space, 2005, 37(7): 1165. DOI:10.1068/a3739 |
| [3] |
SMITH N. New globalism, new urbanism: Gentrification as global urban strategy[J]. Antipode, 2002, 34(3): 427. DOI:10.1111/1467-8330.00249 |
| [4] |
NEWMAN K, WYLY E. The right to stay put, revisited: Gentrification and resistance to displacement in New York City[J]. Urban Studies, 2006, 43(1): 23. DOI:10.1080/00420980500388710 |
| [5] |
HE Shenjing. State-sponsored gentrification under market transition: The case of Shanghai[J]. Urban Affairs Review, 2007, 43(2): 171. DOI:10.1177/1078087407305175 |
| [6] |
HE Shenjing. New-build gentrification in central Shanghai: Demographic changes and socioeconomic implications[J]. Population, Space and Place, 2010, 16(5): 345. DOI:10.1002/psp.548 |
| [7] |
朱喜刚, 周强, 金俭. 城市绅士化与城市更新——以南京为例[J]. 城市发展研究, 2004, 11(4): 33. ZHU Xigang, ZHOU Qiang, JIN Jian. The gentrification and urban renew: In case of Nanjing[J]. Urban Studies, 2004, 11(4): 33. DOI:10.3969/j.issn.1006-3862.2004.04.008 |
| [8] |
WANG Jun, LAU S S Y. Gentrification and Shanghai's new middle-class: Another reflection on the cultural consumption thesis[J]. Cities, 2009, 26(2): 57. DOI:10.1016/j.cities.2009.01.004 |
| [9] |
戴晓晖. 转型期中国大都市中心城旧区的中产阶层化研究——以上海为例[D]. 上海: 同济大学, 2007 DAI Xiaohui. A study on the gentrification of the old urban centers in China during the transformation period: In case of Shanghai[D]. Shanghai: Tongji University, 2007 |
| [10] |
刘玉婷. 转型期中国城市贫困的社会空间[M]. 北京: 科学出版社, 2005. LIU Yuting. The social space of urban poverty in China during the transition period[M]. Beijing: Science Press, 2005. |
| [11] |
吴启焰. 大城市居住空间分异研究的理论与实践[M]. 北京: 科学出版社, 2001. WU Qiyan. The theory and practice of the study on residential space differentiation in large cities[M]. Beijing: Science Press, 2001. |
| [12] |
程晓曦. 混合居住视角下的北京旧城居住密度问题研究[D]. 北京: 清华大学, 2011 CHENG Xiaoxi. Research on residential density of the old city zone of Beijing in the perspective of mixed-income housing[D]. Beijing: Tsinghua University, 2011 |
| [13] |
LYNCH K. Good city form[M]. Cambridge: MIT Press, 1984.
|
| [14] |
顾朝林. 中国大都市空间增长形态[J]. 城市规划, 1994(6): 45. GU Zhaolin. The spatial growth pattern of China's metropolises[J]. City Planning Review, 1994(6): 45. |
| [15] |
张京祥. 城镇群体空间组合[M]. 南京: 东南大学出版社, 2000. ZHANG Jingxiang. Combination of urban group space[M]. Nanjing: Southeast University Press, 2000. |
| [16] |
武进. 中国城市形态: 结构、特征及其演变[M]. 南京: 江苏科学技术出版社, 1990. WU Jin. The morphology of Chinese cities: Structure, characteristic and evolution[M]. Nanjing: Phoenix Science Press, 1990. |
| [17] |
胡俊. 中国城市: 模式与演进[M]. 北京: 中国建筑工业出版社, 1995. HU Jun. Chinese cities: Their evolution and patterns[M]. Beijing: China Architecture & Building Press, 1995. |
| [18] |
杨上广. 中国大城市社会空间的演化[M]. 上海: 华东理工大学出版社, 2006. YANG Shangguang. Evolution of social space in Chinese metropolis[M]. Shanghai: East China University of Science and Technology Press, 2006. |
| [19] |
熊国平. 90年代以来中国城市形态演变研究[D]. 南京: 南京大学, 2005 XIONG Guoping. Study on the morphology evolution of Chinese cities since 1990s[D]. Nanjing: Nanjing University, 2005 |
| [20] |
HILLIER B. Space is the machine: A configurational theory of architecture[M]. Cambridge: Cambridge University Press, 1996.
|
| [21] |
RATTI C. Space syntax: Some inconsistencies[J]. Environment and Planning B: Planning and Design, 2004, 31(4): 487. DOI:10.1068/b3019 |
| [22] |
SOUTHWORTH M, BEN-JOSEPH E. Streets and the shaping of towns and cities[M]. Washington DC: Island Press, 2003.
|
| [23] |
SONG Yan, KNAAP G J. Measuring urban form: Is Portland winning the war on sprawl?[J]. Journal of the American Planning Association, 2004, 70(2): 210. DOI:10.1080/01944360408976371 |
| [24] |
董春方. 密度与城市形态[J]. 建筑学报, 2012(7): 22. DONG Chunfang. Density and urban form[J]. Architectural Journal, 2012(7): 22. DOI:10.3969/j.issn.0529-1399.2012.07.005 |
| [25] |
BHAT C R, GOSSEN R. A mixed multinomial logit model analysis of weekend recreational episode type choice[J]. Transportation Research Part B: Methodological, 2004, 38(9): 767. DOI:10.1016/j.trb.2003.10.003 |
| [26] |
JIANG Bin, CLARAMUNT C, KLARQVIST B. Integration of space syntax into GIS for modelling urban spaces[J]. International Journal of Applied Earth Observation and Geoinformation, 2000, 2(3/4): 161. DOI:10.1016/S0303-2434(00)85010-2 |
| [27] |
汪培庄. 模糊集合论及其应用[M]. 上海: 上海科技出版社, 1983. WANG Peizhuang. Fuzzy set theory and its applications[M]. Shanghai: Shanghai Scientific & Technical Publishers, 1983. |
| [28] |
ZIMMERMANN H J. Fuzzy set theory[J]. WIREs Computational Statistics, 2010, 2(3): 317. DOI:10.1002/wics.82 |
| [29] |
江高. 模糊层次综合评价法及其应用[D]. 天津: 天津大学, 2005 JIANG Gao. Fuzzy AHP synthetical appraise method and application[D]. Tianjin: Tianjin University, 2005 |
| [30] |
OCAMPO-DUQUE W, FERRE-HUGUET N, DOMINGO J L, et al. Assessing water quality in rivers with fuzzy inference systems: A case study[J]. Environment International, 2006, 32(6): 733. DOI:10.1016/j.envint.2006.03.009 |
| [31] |
YANG Tao, YANG Xinmiao. Fuzzy comprehensive assessment, fuzzy clustering analysis and its application for urban traffic environment quality evaluation[J]. Transportation Research Part D: Transport and Environment, 1998, 3(1): 51. DOI:10.1016/S1361-9209(97)00021-7 |
| [32] |
朱慧琴. 应用模糊数学对住宅建筑功能的综合评价[J]. 华南热带农业大学学报, 2003, 9(4): 38. ZHU Huiqin. Synthetical evaluation of residence functions by means of fuzzy mathematics[J]. Journal of South China University of Tropical Agriculture, 2003, 9(4): 38. DOI:10.3969/j.issn.1674-7054.2003.04.009 |
| [33] |
佀同光, 刘加云, 王传慧. 模糊数学方法在绿色建筑评估中的应用[J]. 山东建筑工程学院学报, 2005, 20(1): 32. SI Tongguang, LIU Jiayun, WANG Chuanhui. Fuzzy approach in green building assessment[J]. Journal of Shandong University of Architecture and Engineering, 2005, 20(1): 32. DOI:10.3969/j.issn.1673-7644.2005.01.009 |
| [34] |
郭笑笑, 刘丛强, 朱兆洲, 等. 土壤重金属污染评价方法[J]. 生态学杂志, 2011, 30(5): 889. GUO Xiaoxaio, LIU Congqiang, ZHU Zhaozhou, et al. Evaluation methods for soil heavy metals contamination: A review[J]. Chinese Journal of Ecology, 2011, 30(5): 889. |
| [35] |
刘张强, 马民涛, 朴锦泉. 基于模糊综合评价法的河北省大气环境质量评价[J]. 四川环境, 2015, 34(5): 94. LIU Zhangqiang, MA Mintao, PIAO Jinquan. Atmospheric environmental quality evaluation in Hebei province based on fuzzy comprehensive evaluation method[J]. Sichuan Environment, 2015, 34(5): 94. DOI:10.3969/j.issn.1001-3644.2015.05.018 |
| [36] |
梁缙, 李志宪, 王海燕. 加油站模糊数学安全评价模型及应用[J]. 中国安全科学学报, 2004, 14(8): 106. LIANG Jin, LI Zhixian, WANG Haiyan. Fuzzy safety evaluation model for gas station and its application[J]. China Safety Science Journal, 2004, 14(8): 106. DOI:10.3969/j.issn.1003-3033.2004.08.027 |
| [37] |
杨梅, 陈梦迪, 王珂莉, 等. 基于模糊数学评判法优化调味鱼的腌制工艺[J]. 食品研究与开发, 2020, 41(8): 83. YANG Mei, CHEN Mengdi, WANG Keli, et al. Optimization on brining process of flavored fish based on fuzzy mathematics comprehensive evaluation[J]. Food Research and Development, 2020, 41(8): 83. DOI:10.12161/j.issn.1005-6521.2020.08.013 |
| [38] |
于声. 模糊评价法在区域工业用地适宜性评价中应用[D]. 北京: 中国农业科学院, 2007 YU Sheng. The application of fuzzy evaluation method in the regional industrial land suitability evaluation[D]. Beijing: Chinese Academy of Agricultural Sciences, 2007 |
| [39] |
WEY W M, HSU J. New urbanism and smart growth: Toward achieving a smart National Taipei University District[J]. Habitat International, 2014, 42: 164. DOI:10.1016/j.habitatint.2013.12.001 |
| [40] |
李伟. 基于变异系数法的模糊数学模型在城市生态系统健康评价中的应用[J]. 环境保护与循环经济, 2013, 33(11): 24. LI Wei. Application of fuzzy mathematical model based on coefficient of variation method in the evaluation of urban ecosystem health[J]. Environmental Protection and Circular Economy, 2013, 33(11): 24. |
 2021, Vol. 53
2021, Vol. 53


