2. 北京建筑大学 土木与交通工程学院,北京 100044
2. School of Civil and Transportation Engineering, Beijing University of Civil Engineering and Architecture, Beijing 100044, China
非饱和土在中国中西部分布广泛.随着中国交通基础设施建设不断向西部纵深发展,尤其是“一带一路”战略的实施,公(铁)路的非饱和土地(路)基在循环荷载作用下的长期稳定性分析已成为一个亟待解决的问题.非饱和土的受力变形不仅与所受荷载有关,还与内部含水率的变化密切相关.因此,研究循环荷载作用下非饱和土的力学特性需要考虑水-力耦合作用的影响.
对于静力作用下非饱和土本构模型的研究国内外已有不少成果.Alonso等[1]最早建立了非饱和土的弹塑性模型,该模型考虑了加载湿陷屈服,可以描述非饱和土的湿化变形及屈服应力随吸力变化等特性.在此基础上,Gens等[2-6]采用独立的净平均应力和基质吸力作为应力状态变量,提出了不同形式的弹塑性本构模型.为了描述非饱和土土水特性和受力变形间的耦合效应,不少学者做了有益尝试,如Wheeler等[7]考虑饱和度影响,采用Bishop应力和修正的基质吸力建立了较完整的水-力耦合模型.缪林昌[8]引用骨架应力的概念推导了LC屈服面的函数和硬化规律,建议了体应变引起饱和度变化的关系式.Sheng等[9-10]指出在非饱和土土水特性中饱和度不仅与吸力有关,还与体应变有关.Sun等[11-14]通过干湿循环得到具有不同初始饱和度的试样,然后基于控制吸力的等向压缩和三轴剪切试验结果,提出了能够统一预测吸力控制下沿不同应力路径的非饱和土水力-力学特性耦合的弹塑性本构模型.
对于循环荷载作用下土的弹塑性模型自20世纪70年代以来已多有研究.Provest[15]和Mroz等[16]最早建立了饱和土的多(屈服)面模型,Dafalias等[17]则提出了首个土的边界面(塑性)模型.此后,Mroz等[18]将多面模型简化为双(屈服)面模型,其中加载面收缩为一个弹性核.Li和Meissner等[19-20]将著名的Masing准则[21]推广到了多维应力空间,提出了一种新型塑性硬化准则,并据此建立了饱和黏性土的弹塑性双面模型,该模型可以较好地模拟循环荷载作用下土的动态力学特性.近年来,Hu等[22]基于这一塑性硬化准则,把饱和黏土的循环加载过程分为3类不同加载事件,提出了一个针对海洋波浪荷载作用的弹塑性模型.
非饱和土在复杂动态荷载作用下力学特性的研究还不多,同时考虑水-力耦合特性影响的本构模型研究则更少.Meissner等[23-24]采用自己研制的非饱和土动三轴仪测试了非饱和砂和黏性土在循环荷载作用下的力学特性,分析了影响非饱和土循环塑性的因素.彭丽云等[25]进行了系列循环荷载作用下非饱和击实粉土变形特性的试验研究,给出了不同吸力、净应力和动应力幅值下的应力应变关系.Yang等[26]以边界面塑性和胶结体损伤理论为基础,提出了考虑循环荷载作用下结构损伤的非饱和土弹塑性模型.Khalili等[27]研究了土-水特征曲线(SWCC)对非饱和土全耦合渗流变形特性的影响,建立了可以较好地反映加载过程中水力滞后现象的边界面模型.Xiong等[28]在临界状态土力学框架内,以Bishop骨架应力和饱和度为状态变量,建立了描述非饱和土水-力耦合行为的弹塑性本构模型.
中国西北部地区的公(铁)路地(路)基土中的吸力会受到气候、温差和外荷载影响而变化.由于长期气候和车辆荷载作用下非饱和土水-力耦合行为非常复杂,作为研究的第一步,本文仅研究常吸力循环荷载作用下非饱和黏性土水-力耦合特性的弹塑性模拟方法.为此,首先将Li等[19]提出的塑性硬化法则与BBM模型[1]相结合,考虑非饱和土典型的土水特征,尝试建立能够统一反映非饱和黏性土在常吸力循环荷载作用下水-力耦合特性的弹塑性双面模型;其次利用相关的室内试验结果对模型模拟和预测结果进行对比,以验证所建模型的合理性.
1 非饱和土水-力耦合弹塑性双面模型 1.1 基本假设1) 土颗粒不可压缩;2)不考虑温度效应和流体黏滞性;3)吸力变化不引起偏应变;4)吸力变化不改变临界状态线斜率;5)塑性体积应变εvp为硬化参量;6)采用相关联流动法则.其他假设详见文献[1, 19].
1.2 状态变量选取选取土的骨架应力σ′ij和吸力s为应力状态变量,土的骨架应变ε′ij和饱和度Sr为应变状态变量[8, 12, 28].在等向压缩状态下,σ′ij可以表示为
| $ p^{\prime}=p_{\mathrm{n}}+S_{\mathrm{r}} \cdot s. $ | (1) |
式中,净平均应力pn=p-ua,ua为孔隙气压力,Sr为饱和度,s为吸力.对于常规三轴压缩试验,总应力p=(σ1+2σ3)/3,其中σ1和σ3为大和小主应力.
在常规三轴试验应力状态下有偏应力
| $ {q^\prime } = q = {\sigma _1} - {\sigma _3}. $ | (2) |
非饱和土在干湿循环过程中吸力与饱和度不具有一一对应关系,考虑到非饱和黏性土中饱和度的变化主要由体积变化和吸力改变所决定[10],故有
| $ \mathrm{d} S_{\mathrm{r}}=\frac{\partial S_{\mathrm{r}}}{\partial s} \mathrm{~d} s+\frac{\partial S_{\mathrm{r}}}{\partial e} \mathrm{~d} e. $ | (3) |
式中:e为孔隙比,等号右边第一项表示常净应力条件下吸力与饱和度之间的变化关系,而第二项反映常吸力状态下孔隙比随饱和度的变化.
为简化模型推导采用图 1所示线性SWCC,在主吸湿和主干燥线(边界线)有
| $ \frac{\partial S_{\mathrm{r}}}{\partial s} \mathrm{~d} s=-\lambda_{\mathrm{sr}} \frac{\mathrm{d} s}{s+p_{\mathrm{a}}}. $ | (4) |

|
图 1 土水特征曲线简化模型 Fig. 1 Simplified model for soil-water characteristic curves |
而在扫描线有
| $ \frac{\partial S_{\mathrm{r}}}{\partial s} \mathrm{~d} s=-\kappa_{\mathrm{sr}} \frac{\mathrm{d} s}{s+p_{\mathrm{a}}}. $ | (5) |
式中:λsr为主吸湿和主干燥线的斜率,κsr为扫描线的斜率,pa为大气压力.
根据文献[14],常吸力状态下的三轴试验中非饱和黏性土的饱和度和孔隙比呈线性关系,故式(3)等号右边第二项可表示为
| $ \frac{\partial S_{\mathrm{r}}}{\partial e} \mathrm{~d} e=-\lambda_{\mathrm{se}} \mathrm{d} e. $ | (6) |
式中λse为常吸力状态下饱和度和孔隙比关系曲线的斜率.
利用式(3)~(6)可得沿边界线和扫描线的饱和度增量分别为
| $ \mathrm{d} S_{\mathrm{r}} =-\lambda_{\mathrm{sr}} \frac{\mathrm{d} s}{s+p_{\mathrm{a}}}-\lambda_{\mathrm{se}} \mathrm{d} e , $ | (7a) |
| $ \mathrm{~d} S_{\mathrm{r}} =-\kappa_{\mathrm{sr}} \frac{\mathrm{d} s}{s+p_{\mathrm{a}}}-\lambda_{\mathrm{se}} \mathrm{d} e. $ | (7b) |
假设边界面和加载面几何相似,按照文献[19]中提出的硬化法则,当应力路径在应力空间中改变加载方向时,边界面和加载面的运动及记忆中心的位置遵循以下准则:
1) 边界面可以在应力空间中改变大小和位置,其内部任意应力增量均引起塑性变形.
2) 边界面是加载面的几何边界,加载面与边界面始终在一点相切,加载面可以在应力空间内移动和膨胀但不能收缩.
3) 初始固结加载时,记忆中心位于应力空间某常吸力平面的坐标原点;对后续加载,它移动到应力路径改变方向(加卸载转换)的点.
4) 一旦记忆中心移动到新的位置,上一次加载中形成的边界面和加载面将消失;而在新记忆中心则出现新的边界面和加载面来描述下一次加载事件.为了保证变形的连续性,新的边界面刚出现时具有和旧的边界面同样的大小.
利用该硬化法则可将一个连续的循环加载过程分解成一个个独立的加载事件进行处理,从而为模拟材料在循环加载时复杂的力学特性提供方便.
为了对加载事件进行记忆,以m为加载事件的序号,如m=0表示初始固结加载,m=1表示第一次加载,余类推.
1.5 边界面和加载面方程在BBM模型中常吸力条件下的屈服面方程为椭圆,若以平均骨架应力p′代替其中的净平均应力,在(p′-q-s)空间中第m次加载时的边界面方程为
| $ F_{\mathrm{s}}^{(m)}=\left[p^{\prime}-\alpha_{\mathrm{p}^{\prime}}^{(m)}\right]^{2}+r^{2}\left[q-\alpha_{\mathrm{q}}^{(m)}\right]^{2}-\left[a_{\mathrm{F}}^{(m)}\right]^{2}=0. $ | (8) |
式中:αp′(m)和αq(m)为边界面圆心OF(m)的坐标,边界面长轴的半径aF(m)为塑性体积应变εvp的函数,r为边界面长短半轴之比.考虑到土在压缩和伸长状态下强度不同,从而有
| $ r=M^{-1}=\left\{\begin{array}{l} \left(\tan \theta_{\mathrm{c}}\right)^{-1}, q>\alpha_{\mathrm{q}}^{(m)}, \\ \left(\tan \theta_{\mathrm{e}}\right)^{-1}, q<\alpha_{\mathrm{q}}^{(m)} . \end{array}\right. $ | (9) |
式中M为临界状态线(CSL)的斜率.
类似地,吸力一定时加载面的方程为
| $ f_{\mathrm{s}}^{(m)}=\left[p^{\prime}-\xi_{\mathrm{p}^{\prime}}^{(m)}\right]^{2}+r^{2}\left[q-\xi_{\mathrm{q}}^{(m)}\right]^{2}-\left[a_{\mathrm{f}}^{(m)}\right]^{2}=0. $ | (10) |
式中:ξp′(m)和ξq(m)为加载面圆心Of(m)的坐标,af(m)为加载面长轴的半径.
在常吸力(s=sc)条件下,边界面和加载面在应力空间中的形状和位置如图 2所示.在图 2(a)中,非饱和土试样首先经吸力平衡达到X点(初始吸力sc),假设后续加卸载中该吸力保持不变,则应力路径位于s=sc的平面内.在图 2(b)中,如果在常吸力平面采用莫尔-库仑屈服准则,则在压缩和拉伸方向上,CSL的倾角分别为
| $ \tan \theta_{\mathrm{c}}=\frac{6 \sin \varphi}{3-\sin \varphi}, \tan \theta_{\mathrm{e}}=\frac{6 \sin \varphi}{3+\sin \varphi}. $ | (11) |

|
图 2 应力空间中的边界面和加载面 Fig. 2 Bounding surface and loading surface in stress space |
式中φ为土的有效内摩擦角.
1.6 边界面和加载面的演化规则假设边界面长轴半径为
| $ a_{\mathrm{F}}^{(m)}=a_{\mathrm{F}}^{(0)} \exp \left\{\chi_{\mathrm{s} 0}\left[\left(\varepsilon_{\mathrm{v}}^{\mathrm{p}}\right)_{m}-\left(\varepsilon_{\mathrm{v}}^{\mathrm{p}}\right)_{0}\right]\right\}. $ | (12) |
式中:χs0=(1+e0)/[λ(s)-κ];e0和(εvp)0为土样初始固结完成后的孔隙比和塑性体积应变;κ为非饱和黏性土的回弹指数;λ(s)为吸力为s时非饱和土压缩曲线的斜率,λ(s)=λ(0)[rs+(1-rs)exp(-βs)],λ(0)为饱和土压缩曲线的斜率;rs和β为材料参数; aF(0)为初始固结面长轴半径,其值与土在某吸力状态下的前期固结压力有关.
考虑到边界面和加载面几何相似和始终相切,可推导出边界面中心的位置为
| $ \alpha_{\mathrm{p}^{\prime}}^{(m)}=p_{m-1}^{\prime}-a_{\mathrm{F}}^{(m)}\left[p_{m-1}^{\prime}-\xi_{\mathrm{p}^{\prime}}^{(m-1)}\right] / a_{\mathrm{f}}^{(m-1)}, $ | (13) |
| $ \alpha_{\mathrm{q}}^{(m)}=q_{m-1}-a_{\mathrm{F}}^{(m)}\left[q_{m-1}-\xi_{\mathrm{q}}^{(m-1)}\right] / a_{\mathrm{f}}^{(m-1)}. $ | (14) |
要计算加载面fs(m)的中心位置ξp(m)′和ξq(m),只须将上两式中的aF(m)换成af(m)即可.
如图 2(b)所示,根据记忆中心M、当前应力点P及其共轭点R在应力空间中的位置以及两个面的相似性,可以通过它们之间的几何关系求出加载面的半径:
| $ \begin{array}{l} a_{\rm{f}}^{(m)} = \left( {{q_{m - 1}} - {q_m}} \right)a_{\rm{F}}^{(m)}/\left\{ {\left[ {p_{m - 1}^\prime - \alpha _{{{\rm{p}}^\prime }}^{(m)}} \right] \times } \right.\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {\left[ {{t_m} + \sqrt {t_m^2 - l_{m - 1}^2\left( {r_R^2 - r_M^2} \right)/\left( {k_m^2 + r_R^2} \right)} } \right]} \right\}, \end{array} $ | (15) |
| $ {k_m} = \left( {p_m^\prime - p_{m - 1}^\prime } \right)/\left( {{q_m} - {q_{m - 1}}} \right), $ |
| $ {l_m} = \left[ {{q_m} - \xi _{\rm{q}}^{(m)}} \right]/\left[ {p_m^\prime - \xi _{\rm{p}}^{(m)}} \right], $ |
| $ {t_m} = \left( {{k_m} + {l_{m - 1}}r_R^2} \right)/\left( {k_m^2 + r_R^2} \right). $ |
式中rM和rR分别为M点和R点处r的值.
1.7 常吸力各向等压加载如图 3所示,在非饱和土三轴试验中当增加吸力至X点(s=sc)达到平衡后,控制吸力不变,增加净围压至Y点.在这一各向等压加载(m=0)事件中,加载面和边界面始终重合.当应力点超过LC屈服面后,可根据产生的塑性体应变计算饱和度和孔隙比.

|
图 3 常吸力下初始各向等压加载 Fig. 3 Initial isotropic compression under constant suction |
对于BBM模型的LC屈服面,用平均骨架应力代替净平均应力可得
| $ {p^{\prime}}_{0 \mathrm{~F}}={p^{\prime}}_{\mathrm{c}}\left(p_{0}^{*} / {p^{\prime}}_{\mathrm{c}}\right)^{\frac{\lambda(0)-\kappa}{\lambda(s)-\kappa}} . $ | (16) |
式中: p0*为饱和土的屈服应力, p′c为参考应力.
等向压缩产生的弹性体应变增量为
| $ \mathrm{d} \varepsilon_{\mathrm{vp}}^{\mathrm{e}}=\frac{\kappa}{\nu} \frac{\mathrm{d} p^{\prime}}{p^{\prime}}. $ | (17) |
式中ν为比体积.
对式(1)微分可得
| $ \mathrm{d} p^{\prime}=\mathrm{d} p_{\mathrm{n}}+s \mathrm{~d} S_{\mathrm{r}}+S_{\mathrm{r}} \mathrm{d} s. $ | (18) |
考虑到ds=0,联立式(7)、(17)和(18)可得
| $ \mathrm{d} p^{\prime}=\frac{\mathrm{d} p_{\mathrm{n}}}{1-s \lambda_{\mathrm{se}} \kappa / p^{\prime}}. $ | (19) |
等向压缩产生的塑性体应变增量为
| $ \mathrm{d} \varepsilon_{\mathrm{vp}}^{\mathrm{p}}=\frac{\lambda(s)-\kappa}{\nu} \cdot \frac{\mathrm{d} {p^{\prime}}_{0 \mathrm{~F}}}{{p^{\prime}}_{0 \mathrm{~F}}}. $ | (20) |
联立式(7)、(18)和(20)可得
| $ \mathrm{d} {p^{\prime}}_{0 \mathrm{~F}}=\frac{\mathrm{d} p_{\mathrm{n}}}{1-s \lambda_{\mathrm{se}} \lambda(s) / {p^{\prime}}_{0 \mathrm{~F}}}. $ | (21) |
初始固结完成后若保持吸力为sc不变,第m次剪切加载时的边界面和加载面的形状和位置见图 4.

|
图 4 常吸力三轴剪切加载 Fig. 4 Triaxial shear loading under constant suction |
弹性应力应变关系为
| $ \mathrm{d} \varepsilon_{\mathrm{v}}^{\mathrm{e}}=\mathrm{d} p^{\prime} / K, \mathrm{~d} \varepsilon_{\mathrm{q}}^{\mathrm{e}}=\mathrm{d} q / 3 G. $ | (22) |
式中K和G分别为土的弹性体积和剪切模量.其中,K通常可用下式确定
| $ K=\nu p^{\prime} / \kappa . $ | (23) |
G一般需要由试验确定.
模型采用相关联流动法则,剪切过程中加载面上的塑性体积和剪切应变增量分别为
| $ \mathrm{d} \varepsilon_{\mathrm{v}}^{\mathrm{p}}=\left\langle L_{\mathrm{f}}^{(m)}\right\rangle n_{\mathrm{p}^{\prime}}^{(m)}, \mathrm{d} \varepsilon_{\mathrm{q}}^{\mathrm{p}}=\alpha\left\langle L_{\mathrm{f}}^{(m)}\right\rangle n_{\mathrm{q}}^{(m)}. $ | (24) |
式中: 〈〉为Macauley运算符,当且仅当加载指数Lf(m)为正时取值;α为修正系数,可按下式计算
| $ \alpha=\frac{M(M-9)(M-3)}{9(6-M)} \cdot \frac{1}{1-\kappa / \lambda(0)}. $ | (25) |
在当前应力点P处,加载面外法线单位矢量沿坐标轴p′和q方向的分量分别为
| $ n_{\mathrm{p}^{\prime}}^{(m)}=\left[p^{\prime}-\xi_{\mathrm{p}^{\prime}}^{(m)}\right] / D_{\mathrm{f}}^{(m)}, n_{\mathrm{q}}^{(m)}=r^{2}\left[q-\xi_{\mathrm{q}}^{(m)}\right] / D_{\mathrm{f}}^{(m)}, $ | (26) |
| $ D_{\mathrm{f}}^{(m)}=\left\{\left[p^{\prime}-\xi_{\mathrm{p}^{\prime}}^{(m)}\right]^{2}+r^{4}\left[q-\xi_{\mathrm{q}}^{(m)}\right]^{2}\right\}^{1 / 2} . $ | (27) |
相应地有
| $ L_{\mathrm{f}}^{(m)}=\left[n_{\mathrm{p}^{\prime}}^{(m)} \mathrm{d} p^{\prime}+n_{\mathrm{q}}^{(m)} \mathrm{d} q\right] / h_{\mathrm{m}}. $ | (28) |
其中hm为加载面的塑性模量.
以上公式用于边界面Fs(m)时,只需将np(m)′, nq(m),Lf(m)和hm分别换成Np(m)′, Nq(m),LF(m)和Hm即可.
假设边界面Fs(m)在应力空间中的任何位置都具有与初始固结面相同的特性,其一致性条件为
| $ \mathrm{d} F_{\mathrm{s}}^{(m)}=\frac{\partial F_{\mathrm{s}}^{(m)}}{\partial p^{\prime}} \mathrm{d} p^{\prime}+\frac{\partial F_{\mathrm{s}}^{(m)}}{\partial q} \mathrm{~d} q+\frac{\partial F_{\mathrm{s}}^{(m)}}{\partial \varepsilon_{\mathrm{v}}^{\mathrm{p}}} \mathrm{d} \varepsilon_{\mathrm{v}}^{\mathrm{p}}=0. $ | (29) |
考虑常吸力条件并联立式(8)、(12)、(24)和(29)可求得边界面的塑性模量:
| $ H_{\mathrm{m}}=\frac{\chi_{\mathrm{s} 0} a_{\mathrm{F}}^{(m)}}{\left[D_{\mathrm{F}}^{(m)}\right]^{2}}\left[p^{\prime}-\alpha_{\mathrm{p}^{\prime}}^{(m)}+a_{\mathrm{F}}^{(m)}\right]\left[p^{\prime}-\alpha_{\mathrm{p}^{\prime}}^{(m)}\right]. $ | (30) |
式中DF(m)={[p′-αp′(m)]2+r4[q-αq(m)]2}1/2.
而加载面的塑性模量可用下面的内插关系确定[19]
| $ h_{\mathrm{m}}=H_{R}+\left(H_{M}-H_{R}\right)\left[1-a_{\mathrm{f}}^{(m)} / a_{\mathrm{F}}^{(m)}\right]^{\gamma} . $ | (31) |
式中:HM和HR分别为M点和R点处的塑性模量,HR可用式(30)直接计算;参数γ定义为[19]
| $ \gamma=b \gamma_{\mathrm{b}} \varepsilon_{0} /\left(\gamma_{\mathrm{b}}+b \varepsilon_{\mathrm{Q}}\right). $ | (32) |
式中:b和γb为常数,取决于土的初始孔隙比、超固结比、静强度和动剪应力幅值等因素;εQ为整个加载过程中产生的有效塑性应变,
本文模型涉及参数分别与土的非饱和状态、水力-力学特性和循环加载相关,具体确定方法如下.
1.9.1 非饱和状态相关参数通过控制吸力的各向同性排水压缩试验可以得到λ(0),κ,βs,r,p′c,p0*;通过控制净平均应力的三轴干-湿循环试验可以得到s0,λs和κs;通过同时控制净平均应力和吸力的三轴排水剪切试验,换算整理可得到参数G,M和k.
1.9.2 水力-力学特性相关参数与水力性质相关的λsr和κsr可由实测的非饱和土的土水特征曲线得到;水力-力学性质耦合参数λse可由常吸力下压缩或剪切试验的饱和度和孔隙比关系曲线斜率求出.
1.9.3 循环加载相关参数b和γb与土体的初始状态、加载路径和加载条件等因素有关,可通过控制加载幅值的循环三轴试验结果求出,具体方法可参照文献[19].
2 模型的试验验证 2.1 各向等压加载试验Sun等[12]采用非饱和土三轴仪在恒定吸力条件下对非饱和珍珠黏土(pearl clay)进行了各向等压试验,试验中分别控制吸力为100和150 kPa.为模拟此次试验结果,采用的模型参数如表 1所示.
| 表 1 模拟各向等压和静态三轴剪切试验的模型参数 Tab. 1 Model parameters of isotropic compression and static triaxial shear tests |
图 5和6分别为常吸力等向压缩过程中试样饱和度和孔隙比随净平均应力的变化,从对比图中可以看出,模型模拟结果与试验结果吻合较好.
|
图 5 常吸力下等向压缩加载中饱和度的变化 Fig. 5 Variations of saturation degree during isotropic compression under constant suction |

|
图 6 常吸力下等向压缩过程中孔隙比的变化 Fig. 6 Variations of pore ratio during isotropic compression under constant suction |
图 5中4种不同初始孔隙比试样的饱和度随净应力的增大而逐渐增加,说明非饱和土中存在水-力耦合效应.而图 6中4种不同初始饱和度试样的孔隙比随压力的增大而逐渐减小,符合一般土的压缩规律,其中吸力的改变对土样的压缩性有一定影响.由此对比和分析可知,所建模型较好地反映了非饱和黏性土试样在等向压缩过程中的水-力耦合现象.
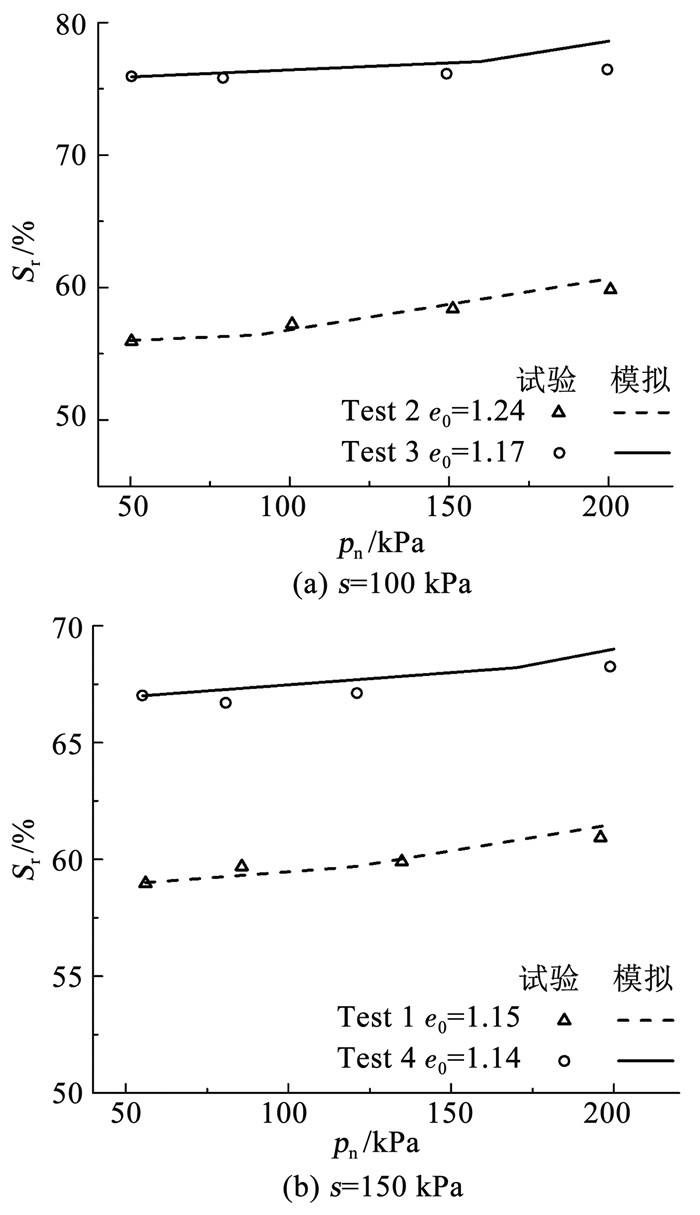
2.2 静态三轴剪切试验Sun等[12]在恒定吸力条件下对非饱和珍珠黏土试样先施加200 kPa的净围压进行各向等向固结,然后在吸力分别为100和150 kPa条件下对具有不同初始饱和度和孔隙比的试样进行静态三轴剪切试验.
采用表 1参数对该试验结果进行模拟,图 7和8分别为常吸力下不同初始饱和度(图 6)试样在剪切过程中的应力-应变曲线和饱和度变化对比,可以看出,模型的模拟结果与试验数据相当吻合.此外,相同吸力条件下试样的饱和度越大,应力应变曲线的峰值越高(图 7),即试样的剪切强度越高.这说明在净应力和吸力均相同的情况下,饱和度能显著影响非饱和黏性土的变形和强度特征.

|
图 7 常吸力下三轴静态剪切试验中应力-应变关系 Fig. 7 Stress-strain relations during static triaxial shear test under constant suction |

|
图 8 常吸力下静态三轴剪切试验中饱和度的变化 Fig. 8 Variations of saturation degree during static triaxial shear test under constant suction |
图 8中,试样的饱和度在剪切过程中不断上升,而吸力变化对其影响不明显.
图 7和8中的对比和验证表明,本文模型能够很好地模拟非饱和黏性土在常吸力条件下静态三轴剪切试验中的水-力耦合效应.
2.3 动态三轴剪切试验通过改进GDS-Tritech50非饱和土三轴仪内置的控制加载模块,在室内开展了控制吸力周期循环加载条件下的非饱和土三轴剪切试验.由于快速加荷引起黏性土内吸力的平衡需要较长时间,为减少试验时间,采用了黏质粉土试样.试样直径和高分别为38.1和80 mm,密度控制在1.98 g/cm3, 含水率为17.9%,初始饱和度(Sr0)为0.78.试验中采用了不同的吸力s和净围压pnet.为了让周期循环加载期间吸力的测量尽可能可靠,经过反复测试,选择加载频率为0.001 Hz;此外,荷载波形采用正弦波,动应力幅值qd为250和320 kPa.有关动三轴试验的具体实施方法见文献[25].
限于篇幅,仅给出净围压为100 kPa和qd=250 kPa的模型模拟结果,模拟采用的模型参数为: λ(0)=0.09, κ=0.015,e0=0.63, G=8 000 kPa, φ=26°, k=1.1, p0*=55 kPa, p′c=43 kPa, β=16.4, rs=0.26, λs=0.073, κs=0.015, s0=1 000 kPa, b=13.4, γb=12.7.
图 9为两种不同吸力下非饱和土循环三轴剪切加载时的应力应变曲线.可以看出,相同试样仅由于吸力不同,呈现出不同的应力应变特征.另外,由于所施加的动应力幅值小于试样的临界动应力,随着循环加载的不断进行,试验的塑性变形越来越小,应力应变滞回圈最终趋于稳定,土样不会发生破坏.图 9的对比表明,所建模型较好地再现了非饱和土在循环荷载作用下的循环塑性特征.

|
图 9 常吸力循环三轴剪切试验结果的模拟与对比 Fig. 9 Comparison between simulation and cyclic triaxial shear test results under constant suction |
目前,非饱和土水-力耦合三轴剪切试验,尤其是动三轴剪切试验数据极其匮乏.为了进一步检验模型的合理性,针对2.3节所示的试验条件并采用相同的模型参数,对非饱和土试样的水-力耦合效应及相关因素影响进行预测和分析.
图 10为两种不同吸力条件下初始饱和度为0.61的土的应力应变曲线.与图 9相比,在其他条件不变的情况下,初始饱和度的降低导致循环荷载产生的累积应变增大,说明饱和度的减少会影响非饱和土的长期强度,这与前述静载试验结果一致.

|
图 10 饱和度对变形特性的影响 Fig. 10 Effects of saturation degree on deformation behavior |
图 11为在不同初始饱和度、吸力、净围压和动应力幅值条件下饱和度的变化.可以看出,饱和度随着循环加载呈现振荡变化,并最终趋于一种循环稳定状态.这是因为在加载初期,土样孔隙比的变化较大,因而饱和度也呈现明显的振荡变化.随着加载的进行,土样逐渐密实,饱和度不再发生明显的变化.土的初始饱和度越大,达到这种稳定状态所需要的变形越小,说明饱和度的增大明显影响土的变形特征(图 11(a));对初始饱和度相同的土样,吸力不同会影响饱和度的变化(图 11(b));另外,动应力幅值对饱和度振幅也有一定影响(图 11(c)).

|
图 11 不同加载条件对饱和度的影响 Fig. 11 Effects of loading conditions on saturation degree |
由上可知,非饱和黏性土在循环荷载作用下的水-力耦合效应相当复杂,要明确其规律还需要做更多的系统性研究.
3.3 循环加载应力路径预测图 12为循环荷载作用下非饱和土的应力路径.可以看出,即便加载条件相同,初始饱和度的不同导致应力路径终点发生了较大改变,这再次说明非饱和土循环加载时存在的水-力耦合效应.

|
图 12 循环加载应力路径预测 Fig. 12 Prediction of stress path under cyclic loading |
1) 采用的硬化法则可把一个连续的循环加载过程分解成独立的加载事件进行处理,从而为模拟非饱和土的循环塑性提供了可能.
2) 尽管在模型的建立中采用了一种简化的线性SWCC模型,但仍可采用其他复杂的SWCC模型以扩大其适用范围.
3) 由于仅通过骨架应力反映水力特性对力学特性的影响,而吸力屈服不受应力变化影响,因此,所建模型只实现了水力-力学特性的部分耦合.
4) 没有考虑非饱和黏性土加载过程中的吸力变化,模型的建立假设和所完成循环加载试验的条件(频率、振幅等)与实际非饱和土路基还存在较大差异.
5) 由于非饱和土在动态循环荷载作用下的水-力耦合特性十分复杂,进一步研究的重点是开展室内外试验和现场长期观测,深入了解这种特性及其变化规律,为建立更可靠的本构模型打下坚实的基础.
| [1] |
ALONSO E E, GENS A, JOSA A. A constitutive model for partially saturated soils[J]. Géotechnique, 1990, 40(3): 405. DOI:10.1680/geot.1990.40.3.405 |
| [2] |
GENS A, ALONSO E E. A framework for the behaviour of unsaturated expansive clays[J]. Canadian Geotechnical Journal, 1992, 29(6): 1013. DOI:10.1139/t92-120 |
| [3] |
WHEELER S J, SIVAKUMAR V. An elasto-plastic critical state framework for unsaturated soil[J]. Géotechnique, 1995, 45(1): 35. DOI:10.1680/geot.1995.45.1.35 |
| [4] |
KOHGO Y, NAKANO M, MIYAZAKI T. Theoretical aspects of constitutive modelling for unsaturated soils[J]. Soils and Foundations, 1993, 33(4): 49. DOI:10.3208/sandf1972.33.4_49 |
| [5] |
SUN D A, MATSUOKA H, CUI H B, et al. Three-dimensional elasto-plastic model for unsaturated compacted soils with different initial densities[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2003, 27(12): 1079. DOI:10.1002/nag.313 |
| [6] |
SUN Dean, MATSUOKA H. An elastoplastic model for frictional and cohesive materials and its application to cemented sands[J]. Mechanics of Cohesive-Frictional Materials, 2015, 4(6): 525. DOI:10.1002/(sici)1099-1484(199911)4:6<525::aid-cfm72>3.0.co;2-x |
| [7] |
WHEELER S J, SHARMA R S, BUISSON M S R. Coupling of hydraulic hysteresis and stress-strain behaviour in unsaturated soils[J]. Géotechnique, 2003, 53(1): 41. DOI:10.1680/geot.2003.53.1.41 |
| [8] |
缪林昌. 非饱和土的本构模型研究[J]. 岩土力学, 2007, 28(5): 855. MIAO Linchang. Research of constitutive model of unsaturated soils[J]. Rock and Soil Mechanics, 2007, 28(5): 855. DOI:10.16285/j.rsm.2007.05.002 |
| [9] |
SHENG Daichao, ZHOU Annan. Coupling hydraulic with mechanical models for unsaturated soils[J]. Canadian Geotechnical Journal, 2011, 48(5): 826. DOI:10.1139/t10-109 |
| [10] |
SHENG Daichao. Review of fundamental principles in modelling unsaturated soil behaviour[J]. Computers and Geotechnics, 2011, 38(6): 757. DOI:10.1016/j.compgeo.2011.05.002 |
| [11] |
SUN D A, SHENG D C, CUI H B, et al. A density-dependent elastoplastic hydro-mechanical model for unsaturated compacted soils[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2007, 31(11): 1257. DOI:10.1002/nag.579 |
| [12] |
SUN Dean, SUN Wenjing, XIANG Li. Effect of degree of saturation on mechanical behaviour of unsaturated soils and its elastoplastic simulation[J]. Computers and Geotechnics, 2010, 37(5): 678. DOI:10.1016/j.compgeo.2010.04.006 |
| [13] |
SUN Dean, SHENG Daichao, SLOAN S W. Elastoplastic modelling of hydraulic and stress-strain behaviour of unsaturated soils[J]. Mechanics of Materials, 2007, 39(3): 212. DOI:10.1016/j.mechmat.2006.05.002 |
| [14] |
SUN Dean, SHENG Daichao, XIANG Li, et al. Elastoplastic prediction of hydro-mechanical behaviour of unsaturated soils under undrained conditions[J]. Computers and Geotechnics, 2008, 35(6): 845. DOI:10.1016/j.compgeo.2008.08.002 |
| [15] |
PREVOST J H. Anisotropic undrained stress-strain behavior of clays[J]. Journal of the Geotechnical Engineering Division, 1978, 104(8): 1075. |
| [16] |
MRÓZ Z, NORRIS V A, ZIENKIEWICZ O C. An anisotropic, critical state model for soils subject to cyclic loading[J]. Géotechnique, 1981, 31(4): 451. DOI:10.1680/geot.1981.31.4.451 |
| [17] |
DAFALIAS Y F, HERRMANN L R. A bounding surface soil plasticity model[C]//Proc Int Symp Soils under Cyclic Trans Load.[S.l.]: [s.n.], 1980: 335
|
| [18] |
MRÓZ Z, NORRIS V A, ZIENKIEWICZ O C. Application of an anisotropic hardening model in the analysis of elasto-plastic deformation of soils[J]. Géotechnique, 1979, 29(1): 1. DOI:10.1680/geot.1979.29.1.1 |
| [19] |
LI Tao, MEISSNER H. Two-surface plasticity model for cyclic undrained behavior of clays[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2002, 128(7): 613. DOI:10.1061/(asce)1090-0241(2002)128:7(613) |
| [20] |
李涛, MEISSNERH. 循环荷载作用下饱和黏性土的弹塑性双面模型[J]. 土木工程学报, 2006, 39(1): 92. LI Tao, MEISSNER H. Elastoplastic two-surface model for clays under undrained cyclic loading[J]. China Civil Engineering Journal, 2006, 39(1): 92. DOI:10.3321/j.issn:1000-131X.2006.01.019 |
| [21] |
MASING G. Eigenspannungen and verfestigung beim messing[C]//Proceedings of 2nd International Conference for Applied Mechanics. Zurich: [s.n.], 1926
|
| [22] |
HU Cun, LIU Haixiao. A new bounding-surface plasticity model for cyclic behaviors of saturated clay[J]. Communications in Nonlinear Science and Numerical Simulation, 2015, 22(1/2/3): 101. DOI:10.1016/j.cnsns.2014.10.023 |
| [23] |
MEISSNER H, BECKER A. Dynamic behavior of partially saturated sand[C]// Proceedings of 7th International Conference on Soil Dynamics and Earthquake Engineering. Crete, Greece: [s.n.], 1995: 45
|
| [24] |
BECKER T, LI T. Behaviour of unsaturated cohesive soils subjected to cyclic loads[C]//SCHANZ T. Unsaturated Soils: Experimental Studies. Springer Proceedings in Physics. Heidelberg, Berlin: Springer, 2005, 93: 355. DOI: 10.1007/3-540-26736-0_27
|
| [25] |
彭丽云, 李涛, 刘建坤. 循环荷载作用下非饱和击实粉土变形特性的试验研究[J]. 北京工业大学学报, 2010, 36(11): 1504. PENG Liyun, LI Tao, LIU Jiankun. Deformation property of unsaturated compacted silts under cyclic loading[J]. Journal of Beijing University of Technology, 2010, 36(11): 1504. DOI:10.11936/bjutxb2010111504 |
| [26] |
YANG C, CUI Y J, PEREIRA J M, et al. A constitutive model for unsaturated cemented soils under cyclic loading[J]. Computers and Geotechnics, 2008, 35(6): 853. DOI:10.1016/j.compgeo.2008.08.005 |
| [27] |
KHALILI N, HABTE M A, ZARGARBASHI S. A fully coupled flow deformation model for cyclic analysis of unsaturated soils including hydraulic and mechanical hystereses[J]. Computers and Geotechnics, 2008, 35(6): 872. DOI:10.1016/j.compgeo.2008.08.003 |
| [28] |
XIONG Yonglin, YE Guanlin, XIE Yi, et al. A unified constitutive model for unsaturated soil under monotonic and cyclic loading[J]. Acta Geotechnica, 2019, 14(2): 313. DOI:10.1007/s11440-018-0754-2 |
 2021, Vol. 53
2021, Vol. 53


