沿海地区由于饱和软黏土地基的高压缩性,在荷载作用下建筑容易产生较大沉降,因此, 需对地基进行预先处理,以加快地基的固结速率,其中设计理论大多基于砂井固结理论.Barron[1]首先对砂井地基给出了等应变和自由应变两种假定下径向固结度的计算公式,并指出当固结时间较长时,两者假定下的计算差异很小.在此基础上,Hansbo等[2-3]分别研究了井阻作用对砂井固结的影响.Tang等[4-6]在等应变条件下分别考察了变荷载、影响区形状等因素对砂井地基固结机制的影响,进一步完善了砂井固结理论.同时,为得到更为精确的固结解答,Berry等[7-9]考虑土体非线性压缩关系,采用不同关系式修正砂井径向固结方程,并给出解析解答.然而,上述研究均忽略了软黏土的流变特性和渗流的非达西特性,因而地基沉降的理论值与实际观测值常存在较大差异.
固结试验和现场观测[10-12]表明,软黏土具有显著的流变性.为了更好地反映土体流变固结机制,Taylor等[13]首先采用Kelvin模型分析土体的主次固结耦合过程,随后有学者引入了Merchant模型[14]、广义Voigt模型[15]等.但由于元件模型通过基本流变元件的组合而成,本构方程有时含有较多参数,且形式比较复杂.因此,刘忠玉等[16-17]引入了分数阶导数模型.同时,有学者基于经典的弹塑性理论,提出了弹黏塑性本构模型.其中,Yin等[18]引入等效时间的概念,给出了一个非线性的EVP本构模型,较好地描述了土体的应力-应变-时间关系.姚仰平等[19-20]则在修正剑桥模型的基础上,采用统一硬化参数,得到了考虑时间效应的统一硬化(UH)模型.上述理论多应用于一维固结情况,同时也开始应用于砂井地基等多维固结分析.例如,刘兴旺等[21-23]先后引入Merchant模型和四元件模型描述砂井地基黏弹性固结问题,并分析了黏弹性参数对固结过程的影响.但目前还少有文献对砂井地基的弹黏塑性变形特性进行深入分析.
另外,已有试验[24-26]表明,某些黏性土中的渗流速度与水力梯度之间存在非线性关系,有别于Darcy渗流,称之为非Darcy渗流.为深入探讨非Darcy渗流下土体的固结机制,学者们[27-29]分别引入指数渗流、起始水力梯度渗流、Hansbo渗流等模式来描述砂井地基的非Darcy渗流,并通过与Darcy渗流下的结果对比,分析相应参数对地基整体孔压消散速率的影响.最近,刘忠玉等[30-31]分别在传统Terzaghi固结理论和经典Biot固结理论的基础上,引入Hansbo渗流给予修正,分析了Hansbo渗流参数对多维弹性饱和地基固结的变化规律.不过上述文献并没有考虑土体应力-应变的非线性关系,因而属于线弹性理论范畴.同时需要注意的是,在土体固结时,随着孔隙比的减小,渗透系数也应当是变化的.Taylor[32]首先提出了渗透系数与孔隙比的经验关系式,之后不断有学者[33-34]通过试验研究影响渗透系数变化的主要因素.同时,也不断有学者[35-36]讨论渗透系数变化对固结过程的影响.但是,这些固结分析仅限于渗流或变形的非线性方面,并未考虑土体的流变特性,并不能准确地分析多维饱和软黏土地基的固结过程.
总之,上述研究成果丰富和发展了对固结机理的理解.但相对而言,在多维固结分析中同时考虑渗流非Darcy特性、渗透系数变化及土体流变特性等方面影响的报道还较少.为此,在自由应变条件下,拟引入考虑时间效应的UH本构模型和Hansbo渗流模型,同时考虑变渗透系数的影响,重新推导理想砂井地基固结方程,并初步探讨相关参数对软黏土地基流变固结特性的影响机制.
1 分析模型及推导控制方程 1.1 应力-应变关系在考虑时间效应的UH模型[19]中,体积应变增量的表达式为
| $ \mathrm{d} \varepsilon_{\mathrm{v}}=\left\{\begin{array}{l} \mathrm{d} \varepsilon_{\mathrm{v}}^{\mathrm{e}}+\mathrm{d} \varepsilon_{\mathrm{v}}^{\mathrm{sp}}+\mathrm{d} \varepsilon_{\mathrm{v}}^{\mathrm{tp}}, \mathrm{d} \sigma^{\prime} \geqslant 0 ,\\ \mathrm{~d} \varepsilon_{\mathrm{v}}^{\mathrm{e}}+\mathrm{d} \varepsilon_{\mathrm{v}}^{\mathrm{tp}}, \mathrm{d} \sigma^{\prime}<0, \end{array}\right. $ | (1) |
| $ \mathrm{d} \varepsilon_{\mathrm{v}}^{\mathrm{e}}=C_{\mathrm{s}} \mathrm{d} \sigma^{\prime} /\left[\left(1+e_{0}\right) \sigma^{\prime} \ln 10\right], $ | (2) |
| $ \mathrm{d} \varepsilon_{\mathrm{v}}^{\mathrm{sp}}=\frac{C_{\mathrm{c}}-C_{\mathrm{s}}}{\left(1+e_{0}\right) \ln 10} \frac{M^{4}}{M_{\mathrm{f}}^{4}} \frac{\mathrm{d} \sigma^{\prime}}{\sigma^{\prime}}, $ | (3) |
| $ \mathrm{d} \varepsilon_{\mathrm{v}}^{\mathrm{tp}}=C_{\mathrm{\alpha}} \mathrm{d} t /\left[\left(1+e_{0}\right)\left(t_{\mathrm{a}}+t_{0}\right) \ln 10\right]. $ | (4) |
式中:dεve和dεvsp分别表示有效应力增量dσ′作用下产生的弹性体应变增量和塑性体应变增量,dεvtp表示时间作用产生的塑性体应变增量,ta和t0分别表示老化时间和单位时间,Cc为压缩指数,Cs为回弹指数,Cα为次固结系数,M和Mf分别为临界状态应力比和潜在破坏应力比,且
| $ M =6 \sin \varphi /(3-\sin \varphi), $ | (5) |
| $ M_{\mathrm{f}}=6\left[\sqrt{\frac{\chi}{R}\left(1+\frac{\chi}{R}\right)}-\frac{\chi}{R}\right], $ | (6) |
| $ \chi=M^{2} / 12(3-M) $ | (7) |
| $ R=\frac{\sigma^{\prime}}{{\sigma^{\prime}}_{\mathrm{c} 0}} \cdot \exp \left.[-\left(1+e_{0}\right) \varepsilon_{\mathrm{v}}^{\mathrm{p}} \ln 10 /\left(C_{\mathrm{c}}-C_{\mathrm{s}}\right)\right], $ | (8) |
| $ \left(t_{\mathrm{a}}+t_{0}\right) / t_{0}=R^{-\alpha}, $ | (9) |
| $ \alpha =\left(C_{\mathrm{c}}-C_{\mathrm{s}}\right) / C_{\mathrm{\alpha}}. $ | (10) |
其中:φ为土的内摩擦角;R表示超固结参数;σ′c0类似先期固结压力,若不考虑时间效应即为先期固结压力,此时超固结参数的初值R0为超固结比的倒数;e0为初始孔隙比;εvp=εvsp+εvtp为塑性体应变.
1.2 控制方程推导设某均质饱和软黏土层厚度为H,底部不透水,顶部透水,并且在自重等荷载作用下已经固结完成.其中均匀设置打穿软土层的砂井,其半径为rw,影响区半径为re.现于砂井地基表面瞬时施加均布荷载p0,并假定在固结过程中土体不发生侧向变形[5].为便于计算,设初始有效应力σ′0和与之对应的初始孔隙比e0沿土层深度不变[37].在半径r深度z处,时刻t的有效应力和超孔隙水压力(以下简称孔压)分别为σ′(r, z, t)和u(r, z, t),渗流速度为
| $ \vec{v}=\left\{\begin{array}{ll} K|\vec{i}|^{m-1} /\left(m i_{1}^{m-1}\right) \cdot \vec{i}, & |\vec{i}| \leqslant i_{1}, \\ K\left[1-i_{1}(m-1) /(m|\vec{i}|)\right] \cdot \vec{i}, & |\vec{i}|>i_{1}. \end{array}\right. $ | (11) |
式中:m为由试验确定的常数;i1为直线段起始水力梯度;K为渗透系数,这里采用Taylor经验关系式来描述其与孔隙比e的关系,即
| $ \log K=\log K_{0}-\left(e_{0}-e\right) / C_{\mathrm{k}}. $ | (12) |
式中:K0为初始孔隙比e0对应的初始渗透系数;Ck为渗透指数,反映渗透系数的变化程度.
考虑体积应变εv与孔隙比e的关系,可得
| $ K=K_{0} \exp \left[-\left(1+e_{0}\right) \varepsilon_{\mathrm{v}} \ln 10 / C_{\mathrm{k}}\right]. $ | (13) |
为便于后面计算,将式(11)改写成形如Darcy定律的表达式
| $ \vec{v}=K^{\prime} \vec{i}. $ | (14) |
式中K′称为视渗透系数,即
| $ \begin{array}{c} K^{\prime}=\left\{\begin{array}{ll} K|\vec{i}|^{m-1} /\left(m i_{1}^{m-1}\right), & |\vec{i}| \leqslant i_{1}, \\ K\left[1-i_{1}(m-1) /(m|\vec{i}|)\right], & |\vec{i}|>i_{1} . \end{array}\right. \end{array} $ | (15) |
式中:
考虑土体渗流连续性条件,可得
| $ \frac{\partial \varepsilon_{\mathrm{v}}}{\partial t}=\frac{1}{r} \frac{\partial}{\partial r}\left(r v_{r}\right)+\frac{\partial v_{z}}{\partial z}. $ | (16) |
根据有效应力原理,可得
| $ \frac{\partial u}{\partial r}=-\frac{\partial \sigma^{\prime}}{\partial r}, \frac{\partial u}{\partial z}=-\frac{\partial \sigma^{\prime}}{\partial z}. $ | (17) |
由式(1)、(11)、(16)和(17)联立可得
| $ \frac{1}{r} \frac{\partial}{\partial r}\left(\psi r \frac{\partial \sigma^{\prime}}{\partial r}\right)+\frac{\partial}{\partial z}\left(\psi \frac{\partial \sigma^{\prime}}{\partial z}\right)=\beta \frac{\partial \sigma^{\prime}}{\partial t}+\lambda . $ | (18) |
式中:ψ=K′/γw;λ=Cα/[(1+e0)(ta+t0)ln 10],由于该参数同时含有次固结系数和老化时间,该参数反映了土体流变性和超固结特性;β可表示为
| $ \beta=\left\{\begin{array}{ll} \frac{C_{\mathrm{s}}+\left(C_{\mathrm{c}}-C_{\mathrm{s}}\right) M^{4} / M_{\mathrm{f}}^{4}}{\left(1+e_{0}\right) \sigma^{\prime} \ln 10}, & \mathrm{~d} \sigma^{\prime} \geqslant 0, \\ \frac{C_{\mathrm{s}}}{\left(1+e_{0}\right) \sigma^{\prime} \ln 10}, & \mathrm{~d} \sigma^{\prime}<0. \end{array}\right. $ | (19) |
本课题的初始条件及边界条件如下:
| $ \sigma^{\prime}(r, z, 0)={\sigma^{\prime}}_{0}, r_{w} \leqslant r \leqslant r_{e}, 0 \leqslant z \leqslant H , $ | (20) |
| $ \left\{\begin{array}{l} \sigma^{\prime}\left(r_{\rm{w}}, z, t\right)=\sigma_{0}^{\prime}+p_{0}, 0 \leqslant z \leqslant H, t>0, \\ \sigma^{\prime}(r, 0, t)=\sigma_{0}^{\prime}+p_{0}, r_{\rm{w}} \leqslant r \leqslant r_{\rm{e}}, t>0, \end{array}\right. $ | (21) |
| $ \left\{\begin{array}{l} \frac{\partial \sigma^{\prime}\left(r_{\rm{e}}, z, t\right)}{\partial r}=0,0 \leqslant z \leqslant H, t>0, \\ \frac{\partial \sigma^{\prime}(r, H, t)}{\partial z}=0, r_{\rm{w}} \leqslant r \leqslant r_{\rm{e}}, t>0. \end{array}\right. $ | (22) |
由于求解上述非线性微分方程解析解比较困难,采用隐式有限差分法进行求解.首先,在rw≤r≤re内,将土层沿径向以Δr为步长由内向外离散,节点从0到N编号;在0≤z≤H内,土层沿竖向以Δz为步长从上往下离散,节点编号从0到Z.同时以Δt为时间步长离散时间.这样,方程(18)离散为
| $ \begin{array}{c} {\sigma^{\prime}}_{i, j}^{\prime k+1}={\sigma^{\prime}}_{i, j}^{\prime k}+\varphi_{i^{\prime}, j}^{k+1}\left(\psi_{i^{\prime}+1 / 2, j}^{k+1} r_{i^{\prime}+1 / 2} A_{i^{\prime}, j}^{k+1}-\psi_{i^{\prime}-1 / 2, j}^{k+1}\right. \cdot \\ \left.r_{i^{\prime}-1 / 2} B_{i^{\prime}, j}^{k+1}\right)+\eta_{i^{\prime}, j}^{k+1}\left(\psi_{i^{\prime}, j+1 / 2}^{k+1} C_{i^{\prime}, j}^{k+1}-\psi_{i^{\prime}, j-1 / 2}^{k+1} D_{i^{\prime}, j}^{k+1}\right)+E_{i^{\prime}, j}^{k+1}. \end{array} $ | (23) |
式中:xi′, jk表示变量x在kΔt时刻,点(rw+i′Δr,jΔz)处的值,且
同时,初始条件(20),边界条件(21)和(22)的离散结果如下:
| $ {\sigma^{\prime}}_{i, j}^{0}={\sigma^{\prime}}_{0}, i^{\prime}=0,1,2, \cdots, N ; j=0,1,2, \cdots, Z. $ | (24) |
| $ \left\{\begin{array}{l} {\sigma^{\prime}}_{i, 0}^{\prime k}={\sigma^{\prime}}_{0}+p_{0}, i^{\prime}=0,1, \cdots, N ; k=1,2, \cdots, \\ {\sigma^{\prime}}_{0, j}^{ k}={\sigma^{\prime}}_{0}+p_{0}, j=0,1, \cdots, Z ; k=1,2, \cdots. \end{array}\right. $ | (25) |
| $ \begin{array}{l} {\sigma^{\prime}}_{N,j}^{k + 1} = {\sigma^{\prime}}_{N,j}^k - \varphi _{N,j}^{k + 1}\left( {\psi _{N + 1/2,j}^{k + 1}{r_{N + 1/2}} + \psi _{N - 1/2,j}^{k + 1}} \right. \cdot \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {{r_{N - 1/2}}} \right)B_{N,j}^{k + 1} + E_{N,j}^{k + 1} + \eta _{N,j}^{k + 1}\left( {\psi _{N,j + 1/2}^{k + 1}} \right. \cdot \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {C_{N,j}^{k + 1} - \psi _{N,j - 1/2}^{k + 1}D_{N,j}^{k + 1}} \right). \end{array} $ | (26) |
| $ \begin{array}{l} {\sigma^{\prime}}_{{i^\prime },Z}^{k + 1} = {\sigma^{\prime}}_{{i^\prime },Z}^k + \varphi _{{i^\prime },Z}^{k + 1}\left( {\psi _{{i^\prime } + 1/2,Z}^{k + 1}{r_{{i^\prime } + 1/2}}A_{{i^\prime },Z}^{k + 1} - } \right.\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {\psi _{{i^\prime } - 1/2,j}^{k + 1}{r_{{i^\prime } - 1/2}}B_{{i^\prime },Z}^{k + 1}} \right) + E_{{i^\prime },Z}^{k + 1} - \eta _{{i^\prime },Z}^{k + 1} \cdot \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {\psi _{{i^\prime },Z + 1/2}^{k + 1} + \psi _{{i^\prime },Z - 1/2}^{k + 1}} \right)D_{{i^\prime },Z}^{k + 1}. \end{array} $ | (27) |
这样,由式(23)~(27)构成封闭的方程组,用迭代法可解得各节点的有效应力,然后利用有效应力原理可得其孔压值.最后,引入按孔压定义的砂井地基的平均固结度式(28),来定量地描述地基中孔压的整体消散情况.
| $ {U_{\rm{P}}} = 1 - \frac{{\int_0^H {{\rm{d}}} z\int_{{r_{\rm{w}}}}^{{r_{\rm{e}}}} 2 {\rm{ \mathsf{ π} }}ru{\rm{d}}r}}{{\int_0^H {{\rm{d}}} z\int_{{r_{\rm{w}}}}^{{r_{\rm{e}}}} 2 {\rm{ \mathsf{ π} }}r{p_0}{\rm{d}}r}} = 1 - \frac{{2\Delta z\sum\limits_{j = 0}^{Z - 1} {\sum\limits_{{i^\prime } = 0}^{N - 1} {S_{{i^\prime },j}^k} } }}{{{p_0}H\left( {r_{\rm{e}}^2 - r_{\rm{w}}^2} \right)}}. $ | (28) |
式中:
最后,将上述算法编成了Fortran程序.
3 解法验证令m=1或i1=0,M=Mf,Cα=0,Cc=Ck,本课题将退化成耿雪玉[37]在自由应变假定下曾讨论过的符合Darcy定律的砂井地基非线性固结问题.为便于对比,引入如下无量纲参数:Z=z/H,X=r/rw,U=u/p0,Tv=[(μ12+λ12L)Ch0t]/rw2,Nσ=(σ′0+p0)/σ′0,Ch0=K0(1+e0)σ′0ln 10/(γwCc),同时取Ck=0.6,Cc=0.6,L=0.01,e0=1.5,K0=6.0×10-7m/min,σ′0=50 kPa,λ1=π/2,μ1=0.28,rw=0.2 m,re=1.0 m,Δr=0.01 m,H=2 m,Δz=0.01 m,Δt=0.1 min,迭代精度为10-7.对应Nσ=1,2,4和8,p0分别取0,50,150和350 kPa,按本文方法得到Z=1,X=2.5处的孔压U随时间因素Tv的变化曲线示于图 1,同时图 1中也附上了耿雪玉[37]的解析解.可见两者基本一致,这说明本文算法是有效的.

|
图 1 本文数值解与耿雪玉[37]解析解对比(Z=1,X=2.5) Fig. 1 Comparison of numerical solution of this paper and analytical solution of Geng[37](Z=1, X=2.5) |
为探讨地基土的流变效应、非达西特性及渗透系数变化等因素对砂井地基固结进程的影响,以下采用单因素法进行分析,其中参数分别取σ′0=50 kPa,p0=150 kPa,K0=6.0×10-7 m/min,γw=10 kN/m3, M=0.772,Cc=0.6,Cα=0.04,Cs=0.12,Ck=0.8,R0=0.75,e0=1.5,m=1.5,i1=5,rw=0.05 m,re=1.0 m,N=50,H=10 m,Z=30,Δt=0.1 min,迭代误差为10-7.
4.1 次固结系数Cα的影响图 2给出次固结系数Cα对某些特殊位置处孔压的影响曲线.可以看出,在流变固结初期(t=1 000 min),Cα>0时,远离排水边界处的孔压都超过了初始值p0 =150 kPa,这说明该阶段这些位置处的孔压不是消散而是升高.并且随着次固结系数Cα的增大,这种现象变得更加明显.如图 2(a)所示,当t=1 000 min,且Cα分别等于0.02,0.04和0.06时,z=5 m,r=0.9 m处的孔压值分别为153,164,173 kPa,即大约是初始孔压的1.02,1.09,1.15倍.这种孔压升高现象不同于二维或三维Biot固结课题中的Mandel-Cryer效应,因为本课题仍属于Terzaghi固结理论范畴,刘忠玉等[38]称之为“类曼德尔效应”.实际上一维固结初期也会出现该现象[18].Yin等[18]将其归结为土的黏滞效应或主次固结耦合效应,认为在土体蠕变过程中,由于靠近不排水面处,土体排水不畅,孔隙水出现拥挤情况,导致远离不排水面处的孔压升高,有效应力减小.这也可用来解释本文砂井地基固结初期的孔压升高现象.

|
图 2 Cα对孔压的影响 Fig. 2 Influence of Cα on excess pore water pressure |
同时由图 2(a)可知,在固结中后期,孔压的消散速率随着Cα的增大而变得明显缓慢.例如,当不考虑黏滞性时,在z=5 m,r=0.9 m处的孔压值为12 kPa;当考虑黏滞性时,对应Cα等于0.02,0.04和0.06,同一位置处的孔压值分别为27,47和76 kPa,分别为不考虑黏滞性时的2.25,3.92和6.33倍.很明显,土体的黏滞效应延缓了地基的固结过程.
图 3给出不同次固结系数Cα时的砂井地基平均固结度Up随时间t的变化曲线.可以看出,在流变固结初期,考虑黏滞效应(Cα >0)的曲线都出现了上升段(固结度甚至为负).如t=1 000 min时,与Cα=0,0.02,0.04,0.06对应的平均固结度值分别为0.080,0.059,-0.016,-0.077.这表明随着土体次固结系数的增大,地基中较大范围内都出现了孔压升高的现象.同时,考虑黏滞效应的平均固结度变化曲线都在不考虑土体黏滞效应(Cα=0)计算曲线的上方,也说明了土体黏滞性对砂井地基中整体孔压消散具有滞后作用.这与胡晶等[20, 38]对一维流变固结分析时所得出的结论一致.

|
图 3 Cα对平均固结度的影响 Fig. 3 Influence of Cα on average degree of consolidation |
图 4给出了t=1 000和100 000 min两个时刻下不同初始超固结参数R0时特殊位置处的孔压分布曲线.可以看出,在流变固结过程中,R0越大(即初始超固结程度越低),孔压越大,且类曼德尔效应越明显.例如图 4(b)中,t=1 000 min时,与R0取0.50,0.75和1.00对应的z=1 m,r=0.5 m处的孔压值分别等于145,160和170 kPa.这与胡晶等[20]在一维流变固结下得出的结论一致,他们认为土体所受的应力历史不同,或者说前期固结应力不同,固结速度也会有所不同,即增大超固结比(或减小初始超固结参数R0),会导致主固结与次固结的变形同时有所减小,从而加快孔压的消散速率.

|
图 4 R0对孔压的影响 Fig. 4 Influence of R0 on excess pore water pressure |
图 5给出初始超固结参数R0对地基平均固结度Up的影响曲线.与图 3类似,图 5表明,平均固结度随时间并非都逐渐增大,而是在固结前期,固结度可有所减小,到某个时刻达最小值,且随着R0的增大,固结度减小得更为明显.例如,当t=1 000 min,R0=0.50,0.75,1.00时,对应的平均固结度值分别为0.072,-0.016,-0.070.从图 5整体来看,R0取值越小,Up-t曲线就越靠左下方,可见初始超固结参数R0越小(即初始超固结程度越强),整体孔压消散越快.这里也与胡晶等[20, 38]对一维固结分析得出的结论相同.
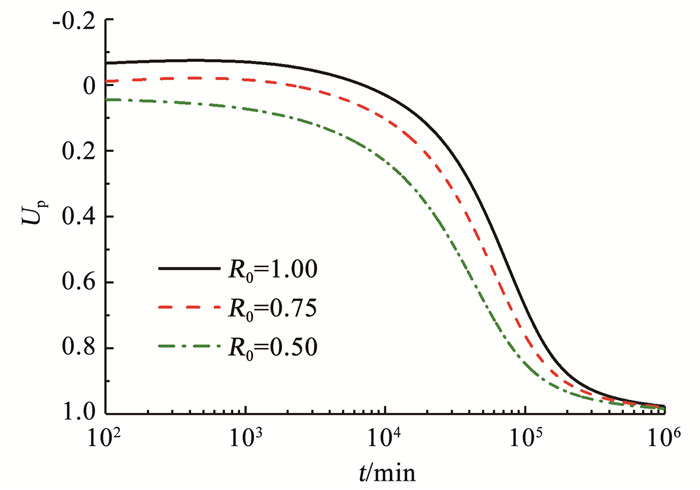
|
图 5 R0对平均固结度的影响 Fig. 5 Influence of R0 on average degree of consolidation |
为分析压缩指数Cc对固结过程的影响,图 6给出了次固结系数Cα=0和Cα=0.04两种情况下,Cc分别取0.6,0.8和1.0时,两个特殊时刻孔压u的分布曲线.可以看出,当不考虑土体黏滞性时,在整个固结过程中,压缩指数Cc越小(即土体的压缩性越低),孔压消散就越快.而当考虑黏滞性(Cα=0.04)时,在固结的前期(t=1 000 min),远离排水面的大部分范围内,压缩指数Cc越小(即土体的压缩性越低),孔压值反而越大,即类曼德尔效应越明显.例如,从图 6(a)中Cα=0.04,t=1 000 min时的孔压分布曲线可以得出,在z=5 m,r=0.9 m处,与Cc=0.6,0.8和1.0对应的孔压值分别为164,159和155 kPa,均明显大于初始孔压值,而Cα=0时,与不同压缩指数对应的同一时刻同一位置处的孔压值均约为150 kPa.这与胡晶等[20]分析压缩指数对土体一维固结影响时的结果类似.

|
图 6 Cc对孔压的影响 Fig. 6 Influence of Cc on excess pore water pressure |
图 7反映了压缩指数Cc对地基平均固结度Up随时间变化的影响.可以看出,当不考虑土体黏滞性(Cα=0)时,每一时刻的平均固结度都随着压缩指数Cc的增大而减小,即压缩性越低,地基中孔压的整体消散越快.而当考虑黏滞效应(Cα=0.04)时,几条曲线是相互交叉的.即在固结前期(对应图 7中交点的左边),固结度可能为负值,且压缩指数越大,地基的平均固结度越大.结合图 6可以看出,当土体压缩性较低时,更容易在地基中较大范围内出现类曼德尔效应;而在固结中后期(对应图 7中交点的右边),平均固结度随压缩指数变化的趋势与Cα=0时相同.同时,从图 7也可以看出相同压缩指数时,考虑土体黏滞性后达到同一固结度需要的时间更长.

|
图 7 Cc对平均固结度的影响 Fig. 7 Influence of Cc on average degree of consolidation |
为考察回弹指数Cs对饱和软黏土地基流变固结过程的影响,图 8给出了z=5 m或r=0.5 m处不同回弹指数Cs时的孔压分布曲线.可以看出,虽然回弹指数Cs的变化对初期孔压升高有一定的影响,但与次固结系数Cα、初始超固结参数R0和压缩指数Cc相比并不显著.例如,图 8(b)中,t=1 000 min,取Cs =0.06,0.12,0.30时,对应z=8 m,r=0.5 m处的孔压值分别为160,161,164 kPa,其差别并不大.
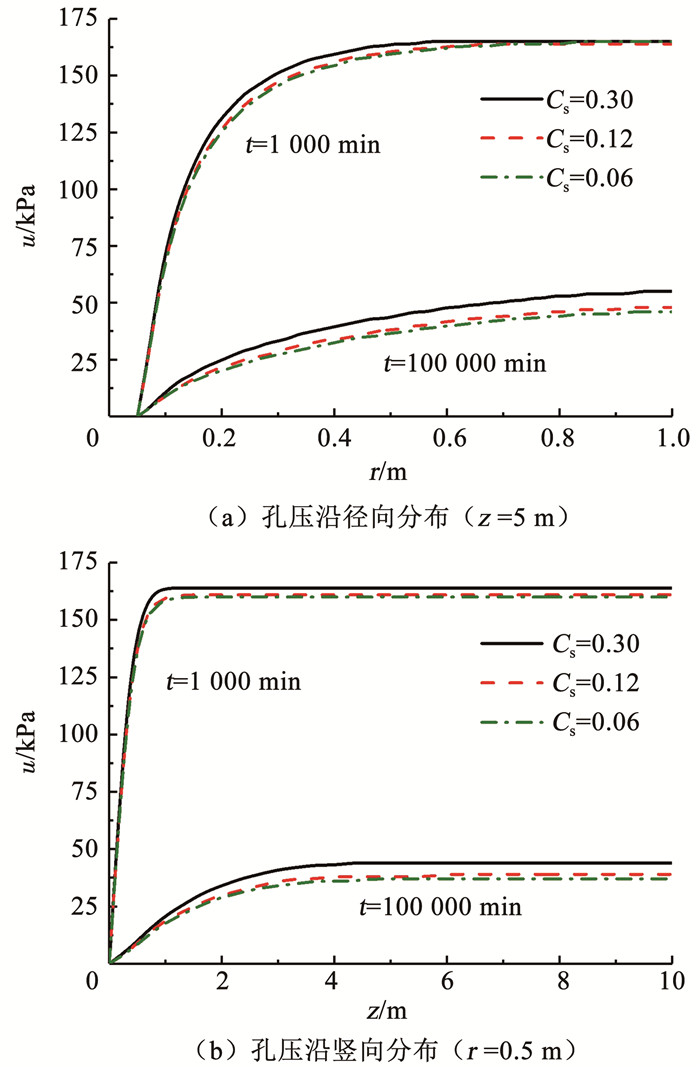
|
图 8 Cs对孔压的影响 Fig. 8 Influence of Cs on excess pore water pressure |
图 9给出了不同回弹指数Cs时的平均固结度随时间的变化曲线.很明显,其变化趋势与图 5类似,即在流变固结初期,随着回弹指数Cs的增大,平均固结度减小的现象也比较明显,同时在固结中后期,达到相同固结度所需时间随着回弹指数的增大也会相应增加.这与胡晶等[20, 38]在一维固结分析时得出的结论类似,即回弹指数越大,土体可恢复的弹性变形部分也越大,这往往会使得地基固结时间延长.

|
图 9 Cs对平均固结度的影响 Fig. 9 Influence of Cs on average degree of consolidation |
对比图 3,5,7和9可以看出,考虑时间效应的UH本构模型中各参数对固结过程的影响程度有所不同.很明显,在本文讨论的参数范围内,相比次固结系数Cα,初始超固结参数R0和压缩指数Cc,回弹指数Cs对固结度的影响相对较弱.
4.5 渗透指数Ck的影响为探讨砂井地基流变固结过程中渗透指数Ck的影响,图 10给出了不同Ck时孔压的分布曲线.可以看出,t=1 000 min时,对应Ck=0.48,0.60,0.80时的几条曲线差别不大,特别在图 10(b)中几乎重叠在一起,在z=1 m,r=0.5 m处,对应不同Ck的孔压值分别为160,161,161 kPa.可见,孔压值均超过了初始孔压,但与前面讨论的UH模型参数Cα、R0和Cc相比,渗透指数Ck的变化对固结初期类曼德尔效应的影响相对较弱.
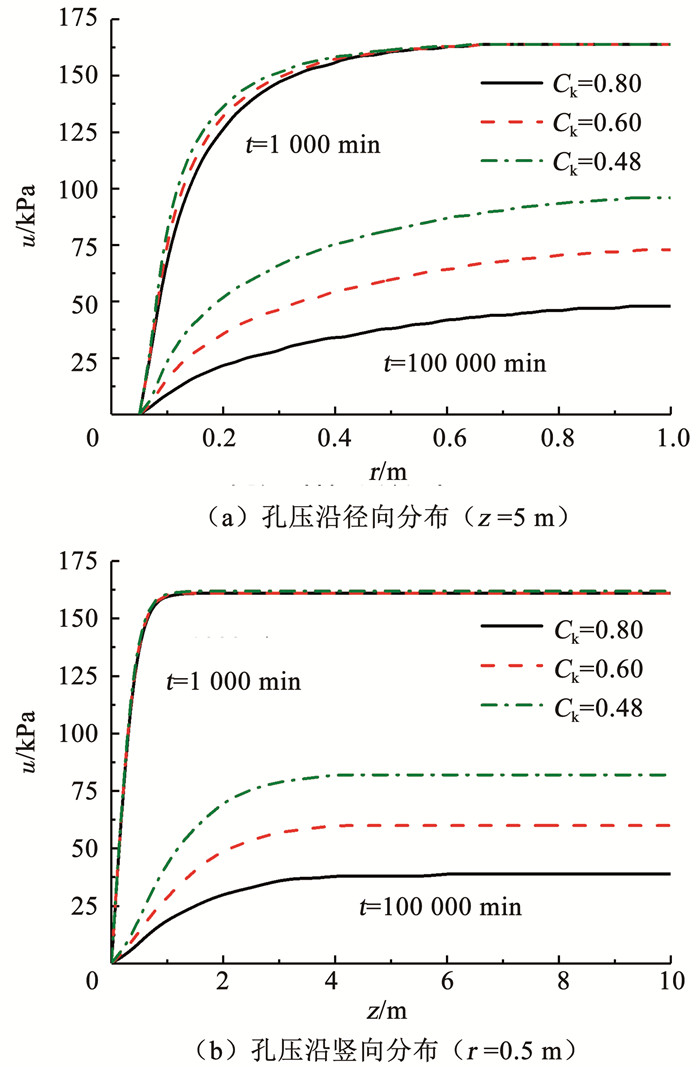
|
图 10 Ck对孔压的影响 Fig. 10 Influence of Ck on excess pore water pressure |
图 11反映了渗透指数Ck对砂井地基平均固结度的影响.可以看出,在固结中后期,随着渗透指数Ck的减小,同一时刻的平均固结度Up也减小.实际上,渗透指数Ck反映了渗透系数K对固结过程中孔隙比变化的敏感程度.在固结过程中,随着有效应力增大,土体变得密实,孔隙比减小,渗透系数也减小.而且,若减小渗透指数Ck,根据式(12)可知,渗透系数减小得更多,从而导致整体孔压消散更为缓慢.例如,当Ck取0.48,0.60,0.80时,对应平均固结度达到90%所需时间分别为189 700,292 600,460 400 min.这一点与李刚等[36]得出的结论一致,他认为随着固结的进行,整个土层有效应力增加,导致土体渗透系数降低,渗流量减少,引起整体孔压消散滞后,地基达到相同固结度的时间也增加.可见,在分析饱和软黏土的固结进程时,应当考虑渗透系数随固结降低所产生的延滞影响.

|
图 11 Ck对平均固结度的影响 Fig. 11 Influence of Ck on average degree of consolidation |
为分析Hansbo渗流模型对固结的影响,图 12,13分别给出了不同m或i1时的孔压分布曲线.二图表明,Hansbo渗流对固结初期的类曼德尔效应有影响,但并不明显.例如,图 12(b)中,t=1 000 min时,z=1 m,r=0.5 m处,与m=1.0,1.2,1.5和1.8对应的孔压值分别为160,160,161和161 kPa.刘忠玉等[30]曾对考虑Hansbo渗流但不计黏滞性的砂井地基固结进程做过分析,并没有发现类曼德尔效应.因此,结合前述分析主、次固结耦合变形机制对地基固结过程的影响规律可知,类曼德尔效应主要是由土体的黏滞效应或主次固结耦合机制引起的.
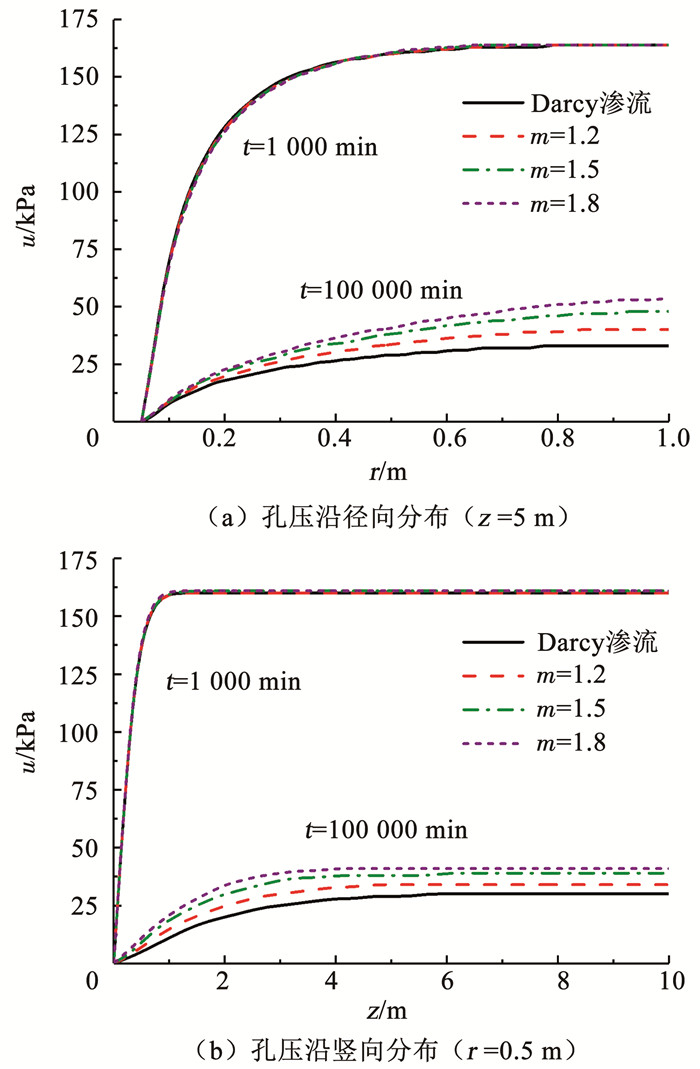
|
图 12 m值对孔压的影响 Fig. 12 Influence of m on excess pore water pressure |
|
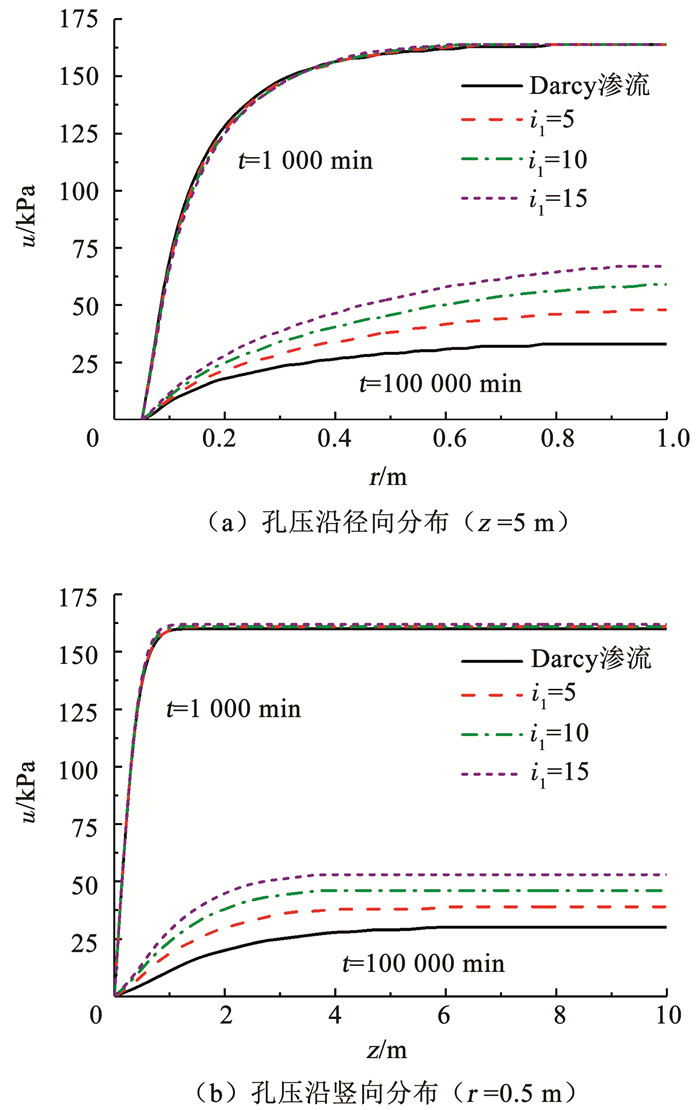
图 13 i1值对孔压的影响 Fig. 13 Influence of i1 on excess pore water pressure |
图 12,13表明,在固结后期(t=100 000 min)时,两种渗流模式计算的孔压值差异比较明显,且m或i1值越大,同一位置处的孔压越大,即孔压消散越慢.例如,图 13(a)中,z=5 m,r=0.9 m,在Darcy渗流模式下(i1=0时)算得的孔压值为33 kPa,当i1取5,10和15时,对应Hansbo渗流模式下计算的结果分别为47,58和67 kPa,大约分别是Darcy渗流下孔压的1.42,1.76和2.03倍,可见,Hansbo渗流延缓了地基中孔压的消散.究其原因是随着固结时间的延长,较大范围土体内的孔压有所消散,水力梯度值也变得较小,当小于直线渗流起始水力梯度i1时,渗流是很缓慢的,且随着Hansbo渗流参数的增大,渗流速度更小,孔隙水更不易排出,所以,孔压消散也更为缓慢.
同时,与前述UH模型参数有关分析图类似的是,图 12,13中孔压沿竖向分布曲线表明,在超过一定深度后,孔压沿竖向基本不再变化,且Hansbo渗流参数越大,孔压不变化的范围也越大.这说明超过某个深度后,水力梯度的竖向分量很小,渗流速度的竖向分量也很小,因此,对于厚度较大的砂井地基,考虑土体黏滞性和非Darcy渗流时径向渗流为主要的排水途径.
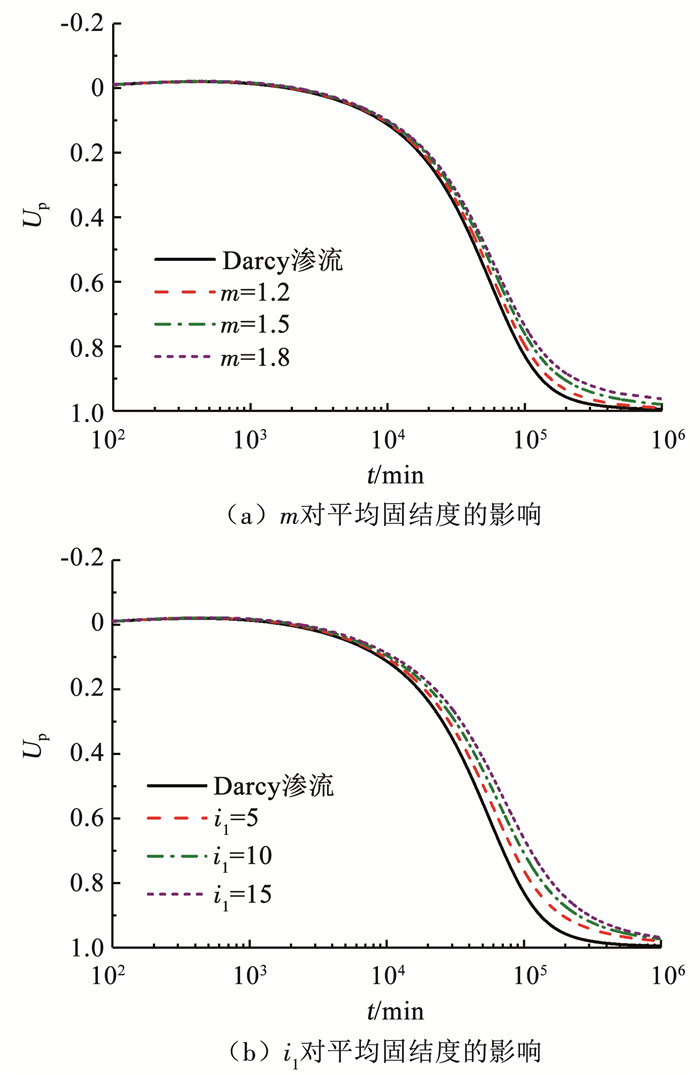
图 14给出m或i1取不同数值时,平均固结度随时间的变化曲线.可以看出,在流变固结中后期,按Hansbo渗流模式计算的平均固结度曲线均在按Darcy渗流模式计算的上方,即地基的固结比基于Darcy定律计算的要慢,并且这一现象随着Hansbo渗流参数的增大而变得更为明显.这也表明在实际工程的固结分析中考虑土体渗流非Darcy特性的必要性,否则将高估砂井地基固结的程度.这与文献[27-30]的结论类似.
|
图 14 Hansbo渗流对平均固结度的影响 Fig. 14 Influence of Hansbo's flow on average degree of consolidation |
1) 固结初期出现的孔压异常升高现象(类曼德尔效应)主要由土体的黏滞效应或主次固结耦合机制引起.增大次固结系数Cα和初始超固结参数R0、或减小压缩指数Cc都会使该现象变得更加明显,但其他参数对此现象的影响较弱.
2) UH模型参数的变化对砂井地基固结过程均有不同程度的影响.随着次固结指数Cα、初始超固结参数R0和压缩指数Cc等参数的增大,砂井地基的固结变慢.与这些模型参数相比,回弹指数Cs变化引起的固结度变化较小.
3) 渗透指数Ck对砂井地基固结进程的影响主要体现在中后期,且该参数越小,孔压消散就越慢,从而砂井地基固结也就越慢.
4) 与Darcy渗流相比,Hansbo渗流使得砂井地基固结变慢.同时考虑Hansbo渗流和土体黏滞性时,砂井地基中的排水更是以径向渗流为主.因此,应该重视渗流非达西特性对砂井地基固结进程的影响.
| [1] |
BARRON R A. Consolidation of fine grained soils by drains wells[J]. Transactions of ASCE, 1948, 113: 718. |
| [2] |
HANSBO S, JAMIOLKOWSKI M, KOK L. Consolidation by vertical drains[J]. Géotechique, 1981, 31(1): 45. DOI:10.1680/geot.1981.31.1.45 |
| [3] |
王贻荪. 考虑砂井阻力的折减井径法[J]. 岩土工程学报, 1982, 4(3): 43. WANG Yisun. Discounted well-diameter method to take the effect of drain well resistance into consideration[J]. Chinese Journal of Geotechnical Engineering, 1982, 4(3): 43. DOI:10.3321/j.issn:1000-4548.1982.03.004 |
| [4] |
TANG Xiaowu, ONITSUKA K. Consolidation by vertical drains under time-dependent loading[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2000, 24(9): 739. DOI:10.1002/1096-9853(20000810)24:9<739::AID-NAG94>3.0.CO;2-B |
| [5] |
谢康和, 曾国熙. 等应变条件下的砂井地基固结解析理论[J]. 岩土工程学报, 1989, 11(2): 3. XIE Kanghe, ZENG Guoxi. Consolidation theories for drain wells under equal strain condition[J]. Chinese Journal of Geotechnical Engineering, 1989, 11(2): 3. DOI:10.3321/j.issn:1000-4548.1989.02.002 |
| [6] |
谢康和, 余坤, 童磊, 等. 考虑影响区真实形状的竖向排水井地基固结解[J]. 岩土力学, 2011, 32(10): 2944. XIE Kanghe, YU Kun, TONG Lei, et al. Analytical solution for consolidation by vertical drains considering actual shape of influence zone[J]. Rock and Soil Mechanics, 2011, 32(10): 2944. DOI:10.3969/j.issn.1000-7598.2011.10.009 |
| [7] |
BERRY P L, WILKNSON W B. The radial consolidation of clay soils[J]. Géotechnique, 1969, 19(2): 253. DOI:10.1680/geot.1969.19.2.253 |
| [8] |
INDRARATNA B, RUJIKIATKAMJORN C, SATHANANTHAN L. Radial consolidation of clay using compressibility indices and varying horizontal permeability[J]. Canadian Geotechnical Journal, 2005, 42: 1330. DOI:10.1139/t05-052 |
| [9] |
郭霄, 谢康和, 卢萌盟, 等. 直排式真空预压法下竖井地基的非线性固结解析解[J]. 中南大学学报(自然科学版), 2018, 49(2): 384. GUO Xiao, XIE Kanghe, LU Mengmeng, et al. Nonlinear analytical solution for consolidation of vertical drains by straight-line vacuum preloading method[J]. Journal of Central South University (Science and Technology), 2018, 49(2): 384. |
| [10] |
殷宗泽, 张海波, 朱俊高, 等. 软土的次固结[J]. 岩土工程学报, 2003, 25(5): 521. YIN Zongze, ZHANG Haibo, ZHU Jungao, et al. Secondary consolidation of soft soils[J]. Chinese Journal of Geotechnical Engineering, 2003, 25(5): 521. DOI:10.3321/j.issn:1000-4548.2003.05.001 |
| [11] |
李西斌, 谢康和, 陈福全. 考虑软土流变特性和应力历史的一维固结与渗透试验[J]. 水利学报, 2013, 44(1): 18. LI Xibin, XIE Kanghe, CHEN Fuquan. One dimensional consolidation and permeability tests considering stress history and rheological characteristic of soft soils[J]. Journal of Hydraulic Engineering, 2013, 44(1): 18. DOI:10.3969/j.issn.0559-9350.2013.01.005 |
| [12] |
FENG Weiqiang, LALIT B, YIN Zhenyu, et al. Long-term non-linear creep and swelling behavior of Hong Kong marine deposits in oedometer condition[J]. Computers and Geotechnics, 2017, 84: 1. DOI:10.1016/j.compgeo.2016.11.009 |
| [13] |
TAYLOR D W, MERCHANT W. A theory of clay consolidation accounting for secondary compression[J]. Journal of Mathematics and Physics, 1940, 19(1/2/3/4): 167. DOI:10.1002/sapm1940191167 |
| [14] |
LO K Y. Secondary compression of clay[J]. Journal of the Soil Mechanics and Foundations Division, 1961, 87(4): 61. DOI:10.1061/JSFEAQ.0000365 |
| [15] |
赵维炳. 广义Voigt模型模拟的饱水土体一维固结理论及其应用[J]. 土木工程学报, 1989, 11(5): 78. ZHAO Weibing. One-dimensional soil consolidation theory of saturated soil based on generalized Voigt model and its application[J]. Chinese Journal of Geotechnical Engineering, 1989, 11(5): 78. |
| [16] |
刘忠玉, 杨强. 基于分数阶Kelvin模型的饱和黏土一维流变固结分析[J]. 岩土力学, 2017, 38(12): 3680. LIU Zhongyu, YANG Qiang. One-dimensional rheological consolidation analysis of saturated clay using fractional order Kelvin's model[J]. Rock and Soil Mechanics, 2017, 38(12): 3680. DOI:10.16285/j.rsm.2017.12.036 |
| [17] |
刘忠玉, 崔鹏陆, 郑占垒, 等. 基于非牛顿指数渗流和分数阶Merchant模型的一维流变固结分析[J]. 岩土力学, 2019, 40(6): 1. LIU Zhongyu, CUI Penglu, ZHENG Zhanlei, et al. Analysis of one-dimensional rheological consolidation with non-Darcy flow described by non-Newtonian index and fractional-order Merchant's model[J]. Rock and Soil Mechanics, 2019, 40(6): 1. DOI:10.16285/j.rsm.2018.1085 |
| [18] |
YIN J H, GRAHAM J. Viscous-elastic-plastic modelling of one-dimensional time-dependent behaviour of clays[J]. Canadian Geotechnical Journal, 1989, 26(2): 199. DOI:10.1139/t89-029 |
| [19] |
YAO Yangping, KONG Lingming, HU Jing. An elastic-viscous-plastic model for overconsolidated clays[J]. Science China Technological Sciences, 2013, 56(2): 441. DOI:10.1007/s11431-012-5108-y |
| [20] |
胡晶, 姚仰平. 基于考虑时间效应UH模型的一维固结分析[J]. 北京航空航天大学学报, 2015, 41(8): 1492. HU Jing, YAO Yangping. 1D-consolidation analysis based on UH model considering time effect[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(8): 1492. DOI:10.13700/j.bh.1001-5965.2014.0583 |
| [21] |
刘兴旺, 谢康和, 潘秋元, 等. 竖向排水井地基粘弹性固结解析理论[J]. 土木工程学报, 1998, 31(1): 10. LIU Xingwang, XIE Kanghe, PAN Qiuyuan, et al. Viscoelastical consolidation theories of soils with vertical drain wells[J]. China Civil Engineering Journal, 1998, 31(1): 10. DOI:10.15951/j.tmgcxb.1998.01.002 |
| [22] |
王瑞春, 谢康和. 变荷载下竖向排水井地基粘弹性固结沉降解析解[J]. 土木工程学报, 2001, 34(6): 93. WANG Ruichun, XIE Kanghe. Analytical solutions for viscoelastic consolidation by vertical drains time-dependent loading[J]. China Civil Engineering Journal, 2001, 34(6): 93. DOI:10.3321/j.issn:1000-131X.2001.06.018 |
| [23] |
张迎春, 刘吉福, 魏金霞. 砂井地基主、次固结度粘弹性分析[J]. 水运工程, 2003(8): 20. ZHANG Yingchun, LIU Jifu, WEI Jinxia. Visco-elastic analysis of the degrees of primary consolidation & secondary consolidation of sand-drained foundation[J]. Port & Waterway Engineering, 2003(8): 20. DOI:10.3969/j.issn.1002-4972.2003.08.009 |
| [24] |
HANSBO S. Consolidation of clay, with special reference to influence of vertical sand drain[C]//Swedish Geotechnical Institute Proceedings No.18. Stockholm: Swedish Geotechnical Institute, 1960: 45
|
| [25] |
DENG Yinger, XIE Heping, HUANG Runqiu. Law of nonlinear flow in saturated clays and radial consolidation[J]. Applied Mathematics and Mechanics, 2007, 28(11): 1427. DOI:10.1007/s10483-007-1102-7 |
| [26] |
孙丽云, 乐金朝, 张杰. 饱和黏土非达西渗透特性试验研究[J]. 郑州大学学报(工学版), 2010, 31(6): 31. SUN Liyun, YUE Jinchao, ZHANG Jie. Experimental study on non-Darcy permeability characteristics of saturated clays[J]. Journal of Zhengzhou University (Engineering Science), 2010, 31(6): 31. DOI:10.3969/j.issn.1671-6833.2010.06.008 |
| [27] |
WALKER R, INDRARATNA B, RUJIKIATKAMJORN C. Vertical drain consolidation with non-Darcy flow and void-ratio-dependent compressibility and permeability[J]. Géotechnique, 2012, 62(11): 985. DOI:10.1680/geot.10.P.084 |
| [28] |
GUO Xiao, XIE Kanghe, DENG Yuebao, et al. Consolidation by prefabricated vertical drains with a threshold gradient[J]. Mathematical Problems in Engineering, 2014, 2014: 410390. DOI:10.1155/2014/410390 |
| [29] |
HANSBO S. Consolidation equation valid for both Darcian and non-Darcian flow[J]. Géotechnique, 2001, 51(1): 51. DOI:10.1680/geot.51.1.51.39357 |
| [30] |
刘忠玉, 焦阳. 基于Hansbo渗流的理想砂井地基固结分析[J]. 岩土工程学报, 2015, 37(5): 792. LIU Zhongyu, JIAO Yang. Consolidation of ground with ideal sand drains based on Hansbo's flow[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(5): 792. DOI:10.11779/CJGE201505004 |
| [31] |
刘忠玉, 张家超, 郑占垒, 等. 考虑Hansbo渗流的二维Biot固结有限元分析[J]. 岩土力学, 2018, 39(12): 4617. LIU Zhongyu, ZHANG Jiachao, ZHENG Zhanlei, et al. Finite element analysis of two-dimensional Biot's consolidation with Hansbo's flow[J]. Rock and Soil Mechanics, 2018, 39(12): 4617. DOI:10.16285/j.rsm.2017.0892 |
| [32] |
TAYLOR D W. Fundamentals of soil mechanics[M]. New York: John Wiley & Sons Inc, 1948.
|
| [33] |
MESRI G, OLSON R E. Mechanisms controlling the permeability of clays[J]. Clays and Clay Minerals, 1971, 19(3): 151. DOI:10.1346/ccmn.1971.0190303 |
| [34] |
蒋玉坤, 孙如华. 深部黏土渗透特性试验研究[J]. 岩土工程学报, 2012, 34(2): 268. JIANG Yukun, SUN Ruhua. Experimental study on permeability of deep clay[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(2): 268. |
| [35] |
MESRI G, ROKHSAR A. Consolidation of normally consolidated clay[J]. Journal of the Soil Mechanics and Foundations Division, 1974, 100(GT8): 889. |
| [36] |
李刚, 张金利, 杨庆, 等. 非达西渗流与变渗透系数下的大变形固结分析[J]. 中南大学学报(自然科学版), 2016, 47(3): 977. LI Gang, ZHANG Jinli, YANG Qing, et al. Analysis of large-strain consolidation with non-Darcy flow and variable permeability coefficient[J]. Journal of Central South University (Science and Technology), 2016, 47(3): 977. DOI:10.11817/j.issn.1672-7207.2016.03.034 |
| [37] |
耿雪玉. 复杂条件下软粘土地基多维固结分析[D]. 杭州: 浙江大学, 2008 GENG Xueyu. Multi-dimensional consolidation of soft soils under complicated conditions[D]. Hangzhou: Zhejiang University, 2008 |
| [38] |
刘忠玉, 张家超, 夏洋洋, 等. 基于分段线性化模型的一维流变固结分析[J]. 同济大学学报(自然科学版), 2019, 47(5): 640. LIU Zhongyu, ZHANG Jiachao, XIA Yangyang, et al. One-dimensional rheological consolidation analysis of saturated soft clay based on piecewise-linear model[J]. Journal of Tongji University (Natural Science), 2019, 47(5): 640. DOI:10.11908/j.issn.0253-374x.2019.05.007 |
 2021, Vol. 53
2021, Vol. 53


