2. 中国矿业大学 力学与土木工程学院, 江苏 徐州 221116;
3. 北京科技大学 土木与资源工程学院,北京 100083;
4. 城市地下空间工程北京市重点实验室 (北京科技大学), 北京 100083;
5. 中国矿业大学 国际学院, 江苏 徐州 221116
2. School of Mechanics and Civil Engineering, China University of Mining and Technology, Xuzhou 221116, Jiangsu, China;
3. School of Civil and Resource Engineering, University of Science and Technology Beijing, Beijing 100083, China;
4. Beijing Key Laboratory of Urban Underground Space Engineering (University of Science and Technology Beijing), Beijing 100083, China;
5. International College, China University of Mining and Technology, Xuzhou 221116, Jiangsu, China
近年来,随着中国冻土区工程建设步伐的加快和深立井、深基坑等地下工程建设中人工冻结法应用的日益增多,冻土-结构接触面物理力学特性研究逐渐引起重视[1-3].冻土与常温土在力学行为上存在巨大差异,为了研究冻土与结构接触面的物理力学特性,已有多位学者开展了相关的研究工作,并取得了很多有价值的成果.董盛时等[4]根据冻结粉土-混凝土接触面剪切试验结果,建立了冻结粉土接触面应力-位移-温度本构方程,分析了不同温度条件下冻结粉土接触面基本力学特征和受力变形规律.杨平等[5]采用损伤力学理论,以不可逆性体应变与最大不可逆性体应变之比作为损伤因子,建立了冻土与结构接触面循环剪切损伤模型.赖远明等[6]对-6 ℃冻结砂土三轴剪切试验,提出了修正的邓肯-张模型和非线性摩尔强度准则,可以同时描述不同应力水平下应力-应变关系的应变软化和应变硬化现象.
以上针对冻土-结构接触面剪切力学特性的研究成果均是在常规试验压力条件下进行的,试验法向应力大多小于700 kPa.然而,目前,中国人工冻结法凿井穿越的表土层厚度已达675.6 m,最深处水平地压已接近9 MPa(按似重液公式估算,水平地压p≈0.013×675.6=8.8 MPa).随着深部地下空间的开发利用,深部高应力水平仍会增加,高应力下冻(融)土-结构接触面剪切力学特性必然有别于常压下研究成果[7-8].另一方面,低温状态冻土具有很高的强度,是立井井筒、地铁联络通道等掘砌施工的保护屏障.工程实际中,低温状态冻土与结构间大多是相对稳定的,冻土-结构间相互作用显著或产生破坏往往发生在地层冻结或解冻过程中.冻结法施工结束后,地下结构周围冻土体逐渐升温至融化状态,经历冻土—正融土—冻融土[9],土体融沉变形、强度降低.冻土升温与降温至相同温度状态时,由于未冻水含量等的影响,土体性质势必存在一定差异,其与剪切面相互作用的力学行为与机理也将不同.因此,有必要开展高应力下、不同融化程度冻(融)土-结构接触面剪切力学响应研究.本文即考虑真实冻土帷幕解冻(融化)过程,以高法向应力冻(融)土-结构接触面直剪试验为基础,分析了高压下不同融化程度冻(融)土-结构接触面剪切行为特征,提出了相应的剪切应力-应变关系经验公式,结果可为冻土区工程或应用冻结法进行相似深部地下工程建设提供必要的支持.
1 直剪试验概况冻结法凿井中,冻结壁解冻是井壁周围土层经历从冻结(约-20 ℃)到完全融化状态(初始地温约6 ℃)的动态转化过程.参考图 1,试验设计选取了冻结壁解冻过程中几个代表性的温度点进行,考虑不同深度的应力条件,共安排了16组不同法向应力和融化程度的冻(融)土与结构接触面直剪试验.

|
图 1 试验设计思路 Fig. 1 Design of test |
高压冻(融)土与结构接触面直剪试验采用课题组研制的DRS-1高压直残剪试验系统进行.试样剪切盒与低温冷浴连接实现对试样冻结和融化程度的控制(温度控制在-40~40 ℃,精度-0.2 ℃),可装载ϕ51.2、ϕ61.8、ϕ79.8 mm 3种规格试样、最大法向应力0~30 MPa、应变控制剪切速率0.001~1.999 mm/min [10].
试验土样采用徐州地铁某施工现场的粉质黏土实验室重塑,经测定该粉质黏土塑性指数Ip=11.0、平均粒径d50=0.06 mm、不均匀系数Cu =5.83、曲率系数Cc=1.38,重塑土样含水率w=20 %、干密度ρd=1.7 g/cm3、直径61.8 mm、高30 mm.试验中选取均匀排列正三角形形状的粗糙钢板模拟结构面,结构面峰谷距0.9 mm,以恒定速率0.8 mm/min剪切至位移达到10 mm时停止.具体试验条件如表 1所示.
| 表 1 试验条件 Tab. 1 Test condition |
以图 2说明试验中如何模拟融化过程中冻土-结构接触面剪切.首先将试样统一冻结至-20 ℃并稳定,之后开始解冻试样(循环冷浴温度高于目标温度0~3 ℃),待试样温度接近目标温度约低2 ℃时,重设循环冷浴温度略低于试样融化设计温度,待试样温度稳定后开始剪切(以Datataker量测的试样温度数据波动小于0.01 ℃/min为稳定判断标准).
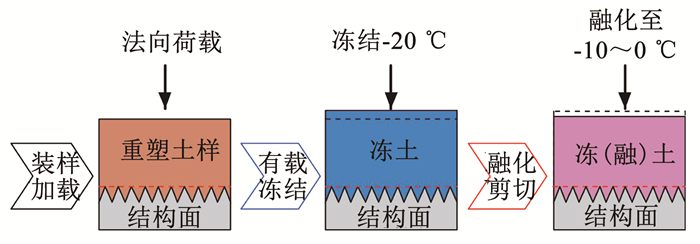
|
图 2 试验过程示意 Fig. 2 Schematic of test process |
试样温度条件是冻土类试验控制的关键.图 3为试样温度量测和控制示意,通过在土样中设置热敏电阻(精度0.01 ℃)对整个试验冻结、融化/解冻、剪切过程中土样的温度进行量测,并以此作为结果分析中试样融化程度和土样-结构剪切面温度的判断依据,以下如无特别说明文中所述试样温度/解冻程度均指该温度数据.综合传感器本身和数据采集精度等因素影响,试验中试样温度量测精度可达0.1 ℃.试样温度通过调节在剪切盒内部循环的冷液温度进行控制,在剪切盒外侧面包裹有保温板起保温隔热作用.
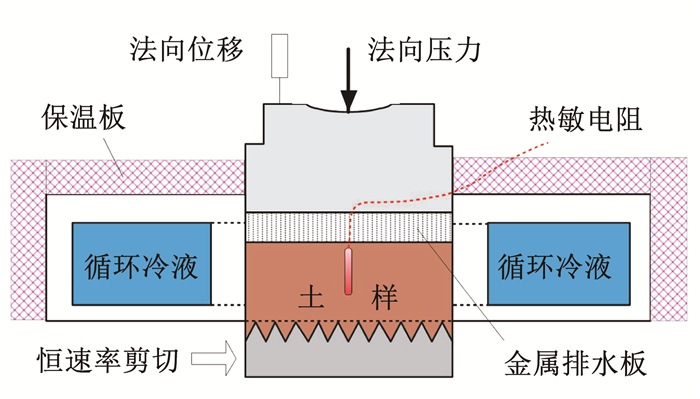
|
图 3 试样温度量测与控制 Fig. 3 Measurement and control of specimen temperature |
图 4为法向应力10 MPa、不同融化程度的试样温度监测数据.可以看出,试样的温度控制符合预期,但冻土试样融化过程中(接近目标温度2 ℃左右)对冷浴温度的调节造成了小幅度的温度波动,之后试样升温速率降低,且稳定时间随着目标温度的升高有所增加.不同试样解冻时间为35~45 min,试样剪切过程持续约13 min,剪切过程中试样温度变化最大幅值Δt=0.12 ℃.因此,表 1中的融化程度准确来讲是一定温度范围.升温至-10~-2 ℃的试样实际仍处于冻结状态,属于冻土.而0 ℃试样基本处于融土状态,属于经历一次完整冻融循环的融土(也有部分学者称其为冻融土),本文中以冻(融)土描述,在此说明.
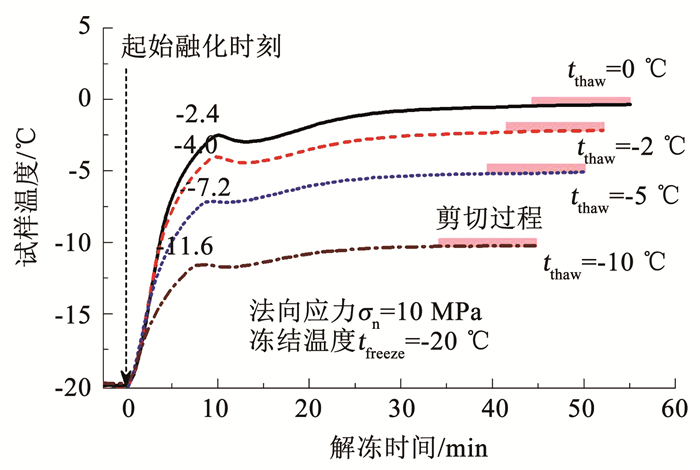
|
图 4 试验中试样温度曲线 Fig. 4 Curves of specimen temperature |
除试样温度数据外,试验系统对剪切过程中剪切荷载、剪切位移、法向荷载、法向位移进行了自动采集和保存.
2 高压冻(融)土-结构接触面剪切应力-位移特征图 5为法向应力10 MPa、融化程度tthaw=-5 ℃条件下剪切应力-剪切应变和法向位移-剪切应变关系曲线.不难看出,试验条件下冻(融)土-结构接触面剪切的整个过程大致可分为以下几个阶段:1)a—b阶段,土-结构触面间以弹性变形为主; 2)b—c阶段,直线逐渐弯曲,b点附近结构面产生整体滑动,表现为剪应力突然下降(试验中有时会伴有轻微的开裂声),之后随着剪切变形的增加剪应力继续上升,表现出应变硬化的特点; 3)c—d阶段,剪切应力达到峰值后逐渐降低,最后趋于定值,呈应变软化特征.
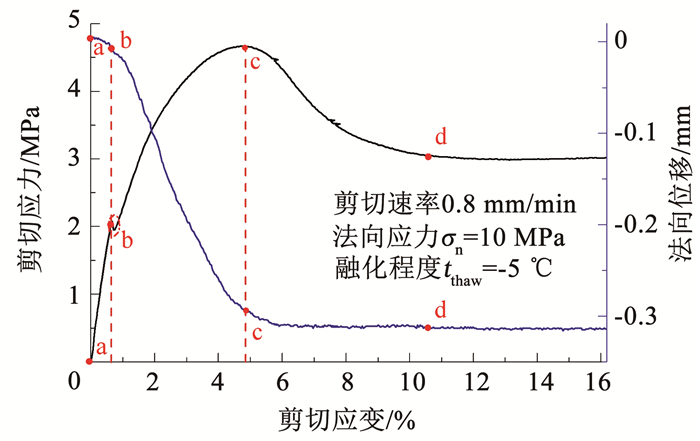
|
图 5 剪切应力和法向位移特征曲线(σn=10 MPa、tthaw=-5 ℃) Fig. 5 Characteristic curves of shear stress and normal displacement (σn=10 MPa, tthaw=-5 ℃) |
与剪切应力-位移关系曲线相对应,剪切过程中法向位移-剪切应变关系曲线表现出相似的阶段性:1)a—b阶段,法向位移会有略微上升,即试样会发生少许剪胀,对应接触面剪切初期的弹性变形阶段; 2)b—c阶段,对应剪切应变硬化阶段,此时法向位移下降最快; 3)c—d阶段,为峰值应力后,剪切应力逐渐降低并趋于稳定,法向位移变化也趋于缓和.
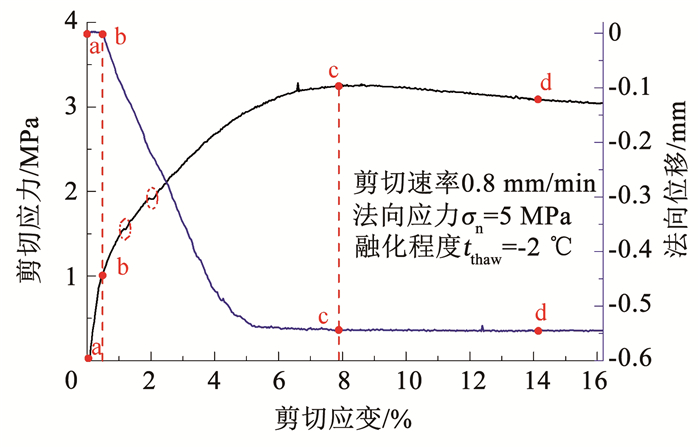
不同法向应力下冻(融)土-结构接触面剪切应力、法向位移-剪切应变曲线具有相似的特征,但随着解冻程度的增加,冻(融)土-结构接触面的剪切应力-应变关系曲线形态逐渐从负温状态的应变软化特征转变为正温状态的应变硬化特征,见图 6.
|
图 6 剪切应力和法向位移特征曲线(σn=5 MPa、tthaw=-2 ℃) Fig. 6 Characteristic curves of shear stress and normal displacement (σn=5 MPa, tthaw=-2 ℃) |
结合相关文献[11-12],升温冻(融)土-结构接触面抗剪强度主要由以下3部分组成:1)接触面上冰-结构面的冻结强度; 2)接触面附近土颗粒-结构面的黏聚力; 3)接触面土颗粒-结构面之间的摩擦力.三者随法向应力和解冻程度等变化而共同影响升温过程中冻(融)土-结构接触面剪切强度特征.接触面冻结强度主要依赖于负温状态,随着试样温度的升高接触面冻结强度逐渐降低,当接触面发生剪切滑动后接触面冻结强度会快速减小,这一现象在图 5中a—b阶段末尾有所体现.接触面黏聚力主要由土颗粒和结构面性质决定,表现为随温度升高和剪切位移的发展而减小,存在于整个剪切过程中,与其他两个组成部分的区别度并不明显.接触面摩擦力主要受法向应力和接触面性状(摩擦系数)共同影响,是剪切后期接触面残余剪切强度的主要来源.
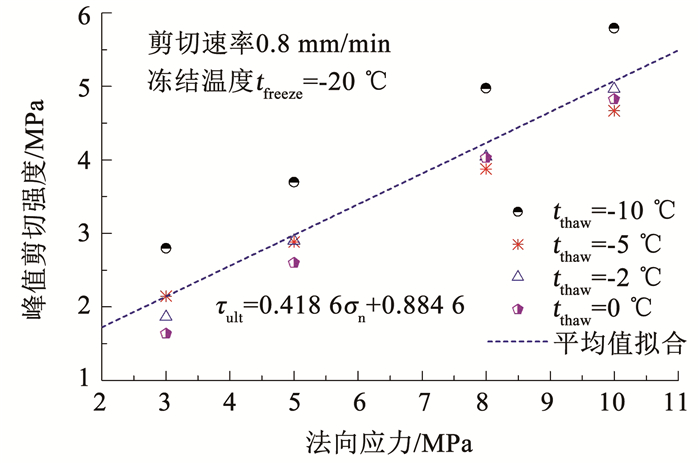
由图 7可知,接触面峰值剪切强度随着法向应力的增加而增大,且变化速率和不同融化程度相关性较小,线性拟合试验结果斜率平均值0.42、最大值0.46、最小值0.36.对比文献[3-4]相近试验低压下结果(随法向应力线性拟合斜率0.85~0.95),高应力下峰值剪切强度随法向应力的变化速率明显减小.随着法向应力增加,接触面摩擦力对峰值强度的贡献度较冻结强度的贡献逐渐占优,使得不同融化程度的试验结果在高应力区有汇聚表现.
|
图 7 峰值剪切强度与法向应力对应关系 Fig. 7 Relation between peak shear strength and normal stress |
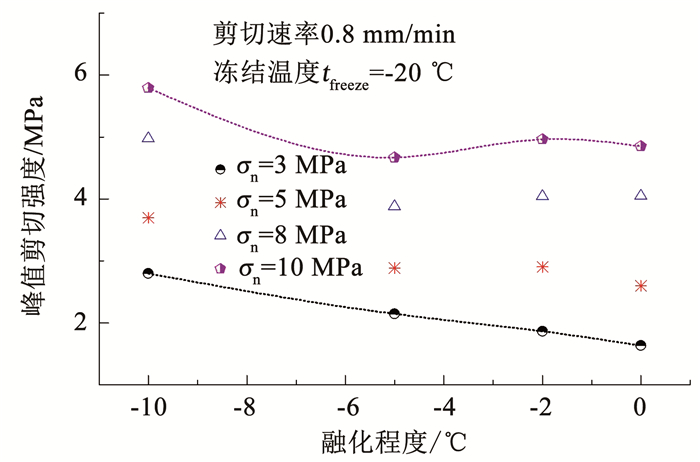
接触面剪切强度与融化程度有明显相关性(如图 8所示),随着融化程度的增加整体呈减小趋势,但由于解冻过程中土体本身性质及应力状态复杂,使得两者的相关关系很难准确获得或描述.高应力下,-5~0 ℃阶段峰值强度略有增加,主要是由于试验中试样的解冻速率基本相同,则试样的解冻时间随着融化程度的增加而增大(意味着试样在高法向应力状态下融化固结的时间增加),而直剪试验盒是相对开放的,使得融化程度较大的试样高压下峰值强度增加.由此说明,高应力状态下冻融造成的土-结构接触面性状以及土体自身的性状改变将有别于低应力状态,需要重视实际深部地下工程冻结法施工中涉及的冻融土-结构相互作用问题研究.
|
图 8 峰值剪切强度与融化程度对应关系 Fig. 8 Relation between peak shear strength and thawing degree |
从前述结果分析可知,随着融化程度的加深,升温冻(融)土-结构接触面剪切应力-应变关系曲线呈应变硬化特征,且在负温条件下如仅考虑剪切应力峰值前部分的曲线形态,与Clough和Duncan提出的接触面上剪切应力-剪切位移双曲线模型相似,因此,有必要对双曲线模型在试验条件下的适用性进行讨论.
根据文献[13]标准双曲线模型为
| $ \tau=\frac{\gamma}{a \cdot \gamma+b}. $ | (1) |
式中:τ为剪切应力(MPa),γ为剪切应变(%),a、b为拟合参数.
将式(1)进行变换,可得
| $ \frac{\gamma}{\tau}=a \cdot \gamma+b $ | (2a) |
其中
| $ \begin{array}{c} \left\{\begin{array}{l} a=1 / \tau_{\mathrm{ult}} \\ b=1 / K_{\mathrm{si}} \end{array}\right. \end{array} $ | (2b) |
式中:Ksi为初始剪切模量,τult为剪切应力极值.
对试验数据进行处理,以γ/τ为纵坐标、γ为横坐标绘图并对试验数据点进行线性拟合,得到相应的直线截距和斜率,即a、b,汇总于表 2.
| 表 2 试验数据拟合结果(峰值前) Tab. 2 Fitting of test data(τ≤τult) |
需要特别说明,由于低温条件下峰值后的应变软化现象与标准双曲线模型特征不符,拟合已无意义,此处拟合数据仅为剪切应力峰值点前的试验数据,即图 9中各曲线箭头所指之前的部分.从图 9可以看出,剪切应力峰值点以前γ/τ与γ均呈较好的线性相关关系,用标准双曲线模型描述此阶段的剪切应力-应变关系是合理的.比较表 2中a、b不难发现,拟合参数a、b与法向应力和融化程度的相关性,可进一步拟合得到a、b的经验表达式
| $ \left\{\begin{array}{l} a=\left(0.6232 \sigma_{\mathrm{n}}-0.1112 t_{\text {thaw }}+0.3539\right)^{-1} , \\ b=\frac{0.0178 t_{\text {thaw }}^{2}+0.3098 t_{\text {thaw }}+1.6481}{\sigma_{\mathrm{n}}^{0.0063 t_{\text {thaw }}^{2}+0.1136 t_{\text {thaw }}+0.7568}}. \end{array}\right. $ | (3) |

|
图 9 融化程度-2 ℃时γ/τ-γ关系拟合曲线 Fig. 9 Fitting of relation between γ/τ and γ at thawing degree of -2 ℃ |
将式(3)代入式(1)即可实现在已知接触面温度和法向应力条件下,预测冻(融)土-结构接触面峰值前剪切应力-应变关系.
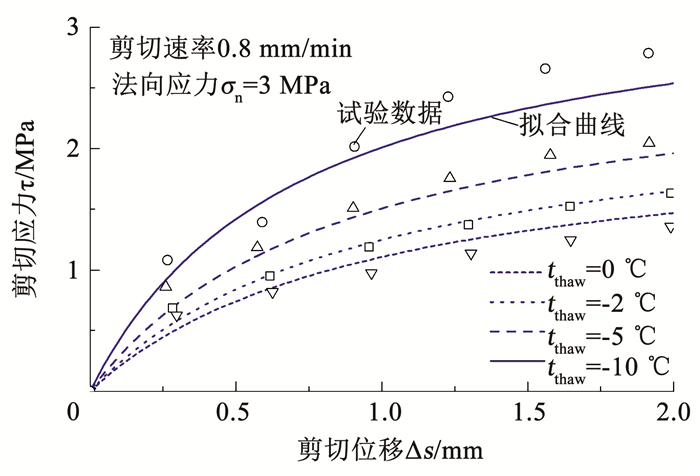
图 10为法向应力σn=3 MPa条件下,不同融化程度试验数据和双曲线模型预测结果曲线之间的比较,在γ≤3.2%时,试验数据和预测结果间的最大残差为0.31,二者变化趋势和量值都比较接近.
|
图 10 3 MPa应力下剪切应力-应变拟合曲线(τ < τf) Fig. 10 Fitting of shear stress-strain at normal stress of 3 MPa (τ < τf) |
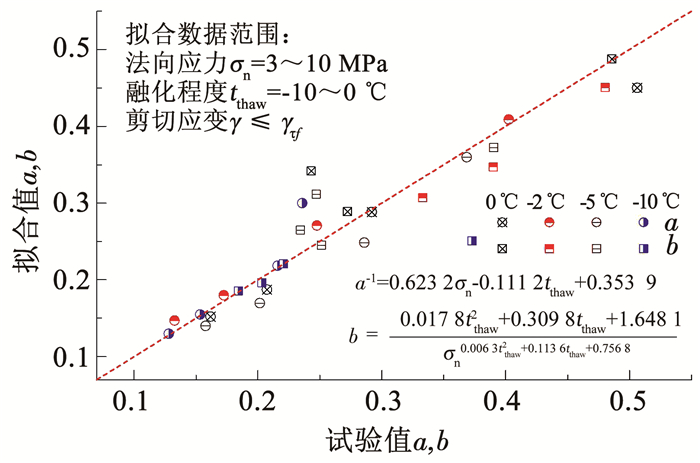
图 11给出了所有试验条件下a、b实测值和双曲线模型拟合值的比较,说明采用上述方法建立的双曲线模型可以较好地描述峰值前剪切应力-应变关系,模型具有良好的适用性.
|
图 11 双曲线模型拟合a、b和实测值比较 Fig. 11 Comparison of fitting results of hyperbolic model with measured values |
由式(2b)知,表 2中参数a的倒数为不同试验条件下拟合得到的升温冻(融)土-结构接触面剪切应力极值.从拟合结果看,接触面剪切应力极值随法向应力的增加和融化程度的降低而呈增大趋势,且在高应力下,剪切应力极值与法向应力关系可用线性函数描述,拟合直线截距随温度升高也呈线性减小趋势.但实测剪切应力-应变曲线达到的剪切应力最大值τf总是比由参数a确定的剪切应力极值τult要小,经统计两者比值(τf/τult)介于0.66~0.85.
3.1.3 初始剪切模量Ksi同理,表 2中参数b的倒数为不同试验条件下拟合得到的冻(融)土-结构接触界面初始剪切模量,其值与接触面形状、法向应力水平、温度条件等密切相关.拟合结果中,b值(1/Ksi)与法向应力呈幂函数关系,且相同应力下,b值(1/Ksi)随着温度的升高而呈增大趋势.
剪切过程中,剪切应力-应变关系曲线的斜率定义为接触面剪切模量Kst.根据式(1),峰值前接触面剪切模量可表达为
| $ K_{\mathrm{st}}=\frac{b}{(a \cdot \gamma+b)^{2}}. $ | (4) |
将表 2中的拟合参数代入上式可得相应试验条件下剪切模量-剪切应变关系式.接触面剪切模量随剪切应变的增大而减小,最终趋于零附近.
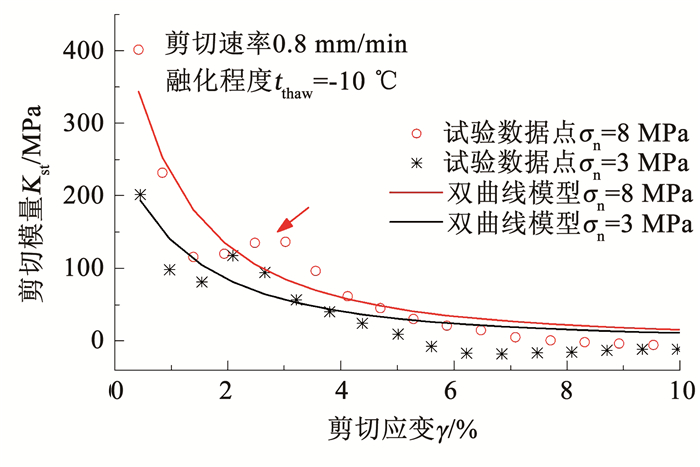
如图 12所示,采用中心差分格式计算试验离散数据点处的斜率,绘制融化程度tthaw=-10 ℃,法向应力分别为3,8 MPa条件下试验剪切模量-剪切应变变化趋势.图中仅绘制了峰值前的试验数据和相同条件下根据式(4)获得的双曲线模型结果.可以看出,双曲线模型可近似地模拟接触面剪切模量随剪切应变变化趋势,但对于试验过程中出现的剪切滑移现象模拟困难(图中箭头处).
|
图 12 接触面剪切模量变化趋势 Fig. 12 Trends of shear modulus of interface |
为描述融化程度较低时冻土-结构接触面剪切应力-应变关系的软化特征,利用文献[4]改进的双曲线模型:
| $ \tau=\frac{\gamma}{l \cdot \gamma^{2}+m \cdot \gamma+n}. $ | (5) |
其中,拟合参数
| $ \left\{\begin{array}{l} l=1 / \tau_{\mathrm{ult}} ,\\ m=1 / \tau_{\mathrm{ult}}-2 /\left(K_{\mathrm{si}} \cdot \gamma_{\mathrm{ult}}\right), \\ n=1 /\left(K_{\mathrm{si}} \cdot \gamma_{\mathrm{ult}}^{2}\right). \end{array}\right. $ | (6) |
式中γult为剪切应力极值时对应的剪切应变值.
参照前文步骤,对试验数据进行拟合分析,得到改进的双曲线模型参数汇总于表 3.
| 表 3 拟合结果(改进的双曲线模型) Tab. 3 Fitting results (improved hyperbolic model) |
分析表 3中参数l、m、n的变化趋势发现,-5 ℃时拟合结果与其他温度时拟合结果差异明显,因此,以下处理并未考虑此温度条件下结果.对表 3中模型参数与法向应力和融化程度进行进一步拟合分析,可以得到统一的经验表达式
| $ \left\{\begin{array}{l} l=0.0173 \mathrm{e}^{-0.143 t_{\text {thaw }}} \sigma_{\mathrm{n}}^{-0.7553}, \\ m=\left(0.0584 t_{\text {thaw }}+1.097\right) \sigma_{\mathrm{n}}^{-0.9927}, \\ n^{-1}=0.2536 \sigma_{\mathrm{n}}-0.1584 t_{\text {thaw }}+0.6774 . \end{array}\right. $ | (7) |
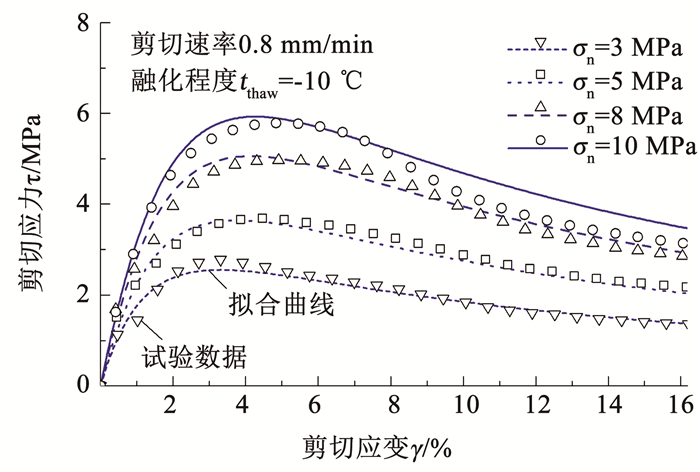
图 13给出了温度-10 ℃下改进的双曲线模型拟合曲线和试验结果曲线比较,可以看出,利用改进的双曲线模型可以较好地模拟具有软化特征的剪切应力-应变关系.
|
图 13 -10 ℃条件下剪切应力-位移拟合曲线 Fig. 13 Fitting of shear stress-displacement at thawing degree of -10 ℃ |
1) 随冻土融化程度的加深,高压下冻(融)土-结构接触面剪切应力-应变关系曲线形态由具有应变软化特征逐渐转变为具有应变硬化特征.
2) 当接触面剪切应变较小时(峰值前),标准的双曲线模型对高压下冻(融)土-结构接触面剪切应力-应变关系具有良好的适用性,建议采用本文拟合公式(1)和(2).对于具有应变软化特征的全过程剪切应力-应变关系模拟可以采用本文拟合公式(5)和(6).需要说明,由于拟合所用的试验数据有限,更准确的结果需要更多的试验数据支撑,作者会在这方面进一步开展工作.
3) 接触面剪切应力极值和初始剪切模量值与法向应力水平、温度条件等密切相关.从拟合结果看,接触面剪切应力极值与法向应力关系可用线性函数描述,拟合直线截距随融化程度升高呈线性减小趋势.接触面初始剪切模量与法向应力呈幂函数关系,且相同应力下,随着融化程度的升高呈减小趋势.
| [1] |
贾艳敏, 郭红雨, 郭启臣. 多年冻土区灌注桩桩-冻土相互作用有限元分析[J]. 岩石力学与工程学报, 2007, 26(增刊1): 3134. JIA Yanmin, GUO Hongyu, GUO Qichen. Finite element analysis of bored pile-frozen soil interactions in permafrost[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(S1): 3134. DOI:10.3321/j.issn:1000-6915.2007.z1.082 |
| [2] |
赵联桢, 杨平, 刘成. 土与结构接触面行为研究综述[J]. 交通科技, 2012(5): 83. ZHAO Lianzhen, YANG Ping, LIU Cheng. Study review of soil-structure interface behavior[J]. Transportation Science & Technology, 2012(5): 83. DOI:10.3963/j.issn.1671-7570.2012.05.029 |
| [3] |
LIU Jiankun, LV Peng, CUI Yinghui, et al. Experimental study on direct shear behavior of frozen soil-concrete interface[J]. Cold Regions Science and Technology, 2014, 104/105: 1. DOI:10.1016/j.coldregions.2014.04.007 |
| [4] |
董盛时, 董兰凤, 温智, 等. 青藏冻结粉土与混凝土基础接触面本构关系研究[J]. 岩土力学, 2014, 35(6): 1629. DONG Shengshi, DONG Lanfeng, WEN Zhi, et al. Study of constitutive relation of interface between frozen Qinghai-Tibet silt and concrete[J]. Rock and Soil Mechanics, 2014, 35(6): 1629. DOI:10.16285/j.rsm.2014.06.038 |
| [5] |
杨平, 赵联桢, 王国良. 冻土与结构接触面循环剪切损伤模型[J]. 岩土力学, 2016, 37(5): 1217. YANG Ping, ZHAO Lianzhen, WANG Guoliang. A damage model for frozen soil-structure interface under cyclic shearing[J]. Rock and Soil Mechanics, 2016, 37(5): 1217. DOI:10.16285/j.rsm.2016.05.001 |
| [6] |
赖远明, 程红彬, 高志华, 等. 冻结砂土的应力-应变关系及非线性莫尔强度准则[J]. 岩石力学与工程学报, 2007, 26(8): 1612. LAI Yuanming, CHENG Hongbin, GAO Zhihua, et al. Stress-strain relationships and nonlinear Mohr strength criterion of frozen sand clay[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(8): 1612. DOI:10.3321/j.issn:1000-6915.2007.08.011 |
| [7] |
郭佳奇, 刘希亮, 苏承东. 高应力下砂土与结构界面单剪试验研究[J]. 土木建筑与环境工程, 2011, 33(4): 120. GUO Jiaqi, LIU Xiliang, SU Chengdong. Simple shear test of interface between sand and structure under high stress[J]. Journal of Civil, Architectural & Environmental Engineering, 2011, 33(4): 120. |
| [8] |
夏红春, 周国庆. 土-结构接触面剪切力学特性及其影响因素试验[J]. 中国矿业大学学报, 2010, 39(6): 831. XIA Hongchun, ZHOU Guoqing. Experimental study of the shear mechanical characteristics at a soil-structure interface and the factors affecting them[J]. Journal of China University of Mining & Technology, 2010, 39(6): 831. |
| [9] |
彭丽云, 刘建坤, 田亚护, 等. 正融土无侧限抗压试验研究[J]. 岩土工程学报, 2008, 30(9): 1338. PENG Liyun, LIU Jiankun, TIAN Yahu, et al. Unconfined compression tests on thawing soil[J]. Chinese Journal of Geotechnical Engineering, 2008, 30(9): 1338. DOI:10.3321/j.issn:1000-4548.2008.09.013 |
| [10] |
梁智. 深厚表土冻融土-井壁接触面剪切力学特性试验研究[D]. 徐州: 中国矿业大学, 2016 LIANG Zhi. Experimental study on shear mechanical characteristics of the deep frozen-thawed soil and shaft lining interface[D]. Xuzhou: China University of Mining and Technology, 2016 |
| [11] |
石泉彬, 杨平, 王国良. 人工冻结砂土与结构接触面冻结强度试验研究[J]. 岩石力学与工程学报, 2016, 35(10): 2142. SHI Quanbin, YANG Ping, WANG Guoliang. Experimental study on adfreezing strength of the interface between artificial frozen sand and structure[J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(10): 2142. DOI:10.13722/j.cnki.jrme.2015.1511 |
| [12] |
刘波, 李东阳, 刘璐璐, 等. 冻土正融过程CT扫描试验及图像分析[J]. 煤炭学报, 2012, 37(12): 2014. LIU Bo, LI Dongyang, LIU Lulu, et al. CT scanning and images analysis during frozen soil thawing[J]. Journal of China Coal Society, 2012, 37(12): 2014. DOI:10.13225/j.cnki.jccs.2012.12.004 |
| [13] |
CLOUGH G W, DUNCAN J M. Finite element analyses of retaining wall behavior[J]. Journal of the Soil Mechanics and Foundations Division, 1973, 97(12): 1657. |
 2021, Vol. 53
2021, Vol. 53


