2. 合肥工业大学 资源与环境工程学院,合肥 230009;
3. 华北理工大学 矿业工程学院,河北 唐山 063009
2. School of Resources and Environmental Engineering, Hefei University of Technology, Hefei 230009, China;
3. School of Mining Engineering, North China University of Science and Technology, Tangshan 063009, Hebei, China
钻爆法是目前岩体工程开挖中最常见、最有效的方法之一. 爆破在导致近区岩体破碎的同时,不可避免地对中远区的岩体产生危害.在多次频繁爆破荷载作用下,中远区岩体内部的损伤程度及范围得到不断的累积增长和扩大以致发生失稳破坏.实践证明,爆破动载荷导致地下工程岩体宏观失效的过程往往并不是由某一次爆破作业造成的,而是多次爆破共同作用的结果.在隧道工程、井巷工程、水利水电工程以及其他岩体工程中都涉及到岩体在频繁冲击扰动作用下的破坏[1-3].
Li等[4]利用改进的SHPB装置对花岗岩进行了单轴循环冲击试验,结果表明动态载荷较低(即小于岩石静态强度的60%)时,循环冲击不会引起岩石内部的明显损伤; Luo等[5]对变粒岩在循环冲击荷载下的疲劳特性进行了研究,发现当循环冲击速度较大时,试样的纵波速度急剧下降; 当循环冲击速度较小时,纵波速度下降趋势逐渐减小; Wang等[6-7]利用SHPB装置研究了不同温度热处理花岗岩在循环冲击荷载下的动态力学特性和能量耗散特性的规律,指出在相同的循环冲击荷载下,600 ℃热处理试样表现出较快的力学性能劣化特性和温度弱化效应; 朱晶晶等[8]利用改进的SHPB装置对花岗岩试件进行单轴循环冲击压缩试验,分析花岗岩在循环冲击载荷下的动力学特性及能量吸收规律,并基于Weibull分布统计损伤本构模型分析了岩石的累积损伤演化规律; 吕晓聪等[9]研究了围压对岩石在循环冲击荷载下动力学性能,发现围压的存在增加了岩石对循环冲击的抵抗能力; 李地元等[10]结合声发射监测技术,研究了花岗岩在多次循环动态冲击下的动力学特性和累积损伤特性; 王志亮等[11]利用改进的SHPB装置研究了单轴循环冲击下花岗岩力学特性与损伤演化机理,并发展出特定应变率下岩样动态裂纹起裂应力的近似确定方法.
然而,值得注意的是,对于深部岩体,在受到频繁多次动荷载之前,其往往已经承受了原岩应力和因工程开挖和工程结构改变而在岩层中产生的次生应力等静载荷.如巷道开挖后,矿柱将出现明显的应力集中现象; 双侧壁导坑法施工的大断面小净距隧道群中,相邻隧道之间的围岩往往受到较大的竖向应力.此时,岩石承受载荷的形式为具有一定一维预应力下的循环动载荷.已有学者对砂岩一维预应力(即含轴压)下循环冲击动力特性开展了不少工作[12-13],但目前对花岗岩在轴压下的循环动力学行为研究较为鲜见.花岗岩作为一种常见的工程材料,在安全防护等大型岩体工程中有着广泛的应用.因此,开展一维静应力下花岗岩在循环冲击荷载下的动态力学特性研究对于合理安排工程爆破设计、地下工程安全防护以及预测动荷载作用下围岩长期稳定性等方面具有重要的意义.
1 试样制备及实验原理 1.1 试样制备试验材料为取自陕西华山地区的黑云母花岗岩.该花岗岩主要由微斜长石、斜长石、石英和黑云母等组成.为减小岩性差异和各向异性对实验结果的影响,测试用的试件均采用水钻法从同一块新鲜完整的岩块上沿同一方向钻孔取得.挑选无明显节理、裂纹等缺陷的试样进行切割、打磨.根据国际岩石力学学会关于冲击荷载下岩石试样长径比的建议[14],将试样加工成ϕ50 mm×25 mm的圆柱体.为减小端部摩擦效应对试验结果的影响,将试样两端面的不平整度控制在±0.05 mm以内.用于循环冲击试验的岩样如图 1所示.

|
图 1 用于循环冲击的花岗岩试样 Fig. 1 Granite samples for cyclic impact |
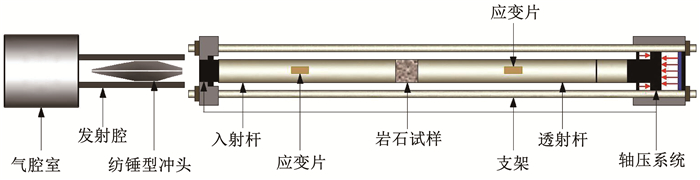
循环冲击压缩试验采用改进的动静组合SHPB装置,如图 2所示.该装置主要由发射系统(包含气腔室和子弹)、传递系统(包含入射杆和透射杆)、预应力(轴压)加载系统和测量系统(应变片、应变仪和示波器等)组成.其中,子弹、入射杆、透射杆和缓冲杆均为高强度40Cr合金钢,其弹性极限达800 MPa,密度为7 795 kg/m3,纵波速度为5 797 m/s. 入射杆、透射杆和缓冲杆的长度分别为2,1.5和0.3 m,直径均为50 mm.
|
图 2 含轴压装置的SHPB原理 Fig. 2 Schematic of SHPB with axial pressure device |
当子弹以一定的冲击速度撞击入射杆时,会在入射杆中产生一压缩脉冲εi(t),当该脉冲传播至入射杆与岩石试件的界面时,一部分脉冲被反射到入射杆中形成反射卸载脉冲εr(t),一部分透过岩石试件在透射杆中产生透射压缩脉冲εt(t). 通过粘贴在入射杆和透射杆上的应变片可测得入射波、反射波和透射波信号. 根据一维应力波理论,并采用适用于脆性材料数据处理的“三波法” [15]对采集到的应变信号进行处理,即可得到试样的应力、应变和应变率计算公式:
| $ {\dot \varepsilon (t) = \frac{c}{{{l_{\rm{s}}}}}\left( {{\varepsilon _{\rm{i}}}(t) - {\varepsilon _{\rm{r}}}(t) - {\varepsilon _{\rm{t}}}(t)} \right), } $ | (1) |
| $ {\varepsilon (t) = \frac{c}{{{l_{\rm{s}}}}}\int\limits_0^t {\left( {{\varepsilon _{\rm{i}}}(t) - {\varepsilon _{\rm{r}}}(t) - {\varepsilon _{\rm{t}}}(t)} \right)} {\rm{d}}t, } $ | (2) |
| $ {\sigma (t) = \frac{{{A_{\rm{e}}}E}}{{2{A_{\rm{s}}}}}\left( {{\varepsilon _{\rm{i}}}(t) + {\varepsilon _{\rm{r}}}(t) + {\varepsilon _{\rm{t}}}(t)} \right).} $ | (3) |
若对试样引入均匀性假设,即代入下面表达式子εi(t)+εr(t)=εt(t),则上式可转换为“二波法”[16]式子:
| $ {\dot \varepsilon (t) = - 2\frac{c}{{{l_{\rm{s}}}}}{\varepsilon _{\rm{r}}}(t), } $ | (4) |
| $ {\varepsilon (t) = - 2\frac{c}{{{l_s}}}\int_0^t {{\varepsilon _{\rm{r}}}} (t){\rm{d}}t, } $ | (5) |
| $ {\sigma (t) = \frac{{{A_{\rm{e}}}E}}{{{A_{\rm{s}}}}}{\varepsilon _{\rm{t}}}(t).} $ | (6) |
式中:Ae和As分别代表压杆和试样的横截面积; E和c分别为压杆的弹性模量和纵波波速; ls为试样的长度.
1.3 循环冲击试验方案利用MTS815电液伺服试验机对花岗岩试样进行了静态单轴压缩试验(应变率为10-5s-1).试验结果表明,花岗岩的静态单轴抗压强度为134.92 MPa.为研究一维预应力(轴压)对花岗岩在循环冲击荷载下动态力学特性的影响,设定5种轴压值(σA),即0,30,60,90和120 MPa,分别对应单轴抗压强度的0%、22.24%、44.47%、66.71%和88.94%.采用相同的入射波峰值电压对不同轴压下的岩样进行等幅循环冲击,入射波峰值电压设为150 mV.
2 试验结果分析表 1为代表性试样的基本参数及总循环冲击次数,所谓代表性试样为其总循环冲击次数最接近相同轴压下所有试样总循环冲击次数的平均值.由表 1可知,在相同的冲击入射波峰值电压下,花岗岩试样的总循环冲击次数随着轴压的增加呈现先增加后减小的趋势.当σA=60 MPa时,试样的总循环冲击次数最大,这也间接地反映了该轴压下花岗岩试样对循环冲击荷载的抵抗能力最强.
| 表 1 代表性试样的基本参数及总循环冲击次数 Tab. 1 Basic parameters of representative samples and total numbers of cyclic impacts |
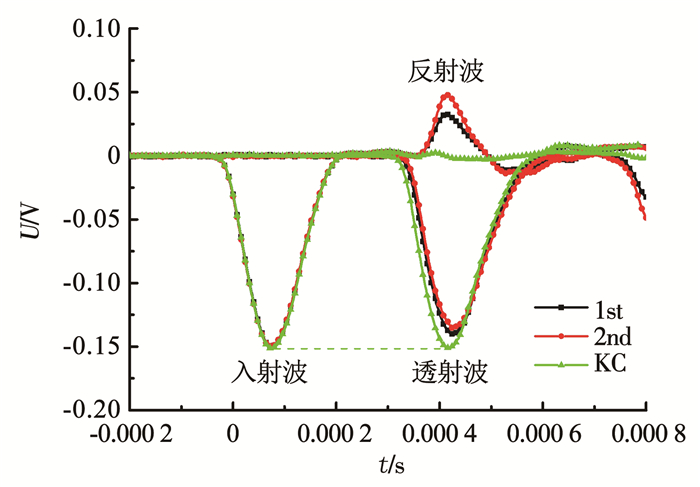
图 3为W0-1试样循环冲击及空冲波形.从空冲(KC)波形可以看出,入射波峰值与透射波峰值基本一致,反射波基本为0,符合SHPB冲击的基本要求.从循环冲击波形可以看出,入射波峰值电压接近150 mV,达到了等幅循环冲击的目的.此外,循环冲击波形中的反射波有明确的“起跳点”,这有益于利用式(1)~(3)进行力学特性参数的求取.W0-1试样首次冲击时的应力均匀性如图 4所示,易见入射波与反射波之和与透射波曲线在峰值应力之前基本重合,说明试样冲击过程中应力已达到均衡.
|
图 3 σA=0 MPa试样冲击及空冲波形 Fig. 3 Waveforms for sample impact and non-sample impact under σA=0 MPa |

|
图 4 σA=0 MPa试样首次冲击应力均匀图 Fig. 4 Stress balance of sample at the first impact under σA=0 MPa |
不同于σA=0 MPa的空冲波形图中反射波接近于零,当σA=30 MPa时,虽入射波峰值与透射波峰值基本一致,反射波却不为零,呈现先上扬后下降的趋势,如图 5所示.这是由于在施加轴压之前,应变片贴于弹性压杆上,施加轴压后,应变片发生挤压变形.通过轴压加油泵可以看出,施加冲击荷载后,仪表盘上的轴压值有稍许的降低,这表明空冲过程中弹性压杆出现了应力卸载,且这一过程是在冲击瞬间完成的.因此,空冲过程中入射杆上应变片采集到反射拉伸波卸载信号正是弹性压杆出现不均匀的瞬间应力卸载造成的.由于入射波和透射波采集到的是压缩信号,入射波峰值与透射波峰值基本一致.

|
图 5 σA=30 MPa试样冲击及空冲波形 Fig. 5 Waveforms for sample impactand non-sample impact under σA=30 MPa |
此外,由图 5还可看出,当对试样进行冲击时,反射波的前段与空冲反射波的前段重合,后段开始出现差异.入射杆上的应变片采集到的反射波信号是弹性杆应力瞬时卸载的反射波信号与入射杆同试样界面处反射回入射杆中的拉伸卸载信号叠加后的结果.此外,无论是空冲还是夹持试样冲击,可以排除是由于入射杆和透射杆未对齐或者试样加工精度不高而造成反射波出现与σA=0时反射波不同的现象.因为冲击试验观察发现,当入射杆和透射杆没有对齐或试样加工精度不高时,施加轴压时弹性杆容易发生“跳杆”现象,而在本次施加轴压的循环冲击试验中,即使当σA=120 MPa时,弹性杆并未出现异常.
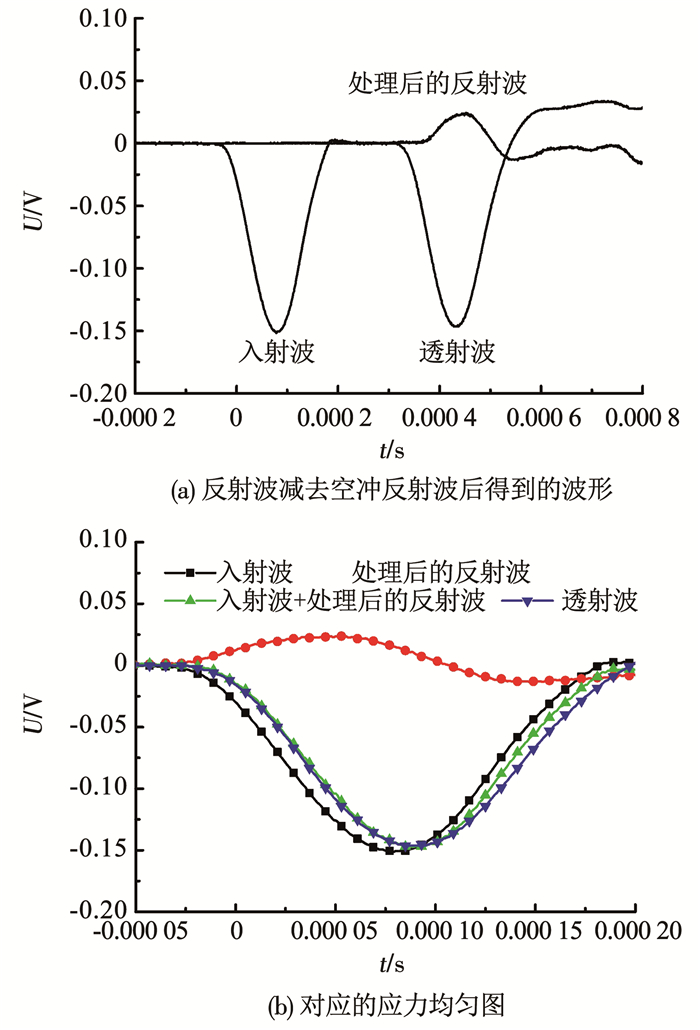
通过以上分析可知,在对施加轴压试样的波形图进行数据处理时,应将试样冲击波形图中的反射波减去空冲波形图中的反射波,据此可得出试样本身在冲击荷载下入射杆与试样界面处反射或透射至入射杆中的拉伸卸载信号.图 6(a)为σA=30 MPa试样首次冲击反射波减去空冲反射波后得到的波形图,可以看出,处理后的反射波经上述处理后有明确的“起跳点”,这样就可以根据式(1)~(3)求得各种力学特性参数.图 6(b)为σA=30 MPa试样首次冲击反射波减去空冲反射波后的应力均匀图,入射波与处理后的反射波之和与透射波曲线在峰值应力之前基本重合,说明施加轴压时试样冲击过程中应力也能达到均衡,满足SHPB冲击的应力均匀性要求.
|
图 6 σA=30 MPa试样首次冲击处理后的波形及其应力均匀图 Fig. 6 Waveforms for sample under σA=30 MPa at the first impact and its dynamic stress balance |
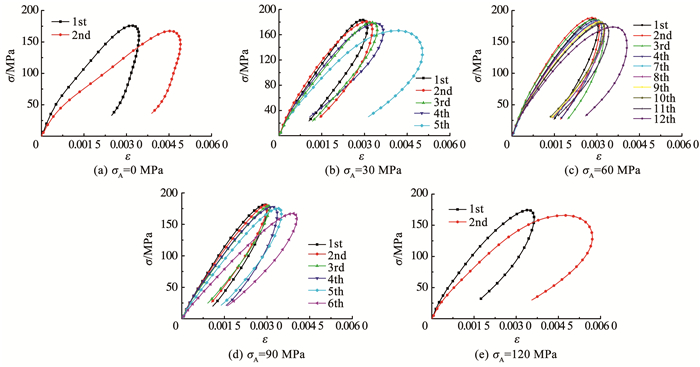
不同轴压下花岗岩试样的循环冲击应力-应变曲线如图 7所示,可见无论是在未施加轴压下还是在施加轴压下,不同轴压下花岗岩试样的应力-应变曲线都表现相似的曲线特征.在加载初期,应力-应变曲线近似为一条直线,此时可认为岩石处于弹性变形阶段.而后,随着应力的逐渐增加,应力-应变曲线的切线斜率逐渐降低,表明试样内部微裂纹逐渐扩展,损伤不断增加,直至达到峰值应力点.接着,随应力的降低达到最大应变(即应力-应变曲线中应变的最大值).最后,应变呈逐渐减小趋势,应力-应变曲线出现明显的“回弹”现象,表现为“Ⅱ”型应力-应变曲线.
|
图 7 不同轴压下花岗岩试样的循环冲击应力-应变曲线 Fig. 7 Cyclic impact stress-strain curves of granite samples under different axial pressures |
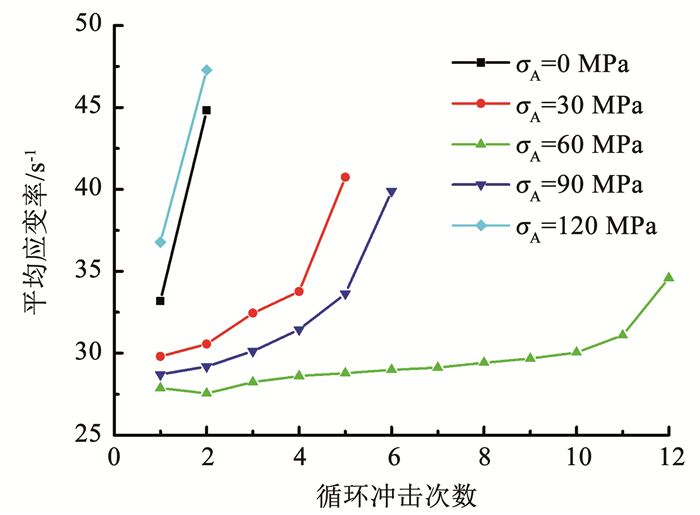
相同循环冲击荷载不同轴压下花岗岩试样的平均应变率随冲击次数的变化如图 8所示,可见首次冲击时,σA=0,30,60,90和120 MPa试样的平均应变率分别为33.18,29.81,27.87,28.70和36.78 s-1,平均应变率随轴压的增加呈现先减小后增加的趋势,施加不同的一维静应力影响了试样在相同冲击荷载下的动力学特性.此外,σA=0,30,90和120 MPa试样的平均应变率随着冲击次数的增加逐渐增大.根据一维应力波理论,应力波在入射杆、试样和透射杆之间发生反射和透射,若仅考虑一次透反射,存在以下关系[17]:
| $ {F = \frac{{{\rho _2}{c_2} - {\rho _1}{c_1}}}{{{\rho _2}{c_2} + {\rho _1}{c_1}}}( - 1 < F < 0), } $ | (7) |
| $ {{\varepsilon _{\rm{r}}}(t) = F{\varepsilon _{\rm{i}}}(t), } $ | (8) |
| $ {{\varepsilon _{\rm{t}}}(t) = \left( {1 - {F^2}} \right){\varepsilon _{\rm{i}}}(t).} $ | (9) |
|
图 8 不同轴压下花岗岩试样的平均应变率随冲击次数的变化 Fig. 8 Variation of average strain rate of granite samples with impact number under different axial pressures |
式中:ρ1c1、ρ2c2分别表示弹性杆和岩石的波阻抗,F为反射系数.
随着冲击次数的增加,在冲击损伤软化作用下,试样内部的损伤逐渐增加,试样的波阻抗将逐渐减小.根据式(7),这将使得反射系数F逐渐减小.对于同一试样(σA=0,30,90和120 MPa)的循环冲击,式(8)显示在相同的入射波εi(t)下,反射波εr(t)将逐渐增加.根据式(4),平均应变率与反射波成正比.因此,试样的平均应变率将随着冲击次数的增加而增加.与此同时,σA=0和120 MPa试样的平均应变率随冲击次数快速增加,相比而言,σA=30和90 MPa试样的平均应变率增长较为缓慢,但在最后一次冲击时应变率增加幅度明显.与σA=0,30,90和120 MPa试样不同,σA=60 MPa试样的平均应变率在第2次冲击时的平均应变率小于首次冲击.这是由于压密作用使得内部微裂纹得到闭合,岩石变得更加致密,力学性能得到了改善.随后,平均应变率在第2~11次冲击时呈现缓慢增加的趋势,在最后一次冲击时平均应变率突然增加,不同轴压下平均应变率的平均增加速率分别为11.64,2.73,0.61,2.24和10.51 s-1/次.
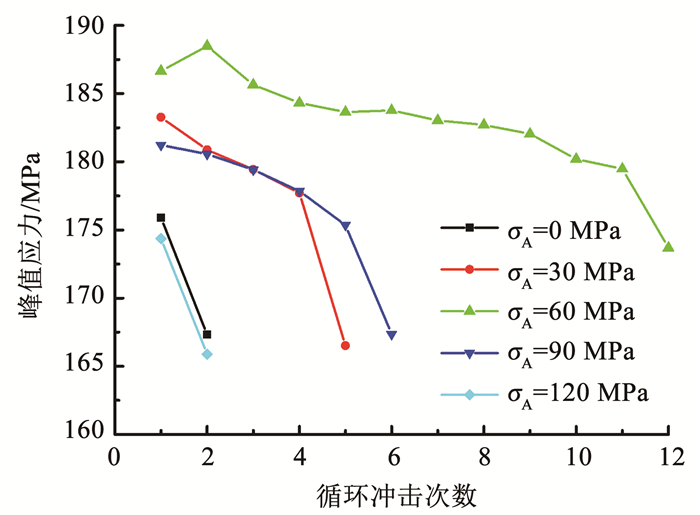
2.4 峰值应力随冲击次数的变化图 9为相同循环冲击荷载不同轴压下花岗岩试样的峰值应力随冲击次数的变化,可见首次冲击时,σA=0,30,60,90和120 MPa试样的峰值应力分别为175.89,183.26,186.65,181.23和174.36 MPa,在σA=60 MPa时峰值应力最大.此外,4种轴压下试样的峰值应力随着冲击次数的增加而不断减小.这同样是由于在冲击损伤软化作用下,岩石的波阻抗不断减小,使得反射系数F渐小.根据式(9),在相同的入射波εi(t)下,随着冲击次数的增加,透射波εt(t)将不断减小.根据式(6),峰值应力与透射波成正比.因此,试样的峰值应力将随着冲击次数的增加而逐渐减小,承载能力不断降低.从图 9还可看出,σA=0和120 MPa试样的峰值应力随冲击次数的增加快速减小.σA=30和90 MPa试样的峰值应力分别在前4次和前5次缓慢减小,最后一次冲击时峰值应力快速减小.与σA=0,30,90和120 MPa试样不同,σA=60 MPa试样的峰值应力在第2次冲击时达到最大值,这是由压密作用所致.从第2次开始,峰值应力呈现“缓慢减小—平缓发展—快速降低”3个阶段.不同轴压下峰值应力的平均减小速率分别为8.58,4.19,1.18,2.78和8.47 MPa/次.
|
图 9 不同轴压下花岗岩试样的峰值应力随冲击次数的变化 Fig. 9 Variation of peak stress of granite samples with impact number under different axial pressures |
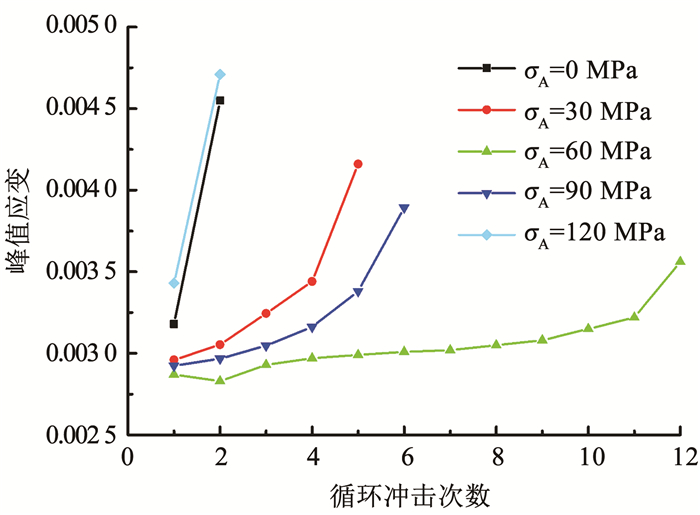
图 10为不同轴压下花岗岩试样的峰值应变(峰值应力对应的应变)随冲击次数的变化.在相同的冲击荷载下,首次冲击时σA=0,30,60,90和120 MPa试样的峰值应变分别为0.003 18,0.002 96,0.002 87,0.002 92和0.003 43.σA=0和120 MPa试样的峰值应变随着冲击次数的增加快速增加,表明试样的变形能力快速增加.σA=30和90 MPa试样的峰值应变随着冲击次数的增加而增加,但分别在前4次和前5次增加速度较缓,最后一次冲击时峰值应变明显增加,显现跳跃的特点.不同于σA=0,30,90和120 MPa试样,σA=60 MPa试样的峰值应变在第2次冲击相比第1次有所降低,第3次峰值应变有所增加,第4~11次峰值应变缓慢增加,最后一次冲击时峰值应变快速增加.不同轴压下峰值应变的平均增加速率分别为0.001 37,0.000 300,0.000 062 7,0.000 194和0.001 28/次.
|
图 10 不同轴压下花岗岩试样的峰值应变随冲击次数的变化 Fig. 10 Variation of peak strain of granite samples with impact number under different axial pressures |
由图 7可以看出,循环冲击下试样的应力-应变曲线上加载段并无明显的直线部分.因此,为更好地反映加载段的变形整体特征,选择应力-应变曲线加载段上对应峰值应力的20%和80%两点间的割线斜率作为加载段的弹性模量[18].其计算式为
| $ E_{\mathrm{c}}=\frac{\sigma_{1}-\sigma_{2}}{\varepsilon_{1}-\varepsilon_{2}}. $ | (10) |
式中:下标1和2分别表示应力-应变曲线上对应0.8σmax和0.2σmax的两点,σ为应力,ε为应变.
循环冲击荷载下花岗岩试样的弹性模量随冲击次数的变化如图 11所示,可以看出,首次冲击时,相同冲击荷载下σA=0,30,60,90和120 MPa下的弹性模量分别为58.37,68.78,74.12,67.61和56.59 GPa,随轴压增加呈现先增加后减小的趋势,即σA=60 MPa时最大,σA=0和120 MPa时,试样弹性模量随着冲击次数增加而快速减小,表明试样抗变形能力快速降低; σA=30和90 MPa试样的弹性模量随着冲击次数的增加而减小,但相对于σA=0和120 MPa试样弹性模量降低速率较缓; σA=60 MPa试样弹性模量呈现先增加后减小的趋势,在第2次冲击时弹性模量达到最大值78.36 GPa.从第2次开始,呈现出“快速下降—缓慢降低—快速降低”趋势.不同轴压下弹性模量平均降低速率分别为21.40,5.06,1.31,4.17和13.928 GPa/次.

|
图 11 不同轴压下花岗岩试样的弹性模量随冲击次数的变化 Fig. 11 Variation of elastic modulus of granite samples with impact number under different axial pressures |
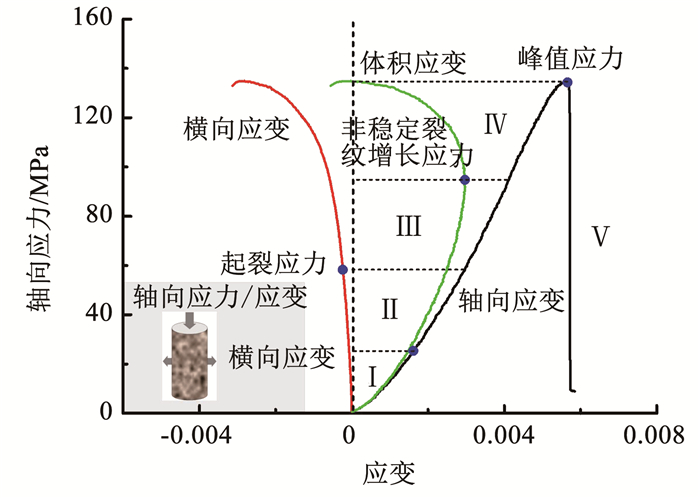
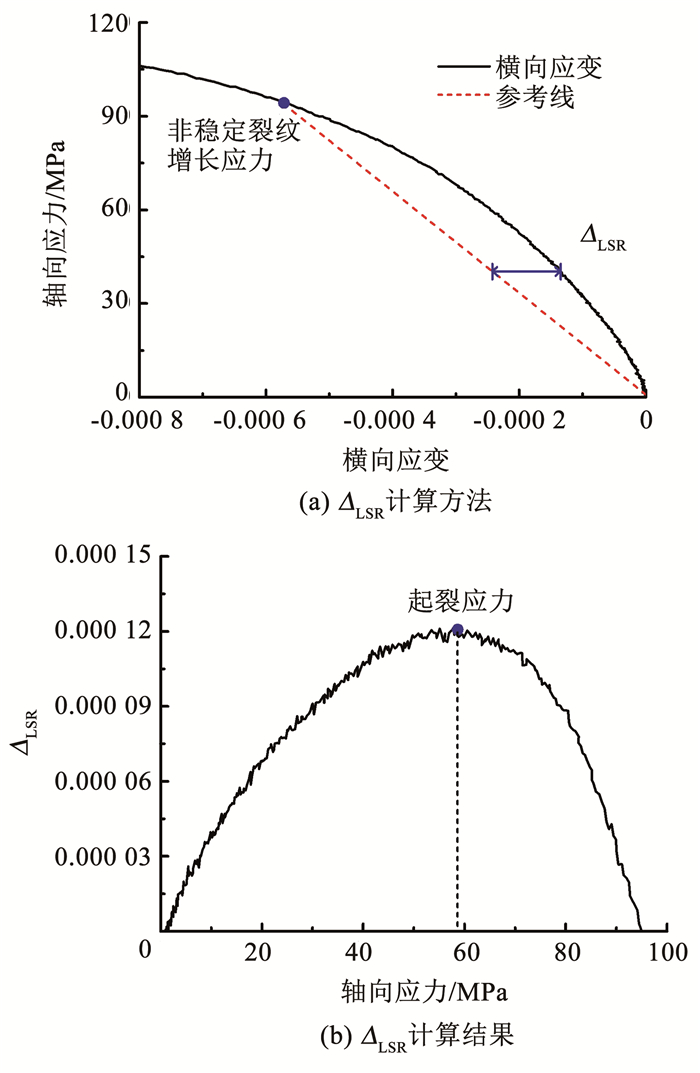
在单轴静态压缩下,脆性岩石的应力-应变曲线可以划分为3个阶段:Ⅰ压密阶段、Ⅱ弹性变形阶段、Ⅲ裂纹起始及稳定增长阶段、Ⅳ裂纹扩展非稳定增长阶段和Ⅴ破坏及峰后阶段,如图 12所示.Brace等[19]提出了利用脆性岩石在单轴压缩下的轴向应力-轴向应变、轴向应力-横向应变和轴向应力-体积应变计算起裂应力和非裂纹增长应力的方法.非稳定裂纹增长应力为体积应变最大点对应的轴向应力.起裂应力可由轴向应力-横向应变曲线中的横向应变响应(ΔLSR)求得,如图 13所示.据此,可求得花岗岩试样的起裂应力为58.63 MPa,非稳定裂纹增长应力为95.03 MPa.
|
图 12 花岗岩试样单轴压缩应力-应变曲线 Fig. 12 Stress-strain curves of granite samples under uniaxial compression |
|
图 13 横向应变响应(ΔLSR)法计算裂纹起裂应力 Fig. 13 Calculation of crack initiation stress using lateral strain response (ΔLSR) |
在一维静应力下的循环冲击试验中,施加轴压的过程近似于常规无侧限静态压缩试验,但所施加的轴压值要小于花岗岩的静态抗压强度(即试样未出现宏观破坏).因此,可利用静态压缩过程中岩样内部损伤演化规律探析后续循环冲击荷载施加前轴压对花岗岩样内部微结构的影响机理.当σA=30 MPa时,试样进入弹性变形阶段.相比σA=0,试样内部的微裂纹得到部分闭合,压密作用导致其力学性质有所改善,表现为首次冲击时平均应变率和峰值应变有所减小,峰值应力和弹性模量得到提高,故总循环冲击次数有所增加,但平均应变率和峰值应变随冲击次数的平均增加速率出现降低,峰值应力和弹性模量随冲击次数的平均降低速率有所减小; 当σA=60 MPa时,静应力处于弹性变形的末端,刚进入裂纹起始及稳定增长阶段,此时在岩石内部产生的微裂纹较少,静应力的增加使得压密程度更高,从而使得σA=60 MPa的总循环冲击次数最大,平均应变率和峰值应变随冲击次数的平均增加速率最小,峰值应力和弹性模量随冲击次数的平均降低速率最小; 当σA=90 MPa时,试样已进入裂纹起始和裂纹稳定增长阶段,此时岩石内部的裂纹已有所萌生,岩石的力学性能得到部分劣化,从而使得其总循环冲击次数相比σA=60 MPa有所降低,各力学参数随冲击次数的劣化速率增加; 当σA=120 MPa时,岩样进入裂纹非稳定增长阶段,其力学性能严重劣化,从而使得其总循环冲击次数较小,平均应变率和峰值应变随冲击次数的平均增加速率增大,峰值应力和弹性模量随冲击次数的平均降低速率增大.
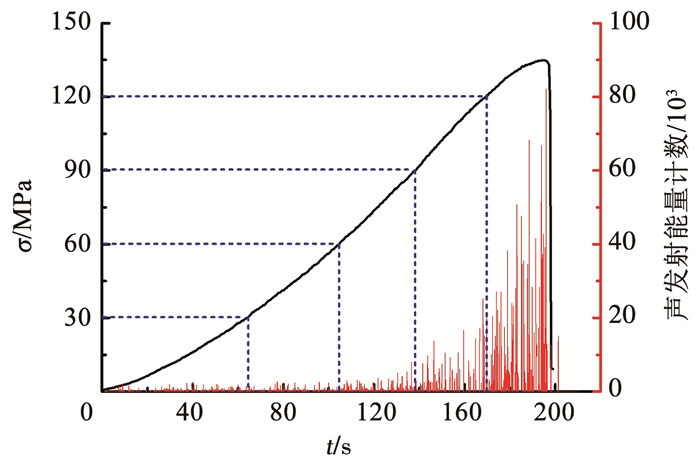
此外,可利用声发射技术监测静应力下岩石内部裂纹的发育过程.图 14为花岗岩试样单轴压缩过程中声发射能量计数与单轴压缩轴向应力-轴向应变曲线的关系.可以看出,在0~60 MPa,声发射能量计数很低,基本可以忽略.说明此应力范围内,岩石内部裂纹并未有明显的萌生或扩展,该阶段岩石处于压密或弹性变形阶段; 60~90 MPa,声发射能量计数开始缓慢增加,说明岩石内部的裂纹开始逐渐被激活; 90~120 MPa,声发射能量计数增加更为明显,裂纹逐渐开始扩展; 120~134.92 MPa,声发射能量计数快速增大,此时岩石内部裂纹迅速汇聚扩展并逐步贯通直至试样发生宏观破坏.
|
图 14 声发射能量计数与单轴压缩轴向应力-轴向应变曲线的关系 Fig. 14 Relation between acoustic emission energy count and axial stress-axial strain curve under uniaxial compression |
1) 在相同的循环冲击荷载下,试样的总循环冲击次数随轴压的增加呈现先增加后减小的趋势,在σA=60 MPa时达到最大.施加轴压时冲击波形中的反射波不同于σA=0时试样,在进行数据处理时需利用空冲反射波对其进行处理.5种轴压下的试样都表现为典型的Ⅱ型应力-应变曲线.
2) 在轴压σA=0,30,90和120 MPa下,试样的平均应变率和峰值应变随着冲击次数的增加而增加,峰值应力和弹性模量变化规律相反.σA=0和120 MPa下试样的力学参数劣化速率较快,σA=60 MPa下试样的平均应变率和峰值应变随着冲击次数的增加呈现先减小后增加的趋势,峰值应力和弹性模量则反之,且力学参数劣化变缓.
3) 通过花岗岩静态单轴压缩应力-应变曲线和声发射能量计数可看出,当轴压小于起裂应力时,压缩作用将导致循环冲击荷载下岩石的动力学性能有所改善; 当轴压大于起裂应力时,由于岩石内部微裂纹的萌生、成核和扩展,岩石的动力学性能将会出现下降.
| [1] |
刘明贵, 张国华, 刘绍波, 等. 大帽山小净距隧道群中夹岩累计损伤效应研究[J]. 岩石力学与工程学报, 2008, 28(7): 1363. LIU Minggui, ZHANG Guohua, LIU Shaobo, et al. Research on accumulative damage effect of interlaid rock in Damaoshan tunnel group with small clear distance[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 28(7): 1363. DOI:10.3321/j.issn:1000-6915.2009.07.009 |
| [2] |
杨国梁, 杨仁树, 车玉龙. 周期性爆破振动下围岩的损伤累积效应[J]. 煤炭学报, 2013, 38(增刊1): 25. YANG Guoliang, YANG Renshu, CHE Yulong. Damage accumulative effect of surrounding rock under periodic blasting vibration[J]. Journal of China Coal Society, 2013, 38(S1): 25. DOI:10.13225/j.cnki.jccs.2013.s1.007 |
| [3] |
肖建清, 冯夏庭, 林大能. 爆破循环对围岩松动圈的影响[J]. 岩石力学与工程学报, 2010, 29(11): 2248. XIAO Jianqing, FENG Xiating, LIN Daneng. Influence of blasting round on excavation damaged zone of surrounding rock[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(11): 2248. |
| [4] |
LI X B, LOK T S, ZHAO J. Dynamic characteristics of granite subjected to intermediate loading rate[J]. Rock Mechanics and Rock Engineering, 2005, 38(1): 21. DOI:10.1007/s00603-004-0030-7 |
| [5] |
LUO Xuedong, JIANG Nan, WANG Mingyang, et al. Response of leptynite subjected to repeated impact loading[J]. Rock Mechanics and Rock Engineering, 2016, 49(10): 4137. DOI:10.1007/s00603-015-0896-6 |
| [6] |
WANG Zhiliang, TIAN Nuocheng, WANG Jianguo, et al. Experimental study on damage mechanical characteristics of heat-treated granite under repeated impact[J]. Journal of Materials in Civil Engineering, 2018, 30(11): 04018274. DOI:10.1061/(asce)mt.1943-5533.0002465 |
| [7] |
WANG Zhiliang, TIAN Nuocheng, WANG Jianguo, et al. Mechanical response and energy dissipation analysis of heat-treated granite under repeated impact loading[J]. Computers Materials and Continua, 2019, 59(1): 275. DOI:10.32604/cmc.2019.04247 |
| [8] |
朱晶晶, 李夕兵, 宫凤强, 等. 单轴循环冲击下岩石的动力学特性及其损伤模型研究[J]. 岩土工程学报, 2012, 35(3): 531. ZHU Jingjing, LI Xibing, GONG Fengqiang, et al. Dynamic characteristics and damage model for rock under uniaxial cyclic impact compressive loads[J]. Chinese Journal of Geotechnical Engineering, 2012, 35(3): 531. |
| [9] |
吕晓聪, 许金余, 葛洪海, 等. 围压对砂岩动态冲击力学性能的影响[J]. 岩石力学与工程学报, 2009, 29(1): 193. LV Xiaocong, XU Jinyu, GE Honghai, et al. Effects of confining pressure on mechanical behaviors of sandstone under dynamic impact loads[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 29(1): 193. |
| [10] |
李地元, 孙小磊, 周子龙, 等. 多次冲击荷载作用下花岗岩动态累计损伤特性[J]. 实验力学, 2016, 31(6): 827. LI Diyuan, SUN Xiaolei, ZHOU Zilong, et al. On the dynamic accumulated damage characteristics of granite subjected to repeated impact load action[J]. Journal of Experimental Mechanics, 2016, 31(6): 827. DOI:10.7520/1001-4888-16-009 |
| [11] |
王志亮, 杨辉, 田诺成. 单轴循环冲击下花岗岩力学特性与损伤演化机理[J]. 哈尔滨工业大学学报, 2020, 52(2): 59. WANG Zhiliang, YANG Hui, TIAN Nuocheng. Mechanical property and damage evolution mechanism of granite under uniaxial cyclic impact[J]. Journal of Harbin Institute of Technology, 2020, 52(2): 59. DOI:10.11918/201811085 |
| [12] |
QIU Jiadong, LI Diyuan, LI Xibing. Dynamic failure of a phyllite with a low degree of metamorphism under impact Brazilian test[J]. International Journal of Rock Mechanics and Mining Sciences, 2017, 94: 10. DOI:10.1016/j.ijrmms.2017.02.013 |
| [13] |
邱加冬, 李地元, 李夕兵, 等. 预制缺陷对花岗岩层裂破坏的影响[J]. 爆炸与冲击, 2018, 38(3): 665. QIU Jiadong, LI Diyuan, LI Xibing, et al. Effect of pre-existing flaws on spalling fracture of granite[J]. Explosion and Shock Waves, 2018, 38(3): 665. |
| [14] |
HATHEWAY A W. The complete ISRM suggested methods for rock characterization, testing and monitoring; 1974-2006[J]. Environmental and Engineering Geoscience, 2009, 15(1): 47. DOI:10.2113/gseegeosci.15.1.47 |
| [15] |
DAI Feng, HUANG Sheng, XIA Kaiwen, et al. Some fundamental issues in dynamic compression and tension tests of rocks using split Hopkinson pressure bar[J]. Rock Mechanics and Rock Engineering, 2010, 43(6): 657. DOI:10.1007/s00603-010-0091-8 |
| [16] |
王礼立. 应力波基础[M]. 北京: 国防工业出版社, 2005. WANG Lili. Foundation of stress waves[M]. Beijing: National Defense Industry Press, 2005. |
| [17] |
李夕兵. 岩石动力学基础与应用[M]. 北京: 科学出版社, 2014. LI Xibing. Rock dynamics fundamentals and applications[M]. Beijing: Science Press, 2014. |
| [18] |
许金余, 吕晓聪, 张军, 等. 围压条件下岩石循环冲击损伤的能量特性研究[J]. 岩石力学与工程学报, 2010, 29(增刊2): 4159. XU Jinyu, LV Xiaocong, ZHANG Jun, et al. Research on energy properties of rock cyclical impact damage under confining pressure[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(S2): 4159. |
| [19] |
NICKSIAR M, MARTIN C D. Evaluation of methods for determining crack initiation in compression tests on low-porosity rocks[J]. Rock Mechanics and Rock Engineering, 2012, 45(4): 607. DOI:10.1007/s00603-012-0221-6 |
 2021, Vol. 53
2021, Vol. 53


