浅层巷道支护主要问题是控制松动岩块在重力作用下的掉落和管理松散岩石[1-2],此时,锚杆的拉伸强度是支护设计的关键参数.如全长黏结式锚杆,在锚杆失效前能充分利用杆体材料拉伸性能而被广泛应用[3].而深部岩层在高地应力作用下,围岩的挤压和裂缝的扩张都能引起开挖面的收敛.因此,深部支承系统除了要考虑支护强度外,还需要考虑围岩的膨胀变形量.在这种环境下,一种既能提供一定支护阻力,又有一定伸长量的新型锚杆孕育而生,称为吸能锚杆或让压锚杆.
吸能锚杆在世界各地已经有近20年的研究历史.吸能锚杆概念最早于20世纪90年代初由南非学者Ortlepp提出[4].1992年,Jager等[5]发明出第一根吸能锚杆,即锥形锚杆(cone bolt).它由一根光滑的金属钢杆和一个在远端锻造的扁平锥形扩口组成.近年来,随着对深部吸能支护理念的深入了解,市场出现了各种类型的吸能锚杆.按吸能机理可概括为结构构件吸能型和杆体吸能型[6].结构构件吸能型是在锚固处增设一种可变形的结构(如套管摩擦式等),如Cone锚杆、Roofex锚杆[7]和CRLD锚杆(横阻大变形)[8]等.杆体吸能型是利用杆体屈服伸长实现变形吸能,如D锚杆[9]、抗冲击新型锚杆[10]等.但是,上述这些吸能锚杆主要通过改变锚杆杆体材料属性(如杆体拉长)或吸能元件相对变形,进而实现锚杆对围岩的让压吸能作用,而其吸能储存量随锚杆延伸不断被消耗.而在深部硬岩类岩层中(如深部金矿中的花岗岩),开采诱发的岩爆类型主要为应变型岩爆,即岩体的破坏是突发的、无征兆的突变.此外,在深部高地应力环境下,单次较小的人工扰动在高地应力叠加后会引起较大的动力响应.因此,急需选择一种小应变高吸能,又能抗重复冲击性能的材料,将其作为结构构件吸能型锚杆的吸能结构,应用于深部坚硬岩体的支护.
高阻尼材料是黏弹性体,具有弹性、黏性、弹簧和流体的性能.可以通过添加炭黑等填料改善材料的抗冲击性和吸能特性,已被广泛应用于结构抗震、军事防爆、设备共振和仪表减震等[11].近年来,国内外学者对高阻尼橡胶材料的力学行为进行了大量的实验研究,如Dall’Asta等[12]通过循环加载实验测试应变率和应变幅值对材料力学性能的影响,并提出橡胶材料在循环荷载作用下的非线性黏弹性损伤模型.Li等[13]采用SHPB装置研究不同应变率下高阻尼橡胶吸能特性,结果表明,材料的吸能能力随加载应变率增大而增大.Amin等[14]对高阻尼橡胶材料的力学性能和本构模型对应变率的依赖进行理论和实验研究. 张伟等[15]采用分离式SHPB实验装置对不同配比的高阻尼橡胶材料进行实验研究,结果表明,橡胶材料的吸能率随应变率增加而增大,而且高应变率对材料吸能率提高幅值明显大于低应变率.顾红军等[16]采用SHPB装置对高聚物复合材料进行冲击实验,讨论了材料的吸能特性.但国内外关于材料几何尺寸对其动力响应和吸能机制方面报道较少,也尚未见将高阻尼橡胶应用于冲击地压巷道支护中的相关报道.因此,本文利用落锤冲击系统和分离式SHPB压杆,对不同厚径比的高阻尼橡胶进行冲击实验,研究不同厚径比对材料的缓冲性能、吸能特性和耐冲性的影响,研究结果为研发新型吸能锚杆的材料参数选择提供依据.最后,对不同厚径比的“橡胶-花岗岩”组合试样进行高速冲击,之后采用分形维数定量描述厚径比对花岗岩缓冲吸能效果的影响.
1 新型小应变吸能锚杆结构与作用机理 1.1 新型小应变吸能锚杆结构小应变吸能锚杆由螺母、托盘、杆体和吸能装置组成(见图 1).吸能装置为阻尼比为20%的高阻尼橡胶材料,与螺母、托盘依次安装于杆体尾部.在实际工程应用中高阻尼橡胶的长宽与托盘长宽相同,均为150 mm×150 mm,厚度依据现场冲击动能和围岩变形量确定.新型小应变吸能锚杆属于结构型吸能锚杆,主要是通过高阻尼橡胶内部大分子链段的内摩擦及链段的协同作用,将外界的大量机械能转化为热能,从而吸收外界激振力.

|
图 1 新型小应变吸能锚杆结构 Fig. 1 New type small strain energy absorbing bolt |
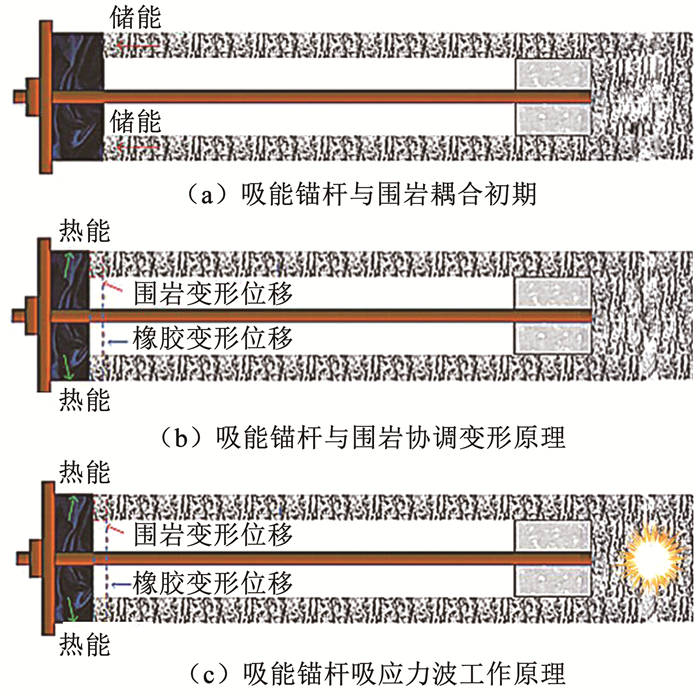
巷道围岩的变形能通过托盘(外锚固段)和内锚固段挤压施加到高阻尼橡胶材料上,图 2给出了小应变吸能锚杆工作原理.
|
图 2 新型小应变吸能锚杆工作原理 Fig. 2 Working principle of new type small strain energy absorbing bolt |
1) 吸能装置变形阶段.当围岩发生变形时,通过托盘和围岩挤压高阻尼橡胶材料的挤压力小于杆体弹性变形的轴向力,此时,小应变吸能锚杆依靠高阻尼橡胶材料变形来吸收围岩的变形能.图 2(a)为锚杆与围岩耦合初期.
2) 杆体弹性变形阶段.当托盘对吸能装置的挤压力逐渐大于杆体弹性变形所需的轴向力时,依靠杆体材料的弹性变形来抵抗围岩变形.
3) 吸能装置和杆体共同变形阶段.当小应变吸能锚杆的轴向力大于杆体材料所需的塑性硬化力时,锚杆依靠高阻尼橡胶材料和杆体的变形,直至巷道围岩再次达到稳定状态,工作示意见图 2(b).
4) 小应变吸能的抗反复冲击吸能.当围岩受到人工开采扰动影响时,扰动应力与高地应力叠加的应力波通过高阻尼橡胶的吸收,降低了应力波对螺母和杆体冲击力,工作示意见图 2(c).外界的冲击能越大,高阻尼橡胶由玻璃态向弹性态转变,其阻尼性能越好,即吸收更多的冲击能[13].
2 实验装置与原理目前,常用缓冲曲线、吸能曲线和能量吸收来评估材料缓冲吸能特性.缓冲曲线借助于落锤试验,主要反映了材料的缓冲效果,是具体缓冲结构物的响应; 吸能曲线法利用材料的应力-应变曲线,主要反映在某一特定应变率下材料的吸能特性; 能量吸收法同时考虑了变形速率和材料密度对材料缓冲吸能的影响,因此,采用缓冲曲线法研究落锤系统冲击下材料缓冲性能,采用能量吸收法研究分离式SHPB冲击下材料吸能性能.
2.1 落锤实验装置与原理实验采用华北理工大学DP-1200型全自动落锤系统,主要由冲击试验平台、电器柜和控制仪表组成,如图 3所示.落锤冲击实验机落锤最高上升高度为1.5 m(除实验夹具和落锤之外),落锤质量配有1,2,5,10 kg共50 kg,冲击速度为1.5~20.0 m/s,冲击能量为2.6~826.0 J.

|
图 3 DP-1200型全自动落锤冲击实验机 Fig. 3 DP-1200 fully automatic drop hammer impact testing machine |
实验选择阻尼为20%的高阻尼橡胶材料.为了确保实验试样材质均匀性,其落锤实验与SHPB实验所用试样均取自直径60 cm、高20 cm的高阻尼橡胶材料.落锤实验所用的试样尺寸为(长mm×宽mm×厚mm):50×50×10、50×50×15、50×50×20、50×50×30、50×50×50、50×50×70,各3件(共18个试样).实验所用的试样见图 4.

|
图 4 落锤实验所用试样 Fig. 4 Samples for drop hammer test |
实验时所用锤头质量为50 kg保持不变,落距分别设计为600,800和1 000 mm.综合考虑试样高度,共设计了6组试验.每组试验有3件试样,每个试样单独重复6次,用于研究厚径比对材料的缓冲性能和耐冲性能的影响.
在落锤冲击试验中,采用加速度传感器获取落锤的加速度时间历程曲线.通过对加速度时程曲线一次数值积分得到速度时程曲线,二次数值积分得到位移时程曲线.将速度时程曲线和落锤质量乘积得到材料在冲击过程所受冲击力.具体如下:
| $ \begin{aligned} V(t) =\int a(t) \mathrm{d} t \end{aligned} $ | (1) |
| $ S(t) =\int V(t) \mathrm{d} t , $ | (2) |
| $ F(t) =M a(t). $ | (3) |
采用直径为50 mm的等截面分离式SHPB压杆系统,压杆弹性模量为250 GPa,密度为7 787 kg/m3,波速为5 667 m/s,撞击杆选用长0.26 m纺锤形子弹,入射杆与透射杆长度均为2.0 m(SHPB装置如图 5所示).

|
图 5 SHPB试验装置 Fig. 5 SHPB test device |
SHPB实验所用的高阻尼橡胶试样尺寸为ϕ50 mm×2 mm(厚)、ϕ50×10、ϕ50×15、ϕ50×20、ϕ50×25,各6件,花岗岩试样尺寸为ϕ50×25,制备15件.实验所用的部分试样见图 6.

|
图 6 SHPB实验所用高阻尼橡胶部分试样 Fig. 6 High damping rubber samples for SHPB test |
为了研究厚径比对高阻尼橡胶力学特性和吸能性能的影响,采用以下两种冲击试验方案:1)保持冲击气压恒定为0.7 MPa,分别对5种不同厚度高阻尼橡胶试样进行冲击,每个试样重复冲击6次; 2)保持冲击气压恒定为0.9 MPa,对5种不同厚度的高阻尼橡胶和花岗岩试样组合试样(简称“橡-岩”试样)进行冲击,之后采用“质量-等效边长筛分法”计算花岗岩破碎后分形维数.在进行“橡-岩”试样冲击时,沿子弹冲击方向花岗岩在前橡胶在后,如图 7所示.

|
图 7 “橡-岩”试件加载方向 Fig. 7 Loading direction of "oak-rock" specimen |
试验时根据SHPB冲击实验一维弹性应力波假设,可以用三波法[17]确定材料的应变率、应变和应力, 即
| $ \begin{array}{c} \dot{\varepsilon}(t)=\frac{c}{l_{0}}\left(\varepsilon_{\mathrm{i}}-\varepsilon_{\mathrm{r}}-\varepsilon_{\mathrm{t}}\right) \end{array} $ | (4) |
| $\varepsilon(t)=\frac{c}{l_{0}} \int_{0}^{t}\left(\varepsilon_{\mathrm{i}}-\varepsilon_{\mathrm{r}}-\varepsilon_{\mathrm{t}}\right) \mathrm{d} t , $ | (5) |
| $ \sigma(t)=\frac{A}{2 A_{0}} E\left(\varepsilon_{\mathrm{i}}+\varepsilon_{\mathrm{r}}+\varepsilon_{\mathrm{t}}\right). $ | (6) |
式中:εi、εr和εt分别为压杆上应变片记录的入射波、反射波和透射波时程; A0和l0分别为试样的横截面面积和厚度; A、c和E分别为压杆横截面面积、波速和杨氏模量.
能量吸收法由Maiti等提出[18],即材料单位体积吸收的能量由试验获得的应力-应变曲线通过积分得到.E表示材料的吸能率,其值越大材料吸能性能越好.
| $ E=\int_{0}^{\varepsilon_{\mathrm{m}}} \sigma \mathrm{d} \varepsilon / \sigma_{\mathrm{m}}. $ | (7) |
式中:E表示当材料在最大压缩应变εm时,材料吸收的能量与最大应力σm比值.
3 实验结果与分析 3.1 厚径比对材料缓冲性能的影响分析高阻尼橡胶材料作为小应变吸能锚杆的吸能构件,除了吸能减震外其缓冲效果对保护托盘和螺母等构件起重要作用.由落锤冲击实验获得不同厚径比试样在落距为600,800和1 000 mm处的力时程曲线,结果如图 8~10所示.

|
图 8 落距为600 mm的时程曲线 Fig. 8 Time-history curves with drop distance of 600 mm |

|
图 9 落距为800 mm的时程曲线 Fig. 9 Time-history curves with drop distance of 800 mm |
|
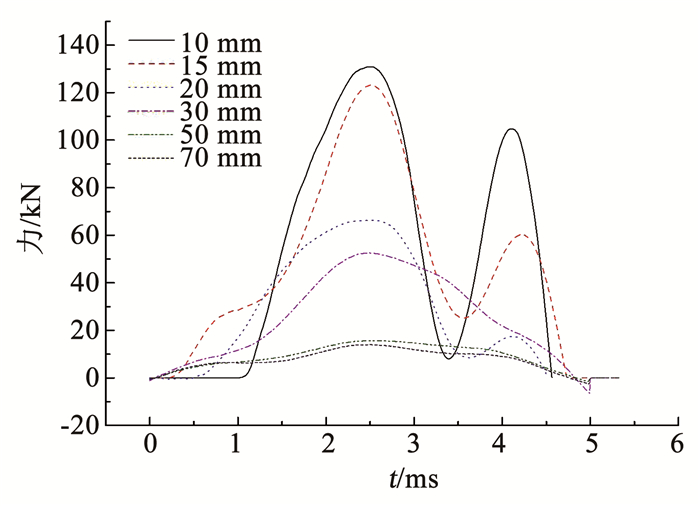
图 10 落距为1 000 mm的时程曲线 Fig. 10 Time-history curves with drop distance of 1 000 mm |
由图 8~10可以看出,同落距下随着试样厚度增大,试样对冲击力响应从零到力峰值的作用时间增大,作用的最大冲击力也显著减小.此外,冲击力随时间变化出现多个峰值,厚径比越小第二个峰值越大.在外界相同冲击能量作用下,由于材料黏滞性作用使荷载出现多次波动从而吸收外界机械能.截面积相同,材料体积越大(即厚度越大),第二个最大冲击力峰值越小,说明材料体积越大缓冲效果越好.
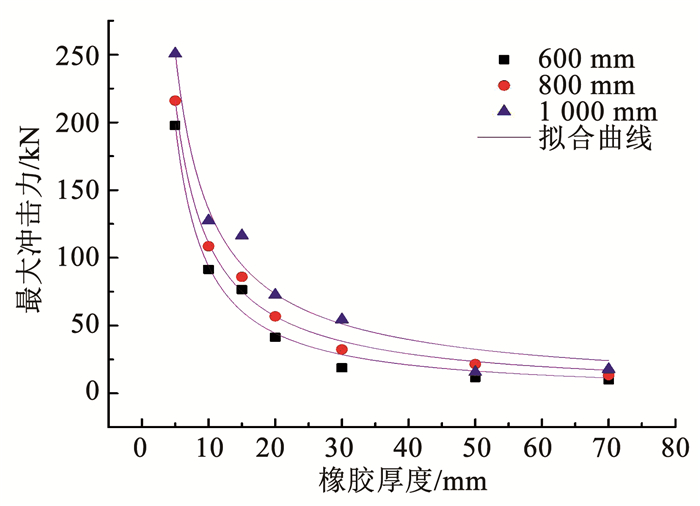
为了直观描述高阻尼橡胶厚度对冲击力缓冲效果,将每种工况下的最大冲击力峰值响应随材料厚径的变化进行对比,结果如图 11所示.可以看出,在相同冲击条件下,锤头不同落距对底座的最大冲击力(y表示)随材料厚径(x表示)变化具有很好的相似性,均呈幂函数(y=axb)趋势变化.将图中数据进行幂函数回归得到相关数据如表 1所示.由表 1可以获得冲击能(E)在294~490 J时,冲击能、最大冲击力和厚度间关系,即y=axb,式中a=0.035 E2-28.03E+6 962.2,b=10-5E2+0.007E-2,由此可以根据锚杆将受到冲击能,设计适合工程应用的材料尺寸.
|
图 11 最大冲击力与橡胶厚度关系 Fig. 11 Relation between maximum impact force and rubber thickness |
| 表 1 数据拟合相关系数 Tab. 1 Correlation coefficients |
由图 11还可以看出,高阻尼橡胶厚径比大于0.6时,材料对冲击力峰值的缓冲变化幅值较小为最优厚径比,即过低的厚径比对冲击力的缓冲作用较小,难于对防护对象起到有效保护作用,而过高的厚径比不利于材料在实际工程中的推广.以落距为800 mm为例,最大冲击力与厚度关系在橡胶厚度30 mm处为变化趋势的拐点,当厚度小于30 mm时,最大冲击力变化幅值较大为183.61 kN,厚度大于30 mm时,变化幅值较小为19.17 kN.
不同落距下材料变形具有较好的相似性,因此,限于篇幅仅分析在落距为800 mm,前5 ms内采集到的最大变形位移,如图 12所示.可以看出,材料位移变形量和材料的厚度间呈较好的线性关系,即y=0.129 7x+9.194 9,相关度为0.977 2,因此,可通过巷道围岩变形量确定材料用量,即可知道材料最小变形量.

|
图 12 位移变形量和材料厚度关系 Fig. 12 Relation between displacement deformation and material thickness |
在深部矿山开采中,较小的人工扰动在高应力场叠加作用下,会放大围岩的动力响应,这时吸能材料的耐冲性能有利于支护体系的长期有效.图 13,14为不同厚径比材料分别在落距为1 000和800 mm冲击下,最大冲击力响应随冲击次数增加的变化曲线.

|
图 13 落距1 000 mm最大冲击力与冲击次数关系 Fig. 13 Relation between maximum impact force and number of impacts with drop distance of 1 000 mm |

|
图 14 落距800 mm最大冲击力与冲击次数关系 Fig. 14 Relation between maximum impact force and number of impacts with drop distance of 800 mm |
由图 13,14可以看出,在每组6次重复实验中,第i+1次冲击的最大冲击力响应相比第i次冲击均有或增或减变化,其中i取1~5.这是由于在冲击后高阻尼橡胶材料内部分子链发生了复杂变化,激振力挤压高阻尼橡胶材料使其内部大分子链发生“拉伸-收缩”往返运动,材料发生局部塑性损伤变形,导致材料缓冲性能下降.如在图 13中,橡胶厚径比为0.2,0.3和0.4试样的第6次冲击的最大冲击力不小于第1次,这是由于材料局部受到冲击损伤,使得材料的动力响应大于或等于第1次.但经计算,试样在1到6次冲击中,试验每次冲击力响应峰值比上一次改变幅度在15%以内,说明高阻尼橡胶材料适合作为缓冲材料多次使用.
3.2 厚径比对材料吸能性能的影响分析图 15为不同厚径比高阻尼橡胶材料在高速冲击下应力-应变曲线.可以看出,在相同气压冲击下,厚径比为0.04(厚度2 mm)试样在较小应变处出现应力峰值,反映了厚径较小时对外界激振力响应明显.在厚径比为0.2~1时,不同厚径比试样的应力应变曲线形状相似.且随着厚径比增大应力幅值越小,应力增加幅值越缓慢.

|
图 15 应力-应变曲线 Fig. 15 Stress-strain curves |
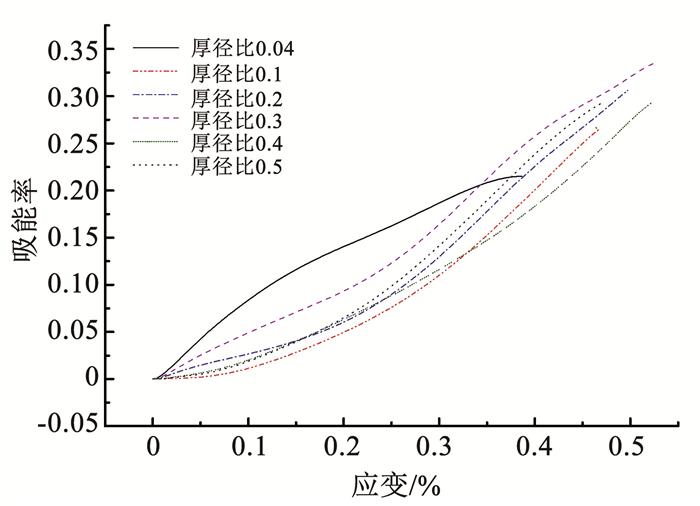
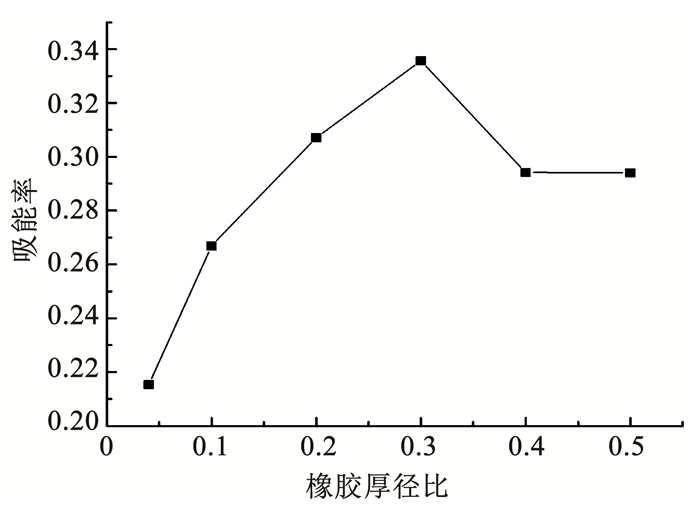
图 16为高阻尼橡胶材料在冲击荷载下材料吸能率E.可以看出,不同厚径比高阻尼橡胶材料受高速冲击荷载作用时,随着应变增加材料吸能率E也随之增大.在应变小于0.33时,厚度为2 mm试样的吸能效率明显大于其他厚度试样.在应变大于0.33时,厚度为15 mm试样的吸能率最大.将图 16中不同材料厚度下最大吸能率提取绘制图 17.可以看出,厚径比为0.3时材料吸能率最大为0.336,说明在相同冲击加载荷载下厚径比为0.3时为最优吸能率.这是由于高阻尼橡胶材料是一种黏弹性体,既有黏性又有弹性和流体的性质.通常采用Ed表示材料每圈耗散能[19],即Ed=(m·π·G2·As·μ02)/h,式中:m为黏弹性层数; As为黏弹性层的剪切面积; h为材料厚度; G2为材料损耗模量,反映材料的耗能性能; μ0为材料的变形位移幅值.对于本试验材料厚度h是影响材料耗能的唯一变量,由于材料吸能能力通常与体积成正比,即在相同作用面积下材料吸能能力随厚度增加呈增大趋势,但在冲击中,黏弹性层太厚会导致材料在振动过程中热量难于散发,从而影响材料实际耗能.
|
图 16 吸能率随应变变化 Fig. 16 Variation of energy absorption rate with strain |
|
图 17 能量吸收率与橡胶厚径比关系 Fig. 17 Relation between energy absorption rate and thickness-diameter ratio of rubber |
为了直观评价材料厚径比缓冲吸能效果,对不同厚度的“橡-岩”组合试样进行SHPB冲击实验.实验后根据花岗岩试样破碎粒径,采用“质量-等效边长筛分法”计算分形维数[20],定量描述花岗岩破碎程度.
“质量-等效边长筛分法”计算等式如下:
| $ \begin{array}{c} D=3-\alpha . \end{array} $ | (8) |
其中
| $ \alpha=\frac{\lg \left(M_{L_{\mathrm{eq}}} / M\right)}{\lg L_{\mathrm{eq}}}. $ | (9) |
式中:D为碎屑的分形维数值; α为lg(MLeq/M)和lg Leq的斜率; MLeq/M为等效边长小于Leq的碎屑百分含量; Leq为碎屑的等效边长; MLeq为直径小于等效边长Leq的碎屑质量; M为试件总质量.
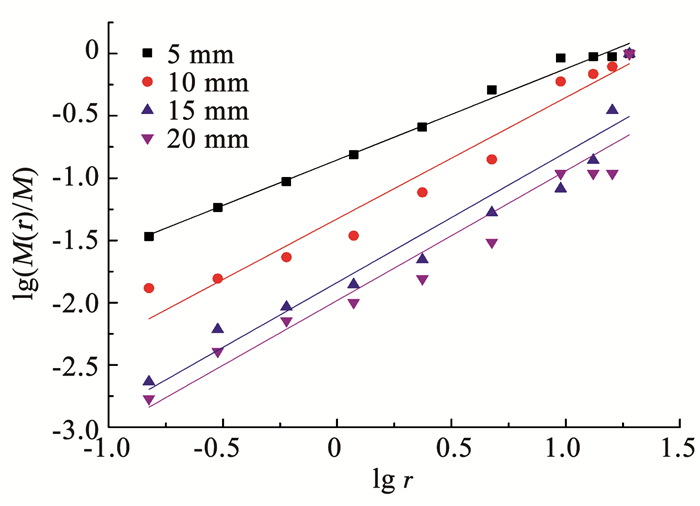
图 18为相同冲击气压下不同“橡-岩”厚度的花岗岩冲击破碎块度曲线.r表示破碎块度粒径.可以看出,在等效边长Leq相同情况下,随着材料厚径比增大,lg(MLeq/M) 的值越小,而且厚径比在0.3~0.4时lg(MLeq/M) 值相差微小.同时,采用式(9)获得岩屑分形维数与橡胶厚度关系见图 19.
|
图 18 冲击破碎块度曲线 Fig. 18 Impact fragmentation curves |

|
图 19 橡胶厚度与分形维数关系 Fig. 19 Relation between rubber thickness and fractal dimensions |
由图 19可以看出,相同冲击条件下材料厚径比越大,花岗岩变形维数越小,而且在厚径比0.3和0.4处发现维数几乎相等.说明随着高阻尼橡胶材料厚径比增大,材料缓冲吸能效果越好,并在厚径比0.3达到材料最佳缓冲吸能.
图 20为不同组合试件的破碎形态.可以直观看出,在相同冲击条件下高阻尼橡胶材料厚度越小,“橡-岩”组合试件的细粒岩屑和微粒岩屑含量越多,而且最大粒径的岩块随厚径比增大块度明显增大,并在厚径比为0.3和0.4处岩屑块度分布相当.

|
图 20 不同组合试件冲击破碎图 Fig. 20 Impact fracture diagram of different composite specimens |
1) 在相同落锤冲击条件下,材料对冲击力响应具有较好的相似性,随着厚径比增大冲击力峰值均呈幂函数趋势递减,并在厚径比0.6处取得最好的缓冲效果.
2) 在6次单独重复落锤冲击中,试样每次冲击力响应峰值相比上一次改变幅度在15%以内,说明高阻尼橡胶材料具有较好的耐冲性,可作为缓冲材料多次使用.
3) SHPB实验结果表明,材料在厚径比0.3处吸能率取得最大值0.336,即0.3为材料最优吸能率.
4) 在组合试样冲击实验中,厚径比表现出显著的缓冲吸能差异性.相同冲击气压下,随着材料厚径比增大,花岗岩破碎分形维数呈幂函数趋势单调减小.在厚径比为0.3处存在分形维数(D)拐点,当厚径比大于0.3时,材料D值变化幅度较小,即在0.3处取得材料最优厚径比.
| [1] |
龙涛, 潘斌, 余斌. 国内外金属矿山地压控制技术研究发展评述[J]. 采矿技术, 2008, 8(3): 58. LONG Tao, PAN Bin, YU Bin. Review of research and development of ground pressure control technology in metal mines at home and abroad[J]. Mining Technology, 2008, 8(3): 58. DOI:10.13828/j.cnki.ckjs.2008.03.016 |
| [2] |
KAISER P K, CAI Ming. Design of rock support system under rockburst condition[J]. Journal of Rock Mechanics and Geotechnical Engineering, 2012, 4(3): 215. DOI:10.3724/SP.J.1235.2012.00215 |
| [3] |
LI C C. A new energy-absorbing bolt for rock support in high stress rock masses[J]. International Journal of Rock Mechanics and Mining Sciences, 2010, 47(3): 396. DOI:10.1016/j.ijrmms.2010.01.005 |
| [4] |
ORTLEPP W D. The design of support for the containment of rockburst damage in tunnels: An engineering approach[M]// KAISER P K, MCCREATH D R. Rock Support in Mining and Underground Construction.[S.l.]: CRC Press, 1992: 593
|
| [5] |
JAGER A J. Two new support units for the control of rockburst damage[M]//KAISER P K, MCCREATH D R. Rock Support in Mining and Underground Construction.[S.l.]: CRC Press, 1992: 621
|
| [6] |
李世民, 李晓军, 徐宝. 新型屈服锚杆发展现状综述[J]. 四川建筑科学研究, 2014, 40(1): 43. LI Shimin, LI Xiaojun, XU Bao. Summarization of the current development state of new yielding bolts[J]. Sichuan Building Science, 2014, 40(1): 43. DOI:10.3969/j.issn.1008-1933.2014.01.011 |
| [7] |
CHARETTE F, PLOUFFE M. Roofex: Results of laboratory testing of a new concept of yieldable tendon[C]// Proceedings of the Fourth International Seminar on Deep and High Stress Mining. Perth: Australian Centre for Geomechanics, 2007: 395. DOI: 10.36487/ACG_repo/711_28
|
| [8] |
张国锋, 于世波, 李国峰, 等. 巨厚煤层三软回采巷道恒阻让压互补支护研究[J]. 岩石力学与工程学报, 2011, 30(8): 1619. ZHANG Guofeng, YU Shibo, LI Guofeng, et al. Research on complementary supporting system of constant resistance with load release for three-soft mining roadways in extremely thick coal seam[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(8): 1619. |
| [9] |
LI C C. Performance of D-bolts under static loading[J]. Rock Mechanics and Rock Engineering, 2012, 45(2): 183. DOI:10.1007/s00603-011-0198-6 |
| [10] |
ANSELL A. Dynamic testing of steel for a new type of energy absorbing rock bolt[J]. Journal of Constructional Steel Research, 2006, 62(5): 501. DOI:10.1016/j.jcsr.2005.08.007 |
| [11] |
JAMES D W. High damping metals for engineering applications[J]. Materials Science and Engineering, 1969, 4(1): 1. DOI:10.1016/0025-5416(69)90033-0 |
| [12] |
DALL'ASTA A, RAGNI L. Experimental tests and analytical model of high damping rubber dissipating devices[J]. Engineering Structures, 2006, 28(13): 1874. DOI:10.1016/j.engstruct.2006.03.025 |
| [13] |
LI Xiudi, MAO Huaiyuan, XU Ke, et al. A SHPB experimental study on dynamic mechanical property of high-damping rubber[J]. Shock and Vibration, 2018, 2018: 3128268. DOI:10.1155/2018/3128268 |
| [14] |
AMIN A F M S, LION A, SEKITA S, et al. Nonlinear dependence of viscosity in modeling the rate-dependent response of natural and high damping rubbers in compression and shear: Experimental identification and numerical verification[J]. International Journal of Plasticity, 2006, 22(9): 1610. DOI:10.1016/j.ijplas.2005.09.005 |
| [15] |
张伟, 郑鹏飞, 刘陈, 等. 动态冲击荷载作用下橡胶材料吸能率分析[J]. 兵器材料科学与工程, 2012, 35(5): 19. ZHANG Wei, ZHENG Pengfei, LIU Chen, et al. Energy absorption ratio of rubber material under dynamic impact load[J]. Ordnance Material Science and Engineering, 2012, 35(5): 19. DOI:10.3969/j.issn.1004-244X.2012.05.005 |
| [16] |
顾红军, 赵国志, 张海波, 等. 高聚物复合材料动力学性能实验研究[J]. 材料科学与工程, 2002, 20(4): 537. GU Hongjun, ZHAO Guozhi, ZHANG Haibo, et al. Experimental study of the dynamic properties of high polymer complex material[J]. Materials Science & Engineering, 2002, 20(4): 537. DOI:10.3969/j.issn.1673-2812.2002.04.019 |
| [17] |
宋力, 胡时胜. SHPB数据处理中的二波法与三波法[J]. 爆炸与冲击, 2005, 25(4): 368. SONG Li, HU Shisheng. Two-wave and three-wave method in SHPB data processing[J]. Explosion and Shock Waves, 2005, 25(4): 368. DOI:10.3321/j.issn:1001-1455.2005.04.014 |
| [18] |
MILTZ J, GRUENBAUM G. Evaluation of cushioning properties of plastic foams from compressive measurements[J]. Polymer Engineering and Science, 1981, 21(15): 1010. DOI:10.1002/pen.760211505 |
| [19] |
周云, 徐赵东, 邓雪松. 粘弹性阻尼器的性能试验研究[J]. 振动与冲击, 2001, 20(3): 71. ZHOU Yun, XU Zhaodong, DENG Xuesong. Experimental study on properties of viscoelastic dampers[J]. Journal of Vibration and Shock, 2001, 20(3): 71. DOI:10.13465/j.cnki.jvs.2001.03.022 |
| [20] |
易顺民, 唐辉明. 三轴压缩条件下三峡坝基岩石破裂的分形特征[J]. 岩土力学, 1999, 20(3): 24. YI Shunmin, TANG Huiming. The fractal characteristics of fracture of dam foundation rock under triaxial compression in the Three Gorges Project[J]. Rock and Soil Mechanics, 1999, 20(3): 24. DOI:10.3969/j.issn.1000-7598.1999.03.005 |
 2021, Vol. 53
2021, Vol. 53


