2. 中铁第一勘察设计院集团有限公司,西安 710043;
3. 北京交通大学 土木建筑工程学院,北京 100044
2. China Railway First Survey and Design Institute Group Co., Ltd., Xi'an 710043, China;
3. School of Civil Engineering, Beijing Jiaotong University, Beijing 100044, China
近年来,由于可利用的中浅层地下空间日趋饱和,盾构掘进面临着更复杂的施工环境与更多变的障碍限制,既有建构筑物的地下桩基、连续墙等成为了盾构掘进路线中愈发常见的障碍物[1-2],从而造成原本用来切削土体的盾构机软土刀具承担切削混凝土的任务.如沈阳地铁1号线、上海轨道交通9、10号线、天津地铁9号线、苏州轨道交通2号线等盾构法施工中都遇到了需要盾构直接破除桥梁、建筑物桩基等混凝土障碍的难题[3-4],这对切刀等软土刀具的可靠性及耐久性提出了更高的要求.盾构刀具的磨损程度对盾构机的正常运行、施工进度及工程成本有重要影响[5],因此,进行刀具设计时须充分考虑软土刀具可能遇到的切削混凝土障碍的工况.研究软土切刀切削混凝土时的动态响应规律可为刀具参数设计提供重要依据,同时,切刀的几何形状、行进参数对盾构机的掘进效率具有重要影响,合理设置相关参数可以有效减小刀具受力,增加刀具行进中的稳定性,降低刀盘旋转的功率负担,减小刀具损坏的几率,延长刀具的使用寿命.
现阶段对于刀具切削作用的研究多集中在数值模拟方面,有学者采用有限元[6-7]、离散元[8-11]手段研究盾构刀具切削力的变化,而切削硬质材料的试验研究主要集中在金属切削和破岩掘进方面.1985年,Ranman等[12]提出了一种锥形刀具在岩石中的实测切削力模型,指出刀具与岩体的接触是以点接触并局部压碎的方式进行,刀具和岩石储存弹性能量并随着切削力增长而增大,直至岩体破碎.王成勇等[13]通过刨床试验详细研究了花岗岩、大理石和辉绿岩的切削性质,指出刀具的切削速度对切削力的影响可以忽略,并指出切削力随岩石材料肖氏硬度的增大而增大.张程焱等[14]考虑了切削刀具的刀刃钝圆度和前后角面摩擦系数因素,建立了预测金属切削刀具受力的局部摩擦因数模型,指出切削速度和刀具前角越大,切削力越小,切削深度增大时,刀具切削力明显增大.Copur等[15]发现在采用锥形刀具切削硬岩时,双螺旋方式比单螺旋方式和三螺旋方式的刀具侧向力低很多,其切削比能比单螺旋时降低了25%,但在软岩和中强度岩石并无太多影响.Rostamsowlat等[16]通过对石灰岩和砂岩进行切削试验指出磨损平面的粗糙度对切削力和磨损系数的影响比较大,切削速度对切削力和磨损系数无影响,在塑性状态下,切削深度对切削力的影响很大.
国内外学者在刀具切削硬质材料方面取得了显著的研究成果,但主要以破岩掘进和金属切削时刀具受力为出发点,针对软土盾构刀具切削混凝土材料的刀具受力问题研究较少.本文基于盾构切削实验平台,根据盾构切刀切削混凝土试块的试验结果,得出了刀具行进过程中切削力的动态响应规律,以期为穿越混凝土障碍物时盾构刀具参数设计和施工掘进参数控制提供一定的参考依据.
1 盾构切削试验原理及试验方案 1.1 盾构切削机试验原理本试验采用的盾构刀具切削机主要由切削机框架结构、液压系统、控制系统和数据采集系统4大部分构成.图 1为盾构刀具切削机连接示意图及实物图.数据采集系统由两个XM2088型压力变送器和1个50XAJ型号的无纸记录仪组成.压力变送器量程为0~12 MPa,输出电流为4~20 mA,两个压力变送器之间并联,并分别串联到无纸记录仪上的通道1和通道2.无纸记录仪最快记录间隔时间为0.25 s.刀具切削时所需的切削力由2只液压千斤顶提供,千斤顶内液压油的压强信号通过压力变送器转换为电信号,最终传到无纸记录仪被记录为可利用的数据.

|
图 1 盾构刀具切削机连接示意图及实物图 Fig. 1 Connection diagram and photograph of shield cutter cutting machine |
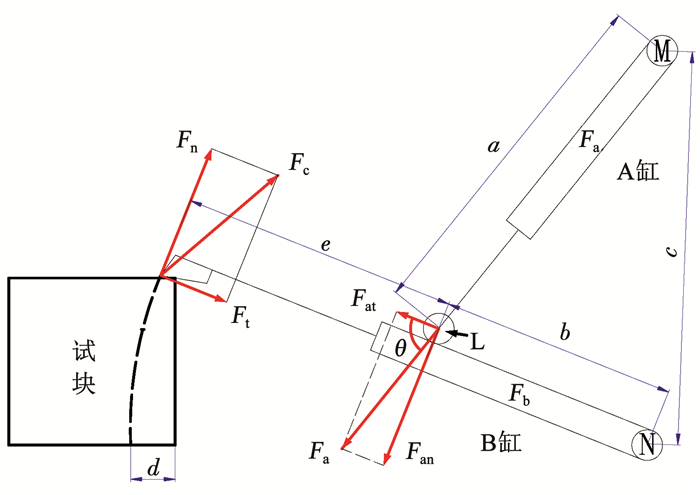
盾构刀具切削时的受力是一个动态过程,刀具直接承受与岩体碰撞产生的突变荷载.在切削试验过程中,切刀做圆周运动.将两个液压千斤顶简化为杆件,刀具简化为受力点,则刀具切削机受力简图如图 2所示.M、N、L分别为3处铰接轴心,a、b、c、e代表各点间长度,其中a、e由于千斤顶伸缩为可变化量,b、c为定值.d为切削深度,在每次试验过程中,根据设计的d值调整千斤顶伸缩量e,并将其固定.伸出Fc为盾构刀具的实际切削力,垂直液压千斤顶B缸方向和沿着B缸方向分解得到刀具法向切削力Fn和刀具切向切削力Ft.同理A缸的受力Fa沿B缸方向和垂直B缸方向可分解为Fat和Fan,Fa与Fat的夹角为θ.整个切削过程中,B缸固定,A缸以恒定速度伸出,故夹角θ为变化量.通过数据采集可得到两只千斤顶的顶推力Fa、Fb,由受力分析可知,Ft=Fb,Fn为
| $ F_{\mathrm{n}}=\frac{F_{\mathrm{an}} b}{b+e}=\frac{F_{\mathrm{a}} b \sin \theta}{b+e}. $ | (1) |
|
图 2 盾构刀具切削机受力分析简图 Fig. 2 Stress analysis diagram of shield cutter cutting machine |
式中θ可根据余弦定理由a、b、c组成的三角形求得
| $ \begin{array}{c} \theta=\arccos \left(\frac{a^{2}+b^{2}-c^{2}}{2 a b}\right), \end{array} $ | (2) |
| $ a=a_{0}+v_{\mathrm{a}} t $ | (3) |
式中:a0为切削前A缸的初始长度; va为A缸伸出速率,所有试验组va设置为8 mm/s; t为切削时间.
在切削试验过程中,切刀的切削路径为圆弧,与实际盾构掘进时切刀所做的等间距螺旋线运动存在一定差异.鉴于室内试验中难以模拟实际工程尺寸下的刀具运动,现有学者的研究多采用数值模拟方法[6-7, 10-11].同时,切刀在破除桩基等混凝土障碍时并非连续性切削,而是以间断的方式进行冲击切削.研究的重点为切削过程中动态切削力的测量,因此,在试验设计中,对切削轨迹进行了适当简化.在切削速度方面,A缸以8 mm/s的速度伸出,切刀以近似匀速的切削速度行进,由非匀速切削产生的切削力误差完全可被忽略.
1.2 试验材料试验以文献[17]给出的配合比配制强度为M2.5、M5、M7.5和M15的4组水泥砂浆立方体试件作为混凝土模拟材料,试件尺寸为200 mm×200 mm×200 mm,经过如图 3所示的单轴压缩试验和劈裂抗拉试验等力学性能试验得到试件的基本力学参数,如表 1所示.

|
图 3 力学性能试验 Fig. 3 Mechanical properties test |
| 表 1 各组水泥砂浆试件强度统计 Tab. 1 Strength of cement mortar test blocks |
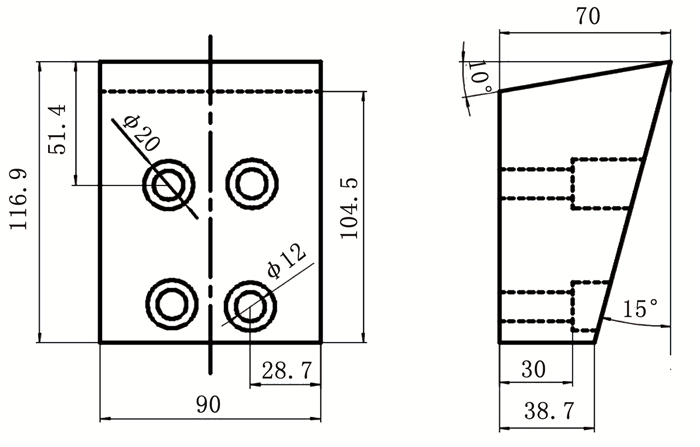
为研究切刀几何参数对破岩过程的作用,试验共制作了7把刀具,各刀具几何参数如表 2所示.以刀具2的几何参数作为对照试验中的不变量,采用单因素法分别对刀具前角、后角和形状展开研究,刀具2的几何尺寸如图 4所示,试验所用全部刀具如图 5所示.
| 表 2 刀具参数 Tab. 2 Parameters of tools |
|
图 4 刀具2的尺寸(单位:mm) Fig. 4 Dimensions of cutter 2 (unit: mm) |

|
图 5 刀具试验组对比 Fig. 5 Contrast of shield cutter test groups |
影响切削过程中切刀受力动态响应的主要参数包括前角、后角和形状等刀具几何参数,被切削体抗压强度fcu,切削深度d.其中,切削深度d为切削开始时刀尖到水泥砂浆试块外边缘的距离,切削速度v为刀尖处的线速度.为分析各主要参数对破岩效果的影响,采用表 3所示参数值展开试验,黑体参数是被选为对照组的不变量.
| 表 3 切刀切削效果影响因素 Tab. 3 Influencing factors of cutters |
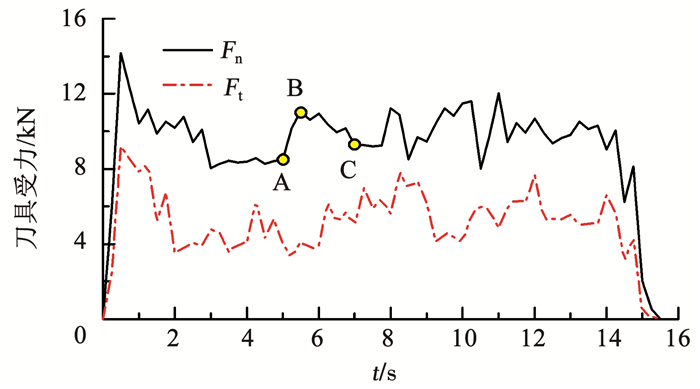
图 6为2号刀具,fcu=7.42 MPa,d=10 mm,v=8 mm/s试验所得刀具受力动态变化过程,整个切削过程刀具受力波动时间大致为16 s,以此为例,分析刀具所受法向切削力与切向切削力变化规律.
|
图 6 刀具法向切削力和切向切削力变化 Fig. 6 Changes of normal cutting force and tangential cutting force of cutter |
在0~1 s,刀具初次接触试件,二者间产生较为强烈的冲击碰撞作用,法向和切向受力均急剧上升; 继续切削,岩块崩落后,刀具受力急剧下降; 整个过程中,刀具与试件之间产生数个接触、切削、剥落的循环,法向和切向切削力均表现出维持在一个固定值附近的反复波动; 待到14~16 s,切削接近结束时,由于试件下部存在临空面,容易出现刀具将试件整块剥落的现象,此后刀具受力骤降到0附近.总体上刀具的切削力波动随时间呈现梯形变化.
刀具对每块水泥砂浆碎屑进行挤压和张拉作用,导致了砂浆试块碎屑的随机剥落,因此,刀具切削力呈现出多个上升和回落的循环过程.以图 6中一个波动循环A—B—C为例进行微观分析.
A点:刀具与该循环内的砂浆块体发生碰撞并开始产生挤压;
A—B段:随着刀具继续切削,试件和刀具之间的挤压作用逐渐加深,刀具受力逐渐增大,接触部分的试块被刀具压实,并产生裂缝;
B点:刀具受力达到该循环的最大值,试件上的裂缝发生贯穿,此时局部试件已经被剥离母体,形成即将剥离的碎屑;
B—C段:刀具继续进行切削,对试件碎屑进行张拉,并剥离母体;
C点:碎屑完全剥离,刀具与新的循环内的试块产生碰撞.
2.2 刀具几何参数对切削力的影响基于上节中对切刀受力的动态分析可知,混凝土试块在切削过程中经历“接触、挤压、压碎、剥离”的破坏周期,因此,切削力始终处于波动循环中.为更清晰地展示切削过程中切削力的波动性及分散程度,对每组数据进行统计分析,并将结果绘制成箱形图(box-plot).箱形图中表述的统计量包括最大值、最小值、上下四分位数Q3和Q1、平均值、中位数、上下边缘值.上下四分位数Q3和Q1的差值被称为四分位距IQR,即IQR=Q3-Q1.由于在切削初始及临近切削结束时,刀具受力陡然变化,此时的切削力值并不具有普遍的参考价值,这些值被认为是数据组中的异常值.异常值被定义为小于Q1-1.5IQR或大于Q3+1.5IQR的值.从上下四分位数Q3和Q1两端向外各画一条线段直到不是异常值的最远数值点,表示该批数据正常值的分布区间,也称上下边缘值.上下边缘值及上下四分位数的区间大小反应了刀具受力的波动情况.
图 7为不同刀具前角下的切削力统计.随着刀具前角角度增大,Fn和Ft均值呈现减小趋势,前角每增加5°,Fn和Ft均值减小1~2 kN,均值减小量并不显著.但前角变化对Fn和Ft的波动性造成显著影响,前角越小,波动性越强,Fn和Ft的上边缘值及上四分位数越大,下四分位数则基本不变.

|
图 7 不同刀具前角因素下的切削力统计 Fig. 7 Cutting force box-plot under different tool rake angles |
图 8为切削得到的试块碎屑.可以看出,随着刀具的前角增大,碎屑粒径不断增大.原因是刀具前角增大,刀尖变得锋利,在切削时切刀切入试件更容易,对试件的拉剪效果更明显,则刀具受力值及波动性减小,碎屑以片状为主.而刀具前角太小,切削时主要以压碎试件为主,试块的抗拉强度远小于其抗压强度,所以,刀具受力值及波动性较大,碎屑以粉末状为主.

|
图 8 不同前角因素下的试件碎屑 Fig. 8 Debris of test blocks under different tool rake angles |
图 9为不同刀具后角下的切削力统计.刀具后角的变化对Fn和Ft的影响较小,3组刀具受力均值基本相同,四分位值区间差距较小,而后角为0°时Fn的边缘值区间较大,这是因为此时后刃面与试块产生一定的摩阻力,摩阻力方向与Fn相同,其大小随刀具运动而产生波动.整体来看,虽然随着后角的增大,刀尖变得锋利,但试件与刀具的接触均发生在前刃面,试件碎屑破碎后沿前刃面运动,因此,刀具的破岩任务主要由前刃面来承担,而后角对刀具受力及波动性基本无影响.

|
图 9 不同刀具后角因素下的切削力统计 Fig. 9 Cutting force box-plot under different tool clearance angles |
图 10为不同刀具形状下的切削力统计.从Fn和Ft的均值和波动性来看,3种刀具的受力情况无明显差别.在切削深度为10 mm时,直线形、圆弧形和三角形切刀与试件的接触边界长分别为110,114.45,113.32 mm,三者数值接近,因此,在刀具受力响应上基本相同.

|
图 10 不同刀具形状因素下的切削力统计 Fig. 10 Cutting force box-plot under different tool shapes |
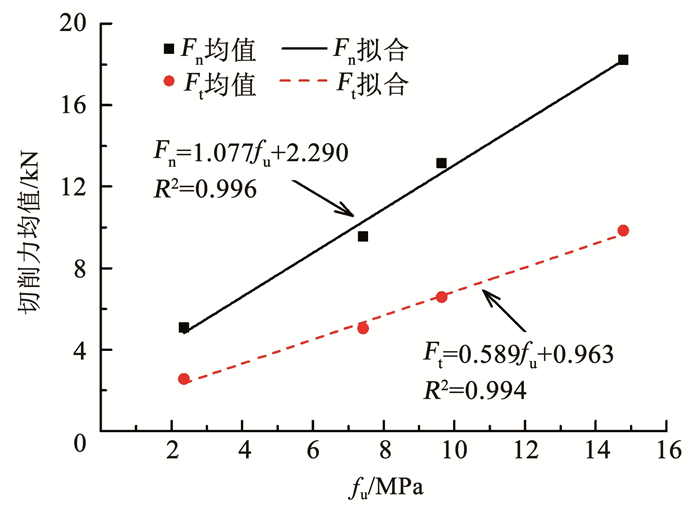
图 11为不同试件强度fu下的切削力统计.Fn和Ft的均值随fu增大而增大,4组数据的波动性并无明显差异,四分位值区间及上下边缘值区间的大小基本相同.因此,在试验设计的试件强度范围内,fu仅会影响切削力的大小,对切削力的波动性几乎没有影响.图 12为Fn和Ft的均值与fu的线性拟合结果.线性拟合的可决系数R2均大于0.99,表明在其他切削影响因素固定的情况下,Fn和Ft的均值随fu线性增长,并且Fn的增长率高于Ft.

|
图 11 不同试件强度fu下的切削力统计 Fig. 11 Cutting force box-plot under different specimen strengths fu |
|
图 12 切削力均值与试件强度fu的关系 Fig. 12 Relation between mean cutting force and specimen strength fu |
图 13为不同强度试件的切削碎屑对比.可以看出,fu越高,切削碎屑的完整性越好,碎屑尺寸越大.在刀具几何因素及切削因素相同的条件下,试块发生破坏的模式相同,强度值fu越高,代表混凝土中颗粒间黏结力越高,在刀具的剪切和挤压作用下,仅剪切面处因拉应力较高试块发生剥离,碎屑本身不易破碎; 而fu较低的试块,颗粒间黏结力低,切削碎屑因刀具挤压而破碎呈粉末或细块状.

|
图 13 不同试件强度fu下的切削碎屑对比 Fig. 13 Debris of test blocks under different specimen strengths fu |
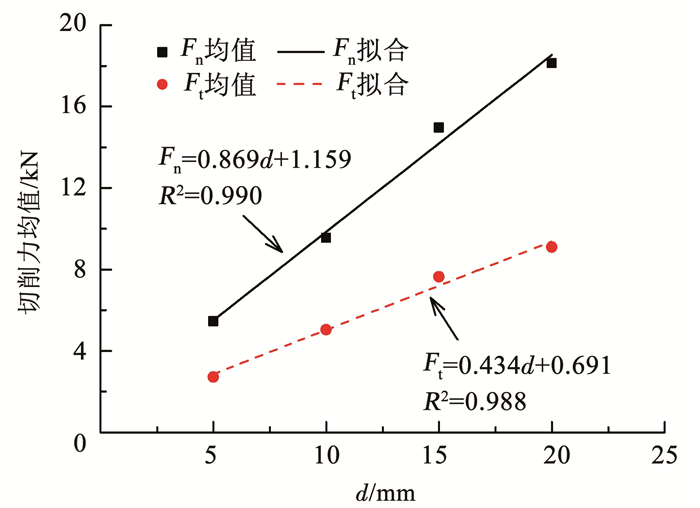
图 14为不同切削深度d下的切削力统计.图 15为Fn和Ft的均值与fu的线性拟合结果.由图可知,d对切削力影响较大,Fn和Ft的均值随d增大而线性增大,文献[18]给出了相同的结论.d对Ft的波动性没有明显影响,但当d>15 mm时,Fn波动性明显增加.一方面,随着d值增加,切刀侧面与试块的摩擦面积增大,刀具侧面受到的摩阻力增大; 另一方面,d值增加导致试块碎屑发生断裂时的不确定性增大,产生的碎屑粒径更大.摩阻力和大块碎屑的存在增大了刀具切削动作的不稳定性,刀具在小幅跳动中完成切削,因此,Fn产生较大波动.

|
图 14 不同切削深度因素下的切削力变化 Fig. 14 Cutting force box-plot under different cutting depths d |
|
图 15 切削力均值与切削深度d的关系 Fig. 15 Relation between mean cutting force and cutting depth d |
图 16为不同切削深度d下的切削碎屑对比.在切削过程中,刀尖扫略过破坏面附近的碎屑因刀尖挤压呈粉末状,而远离刀尖的试块临空面碎屑仅是由于时间张拉破坏而剥落,其完整性较好,因此,4组结果中均有粉末状碎屑分布,d值越大,碎屑中片状碎屑的尺寸越大.

|
图 16 不同切削深度d下的碎屑对比 Fig. 16 Debris of test blocks under different cutting depths d |
切削混凝土过程中刀具切削力始终处于动态波动中,前文分析了各影响因素下Fn和Ft在数值上的响应规律.事实上,Fn和Ft并非独立存在,如图 6所示,二者在数值波动性上具有一定的相关性.以图 7所示的对照组数据为例,以Fn为纵轴,Ft为横轴,将这批数据中的正常值绘制于图 17中,数据点的极坐标代表这一时刻1号切刀切削力的大小和方向.结果表明,刀具切削力在方向上的波动并不是杂乱无序的,数据点集中分布在ρ∈[ρ1, ρ2],θ∈[θ1, θ2]的扇面形区域内.扇面形区域的面积为
| $ \begin{aligned} S=& \iint_{S} \rho \mathrm{d} \rho \mathrm{d} \theta=\int_{\theta_{1}}^{\theta_{2}} \mathrm{~d} \theta \int_{\rho_{1}}^{\rho_{2}} \rho \mathrm{d} \rho=\\ & \frac{\left(\rho_{2}^{2}-\rho_{1}^{2}\right)\left(\theta_{2}-\theta_{1}\right)}{2}. \end{aligned} $ | (4) |

|
图 17 对照组数据的极坐标表示 Fig. 17 Polar coordinates of control group data |
式中:ρ1、ρ2分别为切削力大小的上下限,kN; θ1、θ2分别为切削力方向弧度值的上下限.S值反映了切削力的波动性大小.
按照图 17所述方法,将刀具型式、试件强度、切削深度3个影响因素下试验结果的极坐标表示进行统计,如表 4所示.就刀具型式而言,3号刀具切削过程中ρ值较小且S值最小,对保证刀具强度和可靠性更有利.就试件强度fu,随着fu值增加,ρ1、ρ2值均增大,ρ值区间长度基本不变,始终在7~8 kN,θ值区间长度减小,面积S值变化不大.表明fu值对切削力大小上的波动基本无影响,同时,fu越大,切削力在方向上的波动越小.就切削深度d而言,d值越大,ρ1、ρ2、S值越大,ρ值区间长度越大,θ值区间长度越小.表明随着d值增大,切削力增大,切削力大小上的波动性变大,切削力方向上的波动变小.文献[11]得到的切深6 mm时法向力和切向力的时程变化,通过计算得出θ在1.1~1.35波动,与本文结果相类似.
| 表 4 各组试验结果的极坐标范围统计 Tab. 4 Polar coordinates range of test results |
1) 在切削混凝土过程中,刀具受力始终处于瞬态波动中,切削力因试块碎屑的随机剥落而呈现上升和回落的循环,1个大循环由数个小循环组合而成.切削力的大小及波动性与刀具型式、试件强度和切削深度3个因素均有关系.
2) 切刀前角越大,破岩时对试件的拉剪效果越明显,切削力及波动性均越小,前刃面承担主要破岩任务.切刀后角对切削力的影响并不明显,后角为0°时,切刀后刃面会产生明显的法向摩阻力,造成法向力及其波动性增大.3种形状的刀具在切削力表现上并无明显差异,直线型刀具在切削力稳定性上略优于圆弧型及三角型刀具.
3) 切削力与试件强度、切削深度均呈线性关系,试件强度和切削深度越大,切削力越大,切削力方向上的波动性越小.切削力大小上的波动与试件强度基本无关,但随切削深度增大而增大.
4) 切削后的碎屑粒径与刀具前角、试块强度、切削深度有关.前角越小,试件以挤压破坏为主,碎屑粒径越小.试块强度决定试块颗粒间的黏结力及碎屑的完整程度,因此,强度越高,碎屑越完整.刀尖附近的试块因挤压而破碎,而远离刀尖处的试块仅发生简单的剥离,因此,切削深度越大,因剥离而产生的碎屑粒径越大,而刀尖处碎屑均呈粉末状.
| [1] |
程康, 夏唐代, 梁荣柱, 等. 盾构开挖下邻近既有桩基的竖向响应分析[J]. 岩土工程学报, 2018, 40(增刊2): 42. CHENG Kang, XIA Tangdai, LIANG Rongzhu, et al. Vertical response analysis of adjacent existing single pile under tunneling[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(S2): 42. |
| [2] |
曹宝飞, 朱逢斌. 盾构隧道邻近地下连续墙围护结构施工影响研究[J]. 防灾减灾工程学报, 2017, 37(6): 931. CAO Baofei, ZHU Fengbin. The impact due to shield tunnel adjacent the existing foundation pit[J]. Journal of Disaster Prevention and Mitigation Engineering, 2017, 37(6): 931. DOI:10.13409/j.cnki.jdpme.2017.06.011 |
| [3] |
袁大军, 王飞. 盾构切削大直径钢筋混凝土群桩的理论与实践[M]. 北京: 科学出版社, 2017. YUAN Dajun, WANG Fei. Theory and practice of shield cutting large diameter reinforced concrete piles[M]. Beijing: Science Press, 2017. |
| [4] |
王飞. 盾构直接掘削大直径钢筋混凝土群桩研究[D]. 北京: 北京交通大学, 2014 WANG Fei. Study on shield cutting large diameter reinforced concrete piles directly[D]. Beijing: Beijing Jiaotong University, 2014 |
| [5] |
LI Xingchun, LI Xinggao, YUAN Dajun. Application of an interval wear analysis method to cutting tools used in tunneling shields in soft ground[J]. Wear, 2017, 392: 21. DOI:10.1016/j.wear.2017.09.010 |
| [6] |
夏毅敏, 薛静, 周喜温. 盾构刀具破岩过程及其切削特性[J]. 中南大学学报(自然科学版), 2011, 42(4): 954. XIA Yimin, XUE Jing, ZHOU Xiwen. Rock fragmentation process and cutting characteristics on shield cutter[J]. Journal of Central South University (Science and Technology), 2011, 42(4): 954. |
| [7] |
刘伟. 盾构机刀具切削的三维数值模拟研究及刀盘的有限元分析[D]. 秦皇岛: 燕山大学, 2013 LIU Wei. Three dimensional numerical simulation of shield machine tool cutting process and finite element analysis of the cutterhead[D]. Qinhuangdao: Yanshan University, 2013 |
| [8] |
ROJEK J, OÑATE E, LABRA C, et al. Discrete element simulation of rock cutting[J]. International Journal of Rock Mechanics & Mining Sciences, 2011, 48(6): 996. DOI:10.1016/j.ijrmms.2011.06.003 |
| [9] |
MOON T, OH J. Astudy of optimal rock-cutting conditions for hard rock TBM using the discrete element method[J]. Rock Mechanics and Rock Engineering, 2012, 45(5): 837. DOI:10.1007/s00603-011-0180-3 |
| [10] |
张旭辉, 谭青, 夏毅敏, 等. 盾构切刀切削软岩特性研究[J]. 现代隧道技术, 2015, 52(5): 184. ZHANG Xuhui, TAN Qing, XIA Yimin, et al. Cutting performance of shield cutters in soft rock[J]. Modern Tunnelling Technology, 2015, 52(5): 184. DOI:10.13807/j.cnki.mtt.2015.05.028 |
| [11] |
谭青, 徐孜军, 夏毅敏, 等. 盾构切刀作用下岩石动态响应机制的数值模拟研究[J]. 岩土工程学报, 2013, 35(2): 235. TAN Qing, XU Zijun, XIA Yimin, et al. Numerical simulation of dynamic response mechanism of rock by shield machine cutters[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(2): 235. |
| [12] |
RÅNMAN K E. A model describing rock cutting with conical picks[J]. Rock Mechanics and Rock Engineering, 1985, 18(2): 131. DOI:10.1007/BF01019602 |
| [13] |
王成勇, 刘培德, 胡荣生, 等. 岩石切削力研究[J]. 大连理工大学学报, 1991, 31(1): 53. WANG Chengyong, LIU Peide, HU Rongsheng, et al. Study of rock cutting force[J]. Journal of Dalian University of Technology, 1991, 31(1): 53. |
| [14] |
张程焱, 张发平, 杨瑞生, 等. 基于局部摩擦因数模型的切削力预测建模[J]. 北京理工大学学报, 2018, 38(1): 6. ZHANG Chengyan, ZHANG Faping, YANG Ruisheng, et al. Predictive modeling of cutting force based on local friction coefficient model[J]. Transactions of Beijing Institute of Technology, 2018, 38(1): 6. DOI:10.15918/j.tbit1001-0645.2018.01.002 |
| [15] |
COPUR H, BILGIN N, BALCI C, et al. Effects of different cutting patterns and experimental conditions on the performance of a conical drag tool[J]. Rock Mechanics and Rock Engineering, 2017, 50(6): 1585. DOI:10.1007/s00603-017-1172-8 |
| [16] |
ROSTAMSOWLAT I. Effect of cutting tool properties and depth of cut in rock cutting: An experimental study[J]. Rock Mechanics and Rock Engineering, 2018, 51(6): 1715. DOI:10.1007/s00603-018-1440-2 |
| [17] |
中华人民共和国住房和城乡建设部. 砌筑砂浆配合比设计规程: JGJ/T 98—2010[S]. 北京: 中国建筑工业出版社, 2010 Ministry of Housing and Urban-Rural Development of the People's Republic of China. Specification for mix proportion design of masonry mortar: JGJ/T 98—2010[S]. Beijing: China Architecture and Building Press, 2010 |
| [18] |
夏毅敏, 黄利辉, 周喜温, 等. 盾构切刀切削岩土的试验研究[J]. 矿山机械, 2010, 38(1): 15. XIA Yimin, HUANG Lihui, ZHOU Xiwen, et al. Experimental research on the shield cutter's cutting stones[J]. Mining and Processing Equipment, 2010, 38(1): 15. |
 2021, Vol. 53
2021, Vol. 53


