据美国空间监测网站给出的数据,截至2013年,地球轨道上尺寸大于10 cm的可编目空间物体数量已超过16 000多个.针对日益增多的空间物体,在轨卫星在进行变轨机动时,需对大量空间物体进行高精度的轨道预报计算,以预防在轨航天器与其他空间天体的碰撞.由于卫星高精度的轨道模型具有较高的计算复杂度,而目前计算机上常用的CPU(Central Processing Unit)处理器仅能进行串行计算,进行轨道预报需消耗大量的时间,难以满足军事上及民用上卫星的快速响应需求,因此有必要对轨道模型计算加速方法展开研究.如表 1所示为各类星载计算机的CPU型号与性能参数.
| 表 1 On board computer(OBC)及CPU参数 Tab. 1 On board computer (OBC) and CPU parameters |
对此,国内外都进行了相关的研究.计天阳[1]采用模块化加速方法及英伟达公司提供的CUDA库,配套GPU(Graphics Processing Unit)对SGP4/SDP4轨道模型进行了加速试验,填补了国内在轨道模型GPU并行加速领域研究的空白. Liu等[2]利用GPU并行计算加速方法进行大量空间碎片的轨道预报,通过PMC简化模型(The global point mascon model),可进行15 000颗空间碎片轨道的并行计算,其精度较SGP4/SDP4低,运算速度快,加速比可达10~15倍. Lin等[3]基于CUDA的并行架构,采用块分解算法,对空间碎片进行分批次处理,相邻批次的计算和数据传输操作互相交叠.基于此算法,150个飞行器3 d内的碰撞预报不超过3 h,在大型高性能GPU显卡上计算速度可达CPU加速的30倍.郭松等[4]在FPGA平台上设计并实现了基于VLIW的SGP4/SDP4轨道预报加速器,在单片FGPA上用8个处理单元组成计算阵列,采用指令级并行和任务级并行相结合的方式,将轨道预报速度提升到了CPU的8倍以上.冯森[5]利用CUDA并行架构和GPU硬件作为CPU的协处理器,实现了SGP4轨道预报模型计算时间的大幅缩小,实验结果证明其加速比达到15倍.综上所述,卫星轨道预报并行递推面临解算速度以及解算精度这两个相互冲突的问题,也即如何在保证解算速度的同时尽可能的提高轨道预测精度.目前精度较高的解算方法都为外推法,如四阶龙格库塔法以及HPOP高精度外推模型[6].但由于外推法计算量极大,且其外推的特点在保证精度的同时却无法进行并行计算,外推法难以应用于快速解算之中. 因此,本文基于SGP4/SDP4模型,考虑摄动模型的高精度性质及解析特性,即同一卫星在不同时间点的轨道模型解可独立解得,符合并行计算的特点,提出GPU并行计算方法,使不同卫星的星历、同一颗星不同时间点的星历在不同的线程中同步计算,以达到数倍于CPU处理器速度的加速效果.
Lin等[3]和冯森[5]都在高性能工作站上进行并行解算实验,加速性能达到较高程度.本文拟在小型板卡NVIDIA TX2上完成并行轨道模型加速解算的部署与优化,大大有利于推进基于GPU的卫星轨道并行计算的学术研究与工程应用.
1 轨道预报模型轨道预报是指已知卫星某一时刻位置、速度状态,根据卫星的动力学微分方程来预测卫星未来一段时间内的位置和速度.为了表示卫星的位置、速度信息,北美防空司令部(The north amerian aerospace defense command,NORAD)开发了双行元(two-line element,TLE)[7].其综合考虑了大气阻力、日月引力的长期和周期摄动、地球扁率等影响.TLE作为平均根数,使用特定的方法消除了周期扰动项,解算时必须使用同样的方法重构,因此TLE只适用于特定的轨道预报模型.
针对不同轨道高度的空间目标,NORAD开发了与TLE相应的近地或深空模型,目前定期更新的TLE针对的模型是SGP4/SDP4模型. SGP4模型(Simplified general perturbation version 4)能够对轨道高度较低或绕地飞行周期小于225 min的航天器进行轨道预报,SDP4模型(Simplified deep space perturbation version 4)能够对轨道高度较高或绕地飞行周期大于225 min的航天器进行轨道预报. SGP4/SDP4模型预报精度较高,模型为解析模型,计算复杂度较递推模型低,综合性能高,因此其在卫星轨道预报领域被人们广泛使用[8-9].
SGP4预报模型解算采用解析法,需要将输入数据转换为初始轨道位置.由于TLE中采用平均运动,解算时需要将其重新转换为半长轴,转换方法与正常轨道根数转换方法有差异.
首先,求解平均运动对应半长轴, 即
| $ a_{1}=\left(\frac{\mu}{n_{0}}\right)^{\frac{2}{3}}. $ | (1) |
式中:μ为地球引力常数; n0为平均运动.
J2摄动下的轨道倾角和偏心率分别为:
| $ \delta_{1}=\frac{3}{2} \frac{k_{2}}{a_{1}^{2}} \frac{\left(3 \cos ^{2} i_{0}-1\right)}{\left(1-e_{0}^{2}\right)^{3 / 2}}, $ | (2) |
| $ a_{0}=a_{1}\left(1-\frac{1}{3} \delta_{1}-\delta_{1}^{2}-\frac{134}{81} \delta_{1}^{3}\right). $ | (3) |
式中:k2=0.5J2aE2,J2为地球二阶引力带谐波项; i0、e0分别为平均轨道倾角和平均偏心率.
由此,对半长轴进行修正:
| $ \delta_{0}=\frac{3}{2} \frac{k_{2}}{a_{0}^{2}} \frac{\left(3 \cos ^{2} i_{0}-1\right)}{\left(1-e_{0}^{2}\right)^{3 / 2}} , $ | (4) |
| $ n_{0}^{\prime}=\frac{n_{0}}{1+\delta_{0}} , $ | (5) |
| $ a_{0}^{\prime}=\frac{a_{0}}{1-\delta_{0}}. $ | (6) |
式中:a′0、n′0分别为改进的半长轴和周期参数[10-11].
对于低轨道卫星,即地心距小于98 km,SGP4功率函数中常变量s的表达式为
| $ s=\frac{20}{R_{\oplus}}+a_{E} \text { . } $ | (7) |
计算出如下参数:
| $ \theta=\cos i_{0}, $ | (8) |
| $ \zeta=\frac{1}{a_{0}^{\prime \prime}-s}, $ | (9) |
| $ \eta=a_{0}^{\prime \prime} e_{0} \zeta. $ | (10) |
利用初始参数,进行SGP4轨道预报模型的递推求解.SGP4模型包含大气阻力摄动、非球形轨道摄动、长周期摄动项和短周期摄动项的计算[12].对于低轨道目标,主要摄动项为大气阻力摄动和非球形摄动,表达式如下:
| $ \begin{aligned} M_{\mathrm{DF}}=& M_{0}+\left[1+\frac{3 k_{2}\left(-1+3 \theta^{2}\right)}{2 a_{0}^{\prime\prime 2} \beta_{0}^{3}}+\right.\\ &\left.\frac{3 k_{2}^{2}\left(13-78 \theta^{2}+137 \theta^{4}\right)}{16 a_{0}^{\prime\prime{4}} \beta_{0}^{7}}\right] n_{0}^{\prime \prime}\left(t-t_{0}\right), \end{aligned} $ | (11) |
| $ \begin{aligned} \omega_{\mathrm{DF}}=& \omega_{0}+\left[-\frac{3 k_{2}\left(1-5 \theta^{2}\right)}{2 a_{0}^{\prime\prime 2} \beta_{0}^{4}}+\right.\\ & \frac{3 k_{2}^{2}\left(7-114 \theta^{2}+395 \theta^{4}\right)}{16 a_{0}^{ {\prime\prime 4 }} \beta_{0}^{8}}+\\ &\left.\frac{5 k_{4}\left(3-36 \theta^{2}+49 \theta^{4}\right)}{4 a_{0}^{ {\prime\prime4 }} \beta_{0}^{8}}\right] n_{0}^{\prime \prime}\left(t-t_{0}\right), \end{aligned} $ | (12) |
| $ \begin{aligned} \varOmega_{\mathrm{DF}}=& \varOmega_{0}+\left[-\frac{3 k_{2} \theta}{a_{0}^{\prime\prime 2} \beta_{0}^{4}}+\frac{3 k_{2}^{2}\left(4 \theta-19 \theta^{3}\right)}{2 a_{0}^{\prime\prime{4}} \beta_{0}^{8}}+\right.\\ &\left.\frac{5 k_{4} \theta\left(3-7 \theta^{2}\right)}{2 a_{0}^{\prime\prime 4} \beta_{0}^{8}}\right] n_{0}^{\prime \prime}\left(t-t_{0}\right). \end{aligned} $ | (13) |
式中:M0为某段时间内的平均平近角;Ω0为某段时间内的平均升交点赤经.
大气阻力摄动和非球形摄动造成轨道根数发生变化,有:
| $ \delta \omega=B^{*} C_{3}\left(\cos \omega_{0}\right)\left(t-t_{0}\right), $ | (14) |
| $ \begin{aligned} \delta M=&-\frac{2}{3}\left(q_{0}-s\right)^{4} B^{*} \xi^{4} \frac{a_{E}}{e_{0} \eta}\left[\left(1+\eta \cos M_{\mathrm{DF}}\right)^{3}-\right.\\ &\left.\left(1+\eta \cos M_{0}\right)^{3}\right], \end{aligned} $ | (15) |
| $ M_{P}=M_{\mathrm{DF}}+\delta \omega+\delta M, $ | (16) |
| $ \omega=\omega_{\mathrm{DF}}-\delta \omega-\delta M, $ | (17) |
| $ \varOmega=\varOmega_{\mathrm{DF}}-\frac{21}{2} \frac{n_{0}^{\prime \prime} k_{2} \theta}{a_{0}^{\prime\prime 2} \beta^{2}} C_{1}\left(t-t_{0}\right)^{2}, $ | (18) |
| $ e=e_{0}-B^{*} C_{4}\left(t-t_{0}\right)-B^{*} C_{5}\left(\sin M_{P}-\sin M_{0}\right) \text { , } $ | (19) |
| $ \begin{array}{c} a=a_{0}^{\prime \prime}\left[1-C_{1}\left(t-t_{0}\right)-D_{2}\left(t-t_{0}\right)^{2}-\right. \\ \left.D_{3}\left(t-t_{0}\right)^{3}-D_{4}\left(t-t_{0}\right)^{4}\right]^{2}, \end{array} $ | (20) |
| $ \begin{aligned} I L=& M_{P}+\omega+\varOmega+n_{0}^{\prime \prime}\left[\frac{3}{2} C_{1}\left(t-t_{0}\right)^{2}+\right.\\ &\left(D_{2}+2 C_{1}^{2}\right)\left(t-t_{0}\right)^{3}+\frac{1}{4}\left(3 D_{3}+12 C_{1} D_{2}+\right.\\ &\left.10 C_{1}^{2}\right)\left(t-t_{0}\right)^{4}+\frac{1}{5}\left(3 D_{4}+12 C_{1} D_{3}+6 D_{2}^{2}+\right.\\ &\left.\left.30 C_{1}^{2} D_{2}+15 C_{1}^{25}\right)\left(t-t_{0}\right)\right], \end{aligned} $ | (21) |
| $ \beta=\sqrt{\left(1-e^{2}\right)}, $ | (22) |
| $ n=\frac{k_{e}}{a^{3 / 2}}, $ | (23) |
式中,B*为SGP4典型阻力系数.在近心点距小于220 km时,a和IL的表达式中C1后面的项可舍去,含有C5、δω、δM的项可忽略[13-15].
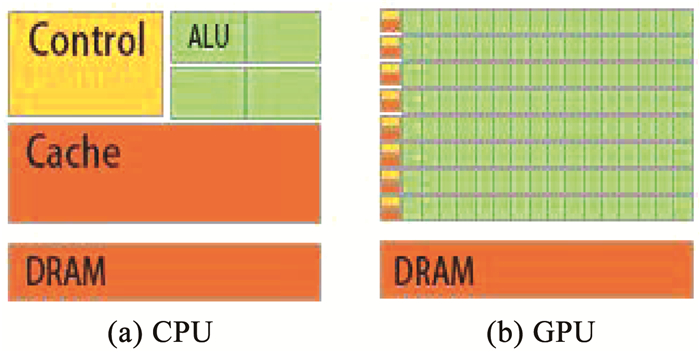
2 基于GPU的并行计算流程设计 2.1 GPU并行计算GPU是一种在个人电脑、工作站、游戏机和一些移动设备(如平板电脑、智能手机等)上专门进行图像运算工作的微处理器.如图 1所示,GPU与CPU组成相同,都由运算基本单元、控制器、寄存器组成. CPU内大部分空间被控制器和寄存器占据,其可利用的临时缓存较大,擅长逻辑控制和串行计算,多用于处理包含不同数据类型的复杂操作.相比于CPU处理器,GPU拥有更多的ALU(算术逻辑单元,是能实现多组算术运算和逻辑运算的组合逻辑电路)用于数据处理,而非数据高速缓存和流控制,此类结构适合于对密集型数据进行并行处理,例如本文中所处理的多卫星轨道数据.
|
图 1 CPU与GPU结构对比示意 Fig. 1 Comparison of structures of CPU and GPU |
因此,GPU可同时调用大量相同类型的数据,并将它们分配入不同线程中进行相同类型的计算操作,其耗费的时间和单独计算一个数据的时间一致,这就是GPU并行计算的概念,即“以空间换时间”的处理方式.
2.2 CUDA计算平台CUDA(Compute unified device architecture)是由NVIDIA公司推出的一种通用并行计算框架,仅适用于NVIDIA公司的产品(以显卡产品为主).其架构包含软硬件体系,硬件为CUDA支持的GPU处理器,软件则包括显卡驱动程序、nvcc编译器、调试模块等组成的开发环境,支持C语言及C++语言编写,通用性较强,易于上手.可将CUDA框架简单理解为一个可通过特定编程模型实现GPU并行加速的C语言函数库.本文中测试程序均于Visual Studio 2013与CUDA 9.0开发平台完成.
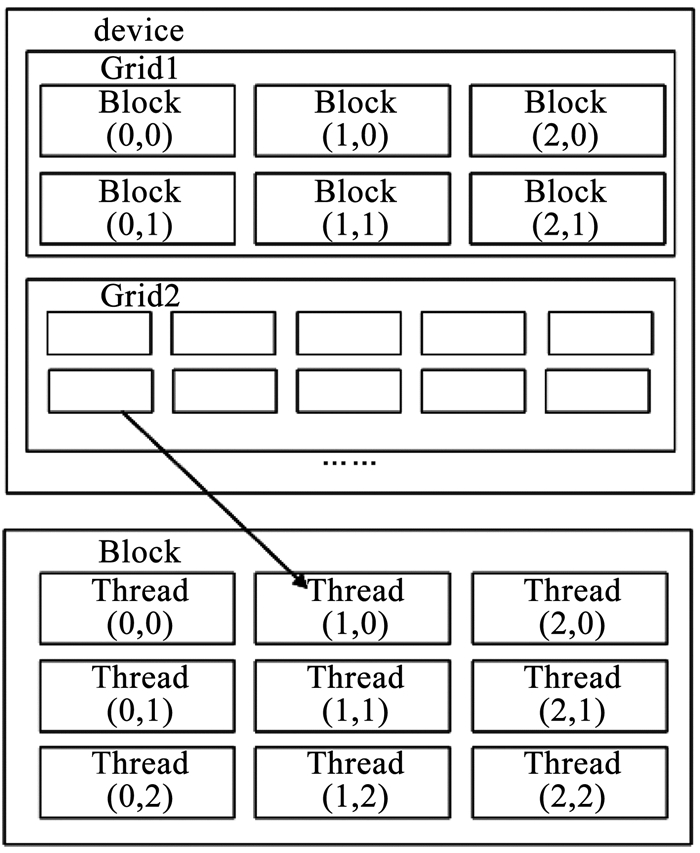
CUDA框架结构中,存在两个必要的程序组成部分:主机程序以及内核函数kernal.主机程序运行在CPU处理器中,实现了CPU部分的计算、CPU与内存间数据传输、CPU与GPU间内存交互、设置GPU并行计算参数的功能.内核函数仅运行于GPU各线程中,为实际并行计算的运算部分,各GPU线程内的相同内核函数带入不同参数同步进行计算.如图 2所示,CUDA框架内GPU线程结构分为3个层次:网格(Grid)、线程块(Block)和线程(Thread).每当一个内核函数被发送到GPU时,即生成一个自定义网格,网格内存在若干自定义维度的线程块,每个线程块内存在同等数量的线程.每个线程都分配有相应的寄存器和本地内存,在其所在的线程块内有一共享内存空间可供该线程块内所有线程读取,同时对于整个网格有可供所有线程访问读取的全局常量及内存,GPU并行计算可根据此原理进行参数设置以达到最优加速效果.
|
图 2 CUDA线程结构示意 Fig. 2 Schematic of CUDA thread structure |
本文集成式框架的输入项为一TXT格式的双行元文件,其包含任意数目卫星的某一时刻双行元数据,表示卫星初始的轨道数据,多颗卫星的双行元数据被统一读取并存入内存.
卫星初始数据读入后,从内存中依次调出每一颗星的双行元数据,并根据双行元数据进行轨道初始参数(轨道六根数)的计算并存入内存,由于此过程单颗卫星参数计算时间小于SGP4模型解算时间的1/10,因此本文中并未对此计算流程进行并行加速.此过程为在CPU运算单元中按顺序进行每一颗星的轨道参数初始化操作.
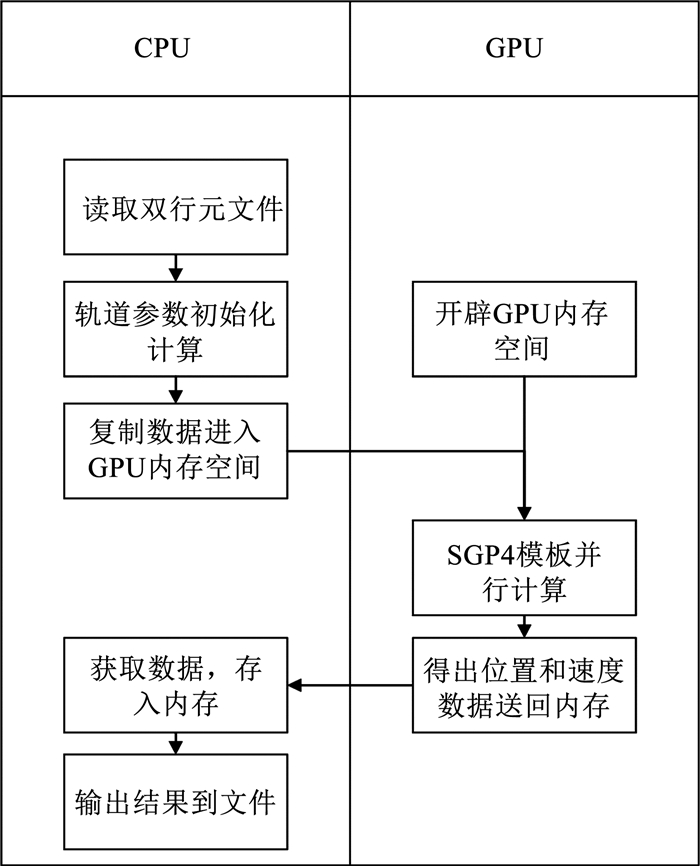
如图 3所示,完成所有双行元数据的轨道初始参数计算后,程序进入第1次数据传输阶段,即CPU至GPU的数据传输.根据双行元数据的个数开辟相应大小的GPU内存空间,每个双行元数据对应的GPU内存空间内分别储存以下4种数据:起始时间、结束时间、解算步长以及卫星星历.其中卫星星历在程序中是以一个结构体变量形式存储的,它包含了每一颗星位置、速度与轨道参数信息.CPU到GPU的数据传输过程是将CPU内存中每颗星起始时间、结束时间、解算步长及起始时刻表示卫星状态的结构体变量数据打包传输到GPU内存空间中,等待GPU调用.
|
图 3 程序流程图 Fig. 3 Program flowchart |
第1次数据传输完成后,GPU将每一颗星对应的结构体变量带入多个独立线程中的核函数进行并行计算.GPU内每一个运算单元为一独立线程,每一独立线程中计算一颗星在某一时间点的星历,则每一颗星的结构体变量需带入计算的线程数量为
| $ n=\frac{t_{s}-t_{0}}{t_{p}}. $ | (24) |
式中:n为单颗星所需线程数量;ts为结束时间;t0为起始时间;tp为步长
在并行计算过程中,多颗星的计算步骤不是顺序进行的,而是同步进行的,即多颗星在独立线程中的解算是同时进行的,以此达到加速效果.所需的并行线程数量为
| $ N=n_{s} \times n. $ | (25) |
式中: N为总线程数量;ns为卫星数;n为单星线程数量.
以计算一颗卫星24 h的星历为例,以1 s为解算步长,所需线程数为86 500个,计算200颗星即为17 300 000个线程,所需的运算单元数超过CPU串行运算2~3个数量级,符合本文“以空间换时间”的理念.但因此,使用本方法进行并行解算的星数会受GPU内存空间大小的限制.例如,在Jetson TX2设备上可同步解算500颗星,但在PC电脑端本方法只可同步递推50颗星的轨道.
GPU并行计算完成后得到卫星星历数据,进行第2次数据传输(GPU至CPU), 将星历数据传输回CPU内存,再输出到文件中结束解算.
3 实验加速效果与分析为了验证所提集成式加速方法的有效性和适应性,即本文提出方法是否达到加速效果,若达到加速效果,在何种计算条件及硬件设备在能达到最好的使用效果,本文分别在两种仿真环境下进行GPU并行加速运行试验:笔记本电脑PC端环境以及JETSON TX2开发板环境.
在笔记本电脑PC端进行的实验对比了CPU解算速度与GPU集成式加速方法解算速度,验证了集成式加速方法的有效性.又将两种环境下的集成式加速结果与模块化加速结果进行比较,得出两种加速方法各自的适用场景.最后通过对比两种环境下集成式加速方法的加速效果,讨论了GPU并行加速方法的设备适用性,提供了卫星在轨解算平台的硬件选择建议.
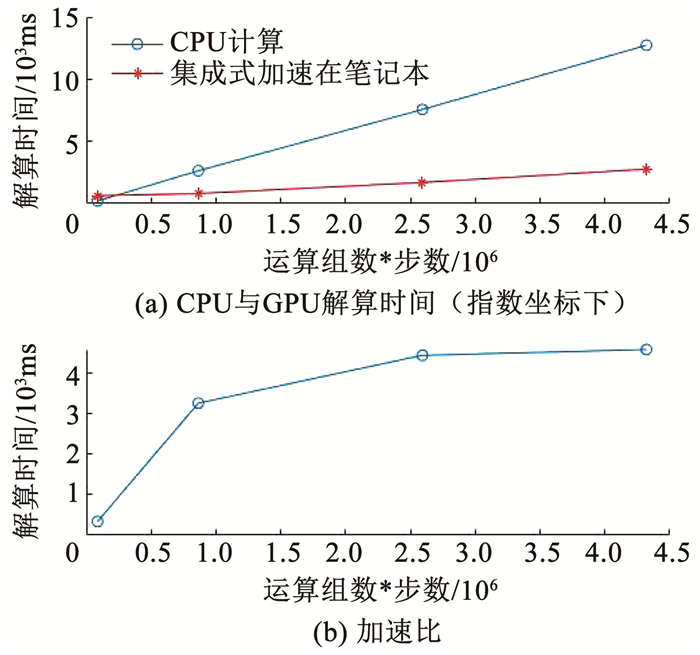
3.1 集成式加速方法有效性分析本文在笔记本电脑PC端环境下首先进行了CPU处理器上的SGP4/SDP4轨道模型解算实验,又于同一台设备上的GPU处理器进行集成式方法的并行加速实验,两次实验结果如表 2和图 4所示.
| 表 2 仿真环境1下仿真结果 Tab. 2 Results of the first simulation environment |
|
图 4 CPU和GPU解算速度对比 Fig. 4 Comparison of calculation speed in CPU and GPU |
仿真过程中每颗星解算步长为1 s,解算时长为24 h,则每颗星计算86 400步,输出86 400组解算结果.
试验验证环境1(笔记本电脑):
操作系统:Windows 10中文版.
CPU:英特尔core i7-6700HQ,2.6 Hz主频,8 GB内存.
GPU:NVIDIA GeForce GTX 950 M,包含640个CUDA单元,4 096 MB显存.
集成式方法需较大的数据储存空间进行运算,鉴于GPU显卡显存及运算单元数量限制,笔记本电脑环境仅能并行解算50颗星星历数据,而TX2开发板能并行解算500颗星的数据.显存空间的大小及GPU运行单元数量决定并行计算所能计算的星数上限,并影响加速效果.
由实验结果如表 2及图 4可知,在星数较少时,总运算步数也较少,CPU解算时间要低于GPU并行解算时间.这是由于CPU处理器在进行单次解算时解算速度为GPU处理器速度的数倍;且进行GPU加速时,CPU调用GPU核函数进入线程的时间为主要消耗时间,真正的GPU线程解算时间都仅为解算一个星历时间点的解算时间.两者的共同因素导致在总运算步数较低时,采用CPU处理器运算效率较高.
当星数增加时,数据量增大,CPU调用核函数的时间随之增加,但调用函数耗费时间增长率较无并行计算的CPU解算时间增长率低,此时GPU并行解算开始呈现速度优势,加速比(即GPU解算速度除以CPU解算速度)最终逐渐稳定于4.6,达到较高加速比.
3.2 集成式加速方法适应性分析上文分析了集成式方法的加速有效性,以下对集成式方法和模块化方法进行对比,提出两种方法各自的适用范围,以及加速方法的设备适用性.
本文于NVIDIA Jetson TX2小型开发板上进行了集成式加速方法的SGP4/SDP4轨道递推模型并行计算实验,将其结果与计天阳[1]中模块化加速方法实验结果进行对比,得出两者方法的适用计算范围.又通过集成式方法在试验环境1、2上加速效果的对比,分析提出轨道模型GPU并行加速的设备适用性.试验结果对比见图 5和表 3.
|
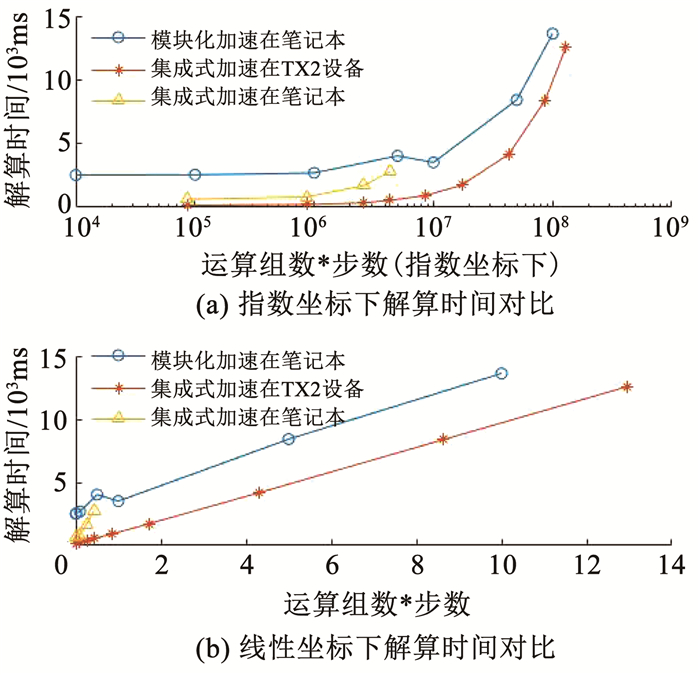
图 5 不同方法GPU解算速度对比 Fig. 5 Comparison of calculation speed in GPU with different methods |
| 表 3 不同GPU解算方法运算时间表 Tab. 3 Calculation time of different GPU computing methods |
试验验证环境2(NVIDIA TX2小型开发板):
操作系统:ARM-LINUX Ubuntu 16.04
GPU:NVIDIA Pascal,256 CUDA核心
在进行GPU并行解算过程中,较GPU的解算速度,CPU调用核函数的速度更为缓慢,如图 6所示为一颗星86 400步数下使用Visual Profiler分析程序得出的各进程占用时间比图,可见建立加速进程的过程较核函数运行时间长.为提高解算速度,本文提出减少调用GPU并行计算核函数次数以达到更高速度的集成式加速方法.

|
图 6 GPU加速后进程时间线(左边黄色为调用创建进程的时间) Fig. 6 Process timeline after GPU acceleration (the left yellow block is the process of calling kernel function) |
集成式解算方法将SGP4解算模型(包括初始常量定义)作为整体加入核函数计算过程中.计算机内存仅需与GPU内存进行一次交互数据传输和一次核函数调用及显存空间分配,相比模块化方法省去多次参数交互和函数调用的时间.但此加速方法单次计算操作复杂,占用显存空间大,当并行计算的星数达到一定数量时,会由于缓存不足出现溢出错误,造成解算失败.
模块化解算方法则将解算过程分为4个模块:重力摄动常数初始化模块、双行元与定轨参数转换模块、SGP4轨道模型初始化模块、SGP4轨道预报模块.除重力摄动常数初始化模块外,其余3个模块在GPU中进行并行计算.分模块进行解算对显存使用需求小,可以实现大规模卫星轨道并行计算.但此方法在CPU与GPU间参数交互的过程中耗费大量时间,加速效果不够理想.
由图 5及表 3,综合分析集成式和模块化两种并行计算方法的试验数据可发现,在运算数较小(本文试验中运算组数*步数 < 400万步)时,宜采用集成式解算方法,在运算数较大(本文试验中运算组数*步数>400万步)时,宜采用模块化解算方法.两种加速方法对比及适用范围可见表 4.
| 表 4 两种解算方法对比及适用范围 Tab. 4 Comparison and range of application of two calculating methods |
在得出加速方法最佳适用范围后,还需讨论加速方法所适用的计算设备,为搭建卫星在轨解算平台提供参考.
由实验结果图 5和表 4可知,低计算量时相同计算量下集成式加速方法解算时间低于模块化加速方法,集成式加速方法在TX2设备上实现解算速度最高.TX2开发板GPU计算性能优越,CPU性能较普通笔记本计算机低,其搭载的专用ARM-LINUX操作系统内核使得其上内存与GPU内存数据传输速率较普通计算高,因此在GPU并行运算时间差距不大的情况下,TX2开发板能够实现最高的解算速度.
由图 5可见,两种解算方法解算时间与计算量都呈现出线性关系,解算时间随计算量线性增长.集成式加速在笔记本上解算时间随时间增长速率最高,经分析认为是WINDOWS操作系统下Visual Studio开发环境下,CUDA程序中由CPU内存至GPU内存的数据传输过程需经由数次内存转移到显卡设备,导致解算速度较低,低于LINUX系统环境效率.此现象也说明,在进行在轨卫星轨道递推解算时,平台应尽量选用搭载结构简约的LINUX系统的计算机,以降低数据传输带来的时间耗费.
4 GPU运算数据精度分析获取在试验环境1下CPU解算和并行解算得出的两份星历递推数据,递推时间为24 h,即86 400步.将数据导入MATLAB中对比,进行二者卫星星历xyz轴上位置误差及直线距离误差计算,因本文实验中笔记本计算机上显卡设备与TX2设备的GPU双精度运算位数相同,试验环境1与试验环境2并行计算解算得到的星历数据一致.用于仿真的双行元数据见表 5,精度仿真结果如图 8所示.
| 表 5 仿真实验中使用的双行元数据 Tab. 5 TLE used in simulation experiment |
|
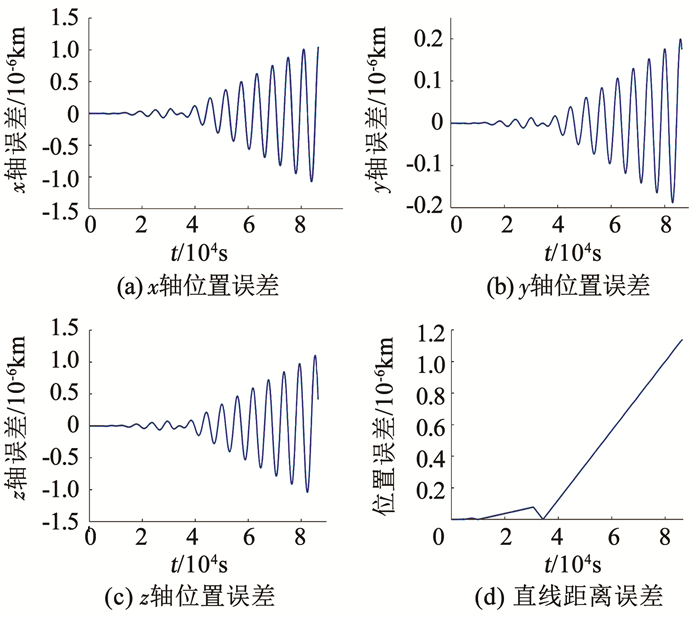
图 7 GPU运算位置与CPU运算对比 Fig. 7 Comparison of position calculated by CPU and GPU |
|
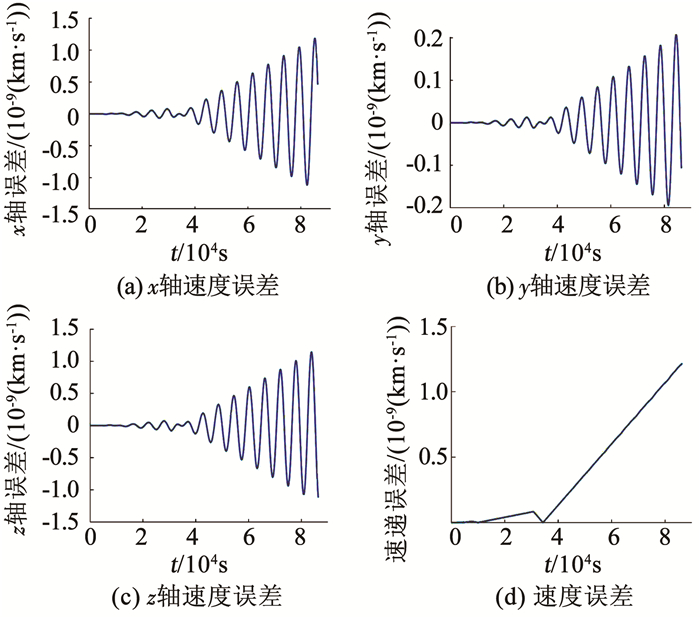
图 8 GPU计算速度与CPU计算对比 Fig. 8 Comparison of velocity calculated by CPU and GPU |
与CPU运算相比,GPU运算的位置误差在10-6 km量级,速度误差在10-9 km量级,误差较小,精度较高,但误差并不收敛,随着运行时间的增长逐渐发散.误差发散的主要原因在于CPU和GPU中的变量精度不同.本文对CPU变量及GPU核函数中变量都以双精度形式保存.CPU中双精度运算位数为80位,GPU中双精度运算位数为64位,随着解算过程的进行,代入解析解的数值增大,GPU双精度计算产生的误差随之增大,结果误差也越大,但总体在可接受范围.
5 结论1) 该方法将完整的SGP4/SDP4轨道预报模型解算过程写入GPU核函数中进行运算.在中小规模计算量下的加速效果优于模块化加速方法.
2) 通过实验仿真对比,集成式加速方法较模块化加速方法在中小规模计算量下加速比更高,且精度损失小.
3) 由于集成式方法占用较大显存容量,因此难以用于超大规模计算量的加速解算,此外,由于GPU内部计算条件限制,导致误差会随着运行时间增长而逐渐发散.针对这两个问题,在后续工作中将采用新的算法尝试进行优化.
| [1] |
计天阳. 基于GPU加速的低轨卫星星座覆盖性能计算与分析[D]. 哈尔滨: 哈尔滨工业大学, 2018 JI Tianyang. Calculation and analysis of coverage performance of LEO satellite constellations based on GPU acceleration[D]. Harbin: Harbin Institute of Technology, 2018. DOI: 10.7666/d.D01587155 |
| [2] |
LIU J, WANG W, GAO Y, et al. Paralleled geopotential computing methods based on GPU[C]//Proceedings of the China Satellite Navigation Conference. Singapore: Springer, 2016: 87. DOI: 10.1007/978-981-10-0940-2_8.
|
| [3] |
LIN Mingpei, XU Ming, FU Xiaoyu. A parallel algorithm for the initial screening of space debris collisions prediction using the SGP4/SDP4 models and GPU acceleration[J]. Advances in Space Research, 2017, 59(9): 2398. DOI:10.1016/j.asr.2017.02.023 |
| [4] |
郭松, 雷元武, 窦勇. 基于VLIW的SGP4/SDP4轨道预测加速器的设计与实现[C]//第十四届计算机工程与工艺会议(NCCET'10)论文集. 扬州: 中国计算机学会, 2010: 147 GUO Song, LEI Yuanwu, DOU Yong. Design and realization of a SGP4/SDP4 orbit prediction accelerator based on VLIW[C]// Proceedings of the 14th Computer Engineering and Technology Conference (NCCET'10). Yangzhou: Chine Computer Federation, 2010: 147 |
| [5] |
冯森. 基于CUDA异构并行加速的两行根数算法的研究[J]. 无线互联科技, 2016(9): 96. FENG Sen. Research on heterogeneous parallel CUDA accelerated two lines of the number of algorithm[J]. Wireless Internet Technology, 2016(9): 96. DOI:10.3969/j.issn.1672-6944.2016.09.044 |
| [6] |
车通宇, 杨力, 张传定, 等. 利用HPOP轨道仿真模型实现接收机自主历书外推[J]. 全球定位系统, 2015, 40(4): 18. CHE Tongyu, YANG Li, ZHANG Chuanding, et al. Executing receiver autonomous ephemeris extrapolation by HPOP model[J]. GNSS World of China, 2015, 40(4): 18. DOI:10.13442/j.gnss.1008-9268.2015.04.004 |
| [7] |
HOOTS F R, ROEHRICH R L. Space track report No. 1-models for propagation of NORAD element sets[R]. Peterson: NORAD, 1980
|
| [8] |
杨嘉墀, 范秦鸿, 张云彤, 等. 航天器轨道动力学与控制[M]. 北京: 中国宇航出版社, 2009: 15. YANG Jiachi, FAN Qinhong, ZHANG Yuntong, et al. Orbit dynamics and control of spacecraft[M]. Beijing: China Astronautic Publishing House, 2009: 15. |
| [9] |
刘林. 航天器轨道理论[M]. 北京: 国防工业出版社, 2000: 5. LIU Lin. Orbit theory of spacecraft[M]. Beijing: National Defense Industry Press, 2000: 5. |
| [10] |
蒋方华, 李俊峰, 宝音贺西. 高精度卫星轨道摄动模型[C]. 中国第十三届空间及运动体控制技术学术年会论文集. 宜昌: 中国自动化学会, 2008 JIANG Fanghua, LI Junfeng, BAOYIN Hexi. High precision orbit perturbation model[C]//Proceedings of the China's 13th Annual Conference on Space and Sports Control Technology. Yichang: Chinese Association of Automation, 2008 |
| [11] |
刘一帆. 基于SGP4模型的低轨道航天器轨道预报方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2009 LIU Yifan. Research on low earth orbit spacecraft orbit prediction strategy based on SGP4 model[D]. Harbin: Harbin Institute of Technology, 2009. DOI: 10.7666/d.D270797 |
| [12] |
韦栋, 赵长印. SGP4/SDP4模型精度分析[J]. 天文学报, 2009, 50(3): 332. WEI Dong, ZHAO Changyin. Analysis on the accuracy of the SGP4/SDP4 model[J]. Acta Astronomica Sinica, 2009, 50(3): 332. DOI:10.3321/j.issn:0001-5245.2009.03.010 |
| [13] |
李梦奇. 基于大气参数修正的低轨航天器SGP4/SDP4模型精度分析轨道预报方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2017 LI Mengqi. Research on low earth orbit spacecraft orbit prediction strategy based on atmospheric coefficient modification[D]. Harbin: Harbin Institute of Technology, 2017. DOI: 10.7666/d.D01333050 |
| [14] |
王明明, 罗建军, 马卫华. IAU1976、1980及2000A岁差章动模型的比较[J]. 中国空间科学技术, 2009, 29(5): 42. WANG Mingming, LUO Jianjun, MA Weihua. Comparison of IAU1976, 1980 and IAU2000A precession-nutation model[J]. Chinese Space Science and Technology, 2009, 29(5): 42. DOI:10.3321/j.issn:1000-758X.2009.05.007 |
| [15] |
郭俊义. 同时顾及章动和极移的地球自转方程[J]. 武汉大学学报(信息科学版), 2000, 25(5): 391. GUO Junyi. Earth rotation equations containing both nutation and polar motion[J]. Geomatics and Information Science of Wuhan University, 2000, 25(5): 391. DOI:10.3969/j.issn.1671-8860.2000.05.003 |
 2021, Vol. 53
2021, Vol. 53


