在海上进行反水雷作战时,往往需要短时间内投放多枚射弹,使敌方防御系统短期内应接不暇.这是典型的运动体并联入水过程.该过程中,两个或多个运动体同时或在极短时间间隔内平行地穿越自由液面进入水中,由于各运动体流场和弹道存在耦合作用,力学环境更加复杂,运动体极易发生运动失稳.
国内外对单个运动体入水开展了大量的研究,包括空泡形态特性、运动体受载特性和弹道特性. Logvinovich[1]提出了空泡独立膨胀原理,为后续的空泡形态研究提供了理论基础;Lee等[2]提出了高速入水空泡形态发展的理论分析方法,该方法可以模拟高速入水过程中空泡的生成及溃灭;Aristoff等[3]基于空泡压力平衡理论和势流理论提出了空泡形态的理论求解方法;王京华等[4]基于空泡独立膨胀原理,研究了空泡的记忆效应及其对空泡形态的影响,详细计算了超空泡航行体各部分所受的流体动力,并提出了避免滑行力出现的预测和控制方法;张伟等[5]进行了不同速度、形状弹体入水试验,得到了3种弹体的入水初期空泡形态与运动特性,建立了平头运动体入水的空泡形态和弹道预测模型;王柏秋等[6]基于动网格技术对超空泡射弹的阻力系数开展了数值研究,结果表明同一模型长细比下,模型阻力系数随时间呈准线性变化;马庆鹏等[7]开展了不同速度下的锥头柱体高速入水过程数值研究,发现入水速度越高,航行体头部压力峰值越大,相同时刻入水空泡最大直径也越大;何乾坤等[8-14]对超空泡射弹的尾拍特性进行了大量数值研究.
目前国内外对并联入水的研究较少.卢佳兴等[15]基于高速摄像技术开展了圆柱体并联入水空泡演化特性的实验研究,发现各深度空泡截面扩张和空泡中心偏移的峰值和持续时间均随弗劳德数增大而先增后减;宋武超等[16]基于势流理论提出了回转体低速并联入水过程空泡形态发展的预测方法.综上所述,对入水问题的研究多针对单体入水,涉及并联入水的研究非常少,且未考虑空化现象对运动体并联入水流体和运动的影响.
本文基于对急动度的限制性假设,推导出描述圆柱体并联入水侧向位移和偏航角的预测公式,研究初始空化数和初始净距等初始条件对侧向和偏航运动特性的影响及其机理,提出避免回转体运动失稳的策略.
1 数值计算方法 1.1 控制方程及其求解本文基于有限体积法对雷诺时均的N-S方程进行离散,使用VOF多相流模型描述各相分布. 混合介质的连续性方程为
| $ \frac{\partial \rho_{m}}{\partial t}+\frac{\partial}{\partial x_{i}}\left(\rho_{m} u_{i}\right)=0, $ | (1) |
其中i=1, 2, 3,下同. 动量方程为
| $ \begin{array}{c} \frac{\partial}{\partial t}\left(\rho_{m} u_{i}\right)+\frac{\partial}{\partial x_{i}}\left(\rho_{m} u_{i} u_{j}\right)= \\ -\frac{\partial p}{\partial x_{i}}+\frac{\partial}{\partial x_{i}}\left[\left(\mu_{m}+\mu_{t}\right)\left(\frac{\partial u_{i}}{\partial x_{j}}+\frac{\partial u_{j}}{\partial x_{i}}\right)\right]. \end{array} $ | (2) |
式中:ρm=αlρl+αgρg+αvρv,μm=αlμl+αgμg+αvμv.αl、αg、αv分别为水、空气和水蒸气的体积分数;ρl、ρg、ρv为三相的密度;μl、μg、μv为三相的动力黏度;μt=ρmCμk2/ε为湍流黏性系数;Cμ为经验常数;k为湍动能;ε为湍动耗散率;ui、uj为速度分量;xi、xj为位移分量.Cμ由下式确定:
| $ C_{\mu}=\frac{1}{A_{0}+\frac{A_{s} k U^{*}}{\varepsilon}}. $ | (3) |
式中: A0=4.04;
本文采用适用于大雷诺数流动的realizable k-ε模型[17],其湍动能和湍动耗散率的输运方程分别为:
| $ \begin{array}{l} \frac{\partial(\rho k)}{\partial t}+\frac{\partial\left(\rho u_{j} k\right)}{\partial x_{j}}=\frac{\partial}{\partial x_{j}}\left[\left(\mu+\frac{\mu_{t}}{\sigma_{k}}\right) \frac{\partial k}{\partial x_{j}}\right]+ \\ G_{k}+G_{b}-\rho \varepsilon-Y_{M}+S_{k}, \end{array} $ | (4) |
| $ \begin{array}{l} \frac{\partial(\rho \varepsilon)}{\partial t}+\frac{\partial\left(\rho \varepsilon u_{j}\right)}{\partial x_{j}}=\frac{\partial}{\partial x_{j}}\left[\left(\mu+\frac{\mu_{t}}{\sigma_{\varepsilon}}\right) \frac{\partial \varepsilon}{\partial x_{j}}\right]+ \\ \rho C_{1} S_{\varepsilon}-\rho C_{2} \frac{\varepsilon^{2}}{k+\sqrt{v \varepsilon}}+C_{1 \varepsilon} \frac{\varepsilon}{k} C_{3 \varepsilon} G_{b}+S_{\varepsilon} . \end{array} $ | (5) |
式中: Gk为时均速度梯度引起的湍动能;Gb为浮力引起的湍动能;YM为脉动扩张在湍流耗散率所占当量;
本文采用Schnerr and Sauer空化模型[18]描述空化现象.水蒸气相输运方程为
| $ \begin{array}{l} \frac{\partial \alpha_{v}}{\partial t}+\frac{\partial}{\partial x_{i}}\left(\alpha_{v} u_{i}\right)=F_{\mathrm{vap}} \frac{2 \alpha_{\text {nuc }}\left(1-\alpha_{v}\right) \rho_{v}}{R_{B}}\cdot \\ \sqrt{\frac{2}{3} \frac{p_{v}-p}{\rho_{l}}}-F_{\text {cond }} \frac{3 \alpha_{v} \rho_{v}}{R_{B}} \sqrt{\frac{2}{3} \frac{p-p_{v}}{\rho_{l}}}. \end{array} $ | (6) |
式中: RB=1×10-6m为气核半径;αnuc=5×10-4为不可凝结气体体积分数;p为远场压力;pv为饱和蒸气压;Fvap=50, Fcond=0.001.
1.2 方法有效性验证文献[4]中给出了同实验结果符合良好的空泡形态模型,其表达式为
| $ R(z)=\left[R_{0}^{2}+2 R_{0} \sqrt{\frac{C_{d}}{2 N}}\left(z-z_{0}\right)-\frac{\sigma}{2 N}\left(z-z_{0}\right)^{2}\right]^{1 / 2}. $ | (7) |
式中: R为空泡半径;R0为头部半径;z为位移;z0为初始位移;σ0、σ分别为初始空化数和空化数;Cd= C0(1+σ), 0.82≤C0≤0.83;N为经验系数,取为2.
为验证计算方法的有效性,对半径5 mm的圆柱体以98.7 m/s入水过程进行数值计算,并和式(7)进行对比.由图 1中可知两者较吻合,说明本文数值计算方法是可信的.

|
图 1 空泡形态对比 Fig. 1 Comparison of cavity shapes |
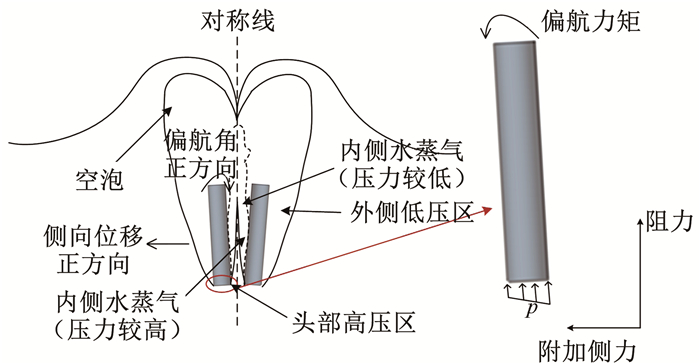
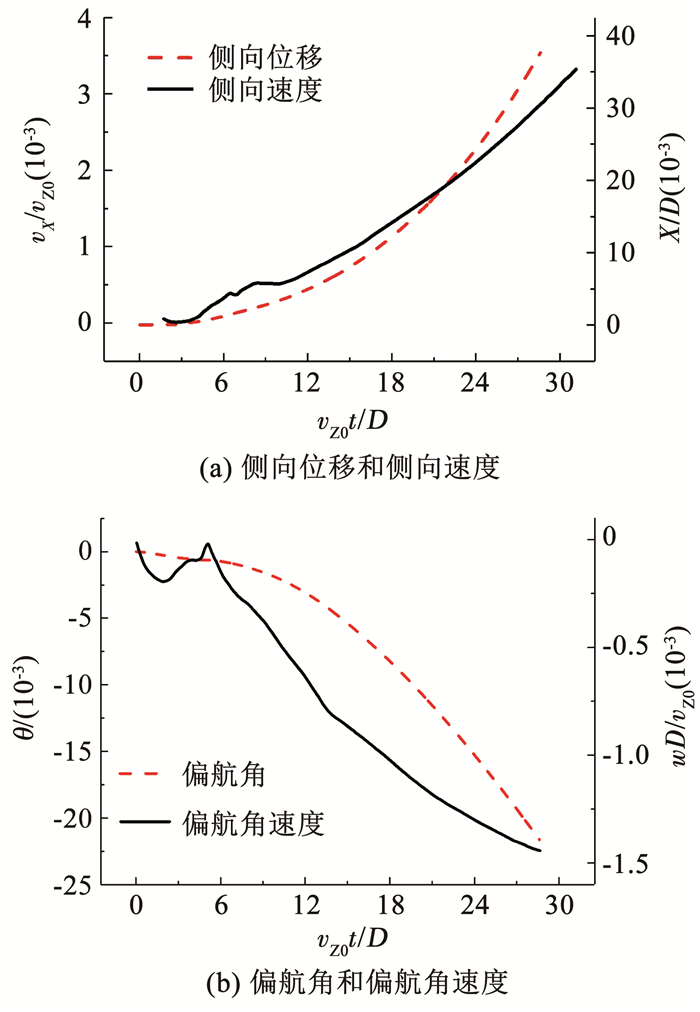
并联入水具有对称性,两回转体的侧向位移和偏航角大小相等,方向相反.本文约定质心相互远离的方向为侧向位移的正方向,头部远离而尾部靠近的旋转方向为偏航角的正方向,如图 2所示. 图 3给出了直径D=10 mm,长l=60 mm铝制圆柱体在初始空化数σ=0.02,初始净距d=0.6D条件下并联入水的侧向和偏航运动曲线. 由图 2可以看出,由于头部靠近内侧的压力较大,回转体受到负方向偏航力矩,导致负方向偏航运动;偏航运动使头部压力对回转体产生正向附加侧力,引起正方向侧向位移.
|
图 2 并联入水示意图 Fig. 2 Schematic of water entry in parallel |
|
图 3 左侧回转体侧向和偏航运动 Fig. 3 Lateral and yaw motions of left rotation body |
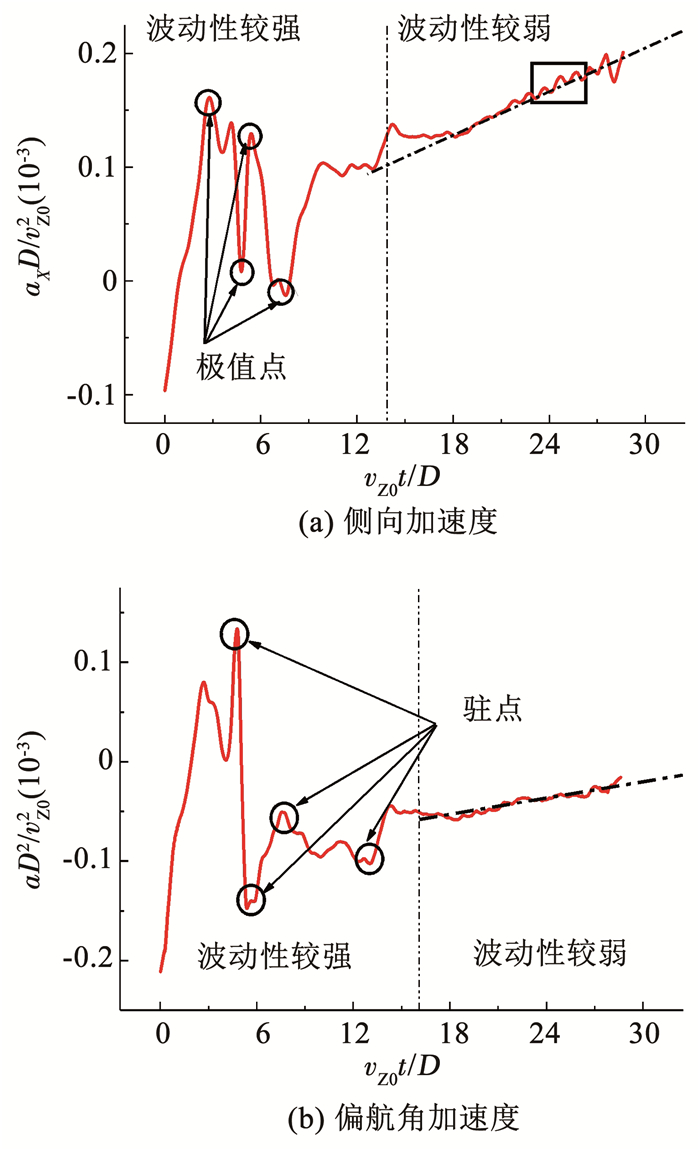
进一步考察侧向加速度和偏航角加速度可知,入水初期两者波动性均较强,随着时间增加逐渐趋于线性变化.因此若忽略波幅较小的波动,可近似认为t较小时侧向加速度和偏航角加速度曲线均有4个极值点,而t充分大时两者为线性变化,如图 4所示.因此由罗尔中值定理可知,侧向急动度和偏航角急动度在t较小时都至少有3个极值点,而当t充分大时两者都几乎为零.于是对侧向急动度和偏航角急动度作如下两个限制性假设:1)侧向急动度和偏航角急动度曲线均有3个极值点;2)侧向急动度和偏航角急动度在t充分大时均收敛于零.
|
图 4 侧向加速度和偏航角加速度的波动性 Fig. 4 Fluctuation characteristics of lateral and yaw angular acceleration |
据此设侧向急动度和偏航角急动度分别为:
| $ j_{X}(t)=\sum\limits_{n=0}^{3} c_{X n} t^{n} f_{X n}(t), j_{\theta}(t)=\sum\limits_{n=0}^{3} c_{\theta n} t^{n} f_{\theta n}(t). $ | (8) |
式中:cXn、cθn为待定参数;fXn(t)、fθn(t)为待定的单调减函数,为使假设成立应满足:
| $ t^{n} f_{X n}(\infty)=0, t^{n} f_{\theta n}(\infty)=0. $ | (9) |
对式(8)积分,并注意到积分第二中值定理可得:
| $ a_{X}=\sum\limits_{n=0}^{3} c_{X n} t^{n} F_{X n}(t), a_{\theta}=\sum\limits_{n=0}^{3} c_{\theta n} t^{n} F_{\theta n}(t), $ | (10) |
其中:FXn(t)、Fθn(t)由下式确定:
| $ \begin{array}{l} F_{X n}(t)=\int_{\xi_{X_{n}}(t)}^{t} f_{X n}(t) \mathrm{d} t, F_{\theta n}(t)=\int_{\xi_{\theta n}(t)}^{t} f_{\theta n}(t) \mathrm{d} t \\ \xi_{X n}(t), \xi_{\theta n}(t) \in[0, t]. \end{array} $ | (11) |
同样地,应用积分第二中值定理对式(10)连续积分两次得到侧向位移和偏航角分别为:
| $ X=\sum\limits_{n=0}^{3} c_{X n} t^{n} \varLambda_{X_{n}}(t), \theta=\sum\limits_{n=0}^{3} c_{\theta n} t^{n} \varLambda_{\theta n}(t). $ | (12) |
令cXi=cθi=0(i=0, 1, 2), 以及cX=6cX3, cθ=6cθ3;并取ΛX3(t)=exp(-crXd
| $ \begin{array}{l} X=c_{X} t^{3} \exp \left(-c_{r X} d \sqrt{t} / \sigma D\right), \\ \theta=c_{\theta} t^{3} \exp \left(-c_{r \theta} d \sqrt{t} / \sigma D\right). \end{array} $ | (13) |
式中: cX、cθ分别为侧向和偏航角名义急动度;crX、crθ分别为侧向和偏航角修正因子.这些参数对于确定的并联入水过程是常数,而对于给定外形和材质的回转体则是初始空化数和初始净距的函数.
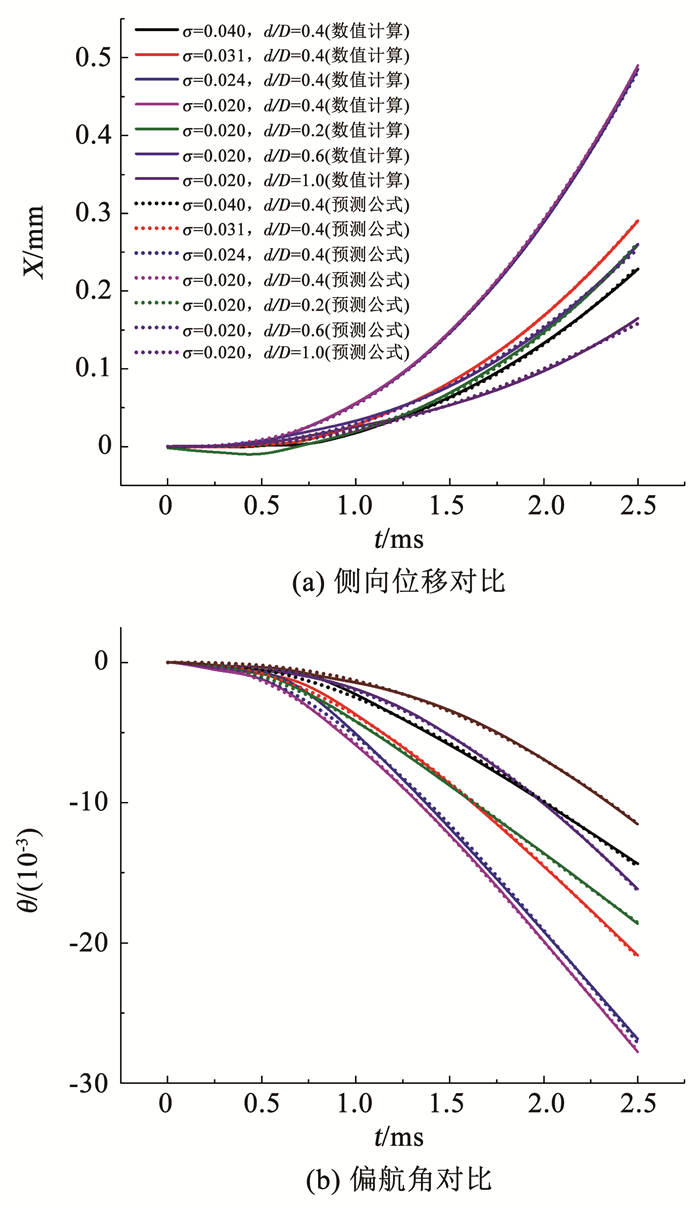
3 运动特性分析取表 1中各初始条件的数值仿真数据对式(13)进行拟合,如图 5所示,拟合结果同式(13)吻合.
| 表 1 初始条件 Tab. 1 Initial conditions |
|
图 5 预测公式与数值计算对比 Fig. 5 Comparison between prediction formulas and numerical calculations |
从图 5还可以看出,同一时刻侧向位移和偏航角随初始空化数减小而增加,随初始净距增加而先增后减.结合图 2对此解释如下:头部压力随初始空化数减小而增大,因此初始空化数越小,回转体所受偏航力矩和附加侧力越大,从而侧向位移和偏航角越大;速度驻点位置随初始净距变小而越靠近内侧,但初始净距较小时,速度驻点位置几乎不再向内侧偏移,故初始净距较大时,偏航力矩随初始净距减小而增大,使偏航角随初始净距减小而增大,进而使附加侧力随初始净距减小而增大,而初始净距较小时,内侧靠近尾部的低压区对回转体有正方向力矩,使偏航力矩和附加侧力随初始净距减小而减小,从而使侧向和偏航运动受到限制.
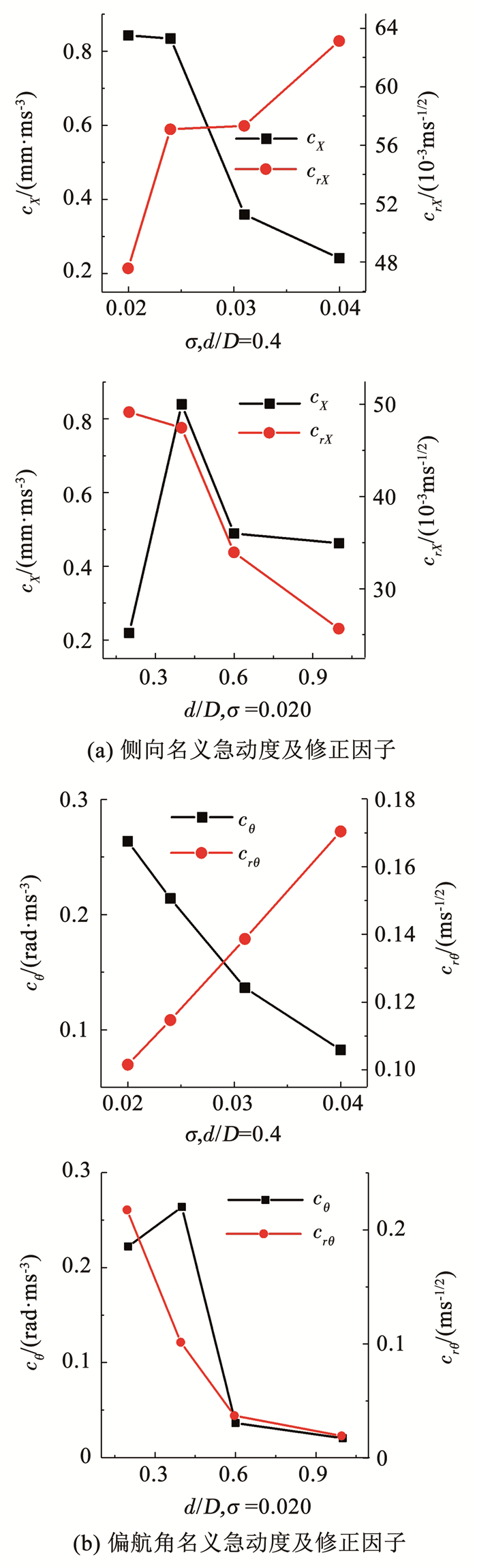
为定量考察初始空化数和初始净距对侧向和偏航运动的影响机理,图 6给出了名义急动度cX、cθ和修正因子crX、crθ随初始条件的变化.可以看出,cX和cθ随着σ减小而增大,而随d/D增大而先增后减;crX和crθ随d/D减小而增大.这进一步说明初始空化数越小,头部压力对侧向和偏航运动的促进作用越强,而初始净距越小,内侧低压对侧向和偏航运动的限制作用越强.
|
图 6 不同初始条件下的名义急动度和修正因子 Fig. 6 Nominal jerkiness and correction factor under different initial conditions |
侧向和偏航运动使回转体逐渐偏离平衡点,可能使回转体碰撞或过度远离,导致运动失稳.因此获得碰撞和过度远离的条件很有必要.
定义运动状态因数β为净距变化量与初始净距之比的相反数,即
| $ \beta=-\frac{2 X+D(1-\sec \theta)+(l+D \tan \theta) \sin \theta}{d}, $ | (14) |
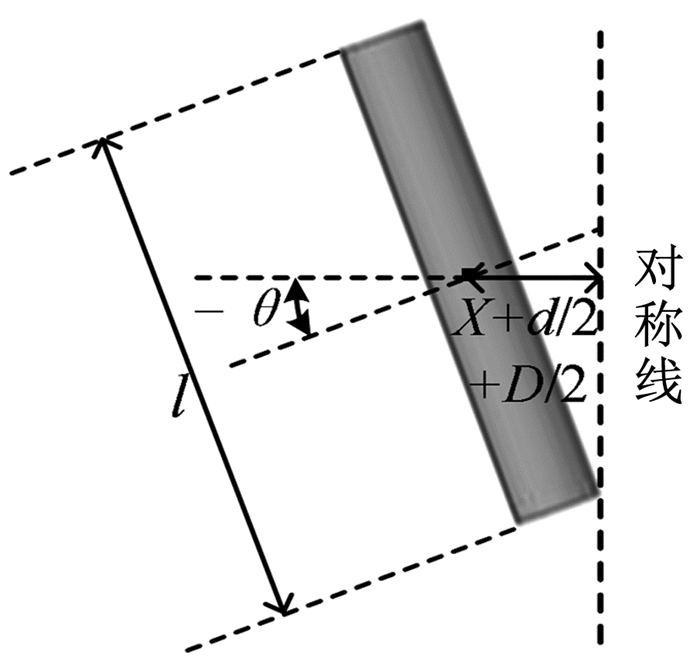
回转体发生碰撞时,头部内侧与对称线接触,如图 7所示.此时满足如下几何关系:
| $ \begin{array}{l} X+\frac{1}{2} d+\frac{1}{2} D-\frac{1}{2} D \sec (-\theta)= \\ \left(\frac{1}{2} l-\frac{1}{2} D \tan (-\theta)\right) \sin (-\theta). \end{array} $ | (15) |
|
图 7 回转体碰撞状态示意 Fig. 7 Schematic of collision state of rotation bodies |
亦即
| $ \beta=-\frac{2 X+D(1-\sec \theta)+(l+D \tan \theta) \sin \theta}{d}=1, $ | (16) |
上式即是碰撞状态的判据.本文约定|β|≤1,当且仅当β=1时回转体碰撞,当且仅当β=-1时为过度远离状态.式(14)可改写为
| $ \beta=-\frac{2 X / D+(1-\sec \theta)+(0.25 \lambda+\tan \theta) \sin \theta}{d / D}, $ | (17) |
其中,λ为长细比,对于本文的回转体λ=24.
将式(13)代入式(17)即得β表达式.该式表明,运动状态不仅和初始条件(初始空化数和初始净距)有关,还同回转体的外形(长细比)相关.
图 8比较了不同初始条件对β的影响.可以看出,对同一初始净距,存在使回转体最接近初始状态的初始空化数;对同一初始空化数,存在使回转体净距最接近初始状态的初始净距.而为避免运动失稳,应当力求|β|尽量小.因此对于已确定形状和材料的回转体,应控制入水初速度和初始净距在合理的范围内.对于本文的圆柱体,若初始净距为0.4D,则入水初速度应控制在79.64 m/s左右(对应于图 8中σ=0.031, d/D=0.4);若入水初速度为98.7 m/s,则初始净距应控制在0.4D~0.6D之间(对应于图 8中σ=0.020, d/D=0.4及σ=0.020, d/D=0.6).

|
图 8 β-t曲线 Fig. 8 β-t curves |
1) 预测公式与数值计算结果符合良好,具有一定的可信度.
2) 入水后同一时刻,运动体的侧向位移和偏航角均随初始空化数减小而增大,随初始净距减小而先增后减.
3) 初始空化数较低时头部压力对侧向和偏航运动具有促进作用,且初始空化数越小,侧向名义急动度和偏航角名义急动度越大,表明侧向和偏航运动所受促进作用越强;初始净距较小时,内侧压力对侧向和偏航运动具有抑制作用,且初始净距越小,侧向修正因子和偏航角修正因子越大,表明侧向和偏航运动所受抑制作用越强
4) 初始条件和回转体外形共同决定了并联入水过程中回转体的运动状态.对于本文运动体,当初始净距为0.4D,则入水初速度应控制在79.64 m/s左右;若入水初速度为98.7 m/s,则初始净距应控制在0.4D~0.6D之间.
| [1] |
LOGVINOVICH G V. Hydrodynamics of flow with free boundaries[M]. Kiev: Naukova Dumka, 1969.
|
| [2] |
LEE M, LONGORIA R G, WILSON D E. Cavity dynamics in high-speed water entry[J]. Physics of Fluids, 1997, 9(3): 540. DOI:10.1063/1.869472 |
| [3] |
ARISTOFF J M, BUSH J W M. Water entry of small hydrophobic spheres[J]. Journal of Fluid Mechanics, 2009, 619: 45. DOI:10.1017/s0022112008004382 |
| [4] |
王京华, 张嘉钟, 于开平, 等. 超空泡高速航行体动力学建模与控制设计[J]. 哈尔滨工业大学学报, 2010, 42(9): 1351. WANG Jinghua, ZHANG Jiazhong, YU Kaiping, et al. Dynamics modeling and control design for a high-speed supercavitating vehicle[J]. Journal of Harbin Institute of Technology, 2010, 42(9): 1351. DOI:10.11918/j.issn.0367-6234.2010.09.002 |
| [5] |
张伟, 郭子涛, 肖新科, 等. 弹体高速入水特性实验研究[J]. 爆炸与冲击, 2011, 31(6): 579. ZHANG Wei, GUO Zitao, XIAO Xinke, et al. Experimental investigations on behaviors of projectile high-speed water entry[J]. Explosion and Shock Waves, 2011, 31(6): 579. DOI:10.11883/1001-1455(2011)06-0579-06 |
| [6] |
王柏秋, 王聪, 魏英杰, 等. 超空泡射弹阻力系数数值模拟[J]. 哈尔滨工业大学学报, 2013, 45(3): 22. WANG Baiqiu, WANG Cong, WEI Yingjie, et al. Drag coefficients of supercavitating projectile based on dynamic mesh[J]. Journal of Harbin Institute of Technology, 2013, 45(3): 22. DOI:10.11918/j.issn.0367-6234.2013.03.004 |
| [7] |
马庆鹏, 魏英杰, 王聪, 等. 锥头圆柱体高速入水空泡数值模拟[J]. 北京航空航天大学学报, 2014, 40(2): 204. MA Qingpeng, WEI Yingjie, WANG Cong, et al. Numerical simulation of high-speed water-entry cavity of cone cylinder[J]. Journal of Beijing University of Aeronautics and Astronautics, 2014, 40(2): 204. DOI:10.13700/j.bh.1001-5965.2014.02.022 |
| [8] |
何乾坤, 魏英杰, 尤天庆, 等. 空泡摆动对超空泡航行体尾拍影响分析[J]. 北京航空航天大学学报, 2012, 38(4): 509. HE Qiankun, WEI Yingjie, YOU Tianqing, et al. Analysis of tail-slaps of supercavitating vehicle influenced by distortion of cavity shape[J]. Journal of Beijing University of Aeronautics and Astronautics, 2012, 38(4): 509. DOI:10.13700/j.bh.1001-5965.2012.04.025 |
| [9] |
魏英杰, 何乾坤, 王聪, 等. 超空泡射弹尾拍问题研究进展[J]. 舰船科学技术, 2013, 35(1): 7. WEI Yingjie, HE Qiankun, WANG Cong, et al. Review of study on the tail-slap problems of supercavitating projectile[J]. Ship Science and Technology, 2013, 35(1): 7. DOI:10.3404/j.issn.1672-7649.2013.1.002 |
| [10] |
何乾坤, 张嘉钟, 魏英杰, 等. 水下通气空泡航行体结构模态及冲击响应研究[J]. 哈尔滨工业大学学报, 2012, 44(3): 1. HE Qiankun, ZHANG Jiazhong, WEI Yingjie, et al. Mode and impulse response of ventilated cavitating underwater vehicles[J]. Journal of Harbin Institute of Technology, 2012, 44(3): 1. DOI:10.11918/j.issn.0367-6234.2012.03.001 |
| [11] |
何乾坤, 张嘉钟, 王聪, 等. 潜射导弹水下发射的模态研究[C]//第八届全国动力学与控制学术会议论文集. 杭州: 中国力学学会, 2008 HE Qiankun, ZHANG Jiazhong, WANG Cong, et al. Mode analyze of submarine-launched missile[C]//Proceedings of the 8th National Conference on Dynamics and Control. Hangzhou: Chinese Society of Theoretical and Applied Mechanics, 2008 |
| [12] |
何乾坤. 超空泡射弹尾拍运动多相流场及结构动力学特性研究[D]. 哈尔滨: 哈尔滨工业大学, 2012 HE Qiankun. Research on multiphase flow and structural dynamics of supercavitating projectile during tail-slapping[D]. Harbin: Harbin Institute of Technology, 2012 |
| [13] |
魏英杰, 何乾坤, 王聪, 等. 亚音速超空泡射弹尾拍动力学响应分析[J]. 振动与冲击, 2012, 31(18): 67. WEI Yingjie, HE Qiankun, WANG Cong, et al. Impact dynamic responses of a supercavitating projectile in subsonic compressible fluid flow[J]. Journal of Vibration and Shock, 2012, 31(18): 67. DOI:10.3969/j.issn.1000-3835.2012.18.016 |
| [14] |
何乾坤, 魏英杰, 王聪, 等. 超空泡射弹尾拍结构动力学响应分析[J]. 工程力学, 2012, 29(11): 370. HE Qiankun, WEI Yingjie, WANG Cong, et al. Dynamic responses of supercavitating projectile impacted by tail forces[J]. Engineering Mechanics, 2012, 29(11): 370. DOI:10.6052/j.issn.1000-4750.2011.03.0157 |
| [15] |
卢佳兴, 魏英杰, 王聪, 等. 圆柱体并联入水过程空泡演化特性实验研究[J]. 力学学报, 2019, 51(2): 450. LU Jiaxing, WEI Yingjie, WANG Cong, et al. Experimental study on cavity evolution characteristics in the water-entry process of parallel cylinders[J]. Chinese Journal of Theoretical and Applied Mechanics, 2019, 51(2): 450. DOI:10.6052/0459-1879-18-288 |
| [16] |
宋武超, 魏英杰, 路丽睿, 等. 基于势流理论的回转体并联入水双空泡演化动力学研究[J]. 物理学报, 2018, 67(22): 224702. SONG Wucao, WEI Yingjie, LU Lirui, et al. Dynamic characteristics of parallel water-entry cavity based on potential flow theory[J]. Acta Physica Sinica, 2018, 67(22): 224702. DOI:10.7498/aps.67.20181375 |
| [17] |
SHIH T H, LIOU W W, SHABBIR A, et al. A new k-ε eddy viscosity model for high Reynolds number turbulent flows[J]. Computers Fluids, 1995, 24(3): 227. DOI:10.1016/0045-7930(94)00032-T |
| [18] |
SCHNERR G H, SAUER J. Physical and numerical modeling of unsteady cavitation dynamics[C]//Proceedings of the 4th International Conference on Multiphase Flow. New Orleans: ICMF, 2001
|
 2021, Vol. 53
2021, Vol. 53


