2. 上海卫星工程研究所,上海 200240
2. Shanghai Institute of Satellite Engineering, Shanghai 200240, China
地磁场提供了丰富的地磁特征[1],利用卫星地磁测量,能够快速地测量全球的地磁场矢量信息.在此基础上完成地磁场模型库的建立与更新,并广泛应用于地磁导航、地震预报等技术领域[2-3].地磁测量的精度受到测量用磁力仪和星敏感器等的仪器安装误差以及坐标系间传递精度的影响[4-7],因此提高卫星地磁测量系统内传感器的精度和磁力仪与星敏感器之间安装矩阵的测量精度具有重要的实用价值.
目前对磁力仪及星敏感器之间安装矩阵的标定方法研究相对较少,张艺腾等[8]对航空地磁测量中的磁力仪与姿态仪的联合标定进行了研究,假设磁力仪三轴与姿态仪三轴之间为欧拉转换的关系,通过多次旋转,由最小二乘通过扫描迭代求出最优的旋转欧拉角,最终得到传感器间的安装矩阵.孙闯等[9]对安装矩阵提出一种户外标定的方法,该方法借助一个标准六面体对伸展杆系统进行多个方向的旋转,测量不同姿态下星敏与磁力仪的输出,并根据测出的星敏感器与磁力仪敏感轴坐标系相对地理坐标系的姿态辨识出星敏与三轴磁力仪间的安装矩阵,但该方法达不到精度要求.王凯强等[10]提出了在实验室环境下利用三轴无磁转台提供姿态信息以及恒星模拟器模拟室外观星环境,通过最小二乘辨识出安装矩阵的方法,但用三轴无磁转台在户外标定既不方便也不经济.
本文提出了一种利用单轴立式无磁转台对磁力仪及星敏感器之间安装矩阵在户外进行地面标定的方法,通过无磁转台提供精确的角位置使磁力仪敏感到不同的地磁场分量的激励,不仅辨识出磁力仪的非正交误差,并在此之上完成安装矩阵的标定.
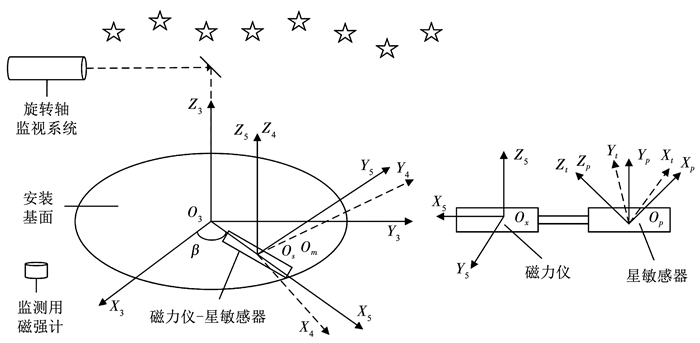
1 地面标定系统介绍针对三轴磁力仪以及3个星敏感器,如果各个敏感轴的方向矢量能够统一在地理坐标系下表示,即可确定他们间的安装矩阵.当星敏感器在地面观星时,可得到星敏光轴在惯性空间的姿态,再利用当地经纬度信息以及测量时刻的格林尼治恒星时推导出星敏光轴在地理坐标系下的表示.在单个位置下三轴磁力仪测量地磁场无法直接解算出其敏感轴的姿态,本文借助单轴无磁转台以及安装夹具,在多个位置进行测量,推导出初始位置下的磁力仪敏感轴在地理坐标系下的表示.最终通过坐标系转换等数学方法,解算出精确的安装矩阵.根据以上原理,整个地面标定系统如图 1所示.
|
图 1 地面标定系统示意 Fig. 1 Schematic of ground calibration system |
磁力仪和星敏感器由刚性杆连接成固联体,安装在单轴立式无磁转台上,构成了无磁实验平台.地面监测系统包括旋转轴监测系统以及地磁场监测磁强计.无磁转台由于必须采用无磁材料等的原因存在着较大的倾角回转误差,使用旋转轴监测装置对转台的回转误差进行实时监测,并对输出进行补偿.标定时需要提供精确的当地磁场矢量信息,故采用监测用磁强计测量当地磁场的变化.
2 坐标系的建立与误差传递根据地面标定系统组成,依次建立以下坐标系.地心惯性坐标系OiXiYiZi,Oi为地球的地心,Xi轴和Yi轴在地球的赤道平面内,Xi轴指向春分点,Zi轴指向地球北极,Yi轴的方向由右手定则来决定.
地理坐标系OXYZ,即东北天坐标系g.如果已知格林尼治恒星时t,测量地点的经度λ以及纬度φ,则可求出惯性系i与地理系g间的转换矩阵为
| $ \boldsymbol{C}_{i}^{g}(t)=\left[\begin{array}{l} -\sin (t+\lambda) & \cos (t+\lambda) & 0 \\ -\cos (t+\lambda) \sin \varphi & -\sin (t+\lambda) \sin \varphi &\cos \varphi \\ \cos (t+\lambda) \cos \varphi & \sin (t+\lambda) \cos \varphi & \sin \varphi \end{array}\right]. $ | (1) |
星敏感器光轴坐标系OpXpYpZp.由3个星敏光轴组成的非正交坐标系.OpXp沿着X星敏光轴,OpYp,OpZp分别沿着其余星敏光轴.
转台轴套坐标系O1X1Y1Z1固联在轴套上.设地理坐标系为单轴无磁转台的参考坐标系,则轴套坐标系相对地理坐标系的变换矩阵为[11]
| $ \boldsymbol{T}_{1}^{0}=\operatorname{rot}\left(x, \Delta \theta_{x 0}\right) * \operatorname{rot}\left(y, \Delta \theta_{y 0}\right), $ | (2) |
式中Δθx0、Δθy0称为主轴轴线的铅垂度,可在试验前通过水平仪精确测量.
主轴坐标系O2X2Y2Z2,主轴坐标系相对于轴套坐标系的姿态矩阵为[11]
| $ \begin{aligned} \boldsymbol{T}_{2}^{1}=& \operatorname{rot}\left(x_{1}, \Delta \theta_{x 1}(\gamma)\right) * \operatorname{rot}\left(y_{1}, \Delta \theta_{y 1}(\gamma)\right) * \\ & \operatorname{rot}\left(z_{1}, \gamma\right), \end{aligned} $ | (3) |
式中Δθx1(γ)、Δθy1(γ)为转台的倾角回转误差,在试验时由旋转轴监视系统进行实时监控.
安装基面坐标系O3X3Y3Z3,为考虑转台安装基面相对于轴系几何轴线的垂直度Δαx2,Δαy2形成,安装基面坐标系相对主轴坐标系的姿态矩阵为[11]
| $ \boldsymbol{T}_{3}^{2}=\operatorname{rot}\left(x_{2}, \Delta \alpha_{x 2}\right) \operatorname{rot}\left(y_{2}, \Delta \alpha_{y 2}\right). $ | (4) |
磁力仪测量坐标系O4X4Y4Z4.为正交坐标系,磁力仪位于初始位置时,O4X4轴与安装基面O3X3轴相差了一个绕O3Z3轴的初始安装角β,磁力仪测量坐标系相对安装基面坐标系的姿态矩阵为
| $ \boldsymbol{T}_{4}^{3}=\operatorname{rot}\left(z_{3}, \beta\right). $ | (5) |
由于磁力仪3个敏感轴存在着三轴非正交误差,初始安装磁力仪时,令磁力仪X轴Y轴处于水平状态,此时磁力仪敏感轴O4Z4与磁力仪敏感轴O5Z5平行,现称为第1种安装方式.设磁力仪敏感轴矢量在磁力仪测量坐标系O4X4Y4Z4的表示为
| $ \boldsymbol{T}_{5}^{4}=\left[\begin{array}{ccc} 1 & \Delta \theta_{y x} & \Delta \theta_{z x} \\ 0 & 1 & \Delta \theta_{z y} \\ 0 & 0 & 1 \end{array}\right], $ | (6) |
式中Δθyx、Δθzx、Δθzy分别为3个敏感轴间的垂直度.若3个参数为正,则表示磁力仪敏感轴之间夹角大于90°.由于加工水平与安装工艺的限制,以及磁力仪的内部存在剩磁,磁力仪输出模型中还存在着标度因子kx, ky, kz和零偏bx, by, bz,可在试验之前通过标定方法求出.设初始安装位置如图 1所示.结合式(2)~(6),此时磁力仪的输出表示为[12]
| $ \left[\begin{array}{c} R_{x} \\ R_{y} \\ R_{z} \end{array}\right]=\left[\begin{array}{lll} k_{x} & & \\ & k_{y} & \\ & & k_{z} \end{array}\right] \boldsymbol{T}_{0}^{5}\left[\begin{array}{c} B_{x} \\ B_{y} \\ B_{z} \end{array}\right]+\left[\begin{array}{c} b_{x} \\ b_{y} \\ b_{z} \end{array}\right]+\varepsilon. $ | (7) |
式中:B =[Bx By Bz]T为地理坐标系下的地磁场强度,由监测设备提供;R =[Rx Ry Rz]T为磁力仪的测量输出;ε为磁力仪噪声.
根据式(7),通过输入B,多个位置的输出R,以及由监测系统得到的监测数据,若能辨识出T05中的各个未知参数的值,就能得到初始位置下磁力仪敏感轴在地理坐标系下的表示,下面给出具体的试验方法.
3 磁力仪误差标定方法称图 1中固联体姿态为第1种安装方式下的初始位置,当单轴无磁转台旋转角度为γ时,采集三轴磁力仪的输出.展开式(7)并忽略二阶小量,有:
| $ \begin{array}{l} {R_{x1}} = \left[ {{k_x}{B_x}\left( {\cos \beta + \Delta {\theta _{yx}}\sin \beta } \right) + {k_x}{B_y}(\sin \beta - } \right.\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {\Delta {\theta _{yx}}\cos \beta } \right) + {k_x}{B_z}\left( { - \Delta {\theta _{y0}}\cos \beta - \Delta {\theta _{y1}}\cos \beta + } \right.\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {\left. {\Delta {\theta _{x0}}\sin \beta + \Delta {\theta _{x1}}\sin \beta } \right)} \right]\cos \gamma + \left[ {{k_x}{B_x}\left( { - \sin \beta + } \right.} \right.\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {\Delta {\theta _{yx}}\cos \beta } \right) + {k_x}{B_y}\left( {\cos \beta + \Delta {\theta _{yx}}\sin \beta } \right) + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {k_x}{B_z}\left( {\Delta {\theta _{x0}}\cos \beta + \Delta {\theta _{x1}}\cos \beta + \Delta {\theta _{y0}}\sin \beta + } \right.}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {\left. {\Delta {\theta _{y1}}\sin \beta } \right)} \right]\sin \gamma + {k_x}{B_z}\left( { - \Delta {\theta _{zx}} - \Delta {\alpha _{y2}}\cos \beta + } \right.}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {\Delta {\alpha _{x2}}\sin \beta } \right) + {b_x},} \end{array} $ | (8) |
| $ \begin{aligned} R_{y 1}=&\left[k_{y} B_{x}(-\sin \beta)+k_{y} B_{y}(\cos \beta)+\right.\\ & k_{y} B_{z}\left(\Delta \theta_{x 0} \cos \beta+\Delta \theta_{x 1} \cos \beta+\Delta \theta_{y 0} \sin \beta+\right.\\ &\left.\left.\Delta \theta_{y 1} \sin \beta\right)\right] \cos \gamma+\left[-k_{y} B_{x} \cos \beta-k_{y} B_{y} \sin \beta+\right.\\ & k_{y} B_{z}\left(\Delta \theta_{y 0} \cos \beta+\Delta \theta_{y 1} \cos \beta-\Delta \theta_{x 0} \sin \beta-\right.\\ &\left.\left.\Delta \theta_{x 1} \sin \beta\right)\right] \sin \gamma+k_{y} B_{z}\left(-\Delta \theta_{z y}+\Delta \alpha_{x 2} \cos \beta+\right.\\ &\left.\Delta \alpha_{y 2} \sin \beta\right)+b_{y}, \end{aligned} $ | (9) |
| $ \begin{aligned} R_{z 1}=&\left[\Delta \alpha_{y 2} k_{z} B_{x}-\Delta \alpha_{x 2} k_{z} B_{y}\right] \cos \gamma+\left[\Delta \alpha_{x 2} k_{z} B_{x}+\right.\\ &\left.\Delta \alpha_{y 2} k_{z} B_{y}\right] \sin \gamma+k_{z} B_{x}\left(\Delta \theta_{y 0}+\Delta \theta_{y 1}\right)-\\ & k_{z} B_{y}\left(\Delta \theta_{x 0}+\Delta \theta_{x 1}\right)+k_{z} B_{z}+b_{z}. \end{aligned} $ | (10) |
式(8)~(10)中存在的辨识参数有β,Δθyx,Δθzx,Δθzy,Δαx2和Δαy2.考虑使用谐波分析辨识,此时一周内采样点个数应大于辨识量的两倍.令γ=2πi/n(i=0, 1, 2, …, n-1),n=24,即单轴转台等间隔旋转24次,每次转台停稳并采集完磁力仪输出后进行下次旋转.
首先应辨识初始旋转角β,因只有在β已知的时才能获取磁力仪敏感轴在地理坐标系下的表示.利用采集到的磁力仪的Y轴输出对式(9)进行谐波分析,有:
| $ \begin{array}{l} {Y_1} = \frac{1}{n}\sum\limits_{i = 0}^{n - 1} {{R_{y1}}} \left( {\frac{{2{\rm{ \mathsf{ π} }}i}}{n}} \right) = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {k_y}{B_z}\left( { - \Delta {\theta _{zy}} + \Delta {\alpha _{x2}}\cos \beta + \Delta {\alpha _{y2}}\sin \beta } \right) + {b_y}, \end{array} $ | (11) |
| $ \begin{array}{l} {Y_2} = \frac{2}{n}\sum\limits_{i = 0}^{n - 1} {\left( {{R_{y1}}\left( {\frac{{2{\rm{ \mathsf{ π} }}i}}{n}} \right)\cos \frac{{2{\rm{ \mathsf{ π} }}i}}{n}} \right)} = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {k_y}{B_z}\left( {\Delta {\theta _{x0}}\cos \beta + \Delta {\theta _{x1}}\cos \beta + \Delta {\theta _{y0}}\sin \beta + } \right.\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {\Delta {\theta _{y1}}\sin \beta } \right) - {k_y}{B_x}\sin \beta + {k_y}{B_y}\cos \beta , \end{array} $ | (12) |
| $ \begin{array}{l} {Y_3} = \frac{2}{n}\sum\limits_{i = 0}^{n - 1} {\left( {{R_{y1}}\left( {\frac{{2{\rm{ \mathsf{ π} }}i}}{n}} \right)\sin \frac{{2{\rm{ \mathsf{ π} }}i}}{n}} \right)} = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {k_y}{B_z}\left( {\Delta {\theta _{y0}}\cos \beta + \Delta {\theta _{y1}}\cos \beta - \Delta {\theta _{x0}}\sin \beta - } \right.\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {\Delta {\theta _{x1}}\sin \beta } \right) - {k_y}{B_x}\cos \beta - {k_y}{B_y}\sin \beta . \end{array} $ | (13) |
由于Δθx0、Δθy0、Δθx1和Δθy1为小量,式(12)、(13)变为
| $ \left\{\begin{array}{l} -k_{y} B_{x} \sin \beta+k_{y} B_{y} \cos \beta \approx Y_{2}, \\ -k_{y} B_{x} \cos \beta-k_{y} B_{y} \sin \beta \approx Y_{3}, \end{array}\right. $ | (14) |
解式(14),求出β的初值β′为
| $ \beta^{\prime}=\arctan \frac{-Y_{2} B_{x}-Y_{3} B_{y}}{Y_{2} B_{y}-Y_{3} B_{x}}. $ | (15) |
精确值满足β=β′+Δβ,其中Δβ为小量.将其代回式(9),并将等式右边的Δθx0、Δθy0、Δθx1和Δθy1项补偿至Ry1,进行整理,并重新进行谐波分析,设补偿后的磁力仪输出为Fy,有:
| $ \begin{array}{l} {Y_4} = \frac{2}{n}\sum\limits_{i = 0}^{n - 1} {\left( {{F_y}\left( {\frac{{2{\rm{ \mathsf{ π} }}i}}{n}} \right)\cos \frac{{2{\rm{ \mathsf{ π} }}i}}{n}} \right)} = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - {k_y}{B_x}\left( {\sin {\beta ^\prime } + \Delta \beta \cos {\beta ^\prime }} \right) + {k_y}{B_y}\left( {\cos {\beta ^\prime } - } \right.\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {\Delta \beta \sin {\beta ^\prime }} \right), \end{array} $ | (16) |
| $ \begin{array}{l} {Y_5} = \frac{2}{n}\sum\limits_{i = 0}^{n - 1} {\left( {{F_y}\left( {\frac{{2{\rm{ \mathsf{ π} }}i}}{n}} \right)\sin \frac{{2{\rm{ \mathsf{ π} }}i}}{n}} \right)} = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {k_y}{B_x}\left( { - \cos {\beta ^\prime } + \Delta \beta \sin {\beta ^\prime }} \right) - {k_y}{B_y}\left( {\sin {\beta ^\prime } + } \right.\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {\Delta \beta \cos {\beta ^\prime }} \right). \end{array} $ | (17) |
联立式(16)、(17),求出Δβ的值为
| $ \Delta \beta=\frac{\left(Y_{5} \sin \beta^{\prime}-Y_{4} \cos \beta^{\prime}\right) B_{x}-\left(Y_{5} \cos \beta^{\prime}+Y_{4} \sin \beta^{\prime}\right) B_{y}}{k_{y}\left(B_{x}^{2}+B_{y}^{2}\right)}. $ | (18) |
至此完成了初始旋转角β的辨识.在此基础上,将等式右边的Δθx0、Δθy0、Δθx1和Δθy1项补偿至Rx1、Rz1,分别对磁力仪的X轴和Z轴输出进行谐波分析.设补偿后的输出分别为Fx和Fz.
| $ \begin{array}{l} {Y_6} = \frac{1}{n}\sum\limits_{i = 0}^{n - 1} {{F_x}} \left( {\frac{{2{\rm{ \mathsf{ π} }}i}}{n}} \right) = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {k_x}{B_z}\left( { - \Delta {\theta _{zx}} - \Delta {\alpha _{y2}}\cos \beta + \Delta {\alpha _{x2}}\sin \beta } \right) + {b_x}, \end{array} $ | (19) |
| $ \begin{array}{l} {Y_7} = \frac{2}{n}\sum\limits_{i = 0}^{n - 1} {\left( {{F_x}\left( {\frac{{2{\rm{ \mathsf{ π} }}i}}{n}} \right)\cos \frac{{2{\rm{ \mathsf{ π} }}i}}{n}} \right)} = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {k_x}{B_x}\left( {\cos \beta + \Delta {\theta _{yx}}\sin \beta } \right) + {k_x}{B_y}(\sin \beta - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {\Delta {\theta _{yx}}\cos \beta } \right), \end{array} $ | (20) |
| $ \begin{array}{l} {Y_8} = \frac{2}{n}\sum\limits_{i = 0}^{n - 1} {\left( {{F_x}\left( {\frac{{2{\rm{ \mathsf{ π} }}i}}{n}} \right)\sin \frac{{2{\rm{ \mathsf{ π} }}i}}{n}} \right)} = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {k_x}{B_x}\left( { - \sin \beta + \Delta {\theta _{yx}}\cos \beta } \right) + {k_x}{B_y}(\cos \beta + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {\Delta {\theta _{yx}}\sin \beta } \right), \end{array} $ | (21) |
| $ {Y_9} = \frac{2}{n}\sum\limits_{i = 0}^{n - 1} {\left( {{F_z}\left( {\frac{{2{\rm{ \mathsf{ π} }}i}}{n}} \right)\cos \frac{{2{\rm{ \mathsf{ π} }}i}}{n}} \right)} = {k_z}{B_x}\Delta {\alpha _{y2}} - {k_z}{B_y}\Delta {\alpha _{x2}}, $ | (22) |
| $ {Y_{10}} = \frac{2}{n}\sum\limits_{i = 0}^{n - 1} {\left( {{F_z}\left( {\frac{{2{\rm{ \mathsf{ π} }}i}}{n}} \right)\sin \frac{{2{\rm{ \mathsf{ π} }}i}}{n}} \right)} = {k_z}{B_x}\Delta {\alpha _{x2}} + {k_z}{B_y}\Delta {\alpha _{y2}}. $ | (23) |
结合式(20)、(21)求出Δθyx,联立式(22)、(23)求出Δαx2和Δαy2,分别为:
| $ \Delta \theta_{y x}=\frac{\left(Y_{7} \sin \beta+Y_{8} \cos \beta\right) B_{x}-\left(Y_{7} \cos \beta-Y_{8} \sin \beta\right) B_{y}}{k_{x}\left(B_{x}^{2}+B_{y}^{2}\right)}, $ | (24) |
| $ \Delta \alpha_{x 2}=\frac{Y_{10} B_{x}-Y_{9} B_{y}}{k_{z}\left(B_{x}^{2}+B_{y}^{2}\right)}, \Delta \alpha_{y 2}=\frac{Y_{9} B_{x}+Y_{10} B_{y}}{k_{z}\left(B_{x}^{2}+B_{y}^{2}\right)}. $ | (25) |
考虑式(11)、(19),可以看出Δθzy和Δθzx项与磁力仪的零偏误差发生混叠,辨识精度会受到严重影响,因此不能直接辨识.至此在第1次安装方式下,可以得到此时的初始旋转角β,磁力仪水平方向两轴之间的非正交误差Δθyx,和安装基面垂直度Δαx2和Δαy2.Δθzx,Δθzy由于不能精确标定,需要改变安装方式进行测量.
重新调整固联体的安装方式,当磁力仪X轴和Z轴位于水平,Y轴竖直时,称为第2种安装方式;当磁力仪Y轴和Z轴位于水平,X轴竖直时,称为第3种安装方式.按照第1种安装方式的步骤进行处理,此时不同安装方式下的初始旋转角将发生变化,进行谐波分析,可以求出各个辨识参数的值.对于第2种安装方式,可以求出水平面两轴垂直度Δθzx的值,对于第3种安装方式,可以求出水平面两轴垂直度Δθzy的值.
在第1次安装方式的初始位置下,磁力仪敏感轴坐标系在地理坐标系下的表示为
| $ \left[\begin{array}{lll} \boldsymbol{l}_{x 1}^{g} & \boldsymbol{l}_{y 1}^{g} & \boldsymbol{l}_{z 1}^{g} \end{array}\right]=\boldsymbol{T}_{1}^{0} \boldsymbol{T}_{2}^{1} \boldsymbol{T}_{3}^{2} \boldsymbol{T}_{4}^{3}, $ | (26) |
其中:
| $ \boldsymbol{l}_{x 1}^{g}=[\cos \beta \quad \sin \beta \quad A]^{\mathrm{T}}, \boldsymbol{l}_{y 1}^{g}=\left[\begin{array}{ccc} -\sin \beta & \cos \beta & B \end{array}\right]^{\mathrm{T}}, $ |
| $ \boldsymbol{l}_{z 1}^{g}\left[\begin{array}{ccc}\Delta \theta_{y 0}+\Delta \theta_{y 1}(0)+\Delta \alpha_{y 2}&-\Delta \theta_{x 0} -\Delta \theta_{x 1}(0)-\Delta \alpha_{x 2} &1\end{array}\right]^{\mathrm{T}}, $ |
| $ \begin{aligned} A=& \sin \beta\left(\Delta \theta_{x 0}+\Delta \theta_{x 1}(0)\right)-\cos \beta\left(\Delta \theta_{y 0}+\Delta \theta_{y 1}(0)\right)+\\ & \Delta \alpha_{x 2} \sin \beta-\Delta \alpha_{y 2} \cos \beta , \end{aligned} $ |
| $ \begin{aligned} B=& \cos \beta\left(\Delta \theta_{x 0}+\Delta \theta_{x 1}(0)\right)+\sin \beta\left(\Delta \theta_{y 0}+\Delta \theta_{y 1}(0)\right)+\\ & \Delta \alpha_{x 2} \cos \beta+\Delta \alpha_{y 2} \sin \beta. \end{aligned} $ |
磁力仪测量磁场的同时,利用星敏感器进行观星.在第1次安装方式的初始位置,假定3个星敏感器均能够观星.设某星敏感器视场内能观测到的某颗恒星的赤经为α,赤纬为δ.则在惯性坐标系下的单位恒星矢量为[13]
| $ \boldsymbol{A}=[\cos \alpha \cos \delta \quad \sin \alpha \cos \delta \quad \sin \delta]^{\mathrm{T}}, $ | (27) |
星敏感器观测该恒星,得到该恒星发出的光映射在该星敏感器测量坐标系下的坐标:
| $ \boldsymbol{S}=\frac{1}{\sqrt{x^{2}+y^{2}+f^{2}}}\left[\begin{array}{lll} -x & -y & f \end{array}\right]^{\mathrm{T}} $ | (28) |
星敏感器在同一时刻能够观测多个恒星,得到了多组矢量对Ai和Si.根据坐标系间变换关系,有
| $ \boldsymbol{A}_{i}=\boldsymbol{T}_{s}^{i} \boldsymbol{S}_{i}. $ | (29) |
根据不同坐标系中矢量组计算坐标系间姿态矩阵又称为Wahba问题[14],常用的方法为QUEST算法[15].求出此时3颗星敏在惯性系的姿态Tsi,并将各个星敏的光轴矢量提出,组成星敏光轴坐标系矢量在惯性系下的表示,设为lpxi,lpyi,lpzi. 在星敏观星时记录格林尼治恒星时t,结合当地经纬度信息,利用式(1)将星敏光轴矢量转化为地理坐标系下的表示为
| $ \left[\begin{array}{lll} \boldsymbol{l}_{p x}^{g} & \boldsymbol{l}_{p y}^{g} & \boldsymbol{l}_{p z}^{g} \end{array}\right]=\boldsymbol{C}_{i}^{g}\left[\begin{array}{lll} \boldsymbol{l}_{p x}^{i} & \boldsymbol{l}_{p y}^{i} & \boldsymbol{l}_{p z}^{i} \end{array}\right]. $ | (30) |
由于3颗星敏安装工艺的限制,三轴之间存在着垂直度误差,将星敏光轴进行正交化,建立星敏感器正交坐标系OXtYtZt,其与星敏感器光轴坐标系的关系为
| $ \left[\begin{array}{lll} \boldsymbol{x}_{t}& \boldsymbol{y}_{t} & \boldsymbol{z}_{t} \end{array}\right]=\left[\begin{array}{lll} \boldsymbol{l}_{p x}^{g} & \boldsymbol{l}_{p y}^{g} & \boldsymbol{l}_{p z}^{g} \end{array}\right]\left[\begin{array}{ccc} 1 & 0 & 0 \\ -\boldsymbol{l}_{p x}^{g} \cdot \boldsymbol{l}_{p y}^{g} & 1 & 0 \\ -\boldsymbol{l}_{p x}^{g} \cdot \boldsymbol{l}_{p z}^{g} & -\boldsymbol{l}_{p y}^{g} \cdot \boldsymbol{l}_{p z}^{g} & 1 \end{array}\right] . $ | (31) |
由于星敏感器与磁力仪通过夹具体固联,二者的夹角不会发生变化,磁力仪三轴垂直度以及星敏感器三轴垂直度也不会发生变化,所以由三轴磁力仪至星敏感器的正交安装矩阵表示为
| $ \boldsymbol{L}_{s}^{t}=\left[\begin{array}{lll} \boldsymbol{l}_{x}^{g} \cdot \boldsymbol{x}_{t} & \boldsymbol{l}_{y}^{g} \cdot \boldsymbol{x}_{t} & \boldsymbol{l}_{z}^{g} \cdot \boldsymbol{x}_{t} \\ \boldsymbol{l}_{x}^{g} \cdot \boldsymbol{y}_{t} & \boldsymbol{l}_{y}^{g} \cdot \boldsymbol{y}_{t} & \boldsymbol{l}_{z}^{g} \cdot \boldsymbol{y}_{t} \\ \boldsymbol{l}_{x}^{g} \cdot \boldsymbol{z}_{t} & \boldsymbol{l}_{y}^{g} \cdot \boldsymbol{z}_{t} & \boldsymbol{l}_{z}^{g} \cdot \boldsymbol{z}_{t} \end{array}\right]. $ | (32) |
在实际的卫星地磁测量中,通过磁力仪测量磁场,并瞬时测得星敏相对惯性空间的姿态,以及此时的经纬度和格林尼治恒星时,结合式(32)的正交安装矩阵以及辨识出的磁力仪三轴垂直度误差Δθyx,Δθzx,Δθzy,星敏感器3个光轴的垂直度,即可解算出该位置下的地磁场矢量信息,为地磁场信息库的建立打下基础.
5 仿真验证为了验证本文基于误差模型提出的标定方法的正确性,利用Monte Carlo方法验证.假定测量位置地磁场强度为三分量Bx为-3 275.9 nT,By为27 102.2 nT,Bz为-48 085.0 nT.各个参数初值见表 1.
| 表 1 误差参数初值 Tab. 1 Initial values of error parameters |
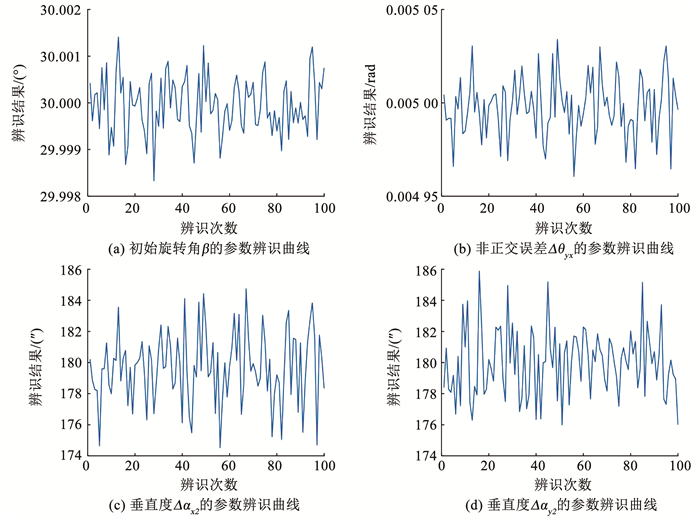
以第1次安装方式为例,选择矢量磁力仪测量噪声为σ=1.00 nT的零均值高斯白噪声,单轴转台每次安装方式等间隔旋转24次,利用Monte Carlo方法设计仿真算法辨识误差参数,共辨识100次,将计算结果绘制成曲线,如图 2所示.
|
图 2 误差参数辨识曲线 Fig. 2 Error parameters identification curves |
针对得到的辨识结果,计算出各个参数的残差εi(β),εi(Δθyx),εi(Δαx2)和εi(Δαy2).残差的计算公式和残差的标准差公式分别为:
| $ \begin{array}{*{20}{l}} {{\varepsilon _i}(\beta ) = \beta (i) - \bar \beta ,{\varepsilon _i}\left( {\Delta {\theta _{yx}}} \right) = \Delta {\theta _{yx}}(i) - \bar \Delta {\theta _{yx}},}\\ {{\varepsilon _i}\left( {\Delta {\alpha _{x2}}} \right) = \Delta {\alpha _{x2}}(i) - \bar \Delta {\alpha _{x2}},{\varepsilon _i}\left( {\Delta {\alpha _{y2}}} \right) = \Delta {\alpha _{y2}}(i) - \bar \Delta {\alpha _{y2}},}\\ {{\sigma _\varepsilon } = \sqrt {\frac{{\sum\limits_{i = 0}^{n - 1} {\varepsilon _i^2} }}{{n - k}}} = \sqrt {\frac{{{\mathit{\boldsymbol{\varepsilon }}^{\rm{T}}}\mathit{\boldsymbol{\varepsilon }}}}{{n - k}}} .} \end{array} $ | (33) |
式中: β、Δθyx、Δαx2、Δαy2分别为各个参数的辨识输出;β、Δθyx、Δαy2、Δαy2分别为各个参数的辨识输出均值;ε为实际输出值与辨识输出值之间的残差向量;n为测量次数;k为辨识的系数数量.
利用式(33)求出辨识参数的不确定度为: σ(β)=2.29″,σ(Δθyx)=3.17″,σ(Δαx2)=2.20″,σ(Δαy2)=2.20″.
由于3次安装方式下的条件相同,可以认为Δθzx,Δθzy的辨识精度与Δθyx相同.利用不确定度合成公式,结合求出的各个辨识参数的不确定度即可求出磁力仪敏感轴的辨识值以及辨识精度.忽略小量,有:
| $ \sigma \left( {\mathit{\boldsymbol{l}}_{x1}^g} \right) = {\left[ {\begin{array}{*{20}{l}} {|\cos \beta |\sigma (\beta )}&{|\sin \beta |\sigma (\beta )}&{\sigma \left( {\Delta {\alpha _{x2}}} \right)} \end{array}} \right]^{\rm{T}}}, $ | (34) |
| $ \sigma \left( {\mathit{\boldsymbol{l}}_{y1}^g} \right) = {\left[ {\begin{array}{*{20}{l}} {|\sin \beta |\sigma (\beta )}&{|\cos \beta |\sigma (\beta )}&{\sigma \left( {\Delta {\alpha _{x2}}} \right)} \end{array}} \right]^{\rm{T}}}, $ | (35) |
| $ {\sigma \left( {\mathit{\boldsymbol{l}}_{z1}^g} \right) = {{\left[ {\begin{array}{*{20}{l}} {\sigma \left( {\Delta {\alpha _{x2}}} \right)}&{\sigma \left( {\Delta {\alpha _{x2}}} \right)}&0 \end{array}} \right]}^{\rm{T}}}.} $ | (36) |
假定经过长时间观星后,星敏感器光轴指向精度Δα为1",设X星敏感器的光轴矢量为
| $ \boldsymbol{l}_{p x}^{i}=\left[\begin{array}{lll} l_{x} & l_{y} & l_{z} \end{array}\right]^{\mathrm{T}}. $ | (37) |
按照不确定度的分配规律,则此时的不确定度为:
| $ \begin{array}{c} \sigma\left(l_{x}\right)=\frac{\sqrt{2}}{2} \sqrt{l_{y}^{2}+l_{z}^{2}} \Delta \alpha, \sigma\left(l_{y}\right)=\frac{\sqrt{2}}{2} \sqrt{l_{x}^{2}+l_{z}^{2}} \Delta \alpha ,\\ \sigma\left(l_{z}\right)=\frac{\sqrt{2}}{2} \sqrt{l_{x}^{2}+l_{y}^{2}} \Delta \alpha. \end{array} $ | (38) |
当星敏观测时刻惯性坐标系到地理坐标系的转换矩阵为
| $ \boldsymbol{C}_{i}^{g}=\left[\begin{array}{lll} m_{11} & m_{12} & m_{13} \\ m_{21} & m_{22} & m_{23} \\ m_{31} & m_{32} & m_{33} \end{array}\right]. $ | (39) |
于是X星敏光轴矢量在地理系下表示和不确定度为:
| $ \boldsymbol{l}_{p x}^{\mathrm{g}}=\left[\begin{array}{c} m_{11} l_{x}+m_{12} l_{y}+m_{13} l_{z} \\ m_{21} l_{x}+m_{22} l_{y}+m_{23} l_{z} \\ m_{31} l_{x}+m_{32} l_{y}+m_{33} l_{z} \end{array}\right], $ | (40) |
| $ \sigma\left(\boldsymbol{l}_{p x}^{g}\right)=\left\{\begin{array}{l} \sqrt{\left[m_{11} \sigma\left(l_{x}\right)\right]^{2}+\left[m_{12} \sigma\left(l_{y}\right)\right]^{2}+\left[m_{13} \sigma\left(l_{z}\right)\right]^{2}}, \\ \sqrt{\left[m_{21} \sigma\left(l_{x}\right)\right]^{2}+\left[m_{22} \sigma\left(l_{y}\right)\right]^{2}+\left[m_{23} \sigma\left(l_{z}\right)\right]^{2}}, \\ \sqrt{\left[m_{31} \sigma\left(l_{x}\right)\right]^{2}+\left[m_{32} \sigma\left(l_{y}\right)\right]^{2}+\left[m_{33} \sigma\left(l_{z}\right)\right]^{2}}. \end{array}\right. $ | (41) |
对于Y和Z星敏光轴矢量不确定度可由相同公式求出.由于星敏光轴间垂直度为小量,根据不确定度合成公式可忽略其对测量精度的影响,认为正交化前后精度一致.即有σ(xt)=σ(lpxg).
对于任意两矢量F =[f1 f2 f3]T,G =[g1 g2 g3]T,其点积F·G的不确定度为
| $ \begin{aligned} \sigma(\boldsymbol{F} \cdot \boldsymbol{G})^{2}=&\left(g_{1} \sigma\left(f_{1}\right)\right)^{2}+\left(g_{2} \sigma\left(f_{2}\right)\right)^{2}+\left(g_{3} \sigma\left(f_{3}\right)\right)^{2}+\\ &\left(f_{1} \sigma\left(g_{1}\right)\right)^{2}+\left(f_{2} \sigma\left(g_{2}\right)\right)^{2}+\left(f_{3} \sigma\left(g_{3}\right)\right)^{2}. \end{aligned} $ | (42) |
对于安装矩阵式(32),由式(42)即可求出安装矩阵中各元素的不确定度.以安装矩阵Lst中首行首列的元素L11为例,若xt=[xx xy xz]T,有
| $ \begin{aligned} \sigma\left(L_{11}\right)^{2}=&\left(x_{x}|\cos \beta| \sigma(\beta)\right)^{2}+\left(x_{y}|\sin \beta| \sigma(\beta)\right)^{2}+\\ &\left(x_{z} \sigma\left(\Delta \alpha_{x 2}\right)\right)^{2}+\left(\cos \beta \sigma\left(x_{x}\right)\right)^{2}+\\ &\left(\sin \beta \sigma\left(x_{y}\right)\right)^{2}+\left(A \sigma\left(x_{z}\right)\right)^{2}. \end{aligned} $ | (43) |
假设观测地的经纬度信息为北纬40.9°,东经115.5°,取对应的格林尼治恒星时为218.63°.利用式(1)得到惯性坐标系到地理坐标系的转换矩阵:
| $ \boldsymbol{C}_{i}^{g}=\left[\begin{array}{rrrrrrr} 0.436\ 271\ 5 & 0.899\ 815\ 1 & 0 .\ 000\ 000 \ 0 \\ -0.589\ 145\ 7 & 0.285\ 644\ 8 & 0.755\ 853\ 5 \\ 0.680\ 128\ 3 & -0.329\ 757\ 3 & 0.654\ 740\ 8 \end{array}\right] . $ | (44) |
3个星敏感器的光轴矢量分别为:
| $ \boldsymbol{l}_{x}^{i}(1)=\left[\begin{array}{llllll} 0.359\ 680\ 0 & -0.799\ 400\ 0 & 0.481\ 240\ 0 \end{array}\right]^{\mathrm{T}}, $ | (45) |
| $ \boldsymbol{l}_{y}^{i}(1)=\left[\begin{array}{lllllll} 0.479\ 200\ 0 & 0.600\ 000\ 0 & 0.640\ 600\ 0 \end{array}\right]^{\mathrm{T}}, $ | (46) |
| $ \boldsymbol{l}_{z}^{i}(1)=\left[\begin{array}{lllllll} -0.800\ 000\ 0& 0 & 0.600\ 000\ 0 \end{array}\right]^{\mathrm{T}} . $ | (47) |
按照上述方法计算,最终求出安装矩阵及各个元素不确定度为:
| $ \boldsymbol{L}_{s}^{t}=\left[\begin{array}{rrrrrrr} -0.526\ 586\ 27 & 0.215\ 113\ 58 & 0.822\ 456\ 27 \\ 0.834\ 889\ 03 & -0.051\ 464\ 25 & 0.548\ 007\ 62 \\ 0.160\ 210\ 40 & 0.975\ 232\ 79 & -0.152\ 495\ 61 \end{array}\right], $ | (48) |
| $ \sigma\left(\boldsymbol{L}_{s}^{t}\right)=\left[\begin{array}{lll} 10.6 & 11.4 & 7.82 \\ 8.95 & 10.1 & 9.80 \\ 9.42 & 6.71 & 11.0 \end{array}\right] \times 10^{-6} $ | (49) |
1) 在建立误差模型的基础上,利用谐波分析法可以辨识得到包括磁力仪三轴垂直度、初始安装角、安装误差等误差参数.
2) 根据辨识结果求出磁力仪测量坐标系在地理坐标系下的表示,结合星敏感器观星确定星敏感器在惯性空间姿态并转化到地理坐标系,最终推导了磁力仪测量坐标系到星敏感器正交坐标系的安装矩阵计算公式.
3) 通过仿真验证,在1 nT的磁力仪测量噪声以及1″的星敏测量精度下,求出安装矩阵内各个元素的精度在1.14×10-5 rad以内.
| [1] |
杨云涛, 石志勇, 关贞珍, 等. 地磁场在导航定位系统中的应用[J]. 中国惯性技术学报, 2007, 15(6): 686. YANG Yuntao, SHI Zhiyong, GUAN Zhenzhen, et al. Application of geomagnetic field in navigation and localization system[J]. Journal of Chinese Inertial Technology, 2007, 15(6): 686. DOI:10.3969/j.issn.1005-6734.2007.06.012 |
| [2] |
LI Ji, ZHANG Qi, CHEN Dixiang, et al. Magnetic interferential field compensation in geomagnetic measurement[J]. Transactions of the Institute of Measurement and Control, 2014, 36(2): 244. DOI:10.1177/0142331213497620 |
| [3] |
常宜峰. 卫星磁测数据处理与地磁场模型反演理论与方法研究[D]. 郑州: 解放军信息工程大学, 2015 CHANG Yifeng. Research on satellite geomagnetic data process and geomagnetic model recovery theory and method[D]. Zhengzhou: Information Engineering University, 2015. DOI: 10.7666/d.D829556 |
| [4] |
SIMPSON D G, VIÑAS A F. NASA computational case study: Modeling planetary magnetic and gravitational fields[J]. Computing in Science & Engineering, 2014, 16(4): 73. DOI:10.1109/MCSE.2014.78 |
| [5] |
HABIB T M A. Fast converging with high accuracy estimates of satellite attitude and orbit based on magnetometer augmented with gyro, star sensor and GPS via extended Kalman filter[J]. Egyptian Journal of Remote Sensing & Space Sciences, 2011, 14(2): 57. DOI:10.1016/j.ejrs.2011.06.002 |
| [6] |
杨照华, 余远金, 祁振强. 空间环境探测卫星用磁强计误差分析及在线标定[J]. 宇航学报, 2012, 33(8): 1104. YANG Zhaohua, YU Yuanjin, QI Zhenqiang. Error analysis and on-board calibration of magnetometer in space environment exploration satellite[J]. Journal of Astronautics, 2012, 33(8): 1104. DOI:10.3873/j.issn.1000-1328.2012.08.015 |
| [7] |
郝寿, 绳涛, 陈小前. 三轴磁强计测量误差修正方法[J]. 航天器环境工程, 2011, 28(5): 463. HAO Shou, SHENG Tao, CHEN Xiaoqian. The error correction of three-axis magnetometer measurement[J]. Spacecraft Environment Engineering, 2011, 28(5): 463. DOI:10.3969/j.issn.1673-1379.2011.05.012 |
| [8] |
张艺腾, 王劲东, 刘振平. 高精度航空矢量磁力仪与姿态仪的联合标定[C]//第三届高分辨率对地观测学术年会分会论文集. 北京: 中国科学院重大科技任务局, 2014: 453 ZHANG Yiteng, WANG Jindong, LIU Zhenping. High precision aviation vector magnetometer and attitude indicator joint calibration[C]//Proceedings of the 3rd China High Resolution Earth Observation Conference. Beijing: Bureau of major R&D Programs Chinese Academy of Sciences, 2014: 453 |
| [9] |
孙闯, 王凯强, 任顺清. 星敏与磁强计安装矩阵的户外标定[J]. 导航定位与授时, 2016, 3(2): 77. SUN Chuang, WANG Kaiqiang, REN Shunqing. Calibration of installing matrix between magnetometer and star sensor[J]. Navigation Positioning and Timing, 2016, 3(2): 77. DOI:10.19306/j.cnki.2095-8110.2016.02.014 |
| [10] |
王凯强. 星敏感器与磁强计安装矩阵的测试监测方法及其误差分析[D]. 哈尔滨: 哈尔滨工业大学, 2016 WANG Kaiqiang. Measuring and monitoring method and error analysis of the installed matrix about star sensors and magnetometers[D]. Harbin: Harbin Institute of Technology, 2016. DOI: 10.7666/d.D01098692 |
| [11] |
任顺清, 房振勇, 吴广玉, 等. 竖直轴系倾角回转误差的两种测试方法的比较[J]. 中国惯性技术学报, 2000, 8(3): 74. REN Shunqing, FANG Zhenyong, WU Guangyu, et al. The contrast of two methods of measuring wobble error in perpendicular axis system[J]. Journal of Chinese Inertial Technology, 2000, 8(3): 74. DOI:10.3969/j.issn.1005-6734.2000.03.017 |
| [12] |
PANG Hongfeng, CHEN Dixiang, PAN Mengchun, et al. Improvement of magnetometer calibration using levenberg-marquardt algorithm[J]. IEEJ Transactions on Electrical and Electronic Engineering, 2014, 9(3): 324. DOI:10.1002/tee.21973 |
| [13] |
易敏, 邢飞, 孙婷, 等. 高精度星敏感器标定方法研究[J]. 仪器仪表学报, 2017, 38(9): 2154. YI Min, XING Fei, SUN Ting, et al. Calibration method of high-accuracy star sensor[J]. Chinese Journal of Scientific Instrument, 2017, 38(9): 2154. DOI:10.3969/j.issn.0254-3087.2017.09.008 |
| [14] |
WAHBA G. A least squares estimate of satellite attitude[J]. SIAM Review, 1965, 7(3): 409. DOI:10.1137/1007077 |
| [15] |
SHUSTER M D. The quest for better attitudes[J]. The Journal of the Astronautical Sciences, 2006, 54(3/4): 657. DOI:10.1007/BF03256511 |
 2021, Vol. 53
2021, Vol. 53


