2. 中国船舶重工集团公司第705研究所,西安 710077
2. The 705 Research Institute, China State Shipbuilding Industry Corporation, Xi'an 710077, China
火箭发动机在水下工作时,其燃气喷射流结构远比大气中复杂[1].由于环境水密度大、压力高等特点,水下火箭发动机工作过程可能发生安全故障[2].“暴风雪”鱼雷推进系统采用的是火箭发动机,通气超空泡会在尾部与喷射气流发生耦合作用,可能会对发动机性能产生影响[3],因此深入研究通气超空化对水下火箭发动机工作性能及安全特性影响,具有十分重要的理论价值和工程应用价值.
国内外众多学者对静水条件下的水下喷射气流开展大量研究.王超等[4-5]重点研究了静水条件下欠膨胀水下超声速喷射流流场变化特性;李婷婷等[6]开展了水下竖直环形喷管喷射流实验,观察到射流颈缩、夹断现象;He等[7]开展矩形喷嘴在不同压比下喷射流实验,得到了管外激波系移动现象;Shi等[8-9]开展了水下喷射流3种膨胀状态系列实验,并分析了诱导喷射流流场脉动的原因;Harby等[10]开展无冷凝气体喷射入水动态实验,得到了气-水交界面不稳定性与喷管出口参数有关;Tang等[11]研究表明水下推力不仅与喷管结构有关,还与射流结构和相应的压力分布有关.
为深入研究水下火箭发动机工作特性,众多学者开展了水流速度对水下喷射气流影响的研究.许海雨等[12]研究了来流速度对超声速喷射流非稳定流场的影响特性,发现水流速有助于流场的稳定;张孝石等[13]开展了有流速的水下超声速射流实验研究,得到了水流速度对喷射流形态影响规律;甘晓松等[14]研究了水流速度对喷射流影响,发现有来流情况下燃气射流没有断裂和回击现象;唐嘉宁等[15]研究了低速工况下水下火箭发动机的推力特性,发现发动机推力剧烈振荡特性.
通气超空化对水下火箭发动机影响的研究较少.党建军等[16]开展了尾部喷射流的试验研究,获得了喷射流对超空泡流型影响规律;Kinzel等[17]研究了通气超空泡与喷射流的相互作用,分析了喷射流强度与空泡形态的关系;Meyon等[18]试验研究了通气超空泡与喷射流的耦合作用.上述研究集中在喷射流对超空泡流型及超空泡泄气率影响,通气超空化对水下喷射流作用特性的研究鲜有报道.
国内外对水下喷射流的研究大多集中在无水流或低水速喷射气流发展及流场变化特性,缺乏高水速、通气超空泡耦合作用对水下发动机工作特性的影响研究.本文在高水流速度条件下,对比研究了无空化、通气空化工况水下火箭发动机不同工作状态射流结构及发动机工作性能,重点分析了通气超空泡对水下火箭发动机工作安全性及流场脉动特性的影响.
1 计算方法 1.1 数值方法 1.1.1 控制方程基于VOF多相流模型的控制方程包括质量守恒方程、动量守恒方程、能量方程,体积分数输运方程[15],控制方程具体如下:
| $ \frac{\partial \rho_{\mathrm{m}}}{\partial t}+\nabla \cdot\left(\rho_{\mathrm{m}} \overrightarrow{\boldsymbol{v}}\right)=0, $ | (1) |
| $ \begin{array}{l} \frac{\partial}{\partial t}\left(\rho_{\mathrm{m}} \overrightarrow{\boldsymbol{v}}\right)+\nabla \cdot\left(\boldsymbol{\rho}_{\mathrm{m}} \overrightarrow{\boldsymbol{v}}\overrightarrow{\boldsymbol{v}}\right)= \\ -\nabla p+\nabla \cdot\left[\mu_{\mathrm{m}}\left(\nabla \overrightarrow{\boldsymbol{v}}+\nabla \overrightarrow{\boldsymbol{v}}^{\mathrm{T}}\right)\right]+\rho_{\mathrm{m}} \overrightarrow{\boldsymbol{f}}, \end{array} $ | (2) |
| $ \begin{array}{l} \frac{\partial}{\partial t}\left(\rho_{\mathrm{m}} E_{\mathrm{m}}\right)+\nabla \cdot\left(\overrightarrow{\boldsymbol{v}}\left(\rho_{\mathrm{m}} E_{\mathrm{m}}+p\right)\right)= \\ \nabla \cdot\left(k_{\mathrm{eff}} \nabla T_{\mathrm{m}}\right)+S_{\mathrm{h}} \cdot \frac{\partial}{\partial t}\left(\alpha_{g} \rho_{\mathrm{g}}\right)+\frac{\partial}{\partial x_{j}}\left(\alpha_{g} \rho_{\mathrm{g}} \boldsymbol{v}\right)=0. \end{array} $ | (3) |
式中:ρm、μm分别为流体微元的各平均密度和动力黏度;
本文采用Realizable k-ε湍流模型对雷诺平均N-S方程进行封闭.该模型的k和ε的输运方程为:
| $ \begin{array}{l} \frac{\partial}{\partial t}(\rho k)+\nabla \cdot(\rho k \vec{\boldsymbol{v}})=\nabla \cdot\left[\left(\mu+\mu_{\mathrm{t}} / \sigma_{\mathrm{k}}\right) \nabla k\right]+\\ G_{\mathrm{k}}+G_{\mathrm{b}}-\rho \varepsilon-Y_{\mathrm{M}}, \end{array} $ | (4) |
| $ \begin{array}{l} \frac{\partial}{\partial t}(\rho \varepsilon)+\nabla \cdot(\rho \varepsilon \vec{\boldsymbol{v}})=\nabla \cdot\left[\left(\mu+\mu_{\mathrm{t}} / \sigma_{\mathrm{k}}\right) \nabla \varepsilon\right]+\\ \rho C_{1} S \varepsilon-\frac{\rho C_{2} \varepsilon^{2}}{k+\sqrt{v \varepsilon}}+C_{1 \varepsilon} \frac{\varepsilon}{k} C_{3 \varepsilon} G_{\mathrm{b}}. \end{array} $ | (5) |
式中:Gk为速度梯度引起的湍流动能; Gb为浮力引起的湍动能; YM为可压缩湍流脉动膨胀对耗散率的影响; μt=ρCμk2/ε为湍流黏性系数,Realizable k-ε湍流模型中Cμ是平均应变率与旋度的函数,在平衡边界层惯性底层Cμ=0.09,模型常数C1=max[0.43, η/η+5],η=Sk/ε,C2=1.9,C1ε=1.44,σk=1.0,σε=1.2,
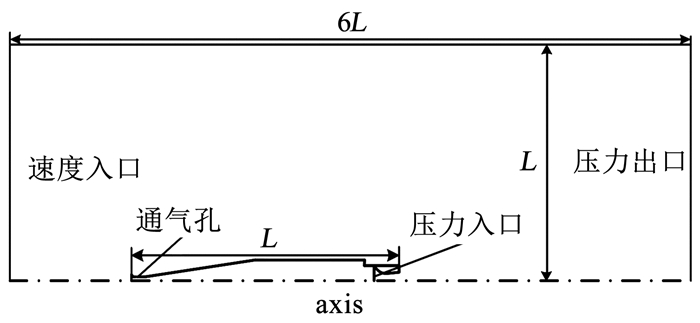
采用二维轴对称模型计算研究通气超空化对水下火箭发动机工作性能影响,经过时间步长无关性检验,计算步长为1×10-6 s,计算域如图 1所示. 以航行器总长度L为基准,流域总长度为6L,宽度为L,喷管进口设置为压力进口边界条件,雷体表面与流场上边界设置为壁面边界条件,左边界为速度进口条件,水流速为50 m/s,距离空化器长度为L,右边界为压力出口条件,距离航行器尾端面4L,通气孔为质量流量入口条件.整个计算域采用结构化网格划分,对喷管及射流核心区网格加密,网格如图 2所示.
|
图 1 计算域及边界条件 Fig. 1 Calculation domain and boundary conditions |

|
图 2 网格分布 Fig. 2 Grid distribution |
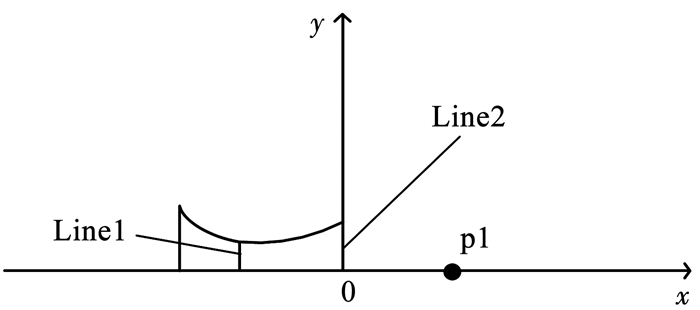
为了研究通气超空化对水下火箭发动机特性影响,选取p1作为监测点,以监测流场压力脉动特性,距离喷管出口位置0.75De,其中De为喷管出口直径;分别选择Line1和Line2,以监测喷管喉部流量和出口平均压力, 如图 3所示.
|
图 3 监测位置设置 Fig. 3 Monitoring points and lines |
文献[4]在水池中进行常温空气超声速水下射流的实验,为了校验数值模型的计算精度,本文采用与此实验相同的工况进行数值仿真,并将数值模拟结果与实验进行对比.
由图 4可知,水下超声速射流由于气液交界不稳定性,气体状态发生时时改变.高速射流大部分时间均处于标称状态(见图 4(a)),其中标称状态指的是超声速燃气射流未发生颈缩、胀鼓、断裂、回击等典型周期现象的气流状态,可将射流区域分为射流区、过渡区与羽流区,水下超声速气体射流会发生间歇性颈缩(见图 4(b)),气流通道便会出现梗阻而导致气体迅速聚集,因而射流发生快速膨胀(见图 4(c));液相的惯性限制了射流在径向方向上持续膨胀,使得膨胀主要在轴向方向上进行,这样沿轴线膨胀的气体分离成两个部分,一部分流向下游,一部分流向上游而产生回击现象(见图 4(d)).

|
图 4 数值结果与实验结果对比 Fig. 4 Comparison of experimental and numerical results |
数值结果可以很好地复现水下喷射流特有的颈缩、胀鼓、回击等现象,表明数值模型的准确性,可用于后文开展水下喷射流特性研究.
2 计算结果及分析本文分别对无空化和通气空化时水下火箭发动机工作性能进行研究.在本文计算中,设计了两种喷管工作状态(完全膨胀和过膨胀)的工况,燃烧室压力P*为7.5 MPa,燃烧室温度T*为2 500 K,具体见表 1.其中压比π定义为燃烧室压力P*与环境背压Pb之比.
| 表 1 计算工况 Tab. 1 Calculation conditions |
图 5给出了在完全膨胀和过膨胀工况燃气射流典型现象的演变过程. 其中A, B, C, D分别为颈缩、断裂、胀鼓和回击4种水下喷射流典型现象.从图 5中可知,完全膨胀工况水下燃气射流演变与在气相环境中的射流发展过程有很大差异.由于水大密度作用,射流的发展受到严重阻滞,燃气射流径向膨胀时间有限,主要延轴向发展,且燃气射流基本保持连续流动,未发生明显断流与回击现象,但在远离喷管的外流场区域中,燃气射流出现了颈缩、胀鼓现象.

|
图 5 燃气喷射流典型工况图 Fig. 5 Typical phenomena of the gas jet flow |
过膨胀工况燃气射流在发展的过程中出现颈缩、断裂、胀鼓、回击等典型的水下射流现象.在A处,可明显观察到燃气射流呈现长细状并形成颈缩,部分燃气由于高压作用向周围翻卷;在B处,由于颈缩程度加强,出现了断裂,但气流未完全夹断;在C处,燃气射流由于断裂而引起压力显著升高,气体开始沿径向发展形成胀鼓,但是在一些时刻胀鼓现象维持的时间极短,气泡没来得及膨胀就已经被水流冲击带动向前流动;在D处,由于气泡膨胀后压力迅速减小,在后面水高压的作用下,会推进一部分燃气向前发展,并且胀鼓现象发生的位置靠近喷管出口,因而射流击打航行器尾部,产生回击现象.相比于完全膨胀状态,过膨胀射流发展速度较快,射流流动更加复杂,并且发生典型周期现象的位置更靠近喷管出口.
2.1.2 无空化工况发动机性能图 6给出了喷管出口平均压力的时变曲线.从图 6中可知,完全膨胀下喷管出口平均压力脉动幅度较小,压力在1.5 MPa上、下小幅度振荡.而在过膨胀工况由于外界水压作用,气-水交界的不稳定性会引起较为剧烈的压力脉动,压力幅值最大为6.1 MPa.造成两种状态出口压力特性迥异的原因有两点,一个是两种工况流场非定常性强度不同,过膨胀工况气/水交界不稳定性更强,射流出现了颈缩、断裂、胀鼓和回击现象,而完全膨胀工况只出现了颈缩、胀鼓现象,这从射流演变图中可知;另一个是发生典型周期现象位置不同,过膨胀工况发生典型周期现象的位置距离喷管出口更近,压力脉动对喷管影响强烈,而完全膨胀工况的典型周期现象发生位置离喷管较远,作用效应弱.

|
图 6 在完全膨胀和过膨胀两种工况喷管出口平均压力脉动特性 Fig. 6 Average outlet pressure of nozzle under full-expansion and over-expansion conditions |
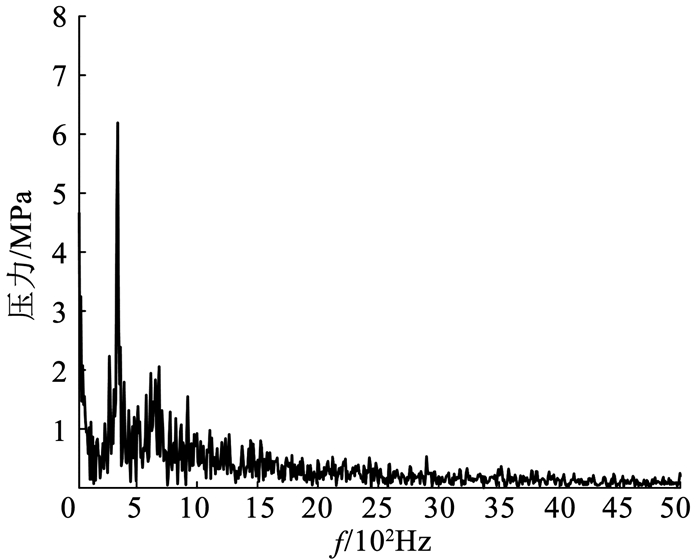
图 7为过膨胀工况喷管出口压力的频谱分析图.由图 7可知,过膨胀喷管出口出现最大压力幅值时,其频率大约为300 Hz,喷管出口压力的机械能量主要分布在0~2 000 Hz范围内,此时压力振荡剧烈,而频率大于2 000 Hz后,能量逐渐减小,流场脉动特性较弱.
|
图 7 过膨胀喷管出口压力频谱图 Fig. 7 FFT of outlet pressure of nozzle under over-expansion condition |
根据射流演变过程分析可知,流场中出现了颈缩、断裂、胀鼓和回击等水下喷射流特有典型周期现象,流场的非稳定性可能会影响水下发动机工作性能,因此靠近喷管出口(p1)的压力时变如图 8所示.图 8中可知在过膨胀工况下压力脉动幅值较大,流场压力峰值最高可达当地流体压力的一倍,在压力峰值处所对应的时间点发现了气体收缩现象.相较于过膨胀工况,完全膨胀工况射流流场压力脉动程度显著较小,压力振荡较弱,因而对喷管出口压力特性影响更弱.

|
图 8 在完全膨胀和过膨胀两种工况监测点p1处压力脉动特性 Fig. 8 Pressure on p1 under full-expansion and over-expansion conditions |
水下火箭发动机的工作安全性是本文最关注的问题,文献[15]指出由于水环境的作用可能使发动机燃烧室工作时出现故障,因此非常有必要研究发动机工作安全特性.在这里,本文通过研究喉部流量的变化特性来分析不同工作状态下燃烧室的安全工作特性.图 9给出了在完全膨胀与过膨胀工况的喉部流量时变线图.从图 9中可知,完全膨胀状态喉部流量没有出现脉动的现象,说明外流场的非稳定特性只影响喷管扩张段,未对喉部流动参数产生影响,进而不会威胁到发动机燃烧室工作时的安全性;在过膨胀的工况下,流量出现了脉动现象,喉部流量最大变化幅度30.4%,说明外界水压力脉动振荡影响到了喷管喉部流体参数,这意味着燃烧室内有相应的燃气并未流出喷管,堆积在燃烧室内,从而亦会导致燃烧室压力增大约30.4%,不仅会导致发动机工作时出现故障,严重时可能会导致燃烧室爆炸.

|
图 9 完全膨胀和过膨胀两种工况喷管喉部流量特性 Fig. 9 Mass flow rate of nozzle throat under full-expansion and over-expansion conditions |
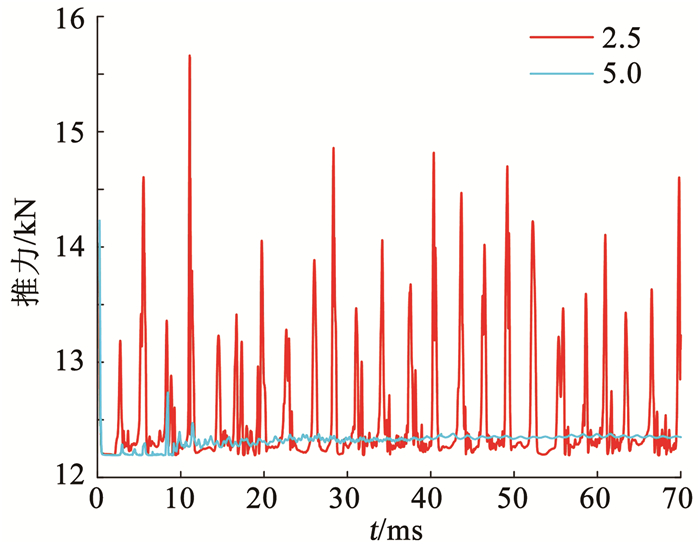
图 10给出了水下火箭发动机推力特性.完全膨胀工况下发动机推力脉动特性较小,推力均值约为12.3 kN. 结合图 5可知,在完全膨胀工况下,尾流场发生颈缩、胀鼓等现象的位置距喷管出口较远,发生的压力脉动对喷管出口影响较小,进而发动机推力脉动特性较小;过膨胀工况,发动机推力产生显著脉动振荡,幅值最大约为15.5 kN.结合图 6、7可知,尾流场发生颈缩、胀鼓、回击等现象的位置靠近喷管,喷管出口压力脉动强烈,压力脉冲作用在喷管内壁,发动机推力产生较大周期振荡.
|
图 10 水下火箭发动机在完全膨胀和过膨胀工况下推力特性 Fig. 10 Thrust of underwater rocket engine under full-expansion and over-expansion conditions |
超空泡航行器在空化器后的通气孔开始通气生成超空泡的同时位于尾部的火箭发动机开始点火,超空泡开始逐渐向后发展,最后与超声速喷射气流耦合.本文目的是为了研究通气超空化对水下发动机工作特性的影响,因此从超空泡与喷射气流开始耦合时作为研究时间起点.即本文时间t表示航行时间与空泡\喷射流耦合时间结点的时间差值.
2.2.1 通气空化工况燃气射流发展过程图 11给出了通气空化工况喷管完全膨胀状态和过膨胀状态时的燃气射流演变过程.由图 11可知,燃气射流在整个发展过程中包括两个部分,一部分是空泡闭合点后的射流区,另一部分是通气空泡闭合区.超空泡闭合点后的区域射流发展过程与无空化时的射流演变过程相似,并且这部分区域距水下火箭发动机较远,因此此处不再重点讨论其发展演变特性.在空泡闭合区内,燃气射流在整个发展过程中未出现无空化工况时的颈缩、断裂、胀鼓、回击等典型的水下射流现象,通气超空泡在航行器尾部与燃气喷射流相互耦合形成了多相尾流.通气超空泡开始接触燃气射流时气流流动复杂,通气空泡与燃气相互掺混,随着通气超空泡的进一步向后发展,喷管附近完全被通入气体与燃气的混合物填充,气体流动趋于稳定.超空泡闭合区后的喷射流压力振荡,导致闭合点前的空泡轮廓发生不同程度的变形.相比较于完全膨胀工况,过膨胀工况超空泡闭合点后的区域射流非稳定性更强,闭合点后的压力振荡更大,导致闭合点前的空泡轮廓形变程度更强.

|
图 11 通气空化时喷射流演变过程 Fig. 11 Jet flow development with ventilated supercavitation |
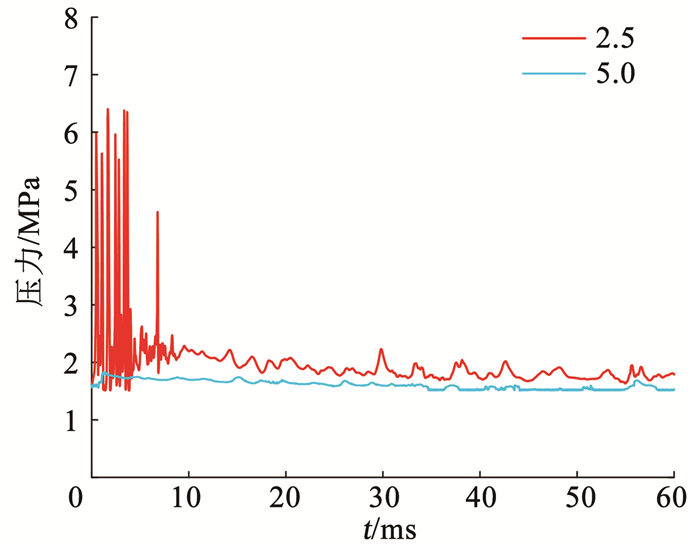
图 12给出了在通气超空化工况下完全膨胀和过膨胀状态的喷管出口平均压力的时变曲线.从图 12中可知,过膨胀状态时喷管出口压力开始剧烈振荡,幅值最大约6 MPa,这与无空化工况条件下的振荡压力近似相同,大于10 ms以后,压力脉动程度显著下降.此时喷管完全处于多相尾流中,出口平均压力为1.85 MPa.完全膨胀状态喷管出口平均压力基本保持平稳,压力约为1.5 MPa,相比较于无空化工况,振荡幅度有所降低.
|
图 12 通气空化时在完全膨胀和过膨胀两种工况喷管出口平均压力脉动特性 Fig. 12 Average outlet pressure of nozzle under full-expansion and over-expansion conditions with ventilated supercavitation |
水下喷射流流场不稳定现象是由气/水界面大密度差条件下混合层流动不稳定所造成的.超空泡航行器工作时位于空化器后的通气孔开始通入非凝气体生成超空泡,同时水下发动机开始工作,这其中涉及到发动机3种工作模态. 第1种是空泡还未完全发展,水下火箭发动机燃气喷射流直接喷入水中,由于大密度差条件导致压力振荡,这是过膨胀喷管出口及发动机推力开始振荡的原因;第2种是空泡闭合在发动机喷管后,此时发动机虽然包裹于空泡内,但空泡形态过小,在超声速喷射流的冲击下,气/水掺混剧烈,这由空泡演变图可知,此时,发动机喷射流仍存在与环境水的接触,这是空泡刚发展到发动机时压力及推力振荡的原因;第3种模式为超空泡继续发展,生成完全包裹航行器的超空泡,且空泡闭合点距离喷管出口较远,发动机完全工作于通入气体中,犹如在空中工作一样,通入的非凝结气体阻隔了发动机喷射流与水的之间接触,避免了由于大密度差造成的混合层不稳定流动,因此压力及推力振荡显著降低.
靠近喷管出口位置流场压力脉动特性会影响水下火箭发动机的工作特性,为研究超声速喷射流流场压力特性,图 13给出了流场中监测点p1的压力时变曲线.图 13中可知在过膨胀工况下监测点p1处的压力开始剧烈振荡,幅值压力最大约为7 MPa,这与无空化工况的压力振荡特性相同,随后压力脉动振荡幅度迅速下降,最大压力值为4 MPa,平均压力为3 MPa.完全膨胀状态时,监测点p1的压力呈现出与过膨胀工况相类似的变化特性,开始时压力振荡剧烈,之后压力脉动较弱.

|
图 13 通气空化时在完全膨胀和过膨胀两种工况监测点p1处压力脉动特性 Fig. 13 Pressure on p1 under full-expansion and over-expansion conditions with ventilated supercavitation |
在通气超空化条件下,喷管过膨胀状态喉部流量稳定在6.33 kg/s,没有出现无空化工况下的喉部流量脉动的现象,说明通气超空泡减弱了喷出射流对喷管内部流动的影响,抑制了发动机喉部气流参数的脉动,稳定了发动机的工作性能,有利于保障水下火箭发动机的安全性;在完全膨胀工况下,喉部流量仍然稳定,没有出现振荡特性,这与无空化条件下的喷管喉部流动特性一致.
图 14给出了通气超空化水下火箭发动机推力特性.过膨胀工况水下发动机推力开始产生显著脉动振荡,这与喷管出口压力的振荡特性一致.推力的振荡正是由于出口压力脉动剧烈,压力脉冲作用在喷管内壁,使发动机推力产生周期振荡所造成的.当在10 ms之后,发动机推力振荡减弱,基本保持平稳,平均推力约为12.3 kN. 完全膨胀工况下发动机推力基本保持平稳,未出现强烈地脉动现象,平均推力约为12.2 kN.

|
图 14 通气空化时水下火箭发动机在完全膨胀和过膨胀工况下推力特性 Fig. 14 Thrust of underwater rocket engine under full-expansion and over-expansion conditions with ventilated supercavitation |
无空化条件下,水下火箭发动机推力与喷管出口压力具有相同的频率特性,主频率约为300 Hz,并且能量主要集中在低频区域.这是因为喷射流发生颈缩、断裂、胀鼓及回击现象时流场振荡特性最强,并且典型现象出现频率较少.结合喷射流的空泡演变过程分析可知,水下超声速喷射流基本分为两种流动模态,一种是湍流度相对平缓的流动模式,主要是燃气向下流方向流动,此流动状态对应高频区;另一种是不稳定模式,出现了剧烈的压力振荡,从而发生颈缩、胀鼓、回击等现象,此流动对应于低频区.
3 结论1) 无通气空化时,火箭发动机尾射流发生颈缩、断裂、胀鼓、回击等非定常现象,相比较于完全膨胀工况,过膨胀工况发动机喉部流量及推力分别产生30.4%、26.1%的振荡幅度.
2) 通气空化时,发动机尾喷流与通气空泡耦合形成多相尾流,尾喷流流场非定常特性显著减小,发动机喉部流量及推力未发生剧烈振荡,发动机工作性能几乎不受工作压力影响.
3) 通气空化时,发动机推力及流场稳定的机理是通气超空泡使喷射流与环境水隔离,减弱了气/水界面因大密度差而形成的混合层不稳定流动.
| [1] |
张有为, 王晓宏. 导弹水下点火推力峰值问题的数值研究[J]. 应用力学学报, 2007, 24(1): 298. ZHANG Youwei, WANG Xiaohong. Numerical research on thrust peak for missile launching underwater[J]. Chinese Journal of Applied Mechanics, 2007, 24(1): 298. DOI:10.3969/j.issn.1000-4939.2007.02.028 |
| [2] |
唐嘉宁, 李世鹏, 王宁飞. 水下固体火箭发动机的负推力现象研究[J]. 固体火箭技术, 2012, 35(3): 325. TANG Jianing, LI Shipeng, WANG Ningfei. Study on the negative thrust of the underwater solid rocket engines[J]. Journal of Solid Rocket Technology, 2012, 35(3): 325. DOI:10.3969/j.issn.1006-2793.2012.03.008 |
| [3] |
孟凡亮, 赵晋宏, 孙继红. 鱼雷水冲压发动机浅析[J]. 工业技术, 2014, 26: 87. MENG Fanliang, ZHAO Jinhong, SUN Jihong. The research development of water-ramjet engine for torpedo[J]. Science & Technology Information, 2014, 26: 87. DOI:10.16661/j.cnki.1672-3791.2014.26.073 |
| [4] |
王超, 施红辉, 汪剑锋. 液体中可压缩气体射流的瞬态特性[J]. 化工学报, 2016, 67(6): 2291. WANG Chao, SHI Honghui, WANG Jianfeng. Transient characteristics of a compressible gas jet in liquid[J]. CIESC Journal, 2016, 67(6): 2291. DOI:10.11949/j.issn.0438-1157.20151874 |
| [5] |
王超, 汪剑锋, 施红辉. 超声速气体浸没射流的数值计算和实验[J]. 化工学报, 2014, 65(11): 4293. WANG Chao, WANG Jianfeng, SHI Honghui. Numerical simulation and experiments on submerged supersonic gas jets[J]. CIESC Journal, 2014, 65(11): 4293. DOI:10.3969/j.issn.0438-1157.2014.11.011 |
| [6] |
李婷婷, 胡俊, 曹雪洁, 等. 环形喷管水下气体射流夹断过程的实验研究[J]. 化工学报, 2017, 68(12): 4565. LI Tingting, HU Jun, CAO Xuejie, et al. Pinch-off process of underwater annular-nozzled gas jet[J]. CIESC Journal, 2017, 68(12): 4565. DOI:10.11949/j.issn.0438-1157.20170666 |
| [7] |
HE Miaosheng, QIN Lizi, LIU Yu. Oscillation flow induced by underwater supersonic gas jets from a rectangular Laval nozzle[J]. Procedia Engineering, 2015, 99: 1531. DOI:10.1016/j.proeng.2014.12.705 |
| [8] |
SHI Honghui, WANG Boyi, DAI Zhenqing. Research on the mechanics of underwater supersonic gas jets[J]. Science China Physics, Mechanics & Astronomy, 2010, 53(3): 534. DOI:10.1007/s11433-010-0150-x |
| [9] |
SHI Honghui, GUO Qiang, WANG Chao, et al. Oscillation flow induced by underwater supersonic gas jets[C]//Proceedings of the 27th International Symposium on Shock Waves. Petersburg: [s. n], 2010, 20: 351. DOI: 10.1007/s00193-010-0270-2
|
| [10] |
HARBY K, CHIVA S, MUÑOZ-COBO J L. An experimental investigation on the characteristics of submerged horizontal gas jets in liquid ambient[J]. Experimental Thermal and Fluid Science, 2014, 53: 26. DOI:10.1016/j.expthermflusci.2013.10.009 |
| [11] |
TANG Jianing, WANG Ningfei, SHYY W. Flow structure of gaseous jets injected into water for underwater propulsion[J]. Acta Mechanica Sinica, 2011, 27(4): 471. DOI:10.1007/s10409-011-0474-4 |
| [12] |
许海雨, 罗凯, 刘日晨. 水下超声速气流流场非定常特性研究[J]. 推进技术, 2019, 40(11): 2618. XU Haiyu, LUO Kai, LIU Richen. Research on unsteady characteristics of underwater supersonic gas jet[J]. Journal of Propulsion Technology, 2019, 40(11): 2618. DOI:10.13675/j.cnki.tjjs.180649 |
| [13] |
张孝石, 许昊, 王聪, 等. 水流冲击超声速气体射流实验研究[J]. 物理学报, 2017, 66(5): 054702. ZHANG Xiaoshi, XU Hao, WANG Cong, et al. Experimental study on underwater supersonic gas jets in water flow[J]. Acta Mechanica Sinica, 2017, 66(5): 054702. DOI:10.7498/aps.66.054702 |
| [14] |
甘晓松, 贾有军, 鲁传敬, 等. 水下燃气射流流场数值研究[J]. 固体火箭技术, 2009, 32(1): 23. GAN Xiaosong, JIA Youjun, LU Chuanjing, et al. Research onnumerical simulation of combustion gas jet under water[J]. Journal of Solid Rocket Technology, 2009, 32(1): 23. DOI:10.3969/j.issn.1006-2793.2009.01.006 |
| [15] |
唐嘉宁, 刘向阳, 李世鹏, 等. 水下固体火箭发动机推力特性研究[J]. 导弹与航天运载技术, 2012, 35(5): 19. TANG Jianing, LIU Xiangyang, LI Shipeng, et al. Study on thethrust characteristics of the underwater solid rocket motor[J]. Missiles and Space Vehicles, 2012, 35(5): 19. DOI:10.3969/j.issn.1004-7182.2012.05.006 |
| [16] |
党建军, 刘统军, 胥银. 尾部喷流对定常超空泡形态影响的数值研究[J]. 水下系统无人学报, 2007, 15(6): 50. DANG Jianjun, LIU Tongjun, XU Yin. Numerical simulation of influence of tail jet on steady supercavitation configuration[J]. Journal of Unmanned Undersea Systems, 2007, 15(6): 50. DOI:10.3969/j.issn.1673-1948.2007.06.013 |
| [17] |
KINZEL M P, KRANE M H, KIRSCHNER I N, et al. A numerical assessment of the interaction of a supercavitating flow with a gas jet[J]. Ocean Engineering, 2017, 136: 304. DOI:10.1016/j.oceaneng.2017.03.042 |
| [18] |
MOENY M J, KRANE M H, KIRSCHNER I N, et al. Jet-supercavity interaction: Insights from experiments[J]. Journal of Physics, 2015, 656: 012162. DOI:10.1088/1742-6596/656/1/012162 |
 2021, Vol. 53
2021, Vol. 53


