平流层一般指海拔高度处于10~55 km的空间,由于平流层的垂直对流效应小,气流稳定,适合布置平流层飞行器完成诸如中继通信、监察和运输等任务,具有极大的军事及民用价值[1].平流层飞艇是一种能定点飞行、效费比高的平流层飞行器,其结构一般包括艇身、吊舱、尾翼和支撑骨架(如图 1所示).对平流层飞艇而言,是否具备长航时是一项重要性能指标[2-3].平流层飞艇飞行过程中受到的阻力由动力系统平衡,阻力系数与动力消耗近似为正比关系,加之飞艇表面积巨大,驻留风阻很高,因此即便阻力系数略微减小,也能极大的减小动力系统的能量消耗,从而提高执行任务时间.通常,艇身阻力占到了全艇阻力的约2/3[4-5],因此找到使艇身具有最小阻力系数的外形具有十分重要的意义[6-7].

|
图 1 飞艇结构示意 Fig. 1 Airship structure diagram |
目前,飞艇减阻一般采用优化方法进行. Lutz等[8]通过在艇身布置周向分布的点源/汇从而得到了压力场和速度场,并利用边界层模型得到了不同雷诺数下的最小阻力外形.Wang等[9]采用势流-边界层耦合方法和混合遗传算法对平流层飞艇艇身外形进行了优化. Geruti等[10]基于粒子群优化算法(PSO)提出了适用于考虑附加质量的非常规布局飞艇的优化框架. Kanikdale等[11]采用GNVR作为飞艇基础外形,提出了飞艇外形的多变量约束方法,并用模拟退火算法对外形进行了优化. Wang等[12]将气动、结构、能源和质量作为优化对象,通过综合目标方程对飞艇外形进行了多学科优化.一般地,飞艇艇身外形廓线可由八参数、四参数、GNVR、椭球形和“海豚”形描述[13-15].但这些方法能包含的外形范围较小,表达过于数学化,效率较低. 翼型参数化方法较上述飞艇外形描述方法丰富很多,能表征更为多样的外形空间.翼型参数化方法主要有Hick-Henne Bump Functions、B-splines、PARSEC和Class/Shape function Transformation (CST)等4种.其中,Hick-Henne Bump Functions方法通过叠加形状函数并改变形状函数因子αi对已有的基础外形进行扰动,例如: Zhong等[16]以RAE2822为基础翼型,通过引入10个形状函数来表示新的翼型;Yang等[17]利用开源软件SU2,引入5个形状函数分别对NACA0012和RAE2822翼型进行了优化;总的来说,Hick-Henne Bump Functions方法适用于对已有外形进行优化,难以形成设计空间.B-Splines方法通过在翼型周围改变控制点位置来更新翼型形状,例如Pérez等[18]使用B-spline方法控制螺旋桨不同展向处叶素的外形,通过设定不同的控制点数和容错系数得到不同的三维螺旋桨CAD模型;Martin等[19]应用扩展的B-spline方法对三维机翼形状进行了优化;该方法具有很强的凸包性和稳定性,但上述控制点没有具体的物理含义,不便于形成明确的设计参考. CST方法通过类函数C(x)和形状函数S(x)的乘积定义外形曲线,例如Masdari等[20]应用CST方法描述翼型形状,结合离散涡方法,以功率系数为目标,对Savonius涡轮进行了优化. 虽然该方法的适应性较强,但表达过于数学化,同样不利于形成明确的设计参考. PARSEC方法通过11个参数控制翼型形状,Chen等[21]通过PARSEC方法描述翼型形状,以功率系数为目标对垂直轴流风力机进行了优化,使功率系数比NACA0015翼型的结果提高了13.26%;PARSEC方法每个参数均有清晰的物理含义,利于形成明确的设计空间. Sripawadkul等[22]系统地研究了上述4种翼型参数化方法的特性,并给出了每种方法在不同指标下的评价结果,其中的正交性指标体现了各参数化方法中参数与外形是否一一对应,该指标在形成设计空间的过程中十分重要,结果表明只有PARSEC方法与CST方法能完全满足正交性.考虑到CST方法表达过于繁复,可选PARSEC方法来描述飞艇外形.
一般而言,优化过程是面向所有参数的,这往往导致在次要参数上会消耗许多不必要的时间.因此提取对艇身阻力系数最敏感的参数,降低优化设计维度,并由这些参数形成飞艇艇身外形设计空间,从而给予艇身初期设计一定的参考是十分必要的.基于此,本文以艇身阻力系数为目标,通过PARSEC参数化方法、CFD方法和Sobol全局敏感度分析方法得到对阻力系数最敏感的参数,进而形成了由这些参数构成的飞艇艇身外形设计空间.
1 数值方法及其验证 1.1 数值方法艇身阻力系数可由势流理论、风洞实验和计算流体力学(CFD)方法得到[23].风洞实验的高耗时和高成本不适用于本文工作,针对飞艇发展的势流理论通常只对细长体预测的较准确,且黏性作用往往使势流理论的结果不准确.随着计算机技术的发展,CFD成为解决气动优化设计和流固耦合问题的重要手段.低速不可压缩流动的NS方程为
| $ \frac{\partial \boldsymbol{u}}{\partial t}+(\boldsymbol{u} \cdot \nabla) \boldsymbol{u}=-\frac{1}{\rho} \nabla p+\mu \nabla^{2} \boldsymbol{u}. $ | (1) |
式中:ρ为流体密度; p为压力; μ为动力黏度; u为速度矢量.对式(1)进行无量纲化可得
| $ \frac{\partial \boldsymbol{u}^{*}}{\partial t^{*}}+\left(\boldsymbol{u}^{*} \cdot \nabla^{*}\right) \boldsymbol{u}^{*}=-\nabla^{*} p^{*}+\frac{1}{R e_{v}} \nabla^{* 2} \boldsymbol{u}^{*}. $ | (2) |
式中:u*= u/U∞,t*=tU∞/L,p*=p/ρU∞2,▽*=L▽,其中L为模型特征长度, U∞为来流速度. 且从式(2)可知,低速流动状态能由雷诺数Rev表征.
选取Spalart-Allmaras模型求解湍流流动,Spalart-Allmaras模型适合求解航空外流场问题,其计算开销低,稳定性好[24].求解器采取不可压缩形式的压力基求解器.压力-速度耦合格式为“coupled”,空间梯度离散方法为“least squares cell based”,压力项采用二阶格式离散,动量和修正湍流黏度采用二阶迎风格式离散.Spalart-Allmaras模型通过求解关于修正湍流黏度的输运方程获得流场信息:
| $ \begin{aligned} \rho \frac{\partial}{\partial t}(\tilde{\nu})+\rho \frac{\partial}{\partial x_{i}}\left(\tilde{\nu} u_{i}\right)=& G_{\nu}+\frac{1}{\sigma_{\tilde{\nu}}}\left\{\frac{\partial}{\partial x_{j}}\left[(\mu+\tilde{\rho \nu}) \frac{\partial \tilde{\nu}}{\partial x_{j}}\right]+\right.\\ &\left.C_{b 2} \rho\left(\frac{\partial \tilde{\nu}}{\partial x_{j}}\right)^{2}\right\}-Y_{\nu}+S_{\tilde{\nu}} . \end{aligned} $ | (3) |
式中:Gν为湍流黏度生成项; Yν为近壁面处产生的湍流黏度损耗项;
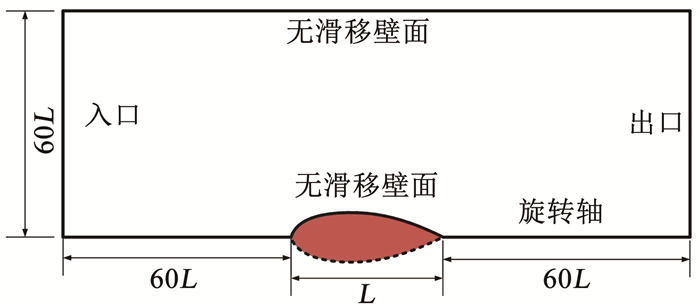
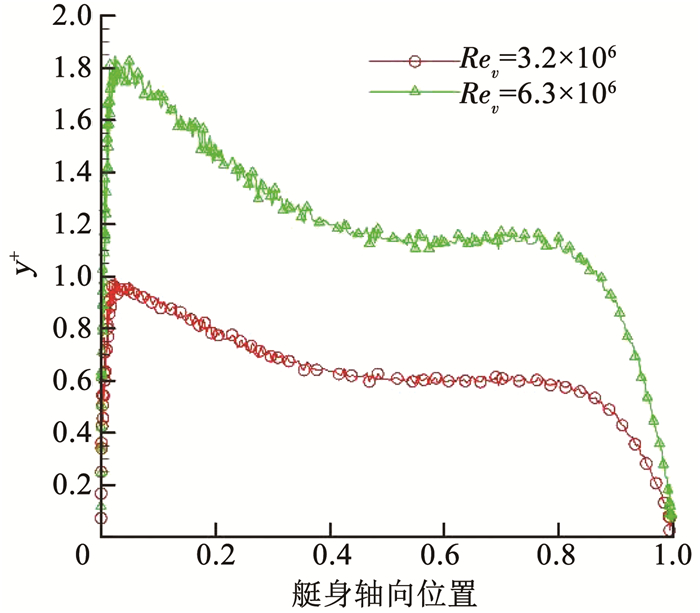
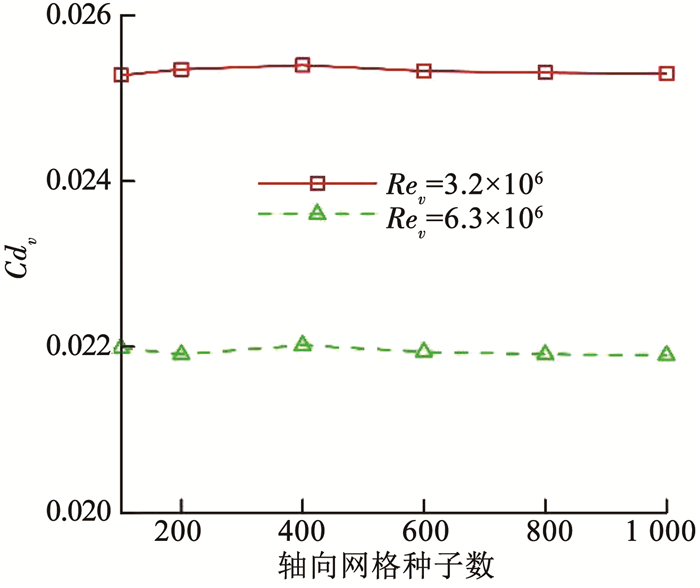
因艇身外形一般为旋成体,故简化为二维轴对称模型.艇身长度为L,艇身与入口和出口的距离均为60L,远场边界与旋转轴的距离也为60L,如图 2所示.模型经过归一化处理,模型长度L取为1.边界条件设置见表 1.流场的数值求解精度主要由y+和艇身沿轴向的网格种子数量决定.设置艇身表面的第1层网格高度为10-6L,计算得到的流线型旋成体模型轮廓线上的y+分布如图 3所示,横坐标为归一化的艇身轴向位置,可见本文设置能使y+满足要求.如图 4所示,对比了在不同Rev下艇身轴向网格种子数量与体积阻力系数Cdv的关系,可见当艇身轴向网格种子数量取为600时,Cdv几乎不再变化.后续数值分析均基于以上述网格划分模式进行.
|
图 2 计算域几何示意图 Fig. 2 Computational domain geometry |
| 表 1 边界条件类型 Tab. 1 Boundary condition types |
|
图 3 不同Rev下Model 4154表面的y+分布 Fig. 3 The y+ distribution of Model 4154 along the hull with different Rev |
|
图 4 网格无关性检验 Fig. 4 Grid independence verification |
文中以飞艇体积的立方根值作为特征长度,因此Rev定义如下:
| $ R e_{v}=\frac{\rho U_{\infty} V^{\frac{1}{3}}}{\mu}, $ | (4) |
式中,V为飞艇体积.
总阻力系数Cdv由压差阻力系数Cdpv和黏性阻力系数Cdfv构成:
| $ C d_{v} =\frac{F_{d}}{\frac{1}{2} \rho U_{\infty}^{2} V^{\frac{2}{3}}} , $ | (5) |
| $ F_{d} =F_{p}+F_{f}, $ | (6) |
| $ C d_{v} =C d p_{v}+C d f_{v} . $ | (7) |
式中:Fd为总阻力; Fp为压差阻力; Ff为黏性阻力.
1.3 算法验证文献[25]中对于流线型旋成体做了详细的流动实验分析记录,在此选取6组模型作为验证对象,模型材质为红木,长度统一为2.74 m,通过在水洞中拖曳模型获取阻力,模型中轴线距离水面深度为2.74 m,模型标签名分别为4 154、4 156、4 158、4 162、4 164和4 175,对应长细比分别为4、6、8、7、7和5. 流体介质的密度和动力黏度分别为998.2 kg/m3和0.001 003 kg/m · s,确保在数值计算中使CFD与实验的雷诺数相等. 对比结果如图 5所示,计算和实验结果的平均相对误差为1.5%,最大相对误差为3.8%,满足工程误差许可,表明本文数值方法是可靠的.

|
图 5 数值方法验证结果 Fig. 5 Verification of numerical simulation method |
为支撑数值方法中雷诺数能表征流动情况这一结论,现从具体算例上进行结果分析.以4 154模型为对象,取流动雷诺数Rev为5×106,固定来流速度U∞为10 m/s,通过调整流体密度ρ与流体动力黏度μ使Rev保持不变.各种参数配合下4 154模型受到的阻力情况见表 2,可见当雷诺数Rev一定时,模型的阻力系数可视为常数.因此不论从控制方程还是计算方法来看,雷诺数均能表征流动情况.
| 表 2 Rev=5×106时的阻力系数 Tab. 2 Drag coefficients at Rev=5×106 |
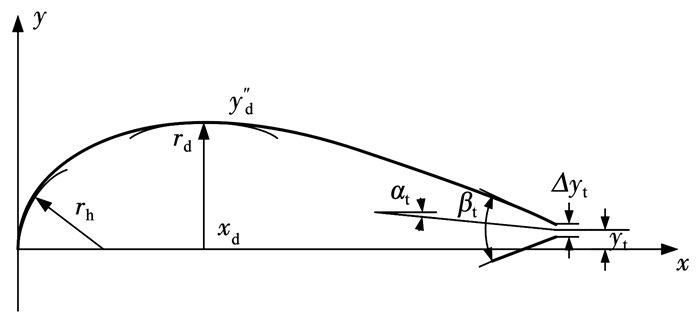
PARSEC方法通过11个参数控制翼型形状,每个参数均有清晰的物理含义.鉴于飞艇艇身的旋成体特性,只需选取上半部分的参数,于是可通过8个参数描述飞艇外形,如图 6所示.
|
图 6 基于“PARSEC”的8参数飞艇艇身外形 Fig. 6 Airship hull geometry defined by eight parameters based on PARSEC |
图中:rh为头部半径;xd为最大半径位置;rd为最大半径;y″d为最大半径处的曲率;αt为尾部偏移角;βt为尾部张开角;Δyt为尾部厚度;yt为尾部高度.
飞艇外形可由6阶多项式表达:
| $ y(x)=\sum\limits_{n=1}^{6} a_{n} x^{n-\frac{1}{2}}, $ | (8) |
式中的待定系数可通过求解下式获得[21],xte为弦长:
| $ \left[\begin{array}{cccccc} 1 & 0 & 0 & 0 & 0 & 0 \\ x_{\mathrm{te}}^{1 / 2} & x_{\mathrm{te}}^{3 / 2} & x_{\mathrm{te}}^{5 / 2} & x_{\mathrm{te}}^{7 / 2} & x_{\mathrm{te}}^{9 / 2} & x_{\mathrm{te}}^{11 / 2} \\ x_{\mathrm{d}}^{1 / 2} & x_{\mathrm{d}}^{3 / 2} & x_{\mathrm{d}}^{5 / 2} & x_{\mathrm{d}}^{7 / 2} & x_{\mathrm{d}}^{9 / 2} & x_{\mathrm{d}}^{11 / 2} \\ 1 / 2 x_{\mathrm{te}}^{-1 / 2} & 3 / 2 x_{\mathrm{d}}^{1 / 2} & 5 / 2 x_{\mathrm{te}}^{3 / 2} & 7 / 2 x_{\mathrm{d}}^{5 / 2} & 9 / 2 x_{\mathrm{te}}^{7 / 2} & 11 / 2 x_{\mathrm{te}}^{9 / 2} \\ 1 / 2 x_{\mathrm{d}}^{-1 / 2} & 3 / 2 x_{\mathrm{d}}^{1 / 2} & 5 / 2 x_{\mathrm{d}}^{3 / 2} & 7 / 2 x_{\mathrm{d}}^{5 / 2} & 9 / 2 x_{\mathrm{d}}^{7 / 2} & 11 / 2 x_{\mathrm{d}}^{9 / 2} \\ -1 / 4 x_{\mathrm{d}}^{-3 / 2} & 3 / 4 x_{\mathrm{d}}^{-1 / 2} & 15 / 4 x_{\mathrm{d}}^{1 / 2} & 35 / 4 x_{\mathrm{d}}^{3 / 2} & 63 / 4 x_{\mathrm{d}}^{5 / 2} & 99 / 4 x_{\mathrm{d}}^{7 / 2} \end{array}\right]\left[\begin{array}{c} a_{1} \\ a_{2} \\ a_{3} \\ a_{4} \\ a_{5} \\ a_{6} \end{array}\right]=\left[\begin{array}{c} \sqrt{2 r_{h}} \\ y_{\mathrm{t}}+\Delta y_{\mathrm{t}} / 2 \\ r_{\mathrm{d}} \\ \tan \left(\alpha_{\mathrm{t}}-\beta_{\mathrm{t}}\right) \\ 0 \\ y_{\mathrm{d}}^{\prime \prime} \end{array}\right]. $ | (9) |
敏感度体现了变量自身的改变对系统的影响程度.一般地,敏感度分析方法分为局部敏感度分析和全局敏感度分析.例如,龙卷风图, 基于分化的方法和筛查法属于前者; 基于回归的方法, 基于方差的方法, 转换不变方法和基于密度的方法属于后者[26].局部敏感度能体现输入空间一点附近的特性,全局敏感度还考虑了参数之间的相互影响,结果更合理可靠.
3.1 Sobol全局敏感度分析方法假设物理模型能被方程f(x)描述,输入x=(x1, x2, …, xn) 是n维空间的一点且xi(i=1, 2, …,n)遵循[0, 1]上的均匀分布.全体x构成一个n维立方体:
| $ C^{n}=\left\{x \mid 0 \leqslant x_{i} \leqslant 1 ; i=1,2, \cdots, n\right\}. $ | (10) |
输出项f(x)能被分解为
| $ \begin{aligned} f(x)=& f_{0}+\sum\limits_{i=1}^{n} f_{i}\left(x_{i}\right)+\sum\limits_{1 \leqslant i<j \leqslant n} f_{i, j}\left(x_{i}, x_{j}\right)+\\ & \sum\limits_{1 \leqslant i<j<k \leqslant n} f_{i, j, k}\left(x_{i}, x_{j}, x_{k}\right)+\\ & \sum\limits_{1 \leqslant i<j<k<l \leqslant n} f_{i, j, k, l}\left(x_{i}, x_{j}, x_{k}, x_{l}\right)+\cdots+\\ & f_{1,2, \cdots, n}\left(x_{1}, x_{2}, \cdots, x_{n}\right), \end{aligned} $ | (11) |
式中f0为常数,且f1, 2, …, s(x1, x2, …, xs)关于它自身变量的积分为0.
| $ \int\limits_{0}^{1} f_{1,2, \cdots, s}\left(x_{1}, x_{2}, \cdots, x_{s}\right) \mathrm{d} x_{k}=0,1 \leqslant k \leqslant s. $ | (12) |
积分式(11)有
| $ f_{0}=\int\limits_{C^{n}} f(x) \mathrm{d} x. $ | (13) |
由于式(11)右侧至少有一个变量是不同的,故具有正交性,再由式(12)可知:
| $ \begin{array}{l} \int\limits_{C^{n}} f_{i_{1}, i_{2}, \cdots, i_{s}}\left(x_{i_{1}}, x_{i_{2}}, \cdots, x_{i_{s}}\right) f_{j_{1}, j_{2}, \cdots, j_{l}}\left(x_{j_{1}}, x_{j_{2}}, \cdots, x_{j_{l}}\right) \mathrm{d} x=\\ 0,\left(i_{1}, i_{2}, \cdots, i_{s}\right) \neq\left(j_{1}, j_{2}, \cdots, j_{l}\right). \end{array} $ | (14) |
对式(11)积分和平方, 即
| $ \begin{array}{c} \int\limits_{C^{n}} f^{2}(x) \mathrm{d} x=f_{0}^{2}+ \\ \sum\limits_{s=1}^{n} \sum\limits_{<\cdots<s}^{n} \int f_{1,2, \cdots, s}^{2} \mathrm{~d} x_{1} \mathrm{~d} x_{2} \cdots \mathrm{d} x_{s} . \end{array} $ | (15) |
式(15)右侧第2项被称为总方差,写为
| $ D=\int\limits_{C^{n}} f^{2}(x) \mathrm{d} x-f_{0}^{2}, $ | (16) |
偏方差定义如下:
| $ D_{1,2, \cdots, s}=\int f_{1,2, \cdots, s}^{2} \mathrm{~d} x_{1} \mathrm{~d} x_{2} \cdots \mathrm{d} x_{s}, $ | (17) |
偏方差和总方差的关系为
| $ D=\sum\limits_{s=1}^{n} \sum\limits_{<\cdots<s}^{n} D_{1,2, \cdots, s}, $ | (18) |
引入比率S1, 2, …, s, 即
| $ S_{1,2, \cdots, s}=\frac{D_{1,2, \cdots, s}}{D}. $ | (19) |
对于具有n个输入变量的离散样本,本文需要计算每个S1, 2…, s的值,但对于需要借助CFD软件才能获得的输出,这样势必造成极大的时间开销.基于此,本文将所有输入变量分为两个子集,子集Xi仅仅包含变量xi, 另一子集Xei包含除了xi的所有变量. 因此总方差可写为
| $ D=D_{i}+D_{\mathrm{e} i}+D_{i, \mathrm{e} i}, $ | (20) |
引入新的参量STi,即
| $ S_{\mathrm{T}i}=S_{i}+S_{i, \mathrm{e} i}=1-S_{\mathrm{e} i}, $ | (21) |
Si表征了变量xi单独对总方差的影响,STi体现了变量xi对系统的“总体”影响,即不仅仅包含变量xi自身也包含了变量xi和余下变量的任意组合对输出的影响.因此,本文称Si和STi为变量xi的一阶敏感度和全局敏感度.
3.2 离散数据的敏感度分析事实上,本文经常面对的是离散的输入与输出数据,其中没有明确的函数关系.现在假设有一具有n个输入变量的系统,抽样产生N个样本.计算之前,本文需要准备两组输入数据x1, x2, …, xn和x′1, x′2, …, x′n,写成矩阵形式如下:
| $ \begin{array}{*{20}{l}} {\left[ {\begin{array}{*{20}{c}} {{x_{11}}}&{{x_{12}}}& \cdots &{{x_{1n}}}\\ {{x_{21}}}&{{x_{22}}}& \cdots &{{x_{2n}}}\\ \vdots & \vdots & \ddots & \vdots \\ {{x_{N1}}}&{{x_{N2}}}& \cdots &{{x_{Nn}}} \end{array}} \right] \to {{\left[ {\begin{array}{*{20}{c}} {{f_1}}\\ {{f_2}}\\ \vdots \\ {{f_N}} \end{array}} \right]}^\prime }\begin{array}{*{20}{c}} |\\ |\\ |\\ | \end{array}\left[ {\begin{array}{*{20}{c}} {x_{11}^\prime }&{x_{12}^\prime }& \cdots &{x_{1n}^\prime }\\ {x_{21}^\prime }&{x_{22}^\prime }& \cdots &{x_{2n}^\prime }\\ \vdots & \vdots & \ddots & \vdots \\ {x_{N1}^\prime }&{x_{N2}^\prime }& \cdots &{x_{Nn}^\prime } \end{array}} \right] \to \left[ {\begin{array}{*{20}{c}} {f_1^\prime }\\ {f_2^\prime }\\ \vdots \\ {f_N^\prime } \end{array}} \right].}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{c}} \uparrow \\ {{x_1}} \end{array}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{c}} \uparrow \\ {{x_2}} \end{array}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{c}} \uparrow \\ {{x_n}} \end{array}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{c}} \uparrow \\ f \end{array}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{c}} \uparrow \\ {x_1^\prime } \end{array}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{c}} \uparrow \\ {x_2^\prime } \end{array}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{c}} \uparrow \\ {x_n^\prime } \end{array}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{c}} \uparrow \\ {{f^\prime }} \end{array}} \end{array} $ | (22) |
有关量可由蒙特卡洛方法近似得到[27]:
| $ f_{0} \approx \frac{1}{N} \sum\limits_{i=1}^{N} f_{i}, $ | (23) |
| $ D+f_{0}{}^{2} \approx \frac{1}{N} \sum\limits_{i=1}^{N} f_{i}^{2}, $ | (24) |
| $ D_{j} \approx D-\sum\limits_{i=1}^{N} \frac{\left(f_{i}-f_{i, j}\right)^{2}}{2 N} , $ | (25) |
| $ D_{T_{j}} \approx \sum\limits_{i=1}^{N} \frac{\left(f_{i}-f_{i, j}^{\prime}\right)}{2 N}. $ | (26) |
式中:fi, j为将变量xj替换为x′ j所得到的输出;f′i, j为将变量x′ j替换为xj所得到的输出.于是本文能通过上述算法和定义获得输入变量的一阶或全局敏感度.
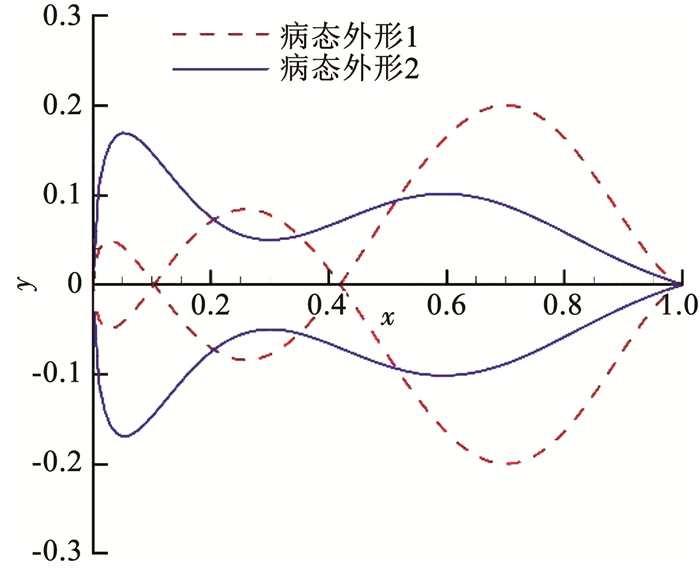
4 敏感度分析和艇身阻力特性研究 4.1 敏感度分析表 3给出了基于PARSEC方法的飞艇外形参数范围.头部半径rh不超过艇身长度1;最大半径rd处于0.05~0.25之间,对应艇身长细比处于2~10之间,能涵盖大多数常规艇身;最大半径位置xd处于0.3~0.5之间,以避免艇身最大截面位置过于靠前或靠后,以此减少艇身外形出现畸变的概率;尾部张开角βt处于20°~40°之间,以保证艇身尾部光滑收缩;尾部偏移角αt,尾部厚度Δyt和尾部高度yt被设定为0,以确保表征的外形为旋成体.如图 7所示,不恰当的参数组合会导致病态外形出现,实线外形包含了负值,虚线外形有多个极值,因此这些病态外形要在抽样时被剔除.基于表 3中的参数范围,得到所有非病态外形样本构成的范围如图 8所示,可见所取的参数能很好地保证艇身廓线的多样性.
| 表 3 飞艇外形参数范围 Tab. 3 Ranges of airship shape parameters |
|
图 7 不合理的参数组合造成的病态外形 Fig. 7 Ill-conditioned shapes caused by inappropriate combinations of parameters |

|
图 8 艇身廓线构成的样本空间 Fig. 8 Sample space formed by airship outlines |
飞艇飞行高度设定为20 km,当地空气密度为0.088 9 kg/m3,空气动力黏度为1.421 61×10-5 kg/ m · s,大气压强为5 529.31 Pa.一般地,平流层飞艇的绕流雷诺数在6.0×106和1.2×107之间,对一典型体积为3.0×105 m3的飞艇而言,当来流速度为20 m/s时,其雷诺数为8.37×106.故本文取雷诺数为8.0×106进行后续研究,进行数值分析时调整流体密度使所有工况的绕流雷诺数一致.
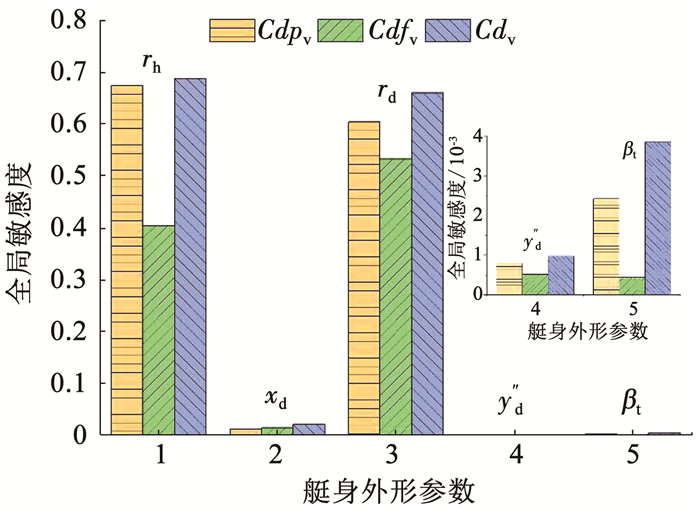
图 9显示了每个外形参数对各阻力系数的总敏感度.可以发现,参数rh和rd对总阻力系数的敏感度分别达到68.8%和66.0%,除了xd以外的其余参数对总阻力系数几乎没有影响,且xd的总敏感度仅为2.1%,故剩余参数可设为确定值.观察由参数rh和rd组成的设计空间,该空间可近似看作被3条线段和1条三次曲线包围形成,如图 10所示.该空间的数学表述为
| $ \text { s. t. }\left\{\begin{array}{l} r_{\mathrm{h}} \leqslant 3.720\ 7 r_{\mathrm{d}}^{3}+6.702\ 7 r_{\mathrm{d}}^{2}+0.420\ 9 r_{\mathrm{d}}-0.038, \\ 0 \leqslant r_{\mathrm{h}} \leqslant 0.50, \\ 0.05 \leqslant r_{\mathrm{d}} \leqslant 0.25. \end{array}\right. $ | (27) |
|
图 9 不同参数的总敏感度 Fig. 9 Global sensitivity of different parameters |

|
图 10 病态和设计空间 Fig. 10 Ill-conditioned space and design space |
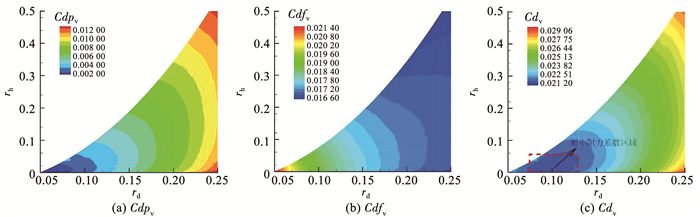
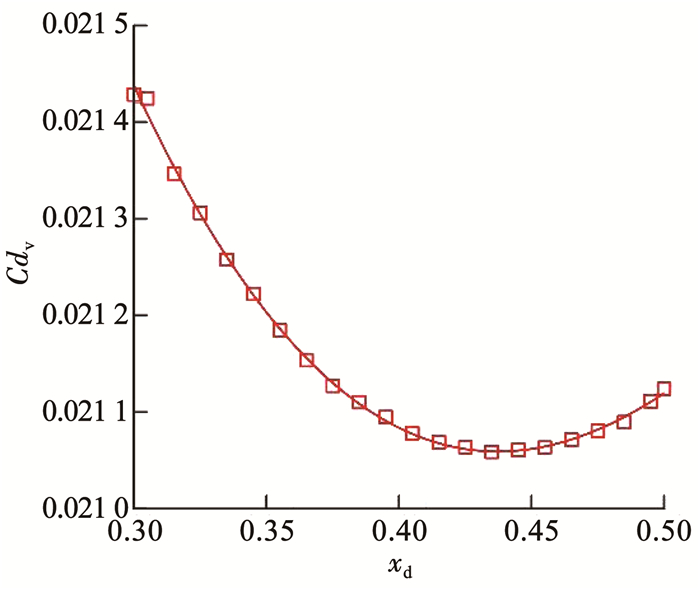
分别设置参数xd,y″d和βt的值为0.35,-0.5和30°.然后将设计空间离散,由同样的计算条件得到参数rh和rd与各阻力系数的关系,如图 11所示,随着设计空间向右上方推进压差阻力系数逐渐升高,而黏性阻力系数与此趋势恰好相反,二者的综合效果使总阻力系数在设计空间上存在极小区域.由此可得到参数rh和rd的最佳组合,另外由图 12可知,在其他参数确定的情况下随着xd的增加,总阻力系数先减小再增大,当xd=0.435时,总阻力系数取最小值.
|
图 11 rh和rd形成的关于各个阻力系数的云图 Fig. 11 Relationship between drag coefficient, rh, and rd |
|
图 12 Cdv和xd的关系 Fig. 12 Relationship between Cdv and xd |
综上所述,可获得使艇身具有最小阻力系数的参数组合,该艇身外形的头部半径rh为0.012 2,最大半径rd为0.95,最大半径位置xd为0.435.上述所得艇身长细比为5.263,与文献[28]中的结论吻合.在实际设计阶段,头部半径rh的范围可取为[0, 0.06],最大半径rd的范围可取为[0.08, 0.12],该范围内的阻力系数大小浮动程度较小,均可较好的降低艇身阻力系数.
5 结论1) 对平流层飞艇而言,动力消耗近似正比于阻力系数,艇身阻力占到了全艇阻力的约2/3,在初期设计阶段,快速找到最佳艇身外形具有十分重要的意义.为降低设计维度,有必要对外形参数进行全局敏感度分析,进一步所得设计空间可为类似设计提供参考.
2) 对流线外形的旋成体,宜采取2维轴对称模型和一方程Spalart-Allmaras湍流模型进行流场求解,所得阻力系数与实验值吻合度较高,具有很高的精度.
3) 在8.0×106这一典型雷诺数下,平流层飞艇阻力对外形参数的敏感度由高到低依次为:rh,rd和xd,其他参数的敏感度相较于这3个量可忽略不计,因此评估飞艇气动特性时应同时考虑以上3个参数,而不只考虑长细比这一参量.
4) 从减阻的角度出发,在实际设计中头部半径rh的范围可取为0~0.06,最大半径rd的范围可取为0.08~0.12.
| [1] |
赵达, 刘东旭, 孙康文, 等. 平流层飞艇研制现状、技术难点及发展趋势[J]. 航空学报, 2016, 37(1): 45. ZHAO Da, LIU Dongxu, SUN Kangwen, et al. Research status, technical difficulties and development trend of stratospheric airship[J]. Acta Aerinautica et Astronautical Sinica, 2016, 37(1): 45. DOI:10.7527/S1000-6893.2015.0332 |
| [2] |
ANDROULAKAKIS S P, JUDY R A. Status and plans of high altitude airship (HAATM) program[C]// AIAA Lighter-Than-Air Systems Technology (LTA) Conference. Daytona Beach: AIAA, 2013. DOI: 10.2514/6.2013-1362
|
| [3] |
张永栋, 翟嘉琪, 孟小君, 等. 基于行为逻辑的平流层飞艇试验自动测试方法[J]. 航空学报, 2018, 39(9): 322185. ZHANG Yongdong, ZHAI Jiaqi, MENG Xiaojun, et al. Approach for automatic testing of stratospheric airship test based on behavior logic[J]. Acta Aerinautica et Astronautical Sinica, 2018, 39(9): 322185. DOI:10.7527/S1000-6893.2018.22185 |
| [4] |
李天娥, 孙晓颖, 武岳, 等. 平流层飞艇气动阻力的参数分析[J]. 工程力学, 2019, 36(1): 248. LI Tiane, SUN Xiaoying, WU Yue, et al. Parameter analysis of aerodynamic drag force in stratospheric airship[J]. Engineering Mechanics, 2019, 36(1): 248. DOI:10.6052/j.issn.1000-4750.2017.11.0814 |
| [5] |
LI Yuwen, NABON M, SHARF I. Airship dynamics modeling: A literature review[J]. Progress in Aerospace Sciences, 2011, 47(3): 217. DOI:10.1016/j.paerosci.2010.10.001 |
| [6] |
CARRION M, BIAVA M, STEIJL R, et al. CFD studies of Hybrid air vehicles[C]//Proceedings of the 54th AIAA Aerospace Sciences Meeting. San Diego, CA: AIAA, 2016. DOI: 10.2514/6.2016-0059
|
| [7] |
冯凯, 赵达, 孟小君, 等. 带辅助安定面平流层飞艇的航向静稳定性分析[J]. 宇航学报, 2018, 39(7): 715. FENG Kai, ZHAO Da, MENG Xiaojun, et al. Directional static stability analysis of an airship with auxiliary stabilizer[J]. Journal of Astronautics, 2018, 39(7): 715. DOI:10.3873/j.issn.1000-1328.2018.07.002 |
| [8] |
LUTZ T, WAGNER S. Drag reduction and shape optimization of airship bodies[J]. Journal of Aircraft, 1998, 35(3): 345. DOI:10.2514/2.2313 |
| [9] |
WANG Xiaoliang, SHAN Xuexiong. Shape optimization of stratosphere airship[J]. Journal of Aircraft, 2006, 43(1): 283. DOI:10.2514/1.18295 |
| [10] |
CERUTI A, GAMBACORTA D, MARZOCCA P. Unconventional hybrid airships design optimization accounting for added masses[J]. Aerospace Science and Technology, 2018, 72: 164. DOI:10.1016/j.ast.2017.10.042 |
| [11] |
KANIKDALE T S, MARATHE A G, PANT R S. Multi-disciplinary optimization of airship envelope shape[C]// Proceedings of the 10th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference. Albany: AIAA, 2004. DOI: 10.2514/6.2004-4411
|
| [12] |
WANG Quanbao, CHEN Jian, FU Gongyi, et al. An approach for shape optimization of stratosphere airships based on multidisciplinary design optimization[J]. Journal of Zhejiang University Science A, 2009, 10(11): 1609. DOI:10.1631/jzus.A0820814 |
| [13] |
宋保维, 李福新. 回转体最小阻力外形优化设计[J]. 水动力学研究与进展, 1994, 9(5): 523. SONG Baowei, LI Fuxin. Optimum shaping design of axisymmetric bodies for minimum drag[J]. Journal of Hydrodynamics, Series A, 1994, 9(5): 523. DOI:10.16076/j.cnki.cjhd.1994.05.003 |
| [14] |
ALAM M I, PANT R S. Multidisciplinary approach for solar area optimization of high altitude airships[J]. Energy Conversion and Management, 2018, 164: 301. DOI:10.1016/j.enconman.2018.03.009 |
| [15] |
MUELLER J B, PALUSZEK M A, ZHAO Yiyuan. Development of an aerodynamic model and control law design for a high altitude airship[C]//Proceedings of the 3rd AIAA "Unmanned Unlimited" Technical Conference, Workshop and Exhibit. Chicago: AIAA, 2004. DOI: 10.2514/6.2004-6479
|
| [16] |
ZHONG Xiaoping, DING Jifeng, LI Weiji, et al. Robust airfoil optimization with multi-objective estimation of distribution algorithm[J]. Chinese Journal of Aeronautics, 2008, 21(4): 289. DOI:10.1016/s1000-9361(08)60038-2 |
| [17] |
YANG Guangda, RONCH A D, DROFELNIK J, et al. Sensitivity assessment of optimal solution in aerodynamic design optimization using SU2[J]. Aerospace Science and Technology, 2018, 81: 362. DOI:10.1016/j.ast.2018.08.012 |
| [18] |
PÉREZ-ARRIBAS F, PÉREZ-FERNÁNDEZ R. A B-spline design model for propeller blades[J]. Advances in Engineering Software, 2018, 118: 35. DOI:10.1016/j.advancesoft.2018.01.005 |
| [19] |
MARTIN M J, ANDRES E, LOZANO C, et al. Volumetric b-spline shape parametrization for aerodynamic shape design[J]. Aerospace Science and Technology, 2014, 37: 26. DOI:10.1016/j.ast.2014.05.003 |
| [20] |
MASDARI M, TAHANI M, NADERI M H, et al. Optimization of airfoil based Savonius wind turbine using coupled discrete vortex method and salp swarm algorithm[J]. Journal of Cleaner Production, 2019, 222: 47. DOI:10.1016/j.jclepro.2019.02.237 |
| [21] |
CHEN Jian, PAN Xiong, WANG Canxing, et al. Airfoil parameterization evaluation based on a modified PARASEC method for a H-Darrious rotor[J]. Energy, 2019, 187: 115910. DOI:10.1016/j.enegy.2019.115910 |
| [22] |
SRIPAWADKUL V, PADULO M, GUENOV M. A comparison of airfoil shape parameterization techniques for preliminary design optimization[C]//Proceedings of the 13th AIAA/ISSMO Multidisciplinary Analysis Optimization Conference. Fort Worth: AIAA, 2010. DOI: 10.2514/6.2010-9050
|
| [23] |
谭惠丰, 康敬天, 卫剑征, 等. 三角形微沟槽飞艇蒙皮表面的流场分析[J]. 哈尔滨工业大学学报, 2014, 46(7): 32. TAN Huifeng, KANG Jingtian, WEI Jianzheng, et al. Flow field analysis of Micro-V shape riblets airship surface[J]. Journal of Harbin Institute of Technology, 2014, 46(7): 32. DOI:10.11918/j.issn.0367-6234.2014.07.006 |
| [24] |
史亚云, 白俊强, 华俊, 等. 基于放大因子与Spalart-Allmaras湍流模型的转捩预测[J]. 航空动力学报, 2015, 30(7): 1670. SHI Yayun, BAI Junqiang, HUA Jun, et al. Transition prediction based on amplification factor and Spalart-Allmaras turbulence model[J]. Journal of Aerospace Power, 2015, 30(7): 1670. DOI:10.13224/j.cnki.jasp.2015.07.019 |
| [25] |
MORTON G. Drag experiments on a systematic series of streamlined bodies of revolution for application to the design of high-speed submarines: C-297[R]. Washington, DC: Navy Department, 1950
|
| [26] |
BORGONOVO E, PLISCHKE E. Sensitivity analysis: A review of recent advances[J]. European Journal of Operational Research, 2016, 248(3): 869. DOI:10.1016/j.ejor.2015.06.032 |
| [27] |
SOBOL I M. Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates mathematics and computers in simulations[J]. Mathematics and Computers in Simulation, 2001, 55(1/2/3): 271. DOI:10.1016/S0378-4754(00)00270-6 |
| [28] |
KHOURY G A, GILLETT J D. Airship technology[M]. Cambridge: Cambridge University Press, 1999.
|
 2021, Vol. 53
2021, Vol. 53


