振动是影响直升机发展的主要问题之一.对于大多数现代直升机而言,机动能力和最大前进速度受到过度振动的限制.发动机、变速箱、尾桨和旋翼质量不平衡都是振动激励源.然而直升机振动的主要来源是主旋翼.振动对直升机操作的几乎所有方面都是有害的,包括飞行员疲劳和结构完整性; 降低电子设备的可靠性和操作准确度; 影响相机和测量设备等机器的精度.旋翼桨叶可以模拟为旋转梁[1],由于弹性变形和刚体运动的耦合,旋转梁的振动特性与非旋转梁的振动特性有很大差异[2].沿着梁长度变化的离心力改变了梁的整体刚度(应力刚化效应),使固有频率和模态发生变化[3].众多研究人员针对不同的课题,采用不同的方法研究了旋转梁的动态特性.例如Southwell原理、积分矩阵法、Rayleigh Ritz法[4]、Galerkin法[5]和扰动法,以及动态刚度法,这涉及到幂级数解及使用Frobenius方法计算相应微分方程的解[6].传统的有限元法(Conventional finite element method, CFEM)[7]已被用于许多分析旋翼固有频率的问题.一种基于低自由度模型的谱有限元法(Spectral finite element method,SFEM)[8]被用于分析旋转锥形梁的运动特性.传递矩阵法用于非旋转锥形梁[9]和带裂纹的旋转梁[10]的自由振动计算.
有限元法和多体系统动力学是武器系统动力学的重要基础.然而,使用这些方法对多刚柔体耦合的复杂武器系统的振动特性计算可能带来很大的计算量和由计算不良条件引起的计算奇点.多体系统传递矩阵方法(MSTMM)[11-13]可以避免复杂线性多系统特征值问题的计算错误,因为系统总矩阵阶次较低,显著提高了振动特性的计算速度[14].本文基于MSTMM,建立了耦合直升机四叶片旋翼/机身的多体系统动力学模型.推导出整体传递方程,并模拟了旋翼振动特性.为了证明所提出方案的准确性,与商业软件ANSYS Workbench仿真结果进行比较.
1 建模与传递矩阵推导 1.1 直升机拓扑模型图 1中所示的典型直升机可以建模为多刚性-柔性耦合系统,直升机主要分为旋翼系统、机身和机尾3个部分.

|
图 1 典型直升机模型 Fig. 1 Typical helicopter model |
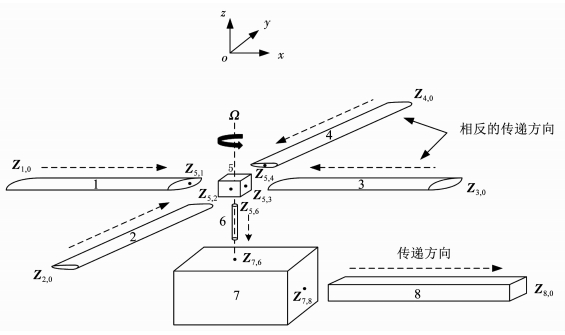
拓扑结构如图 2所示,四桨叶/机身耦合系统的动力学模型在空间内振动.全局惯性系oxyz用于描述系统运动.本文将直升机模型简化为8个元件,分别是4个旋转Euler-Bernoulli梁组成的无铰接柔性桨叶、桨毂、传动轴、机身和尾梁8个部分.元件编号1至4号是桨叶,考虑其在挥舞方向、摆振方向及扭转方向的振动,桨叶通过柔性连接到5号元件桨毂,桨毂处理为一个空间刚体,桨毂连接至元件6传动轴,传动轴处理为一根围绕中心轴旋转的梁,传动轴与元件7机身相连,机身处理为一个刚体,机身与元件8尾梁为刚性连接.旋翼与传动轴以同一转速旋转,旋转角速度为Ω.
|
图 2 直升机拓扑模型 Fig. 2 Helicopter topology model |
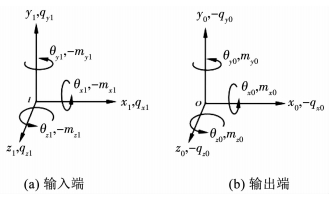
递矩阵法使用状态矢量描述力学系统中任一点的力学状态,坐标系方向及符号约定如图 3所示,状态矢量是由两部分元素构成的一个列阵,一是该点状态变量的位移及角位移(x, y, z, θx, θy, θz),二是内力及内力矩(qx, qy, qz, mx, my, mz).多自由度无阻尼振动系统可由模态振动叠加而成,某阶模态下固有频率ωk对应的状态矢量可以表示为z = Zke-iωkt, Zk为模态坐标下的状态矢量,其状态变量为固有频率ωk对应的位移及内力的模态坐标,为了书写简洁将上标k省略,即Zi, j=[X, Y, Z, Θx, Θy, Θz, Mx, My, Mz, Qx, Qy, Qz]T,其中i为体元件编号,j为铰元件编号.
|
图 3 坐标系及符号约定 Fig. 3 Coordinate system and symbol convention |
系统总传递方程由总传递方程和几何方程构成,总传递方程的状态矢量由所有边界点的状态矢量构成.主传递方程中的每一个系数矩阵为从相应边界点到系统根的传递路径上所有元件传递矩阵的连乘积.几何方程用来描述同一元件不同输入点之间的几何关系,其系数矩阵可以在推导主传递方程的过程中依据同一元件不同输入点之间的几何关系自动导出.对于每一个分支,都可以根据同一个体元件不同输入点的几何关系推导出一组几何方程,几何方程的个数等于系统树梢个数减1.几何方程的系数矩阵为由从边界端到分叉体元件的输入端Ik(k=1, 2, …,L)路径上各个元件的传递矩阵的连乘积,再左乘(- Hj, 1)(若k=1),或左乘(Hj, k)(若k=2, …,L).
在线性系统中ZO= UjZI,其中:ZI为输入点的状态矢量,ZO为输出点状态矢量,Uj为元件j的传递矩阵,由牛顿力学定律推导得到,总传递矩阵Uall为沿传递路径各元件传递矩阵依次连乘之积.最终整理可以得到U all Z all=0,其中Zall为各边界点的状态矢量和,U all即为总传递矩阵.
如图 2拓扑图所示,该模型共有4个边界点,分别为Z1, 0, Z 2, 0, Z 3, 0, Z 4, 0, Z 8, 0, 以Z8, 0为输出点,系统的传递矩阵推导如下:
| $ \begin{array}{l} {Z_{8, 0}} = {U_8}{Z_{7, 8}} = {U_8}{U_7}{Z_{7, 6}} = {U_8}{U_7}{U_6}{Z_{5, 6}} = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {U_8}{U_7}{U_6}\left( {{U_{5, {I_1}}}{Z_{5, 1}} + {U_{5, {I_2}}}{Z_{5, 2}} + } \right.\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {{U_{5, {I_3}}}{Z_{5, 3}} + {U_{5, {I_4}}}{Z_{5, 4}}} \right) = {U_8}{U_7}{U_6}\left( {{U_{5, {I_1}}}{U_1}{Z_{1, 0}} + } \right.\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {{U_{5, {I_2}}}{U_2}{Z_{2, 0}} + {U_{5, {I_3}}}{U_3}{Z_{3, 0}} + {U_{5, {I_4}}}{U_4}{Z_{4, 0}}} \right) = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {U_8}{U_7}{U_6}{U_{5, {I_1}}}{U_1}{Z_{1, 0}} + {U_8}{U_7}{U_6}{U_{5, {I_2}}}{U_2}{Z_{2, 0}} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {U_8}{U_7}{U_6}{U_{5, {I_3}}}{U_3}{Z_{3, 0}} + {U_8}{U_7}{U_6}{U_{5, {I_4}}}{U_4}{Z_{4, 0}}, \end{array} $ | (1) |
或
| $ T_{8-1} Z_{1, 0}+T_{8-2} Z_{2, 0}+T_{8-3} Z_{3, 0}+T_{8-4} Z_{4, 0}-Z_{8, 0}=0, $ | (2) |
其中:
| $ {{T_{8 - 1}} = {U_8}{U_7}{U_6}{U_{5, {I_1}}}{U_1}, {T_{8 - 2}} = {U_8}{U_7}{U_6}{U_{5, {I_2}}}{U_2}, } $ |
| $ {{T_{8 - 3}} = {U_8}{U_7}{U_6}{U_{5, {I_3}}}{U_3}, {T_{8 - 4}} = {U_8}{U_7}{U_6}{U_{5, {I_4}}}{U_4}.} $ |
模型中有一个分叉点,4个分支,所以共有3个几何方程.第1个几何方程如下:
| $ -H_{5, 1} U_{1} Z_{1, 0}+H_{5, 2} U_{2} Z_{2, 0}=0 , $ | (3) |
或
| $ G_{5-1} Z_{1, 0}+G_{5-2} Z_{2, 0}=0, $ | (4) |
其中:
| $ G_{5-1}=-H_{5, 1} U_{1} Z_{1, 0}, G_{5-2}=H_{5, 2} U_{2} Z_{2, 0}. $ |
第2个几何方程如下:
| $ -H_{5, 1} U_{1} Z_{1, 0}+H_{5, 3} U_{3} Z_{3, 0}=0, $ | (5) |
或
| $ G_{5-1} Z_{1, 0}+G_{5-3} Z_{3, 0}=0 , $ | (6) |
其中:
| $ G_{5-1}=-H_{5, 1} U_{1} Z_{1, 0}, G_{5-3}=H_{5, 3} U_{3} Z_{3, 0}. $ |
第3个几何方程如下:
| $ -H_{5, 1} U_{1} Z_{1, 0}+H_{5, 4} U_{4} Z_{4, 0}=0, $ | (7) |
或
| $ G_{5-1} Z_{1, 0}+G_{5-4} Z_{4, 0}=0, $ | (8) |
其中:
| $ G_{5-1}=-H_{5, 1} U_{1} Z_{1, 0}, G_{5-4}=H_{5, 4} U_{4} Z_{4, 0}. $ |
联立式(2)、(4)、(6)、(8),可得
| $ \left.\left.U_{\text {all }}\right|_{30 \times 60} Z_{\text {all }}\right|_{60 \times 1}=0 \text { , } $ | (9) |
其中:
| $ U_{\mathrm{all}}=\left[\begin{array}{c} \left.T_{8-1}\right|_{12 \times 12}& \left.T_{8-2}\right|_{12 \times 12}& \left.T_{8-3}\right|_{12 \times 12}& \left.T_{8-4}\right|_{12 \times 12}& \left.-I\right|_{12 \times 12} \\ \left.G_{5-1}\right|_{6 \times 12} & \left.G_{5-2}\right|_{6 \times 12} & \left.0\right|_{6 \times 12} & \left.0\right|_{6 \times 12} & \left.0\right|_{6 \times 12} \\ \left.G_{5-1}\right|_{6 \times 12} & \left.0\right|_{6 \times 12} & \left.G_{5-3}\right|_{6 \times 12} & \left.0\right|_{6 \times 12} & \left.0\right|_{6 \times 12} \\ \left.G_{5-1}\right|_{6 \times 12} & \left.0\right|_{6 \times 12} & \left.0\right|_{6 \times 12} & \left.G_{5-4}\right|_{6 \times 12} & \left.0\right|_{6 \times 12} \end{array}\right], $ |
| $ \boldsymbol{Z}_{\text {all }}=\left[\begin{array}{lllll} Z_{1, 0} & Z_{2, 0} & Z_{3, 0} & Z_{4, 0} & Z_{8, 0} \end{array}\right]^{\mathrm{T}}. $ |
由系统的边界条件可知,Zall中的第7-12、19-24、31-36、43-48和55-60个元素为零,从Zall中去掉这些零元素,并在Uall中去掉与这些零元素对应的列,得Uall|30×30 Zall|30×30. Uall只与系统固有频率ω相关,可得特征方程Δ= ∣ Uall ∣=0时的频率ω就是固有频率.通过逐步搜索法就可以确定系统的固有频率.
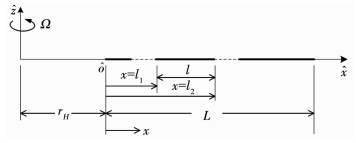
2 主要元件传递矩阵的推导 2.1 旋转梁的传递矩阵的推导直升机旋翼是一根绕一端旋转的细长梁,模型简化为一根欧拉伯努利梁,对一根质心轴与弹性轴重合的欧拉伯努利梁来说,不考虑弯扭耦合.图 4是摆振方向振动平面内的示意图,
|
图 4 旋转梁挥舞方向振动的符号约定和坐标系 Fig. 4 Symbol convention and coordinate system for vibration of rotating beam in flapwise direction |
z为在ẑ轴上的横向位移,梁的势能可以得到:
| $ U=\frac{1}{2} \int_{0}^{L} E I\left(z^{\prime \prime}\right)^{2} \mathrm{~d} x+\frac{1}{2} \int_{0}^{L} F(x)\left(z^{\prime}\right)^{2} \mathrm{~d} x, $ | (10) |
式中rH为梁的输入端距离旋转轴的距离,其中离心力F(x)可以表示为
| $ \begin{aligned} F(x)=& \int_{y}^{L} \bar{m} \varOmega^{2}\left(r_{H}+x\right) \mathrm{d} x+F_{0}=\\ & \bar{m} \varOmega^{2}\left(0.5 L^{2}-r_{H} x-0.5 x^{2}+r_{H} L\right)+F_{0}, \end{aligned} $ | (11) |
式中m为梁的线质量,当梁的末端完全自由时F0=0,离心力对x的一阶导为
| $ F^{\prime}(x)=-\bar{m} \varOmega^{2}\left(r_{H}+x\right). $ | (12) |
梁的动能T由下式给出:
| $ T=\frac{1}{2} \int_{0}^{L} \bar{m} {\dot z}^{2} \mathrm{~d} x. $ | (13) |
Hamilton原理可以表示如下:
| $ \delta \int_{t_{1}}^{t_{2}}(T-U) \mathrm{d} t=0. $ | (14) |
将式(10)、(13)代入式(14)中,可以得到挥舞方向振动的运动微分方程:
| $ \left(E I z^{\prime \prime}\right)^{\prime \prime}-\left(F(x) z^{\prime}\right)^{\prime}+\bar{m} \ddot{z}=0. $ | (15) |
将式(15)中位移改写为谱坐标形式,即z(x, t)= Z(x)eiωt,并代入式(11)、(12),化简方程可得
| $ \begin{array}{c} Z^{\mathrm{IV}}(x)-\left(0.5 C_{1}+r_{H} C_{1} x+C_{2}\right) Z^{\prime \prime}(x)+ \\ C_{1}\left(r_{H}+x\right) Z^{\prime}(x)+C_{3} Z(x)=0, \end{array} $ | (16) |
其中:
| $ C_{1}=\frac{\bar{m} \varOmega^{2}}{E I}, C_{2}=-C_{1} L^{2}\left(0.5+\frac{r_{H}}{L}\right)-\frac{F_{0}}{E I}, $ |
| $ C_{3}=-\frac{\bar{m} \omega^{2}}{E I}. $ |
方程(16)的根是使用幂级数中的Frobenius方法计算的,并且可以假设该微分方程的解如下:
| $ \left\{\begin{array}{l} Z(x, k)=\sum\limits_{i=0}^{\infty} a_{i+1}(k) x^{k+i} , \\ \frac{\mathrm{d} Z(x, k)}{\mathrm{d} x}=\sum\limits_{i=0}^{\infty}(k+i) a_{i+1}(k) x^{k+i-1}, \\ \frac{\mathrm{d}^{2} Z(x, k)}{\mathrm{d} x^{2}}=\sum\limits_{i=0}^{\infty}(k+i)(k+i-1) a_{i+1}(k) x^{k+i-2} , \\ \frac{\mathrm{d}^{3} Z(x, k)}{\mathrm{d} x^{3}}=\sum\limits_{i=0}^{\infty}(k+i)(k+i-1) \times \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (k+i-2) a_{i+1}(k) x^{k+i-3}, \\ \frac{\mathrm{d}^{4} Z(x, k)}{\mathrm{d} x^{3}}=\sum\limits_{i=0}^{\infty}(k+i)(k+i-1)(k+i-2) \times \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (k+i-3) a_{i+1}(k) x^{k+i-4}. \end{array}\right. $ | (17) |
将式(17)代入式(16)中,可以得到:
| $ \begin{array}{l} \sum\limits_{i=0}^{\infty}(k+i-3)(k+i-2)(k+i-1) a_{i+1}(k) x^{k+i-4}+\\ \left(0.5 C_{1} x^{2}+r_{H} C_{1} x+C_{2}\right) \sum\limits_{i=0}^{\infty}(k+i-1)(k+i) a_{i+1}(k) x^{k+i-2}+\\ \left(C_{1} x+C_{1} r_{H}\right) \sum\limits_{i=0}^{\infty}(k+i) a_{i+1}(k) x^{k+i-1}+\\ C_{3} \sum\limits_{i=0}^{\infty} a_{i+1}(k) x^{k+i}=0. \end{array} $ | (18) |
上式也可以写为如下形式:
| $ \begin{array}{l} \sum\limits_{i=-4}^{\infty}\left\{(k+i+1)(k+i+2)(k+i+3)(k+i+4) a_{i+5}+\right. \\ C_{2}(k+i+1)(k+i+2) a_{i+3}+C_{1} r_{H}(k+i+1)^{2} a_{i+2}+ \\ \left.\left[C_{1}(k+i)+0.5 C_{1}(k+i-1)(k+i)+C_{3}\right] a_{i+1}\right\} x^{k+i}. \end{array} $ | (19) |
代入i=-4到式(19)中,可以发现只有a1得系数非零,其他的项都等于0.因此,将i=-4代入式(19)中,发现a1是最低阶非消失系数,得到k(k-1)(k-2)(k-3)a1=0, 其中a1≠0, 那么k只有0,1,2和3这4个根满足方程k(k-1)(k-2)(k-3)=0,并且a1是任意数,这里假设a1=1, 式(19)中的未知系数的一般形式可以用以下表达:
| $ \begin{array}{l} {a_{i + 5}} = - \frac{{{C_2}}}{{(k + i + 3)(k + i + 4)}}{a_{i + 3}} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{{r_H}{C_1}(k + i + 1)}}{{(k + i + 2)(k + i + 3)(k + i + 4)}}{a_{i + 2}} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{{C_1}(k + i) + 0.5{C_1}(k + i - 1)(k + i) + {C_3}}}{{(k + i + 1)(k + i + 2)(k + i + 3)(k + i + 4)}}{a_{i + 1}}. \end{array} $ | (20) |
分别将i=-3, i=-2, i=-1及i=0代入式(20)中,依次得到:
| $ \left\{\begin{array}{l} a_{2}=0, \\ a_{3}=-\frac{C_{2}}{(k+1)(k+2)} a_{1}, \\ a_{4}=-\frac{r_{H} C_{1} k}{(k+1)(k+2)(k+3)} a_{1}, \\ a_{5}=-\frac{C_{2}}{(k+3)(k+4)} a_{3}-\frac{0.5 C_{1} k(k+1)+C_{3}}{(k+1)(k+2)(k+3)(k+4)} a_{1} . \end{array}\right. $ | (21) |
从式(19)、(20)可以确定所有未知系数,对于k=0, 1, 2, 3, 微分方程式(19)的解可以用4个独立线性解的总和乘以任意常数表示如下:
| $ Z(x)=A_{1} f(x, 0)+A_{2} f(x, 1)+A_{3} f(x, 2)+A_{4} f(x, 3), $ | (22) |
式中A =[A1, A2, A3, A4]T是任意常数,方程(22)中k=0, 1, 2, 3的4个独立解f(x, k)可以用函数的形式表示如下:
| $ \begin{array}{l} f(x, k)=\sum\limits_{i=0}^{\infty} a_{i+1}(k) x^{k+i} \Rightarrow \\ f(x, 0)=a_{1}(0) x^{0}+a_{3}(0) x^{2}+a_{4}(0) x^{3}+a_{5}(0) x^{4}+\cdots, \\ f(x, 1)=a_{1}(1) x^{1}+a_{3}(1) x^{3}+a_{4}(1) x^{4}+a_{5}(1) x^{5}+\cdots, \\ f(x, 2)=a_{1}(2) x^{2}+a_{3}(2) x^{3}+a_{4}(2) x^{4}+a_{5}(2) x^{5}+\cdots, \\ f(x, 3)=a_{1}(3) x^{3}+a_{3}(3) x^{4}+a_{4}(3) x^{5}+a_{5}(3) x^{6}+\cdots. \end{array} $ | (23) |
由材料力学可得旋转梁在此平面内的弯矩和剪切力,分别为:
| $ M_{y}=E I \frac{d^{2} Z(x)}{\mathrm{d} x^{2}}, $ | (24) |
| $ \begin{array}{c} Q_{z}=E I Z^{\prime \prime \prime}(x)-0.5 \bar{m} \varOmega^{2}\left(L^{2}+2 r_{H} L-\right. \\ \left.2 r_{H} x-x^{2}\right) Z^{\prime}(x)-F_{0} Z^{\prime}(x). \end{array} $ | (25) |
在MSTMM中,桨叶挥舞方向z-x平面内的边界条件为[Z, Θy, My, Qz]T,根据线性关系可以得到Θy =Z′,联立式(24)、(25),可以写成如下形式Z(x)=D(x) A.
| $ {\left[ {\begin{array}{*{20}{c}} Z\\ {{\Theta _y}}\\ {{M_y}}\\ {{Q_z}} \end{array}} \right]_x} = \left[ {\begin{array}{*{20}{c}} {f(x,0)}&{f(x,1)}&{f(x,2)}&{f(x,3)}\\ {{f^\prime }(x,0)}&{{f^\prime }(x,1)}&{{f^\prime }(x,2)}&{{f^\prime }(x,3)}\\ {EI{f^{\prime \prime }}(x,0)}&{E{I^{\prime \prime }}(x,1)}&{E{I^{\prime \prime }}(x,2)}&{EI{f^{\prime \prime }}(x,3)}\\ {{H_1}}&{{H_2}}&{{H_3}}&{{H_4}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{A_1}}\\ {{A_2}}\\ {{A_3}}\\ {{A_4}} \end{array}} \right], $ | (26) |
其中:
| $ H_{1}=E I\left[f^{\prime \prime \prime}(x, 0)+\gamma f^{\prime}(x, 0)\right], $ |
| $ H_{2}=E I\left[f^{\prime \prime \prime}(x, 1)+\gamma f^{\prime}(x, 1)\right], $ |
| $ H_{3}=E I\left[f^{\prime \prime \prime}(x, 2)+\gamma f^{\prime}(x, 2)\right], $ |
| $ H_{4}=E I\left[f^{\prime \prime \prime}(x, 3)+\gamma f^{\prime}(x, 3)\right], $ |
| $ \gamma=\left(0.5 C_{1} x^{2}+r_{H} C_{1} x+C_{2}\right) . $ |
由式(26)可以得到在x=l1作为输入端的状态适量为Z I=[D (l1)] A,从而这组未知的系数向量可以表示为A =[D (l1)]-1 Z I,那么位于x=l2的输出端的状态矢量为
| $ \boldsymbol{Z}_{O}=\left[\boldsymbol{D}\left(l_{2}\right)\right] \boldsymbol{A}=\left[\boldsymbol{D}\left(l_{2}\right)\right]\left[\boldsymbol{D}\left(l_{1}\right)\right]^{-1} \boldsymbol{Z}_{I}=U^{R B} \boldsymbol{Z}_{I}, $ | (27) |
式中URB=[D (l2)][D (l1)]-1为旋转梁在挥舞平面内横向振动的传递矩阵.
同理,在摆振运动平面内也以此方法获得其传递矩阵,但在离心力部分略有不同,由于离心力的作用方向分为摆振方向和展向分量,因此运动微分方程为
| $ E I_{z} y^{\mathrm{IV}}-F(x) y^{\prime \prime}-F^{\prime}(x) y^{\prime}-\Omega^{2} m y+m \ddot{y}=0 $ | (28) |
非圆截面梁的扭转通过材料力学可以得知微段的扭转角φ与扭矩T的关系为
| $ \varphi=\frac{T}{G \beta h b^{3}}=\frac{T}{G I_{t}}. $ | (29) |
式中:G为剪切模量; h为截面长边; b为截面短边; β为矩形截面杆扭转时的因数,当h/b远大于10时,β近似等于0.333, It=βhb3.在扭转方向上由于螺桨效应的影响,即由离心力Ω引起回复力矩,扭转振动的运动微分方程为
| $ \left(G I_{t} \varphi^{\prime}\right)^{\prime}-I_{\alpha}\left(\ddot{\varphi}+\varOmega^{2} \varphi\right)=0, $ | (30) |
其中Iα为微段绕扭转轴的转动惯量.
通过求解式(30)这个微分方程,最终可以得到长为x的旋转梁扭转振动的传递矩阵如下:
| $ U_{t}=\left[\begin{array}{cc} \cos \gamma x & \frac{1}{\gamma G I_{t}} \sin \gamma x \\ -\gamma G I_{t} \sin \gamma x & \cos \gamma x \end{array}\right], $ | (31) |
式中
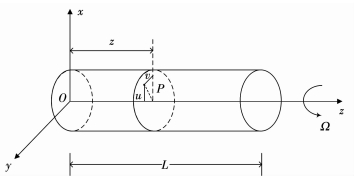
推导传动轴的传递矩阵,首先确定其运动微分方程.建立如图 5所示模型,一根长为L的均质Euler-Bernoulli梁绕Z轴以角速度Ω旋转,线质量为m且在YZ平面与XZ中的主轴弯曲刚度分别是EIxx和EIyy, 距离原点z处的截面质心点P在X轴和Y轴上的位移分别是u和v,通过Hamilton原理得到其运动微分方程为[16]
|
图 5 旋转轴模型 Fig. 5 Spinning axis model |
| $ \left\{\begin{array}{l} E I_{y y} u^{\prime \prime \prime \prime}-2 m \Omega \dot{v}-m \Omega^{2} u+m \ddot{u}=0 , \\ E I_{x x} v^{\prime \prime \prime \prime}-2 m \Omega \dot{u}-m \Omega^{2} v+m \ddot{v}=0. \end{array}\right. $ | (32) |
代入模态坐标u(z, t)=U(z)eiωt和v(z, t)=V(z)eiωt,并引入量纲一的长度ξ =z/L与微分算子D=d/dξ,整理后式(33)变为
| $ \left\{\begin{array}{l} \left(D^{4}-\frac{m \omega^{2} L^{4}}{E I_{y y}}-\frac{m \varOmega^{2} L^{4}}{E I_{y y}}\right) U-\frac{2 m \varOmega \omega L^{4}}{E I_{y y}} V=0, \\ \left(D^{4}-\frac{m \omega^{2} L^{4}}{E I_{x x}}-\frac{m \varOmega^{2} L^{4}}{E I_{x x}}\right) V-\frac{2 m \varOmega \omega L^{4}}{E I_{x x}} U=0. \end{array}\right. $ | (33) |
对式(33)求解后分别得到U(ξ)和V(ξ)的通解:
| $ \begin{aligned} U(\xi)=& A_{1} \sin \sqrt{\alpha} \xi+A_{2} \cos \sqrt{\alpha} \xi+A_{3} \sinh \sqrt{\alpha} \xi+\\ & A_{4} \cosh \sqrt{\alpha} \xi+A_{5} \sin \sqrt{\beta} \xi+A_{6} \cos \sqrt{\beta} \xi+\\ & A_{7} \sinh \sqrt{\beta} \xi+A_{8} \cosh \sqrt{\beta} \xi , \\ V(\xi)=& B_{1} \sin \sqrt{\alpha} \xi+B_{2} \cos \sqrt{\alpha} \xi+B_{3} \sinh \sqrt{\alpha} \xi+\\ & B_{4} \cosh \sqrt{\alpha} \xi+B_{5} \sin \sqrt{\beta} \xi+B_{6} \cos \sqrt{\beta} \xi+\\ & B_{7} \sinh \sqrt{\beta} \xi+B_{8} \cosh \sqrt{\beta} \xi. \end{aligned} $ | (34) |
A1-A8与B1-B8是两组独立的8个常系数,其之间的关系如下:
| $ \begin{array}{l} \left(A_{1}, A_{2}, A_{3}, A_{4}\right)=k_{\alpha}\left(B_{1}, B_{2}, B_{3}, B_{4}\right), \\ \left(A_{5}, A_{6}, A_{7}, A_{8}\right)=k_{\beta}\left(B_{5}, B_{6}, B_{7}, B_{8}\right), \end{array} $ | (35) |
其中:
| $ k_{\alpha}=\frac{2 \lambda_{x}^{2} \eta}{\alpha^{2}-\lambda_{x}^{2}\left(1+\eta^{2}\right)}, k_{\beta}=\frac{2 \lambda_{y}^{2} \eta}{\beta^{2}-\lambda_{y}^{2}\left(1+\eta^{2}\right)} $ |
| $ \lambda_{x}^{2}=\frac{m \omega^{2} L^{4}}{E I_{x x}}, \lambda_{y}^{2}=\frac{m \omega^{2} L^{4}}{E I_{y y}}, \eta^{2}=\frac{\varOmega^{2}}{\omega^{2}}, $ |
| $ \begin{aligned} \alpha=& \frac{1}{2}\left\{\left(\lambda_{x}^{2}+\lambda_{y}^{2}\right)\left(1+\eta^{2}\right)+\right.\\ & \sqrt{\left(\lambda_{x}^{2}+\lambda_{y}^{2}\right)^{2}\left(1+\eta^{2}\right)^{2}+16 \lambda_{x}^{2} \lambda_{y}^{2} \eta^{2}}, \end{aligned} $ |
| $ \begin{aligned} \beta=& \frac{1}{2}\left\{\left(\lambda_{x}^{2}+\lambda_{y}^{2}\right)\left(1+\eta^{2}\right)-\right.\\ & \sqrt{\left(\lambda_{x}^{2}+\lambda_{y}^{2}\right)^{2}\left(1+\eta^{2}\right)^{2}+16 \lambda_{x}^{2} \lambda_{y}^{2} \eta^{2}}. \end{aligned} $ |
由式(32)可以得出扭转角,弯矩与剪切力的表达式如下:
| $ \theta_{x}=-\frac{\mathrm{d} V}{\mathrm{~d} z}=-\frac{1}{L} \frac{\mathrm{d} V}{\mathrm{~d} \xi}, \theta_{y}=-\frac{\mathrm{d} U}{\mathrm{~d} z}=-\frac{1}{L} \frac{\mathrm{d} U}{\mathrm{~d} \xi}; $ | (36) |
| $ \begin{array}{l} M_{x}=E I_{x x} \frac{d^{2} V}{\mathrm{~d} z^{2}}=\frac{E I_{x x}}{L^{2}} \frac{d^{2} V}{\mathrm{~d} \xi^{2}} , \\ M_{y}=-E I_{y y} \frac{d^{2} U}{\mathrm{~d} z^{2}}=\frac{E I_{y y}}{L^{2}} \frac{d^{2} U}{\mathrm{~d} \xi^{2}}; \end{array} $ | (37) |
| $ \begin{array}{l} S_{x}=E I_{y y} \frac{d^{3} U}{\mathrm{~d} z^{3}}=\frac{E I_{y y}}{L^{3}} \frac{d^{3} U}{\mathrm{~d} \xi^{3}}, \\ S_{y}=E I_{x x} \frac{d^{3} V}{\mathrm{~d} z^{3}}=\frac{E I_{x x}}{L^{3}} \frac{d^{3} V}{\mathrm{~d} \xi^{3}}. \end{array} $ | (38) |
将式(34)、(35)分别代入到式(36)~式(38)中,整理后可以得到x=l1处的状态矢量为
| $ \boldsymbol{Z}_{I}=\left[\boldsymbol{D}\left(\frac{l_{1}}{L}\right)\right] \boldsymbol{A}, $ | (39) |
式中ZI=[U, V, θx, θy, Mx, My, Sx, Sy]T,以x=l2为输出端,可以得到:
| $ Z_{0}=\left[D\left(\frac{l_{2}}{L}\right)\right]\left[D\left(\frac{l_{1}}{L}\right)\right]^{-1} Z_{I}=\boldsymbol{U}^{S} Z_{I}, $ | (40) |
| $ \boldsymbol{U}^{S}=\left[D\left(\frac{l_{2}}{L}\right)\right]\left[D\left(\frac{l_{1}}{L}\right)\right]^{-1}, $ | (41) |
式中US为旋转轴的传递矩阵.
3 计算与仿真对比验证 3.1 旋转梁的固有频率验证为验证MSTMM计算旋转梁频率的准确性,分别对转速为0,20,40 rad/s时悬臂梁的频率计算,使用MATLAB编程计算与Ansys Workbench仿真结果的前五阶频率对比.梁的参数分别为,长度L=6 m,横截面长b=0.5 m,高h=0.04 m,密度ρ=334 kg/m3,弹性模量E=7.1 MPa,剪切模量G=2.730 8 MPa,泊松比μ=0.3. ANSYS Workbench的模型有88 413个节点,网格单元数为15 600.
计算结果与对比见表 1,3种转速下前五阶频率结果误差较小.取3次相同计算条件下的平均时间,使用MATLAB编程的计算时间为6.3 s,ANSYS Workbench的计算时间是55.9 s.计算速度提高了8.8倍.
| 表 1 悬臂梁在3种转速下MSTMM计算与ANSYS仿真的固有频率对比 Tab. 1 Comparison of natural frequencies of a cantilever beam obtained from MSTMM calculation and ANSYS simulation at three speeds |
旋转轴的验证模型选择一根各向同性均匀圆截面梁,这个算例选择悬臂边界条件,此方法同样适用于其他边界条件.以量纲一的形式呈现结果直观高效,定义以下量纲一的固有频率ωi*和旋转速度参数Ω*, 从而能够应用于一般情况.
| $ \omega_{i}^{*}=\omega_{i} / \omega_{0}, \varOmega^{*}=\varOmega / \omega_{0}, $ | (42) |
式中
梁的参数分别为,长L=1.29 m,抗弯刚度EIxx=EIyy=582.996 N·m2,线质量m=2.87 kg/m.使用MSTMM方法MATLAB编程计算结果与文献[16]中的前6阶频率对比结果见表 2,计算结果基本相同,在低转速下结果误差在0.15%内,随着转速提高,计算结果也越相近,而且在高转速下MSTMM方法依然可以求得低阶频率.
| 表 2 圆截面悬臂旋转轴的固有频率(EIxx=EIyy) Tab. 2 Natural frequencies of a cantilever spinning axis with circular cross-section (EIxx=EIyy) |
为了验证MSTMM方法计算的准确性,对图 2直升机模型进行验证计算.直升机各部件的参数如下,桨叶密度ρ=334 kg/m3,长度L=6 m,横截面长b=0.5 m,高h=0.04 m,弹性模量E=7.1 MPa,剪切模量G=2.730 8 MPa; 桨毂密度ρ=7 850 kg/m3,尺寸为长和宽为0.5 m,高0.3 m; 传动轴密度ρ=7 850 kg/m3,尺寸为直径0.16 m, ,高为1 m,弹性模量E=2.5 MPa,剪切模量G=9.615 4 MPa; 机身密度ρ=170 kg/m3,长3 m,宽1.8 m,高1.6 m,质心与机身传动轴连接点在X轴上的投影距离0.4 m; 尾梁密度ρ=140 kg/m3,截面高和宽为0.8 m,长为4 m,弹性模量E=2 MPa,剪切模量G=7.692 3 MPa.尾梁末端采用固定约束,旋翼系统的转速为36.651 9 rad/s. ANSYS Workbench模型的节点数88 260,16 056个单元.前12阶频率见表 3.
| 表 3 使用MSTMM方法计算旋转状态直升机固有频率与ANSYS仿真结果对比 Tab. 3 Comparison of natural frequencies of helicopter model obtained from MSTMM calculation and ANSYS simulation in rotating state |
计算结果与仿真结果基本一致.3次相同计算条件下的平均时间,使用MATLAB编程的计算时间为11.5 s,ANSYS Workbench的计算时间是81.2 s.计算速度提高了7.1倍.由此可以使用MSTMM方法计算无约束条件即悬停状态下直升机模型的固有频率,前8阶的计算结果见表 4.
| 表 4 悬停状态下直升机模型固有频率 Tab. 4 Natural frequencies of helicopter model in hovering state |
1) 本文推导了旋转梁在挥舞、摆振和扭转3个自由度的运动方程,得到其传递矩阵,算例通过与ANSYS仿真结果对比,误差在1.5%以内,验证了结果的准确性.
2) 推导了旋转轴的传递矩阵,算例与参考文献结果对比,误差不超过0.15%,验证了准确性.
3) MSTMM可以快速准确地计算动力学问题.并且相较于传统动力学软件Workbench ANSYS,结果相近,计算时间大大缩短,本文算例计算时间缩短了7倍以上.
4) 对直升机旋翼/机身耦合系统验证计算,与仿真结果基本一致,并得到了悬停状态下的前8阶固有频率,对直升机设计具有一定参考价值.
| [1] |
CHENG Jianlian, XU Hui. Inner mass impact damper for attenuating structure vibration[J]. International Journal of Solids and Structures, 2006, 43(17): 5355. DOI:10.1016/j.ijsolstr.2005.07.026 |
| [2] |
YANG J B, JIANG L J, CHEN D C. Dynamic modelling and control of a rotating Euler-Bernoulli beam[J]. Journal of Sound and Vibration, 2004, 274(3/4/5): 863. DOI:10.1016/S0022-460X(03)00611-4 |
| [3] |
VINOD K G, GOPALAKRISHNAN S, GANGULI R. Free vibration and wave propagation analysis of uniform and tapered rotating beams using spectrally formulated finite elements[J]. International Journal of Solids and Structures, 2007, 44(18/19): 5875. DOI:10.1016/j.ijsolstr.2007.02.002 |
| [4] |
PNUELI D. Natural bending frequency comparable to rotational frequency in rotating cantilever beam[J]. Journal of Applied Mechanics, 1972, 39(2): 602. DOI:10.1115/1.3422729 |
| [5] |
FOX C H J, BURDESS J S. The natural frequencies of a thin rotating cantilever with offset root[J]. Journal of Sound and Vibration, 1979, 65(2): 151. DOI:10.1016/0022-460X(79)90509-1 |
| [6] |
BANERJEE J R, SU H, JACKSON D R. Free vibration of rotating tapered beams using the dynamic stiffness method[J]. Journal of Sound and Vibration, 2006, 298(4/5): 1034. DOI:10.1016/j.jsv.2006.06.040 |
| [7] |
PAWAR P M, GANGULI R. On the effect of progressive damage on composite helicopter rotor system behavior[J]. Composite Structures, 2007, 78(3): 410. DOI:10.1016/j.compstruct.2005.11.043 |
| [8] |
WANG Gang, WERELEY N M. Free vibration analysis of rotating blades with uniform tapers[J]. AIAA Journal, 2004, 42(12): 2429. DOI:10.2514/1.4302 |
| [9] |
LEE J W, LEE J Y. Free vibration analysis using the transfer-matrix method on a taperedbeam[J]. Computers & Structures, 2016, 164(C): 75. DOI:10.1016/j.compstruc.2015.11.007 |
| [10] |
LEE J W, LEE J Y. In-plane bending vibration analysis of a rotating beam with multiple edge cracks by using the transfer matrix method[J]. Meccanica, 2017, 52(4/5): 1143. DOI:10.1007/s11012-016-0449-4 |
| [11] |
RONG Bao, RUI Xiaoting, WANG Guoping. New method for dynamics modelling and analysis on flexible plate undergoing large overall motion[J]. Proceedings of the Institution of Mechanical Engineers Part K: Journal of Multi-body Dynamics, 2010, 224(1): 33. DOI:10.1243/14644193JMBD219 |
| [12] |
RUI Xiaoting, ZHANG Jianshu, ZHOU Qinbo. Automatic deduction theorem of overall transfer equation of multibody system[J]. Advances in Mechanical Engineering, 2015, 6: 378047. DOI:10.1155/2014/378047 |
| [13] |
ABBAS L K, ZHOU Qinbo, BESTLE D, et al. A unified approach for treating linear multibody systems involving flexible beams[J]. Mechanism and Machine Theory, 2017, 107: 197. DOI:10.1016/j.mechmachtheory.2016.09.022 |
| [14] |
RUI Xiaoting, WANG Xun, ZHOU Qinbo, et al. Transfer matrix method for multibody systems (Rui method) and its applications[J]. Science China (Technological Sciences), 2019, 62(5): 712. DOI:10.1007/s11431-018-9425-x |
| [15] |
RUI Xiaoting, ABBAS L K, YANG Fufeng. Flapwise vibration computations of coupled helicopter rotor/fuselage: Application of multibody system dynamics[J]. AIAA JOURNAL, 2018, 56(2): 818. DOI:10.2514/1.J056591 |
| [16] |
BANERJEE J R, SU H. Development of a dynamic stiffness matrix for free vibration analysis of spinning beams[J]. Computers & Structures, 2004, 82(23/24/25): 2189. DOI:10.1016/j.compstruc.2004.03.058 |
 2021, Vol. 53
2021, Vol. 53


