2. 工业装备结构分析国家重点实验室(大连理工大学), 辽宁 大连 116024;
3. 高技术船舶与深海开发装备协同创新中心,上海 200240)
2. State Key Laboratory of Structural Analysis for Industrial Equipment (Dalian University of Technology), Dalian 116024, Liaoning, China;
3. Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration, Shanghai 200240, China
由于中国海洋面积广阔、海岸线漫长、海洋环境复杂,各种海洋灾害频发并伴随着巨大的损失,随着有关海洋各项研究工作的开展,海洋的防灾减灾工作就显得极为重要,同时防灾减灾工作也是海洋经济发展以及生态文明建设的基础性工作.目前,中国的海洋预报业务可覆盖全球大部分地区,多种海洋波浪预报处于国际前沿水平,海洋的防灾减灾工作正稳步推进但同时也面临着严峻的挑战.
畸形波是海洋灾害的重点研究对象之一,它来源于1965年Draper[1]提出的“Freak wave”,也可以称为“凶波”或“巨波”,世界上有关畸形波的首次记录是1896年由畸形波引起的葡萄牙Spray号船的倾覆.杨冠声等[2]指出近年来,在南非东南海域、日本海域、挪威北海海域、中国的南海海域以及台湾海峡都有畸形波的观测记录.南海又是中国海洋建设的重点海域,由于畸形波对海上建筑物强大的破坏力以及对人员生命财产的威胁,对畸形波的研究就显得迫在眉睫,畸形波的有效预报也能有助于海洋防灾工作的进一步推进.Kharif等[3]指出波浪对海洋建筑物的影响由许多参数确定,现有的测量和理论并不总是允许对波浪事故进行非常详细的描述,因此畸形波的简化定义就存在一定的意义,本文采用一个简单的定义,即波高大于两倍有义波高的波浪为畸形波.
| $ AI = \frac{{{H_{fr}}}}{{{H_s}}} > 2. $ | (1) |
式中:Hfr为畸形波的高度,cm; Hs为有义波高,cm; AI为定义波浪是否为畸形波的参数.
由于畸形波特性以及外界条件的限制,完整的畸形波记录很难得到,而且相关记录相对较少,因此无法得到大量可靠的实测资料用于畸形波的研究,畸形波的发生机理仍然无法得到统一认识.对于畸形波的研究,学者们大都在实验室通过建立不同的物理模型或者是在计算机上对畸形波进行数值模拟.目前,畸形波的产生机理有如下几种解释:一是由于Lavrenov[4]研究的反向流放大作用,它只能描述特定海域的畸形波的发生; 二是White等[5]研究的波的集中作用,可以理解为一定条件下由于多种环境同时作用,产生畸形波; 三是Dias等[6]研究的波的非线性不稳定性.赵西增等[7]基于高阶谱方法在实验室建立了三维畸形波聚焦模型并对大尺度畸形波的发展过程进行了模拟.裴玉国[8]通过建立多种叠加模型在实验室生成了畸形波同时证实了随机波浪中畸形波的发生,同时通过对试验得到的畸形波进行分析研究得到了畸形波的基本特性.Lu等[9]基于非线性四阶薛定谔方程,数值研究了Peregrine呼吸子解畸形波的产生和演化.Kharif等[10]在经典非线性方程的框架下对畸形波进行了数值模拟,讨论了Benjamin-Feir不稳定性对畸形波的影响.Waseda等[11]利用定向波发生器,在实验室水槽中研究了深水中随机定向波的演化,根据各项参数的变化研究了畸形波发生的条件.刘首华等[12]讨论了目前畸形波研究存在的问题并对各项问题及解决思路进行了探讨.
人工神经网络与小波分析相结合,网络就能避免陷入局部最优,加快收敛速度,又能同时对数据的时——频局部化分析,在非线性信号和突变信号的研究方面更有优势.赵勇[13]对小波的理论基础做了详细的描述并分析了小波数值方法在流体力学方面的若干应用.谭善文等[14]分析了小波基的各项性质,同时对突变信号的小波变换性质进行了详细的描述和实验验证,结果表明小波变换由于其时频局部化特征, 非常适合突发信号的识别.Deka等[15]通过建立小波变换和神经网络结合的松散型小波神经网络,预报了印度西海岸高达48 h的有效波高,结果与传统单一神经网络预报结果相比,小波神经网络的预报精度更高. Doong等[16]建立的人工神经网络的海岸畸形波预警模型结果表明,所提出的预警模型是准确可靠的,并证实了神经网络在自然灾害预警中的应用.孟雷等[17]建立了3种神经网络模型对海浪模式输出的有效波高进行训练学习,结果表明通过神经网络可提高其模拟精度.朱智慧[18]利用SWAN海浪模式和BP神经网络对波浪的有效波高分别进行了预报,结果表明BP神经网络的预报效果更好,SWAN模式预报数值随着有效波高的增大,误差会增大.本文采用的紧致型小波神经网络能够对畸形波进行有效预报,基于某岛礁附近波形演化实验进行了畸形波预报和分析.
1 小波神经网络理论傅里叶变换是整体变换,只能单独对时域或者频域进行分析,信号中时域和频域的信息不能够同时得到,因此更适用于平稳信号的分析.但在实际的研究工作中,所处理的往往是非平稳信号,由于能够对信号进行时间和频率局部化分析,经过伸缩和平移运算后在高频信号处对时间的分辨率高,在低频信号处对频率的分辨率高,可以更好地捕捉信号的任何细节.因此王建忠[19]指出小波变换相对于傅里叶变换对于非稳态信号以及突变信号有更强的处理能力.
小波母函数ψ(t)必须满足容许条件:
| $ \int_{ - \infty }^\infty {\frac{{{{\left| {\hat \psi \left( \lambda \right)} \right|}^2}}}{{\left| \lambda \right|}}} {\rm{d \mathsf{ λ} < + }}\infty . $ | (2) |
小波母函数通过伸缩和平移变换得来得到连续小波公式为
| $ {\psi _{a, b}}\left( t \right) = {\left| a \right|^{ - 1/2}}\psi \left( {\frac{{t - b}}{a}} \right). $ | (3) |
式中:a为尺度参数,b为平移参数.
对于f∈L2
| $ {W_f} = \left\langle {f, {\psi _{a, b}}} \right\rangle = {\left| a \right|^{ - 1/2}}\int_{ - \infty }^\infty {f\left( t \right){\psi _{a, b}}\left( {\frac{{t - b}}{a}} \right){\rm{d}}t} , $ | (4) |
为信号f(t)的连续小波变换.
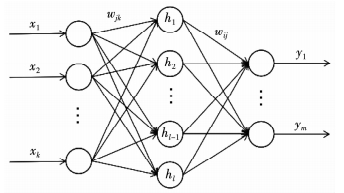
神经网络现广泛应用于各个领域研究当中,由于容错性、鲁棒性以及自适应能力极强,能够对复杂的非线性关系进行有效地学习.小波神经网络(Wavelet Neural Network, WNN)是将小波变换与神经网络理论相结合形成的前馈神经网络.紧致型结合和松散型结合是目前小波理论与神经网络结合的两种方式,紧致型结合方式通常是用小波函数代替传统神经网络的激活函数,小波变换和网络系数之间经过仿射变换建立关系; 松散结合方式则是先将信号进行小波分析得到每一层的高频和低频信号,再将处理后的数据输入到神经网络当中.目前研究工作中广泛采用紧致型小波神经网络的结构形式,它处理数据的能力更强,本文在处理畸形波数据时采用的是紧致型的小波神经网络,其网络拓扑结构如图 1所示.
|
图 1 小波神经网络拓扑结构 Fig. 1 Topology of wavelet neural network |
图 1为3层小波神经网络拓扑结构,x1, …, xk为神经网络的输入层,y1, …, ym为神经网络的输出层,隐含层用小波基函数代替传统神经网络的激活函数,wjk为输入层—隐含层的权值,wij为隐含层—输出层的权值,当输入信号序列为xi(i=1, …, k)时,隐含层的输出公式为
| $ h\left( j \right) = {h_j}\left( {\frac{{\sum\limits_{i = 1}^k {{w_{jk}}{x_k}} - {b_j}}}{{{a_j}}}} \right), {\rm{ }}j = 1, 2, \ldots , l. $ | (5) |
式中:hj为小波基函数; aj为小波基函数的伸缩因子; bj为小波基函数的平移因子; h(j)为隐含层第j个节点的输出值.
小波基函数选用Morlet母小波,其数学公式为
| $ y = {\rm{cos}}(5x){{\rm{e}}^{ - {x^2}/2}}. $ | (6) |
输出层的计算公式为
| $ y\left( i \right) = \sum\limits_{j = 1}^l {{w_{ij}}h} \left( j \right), i = 1, 2, \ldots , m $ | (7) |
网络预报流程图如图 2所示.

|
图 2 小波神经网络预报流程 Fig. 2 Wavelet neural network prediction flow chart |
在实验室中,学者们通常采用在实验水槽内对畸形波进行模拟或者是在计算机上对畸形波进行数值模拟.在实验水槽内通常可以采用聚焦方法模拟畸形波、非线性自聚焦方法模拟畸形波或者是在随机波列模拟畸形波.邹丽等[20-21]通过随机波浪试验对岛礁地形的畸形波演化过程及特性进行了研究,同时得到了含有畸形波的波浪时间序列数据.本文的样本数据来自邹丽等[21]根据某岛礁实测数据建立的岛礁三维模型(1: 100)中测得,在实验中根据不同有效波高、不同周期设置了多个工况,同时在试验水池中选取了50个点设置浪高仪,浪高仪每0.02 s采集一次数据,历时81.92 s,获得4 096个波高序列数据,实验结果发现在多个波高时间序列中存在畸形波.
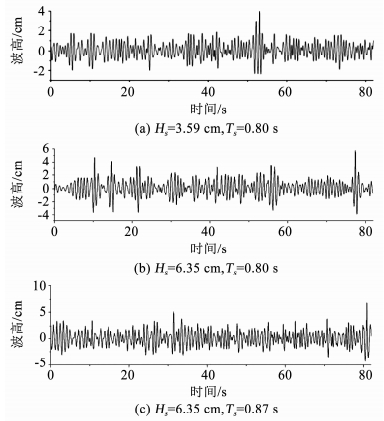
本文选择存在畸形波的时间序列进行分析研究,所选3个波浪数据序列如图 3所示, 图 3(a)是在有义波高Hs=3.59 cm, 有义周期Ts=0.80 s工况下H8地形位置,浪高仪编号13记录下的波浪时间序列,此波浪时间序列T=53.04 s处测得最大波高Hmax=6.36 cm, 波高比达到了AI=2.20,符合畸形波定义. 图 3(b)是在有义波高Hs=6.35 cm, 有义周期Ts=0.80 s工况下G5地形位置,浪高仪编号49记录下的波浪时间序列,此时间序列最大波高Hmax=9.63 cm发生在T=77.34 s这一时刻, 波高比为AI=2.11.与图 3(a)不同的是,在图 3(b)时间序列中T=10.06 s处的波高已经达到了8.35 cm,此处波高比为AI=1.83,已经接近畸形波定义中的2倍,波浪时间序列中多次出现较大的波高时刻,表明此处发生畸形波的概率较高. 图 3(c)是在有义波高Hs=6.35 cm, 有义周期Ts=0.87 s工况下H1地形位置,浪高仪编号16记录下的波浪时间序列,此序列T=80.8 s处达到最大波高Hmax=11.25 cm.此时间序列的非线性很强,最大波高处的波高比达到了AI=2.10,符合畸形波定义,畸形波波峰高度达到了波高的61.6%.
|
图 3 波浪演化的波面时间序列图 Fig. 3 Wave surface time series diagram of wave evolution |
本文属于时间序列预报,岛礁试验中每个浪高仪历时81.92 s共记录4 096个数据,用前60 s测得的3 000个数据的波面时间序列将作为训练数据训练神经网络模型,利用训练好的模型预报后21.92 s内的1 096个数据的波面时间序列,将神经网络输出预报值与实际测量数据进行比较,从而判断神经网络的训练精度.在构建小波神经网络时隐含层神经元个数采用拼凑法确定为24,此时小波神经网络的预报精度更好,输入层神经元个数为4,输出层神经元个数为1,确定网络模型为4-24-1结构.网络权值更新学习速率lr 1=0.01,小波基函数伸缩因子和平移因子的更新学习速率lr 2=0.001,最大训练次数为100次.
误差分析引入平均绝对误差(MAE),平均相对误差(MRE)和均方根误差(RMSE).
平均绝对误差(MAE)公式为
| $ {\rm{MAE}} = \frac{{\sum {\left| {Y - X} \right|} {\rm{ }}}}{N}, $ | (8) |
平均相对误差(MRE)公式为
| $ {\rm{MRE}} = \frac{1}{N}\sum {\left| {\frac{{Y - X}}{Y}} \right|} $ | (9) |
均方根误差(RMSE)公式为
| $ {\rm{RMSE = }}\sqrt {\frac{{\sum\limits_{i = 1}^N {{{\left( {Y - X} \right)}^2}} }}{N}} . $ | (10) |
式中:Y为预报输出; X为实际输出; N为输出数据的数目.
为考察小波神经网络的精度,本文同时引入了传统的BP神经网络,网络模型同样采用4-24-1结构,学习速率为0.01,不同于小波神经网络的是BP神经网络采用的激活函数是sigmod函数.经过实验得到了每个工况的两种神经网络预报的波面时间序列图和预报值与实际值之间的误差曲线图,误差曲线图中的误差为预报值与实际值之间的绝对误差,并根据结果对3个工况的波高时间序列进行了分析.
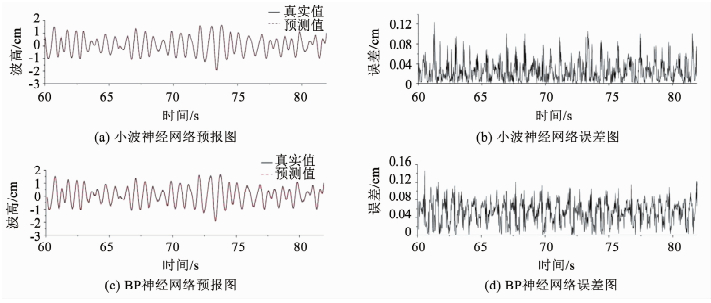
3.1 工况①有义波高Hs=3.59 cm, 有义周期Ts=0.80 s,H8地形位置,浪高仪编号13.两种网络模型预报结果及误差如图 4所示,误差曲线分布较为均匀.
|
图 4 Hs=3.59 cm, Ts=0.80 s Fig. 4 Hs=3.59 cm, Ts=0.80 s |
工况①波面整体预报结果误差见表 1.工况①测点处在地形非线性变化的区域H8地形位置,此时间序列中畸形波形成于53.04 s, 此畸形波数据作为训练样本存在于神经网络当中,预报时间段属于常规波浪.虽然是常规波预报,用畸形波数据预报常规波,预报精度相对较高但并无明显优势.
| 表 1 工况①预报误差分析 Tab. 1 Error analysis of prediction case ① |
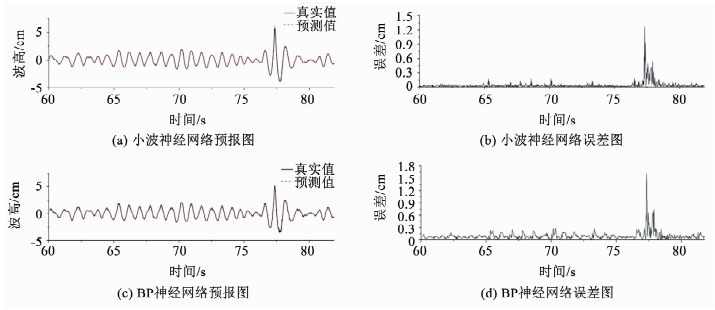
有义波高Hs=6.35 cm, 有义周期Ts=0.80 s,G5地形位置,浪高仪编号49测点预报结果如图 5所示,误差集中在畸形波附近.
|
图 5 Hs=6.35 cm, Ts=0.80 s Fig. 5 Hs=6.35 cm, Ts=0.80 s |
工况②波面整体预报结果误差见表 2.工况②的G5地形位置与工况①的H8同样处于地形非线性变化的区域,总体来看在这种区域内畸形波生成的概率偏大,说明在一定条件下,地形变化区域有可能发生畸形波.此工况预报样本中存在近似畸形波,两种神经网络的各项误差值普遍会比工况①的常规波浪的误差值稍大,但不明显.从误差图来看,小波神经网络预报畸形波部分的平均绝对误差值为0.226,BP神经网络在此处的误差值为0.316,可见,小波神经网络对畸形波部分的预报效果更好.结合表 2分析,小波神经网络在各项误差均明显低于BP神经网络.
| 表 2 工况②预报误差分析 Tab. 2 Error analysis of prediction case ② |
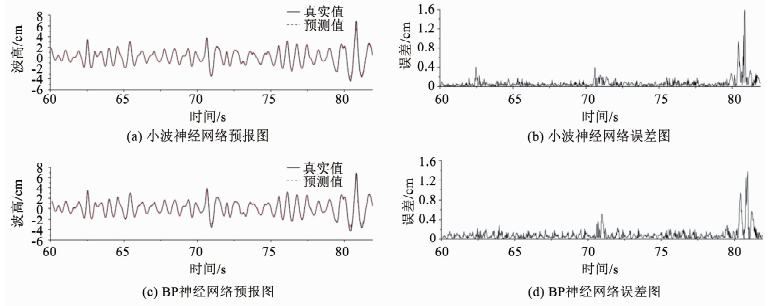
有义波高Hs=6.35 cm, 有义周期Ts=0.87 s,H1地形位置,浪高仪编号16测点预报及误差曲线如图 6所示,误差在常规波段较小,主要集中在畸形波附近.
|
图 6 Hs=6.35 cm, Ts=0.87 s Fig. 6 Hs=6.35 cm, Ts=0.87 s |
工况③波面整体预报结果误差见表 3.工况③处于H1地形位置,不属于地形非线性变化的区域,由此可见地形不是畸形波产生的唯一条件,地形线性区域同样有可能发生畸形波.神经网络中,此工况的训练样本中不存在畸形波,畸形波存在于预报数据部分,小波神经网络对于畸形波部分的预报的平均绝对误差为0.312,BP神经网络的误差为0.406,小波神经网络对畸形波部分的预报效果更好,曲线波峰和波谷部分小波神经网络的拟合效果更好.同时,结合表 3分析可知此工况的小波神经网络预报结果的各项误差明显大于工况②中小波神经网络的各项误差,工况③中小波神经网络的各项误差精度也明显高于BP神经网络.
| 表 3 工况③预报误差分析 Tab. 3 Error analysis of prediction case ③ |
1) 对3种工况的典型预报,无论是采用平均绝对误差MAR、平均相对误差MRE还是均方根误差RMSE指标评价,小波神经网络预报的各项误差精度都明显高于常规BP神经网络,畸形波部分小波神经网络预报曲线与实际曲线的拟合效果更好,符合小波具有捕捉局部结构特征的预期,适合用来预报畸形波突发性事件.
2) 基于试验数据的分析方法,可见小波神经网络应用于畸形波预报并不困难,且精度较高.从工况②和工况③来看如果训练样本中包含畸形波特征,神经网络建立的畸形波模型将会更为准确,那么对未来畸形波的预报精度将会进一步提高,可见对于实际的畸形波预报来说,实测的畸形波波高时间序列资料也是极为重要的.
3) 本文后续工作将针对畸形波进行集中试验,丰富畸形波预报样本数据,提高预报精度延长预报时间等.
| [1] |
DRAPER L. 'Rouge'waves[J]. Marine Observer, 1965, 35: 193. |
| [2] |
杨冠声, 董艳秋, 陈学闯. 畸形波(freak wave)[J]. 海洋工程, 2002, 20(4): 105. YANG Guansheng, DONG Yanqiu, CHEN Xuechuang. Freak wave[J]. The Ocean Engineering, 2002, 20(4): 105. |
| [3] |
KHARIF C, PELINOVSKY E, SLUNYAEV A. Rogue waves in the ocean[M]. Berlin: Springer-Verlag, 2009. DOI:10.1007/978-3-540-88419-4
|
| [4] |
LAVRENOV I V. The wave energy concentration at Agulhas current of South Africa[J]. Natural Hazards, 1998, 17(2): 117. DOI:10.1023/A:1007978326982 |
| [5] |
WHITE B S, FORNBRG B. On the chance of Rouge wave at sea[J]. Journal of Fluid Mechanics, 1998, 355(1): 113. DOI:10.1017/S0022112097007751 |
| [6] |
DIAS F, KHARIF C. Nonlinear gravity and capillary-gravity waves[J]. Annual Review of Fluid Mechanics, 1999, 31: 301. DOI:10.1146/annurev.fluid.31.1.301 |
| [7] |
赵西增, 孙昭晨, 梁书秀. 高阶谱方法建立三维畸形波聚焦模拟模型[J]. 海洋工程, 2009, 27(1): 33. ZHAO Xizeng, SUN Zhaochen, LIANG Shuxiu. Focusing model for generating 3-D freak waves based on HOS method[J]. The Ocean Engineering, 2009, 27(1): 33. |
| [8] |
裴玉国.畸形波的生成及基本特性研究[D].大连: 大连理工大学, 2008 PEI Yuguo. The generation of freak waves and its behaviors[D]. Dalian: Dalian University of Technology, 2008 |
| [9] |
LU Wenyue, YANG Jianmin, FU Shixiao. Numerical study of the generation and evolution of breather-type rogue waves[J]. Ships and Offshore Structures, 2017, 12(1): 66. DOI:10.1080/17445302.2015.1112177 |
| [10] |
KHARIF C, PELINOVSKY E. Physical mechanisms of the rogue wave phenomenon[J]. European Journal of Mechanics, B/Fluids, 2003, 22(6): 603. DOI:10.1016/j.euromechflu.2003.09.002 |
| [11] |
WASEDA T, KINOSHITA T, TAMURA H. Evolution of a random directional wave and freak wave occurrence[J]. Journal of Physical Oceanography, 2009, 39(3): 621. DOI:10.1175/2008jpo4031.1 |
| [12] |
刘首华, 牟林, 刘克修, 等. 畸形波研究的进展及存在问题[J]. 地球科学进展, 2013, 28(6): 665. LIU Shouhua, MU Lin, LIU Kexiu, et al. Research advance and problems in freak wave[J]. Advances in Earth Science, 2013, 28(6): 665. DOI:10.11867/j.issn.1001-8166.2013.06.0665 |
| [13] |
赵勇.小波数值方法在船舶流体力学中的若干应用[D].大连: 大连理工大学, 2011 ZHAO Yong. Wavelet numerical method with some applications to marine hydrodynamics[D]. Dalian: Dalian University of Technology, 2011 |
| [14] |
谭善文, 秦树人, 汤宝平. 小波基时频特性及其在分析突变信号中的应用[J]. 重庆大学学报(自然科学版), 2001, 21(2): 12. TAN Shanwen, QIN Shuren, TANG Baoping. Time-frequency characteristic of wavelet base and its application transient signal detection[J]. Journal of Chongqing University (Natural Science Edition), 2001, 21(2): 12. DOI:10.11835/j.issn.1000-582X.2001.02.004 |
| [15] |
DEKA P C, PRAHLADA R. Discrete wavelet neural network approach in significant wave height forecasting for multistep lead time[J]. Ocean Engineering, 2012, 43: 32. DOI:10.1016/j.oceaneng.2012.01.017 |
| [16] |
DOONG D J, PENG J P, CHEN Y C. Development of a warning model for coastal Rouge wave occurrences using an artificial neural network[J]. Ocean Engineering, 2018, 169: 270. DOI:10.1016/j.oceaneng.2018.09.029 |
| [17] |
孟雷, 闻斌, 于福江, 等.基于神经网络方法的海浪数值模拟[C]//中国海洋学会2007年学术年会论文汇编.湛江: 中国海洋学会, 2007: 702 MENG Lei, WEN Bin, YU Fujiang, et al. Ocean wave numerical simulation with neural networks[C]//Proceedings of the 2007 Annual Conference of the Chinese Society for Oceanography. Zhanjiang: Chinese Society for Oceanography, 2007: 702 |
| [18] |
朱智慧. BP神经网络方法在海浪数值预报中的释用研究[J]. 大气科学研究与应用, 2011(1): 84. ZHU Zhihui. Study on the BP neural network application to wave model forecast[J]. Atmospheric Science Research and Application, 2011(1): 84. |
| [19] |
王建忠. 小波理论及其在物理和工程中的应用[J]. 数学进展, 1992, 21(3): 289. WANG Jianzhong. Wavelet theory and its application in physics and engineering[J]. Advances in Mathematics, 1992, 21(3): 289. |
| [20] |
邹丽, 王爱民, 江晖, 等.岛礁地形畸形波特性的二维实验研究[C].第十四届全国水动力学学术会议暨第二十八届全国水动力学研讨会文集(上册).北京: 海洋出版社, 2017: 492 ZOU Li, WANG Aimin, JIANG Hui, et al. The freak wave characteristics of the reef profile on 2D experimental study[C]//Proceedings of the 14th National Symposium on Hydrodynamics and the 28th National Symposium on Hydrodynamics. Beijing: China Ocean Press, 2017: 492 |
| [21] |
邹丽, 王爱民, 宗智, 等. 岛礁地形畸形波演化过程的试验及小波谱分析[J]. 哈尔滨工程大学学报, 2017, 38(3): 344. ZOU Li, WANG Aimin, ZONG Zhi, et al. Experiment and wavelet analysis of the evolution process of freak waves around reefs[J]. Journal of Harbin Engineering University, 2017, 38(3): 344. DOI:10.11990/jheu.201603097 |
 2021, Vol. 53
2021, Vol. 53


