2. 北京智芯微电子科技有限公司, 北京 100192
2. Beijing Smart-Chip Microelectronics Technology Co., Ltd., Beijing 100192, China
侵入式攻击通常使用聚焦离子束(FIB)和微探针等手段[1],对芯片内部电路直接进行探测和修改.安全芯片使用顶层或次顶层金属走线作为金属屏蔽层,遮蔽芯片的重要区域和电路连线,保证其芯片内部电路的安全.主动式屏蔽层在顶层金属网络中通入数字信号,通过对比屏蔽层信号的完整性和一致性,判断屏蔽层是否受到攻击.主动屏蔽层易受到针对性的侵入式攻击,许多学者对此展开了研究. Cioranesco等[2]提出了在主动屏蔽层的走线中通入加密数字信号的方法,提高检测信号的安全性;Wang等[3]提出节点式布线的方法,复杂化主动屏蔽层的拓扑结构.这些手段可以提高攻击者进行逆向工程的难度,但是在花费一定时间对屏蔽层数据进行截取和分析后,攻击者仍然能找到走线的互联关系[4].Feng等[5]提出一种通过路由节点改变屏蔽层数据传输路径的抗重布线攻击方法,路由节点每次重构都会从节点的4个端口中选择两个进行随机连接.多个节点形成阵列,可控制主动屏蔽层的拓扑结构,但该方法的节点在每次重构后都存在两个未连接的端口,与其相连的主动屏蔽线未被通入信号,存在一定安全隐患.
针对主动屏蔽层的安全问题,本文结合随机哈密顿回路填充算法[6],提出了一种基于Galois环振[7]的随机重构主动屏蔽层电路.将主动屏蔽层进行分段重构,同时利用屏蔽层走线与重构节点的驱动器实现Galois环振真随机数生成器结构,产成高熵值的真随机数,利用该真随机数作为种子产生屏蔽层的检测随机数码流序列.以Trivium密码算法电路为目标进行防护,并利用该算法生成加密数据流对屏蔽层中的检测码流进行加密,构建了屏蔽层安全系统.本文在8通道并行随机哈密顿回路走线的主动屏蔽层中实现,解决了屏蔽层随机数检测码流上电后初始状态相同的问题,并且极大地减少重布线攻击的失效区域,可以有效提高屏蔽层安全性.
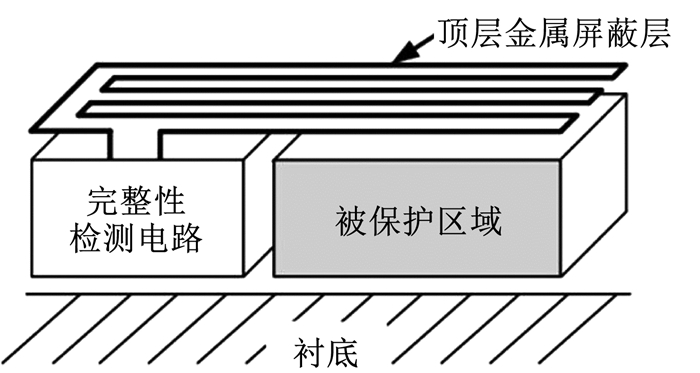
1 重布线攻击原理主动屏蔽层结构如图 1所示,屏蔽层金属导线以规定的方式在芯片顶层走线,填满整个顶层金属层.通过向金属线的输入端发送生成的随机数码流信号,并在接收端同步检测数据的真实性与完整性,达到检测物理攻击的效果.若想获取芯片内部数据,就必须绕开主动屏蔽层,或是对其进行部分移除.攻击者通过FIB和微探针等先进的芯片分析和电路修改工具来修改屏蔽层,从而将感应电路短路,让屏蔽层的保护失效的操作被称为重布线攻击.
|
图 1 主动屏蔽层 Fig. 1 Active shield |
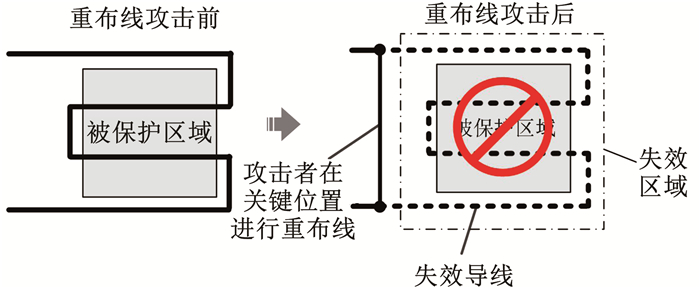
重布线攻击的过程如图 2所示,通过对主动屏蔽层走线连接关系的分析,攻击者找出长距离走线上相隔较近的节点进行重布线,使主动屏蔽层部分面积失效,失效导线的长度称为失效距离,失效导线覆盖的被保护区域面积称之为失效面积.
|
图 2 重布线攻击 Fig. 2 Shield rerouting attack |
若屏蔽层拓扑结构较为简单,攻击者只需短路较小的距离,就能使大面积屏蔽层失效.提高屏蔽层拓扑结构的复杂度,会提升攻击者识别屏蔽层连接关系的时间,但对重布线攻击手段没有直接进行防护.本文在主动屏蔽层中插入可重构节点,实现了屏蔽层中数据流的通道换序与加密操作,可以将屏蔽层的最大失效面积减小,直接降低了重布线攻击的成功率.插入节点的数量N与屏蔽层导线长度L的关系为
| $ L = \sum\limits_{N + 1}^i {{L_{{\rm{pi}}}}} , {\rm{ }}N \ge 0 $ | (1) |
式中Lpi为节点之间每段线的长度,在插入节点较为均匀分布的情况下Lpi可以表示为
| $ {L_{{\rm{pi}}}} \approx \frac{L}{{N + 1}}, {\rm{ }}N \ge 0 $ | (2) |
假定屏蔽层的总面积为A,失效面积为C,失效距离为S,根据失效导线覆盖的面积为失效面积这一原则,失效面积与总面积之间的比例可以表示为
| $ \frac{C}{A} \approx \frac{S}{L}. $ | (3) |
若走线处于最差情况,即攻击者可以直接对两个节点间的导线进行重布线,根据式(2)、(3)可以推得此时失效距离Smax为
| $ {S_{{\rm{max}}}} = \frac{L}{{N + 1}}, $ | (4) |
而最差情况下的节点间最大失效面积Cmax,可以根据式(3)、(4)推得:
| $ {C_{{\rm{max}}}} = \frac{L}{{N + 1}} \times A. $ | (5) |
插入可重构节点使得屏蔽层走线在节点前后的数据不同,因此跨越节点的走线不能被短路,屏蔽层的最大失效面积可以等效为节点间的最大失效面积.若未插入可重构节点的主动屏蔽层最大失效面积为Cn,插入N个节点后的最大失效面积为Ce,则最大失效面积的差值ΔC可以表示为
| $ \Delta C = {C_n} - {C_e}. $ | (6) |
而根据式(5)、(6)可以得出
| $ \Delta C = \left( {1 - \frac{L}{{N + 1}}} \right) \times A. $ | (7) |
由式(7)可知,插入节点操作后的最大失效面积减小了
可重构节点N的数目与芯片的安全等级、电路资源的占比、芯片IP的面积等因素相关.在保证芯片安全性的同时,需要确保节点不会占用过多资源,打乱芯片IP的摆放.本文主动屏蔽层总面积为1×106 μm2,IP的单元面积约为220 000 μm2,为了达到较好的防护效果,最大失效面积应该小于IP面积,根据式(5)、(7)得出,节点的个数至少为4个,综合考虑资源占用与安全性本文在屏蔽层中布置了4个可重构节点.
2 主动屏蔽层随机重构电路设计本文提出的主动屏蔽层随机重构电路,在主动屏蔽层中增加了可重构节点来抗重布线攻击,并利用屏蔽层产生亚稳态振荡,通过种子采集等模块对振荡进行采样获取真随机数.屏蔽层分为检测模式与随机数产生模式,具体结构如图 3所示.

|
图 3 主动屏蔽层系统 Fig. 3 Active shield system |
图 3中随机数码流生成模块使用线性移位反馈寄存器(LFSR)结构,负责产生屏蔽层检测码流与重构节点随机控制信号;种子采样部分为D触发器组与异或网络,用来实现屏蔽层真随机数生成器功能,在随机数产生模式下收集屏蔽层环振产生的真随机数并暂存,之后将其作为种子发送给LFSR与密码算法模块;可重构节点为设计的核心部分,其随机重构功能用来抗重布线攻击,加密功能用来混淆出入节点的数据流.密码算法模块为4组Trivium算法电路,在本文中作为被保护电路,算法也使用真随机数种子产生密码随机数序列,通入可重构节点对屏蔽层中检测码流进行进一步加密;检测电路对屏蔽层中的数据流进行解密与比对,输出报警信号.
2.1 真随机数种子生成器设计与主动屏蔽层系统配套的电路结构需要较小的资源占用,并且在每次上电后其检测码流生成结构都可以产生不同的数据流.真随机数生成器作为安全芯片中的重要结构,可以达到上电后随机数据状态的效果.
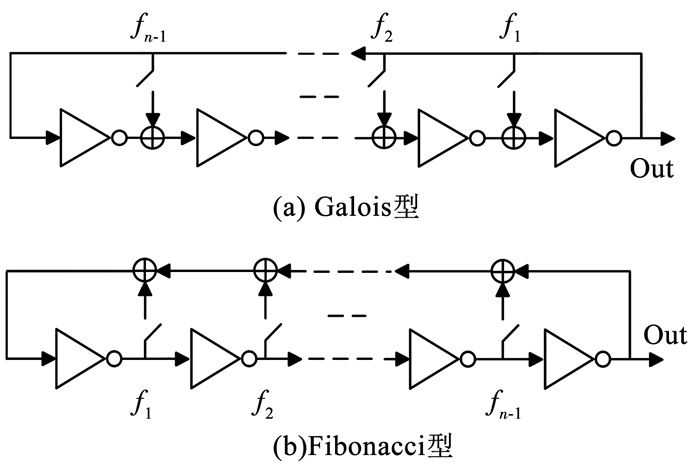
在数字电路中通常使用低频时钟信号控制D触发器,对奇数个反相器形成的环形振荡器的高频振荡进行采样来获取真随机数.该方法简单、容易实现,但缺点明显,此方法得到的真随机数统计属性受环振频率与时钟频率的影响较大,熵值较低,通常需要较多的后处理电路来满足高质量随机数的使用要求.带有反馈的环形振荡器能够产生高熵不稳定振荡状态,Dichtl等[8]在2006年首先提出了两种带有反馈连接的Fibonacci环振和Galois环振的概念,其具体结构如图 4所示.
|
图 4 Galois和Fibonacci环形振荡器 Fig. 4 Galois and Fibonacci ring oscillator |
图中fi决定环振的反馈连接,fi=1时反馈开关闭合,fi=0反馈连接断开,可以用公式表示为
| $ {f\left( x \right) = \sum\limits_{i = 0}^n {{f_i}{x_i}} , {\rm{ }}{f_0} = {f_n} = 1, } $ | (8) |
式中n为反相器个数.为保证输出不会有固定不变的状态,反馈多项式需要满足条件:
| $ {f\left( x \right) = \left( {1 + x} \right)h\left( x \right), } $ | (9) |
f(x)可以被1+x整除,但h(x)不可以被1+x整除[9].Fibonacci环振的级数不能为2且h(1)必须为1,Galois环振的级数只能是奇数.
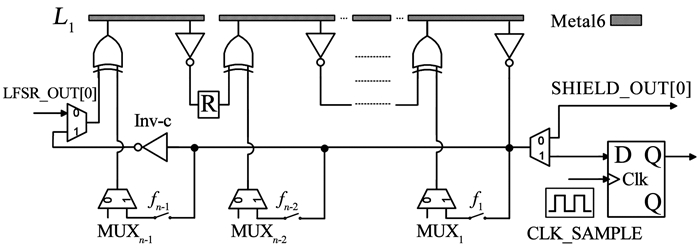
Fibonacci环振的反馈是每级反相器的输出分别异或后送入第1级,而Galois环振的反馈是第1级输出分别与每一级的输入异或,Galois环振这种异或与反相器在同侧相间隔的电路特点与本文的可重构节点设计匹配,并且符合屏蔽层驱动的设计思路.因此,本文改进了主动屏蔽层结构,使其集成Galois环形振荡器,作为数字真随机数的熵源结构.采用多路选择器与开关控制反馈连接的通断,实际电路中根据效果选择最大熵值的环振反馈连接,屏蔽层Galois环振的剖面示意图如图 5所示.
|
图 5 主动屏蔽层Galois环形振荡器 Fig. 5 Active shield Galois ring oscillator |
图 5中R为可重构节点,本文将主动屏蔽层的驱动端口,分别替换为异或门与反相器,并与节点相连.系统会根据不同工作状态下的控制信号,使用MUXn-1,MUXn-2等多路选择器,选择通过异或门注入屏蔽层中的数据类型.MUX的控制信号为0时,屏蔽层为检测模式,异或门作为异或加密的运算模块接收密码算法产生的密码随机数流,屏蔽层通道中输入检测码流,可重构节点R对通道之间进行随机重构;控制信号为1时,屏蔽层为随机数产生模式,每个通道走线的输出都通过一个反相器Inv-c连接到自己的输入端,在随机数产生模式下节点不对屏蔽层进行重构,作为开关直接导通,异或门作为反馈输入,由另一组选通开关根据给定的反馈多项式决定fi是否闭合.
屏蔽层的每个通道都形成了一个Galois型环振结构,通过采样时钟对环振进行采样,并将每个通道的采样输出进行异或,就可以得到较高熵值的真随机数种子.主动屏蔽层真随机生成器结构如图 6表示,L1~L8为8通道的主动屏蔽层形成了多个反馈连接不同的Galois环振,分别用D触发器对其采样,并对获得的采样数据进行异或,最终得到真随机数输出TRNG_OUT信号.

|
图 6 主动屏蔽层真随机数生成器 Fig. 6 Active shield true random number generator |
Galois环形振荡器在反相器环振的基础上引入了反馈抽头结构,结合了数学方法[10],得到了较为混沌的振荡特性.复用屏蔽层的Galois型环振真随机数电路,符合在小面积下能产生高熵值随机数的设计要求.
2.2 可重构节点与密码算法设计可重构节点由切换单元和加密单元构成.切换单元包含多组多路选择器,根据控制信号码流和预设的通道准入规则选择节点两端屏蔽层金属线的连接顺序.加密单元复用主动屏蔽层的驱动异或门,其作用是在屏蔽层连接顺序改变后,对每条线的数据进行异或加密,以防止长时间的微探针攻击观测到并行金属线通道的切换顺序.
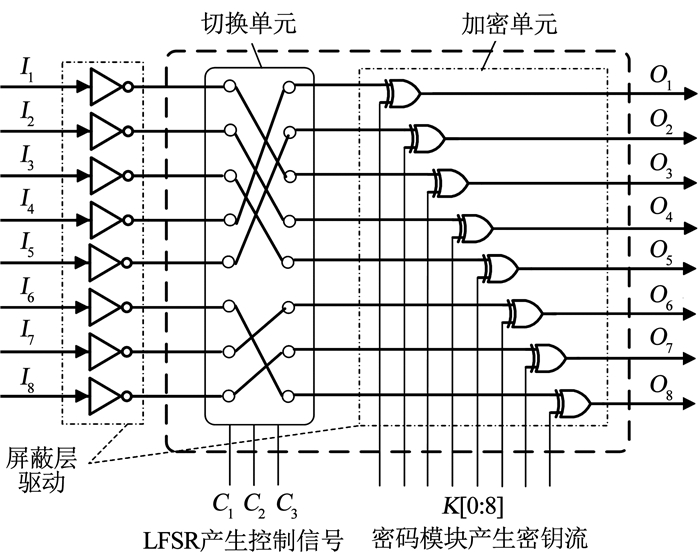
图 7是重构节点的结构图,I, O分别为流入与流出重构节点的屏蔽层数据流,C1C2C3为发送端的LFSR产生的3 bit随机数控制信号,K[7:0]为密码算法模块产生的密钥随机数流.检测模式下,屏蔽层数据首先由切换单元进行通道切换,通道中的数据根据控制信号进行多次随机更换“信息通路”,之后进入加密单元与密钥随机数流进行异或加密,最后输出重构单元进入屏蔽层中继续传输.
|
图 7 可重构节点电路原理图 Fig. 7 Reconfigurable node circuit |
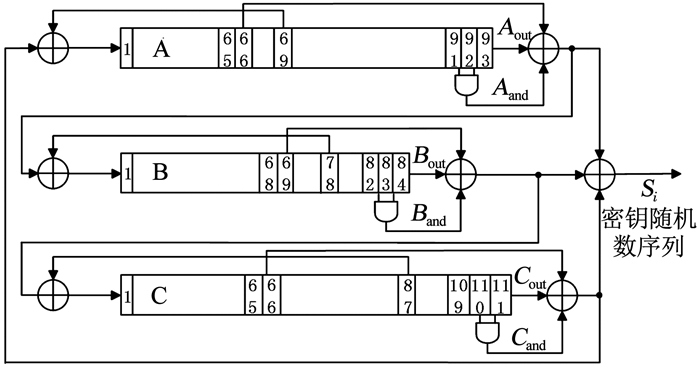
本文中密码算法模块利用真随机数种子,产生高质量随机数密码序列,提供给可重构节点的加密单元作为异或加密的密钥流,该随机数也可以供芯片其他模块使用.模块使用的Trivium算法,是由Canniàre等[11]提出的eSTREAM计划入选流密码算法之一,其结构由3个非线性移位反馈寄存器(NFSR)组成,长度分别为93、84、111 bit,如图 8所示.
|
图 8 Trivium算法电路结构 Fig. 8 Trivium algorithm circuit structure |
Trivium算法的密钥输出来自多个级联的NFSR,密钥输出部分对其状态转移周期无影响,因此本文对该算法的密钥输出部分进行了修改,使用后续电路分别提取了A,C寄存器的59~66 bit,B寄存器的61~69 bit,与原寄存器的输出部分进行异或,以获得多通道随机数密钥输出.
2.3 主动屏蔽层随机重构电路工作模式本文中采用16位LFSR并使用本原多项式进行连接,产生的状态序列包含65 535个时钟周期.但如果攻击者获取了整个序列,便可以推算出LFSR的初始状态,因此本文通过在状态转移序列的半周期中更换LFSR的种子,防止攻击者进行长时间监控屏蔽层获取LFSR的反馈连接与初始状态.
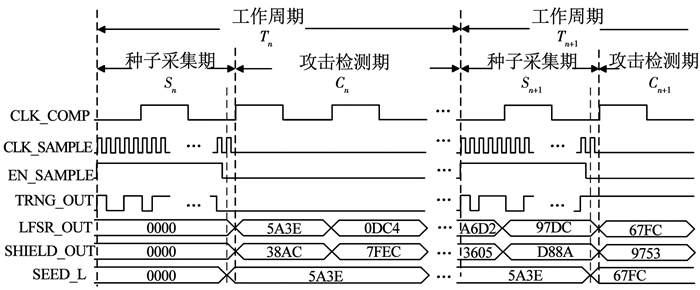
这一过程体现在系统的工作时序中,由图 9所示.屏蔽层工作状态由数个工作周期Tn组成,随机数产生模式与检测模式在工作周期内分别对应两个时期:种子采集期Sn和攻击检测期Cn.在种子采集期中,采样时钟使能信号EN_SAMPLE置高,高频随机数采样时钟CLK_SAMPLE启动,MUX选择可重构节点的异或门接入反馈连接,屏蔽层进入环振状态并开始真随机数生成.在采样到足够数量的真随机数种子后,EN_SAMPLE信号置低,采样时钟关闭,降低系统功耗.同时真随机数种子被赋给屏蔽层发送端的LFSR与Trivium算法模块,系统此时进入攻击检测期,采样模块关闭,其余模块在低频检测时钟CLK_COMP下工作,主动屏蔽层中开始通入检测码流,可重构节点对其进行重构与加密.在经过较多的时钟周期数后,攻击检测期结束,系统开始重新采集屏蔽层随机数种子,进入新一轮工作周期Tn+1.
|
图 9 系统工作时序 Fig. 9 System working sequence |
在系统首次上电后,会进入初始化状态,此时为种子采集期S1,采样到的种子中,有160 bit提供给密码算法模块,用来产生密钥随机数流. Trivium算法的周期由经验公式[12]表明,包含一个周期长度不小于296-3-1的随机序列;其次,如果该算法的初始值足够随机,则生成的序列周期长度为2288,因此可以近似的认为在有限的观察时间内,该算法是足够安全的.
本文中,系统的检测时钟周期长度为采样时钟的1 000倍,由于中途只更换LFSR的种子,因此除初始采集期S1稍长外,每个采集期Sn仅需占用较少的时间进行采集,不影响屏蔽层的检测效果.
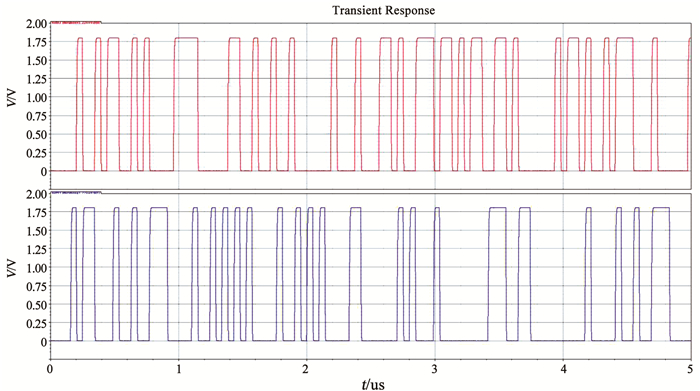
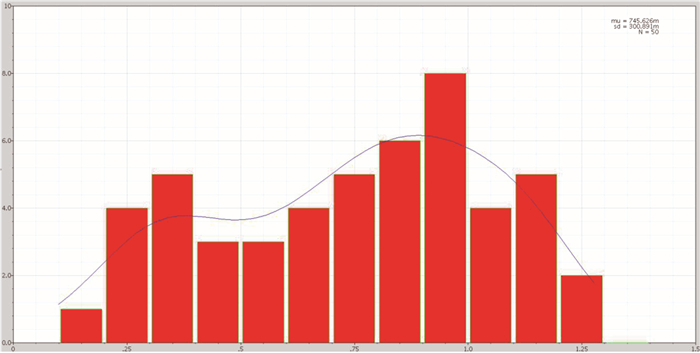
3 仿真结果及分析 3.1 真随机数种子功能验证根据电路原理图,使用SMIC0.18 μm工艺实现了8通道主动屏蔽层设计,完成可重构节点的布置与真随机数采样部分的搭建.利用蒙特卡洛分析和传输噪声分析的方法,对真随机数种子生成器进行了仿真.图 10为真随机数生成器的瞬态仿真结果,证明在不同的噪声环境下TRNG有不同的输出曲线.图 11是蒙特卡洛仿真结果图,表示的是环振在2 us时的电压分布,其输出处于亚稳态,有较高的熵值.
|
图 10 真随机数仿真结果 Fig. 10 Simulation results of true random number |
|
图 11 蒙特卡洛仿真结果 Fig. 11 Monte Carlo simulation results |
在真随机数采样期间,平均功耗为6.123 6 mW.不同噪声频率下得到的16位随机数种子部分输出结果见表 1所示,表中噪声种子是Spectre传输噪声分析工具噪声产生器的初始值,可以用于生成不同的噪声状态,利用同一个种子产生的噪声可以被复现[13].
| 表 1 不同噪声环境真随机数种子 Tab. 1 True random number seeds in different noise environments |
得到的种子通过后处理并使用Trivium密码算法产生高质量真随机数序列,对生成的8组10 M数据量的随机数进行NIST SP800-22测试[14],输出P值大于0.000 1即可认为该项测试通过.测试结果见表 2,产生的随机数可以通过测试,且每项测试的通过率较高.
| 表 2 随机数NIST测试结果 Tab. 2 Random number NIST test results |
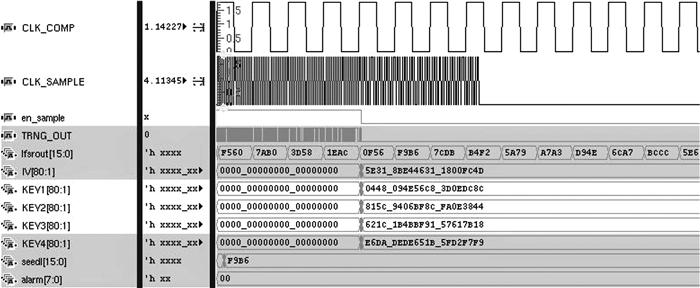
根据系统原理,使用Verilog硬件描述语言对系统数字电路进行自顶向下的设计,利用AMS工具对数字和模拟部分进行混合后仿,得到系统的运行仿真结果如图 12、13所示.
|
图 12 起始阶段 Fig. 12 Initial stage |
|
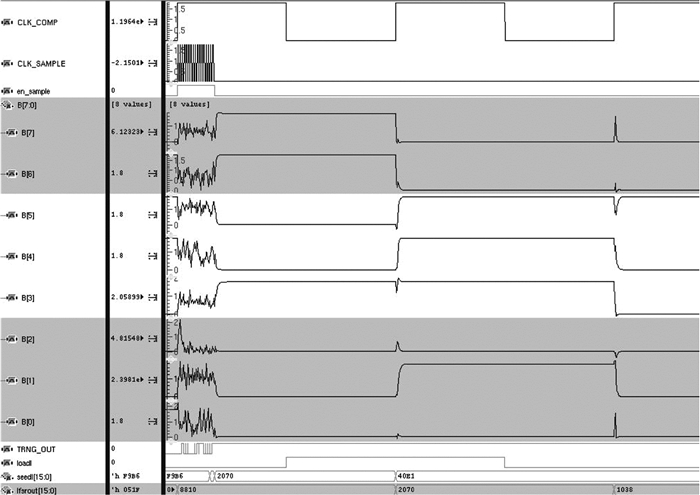
图 13 工作过程中种子采集阶段 Fig. 13 Seed collection stage during work |
图 12中显示的是系统的第1个周期T1中种子采集期S1和攻击检测期C1,采集到的真随机数在采样使能信号en_sample置低后被赋予给seedl和KEY信号,作为LFSR和密码算法起始种子.采样时钟CLK_SAMPLE额外工作了一段时间是为了满足Trivium算法的初始化过程,之后采样时钟关闭,系统进入攻击检测期C1.图 13中所示为系统工作中的一个种子采集期Cn,图 13中B信号为主动屏蔽层通道输出,可以清晰的看出通过采样时钟对屏蔽层中的亚稳态震荡进行了采样,输出随机数为TRNG_OUT信号,并获得了新的随机数种子seedl,在下一个CLK_COMP信号的上升沿被赋给主动屏蔽层的输入lfsr_out信号.
在完成芯片后端设计之后,得到系统的各个模块资源占用见表 3. 其中,攻击检测与重构节点部分占总面积的20%,插入式重构节点与真随机数采样结构占比2.2%,对于更大面积的芯片,重构节点部分将有更小的资源占比.
| 表 3 模块资源消耗 Tab. 3 Module resource consumption |
插入重构节点与真随机数模块前后电路指标对比见表 4.增加的主动屏蔽层节点,只占用较小的系统资源,并获得较高的防护效果.
| 表 4 插入重构节点与真随机数模块前后电路指标对比 Tab. 4 Comparison of circuit indicators before and after inserting reconfigurable nodes and true random number modules |
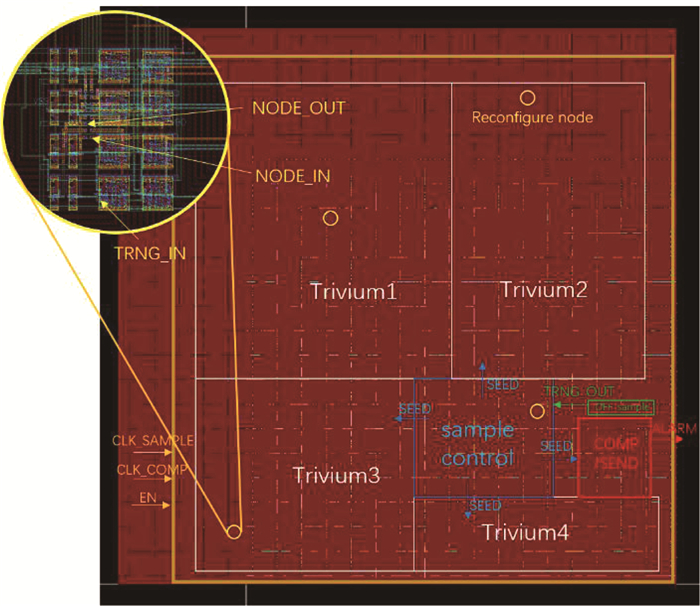
芯片版图如图 14所示,红色区域为芯片主动屏蔽层,框图为芯片各主要模块的布局,箭头为各模块之间的端口连接关系,图中橙色圆圈为重构节点的布置位置,放大的图中可以看到可重构节点屏蔽层驱动器的具体电路版图.
|
图 14 抗物理攻击主动屏蔽层系统版图 Fig. 14 Anti-physical attack active shield system layout |
表 5列出了本文与部分已发表设计的对比,本文在屏蔽层图形上使用了多通道随机哈密顿回路填充,相较于迂回、平行等简单走线方式安全性较高,相较于文献[15]中的单通道多层哈密顿回路,在结构上占用面积较少,且容易布置,适用范围较广.相较于其他文献中的可重构节点布置方式,本文的节点位置较为自由,并且不会引入未通入信号的屏蔽层走线.对比其他文献中的使用伪随机数对屏蔽层数据进行加密的方法,本设计中使用屏蔽层产生的真随机数密码,再重新加密主动屏蔽层中的检测码流,资源占用少并且安全性较高.此外,本文在功耗和面积上控制的较为均衡.由此可见,本文较其他设计在综合性能上有明显的提升.
| 表 5 本文与其他设计指标对比 Tab. 5 Comparison between this paper and other design indicators |
1) 本文使用重构和复用的方法,设计了一种随机重构的改良型主动屏蔽层控制电路.在主动屏蔽层中插入可重构节点,使屏蔽层中数据重构与加密.
2) 本文复用通道与节点驱动,在占用较小电路资源的基础上,实现了能产生较高熵值的真随机数生成器,并利用该真随机数作为种子产生密码序列,对芯片进行进一步防护.
3) 本文的电路功耗和面积较小,芯片在加入可重构节点之后资源开销无明显增加.电路适用于多通道主动屏蔽层,能为小硬件开销的芯片提供高等级的安全防护.
| [1] |
SKOROBOGATOV S. How microprobing can attack encrypted memory[C]//2017 Euromicro Conference on Digital System Design (DSD). Vienna: IEEE, 2017: 244. DOI: 10.1109/DSD.2017.69
|
| [2] |
CIORANESCO J M, DANGER J L, GRABA T, et al. Cryptographically secure shields[C]//2014 IEEE International Symposium on Hardware-Oriented Security and Trust (HOST). Arlington: IEEE, 2014: 25. DOI: 10.1109/HST.2014.6855563
|
| [3] |
WANG Kan, GU Yong, ZHOU Tong, et al. Multi-pair active shielding for security IC protection[J]. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2019, 38(12): 2321. DOI:10.1109/TCAD.2018.2878175 |
| [4] |
BRIAIS S, CIORANESCO J M, DANGER J L, et al. Random active shield[C]//2012 Workshop on Fault Diagnosis and Tolerance in Cryptography. Leuven: IEEE, 2012: 103. DOI: 10.1109/FDTC.2012.11
|
| [5] |
FENG Ting, LI Kenli, QIN Yunchuan, et al. A dynamic active shield against shield rerouting attack[J]. International Journal of High Performance Computing and Networking, 2016, 9(5/6): 462. DOI:10.1504/IJHPCN.2016.080419 |
| [6] |
XIN Ruishan, YUAN Yidong, HE Jiaji, et al. High-efficient generation algorithm for large random active shield[J]. Science China Information Sciences, 2019, 62(3): 039108. DOI:10.1007/s11432-018-9474-3 |
| [7] |
SCHRAMM M, DOJEN R, HEIGL M. Experimental assessment of FIRO-and GARO-based noise sources for digital TRNG designs on FPGAs[C]//2017 International Conference on Applied Electronics (AE). Pilsen: IEEE, 2017: 1. DOI: 10.23919/AE.2017.8053618
|
| [8] |
DICHTL M, GOLIC J D. High-speed true random number generation with logic gates only[C]//International Workshop on Cryptographic Hardware and Embedded Systems. Berlin: Springer, 2007: 45
|
| [9] |
DICHTL M. Fibonacci ring oscillators as true random number generators—A security risk[J]. IACR Cryptology ePrint Archive, 2015, 2015: 270. |
| [10] |
樊凌雁, 朱亮亮, 骆建军, 等. 一种基于亚稳态的真随机数发生器[J]. 微电子学, 2017, 47(4): 519. FAN Lingyan, ZHU Liangliang, LUO Jianjun, et al. A true random number generator based on metastable state[J]. Microelectronics, 2017, 47(4): 519. DOI:10.13911/j.cnki.1004-3365.2017.04.017 |
| [11] |
CANNIÀRE C, PRENEEL B. Trivium specifications[EB/OL]. http://www.ecrypt.eu.org/stream/p3ciphers/trivium/trivium_p3.pdf, 2007
|
| [12] |
高博. 基于半张量积的几类密码算法的研究[D]. 北京: 北京交通大学, 2014 GAO Bo. Research on encryption algorithm based on semi-tensor product[D]. Beijing: Beijing Jiaotong University, 2014 |
| [13] |
NAKHLA N, NAKHLA M, ACHAR R. A general approach for sensitivity analysis of distributed interconnects in the time domain[J]. IEEE Transactions on Microwave Theory and Techniques, 2011, 59(1): 46. DOI:10.1109/TMTT.2010.2091205 |
| [14] |
BASSHAM L E, RUKHIN A L, SOTO J, et al. A statistical test suite for random and pseudorandom number generators for cryptographic applications: NIST 800-22[R]. Gaithersburg: U.S. Department of Commerce, 2010
|
| [15] |
BRIAIS S, CARON S, CIORANESCO J M, et al. 3D hardware canaries[C]//International Workshop on Cryptographic Hardware and Embedded Systems. Berlin: Springer, 2012: 1. DOI: 10.1007/978-3-642-33027-8_1
|
| [16] |
MUN Y, KIM H, LEE B, et al. Secure integrated circuit with physical attack detection based on reconfigurable top metal shield[J]. Journal of Semiconductor Technology and Science, 2019, 19(3): 260. DOI:10.5573/JSTS.2019.19.3.260 |
 2021, Vol. 53
2021, Vol. 53


