滚动轴承是很多旋转机械设备传动装置的关键部件,由于其运行环境复杂多样,因此也是发生故障最多部件之一[1].一旦发生故障,轻则影响设备的正常运行,重则引起严重的安全事故,并造成巨大的经济损失及人员伤亡,因此为了提高滚动轴承的安全性,防范事故的发生,对滚动轴承的运行状态进行监测及诊断是十分有意义的.
当前针对像滚动轴承的故障诊断方法主要分为两类:一类是以信号分析为主的传统诊断方法,这类分析方式需要大量的专家知识;一类是以数据驱动为主的智能机器学习方法,这类方法不需要大量的专家知识,而是依靠模型自动学习数据中的特征信息,从而实现故障诊断,然而对于数据量大,数据维度更高,非线性关系更强的大数据,传统智能方法特征提取能力很有限,无法完全提取数据的本质特征.因此需要学习能力更强的方法去提取数据的本质特征.
随着2006年深度学习概念的提出,为解决复杂数据的学习问题提供了有效解决途径[2-3].经过近几年的不断发展,目前深度学习已成为机器学习中最流行的一个分支,它的实用性范围广,极大地促进了人工智能的发展.当前已有一些采用深度神经网络去解决滚动轴承故障诊断问题的研究成果,文献[4]提出深度置信网络对滚动轴承进行诊断,并用粒子群算法对网络结构进行了优化,采用模拟数据和实验数据验证了方法的可靠性.针对旋转机械的运行条件总是复杂多变,难以从测得的振动信号中自动有效地捕获有用的故障特征的问题,文献[5]提出了一种基于深度自编码器的故障诊断方法,并采用人工鱼群算法优化深度自动编码器的关键参数,最后用齿轮箱和电力机车滚动轴承的实验数据对所提方法进行了验证.针对传统基于最小二乘支持向量机的故障诊断方法需要手动去提取故障特征的不足,文献[6]提出了深度栈式最小二乘支持向量机故障诊断模型去自动学习故障特征,所提出的方法在滚动轴承实验中取得了良好的诊断效果.
考虑到深度学习方法具有强大的学习能力,因此可以获得比浅层学习方法更好的结果,然而若要使用神经网络提取到数据的本质特征,则需要的神经网络层数越多,随着神经网络的层数加深,所需要训练的参数越来越多,计算量也会成倍增长,神经网络的性能也会出现退化,为了改善这种现象,本文拟采用残差神经网络(Residual neurnal network, RNN)来对这种现象进行改进.同时为了增强模型的鲁棒性,本文采用多传感器技术对RNN模型进行改进,建立了多传感器融合改进的深度残差神经网络(Deep residual neural netuork, DRNN)故障诊断模型:DRNN-3S.
1 方法介绍 1.1 卷积神经网络(Convolutional neural netwoks, CNN)CNN模型起源于生物神经视觉研究,通过3个重要思想(稀疏交互、参数共享、等变表示)减少了自由变量的数量,提高了模型的泛化能力,并且提高了训练速度.经过多年的发展,已有相对成熟的结构.CNN的基本结构由输入层、卷积层、池化层、全连接层及输出层构成[7].卷积过程可视为特征提取的过程,用一张二维图像I作为输入,K为卷积核,Z为卷积结果,则卷积过程定义为
| $ \mathit{\boldsymbol{Z}}\left( {i, j} \right) = \sum\limits_m {\sum\limits_n {\mathit{\boldsymbol{I}}\left( {i + m, j + n} \right)\mathit{\boldsymbol{K}}\left( {m, n} \right)} } . $ | (1) |
式中:(m, n)为卷积核K的大小,(i,j)为卷积位置.一个卷积层中一般包含多个卷积核,以便提取更多的特征信息.然后将卷积结果输入到激活函数,计算后得到卷积层的输出y,计算过程定义为
| $ \mathit{\boldsymbol{y}} = g(\mathit{\boldsymbol{Z}} \cdot \mathit{\boldsymbol{W}} + \mathit{\boldsymbol{b}}). $ | (2) |
式中:W为权值矩阵;b为偏置;g(·)为激活函数.本文设置为常用的线性整流函数(ReLU)[8],定义为
| $ g\left( x \right) = {\rm{max}}\left( {x, 0} \right). $ | (3) |
池化层也称为子采样层,通常跟随在卷积层之后,依据一定的下采样规则对特征图进行下采样,常用的下采样方法有max-pooling,mean-pooling等.假设Zsub是池化层的输出,subsampling(·)为采样函数,则
| $ {\mathit{\boldsymbol{Z}}_{{\rm{sub}}}} = {\rm{subsampling}}(\mathit{\boldsymbol{y}}). $ | (4) |
理论上来说深度神经网络的结构越深,越能提取到数据的本质特征,然而现有的研究表明深度卷积神经网络(Deep Convolution neural network, DCNN)将层数提高到一定层数时,模型会出现退化,比如梯度消失或者爆炸.因此,研究人员不断寻求新的思路来改进模型,现有的改进思路主要分为两种,一种是改进神经网络的求解器,然而这种思路在短时间内很难有很大的突破,模型性能提升有限;另一种是改进模型的结构,比如文献[7, 9-10]等提出的深度神经网络模型.本文选择新型神经网络模型RNN作为故障诊断识别模型,它由He等[11]在2015年提出,作为一种新的网络结构使性能得到很大的提升,并在图像识别,目标检测,目标定位等公开数据及上取得了很高的识别率.
一般的CNN是由卷积层、池化层交替堆叠,而RNN由残差块构成,其基本结构如图 1所示.

|
图 1 残差网络结构简图 Fig. 1 Schematic diagram of residual network |
图中x为残差模块的输入,F(x, {Wi})为待训练的残差函数,通过跳层连接技术将恒等映射x与F(x, {Wi})相加得到x的估计值H(x),这样不仅提高了随机梯度下降算法的学习能力,而且加快了模型收敛速度,提高了模型的泛化能力[12].
1.3 神经网络训练本文采用随机梯度下降法(Stochastic gradient descent, SGD)训练DRNN,SGD是一种神经网络优化算法,通过在每次迭代训练过程中从总样本集中随机抽取独立同分布的小样本,然后用梯度下降法训练深度神经网络,这样能够提高在样本集很大时的训练效率,因此成为了目前深度神经网络训练过程中用的最多方法[13].训练流程如图 2所示,训练过程可以看作是对DRNN的参数θ={W, b}进行迭代更新求解,其中W为权值矩阵,b为偏置向量,训练结束后将最后一次训练的结果保存,作为测试模型.

|
图 2 神经网络训练过程 Fig. 2 Training process of neural network |
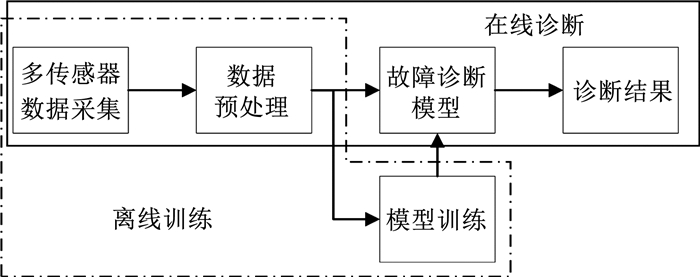
根据滚动轴承的特征,设计了如图 3所示故障诊断流程,包括离线训练和在线诊断两个步骤构成.在离线训练过程中,首先通过多传感器采集设备的运行状态数据,然后通过数据预处理技术从原始数据中提取特征数据,最后用特征数据去训练故障诊断模型.在线诊断过程中,首先将在线采集的数据输入到预处理模块得到特征数据,然后将特征数据输入到训练好的诊断模型中,最后经过识别得到诊断结果.
|
图 3 滚动轴承故障诊断流程 Fig. 3 Fault diagnosis process for rolling bearing |
为了验证本文提出方法的有效性,用西储大学的轴承故障实验数据集[14]测试所提出的方法,实验台架如图 4所示.数据集包含3个分别布置在马达驱动端,风扇端和支撑基板的加速度传感器(SDE,SFE,SBA)所采集的数据,采样频率为12 000 Hz.由于正常状态缺乏位于支撑基板传感器的数据,故用0补全正常状态下该传感器的数据.当前多数研究只针对10种(包括正常、3种不同故障直径的滚珠故障、3种不同故障直径的内圈故障、3种不同故障直径的外圈故障)或者4种(包括正常、滚珠故障、内圈故障、外圈故障)故障状态进行诊断识别[15-19],为了体现算法的优势,本文针对其中40种故障状态(包括上述10种和4种故障类型)展开了研究,包含4种正常运行状态,12种滚珠故障,12种内圈故障,12种外圈故障,详细故障类型及编码见表 1.

|
图 4 轴承实验台 Fig. 4 Bearing test rig |
| 表 1 故障类型及编码 Tab. 1 Fault types and encoding |
当前很多针对振动信号分析方式采用的是频域分析或时域分析,这样有可能造成部分特征信息缺失,为了综合利用时域和频域的特征信息,本文采用STFT对振动信号进行初级特征提取[20].STFT是一种时频分析方法,它可以通过窗函数获取信号特定时间的频率分布,同时通过在时间轴上移动窗函数,又可以获取不同频率的时间分布,因此可以同时提取频域特征,又可以提取时域特征.短时傅里叶变换的表达式为
| $ {S\left( {\omega , \tau } \right) = \int {f\left( t \right)} {g^*}\left( {t - \tau } \right){{\rm{e}}^{ - {\rm{j}}\omega {\rm{t}}}}{\rm{d}}t.} $ | (5) |
式中:*为复共轭符号;g(t)为窗函数;f(t)为待分析信号.信号的STFT结果S(ω, τ)反映了待分析信号在τ时刻、频率为ω的信号分量.
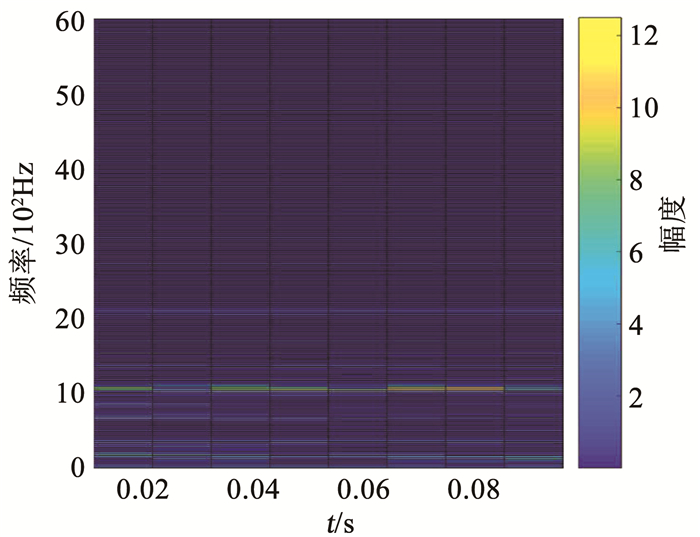
本文窗函数选择汉明窗函数,窗长度为512,相邻窗函数采样重叠率为384,选取连续8个窗函数提取的频域特征组成大小为256*8的时频谱,其时间分辨率为0.085 3 s,频率范围为0~6 000 Hz,图 5为一组正常信号的时频谱,横坐标包含8个时间点,纵坐标包含256个频率点,幅值大小用不同的颜色表示,本文既可观察某一时刻的频率分布,又可以观察到某一频率的时间分布.通过对3个传感器采集的数据分别进行STFT,然后将单个传感器信号的时频谱合并,得到单个大小为256*8*3的样本数据.将所有故障的特征信号进行变换后,得到大小为5 909的故障样本集,故障样本的分布见表 2.
|
图 5 时频特征频谱图 Fig. 5 Time-frequency characteristic spectrum |
| 表 2 故障样本分布 Tab. 2 Fault sample distribution |
在使用机器学习算法之前,常常需要对数据进行标准化处理,这样可以避免不同量纲的特征参量降低机器学习算法的性能,从而提高训练效率和准确度.本文采用z-score标准化方法[21]对样本数据进行预处理,公式定义为
| $ {x\prime = \frac{{x - \mu }}{\sigma }.} $ | (6) |
式中:x为原始数据;x′为标准化后的数据;μ为原始数据的平均值;σ为原始数据的标准差,标准化后的数据服从均值为0,方差为1的标准正态分布.
3.3 故障诊断模型构建本文采用的DRNN-3S模型包含8个残差模块,1个卷积层和1个逻辑回归层,共18层网络,其结构简图如图 6所示,相关结构参数见表 3.网络的输入包含3个通道,输入值分别为每个传感器标准化后的初级特征矩阵,每个残差模块都可以视为一个特征提取器,它包含两个卷积层,输出层的输出为每种故障的概率.

|
图 6 残差网络结构 Fig. 6 Structure of DRNN-3S |
| 表 3 DRNN-3S的参数设置 Tab. 3 Parameter setting of DRNN-3S |
针对滚动轴承故障诊断问题,DCNN是目前研究最多,且诊断精度较高的深度学习方法,故本文选取DCNN作为对比方法进行测试,并基于3个传感器的特征数据,建立了深度卷积神经网络故障诊断模型:DCNN-3S;DCNN-3S的结构与参数初始值和DRNN-3S均保持一致,每个卷积层之间用池化层进行优化,但没有跳层连接. 神经网络训练参数设置为:学习率α=1,最大迭代次数N=720,小批量大小m=128,训练方式:GPU;样本集按照8∶2的比例分为训练样本和测试样本.
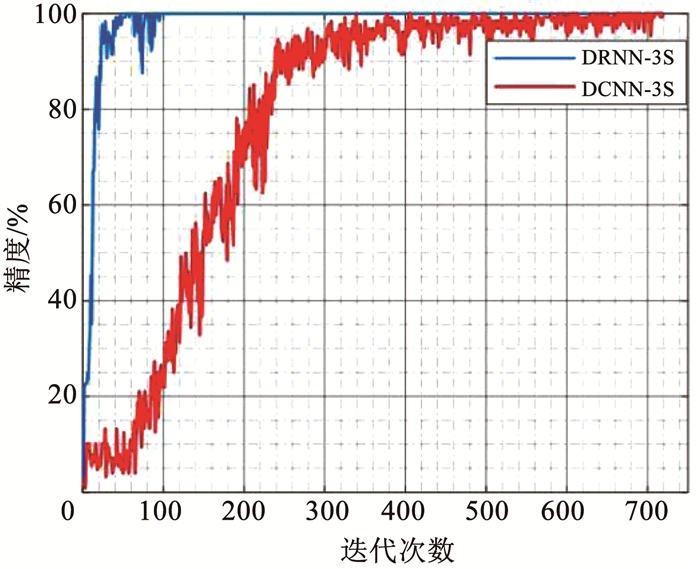
图 7为DRNN-3S模型与DCNN-3S模型的训练精度随迭代次数变化曲线图,从中可以看出DRNN-3S的收敛速度明显要比DCNN-3S快很多,约100次迭代就达到了100%的训练精度,而DCNN的训练精度最终在99%处上下波动;图 8为DRNN-3S与DCNN-3S损失函数随迭代次数变化曲线图,从中可以看出DRNN-3S的损失函数值的收敛速度也比DCNN-3S快,损失函数值的收敛数量级达到了10-5,而DCNN-3S损失函数值的收敛数量级只有10-3.
|
图 7 训练精度变化曲线 Fig. 7 Training accuracy curves with iterations |

|
图 8 损失函数变化曲线 Fig. 8 Loss function value curves with iterations |
训练完成后,用测试数据测试两个模型的泛化性能,针对40类故障的测试数据,最终,DRNN-3S模型的测试精度为100%,DCNN-3S的测试精度为99.74%.
综上所述,DRNN-3S在训练过程中,性能表现更好,充分说明优化残差函数要比原函数要容易的多,且更容易收敛,在测试过程中,DRNN-3S模型的测试精度比DCNN-3S要高,说明DRNN-3S的泛化性能要比DCNN-3S好.
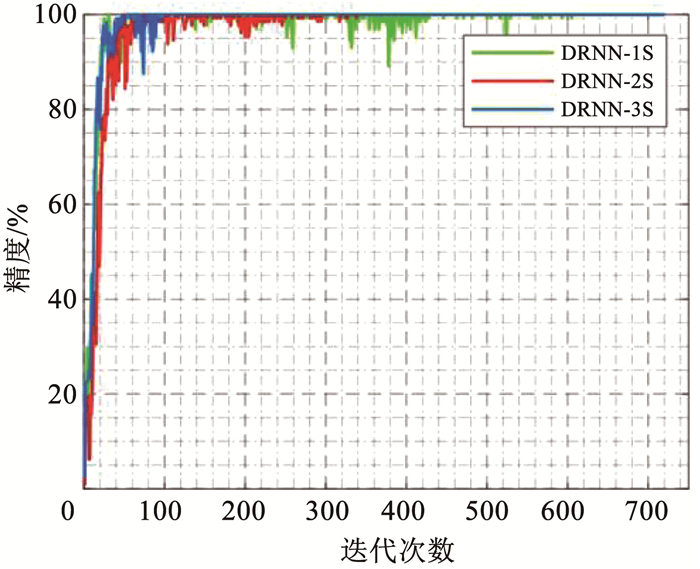
3.5 多传感器性能测试为体现多传感器融合的优势,分别用一个传感器(SDE)、两个传感器(SDE,SFE)和3个传感器(SDE,SFE,SBA)采集的数据去构建3个DRNN模型: DRNN-1S, DRNN-2S, DRNN-3S,模型输入层数据输入通道分别为1,2和3,其他结构参数和训练参数均与模型训练保持一致,图 9、10分别是不同传感器数据下的训练精度收敛曲线和损失函数收敛曲线,从中可以发现,3个模型的训练精度最终都可以达到100%,当模型精度达到100%,且损失函数值趋于稳定时,模型DRNN-1S, DRNN-2S, DRNN-3S训练所用的次数分别约为600,350,100次.综上所述,训练数据所用的传感器数量越多,训练过程收敛速度越快,越稳定,因为数据源越多,所提供的信息越丰富,只需要较低的迭代次数,便能找到数据的内在规律.
|
图 9 不同传感器数下训练精度变化曲线 Fig. 9 Training accuracy curves with different sensor numbers |

|
图 10 不同传感器数下损失函数变化曲线 Fig. 10 Loss function value curves with different sensor numbers |
实际运行环境中,采集到的滚动轴承振动信号基本上会受到噪声的影响,这对故障诊断模型的适应能力形成巨大的考验.本文通过在原始振动信号中加入高斯白噪声来模拟实际嘈杂的工作环境中采集的数据,并用含噪声的数据来评估故障诊断模型的抗噪性能.根据不同环境下,噪声程度不同,本文用信噪比(SNR)来衡量噪声程度,定义如下:
| $ {{\rm{SNR}} = 10{\rm{lg}}\left( {\frac{{Ps}}{{Pn}}} \right).} $ | (7) |
式中: Ps为信号功率,Pn为噪声功率.本文分别用SNR范围为0~10 dB的噪声对单个传感器的数据和所有传感器的数据进行污染,共得到4组含噪声的测试数据,然后用包含噪声的测试数据对DRNN-3S和DCNN-3S模型进行测试,测试结果见表 4.从表 4中可以看出,在单一传感器受到噪声污染的情况下,在不同噪声程度下,DRNN-3S模型的性能均比DCNN-3S要好,即使信噪比低至0 dB时,DRNN-3S模型均能保持94%以上的诊断精度,其中在只有传感器SBA受到噪声感染情况下,模型诊断精度在99.9%以上.当模型的诊断精度保持在100%时,传感器SDE,SFE,SBA信号的最低SNR分别为8, 6, 2 dB,因此对DRNN-3S模型而言,传感器的抗噪能力排名为:SBA>SFE>SDE.在所有传感器均受到噪声污染的情况下,相比于单个传感器受到噪声污染,模型性能会有所下降,但DRNN-3S模型的性能依旧要比DCNN-3S出色,当噪声程度SNR≥6 dB时,模型诊断精度在99%以上,而DCNN-3S模型最大诊断精度也只有83.49%.
| 表 4 DRNN-3S模型和DCNN-3S模型的抗噪测试结果 Tab. 4 Anti-noise test results of DRNN-3S and DCNN-3S |
为了体现多传感器融合的优势,本文同样测试了基于单个传感器采集的数据建立的DRNN诊断模型的抗噪能力.分别用SDE、SFE、SBA采集的数据训练了3个单传感器DRNN故障诊断模型:DRNN-DE,DRNN-FE和DRNN-BA,用不含噪声的测试数据对模型进行测试,可得到模型的测试精度分别为100.00%,100.00%,80.14%.因为传感器SBA采集的数据没有正常状态的数据,本文中正常状态下的数据均由0补充,故造成识别率偏低.
本文首先用信噪比为0~10 dB的噪声分别对SDE、SFE、SBA采集的数据进行污染,然后用含噪声的数据对上述模型进行测试,测试结果见表 5,通过将结果与表 4中的DRNN-3S模型结果进行对比,可以发现多传感器融合改进模型在不同信噪比下,诊断精度都比单传感器模型的精度高,尤其在传感器SBA受到噪声污染时,DCNN-BA模型的诊断精度低并且抗噪能力低,然而DRNN-3S模型却没有这些短板,这充分说明了多传感器融合改进模型的抗噪能力更好.
| 表 5 单传感器故障诊断模型抗噪测试结果 Tab. 5 Anti-noise test results of single sensor-based model |
综上所述,基于多传感器融合改进的DRNN故障诊断模型DRNN-3S的抗噪能力是相当突出的,不仅提升故障诊断模型的鲁棒性,而且具有较强的环境适应能力.
4 结论1) 本文针对滚动轴承的故障诊断问题提出了一种基于多传感器融合改进的深度残差神经网络的故障诊断方法,构建了故障诊断模型DRNN-3S,并用滚动轴承实验数据集对所提出方法的有效性进行了验证.
2) 在模型训练和多传感器性能测试阶段,DRNN-3S模型的训练收敛速度更快,且能保持较高的训练精度和测试精度,均达到100%,充分体现了残差模型和多传感器融合的优势.
3) 在抗噪能力测试中,DRNN-3S模型表现出良好的抗噪能力.当单一传感器采集的数据受到噪声污染时,DRNN-3S模型能保持至少93.78%的诊断精度,当所有传感器采集的数据受到噪声污染时,DRNN-3S模型能保持至少82.54%的诊断精度.
| [1] |
于军, 丁博, 何勇军. 基于平均多粒度决策粗糙集和NNBC的滚动轴承故障诊断[J]. 振动与冲击, 2019, 38(15): 209. YU Jun, DING Bo, HE Yongjun. Rolling bearing fault diagnosis based on mean multi-granularity decision rough set and NNBC[J]. Journal of Vibration and Shock, 2019, 38(15): 209. DOI:10.13465/j.cnki.jvs.2019.15.029 |
| [2] |
HINTON G E, OSINDERO S, TEH Y W. A fast learning algorithm for deep belief nets[J]. Neural Computation, 2006, 18(7): 1527. DOI:10.1162/neco.2006.18.7.1527 |
| [3] |
PENG Binsen, XIA Hong, LIU Yongkuo, et al. Research on intelligent fault diagnosis method for nuclear power plant based on correlation analysis and deep belief network[J]. Progress of Nuclear Energy, 2018, 108: 419. DOI:10.1016/j.pnucene.2018.06.003 |
| [4] |
SHAO Haidong, JIANG Hongkai, ZHANG Xun, et al. Rolling bearing fault diagnosis using an optimization deep belief network[J]. Measurement Science and Technology, 2015, 26(11): 115002. DOI:10.1088/0957-0233/26/11/115002 |
| [5] |
SHAO Haidong, JIANG Hongkai, ZHAO Huiwei, et al. A novel deep autoencoder feature learning method for rotating machinery fault diagnosis[J]. Mechanical Systems and Signal Processing, 2017, 95: 187. DOI:10.1016/j.ymssp.2017.03.034 |
| [6] |
LI Xin, YANG Yu, PAN Haiyang, et al. A novel deep stacking least squares support vector machine for rolling bearing fault diagnosis[J]. Computers in Industry, 2019, 110: 36. DOI:10.1016/j.compind.2019.05.005 |
| [7] |
KRIZHEVSKY A, SUTSKEVER I, HINTON G E. ImageNet classification with deep convolutional neural networks[C]//Proceedings of the 25th International Conference on Neural Information Processing Systems. New York: ACM, 2012: 1097. DOI: 10.1145/3065386
|
| [8] |
NAIR V, HINTON G E. Rectified linear units improve restricted Boltzmann machines[C]//Proceedings of the 27th International Conference on Machine Learning (ICML-10). Haifa: [s. n], 2010: 807. DOI: 10.5555/3104322.3104425
|
| [9] |
LECUN Y, BOTTOU L, BENGIO Y, et al. Gradient-based learning applied to document recognition[J]. Proceedings of the IEEE, 1998, 86(11): 2278. DOI:10.1109/5.726791 |
| [10] |
SIMONYAN K, ZISSERMAN A. Very deep convolutional networks for large-scale image recognition[Z]. arXiv: 1409.1556, 2014. https://arxiv.org/abs/1409.1556
|
| [11] |
HE Kaiming, ZHANG Xiangyu, REN Shaoqing, et al. Deep residual learning for image recognition[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas, NV: IEEE Computer Society, 2016: 770. DOI: 10.1109/CVPR.2016.90
|
| [12] |
RAIKO T, VALPOLA H, LECUN Y. Deep learning made easier by linear transformations in perceptrons[C]//Proceedings of the 15th International Conference on Artificial Intelligence and Statistics. La Palma, Canary Islands: JMLR W & CP, 2012: 924
|
| [13] |
LECHEVALLIER Y, SAPORTA G. Large-scale machine learning with stochastic gradient descent[M]//Proceedings of COMPSTAT'2010. Berlin: Springer-Verlag, 2010: 177. DOI: 10.1007/978-3-7908-2604-3
|
| [14] |
SMITH W A, RANDALL R B. Rolling element bearing diagnostics using the Case Western Reserve University data: A benchmark study[J]. Mechanical Systems and Signal Processing, 2015, 64/65: 100. DOI:10.1016/j.ymssp.2015.04.021 |
| [15] |
HOANG D T, KANG H J. Rolling element bearing fault diagnosis using convolutional neural network and vibration image[J]. Cognitive Systems Research, 2019, 53: 42. DOI:10.1016/j.cogsys.2018.03.002 |
| [16] |
DU Wenliao, TAO Jianfeng, LI Yanming, et al. Wavelet leaders multifractal features based fault diagnosis of rotating mechanism[J]. Mechanical Systems & Signal Processing, 2014, 43(1/2): 57. DOI:10.1016/j.ymssp.2013.09.003 |
| [17] |
JIN Xiaohang, ZHAO Mingbo, CHOW T W S, et al. Motor bearing fault diagnosis using trace ratio linear discriminant analysis[J]. IEEE Transactions on Industrial Electronics, 2013, 61(5): 2441. DOI:10.1109/TIE.2013.2273471 |
| [18] |
ZHANG Xiaoyuan, LIANG Yitao, ZHOU Jianzhong. A novel bearing fault diagnosis model integrated permutation entropy, ensemble empirical mode decomposition and optimized SVM[J]. Measurement, 2015, 69: 164. DOI:10.1016/j.measurement.2015.03.017 |
| [19] |
LI Xiang, ZHANG Wei, DING Qian. Understanding and improving deep learning-based rolling bearing fault diagnosis with attention mechanism[J]. Signal Processing, 2019, 161: 136. DOI:10.1016/j.sigpro.2019.03.019 |
| [20] |
WELCH P D. The use of fast Fourier transform for the estimation of power spectra: A method based on time averaging over short, modified periodograms[J]. IEEE Transactions on Audio and Electroacoustics, 1967, 15(2): 70. DOI:10.1109/TAU.1967.1161901 |
| [21] |
CARLO C, GEORGE H, SCOTT Z, et al. SNOMAD (Standardization and NOrmalization of MicroArray Data): Web-accessible gene expression data analysis[J]. Bioinformatics (Oxford, England), 2002, 18(11): 1540. DOI:10.1093/bioinformatics/18.11.1540 |
 2021, Vol. 53
2021, Vol. 53


