2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
FIR数字滤波器为对称型结构,阶数和量化位宽是决定数字滤波器硬件资源的两个重要因素,通常情况下,阶数越高、量化位宽越大,硬件资源消耗越多.考虑到FIR滤波器的参数是固定的,人们引入了固定乘数优化算法进行优化处理[1],即将乘法分解成加法和移位计算,降低运算复杂度.在已有的数字滤波器的固定乘数优化算法中,加法深度LD(logic depth)和加法器个数LA(logic adder)是衡量算法优劣性的两个重要指标.降低加法器个数需要尽可能复用系数中的公共项,从而带来加法深度的增加;降低加法深度则意味着降低公共项的复杂度,带来加法器LA的增加.LD和LA的结果不仅取决于系数的量化位宽、阶数,也取决于用户的优化方式,是一个综合性的优化问题.考虑到常系数乘法的加法器个数与系数非零项直接相关,Park等[2-3]提出采用CSD、MSD表示法表示滤波器系数,在后续的算法中得到了广泛应用.在此基础上, 人们提出了采用递归式算法和非递归式算法的不同公共项提取思路来降低电路中的加法器消耗.前者[4-9]以BHM[4]、RAG-n[5-6]、HARTLEY[7]和HCUB[8]为代表,采用迭代运算穷举固定系数的所有公共项,可以达到最优的降低MCM加法器的效果.RAG-n、BHM和HCUB算法均采取图形启发式方式进行优化,即先对系数进行排序,以最小的系数为公因子,穷举各个系数的公因子组合方式,选取代价最小的作为最优解.其中Bull等[4]最早提出采用图形化的方法来从小到大组合滤波器系数,取得了较好的效果;Dempster等[5]在此基础上进行了改良,扩展了系数范围,提出了BHM算法;而RAG-n则更进一步,采用查表法遍历了所有可能,所以加法器个数LO最少,但是代价是需要预存分解表,算法复杂度最高,运算时间最长,加法深度最高. HCUB算法则是在此基础上,引入了中间变量算子,降低了算法对分解表的要求,是目前最优的启发式优化算法. 然而,上述图形启发式优化方法均存在算法复杂度高、求解时间随量化位数增加急剧上升的问题,同时由于采用公共项的多次复用,逻辑深度居高不下,引入大量的路径延时,对后期电路的设计和综合非常不友好.非递归式[10-16]则以直接提取公共项进行有限次数迭代,具有算法复杂度低、可综合性好等优点,代表性的有NR-SCSE、HSSE、VSSE算法等.其中Peiro等[14]提出的非递归有符号公共项消去算法(Non-recursive signed common sub-expression elimination, NRSCSE),采用一维搜索频次最高的公共项的算法,算法复杂度低,逻辑深度低,取得了非常好的同时降低LO和LD的效果.为了达到降低逻辑深度的目的,该算法只启用包含2个非零项的公共项,具有最低逻辑深度特性. 然而,上述非递归式算法均只进行了一维的共同项(单独的系数矩阵的行公共项或者单独的列公共项)的提取,并没有考虑到系数矩阵的二维特性,在加法器个数的指标上整体落后于递归算法.
为了达到逻辑深度和加法器个数的双重优化效果,本文提出了一种新的二维非递归优化算法. 其在一维非递归式算法的基础上,对系数矩阵的第2个维度进行公共项提取,从而达到进一步降低加法器个数的效果.仿真结果表明,相比于一维的NRSCSE,本文设计的滤波器优化算法(后文简称ONRSCSE)可以降低10%左右的系数加法器数量,具有良好的推广价值.
1 一维非递归算法数字滤波器的滤波效果是通过输入信号与滤波系数的卷积运算来实现的,具体来说,输入信号x进入一个N阶的数字FIR滤波器后,需要与N-1个系数进行乘法运算,之后进行累加,得到输出值.假定N阶FIR滤波器的系数由低阶到高阶分别为:h(0), h(1), …,h(N-1), 则有该滤波器的响应为
| $ \begin{aligned} y(n)=& \sum\limits_{i=0}^{N-1} h(i) \times x(n-i)=\\ & \sum\limits_{i=0}^{N-1} h(i) \times x(n) \times z^{-i} . \end{aligned} $ | (1) |
式中:x(n)、y(n)分别为滤波器的输入和输出.假定滤波器的系数矩阵为H,H=[h0, h1, …, hN-1],当前输入为x(n),则输出Y=H×X,X=x(n)×[z0, z-1, z-2, z-3]为输入矢量.
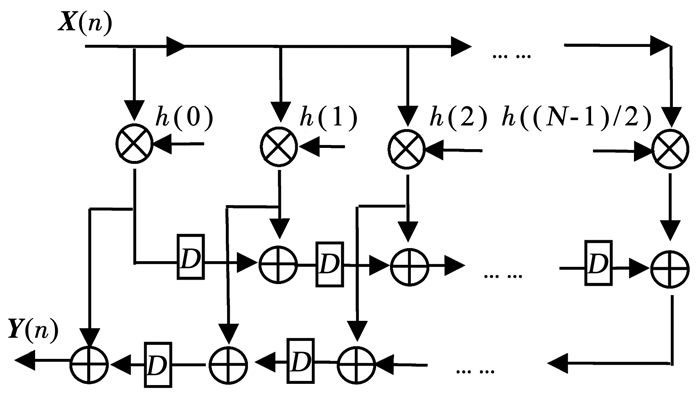
考虑到FIR滤波器的系数对称性,通常采用优化的转置式实现,假定FIR为Ⅰ型滤波器,N为奇数,则实现的滤波器结构如图 1所示.由于其系数对称性,即h0=hN-1,h1=hN-2,对系数的优化只需要对其前1/2系数h0,h1,…,h(N-1)/2进行即可.
|
图 1 FIR滤波器的优化转置结构 Fig. 1 Optimized transposed structure of FIR filter |
传统的非递归优化算法在将系数hi采用CSD法表示后,对各个系数的非零项进行统计,依次提取出现频率最高的间距相同、符号相同/相反的非零项作为公共项,对系数进行分解,直到系数无法再提取公共项为止,通常为一维搜索算法.以NRSCSE[14]算法为例,其只搜索系数内的任意间距2个非零位公共项,在量化位数为b时,单个系数最多存在2×(b-1)个公共项,逻辑深度最多为
| $ \begin{array}{l} h(0)=1288, h(1)=776, h(2)=1077, \\ h(3)=1189 . \end{array} $ | (2) |
将其表示为12 bit的CSD数后,系数如下:
| $ \begin{array}{l} \mathit{\boldsymbol{h}}\left( 0 \right) = 0{\rm{x}}508 = {\left( {010100001000} \right)_{{\rm{CSD}}}}, \\ h\left( 1 \right) = 0{\rm{x}}308 = {\left( {010 - 100001000} \right)_{{\rm{CSD}}}}, \\ h\left( 2 \right) = 0{\rm{x}}435 = {\left( {0100010 - 10101} \right)_{{\rm{CSD}}}}, \\ h\left( 3 \right) = 0{\rm{x}}4{\rm{a}}5 = {\left( {010010100101} \right)_{{\rm{CSD}}}}. \end{array} $ | (3) |
采用NRSCSE提取公共项101/10-1后,得到剩余矩阵(后文称为残余矩阵)为
| $ \boldsymbol{H}_{\text {remain }}=\left[\begin{array}{l} 1 \ll 3 \\ 1 \ll 3 \\ 1 \ll 11 \\ 1 \ll 11 \end{array}\right], $ | (4) |
则整体表示法为
| $ y_{0}=\boldsymbol{H} \times \boldsymbol{X}=\left[\begin{array}{c} S_{0} \ll 8+x_{0} \ll 3 \\ S_{1} \ll 8+x_{0} \ll 3 \\ S_{1} \ll 4+S_{0}+x_{0} \ll 10 \\ S_{0} \ll 5+S_{0}+x_{0} \ll 10 \end{array}\right] \times\left[\begin{array}{c} z^{0} \\ z^{-1} \\ z^{-2} \\ z^{-3} \end{array}\right]^{\mathrm{T}} $ | (5) |
式中: 公共项S0=x0≪2+x0,S1=x0≪2-x0,如图 2中红色方框内所示.共需要加法器8个,逻辑深度(系数中最大加法器个数+1)为2层.

|
图 2 滤波器系数的NRSCSE优化示例 Fig. 2 Example of NRSCSE coefficient optimization |
考虑到经过系数内的公共项提取后,系数残余矩阵内还存在冗余信息,如图 2中蓝色圆框所示,可以进一步进行优化.
2 二维非递归优化算法二维非递归优化算法(Optimized non-recursive signed common sub-expression elimination,ONRSCSE)是行公共项和列公共项提取的结合,是一种典型的非递归固定乘数优化方法.其大致思路为:首先采用CSD法表示FIR滤波器的前1/2系数,将系数表示为{-1,0,1}的初始系数矩阵;然后采用行公共项提取的方法依次分解系数矩阵的行系数,直到满足行分解的终止条件为止;之后对分解后剩余的非0系数矩阵(后文称为残余矩阵)进行列公共项分解,直到满足终止条件为止;最后将系数表示成分解出的行与列公共项的移位与加法组合,完成整个算法优化.
以一维优化为例,本文在一维非递归算法的基础上,对上述残余矩阵式6进行列公共项的提取,得到列公共项[1 1]T,记为S2=x0+x0[-1],[-1]表示对系数进行一个单位的延时,则滤波器此部分的输出为
| $ y_{0}=\left[\begin{array}{c} S_{0} \ll 8 \\ S_{1} \ll 8 \\ S_{1} \ll 4+x_{0} \ll 10 \\ S_{0} \ll 5+S_{0} \end{array}\right]+\left[\begin{array}{c} 0 \\ S_{2} \ll 4 \\ 0 \\ S_{2} \ll 10 \end{array}\right] *\left[\begin{array}{c} z^{0} \\ z^{-1} \\ \ldots \\ z^{-3} \end{array}\right]^{\mathrm{T}} $ | (6) |
整体实现一共需要加法器7个,逻辑深度2层. 因此,相比于一维的NRSCSE算法,本算法(ONRSCSE)增加了列系数的非零项搜索,节省了1个加法器资源.
不难推算,NRSCSE算法优化的残余矩阵中非零项越多,列公共项出现次数越多,本算法的优化效果越显著.
2.1 名词定义 2.1.1 系数矩阵由CSD表示后的滤波器系数组成的矩阵,矩阵元素为{-1,0,1},假定滤波器系数量化位宽为b,阶数为n,本算法通常取前1/2系数第0~m阶组成系数矩阵(如果n为偶数,m=n/2;如果n为奇数则m=(n-1)/2).系数矩阵记为Hi,下标i代表第i次系数分解,H0为初始化系数矩阵.
2.1.2 残余矩阵系数矩阵减去公共项元素后剩余的非0矩阵.
2.2 算法描述在系数矩阵的基础上,对公共项进行二维搜索,遵循规则为——先迭代搜索行公共项,再搜索列公共项.
1) 首先对n阶、系数量化为b bit的FIR滤波器进行CSD表示,产生n*b的系数矩阵, 取前1/2系数0~m项Cb/22(m=(n-1)/2)组成系数矩阵H0;
2) 对系数矩阵Hi进行行系数分解,方法为统计在整个系数矩阵中出现次数最多的行公共项,将其作为最优公共项;
3) 在系数矩阵Hi中消去最优公共项,得到残余矩阵Hi+1,则Hi可以表示为Hi+1与最优公共项的移位和加法组合;
4) 返回步骤2)继续分解残余矩阵Hi+1,直到满足行分解的终止条件——公共项矩阵中最优公共项出现次数小于2为止,进入步骤5).假定此时已经进行了j次迭代,得到了残余矩阵Hj;
5) 对残余系数矩阵Hj进行列分解,方法为统计在整个系数矩阵中出现次数最多的列公共项,将其作为最优公共项;
6) 在系数矩阵Hj中消去最优公共项,得到残余矩阵Hj+1,则Hj可表示为Hj+1与最优列公共项的移位和加法组合;
7) 返回步骤5)继续分解残余矩阵Hj+1,直到满足列分解终止条件为止,进入步骤8);
8) 将滤波器的输出y表示为所有行、列公共项的移位和累加*输入的组合.
2.3 算法复杂度分析基于上述算法描述,对ONRSCSE的复杂度进行分析.假定待优化滤波器的阶数为n,量化位宽为b,则系数矩阵的行系数最多有b/2个非零项,每个系数的行公共项搜索最多进行Cb/22次运算,一次系数矩阵的行公共项搜索最多进行n*Cb/22次计算.由于行公共项最多有(b-2)个,故行分解的运算次数为n*(b-2)*Cb/22次.完成行分解后,残余矩阵已经是稀疏矩阵,只有少量的非零项,因此列分解运算不影响算法复杂度.故ONRSCSE的整体算法复杂度与一维非递归算法NRSCSE相当,均为o(nb3).相比于现有递归算法HCUB[8]的o(n3b5),算法复杂度得到了极大的降低.
3 结果及分析 3.1 实验数据集本文采用通用的滤波器设计方法,一共设计了19个不同特性的滤波器,并对其进行不同量化位宽、不同阶数的例化,产生了共82个滤波器,此为算法优化的对象.
其中为对比本算法与一维非递归算法,采用MATLAB的FDAtool工具产生了12组数字FIR带通滤波器,阶数从37阶到649阶,并对每组滤波器系数进行了12、16 bit的量化,覆盖了常用的数字滤波器范围,此为数据集1.
为对比本算法与递归型优化算法,采用Parks-McClellan法设计7种不同阶数的数字带通滤波器,每种阶数内有10组不同的滤波器系数,分别对应不同的带通特性,此为数据集2.采用Voronenko等[18]提供的优化算法库对数据集2内的滤波器进行优化. Voronenko[18]算法库为卡内基梅隆大学SPIRAL算法库的一部分,滤波器优化部分由HCUB算法的提出者Voronenko[18]提供,是一个集成多个主流递归式滤波器优化算法的经典算法实现库,已经被Vinod等[16-17]多位学者引用,可以实现包括BHM、RAG-n、HCUB在内的3种递归式滤波器优化算法,量化位宽支持到12 bit,滤波器阶数支持到100阶左右.由于Parks-McClellan设计法和算法库的限制,只产生了70组30-100阶的滤波器,量化位宽均为12 bit.
3.2 本算法与一维非递归算法及传统CSD表示法的对比对数据集1内的18组滤波器进行了优化,统计采用CSD表示法、NRSCSE算法和ONRSCSE算法时运算需要的加法器资源,得到结果见表 1、2.
| 表 1 CSD表示法的加法器资源 Tab. 1 Logic adder number of CSD representation |
| 表 2 NRSCSE与ONRSCSE算法优化后的加法器资源 Tab. 2 Logic adder number after NRSCSE and ONRSCSE optimization |
可以看到,与CSD表示法相比,NRSCSE与ONRSCSE优化效果都很显著.在阶数低于100时,优化后的加法器资源均控制在传统CSD表示法的30%左右;阶数高于100时,优化后的加法器资源控制在传统CSD表示法的50%以内.
比较NRSCSE与ONRSCSE的优化效果发现,同等情况下,ONRSCSE均优于NRSCSE,优化效率见表 3.可以看到,ONRSCSE对NRSCSE的优化效率不随着滤波器阶数和量化位宽线性变化,而是主要取决于滤波器经过一维非递归优化后的加法器资源.普遍来说, 同样量化位宽的条件下, ONRSCSE对NRSCSE的优化效果呈现一定的比例关系,NRSCSE优化后的加法器个数越多,ONRSCSE节省的加法器个数就相对更大.然而由于经过NRSCSE优化后的残余系数矩阵的非零位在不同滤波器系数矩阵中分布各异,所以优化效果会体现出个体差异,如FIR10与FIR11,12 bit量化时经过NRSCSE优化后加法器个数分别为109/122个,但是ONRSCSE的节省加法器个数却是12/9个,FIR11的ONRSCSE优化效果略差于FIR10.这是因为FIR11经过行系数公共项提取后,残余稀疏矩阵非零位分布相对发散,可以提取的列公共项个数少于FIR10.
| 表 3 ONRSCSE对NRSCSE的提升效果 Tab. 3 Optimization effect of ONRSCSE versus NRSCSE |
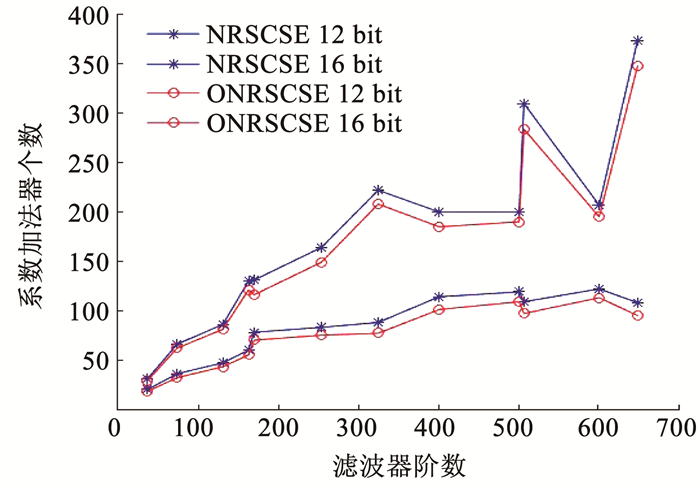
对上述优化结果的加法器资源进行绘图,得到ONRSCSE与NRSCSE加法器个数对比, 如图 3所示.
|
图 3 ONRSCSE与NRSCSE加法器个数对比 Fig. 3 Comparison of adder number between ONRSCSE and NRSCSE |
与传统一维非递归算法NRSCSE算法相比,采用ONRSCSE算法的优化效果更高,降低加法器资源的比率平均为10.05%(12 bit量化)和7.21%(16 bit量化).同时,优化的效果受阶数的变化影响较小,呈现非常稳定的特性.由于ONRSCSE对相邻系数的共同项提取结果直接通过D触发器进入下一级运算,对滤波器的逻辑深度没有影响,因此ONRSCSE和一维非递归算法一样,仍然具有最低逻辑深度特性.
3.3 本算法与传统算法的比较对数据集2的7种12 bit量化的滤波器进行优化,分别采用BHM、RAG-n、HCUB、NRSCSE、ONRSCSE算法进行设计,每种滤波器的10组系数优化结果LA与LD进行平均,得到相同阶数内滤波器优化的平均优化结果.记录最终得到的平均加法器个数(Mean logic adder, MLA)和平均逻辑深度(Mean logic depth, MLD),进行优化效果对比.其中BHM、RAG-n、HCUB的滤波器优化算法由Voronenko[18]提供,优化结果对比见表 4.
| 表 4 ONRSCSE与NRSCSE、BHM、RAG-n、HCUB的优化效果对比 Tab. 4 Comparison of optimization effect among ONRSCSE, NRSCSE, BHM, RAG-n, and HCUB |
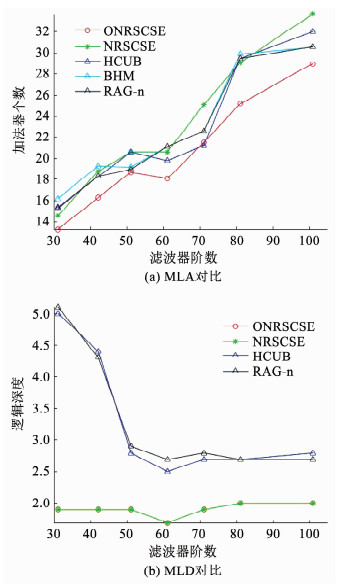
对优化结果的加法器资源和逻辑深度进行绘图,得到算法性能对比如图 4所示。可以看到,在31~101阶的一共70组12 bit系数量化滤波器中,非递归的滤波器优化算法NRSCSE算法相比于递归式算法HCUB、BHM、RAG-n,逻辑深度最低,加法器资源最高,优化后的ONRSCSE算法逻辑深度与NRSCSE算法相同,均保持为最低,但是加法器资源已经明显优于HCUB、BHM、RAG-n,取得了最好的效果.由于ONRSCSE只依靠系数内的公共项,不利用系数值进行下一步的系数优化,系数间不存在依赖关系,不会对后续的综合产生影响,非常有利于算法的综合与实现.
|
图 4 ONRSCSE/NRSCSE/HCUB/BHM/RAG-n算法的加法器资源与逻辑深度对比 Fig. 4 Mean logic adder and mean logic depth of ONRSCSE/NRSCSE/HCUB/BHM/RAG-n |
1) 本文首次提出了结合系数行公共项优化和列公共项优化的系数矩阵二维优化方法,并将其运用到了非递归的FIR滤波器优化算法中,取得了较好的效果. 首先将系数用CSD法表示,降低了系数中的非0值个数;然后对系数矩阵进行行系数分解,降低行系数中的加法器个数;之后对残余矩阵进行公共项提取,进一步降低整体加法器个数.
2) 相比于现有的一维非递归算法,本算法可节省10.05%(12 bit量化)和7.21%(16 bit量化)加法器个数.在低阶滤波器的优化中,加法器使用量降低到了传统的CSD表示法的30%左右.仿真结果表明,在阶数低于100、量化位宽为12 bit时平均加法器个数和深度指标均优于已发表的NRSCSE、BHM、RAG-n、HCUB算法.
3) 由于只采用2个非零项作为公共项,逻辑深度保持在log2
| [1] |
CHANDRA A, CHATTOPADHYAY S. Design of hardware efficient FIR filter: A review of the state-of-the-art approaches[J]. Engineering Science and Technology, an International Journal, 2016, 19(1): 212. DOI:10.1016/j.jestch.2015.06.006 |
| [2] |
PARK I C, KANG H J. Digital filter synthesis based on minimal signed digit representation[C]//Proceedings of the 38th Design Automation Conference. Las Vegas, NV: IEEE, 2001: 468. DOI: 10.1109/DAC.2001.156185
|
| [3] |
HARTLEY R. Optimization of canonic signed digit multipliers for filter design[C]//Proceedings of the IEEE International Sympoisum on Circuits and Systems. Piscataway, NJ: IEEE, 1991: 1992. DOI: 10.1109/ISCAS.1991.176054
|
| [4] |
BULL D R, HORROCKS D H. Primitive operator digital filters[J]. IEE Proceedings-Circuits, Devices and Systems, 1991, 138(3): 401. DOI:10.1049/ip-g-2.1991.0066 |
| [5] |
DEMPSTER A G, MACLEOD M D. Constant integer multiplication using minimum adders[J]. IEE Proceedings-Circuits, Devices and Systems, 1994, 141(5): 407. DOI:10.1049/ip-cds:19941191 |
| [6] |
DEMPSTER A G, MACLEOD M D. Use of minimum-adder multiplier blocks in FIR digital filters[J]. IEEE Transactions in Circuits and Systems Ⅱ: Analog and Digital Signal Processing, 1995, 42(9): 569. DOI:10.1109/82.466647 |
| [7] |
HARTLEY R I. Subexpression sharing in filters using canonic signed digit multipliers[J]. IEEE Transactions on Circuits and Systems Ⅱ: Analog and Digital Signal Processing, 1996, 43(10): 677. DOI:10.1109/82.539000 |
| [8] |
BOUDJELABA K, CHIKOUCHE D, ROS F. Evolutionary techniques for the synthesis of 2-D FIR filters[C]// Proceedings of the IEEE Statistical Signal Processing Workshop. Nice, France: IEEE, 2011: 601. DOI: 10.1109/SSP.2011.5967771
|
| [9] |
VORONENKO Y, PUSCHEL M. Multiplierless multiple constant multiplication[J]. ACM Transactions on Algorithms, 2007, 3(2): 1. DOI:10.1145/1240233.1240234 |
| [10] |
PASKO R, SCHAUMONT P, DERUDDER V, et al. A new algorithm for elimination of common subexpressions[J]. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 1999, 18(1): 58. DOI:10.1109/43.739059 |
| [11] |
DEMPSTER A G, DEMIRSOY S S, KALE I. Designing multiplier blocks with low logic depth[C]//Proceedings of the IEEE International Symposium on Circuits and Systems. Phoenix-Scottsdale, AZ: IEEE, 2002: 773. DOI: 10.1109/ISCAS.2002.1010818
|
| [12] |
DEMPSTER A G, MACLEOD M D. Using all signed-digit representations to design single integer multipliers using subexpression elimination[C]//Proceedings of the IEEE International Symposium on Circuits and Systems. Vancouver, BC: IEEE, 2004: III-165. DOI: 10.1109/ISCAS.2004.1328709
|
| [13] |
JANG Y, YANG S. Low-power CSD linear phase FIR filter structure using vertical common sub-expression[J]. Electronics Letters, 2005, 38(15): 777. DOI:10.1049/el:20020529 |
| [14] |
PEIRO M M, BOEMO E I, WANHAMMAR L. Design of high-speed multiplierless filters using a nonrecursive signed common subexpression algorithm[J]. IEEE Transactions on Circuits and Systems Ⅱ: Analog and Digital Signal Processing, 2002, 49(3): 196. DOI:10.1109/TCSII.2002.1013866 |
| [15] |
YAO C Y, CHEN H H, LIN T F, et al. A novel common-subexpression-elimination method for synthesizing fixed-point FIR filters[J]. IEEE Transactions on Circuits and Systems Ⅰ: Regular Papers, 2004, 51(11): 2215. DOI:10.1109/TCSI.2004.836853 |
| [16] |
VINOD A P, LAI E M-K. Comparison of the horizontal and the vertical common subexpression elimination methods for realizing digital filters[C]//Proceedings of the IEEE International Symposium on Circuits and Systems. Kobe, Japan: IEEE, 2005: 496. DOI: 10.1109/ISCAS.2005.1464633
|
| [17] |
MAHESH R, VINOD A P. A new common subexpression elimination algorithm for realizing low-complexity higher order digital filters[J]. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2008, 27(2): 217. DOI:10.1109/TCAD.2007.907064 |
| [18] |
VORONENKO Y, PUSCHEL M. Multiplier block generator. (2019-01-14). http://spiral.ece.cmu.edu/mcm/gen.html
|
 2021, Vol. 53
2021, Vol. 53


