2. 中国地震局地震工程与工程振动重点实验室 (中国地震局工程力学研究所),哈尔滨 150080;
3. 北京市煤气热力工程设计院有限公司,北京 100032
2. Key Laboratory of Earthquake Engineering and Engineering Vibration of China Earthquake Administration(Institute of Engineering Mechanics, China Earthquake Administration), Harbin 150080, China;
3. Beijing Gas and Heating Engineering Design Institute Co., Ltd., Beijing 100032, China
随着中国经济发展和城市化进程的加快,准确真实评估城市燃气管网不同地震动强度下的抗震性能变得尤为重要.根据研究尺度的不同,城市燃气系统的易损性分析分为燃气管线(微观)和燃气管网(宏观)两种,目前国内的研究多集中在前者[1],即多局限于通过有限元分析等数值模拟手段对埋地管线、调压站、储气罐等要素进行易损性分析;对城市燃气管网整体的易损性分析关注较少,基于连通性的城市燃气管网易损性可以定义为:城市燃气管网在不同强度地震作用下,其连通性发生各种破坏状态的发生概率.
基于图论知识,燃气管网的连通可靠性分析主要有解析算法和蒙特卡罗模拟法两种:如李杰等[2]针对供燃气管网系统提出了用于大型网络抗震连通可靠度分析的递推分解算法. 2012年, Poljanšek等[3]假设燃气管网各单元失效相互独立,运用蒙特卡罗模拟的方法对燃气管网进行了地震风险评估.基于蒙特卡罗模拟进行燃气管网连通可靠性分析具有建模难度低,适用性强,以及收敛快速等多个优点,本文拟基于该分析思路来进行城市燃气管网的连通易损性分析.此外地震动强度评估作为易损性分析的重要基础环节是本文关注的另一个关键问题.目前国内大多采用GB18306-2015《中国地震动参数区划图》或GB 50032-2003《室外给水排水和燃气热力工程抗震设计规范》对城市的地震动参数进行宏观估计[4]. 但是这种评估方式无法体现燃气管网系统不同位置的地震动差异与不确定性. 2014年, Esposito等[5]在进行燃气管网的地震风险评估时,提出了采用地面运动预测方程(GMPE)来评估意大利中部阿奎拉市的燃气管网各位置的地震动强度. 本文借鉴该思路,尝试将中国地震动预测方程(GMPE)应用到城市燃气管网连通易损性分析中,同时将地震动预测方程中不确定性也通过随机误差变量抽样来一并考虑.
综上所述,为了综合考虑地震动的区域分布差异性和地震动的不确定性,本文提出基于蒙特卡罗模拟的城市燃气管网连通易损性分析方法.为验证其适用性,以中国某城市燃气管网作为实例进行了连通易损性分析,同时针对地震动预测方程中不确定性的影响进行重点对比研究.
1 城市燃气管网连通易损性分析流程城市燃气管网系统由燃气管线、燃气门站、调压站、用户等部分组成,各功能单元相互连接构成网络结构[6]. 将燃气门站、调压站、管线交汇处、用户抽象为网络节点,燃气管线抽象为网络的边,其中燃气门站记作网络的源点,用户端记作汇点便构成复杂网络记为图G,表示为G=(V, E), 其中V为非空的节点集,E为不与V相交的边集.图G的节点和边的连接关系可以表达为邻接矩阵,记为A,称A=A(G)=(aij)n×n为图G的邻接矩阵,n为节点数量,aij可表示为
| $ a_{i j}=\left\{\begin{array}{l} 1, \text { 存在由节点 } i \text { 流向 } j \text { 的边; } \\ 0, \text { 不存在由节点 } i \text { 流向 } j \text { 的边. } \end{array}\right. $ | (1) |
对于拓扑网络一般采用可达矩阵法进行连通性估计:即计算M=A+A2+A3+…+An-1, 若Mij≠0, 则表示i、j两节点连通,反之,则i、j两节点不连通[7].
下面首先介绍作为连通性计算依据的地震动强度指标估计方法,然后介绍燃气管网中点、边类单元的失效概率估计方法,最后给出基于蒙特卡罗模拟的燃气管网连通易损性计算流程.
1.1 基于GMPE的燃气管网地震动强度指标确定由于城市燃气管网系统其研究尺度一般在数百甚至上千平方公里,因此需要合理评估管网系统不同位置的地震动强度,并且需要考虑地震动自身的不确定性.如果以该地某一历史地震或者目标活跃断层的位置作为假想震源,则该城市燃气管网各节点的地震动强度可以根据适用于该城市或区域的地震动预测方程进行评估计算.
本文采用了目前地震安全性评价工程中广泛使用的文献[8]地震动土层预测方程进行计算,长、短轴采用的预测方程模型为
| $ \lg Y=C_{1}+C_{2} \cdot M+C_{4} \cdot \lg \left[R+C_{5} \cdot \exp \left(C_{6} \cdot M\right)\right]+\varepsilon. $ | (2) |
式中: Y为目标地震动强度指标(本文中为Pga和Pgv); M为面波震级; R为震中距; C1、C2、C4、C5、C6分别为回归分析得到的参数; ε为体现不确定性的随机误差变量,呈均值为0,标准差为σlg(Y)的正态分布.
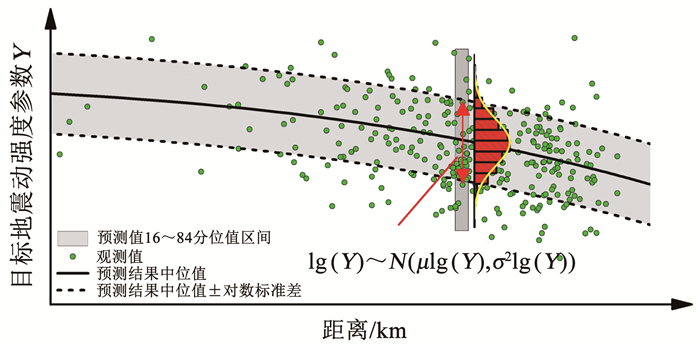
由图 1的某次地震动算例可知,地震动预测方程给出的其实是一定范围的地震动强度指标预测区间,体现实际地震动观测值的不确定性.对数强度指标预测值加减一倍对数标准差表征了16~84分位值的预测区间.
|
图 1 考虑地震动不确定性的地震动预测方程示意 Fig. 1 Schematic of GMPE considering uncertainty |
城市燃气管网系统单元可以分为:1)点状关键设施,如燃气门站、调压站、用户端等;2)埋地燃气管道.大量的震害调查研究表明[9],相比于供水网络等边权网络,以及供电网络等点权网络,城市燃气管网系统震后应同时考虑点状设施及管道失效的可能性.假定燃气管网各单元之间失效相互独立,某一部分单元在地震后失效,也会改变了整个管网的连通性.本文从节点和边的角度分别给出两类单元失效概率的估计方法.
1.2.1 节点失效概率对于城市燃气管网的点状设施,本文仅考虑燃气门站(源点)具有失效的可能性,而不考虑用户端等其他节点的失效[10].作为主导燃气门站失效的地震动参数Pga由上文的GMPE得到.本文中,燃气门站的失效概率采用易损性曲线与故障树分析相结合的方法.
不同功能设施的易损性曲线可以使用文献[11]中的经验统计模型,可表示为对数正态分布的函数,其可以转换为标准正态分布进行计算,即
| $ P\left(D \mid P_{\mathrm{ga}}\right)=\boldsymbol{\varPhi}\left[\frac{\ln \left(P_{\mathrm{ga}} / P_{\mathrm{ga}}^{m}\right)}{\sigma_{\ln \left(P_{\mathrm{ga}}\right)}}\right]. $ | (3) |
式中:D为目标设施的破坏状态; Pgam、σln(Pga)为目标破坏状态D下的Pga中位值与对数标准差.
燃气门站中影响地震后使用功能的重要设施可划分为储气罐与计量调压间,两部分失效独立,且失效状态均设为严重破坏.本文采用文献[12]中建议的储气罐与计量调压间在严重破坏下的易损性函数参数值,见表 1. 通过式(3)可以得到该源点地震作用强度达到Pga值时各子结构设施的失效概率,最后采用故障树方法,计算出整个燃气门站的失效概率(当考虑地震动预测方程中不确定性后,该失效概率为随机变量),即
| $ P_{\text {燃气门站失效 }}=1-\left(1-P_{\text {计量减压间失效 }}\right) \times\left(1-P_{\text {储气罐失效 }}\right) . $ | (4) |
| 表 1 燃气门站功能设施易损性函数参数值 Tab. 1 Fragility function parameters for gas gate station facilities |
考虑影响埋地管线失效概率的地震动参数时,本文主要考虑Pgv[7]与Pgd[13-14](Permanent Ground Deformation, 永久地面位移)的影响.
首先,由GMPE计算出各节点的Pgv后,边(管线)的Pgv可以近似取所连两节点的Pgv的平均值.
基于Pgv影响下管线平均震害率的经验函数与管线的破裂沿管线遵循泊松分布的假设,同时考虑到城市燃气管线较其他生命线系统最大的区别在于其不允许带渗漏作业,采用两态破坏准则,只有连通与失效两种工作状态,当埋地管线至少发生1处破坏时,管线失效.
本文采用文献[12]中的震害率模型,表示为
| $ R_{\mathrm{f}_{1}}=0.0024 \times K_{1} \times P_{\mathrm{gv}}. $ | (5) |
式中:Rf1为埋地管线平均震害率,处/km;K1为与管材、接头形式、场地土、管径相关调整系数;Pgv为峰值地面速度. 其中
| $ P_{\mathrm{f}_{1}}=1-P(0)=1-\mathrm{e}^{-R_{\mathrm{f}_{1}} L}. $ | (6) |
式中:Pf1为Pgv影响下埋地管线震后失效概率(当考虑地震动预测方程中不确定性后,该失效概率为随机变量);L为计算管线的长度.
对于震后易发生永久地面位移地区管线以及一些因服役年限过长或腐蚀严重的管线,本文采用文献[15]中的方法通过修正系数对Pgv影响下的燃气管线失效概率进行修正,其失效概率Pf2为
| $ P_{\mathrm{f}_{2}}=\beta_{1} \cdot \beta_{2} \cdot \beta_{3} \cdot \beta_{4} \cdot P_{\mathrm{f}_{1}}. $ | (7) |
式中:β1为使用年限修正系数;β2为震陷修正系数;β3为液化修正系数;β4为腐蚀等其他因素修正系数.
1.3 基于蒙特卡罗模拟的燃气管网地震连通易损性计算首先定义燃气管网的连通性评价指标.燃气管网系统的连通性可以通过地震前后的接收燃气用户数量的比例来表示,并用CL(Connectivity loss)指标表示燃气管网连通性的损失程度:
| $ C_{\mathrm{L}}=1-\frac{n^{\mathrm{pos}}}{N^{\mathrm{pre}}}. $ | (8) |
式中:npos为地震作用后,可以接收到燃气的用户数量;Npre为地震作用前,可以接收到燃气的用户数量.
破坏等级划分方法见表 2.
| 表 2 城市燃气管网基于CL值的破坏等级划分 Tab. 2 Seismic damage level of urban gas network based on CL values |
对于含有n个燃气门站,m条埋地管线的燃气管网模型,假设离散型随机变量X=(X1, X2, …, Xn, Xn+1, …, Xn+m)表示燃气管网震后状态,x=(x1, x2, …, xn, xn+1, …, xn+m)表示X的一个样本取值,xi表示第i个管网单元,有失效xi=0和不失效xi=1两种状态.CL(x)表示X=x时燃气管网的CL值.
在某震级下,设定蒙特卡罗模拟次数N.若不考虑GMPE中不确定性ε,各节点的Pga、Pgv在每一次蒙特卡罗模拟中为定值(预测值),但若考虑GMPE中地震动不确定性的影响,则用服从正态分布的随机数模拟随机误差变量.每一次蒙特卡罗模拟中不同节点的Pga、Pgv不确定性是完全随机的,同时因为地震动的不确定性,网络中各单元的失效概率在每一次模拟中也均不相同.对所有单元产生服从0~1之间均匀分布的随机数,当产生的随机数小于该单元失效概率时,该单元失效,并生成新的受损网络,形成新的邻接矩阵,得到该次模拟下受损网络的CL值.重复N次蒙特卡罗模拟,然后计算超过某CL值的次数与N的比值,得到该震级下,该城市燃气管网的连通性指标CL的超越概率曲线.并求解N次模拟结果中CL值的均值和标准差即可得到CL的期望估计值与离散性.
连通损伤指标μ定义如下式所示,反映了燃气管网在不同震级下连通性的平均损失程度,其值越大,表征燃气管网的抗震能力越弱.
| $ \mu=\frac{1}{N} \sum\limits_{k=1}^{N} C_{\mathrm{L}}(x(k)). $ | (9) |
式中: N为蒙特卡罗模拟的次数; x(k)为第k次模拟抽样得到的样本值.
调整震级大小,重复上述步骤,得到不同震级下超过某破坏状态的次数与N的比值,假设不同破坏状态所对应的易损性曲线为对数分布函数,即可拟合得到城市燃气管网连通性易损性曲线.

|
图 2 单元水平易损性——网络水平易损性 Fig. 2 Seismic fragility at elemental level and network level |
|
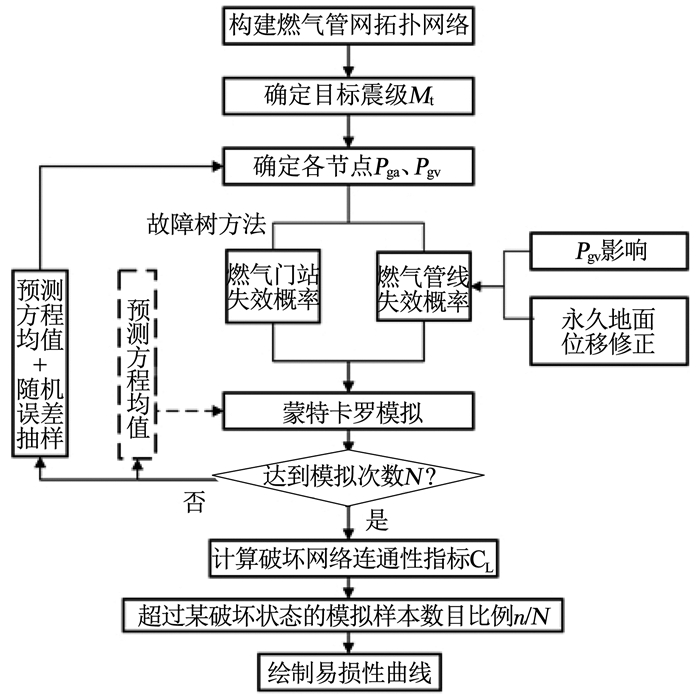
图 3 城市燃气管网连通易损性分析流程 Fig. 3 Seismic connectivity fragility analysis process of urban gas network |
本文选取中国华北某城市部分燃气管网作为算例,采用上文的计算流程进行连通易损性分析,并对比讨论了地震动预测方程中不确定性的影响.
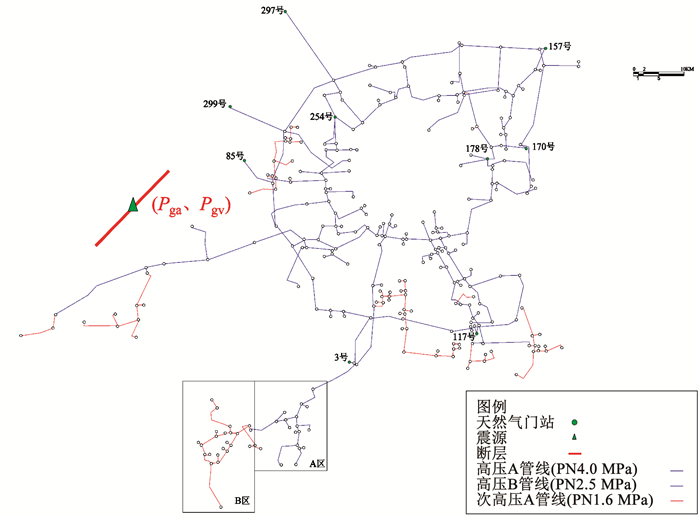
2.1 燃气管网拓扑建模该市燃气管道总长1 037.1 km,设计压力分级为高压A管线PN(公称压力)4.0 MPa,高压B管线PN2.5 MPa,次高压A管线PN1.6 MPa,对该市的燃气管网进行拓扑网络的构建,其中共9个燃气门站,110个用户,共306个节点,共326条边.源点编号分别为:3、85、117、157、170、178、254、297、299.该市燃气管网简化图如图 4所示.
|
图 4 该市燃气管网简化网络图 Fig. 4 Simplified network diagram of the city's gas network |
部分管段信息及节点编号见表 3.
| 表 3 燃气管道属性表 Tab. 3 Attributes of gas pipeline |
本文以该市历史发生过破坏性地震的某个活断层为假想震源所在断层(如图 4所示),长轴方向依据所在活动断层走向确定.由于工程场地勘测钻孔资料的缺失,本文暂不考虑燃气管网所在地区的场地类型差异.通过联立求解文献[8]的长、短轴土层地震动预测方程得到震级5.0~8.0级(0.5级间隔)下管网各节点的Pga、Pgv值.取蒙特卡罗模拟次数N为10 000,其中5.0~8.0级地震发生时某一次模拟下的燃气管网各节点Pga、Pgv与震中距的关系如图 5所示.从图 5中可以看出,在不考虑地震动不确定性时,各节点的地震动参数对数预测值在长短轴对数预测均值曲线之间;当引入随机误差变量时,模拟得到的各节点计算结果大致分布在长、短轴对数预测值加减一倍标准差的范围.下文将对比讨论是否考虑地震动不确定性对结果的影响.

|
图 5 不同震级下地震动参数考虑不确定性单次模拟结果与预测值对比 Fig. 5 Comparison between single simulation results and prediction values of ground motion parameters at different magnitudes |
基于GMPE确定各门站Pga后,采用表 1中参数及式(3)、(4)计算各源点的失效概率.
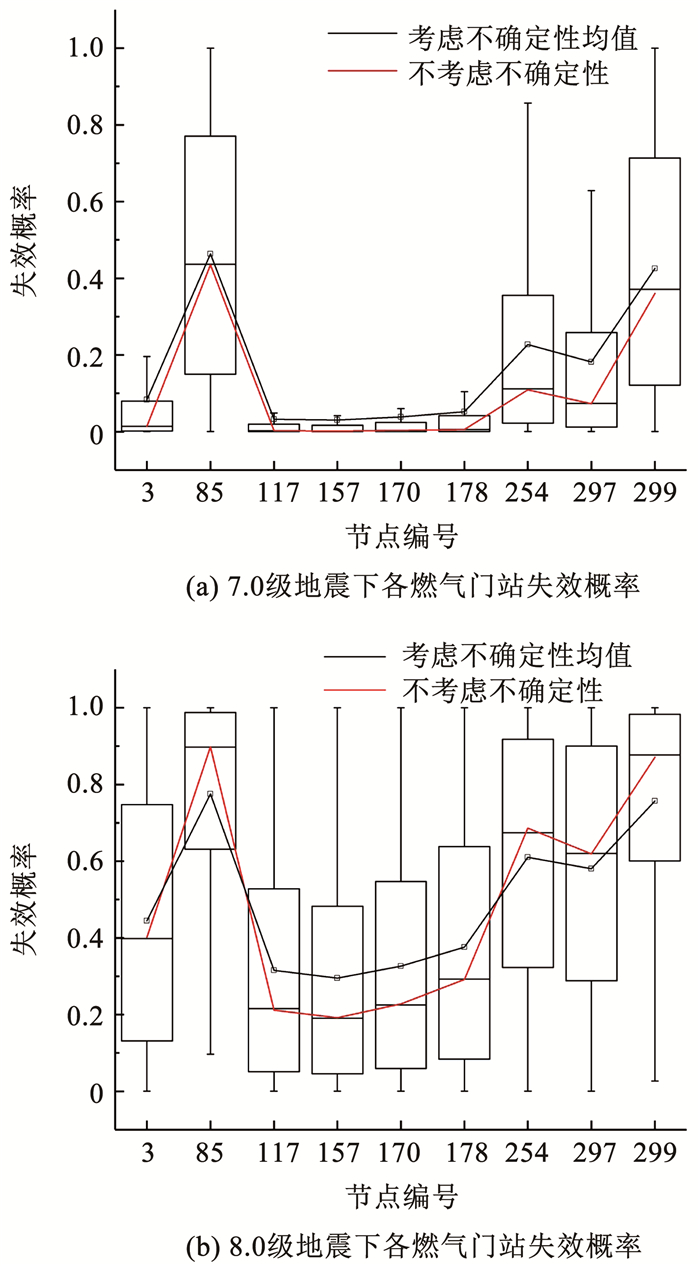
当考虑地震动不确定性时,由于同一点每一次模拟中的地震动强度指标分布情况都是不同的,导致不同模拟中得到的燃气门站失效概率也各不相同.以7.0、8.0级地震为例,计算各源点考虑地震动不确定性后失效概率值的分布箱型图如图 6所示.可以看到7.0级地震下,考虑地震动不确定性时各源点失效概率的均值均大于不考虑不确定性时的失效概率;造成该差异的原因是,由于地震动预测方程中地震动参数服从对数正态分布,所以在考虑GMPE中不确定性时抽样得到的地震动参数样本为偏态分布,其均值与地震动预测方程预测值(中位值)是不同的,这种差异也传递到了最后的计算结果中.在8.0级地震下,由于85,254,297,299节点(其空间分布如图 4所示)失效概率的中位值偏大,导致当Pga大于某值后其失效概率恒为1,故出现均值小于中位值的结果.
|
图 6 7.0、8.0级地震下各燃气门站失效概率 Fig. 6 Failure probability of gas gate stations under earthquake events with magnitudes 7.0 and 8.0 |
国内外均有学者在做燃气管网连通可靠性分析时将燃气管网系统作为边权网络系统,即仅考虑各边失效的可能性[16].由图 6中各燃气门站失效概率分布可知,某些门站失效概率均值也很大.因此无论在进行燃气管网的可靠性,还是易损性分析时,燃气门站的失效概率不可忽略.
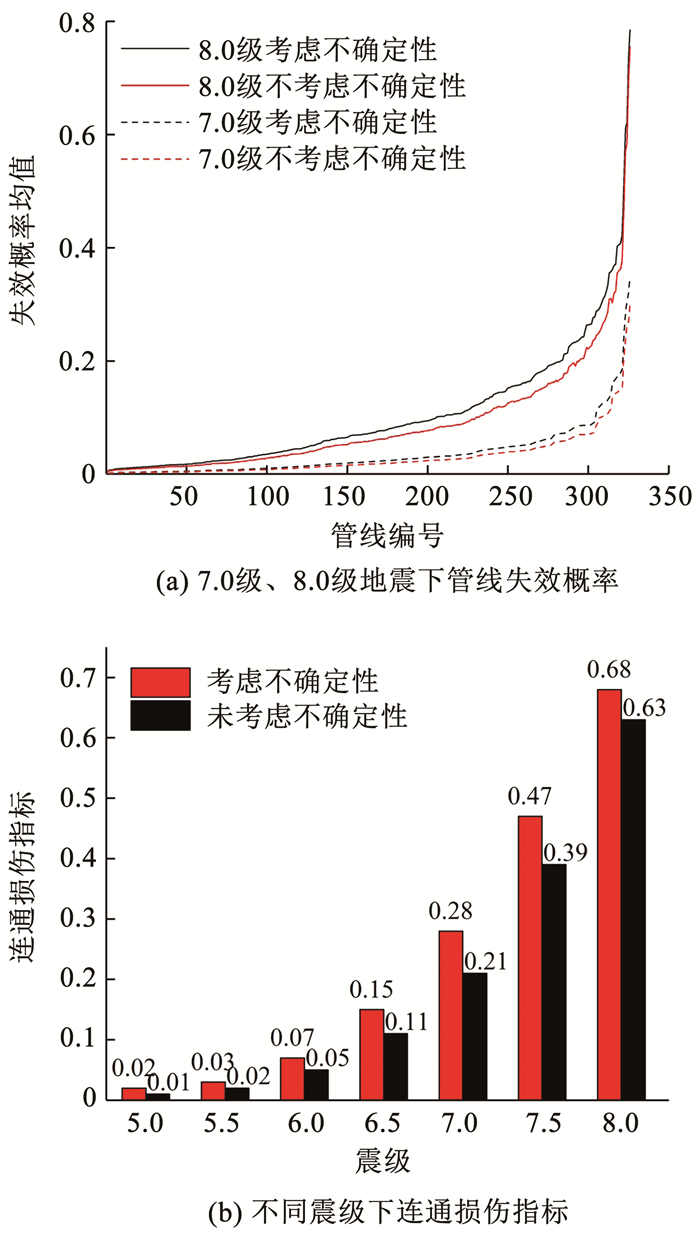
2.3.2 埋地管线失效概率计算埋地管线的失效概率时,式(5)中K1依据文献[12],综合考虑管材、接头形式、场地土、管径等因素分别取0.60与0.15.依据文献[15],建设于2015—2019年的管线β1=1.0,建设于2010—2014年的管线β1=1.1,建设于2010年之前的管线β1=1.2;由该市的地质资料可知,该市A、B区是震陷高发区,故在小于7.0级地震发生时,A、B区的埋地管线在计算失效概率时,修正系数β2=1.2,当发生大于等于7.0级地震时,修正系数β2=1.5;各管线的β3、β4均取值为1.各管线在7.0、8.0级地震发生时,按考虑地震动不确定性时各管线失效概率均值由小到大排列,并与相同管线在不考虑不确定性时的失效概率值相比较,结果如图 7(a)所示.可以看出由于受到Pgv服从对数正态分布影响,在考虑不确定性时各管线的失效概率均值均大于未考虑不确定性时各管线的失效概率.
|
图 7 燃气管线失效概率和不同震级下连通损伤指标 Fig. 7 Gas pipeline failure probability and connection damage index |
不同震级下连通损伤指标结果如图 7(b)所示,由表 2中的破坏等级划分可知,考虑地震动不确定性时,在发生7.0级地震后,该市的燃气管网的连通性能发生轻微破坏,发生8.0级地震时燃气管网的连通性能发生中等破坏.由上述分析可见,本文提出的连通损伤指标可以通过具体数值刻画某市燃气管网在不同震级下连通性的损失程度,可以作为衡量燃气管网的鲁棒性的指标之一,指导管网建设决策,同时为接下来城市燃气管网可恢复性的研究做铺垫,具有较好的工程应用价值.
2.4 燃气管网连通易损性曲线不同震级下,该城市燃气管网的连通性指标CL的超越概率曲线及不同破坏状态的易损性曲线如图 8所示.不同破坏状态下震级均值与标准差见表 4.

|
图 8 城市燃气管网连通易损性计算结果 Fig. 8 Seismic connectivity fragility curves for urban gas network |
| 表 4 不同破坏状态下震级均值与标准差 Tab. 4 Mean and standard deviation of magnitudes under different failure states |
由该计算结果可知,考虑地震动不确定性时,在发生5.0、5.5、6.0级地震后,该市燃气管网连通性能完好的概率为56%、38%、6%. 各震级下,考虑地震动预测方程中不确定性后的该市燃气管网的连通损失超越概率均大于不考虑不确定性时的数值,易损性曲线也反映了在考虑不确定性时,该市燃气管网在不同震级下连通性能超过某破坏状态的概率均偏大.原因在于在考虑某一震级下各地地震动参数的不确定性时,其地震动参数为偏态分布,均值大于中位值,故导致燃气管网中单元的失效概率均值增大,导致整个管网的连通性更易损坏.
3 结论1) 基于地震动预测方程(GMPE)确定燃气管网各位置的地震动强度指标,然后确定燃气管网点状设施、边单元(埋地管道)的失效概率.最后通过蒙特卡罗模拟,统计震后的管网中未通气的节点数量确定反映系统连通性能损失的指标,最后在多个震级下重复该过程,可以得到燃气管网的整体连通易损性曲线.
2) 算例城市在不同震级下的连通损伤指标结果表明,在目标断层位置发生7.0级地震后,该市的燃气管网的连通性能发生轻微破坏,发生8.0级地震时燃气管网的连通性能发生中等破坏.在发生5.0级、5.5级、6.0级地震后,该市燃气管网连通性能完好的概率为56%、38%、6%.
3) 地震动的不确定性对连通性指标CL的超越概率曲线及不同破坏状态的易损性曲线计算结果影响较大.考虑地震动预测方程中不确定性后,该市燃气管网的连通损失超越概率均大于忽视不确定性时的数值,后者可能会低估实际地震下管网连通性能的损失.
| [1] |
丽娃. 埋地天然气管线的地震损伤与易损性评估[D]. 哈尔滨: 哈尔滨工业大学, 2014 INDIRA Y. Seismic damage and fragility assessment of buried gas pipelines[D]. Harbin: Harbin Institute of Technology, 2014 |
| [2] |
李杰, 刘威. 大型城市管网抗震可靠性分析与优化[J]. 地震工程与工程振动, 2006, 26(3): 172. LI Jie, LIU Wei. Large-scale urban network seismic reliability analysis and optimization[J]. Earthquake Engineering and Engineering Vibration, 2006, 26(3): 172. DOI:10.3969/j.issn.1000-1301.2006.03.048 |
| [3] |
POLJANŠEK K, BONO F, GUTIÉRREZ E. Seismic risk assessment of interdependent critical infrastructure systems: The case of European gas and electricity networks[J]. Earthquake Engineering and Structural Dynamics, 2012, 41(1): 61. DOI:10.1002/eqe.1118 |
| [4] |
武百超. 考虑依赖性的生命线网络性态评估方法[D]. 哈尔滨: 哈尔滨工业大学, 2017 WU Baichao. Performance assessment of the lifeline network considering dependencies[D]. Harbin: Harbin Institute of Technology, 2017 |
| [5] |
ESPOSITO S, IERVOLINO I, D'ONOFRIO A, et al. Simulation-based seismic risk assessment of gas distribution networks[J]. Computer-Aided Civil and Infrastructure Engineering, 2015, 30(7): 508. DOI:10.1111/mice.12105 |
| [6] |
刘小坛. 城市供燃气管网系统的抗震可靠性优化[D]. 上海: 同济大学, 2007 LIU Xiaotan. Seismic reliability optimization of urban gas supply network system[D]. Shanghai: Tongji University, 2007 |
| [7] |
李杰. 生命线工程抗震—基础理论与应用[M]. 北京: 科学出版社, 2005: 103. LI Jie. Lifeline aseismic engineering—Basic theory and applications[M]. Beijing: Science Press, 2005: 103. |
| [8] |
霍俊荣. 近场强地面运动衰减规律的研究[D]. 哈尔滨: 中国地震局工程力学研究所, 1989 HUO Junrong. Study on the near-field strong ground motion attenuation relationship[D]. Harbin: Institute of Engineering Mechanic, China Earthquake Administration, 1989 |
| [9] |
高乃辉, 赵鸣, 李素贞, 等. 汶川8.0级地震都江堰市天然气系统震害分析及救灾过程[J]. 灾害学, 2010, 25(3): 71. GAO Naihui, ZHAO Ming, LI Suzhen, et al. Seismic damage investigation and relief procedures of natural gas system in Dujiangyan city in M8. 0 Wenchuan earthquake[J]. Journal of Catastrophology, 2010, 25(3): 71. DOI:10.3969/j.issn.1000-811X.2010.03.015 |
| [10] |
CIMELLARO G P. Urban resilience for emergency response and recovery-fundamental concepts and applications[M]. Cham: Springer International Publishing, 2016: 270. DOI:10.1007/978-3-319-30656-8
|
| [11] |
Federal Emergency Management Agency. HAZUS-MH MR1-ADVANCED: Engineering building module technical and user's manual[R]. Washington DC: FEMA, 2003
|
| [12] |
GEHL P, DESRAMAUT N, RÉVEILLÈRE A, et al. Fragility functions of gas and oil networks[M]//SYNER-G: typology definition and fragility functions for physical elements at seismic risk. Dordrecht: Springer, 2014: 187. DOI: 10.1007/978-94-007-7872-6_7
|
| [13] |
刘爱文, 胡聿贤, 李小军, 等. 大口径埋地钢管在地震断层作用下破坏模式的研究[J]. 工程力学, 2005, 22(3): 82. LIU Aiwen, HU Yuxian, LI Xiaojun, et al. Damage behavior of large-diameter buried steel pipelines under fault movements[J]. Engineering Mechanics, 2005, 22(3): 82. DOI:10.3969/j.issn.1000-4750.2005.03.016 |
| [14] |
刘爱文, 张素灵, 胡聿贤, 等. 地震断层作用下埋地管线的反应分析[J]. 地震工程与工程振动, 2002, 22(2): 22. LIU Aiwen, ZHANG Suling, HU Yuxian, et al. A method for analyzing response of buried pipeline due to earthquake fault movement[J]. Earthquake Engineering and Engineering Vibration, 2002, 22(2): 22. DOI:10.13197/j.eeev.2002.02.004 |
| [15] |
王祥建, 郭恩栋, 于天洋, 等. 基于不同翔实程度数据的燃气管网地震破坏评估方法研究[J]. 地震工程与工程振动, 2018, 38(2): 84. WANG Xiangjian, GUO Endong, YU Tianyang, et al. Study on seismic damage assessment method of gas pipeline network based on the obtained data with different detailed levels[J]. Earthquake Engineering and Engineering Dynamics, 2018, 38(2): 84. DOI:10.13197/j.eeev.2018.02.84.wangxj.010 |
| [16] |
刘威, 李杰. 考虑腐蚀的城市燃气管网抗震可靠度分析[J]. 华中科技大学学报(城市科学版), 2008, 25(4): 138. LIU Wei, LI Jie. Seismic response analysis of urban gas networks considering corrosion[J]. Journal of HUST (Urban Science Edition), 2008, 25(4): 138. DOI:10.3969/j.issn.2095-0985.2008.04.037 |
 2021, Vol. 53
2021, Vol. 53


