准确的动力学模型是获得良好控制效果的前提之一,因此在对实际机器人进行控制实验之前,往往需要进行参数辨识,以减少控制器中理论模型的误差。参数辨识的研究对象大多为机器人操作臂等有根系统[1-3],对系统的Lagrange方程或牛欧方程进行线性化[4-5],可得到如下方程:
| $ \boldsymbol{\tau}=\boldsymbol{Y}(\boldsymbol{q}, \dot{\boldsymbol{q}}, \ddot{\boldsymbol{q}}) \boldsymbol{\varPhi}+\boldsymbol{\tau}_{f} $ | (1) |
式中:τ和τf分别为关节的驱动力矩和摩擦力矩矢量,q为关节角矢量,Y为由关节运动确定的回归矩阵,Φ为由待辨识的基底参数组成的矢量。
根据回归矩阵Y的行列式[6]或条件数[7]对参数辨识时机器人的运动轨迹进行优化,使Φ中的参数得到充分激励,对不同时刻的测量数据进行组合,使用最小二乘法[1-2]或其他优化求解算法[3]对式(1)中的函数进行拟合,即可得到最优的模型参数。
近年来,随着机器人操作臂的参数辨识技术日趋成熟,研究者们将目光转向了包含双足机器人在内的多支链无根系统,一部分研究中直接使用与机器人操作臂相同的方法,将双足机器人的某个杆件固定,对不同的运动学支链单独进行识别。例如He等[8]将仿人机器人的躯干固定,根据关节力矩数据对机器人的手臂惯性参数进行了辨识;熊文英[9]将双足机器人的躯干固定,对大腿和小腿的惯性参数进行了参数辨识;Iwasaki等[10]固定双足机器人的右脚,进行了HRP-2机器人的参数辨识仿真。
上述参数辨识方法无法得到被固定杆件的惯性参数,且辨识结果受关节摩擦的不确定性影响,会产生一定误差。为解决上述问题,Ayusawa等[11]对足式机器人的一般动力学模型[12]进行变形处理,得到参数辨识方程:
| $ \boldsymbol{Y}_{\rm{O}}\left(\boldsymbol{q}_{\rm{O}}, \dot{\boldsymbol{q}}_{\rm{O}}, \ddot{\boldsymbol{q}}_{\rm{O}}\right) \boldsymbol{\varPhi}=\sum\limits_{i=1}^{N_{\mathrm{L}}} \boldsymbol{J}_{i}^{\mathrm{T}} \boldsymbol{F}_{i} $ | (2) |
提出了足式机器人惯性参数辨识的基准杆件方法。其中: qO为由基准杆件位姿矢量qB和机器人关节角矢量q组成的观测矢量,qO=[qBT, qT]T;YO是考虑基准杆件运动的回归矩阵;NL是机器人足的数量;Fi是第i个足的六维力矢量;Ji是第i个足到基准杆件的雅可比矩阵。
对式(2)参数辨识方程使用最小二乘法即可直接得到惯性参数Φ的辨识结果。一些研究者在此基础上进行了进一步研究,2015年Ogawa等[13]将式(1)和式(2)结合进行了TORO仿人机器人的参数辨识实验;Jovic等[14]2015年提出了一种足式机器人参数辨识的激励运动优选方法,考虑杆件惯性参数的实际取值范围,又于2016年提出了一种基于二次规划的分层优化参数辨识方法[15];Bonnet等[16]对参数辨识的激励运动进行参数化建模,提出了一种能使回归矩阵列满秩的激励轨迹优化方法。用该方法进行双足机器人的惯性参数辨识时,需要使用运动捕捉设备采集机器人躯干的运动(对应qB及其导数),并同时记录机器人各关节的运动(对应q及其导数)和每个足上完整的6维力信息(对应Fi),因此难于应用在足底只装有接触力传感器的机器人上。
针对上述问题,本文提出基于足底ZMP的双足机器人惯性参数辨识方法,其优势在于:1)与使用式(1)的参数辨识方法相比;不受关节摩擦阻尼的影响,能够得到精度更高的辨识结果;2)与使用式(2)的参数辨识方法相比,所提出的方法不需要额外的运动捕捉和测力设备,只需要使用机器人自带的接触力传感器就能完成参数辨识。
本文首先基于足底ZMP数据建立双足机器人惯性参数辨识的优化模型;然后,给出求解此最优参数的算法;最后,对GoRoBoT-II机器人的双足部分进行参数辨识实验,对比所提出的方法和基于关节力矩的参数辨识方法(式(1))的结果。
1 基于ZMP数据的参数辨识模型 1.1 双足机器人的通用模型如图 1为双足机器人的通用模型,其中忽略了机器人的具体机构,仅考虑机器人的质心、足底支撑区以及构成本体的n个杆件(图中仅画出了第i个杆件),且在本文后续的推导中,认为足底支撑区与地面不滑移。ΣO-xyz是与地面固连的基坐标系,将机器人各杆件的重力和惯性力向质心C简化,得到的合力与合力矩矢量分别以F和M表示。将双足机器人的关节角表示为θj(j=1, 2, …, n-1),则可定义关节角矢量q=[θ1, θ2, …, θn-1]T,机器人的运动状态矢量可用

|
图 1 双足机器人的一般模型 Fig. 1 General model of biped robot |
机器人第i个杆件的质心为Ci,杆件坐标系设为ΣOi-xiyizi,杆件i的惯性参数共有10个,包括:杆件质量mi,杆件系内的质心位置坐标xi、yi、zi,杆件的惯性矩Ixxi、Iyyi、Izzi、Ixyi、Ixzi、Iyzi,上述参数可被写成参数矢量Φi(i=1, 2, …, n)的形式:
| $ \boldsymbol{\varPhi}_{i}=\left[\begin{array}{llllllllll} m_{i} & x_{i} & y_{i} & z_{i} & I_{xxi} & I_{yyi} & I_{zzi} & I_{x y i} & I_{xzi} & I_{y z i} \end{array}\right]^{\mathrm{T}} $ | (3) |
将各杆件的参数矢量进行组合,可得到机器人的总体参数矢量:
| $ \boldsymbol{\varPhi}=\left[\begin{array}{llll} \boldsymbol{\varPhi}_{1}^{\mathrm{T}} & \boldsymbol{\varPhi}_{2}^{\mathrm{T}} & \cdots & \boldsymbol{\varPhi}_{n}^{\mathrm{T}} \end{array}\right]^{\mathrm{T}} $ | (4) |
其中共含10n个惯性参数。根据机器人系统的动力学模型,ZMP的理论位置坐标(x’, y’)为
| $ \left\{\begin{array}{l} x^{\prime}=x_{C}-\left(F_{X} z_{C}+M_{Y}\right) / F_{Z} \\ y^{\prime}=y_{C}-\left(F_{Y} z_{C}-M_{X}\right) / F_{Z} \end{array}\right. $ | (5) |
| $ \begin{aligned} \boldsymbol{P}_{C}=&\left[\begin{array}{lll} x_{C} & y_{C} & z_{C} \end{array}\right]^{\mathrm{T}}=\sum\limits_{i=1}^{n} m_{i} \boldsymbol{P}_{C i} / M=\\ & \sum\limits_{i=1}^{n} m_{i}\left(\boldsymbol{P}_{i}+\boldsymbol{R}_{i} \boldsymbol{p}_{C i}\right) / M \end{aligned} $ | (6) |
其中,xC、yC、zC是质心的位置坐标,FX、FY、FZ是质心处惯性力的三轴分量,且
| $ \boldsymbol{F}=\left[\begin{array}{lll} F_{X} & F_{Y} & F_{Z} \end{array}\right]^{\mathrm{T}}=\sum\limits_{i=1}^{n} m_{i}\left(\boldsymbol{g}-\boldsymbol{a}_{C i}\right) $ | (7) |
MX、MY分别是质心处惯性力矩的x轴、y轴分量,
| $ \boldsymbol{M}=\left[\begin{array}{lll} M_{X} & M_{Y} & M_{Z} \end{array}\right]^{\mathrm{T}}=-\sum\limits_{j=1}^{n} m_{j}\left(\boldsymbol{P}_{C j}-\boldsymbol{P}_{C}\right) \times \boldsymbol{a}_{C j} $ | (8) |
式中:M为测得的机器人总质量;PCi和aCi分别为杆件i的质心在基坐标系内的位置和加速度矢量;pCi为杆件i的质心在第i个杆件坐标系内的位置矢量,pCi=[xi, yi, zi]T;Pi和Ri分别为ΣOi系在基坐标系内的位置矢量和旋转矩阵;g为重力加速度矢量。
1.2 参数辨识建模参数辨识的基本思想是通过修改参数标称值,使理论计算和实测的物理量偏差最小。这里将ZMP的理论坐标(x′, y′)表示成运动状态矢量S和参数矢量Φ的函数,可定义如下的ZMP偏差函数:
| $ e(\boldsymbol{S})=\sum\limits_{j=1}^{N}\left[x^{\prime}\left(\boldsymbol{S}_{j}, \boldsymbol{\varPhi}\right)-x_{j}\right]^{2}+\left[y^{\prime}\left(\boldsymbol{S}_{j}, \boldsymbol{\varPhi}\right)-y_{j}\right]^{2} $ | (9) |
式中:Sj为第j个采样周期测得的S矢量,xj、yj分别为第j个采样周期测得的ZMP位置x轴和y轴坐标,N为参数辨识过程中的采样周期总数。
参数识别的优化模型可被表示为
| $ \begin{array}{c} \boldsymbol{\varPhi}^{*}=\arg \min e(\boldsymbol{\varPhi}) \\ \text { s.t. } \quad \boldsymbol{\varPhi}_{\min } \leqslant \boldsymbol{\varPhi} \leqslant \boldsymbol{\varPhi}_{\max } \\ \boldsymbol{c} \cdot \boldsymbol{\varPhi}=M \end{array} $ | (10) |
式中Φ*为最优参数矢量;Φmin和Φmax分别是由各参数下限和上限组成的矢量;c为质量约束矢量,c=[b1T, b2T, …, bnT]T,其中bi(i=1, 2…, n)均是只有第一个元素为1其余元素均为0的10维矢量。
在式(10)的优化模型中,第二个约束条件的物理含义为按参数标称值计算的机器人总质量应等于事先测量的值M。
2 参数辨识优化模型的求解算法由于式(5)中ZMP的理论位置坐标(x′, y′)无法写成像式(1)或式(2)那样的关于参数矢量Φ的线性形式,因此不能使用最小二乘法进行求解,这里考虑c∙Φ=M的等式约束,使用如下的迭代法对式(10)中的优化模型进行求解:
| $ \boldsymbol{\varPhi}^{(k)}=\boldsymbol{\varPhi}^{(k-1)}+\left[\boldsymbol{E}-\boldsymbol{c}\left(\boldsymbol{c}^{\mathrm{T}} \boldsymbol{c}\right)^{-1} \boldsymbol{c}^{\mathrm{T}}\right] \Delta \boldsymbol{\varPhi} $ | (11) |
式中上标(k)表示迭代的步数,E为与Φ同阶的单位矩阵,ΔΦ是每次迭代的参数增量矢量。
一般情况下,增量ΔΦ按牛顿迭代法确定,
| $ \Delta \boldsymbol{\varPhi}=-\boldsymbol{H}^{-1} \boldsymbol{G} $ | (12) |
其中G和H分别为误差函数e的梯度矢量和海塞矩阵。当海塞矩阵H奇异时,使用式(13)所示的最速下降法求解ΔΦ,
| $ \Delta \boldsymbol{\varPhi}=-\alpha \boldsymbol{G} $ | (13) |
其中α为学习率(α>0)。上述迭代过程的收敛条件可表示为
| $ \|\Delta \boldsymbol{\varPhi}\| \leqslant \varepsilon $ | (14) |
其中,ε为预设的误差限。综合式(11)~(14),图 2给出了上述优化模型求解算法的具体计算流程。

|
图 2 参数辨识模型的求解算法流程图 Fig. 2 Flowchart for solving the parameter identification model |
上述算法中的海塞矩阵H和梯度矢量G分别为
| $ \begin{array}{l} \boldsymbol{H}=\frac{\partial^{2} e}{\partial \boldsymbol{\varPhi}^{2}}=2 \sum\limits_{i=1}^{N}\left\{\frac{\partial^{2} x_{j}^{\prime}}{\partial \boldsymbol{\varPhi}^{2}}\left[x_{j}^{\prime}-x_{j}\right]+\frac{\partial^{2} y_{j}^{\prime}}{\partial \boldsymbol{\varPhi}^{2}}\left[y_{j}^{\prime}-y_{j}\right]+\right. \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left.\left[\frac{\partial x_{j}^{\prime}}{\partial \boldsymbol{\varPhi}}\right]\left[\frac{\partial x_{j}^{\prime}}{\partial \boldsymbol{\varPhi}}\right]^{\mathrm{T}}+\left[\frac{\partial y_{j}^{\prime}}{\partial \boldsymbol{\varPhi}}\right]\left[\frac{\partial y_{j}^{\prime}}{\partial \boldsymbol{\varPhi}}\right]^{\mathrm{T}}\right\} \end{array} $ | (15) |
| $ \boldsymbol{G}=\frac{\partial e}{\partial \boldsymbol{\varPhi}}=2 \sum\limits_{j=1}^{N}\left\{\frac{\partial x_{j}^{\prime}}{\partial \boldsymbol{\varPhi}}\left(x_{j}^{\prime}-x_{j}\right)+\frac{\partial y_{j}^{\prime}}{\partial \boldsymbol{\varPhi}}\left(y_{j}^{\prime}-y_{j}\right)\right\} $ | (16) |
其中xj′=x′(Sj, Φ),y′j=x′(Sj, Φ),x′和y′关于Φ的一阶偏导为:
| $ \frac{\partial x^{\prime}}{\partial \boldsymbol{\varPhi}}=\dot{x}_{C}-\frac{\dot{F}_{X} z_{C}+F_{X} \dot{z}_{C}+\dot{M}_{Y}}{F_{Z}}+\frac{F_{X} z_{C}+M_{Y}}{F_{Z}^{2}} \dot{F}_{Z} $ | (17) |
| $ \frac{\partial y^{\prime}}{\partial \boldsymbol{\varPhi}}={\dot y}_{C}-\frac{\dot{F}_{Y} z_{C}+F_{Y} \dot{z}_{C}-\dot{M}_{X}}{F_{Z}}+\frac{F_{Y} z_{C}-M_{X}}{F_{Z}^{2}}{\dot{F}}_{Z} $ | (18) |
式中
x′和y′关于Φ的二阶偏导为
| $ \begin{aligned} \frac{\partial^{2} x^{\prime}}{\partial \boldsymbol{\varPhi}^{2}}=& \ddot{x}_{C}-\frac{\ddot{F}_{X} z_{C}+\dot{F}_{X} \dot{z}_{C}^{\mathrm{T}}+\dot{z}_{C} \dot{F}_{X}^{\mathrm{T}}+F_{X} \ddot{z}_{C}+\ddot{M}_{Y}}{F_{Z}}+\\ &\left(\ddot{F}_{Z}-2 \dot{F}_{Z} \dot{F}_{Z}^{\mathrm{T}} / F_{Z}\right)\left(F_{X} z_{C}+M_{Y}\right) / F_{Z}^{2}+\\ &\left(\dot{F}_{X} z_{C}+F_{X} \dot{z}_{C}+\dot{M}_{Y}\right) \dot{F}_{Z}^{\mathrm{T}} / F_{Z}^{2}+\\ & \dot{F}_{Z}\left(\dot{F}_{X} z_{C}+F_{X} \dot{z}_{C}+\dot{M}_{Y}\right)^{\mathrm{T}} / F_{Z}^{2}. \end{aligned} $ | (19) |
| $ \begin{aligned} \frac{\partial^{2} y^{\prime}}{\partial \boldsymbol{\varPhi}^{2}}=& \ddot{y}_{C}-\frac{\ddot{F}_{Y} z_{C}+\dot{F}_{Y} \dot{z}_{C}^{\mathrm{T}}+\dot{z}_{C} \dot{F}_{Y}^{\mathrm{T}}+F_{Y} \ddot{z}_{C}-\ddot{M}_{X}}{F_{Z}}+\\ &\left(\ddot{F}_{Z}-2 \dot{F}_{Z} \dot{F}_{Z}^{\mathrm{T}} / F_{Z}\right) F_{Y} z_{C}-M_{X} / F_{Z}^{2}+\\ &\left(\dot{F}_{Y} z_{C}+F_{Y} \dot{z}_{C}-\dot{M}_{X}\right) \dot{F}_{Z}^{\mathrm{T}} / F_{Z}^{2}+\\ & \dot{F}_{Z}\left(\dot{F}_{Y} z_{C}+F_{Y} \dot{z}_{C}-\dot{M}_{X}\right)^{\mathrm{T}} / F_{Z}^{2}. \end{aligned} $ | (20) |
式中:
本文中待参数辨识的机器人是作者所在研究室自行研制的GoRoBoT-II型类人猿机器人的双足部分,该机器人的左右两腿完全对称,图 3给出了其照片、机构简图、以及脚部拆解后的照片。

|
图 3 GoRoBoT-II机器人双足部分的照片和机构简图 Fig. 3 Photo and mechanism of biped part of GoRoBoT-II robot |
上述机器人的左右两腿各有6个转动关节,关节角分别表示为θLi和θRi(i=1, 2, …, 6),每只脚掌的四角分别嵌入压力传感器,测量机器人与地面接触的法向力,用于计算机器人的ZMP位置。图 3(b)中m0、m1、m2、m3分别是躯干、大腿、小腿、脚掌杆件的质量,lc0、lc1、lc2、lc3分别是上述4种杆件的质心位置参数,图 3(b)中标出的其他参数均是机器人的机构参数,其测量值由表 1给出。
| 表 1 GoRoBoT-II双足机器人的机构参数 Tab. 1 Mechanism parameters of GoRoBoT-II biped robot |
如图 4所示,本文所使用的GoRoBoT-II型机器人采用上位机+IPM-100运动控制板卡进行关节位置伺服控制,上位机的运动控制指令通过RS-485网络发送到驱动和控制各关节电机的IPM-100板卡上,上位机的指令周期为50 ms,IPM-100板卡内的位置伺服控制周期为1 ms。
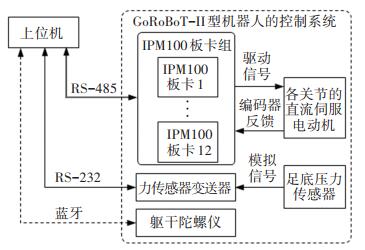
|
图 4 GoRoBoT-II型双足机器人的控制系统硬件框图 Fig. 4 Control system hardware diagram of GoRoBoT-II biped robot |
考虑机器人的实际情况,从以下3个方面对第1节中定义的惯性参数矢量Φ进行了简化:
1) 机器人左右两腿对应杆件相同,因此待辨识的杆件只有4种,即脚掌、小腿、大腿、躯干;2)由于各杆件均是形状大体规则的长方体,这里忽略了其质心与杆长方向相垂直的偏移量;3)由于激励运动需考虑双足机器人的平衡问题,机器人运动速度一般不快,杆件惯性矩参数Ixx、Iyy、Izz、Ixy、Ixz、Iyz不能得到充分激励,因此这些参数的值将由三维几何建模的结果进行近似。
经简化,待识别的机器人惯性参数矢量为Φ=[lc0, lc1, lc2, lc3, m0, m1, m2, m3]T,分别包含躯干、大腿、小腿、脚掌4种杆件的质心位置和质量。
3.2 参数辨识的实验过程在对图 3所示的机器人进行参数辨识实验时,首先令机器人在单脚站立状态下做限幅随机运动,运动样本由文献[17]中提出的方法按随机的参考ZMP轨迹规划得到。实验过程中以50 ms为周期实时采集传感器数据,共进行5次时长约为95 s的实验,其中1次实验录像的截图如图 5所示。

|
图 5 一次参数辨识实验的视频截图 Fig. 5 Screenshots of parameter identification experiment |
由图 5可见,机器人首先向支撑脚(右脚)偏移质心并抬起左脚,之后左脚在空中进行目标位置随机的平移运动,右腿负责保持机器人平衡,使机器人实际ZMP追踪随机的参考ZMP,如此在保证机器人平衡的基础上,各关节的角度、角速度、角加速度均呈现连续变化的随机波动。
3.3 数据采集结果参数辨识计算需要以下3类数据:
1) 机器人的关节角。由各关节的伺服电机编码器反馈和关节减速比算得,再通过差分运算得到各关节的角速度和角加速度;2)机器人的关节力矩。由各关节伺服电机的电流计算电机转矩,根据关节减速比计算关节力矩;3)足底ZMP。根据安装在机器人脚底的接触力传感器反馈,经惯性滤波得到ZMP位置。
图 6给出了一次实验中机器人支撑腿和游腿的关节角曲线,由于实验过程中机器人的髋关节立转自由度始终处于保持力矩状态,静止不动,因此图 6中没有给出髋关节立转角的曲线。
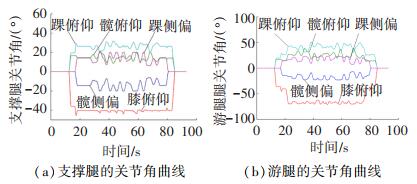
|
图 6 一次参数辨识实验中的机器人关节角曲线 Fig. 6 Joint angle curves in parameter identification experiment |
图 7给出了一次实验中支撑脚4个压力传感器采集的原始接触力曲线,可知压力原始数据中含有高频扰动信号,不能直接用于参数辨识计算。
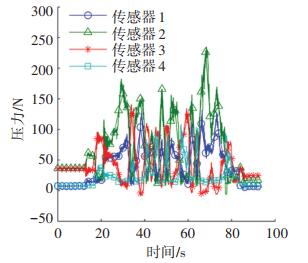
|
图 7 一次实验中机器人足底压力传感器原始数据曲线 Fig. 7 Raw data curves of contact force sensors obtained in parameter identification experiment |
使用上述接触力数据计算ZMP位置,得到的x轴(前后向)、y轴(侧向)坐标曲线如图 8所示。
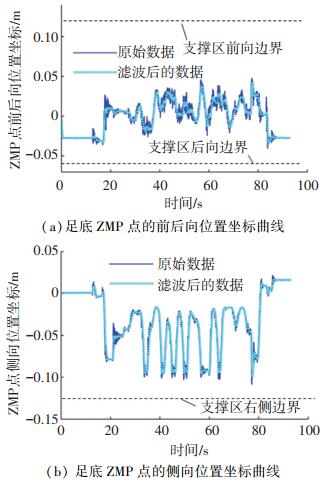
|
图 8 一次参数识别实验得到的足底ZMP位置坐标曲线 Fig. 8 ZMP curves in parameter identification experiment |
由图 8可知,经惯性滤波后ZMP坐标的高频波动显著减小,且曲线滞后不明显,因此后续的参数辨识计算将使用滤波后的ZMP位置数据。
图 9(a)、(b)分别给出了一次实验中机器人支撑腿和游腿的关节力矩曲线,可以看到,实验过程中机器人各关节的转矩呈现随机波动的变化规律,由于游腿的脚掌地面始终与支撑面平行(见图 5),因此游腿脚踝侧偏关节的力矩始终较小。
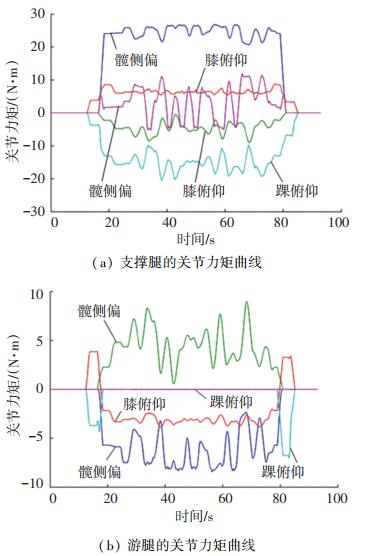
|
图 9 一次参数识别实验得到的关节力矩曲线 Fig. 9 Joint torque curves in parameter identification experiment |
用第3节获得的实验数据,按第2节给出的参数辨识求解算法计算最优参数。求解过程中的学习率α由试错过程确定,初始值设为1,即按照100%的梯度矢量确定参数矢量Φ的调整量,然后逐渐减小α的值,直到连续的3次计算均能收敛于相同结果,此时认为参数辨识算法达到了稳定收敛的结果,在本文中算法稳定收敛对应的α值为0.02;确定参数矢量增量的阈值ε时,考虑到长度参数和质量参数分别辨识到0.1 mm和0.1 g的精度即能满足控制要求,因此将ε设为1×10-4。图 10给出了对一次实验数据进行计算得到的误差函数(见式(9))和收敛指标(见式(14)),收敛于第121次迭代。
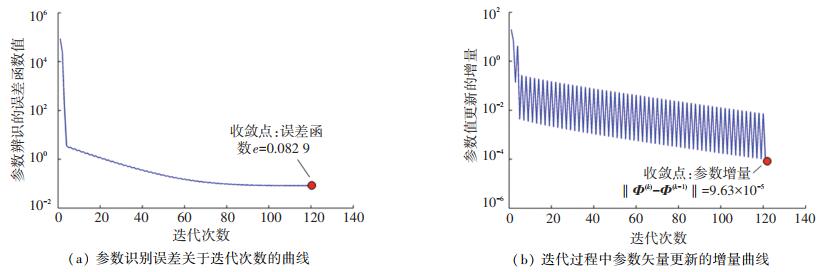
|
图 10 参数辨识计算过程中误差函数曲线和参数增量曲线 Fig. 10 Error and parameter increment curves in identification calculation process |
用机器人的关节力矩进行了参数辨识计算,计算过程中将机器人的支撑脚作为固定不动的杆件,具体计算方法已在文献[8-10]中给出,这里不详细展开。表 2分别给出了基于ZMP和基于关节力矩的参数辨识结果。包括5次实验数据分别计算得到的参数均值和标准差,以及由三维几何建模得到的参数标称值。
| 表 2 GoRoBoT-II双足机器人的参数识别结果 Tab. 2 Parameter identification results of GoRoBoT-II robot |
一般情况下,参数标称值的误差由加工装配误差、软管配线等无法在三维几何建模中体现的因素引起,因此参数标称值与真值的差距不会很大。由表 2数据可见,基于ZMP的辨识结果更接近三维几何建模得到的参数标称值,且除去参数m0,基于ZMP的辨识方法在其他7个参数上均得到了比传统方法更小的标准差,说明基于ZMP的参数辨识方法得到的结果好于基于关节力矩的参数辨识结果。
表 2中参数m3的辨识结果与三维几何建模的参数标称值偏差较大,是由于m3对应的脚掌杆件处配线相对集中(有2个电机和4个力传感器的线缆),对机器人杆件的牵拉作用更强,且所进行的激励运动中支撑脚的脚掌与地面始终相对静止,激励效果弱于其他杆件,因辨识结果的偏差较大。
为进一步比较两种方法所得结果的优劣,在与第3节相同的条件下,单独进行了一次机器人的随机运动实验,并记录机器人的关节运动数据和ZMP位置,将表 2中给出的参数均值和新得到的运动数据代入机器人的动力学模型,计算了理论ZMP的位置坐标,图 11中给出了不同参数值对应的理论ZMP与实验测得的ZMP的距离偏差曲线,其中的水平虚线是不同曲线对应的ZMP偏差均值线,还标出了各曲线的偏差均值。

|
图 11 不同参数取值下的理论ZMP与实际ZMP偏差 Fig. 11 Deviation between theoretical ZMP and actual ZMP under different parameter values |
由图 11可知,参数标称值ZMP偏差最大,平均为33.8 mm;基于ZMP的参数辨识结果的平均ZMP偏差为4.6 mm,好于基于关节力矩的参数辨识结果的12.4 mm,说明了所提出的基于ZMP的双足机器人惯性参数辨识方法的有效性。
5 结论本文仅依靠双足机器人自带的传感器,提出了基于足底ZMP数据的机器人惯性参数辨识方法,并在研究室自主研制的GoRoBoT-II型机器人上进行了惯性参数辨识的实验研究,主要结论如下:
1) 建立了基于ZMP数据的参数辨识优化模型,并推导了目标函数的梯度矢量和海塞矩阵,使用最速下降法和牛顿法解决了非线性的参数辨识模型的优化求解问题。
2) 使用GoRoBoT-II型机器人进行了双腿的惯性参数辨识实验,实验结果表明:与传统的基于关节力矩的辨识方法相比,所提出的参数辨识方法能够得到更接近于参数标称值的辨识结果,在实验中将将理论ZMP与实际ZMP的平均偏差由12.4 mm降低到了4.6 mm,使平均ZMP偏差缩小了62.9%,得到了更为准确的机器人惯性参数辨识结果。
综上,本文所提出的基于ZMP的参数辨识方法容易实现,且相对于传统的方法能进一步获得更准确的辨识结果,为双足机器人的平衡控制提供了更准确的动力学模型参数。
| [1] |
李永泉, 吴鹏涛, 张阳, 等. 球面二自由度冗余驱动并联机器人系统动力学参数辨识及控制[J]. 中国机械工程, 2019, 30(16): 1967. LI Yongquan, WU Pengtao, ZHANG Yang, et al. Dynamics parameter identification and control of a spherical 2-DOF redundant driven parallel robot system[J]. China Mechanical Engineering, 2019, 30(16): 1967. DOI:10.3969/j.issn.1004-132X.2019.016.011 |
| [2] |
潘炳伟, 吕燕, 蒋劲峰, 等. 协作机器人动力学参数辨识方法研究[J]. 上海电气技术, 2019, 12(4): 1. PAN Bingwei, LV Yan, JIANG Jinfeng, et al. Research on dynamic parameters identification of collaborative robot[J]. Shanghai Electric Technology, 2019, 12(4): 1. |
| [3] |
席万强, 陈柏, 丁力, 等. 考虑非线性摩擦模型的机器人动力学参数辨识[J]. 农业机械学报, 2017, 48(2): 393. XI Wanqiang, CHEN Bai, DING Li, et al. Dynamic parameter identification for robot manipulators with nonlinear friction model[J]. Transactions of the Chinese Society of Agricultural Machinery, 2017, 48(2): 393. DOI:10.6041/j.issn.1000-1298.-2017.02.053 |
| [4] |
GAUTIER M, KHALIL W. On the identification of the inertial parameters of robots [C]// 27th IEEE Conference on Decision and Control. Piscataway: IEEE, 1988: 1682. DOI: 10.1109/CDC.1988.194738
|
| [5] |
FISETTE P, RAUCENT B, SAMIN J C. Minimal dynamic characterization of tree-like multibody systems[J]. Nonlinear Dynamics, 1996, 9: 165. DOI:10.1007/BF01833299 |
| [6] |
SWEVERS J, GANSEMAN C, TUKEL D B, et al. Optimal robot excitation and identification[J]. IEEE Transactions on Robotics and Automation, 1997, 13(5): 730. DOI:10.1109/70.631234 |
| [7] |
HAN Y, WU J, LIU C, et al. Static model analysis and identification for serial articulated manipulators[J]. Robotics & Computer Integrated Manufacturing, 2019, 57: 155. DOI:10.1016/j.rcim.2018.11.010 |
| [8] |
HE W, GE W, LI Y, et al. Model identification and control design for a humanoid robot[J]. IEEE Transactions on Systems Man & Cybernetics Systems, 2017, 47(1): 45. DOI:10.1109/TS-MC.2016.2557227 |
| [9] |
熊文英. 下肢外骨骼机器人系统参数辨识与控制器设计[D]. 成都: 电子科技大学, 2020 XIONG Wenying. Parameter identification and controller design of lower limb exoskeleton robot system[D]. Chengdu: University of Electronic Science and Technology of China, 2020 |
| [10] |
IWASAKI T, VENTURE G, YOSHIDA E. Identification of the inertial parameters of a humanoid robot using grounded sole link [C]//2012 12th IEEE-RAS International Conference on Humanoid Robots (Humanoids 2012). Piscataway: IEEE, 2012: 449. DOI: 10.1109/HUMANOIDS.2012.6651558.
|
| [11] |
AYUSAWA K, VENTURE G, NAKAMURA Y. Identifiability and identification of inertial parameters using the underactuated base-link dynamics for legged multibody systems[J]. International Journal of Robotics Research, 2013, 33(3): 446. DOI:10.1177/0278364913495932 |
| [12] |
FUJIMOTO Y, OBATA S, KAWAMURA A. Robust biped walking with active interaction control between foot and ground [C]// 1998 IEEE International Conference on Robotics and Automation. Piscataway: IEEE, 1998: 2030. DOI: 10.1109/ROBOT.1998.680613
|
| [13] |
OGAWA Y, VENTURE G, OTT C. Dynamic parameters identification of a humanoid robot using joint torque sensors and/or contact forces[C]// 2014 IEEE-RAS International Conference on Humanoid Robots. Piscataway: IEEE, 2014: 457. DOI: 10.1109/HUMANOIDS.2014.7041401
|
| [14] |
JOVIC J, PHILIPP F, ESCANDE A, et al. Identification of dynamics of humanoids: Systematic exciting motion generation [C]//IEEE/RSJ International Conference on Intelligent Robots & Systems. Piscataway: IEEE, 2015: 2173. DOI: 10.1109/HUMANOIDS.2014.7041401
|
| [15] |
JOVIC J, ESCANDE A, AYUSAWA K, et al. Humanoid and human inertia parameter identification using hierarchical optimization[J]. IEEE Transactions on Robotics, 2016, 32(3): 726. DOI:10.1109/TRO.2016.2558190 |
| [16] |
BONNET V, FRAISSE P, CROSNIER A, et al. Optimal exciting dance for identifying inertial parameters of an anthropomorphic structure[J]. IEEE Transactions on Robotics, 2016, 32(4): 823. DOI:10.1109/TRO.2016.2583062 |
| [17] |
吴伟国, 侯月阳, 姚世斌. 基于弹簧小车模型和预观控制的双足快速步行研究[J]. 机械设计, 2010, 27(4): 84. WU Weiguo, HOU Yueyang, YAO Shibin. Research on biped fast walking based on spring-car model and preview control[J]. Journal of Machine Design, 2010, 27(4): 84. |
 2021, Vol. 53
2021, Vol. 53


