2. 航空气动声学工信部重点实验室(北京航空航天大学),北京 100191
2. Key Lab of Aero-Acoustics Ministry of Industry and Information Technology (Beihang University), Beijing 100191, China
随着航空技术的发展,未来战场对战斗机的过失速机动提出了更高的要求,后掠翼布局(单三角翼,双三角翼和鸭式布局)由于能在大迎角下产生稳定的前缘涡升力而受到越来越多的重视[1-3]。与其他后掠翼布局相比,鸭式布局在静态条件下通过借助鸭翼涡与主翼涡之间的有利干扰能明显推迟主翼的失速迎角并获得更大的最大升力系数[4]。近些年,高速计算机的问世和数值模拟技术的成功应用,使得人们对探究更为复杂的鸭式布局瞬态机动问题成为了可能。
当飞机进行过失速机动飞行时,机体表面的气动力与周围的流场均与同等迎角下的静态工况明显不同,存在着大量的气动迟滞行为,但此类研究目前主要集中于单三角翼[5-10]。Gad-el-hak等[5]借助染色液显示技术研究了三角翼俯仰运动中的空间流场,发现染色液的厚度大小随着模型的运动呈现明显的迟滞现象。Lemay等[6]通过烟雾示踪实验研究了三角翼俯仰振荡中的前缘涡破裂现象,发现破裂点的位置与缩减频率有关,频率越高,涡破裂的滞后效应越强。Soltani等[7]开展了三角翼俯仰运动的动态测力实验,指出引起气动力产生迟滞的根本原因来自于俯仰振荡中的涡破裂滞后。Ericsson[8]利用运动产生的虚拟弯度效应分析了动态俯仰中三角翼涡破裂位置的滞后现象。Gursul[9-10]总结了前人的研究成果,指出对于不同形式的三角翼非定常运动,涡破裂的延迟响应都是一致的,并利用涡流动的波传播理论进行了统一解释。与三角翼的研究内容相比,人们对鸭式布局的研究仍主要集中在静态的气动特性方面[11-15],而对动态特性的认识较少[16-17]。Oelker和Hummel等[11-12]开展了鸭式布局的表面测压与流场测量实验,发现鸭翼涡在往下游对流的过程中会运动到主翼的内侧并靠近主翼翼面,同时鸭翼涡对主翼前缘尖点处的下洗作用能明显抑制该处主翼涡的形成。Tu[13-14]数值分析了鸭式布局的静态流场特征,指出鸭翼涡的存在能明显推迟主翼涡的失速迎角; 还讨论了不同鸭翼高度对鸭式布局静态气动特性的影响,发现高置与中置鸭翼对鸭翼涡与主翼涡的干扰会带来有利的影响,而低置鸭翼会起到不利的作用。Bergmann等[15]通过表面测压和流显实验分析了鸭翼位置对鸭式布局气动特性的影响,认为大迎角下主翼涡对鸭翼涡尾流的加速效应使得高置鸭翼的鸭式布局具有更高的最大升力系数[15]。相比鸭式布局的静态研究结果,人们对其动态特性认识有限[16-17]。Myose等[16]实验研究了鸭式布局俯仰运动中的涡破裂现象,相比静态测量结果,动态俯仰中主翼涡的破裂位置发生了明显的滞后,且最有利的滞后发生在模型的高频上仰与低频下俯阶段。Davari等[17]对鸭式布局的俯仰运动过程开展了大量的风洞测压和测力实验,发现鸭式布局的表面压力与气动力同样存在着迟滞现象,且迟滞环的尺寸大小与模型俯仰频率和平均迎角有关。
文献[16]和[17]中鸭式布局的鸭翼与主翼是共面的,而对于实际应用中的鸭式布局(如法国阵风、瑞典鹰狮和中国歼10等),鸭翼与主翼之间往往存在一定的高度差。早期的静态研究结果表明, 鸭翼高度能明显影响鸭式布局的纵向气动特性[14-15]。当模型进行非定常俯仰振荡时,为揭示鸭翼高度对模型表面气动力与空间涡系演化的影响,本文开展了相关的水槽实验测力与CFD数值模拟研究。
1 实验及计算 1.1 实验设备、模型及方法实验在北京航空航天大学航空气动声学工信部重点实验室的回流水槽中进行[18]。该水槽是一座低湍流度、低噪声的直流式水槽,实验段尺寸4 000 mm(长)×400 mm(宽)×525 mm(高),能提供0~0.5 m/s的稳定流速,实验段的湍流度小于来流速度的1%。实验模型采用厚度为3 mm的铝合金制式的半模鸭式布局(鸭翼后掠角Λc = 45°,根弦长cc =80 mm,主翼后掠角Λ=40°,根弦长cw=155 mm),在模型的鸭翼与主翼前后缘进行双边45°对称倒角处理。实验中水槽的平均流速为U∞=0.162 m/s,水温为20 ℃,基于主翼根弦长的来流雷诺数Rec = ρU∞cw/μ=2.5×104。实验中,为削弱水槽自由液面对动态测力的影响,在模型根弦长处采用端板机构以模拟对称面边界条件,如图 1所示。
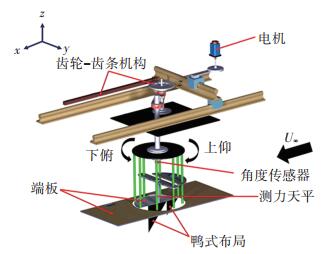
|
图 1 回流水槽动态俯仰机构示意图 Fig. 1 Schematic of dynamic pitching rig of closed-loop water tunnel |
实验模型的俯仰运动由预先设计的大振幅高频俯仰机构控制(图 1),在该机构的控制下,模型可实现0到60°迎角范围的正弦俯仰运动,关于该机构的详细介绍见文献[19]。在实验过程中,转轴位于2/3倍主翼根弦长处,俯仰频率f取0.012 5 Hz与0.200 0 Hz,对应的无量纲缩减频率k=πfcw/U∞为0.037 5与0.600 0,分别代表典型的准定常与非定常运动频率[20]。角度传感器固连于旋转机构上,用于记录模型俯仰运动中的瞬时迎角;测力天平安装在模型主翼的上方,用于测量鸭式布局俯仰运动中的主翼气动力。实验测力的最终值取为连续正弦俯仰50个周期的瞬时结果的相位平均值。另外,为研究鸭翼高度(g/cw,其中g为鸭翼距主翼的垂向高度)的影响,本文选取5个不同鸭翼位置进行实验研究,见图 2。其中,低置鸭翼工况为g/cw = -0.15和-0.05;共面鸭翼工况为g/cw = 0;高置鸭翼工况为g/cw = 0.05和0.15。
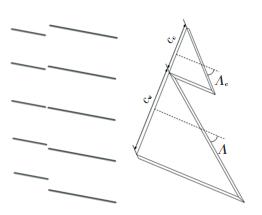
|
图 2 实验模型示意图 Fig. 2 Schematic of experimental model |
在实验测力的基础上,本文开展了详细的CFD数值计算。计算域选用长方体计算域,借助ICEM网格划分软件实现全流场的结构网格划分(近壁面y+~o(1),在剪切层及前缘涡的作用区域进行网格局部加密),如图 3所示。通过编译的UDF文件完成模型的运动控制,并利用整体动网格技术实现网格与模型的同步俯仰运动[21]。计算域入口和远场边界距离鸭翼前缘尖点20cw,采用速度入口边界条件;出口边界距离主翼尾缘30cw,采用压力出口边界条件;在模型根部应用对称面边界条件。基于FLUENT流体计算软件,采用S-A-方程RANS模型的延迟分离涡模拟(DDES)方法进行俯仰振荡的非定常不可压流场求解[22]。DDES方法属于广义的RANS-LES混合模型,由于单纯的RANS模型对于由大范围分离流动占主导的复杂流场模拟一直不太理想,而LES对空间分离流场具有较好的模拟效果,但对于近壁区模拟需要耗费大量网格,后人针对这种情况提出了DDES方法,该方法在物面附近采用RANS模型有效地处理边界层的流动,在远离物面的流动区域内采用LES计算大范围分离流动,综合了RANS和LES的优势,提高了大分离流动下的数值模拟能力[23]。DDES-SA计算方法如今已被广泛应用于后掠翼布局旋涡流动数值模拟[19, 24-25]。
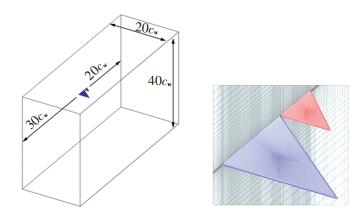
|
图 3 计算域及流场网格示意图 Fig. 3 Computational domain and flow field grids |
为进行网格无关性验证,本文选择了3种网格密度(粗网格600万,中等网格900万和密网格1 200万)来求解共面鸭式布局(g/cw=0)在k=0.075 0下的正弦俯仰运动,主翼升力的计算结果如图 4所示。可以看到,尽管3种网格密度下的工况计算出的主翼升力值整体重合度较好,但粗密度网格在下俯至10°迎角时出现小幅度偏离。因此,本文均采用中等密度的网格来捕捉鸭式布局俯仰运动的非定常流场特征。

|
图 4 网格无关性验证 Fig. 4 Verification of grid independence |
图 5给出了实验中5种鸭翼高度(g/cw分别为-0.15、-0.05、0、0.05和0.15)的模型在k=0.037 5与0.600 0时主翼升力系数随时间的变化曲线。当k=0.037 5时,在上仰的初期(t*<0.2)与下俯的末期(t*>0.8)主翼升力系数对鸭翼位置的变化不敏感;当0.2≤t*≤0.8时,随鸭翼位置的升高,主翼的升力系数有了明显的增加,且高置布局往往拥有更高的主翼最大升力系数[15]。当k = 0.600 0时,鸭翼位置对主翼升力产生的影响更为明显,与图 5(a)不同,上仰的初期不同布局的升力系数就出现一定的区别,即高置布局的主翼升力系数整体要高于低置布局的;但在下俯阶段,低置布局的主翼升力系数在较长时间内要高于前者。

|
图 5 不同鸭翼布局的主翼升力系数随时间的变化曲线 Fig. 5 Relation between wing lift coefficients for cases with different canard-position configurations and time |
图 6(a)给出共面鸭式布局(g/cw= 0)进行俯仰运动时(k = 0.0375与0.6000)主翼升力系数的实验与数值结果对比。可以看出,同一频率下实验与数值模拟得到的主翼升力系数整体趋势吻合较好。在高频上仰至较大迎角和低频下俯至较小迎角时,由于存在着与黏性效应密切相关的前缘涡破裂与再附过程[1],计算结果与实验值出现了一定的差异[19]。此外,受当前实验条件的限制,只能开展高置鸭式布局(g/cw= 0.15)俯仰运动中的鸭翼气动力测量,相应的实验与计算结果如图 6(b)所示。可以看出,数值计算的鸭翼气动力在趋势与量级上均与实验值对应较好,数值模拟的有效性得到进一步验证。由于无法通过实验手段直接测量其他鸭式布局(除g/cw=0.15之外)俯仰运动中鸭翼的升力系数,本文主要借助CFD数值计算结果对鸭翼的动态气动力及流场展开分析。
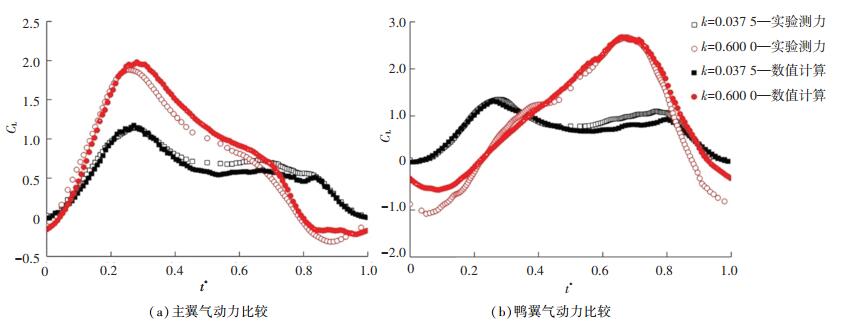
|
图 6 实验与计算的气动力结果比较 Fig. 6 Comparison between experimental and computational aerodynamic results |
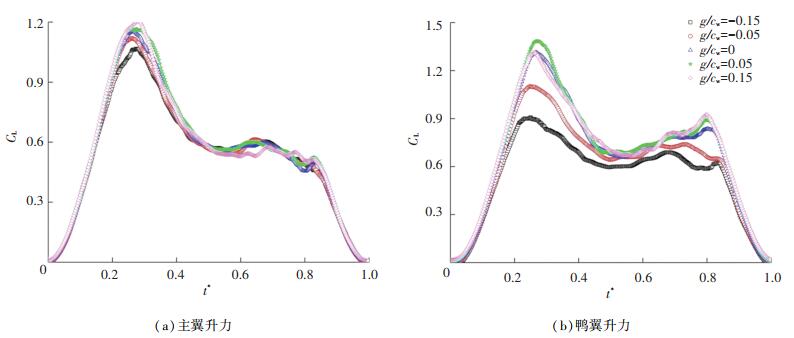
图 7给出k=0.037 5时不同鸭翼高度的鸭式布局俯仰运动中主翼与鸭翼的升力系数变化曲线。从图 7(a)可以看到,上仰阶段计算结果呈现的规律与实验发现(图 5)十分吻合,只是在下俯阶段出现了一定的偏差(图 6),但整体而言CFD模拟的结果可以较好地刻画鸭翼高度对主翼升力产生的影响。另外,从图 7(b)可以看到,鸭翼高度对鸭翼升力产生的影响更明显,低置鸭翼的升力系数要明显低于高置鸭翼的,尽管最大高度的鸭翼(g/cw = 0.15)在上仰阶段的升力特性有所降低。
|
图 7 k=0.037 5时,鸭式布局的升力系数随时间的变化曲线 Fig. 7 Relation between lift coefficients for different canard deployed cases and time(k=0.037 5) |
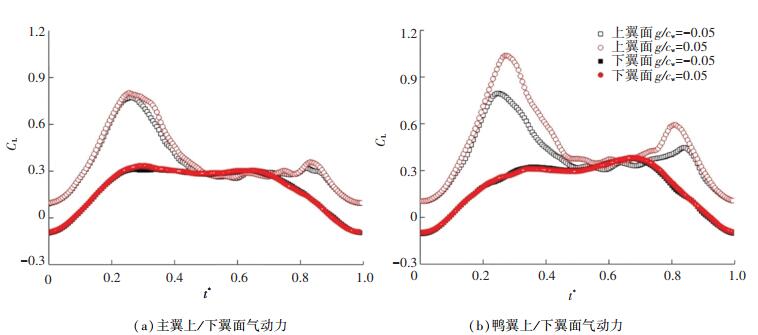
图 8给出了低置(g/cw=-0.05)与高置(g/cw=0.05)鸭式布局俯仰运动中主翼与鸭翼上下翼面升力系数的变化情况,其中空心点表示上翼面的值,实心点表示下翼面的值。可以看到,无论是主翼还是鸭翼,在低频俯仰时不同构型间升力系数的差异主要源于上表面的贡献,下表面的升力系数差别很小。
|
图 8 k=0.037 5时,鸭式布局主翼与鸭翼上/下翼面在俯仰运动中的升力系数变化曲线 Fig. 8 Variation of lift coefficients on upper/lower surface for wing and canard during pitching motions (k=0.037 5) |
图 9给出低置(g/cw = -0.05)与高置(g/cw = 0.05)鸭式布局在低频俯仰至α = 20°和40°时上翼面的静压分布云图,其中迎角-时间曲线下侧为低置布局计算结果,上侧为高置布局的计算结果。可以看到,在上仰阶段,与低置鸭翼的结果相比,高置布局的鸭翼上翼面负压分布更明显(图 8(b)),具体的原因将在下文给予解释。另外,基于涡识别的Q准则[26-27],上仰至20°和40°迎角时的流场涡结构(Q=100)也在图 9中给出,并用无量纲化的流向速度(Ux/U∞)渲染,范围介于-0.5到1.0。由图 9可以发现,在上仰阶段,与低置布局的涡结构相比,高置鸭翼的工况在同等迎角下往往拥有更为集中的主翼前缘涡分布,导致主翼面存在大范围的负压区(α=40°);在下俯阶段,当前的数值模拟无法精确捕捉主翼前缘涡的再生成过程(图 6),因而计算出的低置与高置鸭式布局在同一迎角下的主翼面静压分布比较接近(图 8(a))。

|
图 9 k=0.037 5时,低置与高置布局俯仰运动中上翼面压强系数及涡结构分布 Fig. 9 Distribution of pressure coefficients on upper surface and vortical structures for lower and higher canard deployed cases during pitching motions(k=0.037 5) |
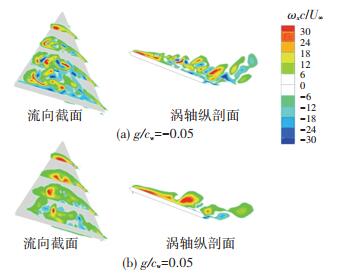
图 10给出上仰至20°时,低置(g/cw = -0.05)与高置(g/cw = 0.05)布局鸭翼前缘涡(ωxc/U∞)的截面分布结果,其中左侧为鸭翼涡的流向截面分布(沿鸭翼弦向4等分),右侧为过鸭翼前缘涡涡轴的纵剖面上的涡量分布,为便于观察比较,下游的主翼未予显示。相比高置鸭翼的布局(图 10(b)),低置布局的鸭翼前缘涡更不稳定,在第2个1/4流向截面就出现了负涡量,而前者在第3个流向截面才有较弱的负涡量产生。对比过鸭翼涡涡轴的纵剖面上的涡量分布发现,低置鸭翼的布局在更靠前的位置(约1/3倍鸭翼弦长处)出现了正负涡量交错分布的现象,说明低置布局的鸭翼涡卷起位置相对较低,下游较高位置的主翼能对鸭翼涡的流动产生明显的干扰作用,使得上游的鸭翼涡较早出现双螺旋不稳定性,诱发鸭翼涡的提前破裂[28-29]。相反,高置布局由于鸭翼涡卷起位置较高,下游处于较低位置的主翼对鸭翼涡尾流的干扰效应被明显减弱,因而在低频上仰时,同等迎角下的高置布局鸭翼涡会更集中,鸭翼上翼面的负压分布也更明显(图 9)。同时,受到鸭翼涡对主翼前缘的下洗及卷绕作用,高置鸭翼的布局在中大迎角下能更明显地延缓主翼涡的涡破裂[30],导致主翼前缘形成更强的负压区(图 9)。
|
图 10 上仰至α=20°时,低置与高置布局鸭翼涡的截面分布 Fig. 10 Section distribution of canard vortex for lower and higher canard deployed cases, when pitching up to α=20° |
回顾图 7(b),与主翼的计算结果不同,鸭翼下俯阶段的升力系数随着鸭翼高度的不同仍存在着显著的差异。图 11给出低频下俯至20°(t*≈0.8)时,低置(g/cw = -0.05)与高置(g/cw = 0.05)布局鸭翼涡的流向截面分布,由图 11可以发现,高置布局在第1个流向截面已经形成稳定的鸭翼涡结构,而低置布局仍存在着明显的负涡量区。本文初步认为,低置布局在鸭翼涡重新生成的过程中更易受到下游主翼的干扰作用,后者产生的扰动会以波的形式往上游传播,延缓了鸭翼前缘涡的恢复[31-32];相反,对于高置鸭翼,干扰效应被明显减弱,鸭翼涡在第1个流向截面开始恢复,所以下俯至20°时高置布局鸭翼的升力系数较高(图 8(b))。

|
图 11 下俯至α = 20°时,低置与高置布局鸭翼涡的流向截面分布 Fig. 11 Section distribution of canard vortex for lower and higher canard deployed cases, when pitching down to α=20° |
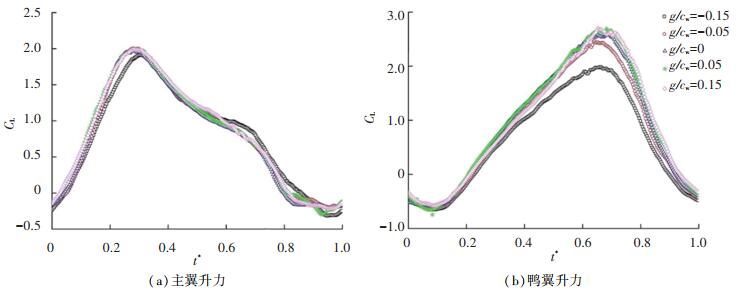
图 12给出k=0.600 0时不同鸭翼高度的鸭式布局主翼与鸭翼在俯仰运动中的升力系数变化曲线。与图 5(b)的规律一致,随着鸭翼位置的升高,上仰阶段主翼的气动力系数有所增大;但在下俯阶段,低置布局的主翼升力系数往往较高,尤其是g/cw=-0.15的工况。由图 12(b)可知,高置布局的鸭翼升力系数在整个俯仰周期内较低置布局均有了明显的增加。
|
图 12 k=0.600 0时,鸭式布局的升力系数随时间的变化曲线 Fig. 12 Relation between lift coefficients for different canard deployed cases and time (k = 0.600 0) |
图 13给出低置(g/cw = -0.05)与高置(g/cw = 0.05)鸭式布局高频俯仰运动中主翼与鸭翼上下翼面升力系数的变化情况,其中空心点表示上翼面的值,实心点表示下翼面的值。与低频结果(图 8(a))相比,在高频上仰初期(t*≤0.2),两种布局主翼下翼面的升力系数出现了较大的差别;当t*>0.2时,主翼下翼面升力系数的差别不再明显,上翼面升力系数的不同是导致主翼升力系数差异的主要原因。对鸭翼而言,与图 8(b)一致,高频俯仰运动中鸭翼上翼面升力系数的差异是导致鸭翼升力系数不同的主要来源。需要说明的是,当模型高频下俯时(t*>0.6),两种布局的主翼与鸭翼上翼面升力系数的大小关系是正好相反的,具体原因将在下文给予解释。
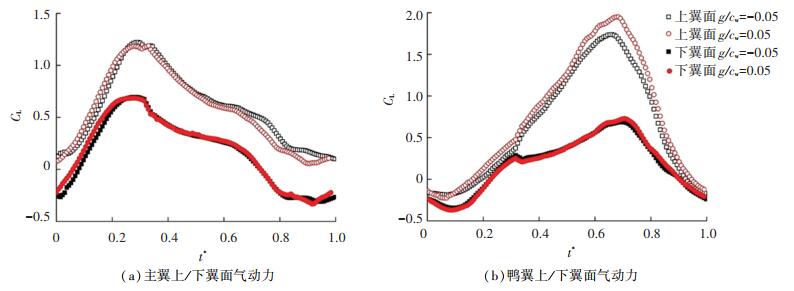
|
图 13 k=0.600 0时,鸭式布局主翼与鸭翼上/下翼面在俯仰运动中的升力系数变化曲线 Fig. 13 Variation of lift coefficients on upper/lower surface for wing and canard during pitching motions (k=0.600 0) |
图 14为高频上仰阶段低置(g/cw=-0.05)与高置(g/cw = 0.05)布局在不同迎角下的翼面压强及前缘涡(Q = 100)分布,其中迎角-时间曲线下侧为低置布局的计算结果,上侧为高置布局的计算结果。
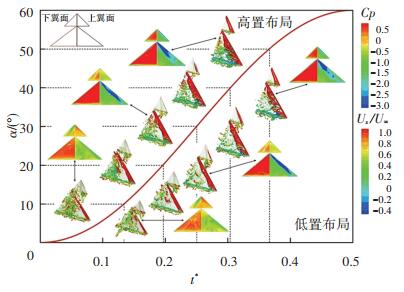
|
图 14 k=0.600 0时,低置与高置布局上仰阶段翼面压强系数及涡结构分布 Fig. 14 Distribution of pressure coefficients and vortical structures for lower and higher canard deployed cases during pitching-up process(k=0.600 0) |
模型快速上仰运动时,两种布局的鸭翼涡起初均形成于下翼面,后随着迎角的增大,逐渐在上翼面形成并发展,早期的研究认为,这与模型快速上仰明显减小了鸭翼前缘的有效迎角有关[33-34]。与高置布局相比,低置布局卷起的下翼面鸭翼涡相对主翼的位置更低,随着模型的快速上仰,鸭翼涡尾流更容易流至主翼下翼面(如α=10°),引起主翼下表面的静压损失(图 13(a))。与图 9不同,在整个上仰阶段,低置与高置布局的鸭翼涡沿整个弦向都存在着集中的前缘涡结构,下游主翼的干扰作用未诱发鸭翼涡的提前破裂[29]。
当模型进行快速下俯时,流体相对模型运动存在着明显的滞后效应[35],下俯至小迎角时的空间流场结构可视为大迎角下的流动发展形成的。图 15给出了下俯至50°时低置与高置布局主翼上方的流向截面涡量云图(沿主翼弦向4等分)。

|
图 15 k=0.600 0时,鸭式布局下俯至50°时主翼上方的流向涡量云图 Fig. 15 Distributions of streamwise vorticity contours above the wing, when pitching down to α= 50° (k=0.600 0) |
由图 15可以看到,低置布局的主翼涡在第1个1/4流向截面仍存在比较集中的前缘涡结构,它能与上游流过来的鸭翼涡产生一定的相互作用,捕获部分的鸭翼涡涡量[36];受鸭翼低置的影响,鸭翼涡在向下游对流的过程中将更靠近主翼上翼面,起到充当主翼涡的作用,提升了下俯后期主翼上翼面的升力贡献量(图 13(a),t*>0.6)。相反,高置布局在第1个流向截面主翼涡就已明显破裂,且鸭翼高置显著地拉开了鸭翼涡与主翼背风侧碎涡结构的距离,削弱了彼此之间的相互作用,导致主翼近壁面总是被离散的碎涡结构所占据,集中的鸭翼涡只会简单地对流至主翼的下游,致使下俯后期高置布局主翼上翼面的升力贡献量较低(图 13(a),t*>0.6)。
图 16给出了模型下俯至50°时对称面处的压强分布云图,其中图 16(a)为g/cw = -0.05(左)与g/cw = 0.05(右)的布局计算结果,图 16(b)为g/cw =-0.15(左)与g/cw = 0.15(右)的布局计算结果。与高置布局的压强云图相比,同一组内的低置布局在鸭翼尾缘处往往拥有更低的压强梯度,这与主翼前缘明显的集中涡结构有关(图 15(a))。早期的研究认为,主翼前缘涡的存在能加快鸭翼涡尾流的对流速度[37],使得同等迎角下的低置布局鸭翼上方的涡残留更少[19],减小了高频下俯阶段鸭翼的升力系数(图 13(b))。

|
图 16 高频下俯至50°时,鸭式布局对称面处的压强分布云图 Fig. 16 Pressure distribution contours for symmetric planes of different canard configurations, when pitching down to α=50° |
本文通过实验与数值模拟的方法研究了5种鸭翼高度(g/cw分别为-0.15、-0.05、0、0.05和0.15)下的鸭式布局进行低频与高频(k = 0.037 5与0.600 0)俯仰振荡的升力特性,结果表明:
1) 在低频上仰阶段,低置布局的鸭翼涡较早地发生了双螺旋破裂,导致鸭翼升力系数明显减小;随着鸭翼位置的升高,同等迎角下的鸭翼升力系数有了较大地提升。在低频下俯阶段,主翼产生的扰动会明显干扰低置布局鸭翼涡的重新生成,降低了鸭翼的升力系数。
2) 在高频上仰阶段,主翼对鸭翼涡破裂的影响被明显削弱。由于模型的快速上仰明显减小了鸭翼前缘的有效迎角,使得鸭式布局的鸭翼涡优先生成于下翼面。在高频下俯阶段,大迎角下低置布局的主翼前缘存在集中的前缘涡结构,它产生的低压区能明显减小鸭翼尾缘的压力梯度,加快鸭翼涡残留往下游的对流速度,使得低置布局的鸭翼升力系数明显减小。
3) 对主翼而言,低频俯仰时低置布局的主翼最大升力系数较低,但在高频俯仰时,受到主翼前缘集中涡量与鸭翼高度的共同影响,低置布局的鸭翼涡尾流在向下游对流的过程中会更靠近主翼上翼面,起到充当主翼涡的作用,提升了下俯后期低置布局的主翼升力系数。
| [1] |
NELSON R C, PELLETIER A. The unsteady aerodynamics of slender wings and aircraft undergoing large amplitude maneuvers[J]. Progress in Aerospace Sciences, 2003, 39(2): 188. DOI:10.1016/S0376-0421(02)00088-X |
| [2] |
GURSUL I, GORDNIER R, VISBAL M. Unsteady aerodynamics of nonslender delta wings[J]. Progress in Aerospace Sciences, 2005, 41(7): 519. DOI:10.1016/j.paerosci.2005.09.002 |
| [3] |
肖志祥, 崔文瑶, 刘健, 等. 新一代战斗机非定常流动数值研究综述[J]. 航空学报, 2020, 41(6): 6. XIAO Zhixiang, CUI Wenyao, LIU Jian, et al. Review of numerical research on unsteady flows of the new generation fighters[J]. Acta Aeronautica et Astronautica Sinica, 2020, 41(6): 6. DOI:10.7527/S1000-6893.2019.23451 |
| [4] |
BEHRBOHM H. Basic low speed aerodynamics of short-coupled canard configuration of small aspect ratio[R]. Linkoping: SAAB, 1965
|
| [5] |
GAD-EL-HAK M, HO C M. The pitching delta wing[J]. AIAA Journal, 1985, 23(11): 1663. DOI:10.2514/3.9147 |
| [6] |
LEMAY S P, BATILL S M, NELSON R C. Vortex dynamics on a pitching delta wing[J]. Journal of Aircraft, 1990, 27(2): 67. DOI:10.2514/3.45908 |
| [7] |
SOLTANI M R, BRAGG M B, BRANDON J M. Measurements on an oscillating 70-deg delta wing in subsonic flow[J]. Journal of Aircraft, 1990, 27(3): 213. DOI:10.2514/3.45921 |
| [8] |
ERICSSON L E. Nonlinear unsteady aerodynamics of pitching delta wings [C]//16th AIAA Applied Aerodynamics Conference. Albuquerque: AIAA, 1998: 212. DOI: 10.2514/6.1998-2518
|
| [9] |
GURSUL I. Proposed mechanism for time lag of vortex breakdown location in unsteady flows[J]. Journal of Aircraft, 2000, 37(4): 734. DOI:10.2514/2.2661 |
| [10] |
GURSUL I. Recent developments in delta wing aerodynamics[J]. The Aeronautical Journal, 2004, 108(1087): 448. DOI:10.1017/S0001924000000269 |
| [11] |
OELKER H C, HUMMEL D. Investigations on the vorticity sheets of a close-coupled delta-canard configuration[J]. Journal of Aircraft, 1989, 26(7): 660. DOI:10.2514/3.45817 |
| [12] |
HUMMEL D, OELKER H C. Low-speed characteristics for the wing-canard configuration of the international vortex flow experiment[J]. Journal of Aircraft, 1994, 31(4): 874. DOI:10.2514/3.46573 |
| [13] |
TU E L. Navier-Stokes simulation of a close-coupled canard-wing-body configuration[J]. Journal of Aircraft, 1992, 29(5): 836. DOI:10.2514/3.46253 |
| [14] |
TU E L. Effect of canard position on the longitudinal aerodynamic characteristics of a close-coupled canard-wing-body configuration [C]//Astrodynamics Conference. Hilton Head Island: AIAA, 1992: 4. DOI: 10.2514/6.1992-4632
|
| [15] |
BERGMANN A, HUMMEL D. Aerodynamic effects of canard position on a wing body configuration in symmetrical flow [C]//39th Aerospace Sciences Meeting and Exhibit. Reno: AIAA, 2001: 5. DOI: 10.2514/6.2001-116
|
| [16] |
MYOSE R Y, HAYASHIBARA S, YEONG P C, et al. Effect of canards on delta wing vortex breakdown during dynamic pitching[J]. Journal of Aircraft, 1997, 34(2): 170. DOI:10.2514/2.2168 |
| [17] |
DAVARI A R, ASKARI F, SOLTANI M R. Canard flow improvement in a split canard configuration[J]. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, 2015, 229(6): 1082. DOI:10.1177/0954410014544180 |
| [18] |
王亚平. 近距耦合鸭式布局旋涡卷绕融合机理实验研究[D]. 北京: 北京航空航天大学, 2017 WANG Yaping. Experimental investigation on the vortex merger mechanism of close-coupled canard configurations [D]. Beijing: Beihang University, 2017 |
| [19] |
YI Yuan, HU Tianxiang, LIU Peiqing, et al. Dynamic lift characteristics of nonslender delta wing in large-amplitude-pitching[J]. Aerospace Science and Technology, 2020, 105: 3. DOI:10.1016/j.ast.2020.105937 |
| [20] |
LEISHMANN J G. Principles of helicopter aerodynamics[M]. 2nd ed. Cambridge: Cambridge University Press, 2006: 427.
|
| [21] |
QU Qiulin, HU Mingxuan, GUO Hao, et al. Study of ditching characteristics of transport aircraft by global moving mesh method[J]. Journal of Aircraft, 2015, 52(5): 1551. DOI:10.2514/1.C032993 |
| [22] |
LÜDELE H, LEICHER S. Unsteady CFD analysis of a delta wing fighter configuration by delayed detached eddy simulation[J]. Notes on Numerical Fluid Mechanics and Multidisciplinary Design, 2008, 97: 4. DOI:10.1007/978-3-540-77815-8_21 |
| [23] |
陈名乾. 近距耦合鸭式布局动态机动中涡系干扰机理的数值研究[D]. 北京: 北京航空航天大学, 2014 CHEN Mingqian. Numerical study on the mechanism of dynamic vortex interaction on a maneuvering close-coupled canard configuration [D]. Beijing: Beihang University, 2014 |
| [24] |
CHEN Mingqian, LIU Peiqing, GUO Hao, et al. Effect of sideslip on high-angle-of-attack vortex flow over close-coupled canard configuration[J]. Journal of Aircraft, 2016, 53(1): 218. DOI:10.2514/1.C033305 |
| [25] |
赵悦, 胡天翔, 陈庆民, 等. 双三角翼非定常俯仰运动实验与数值模拟[J]. 气体物理, 2020, 5(5): 48. ZHAO Yue, HU Tianxiang, CHEN Qingmin, et al. Experimental and numerical studies on large-amplitude-pitching double-delta wings[J]. Physics of Gases, 2020, 5(5): 48. DOI:10.19527/j.cnki.2096-1642.0796 |
| [26] |
HUNT J C R, WRAY A A, MOIN P. Eddies, stream, and convergence zones in turbulent flows [C]//Proceedings of the Summer Program, Center for Turbulence Research. [S. l. ]: Center for Turbulence Research, 1989: 196
|
| [27] |
GREEN M A, ROWLEY C W, HALLER G. Detection of Lagrangian coherent structures in three-dimensional turbulence[J]. Journal of Fluid Mechanics, 2007, 572: 111. DOI:10.1017/S0022112006003648 |
| [28] |
GORDNIER R E, VISBAL M R. Numerical simulation of the impingement of streamwise vortex on a plate[J]. International Journal of Computational Fluid Dynamics, 1999, 12(1): 55. DOI:10.1080/10618569908940815 |
| [29] |
SUN Zhijun, GU Yunsong, ZHAO Hang. Experimental investigation on the streamwise vortex-surface interaction[J]. Journal of Visualization, 2019, 22: 2. DOI:10.1007/s12650-018-00544-3 |
| [30] |
刘沛清, 王亚平, 刘杰, 等. 近距耦合鸭式布局复杂涡系的干扰机理[J]. 北京航空航天大学学报, 2012, 38(7): 876. LIU Peiqing, WANG Yaping, LIU Jie, et al. Vortex interaction mechanism over close-coupled canard configuration[J]. Journal of Beijing University of Aeronautics and Astronautics, 2012, 38(7): 876. DOI:10.13700/j.bh.1001-5965.2012.07.014 |
| [31] |
ÖZGÖRENM, SAHINB, ROCKWELLD. Vortex breakdown from a pitching delta wing incident upon a plate: flow structure as the origin of buffet loading[J]. Journal of Fluids and Structures, 2002, 16(3): 304. DOI:10.1006/jfls.2001.0427 |
| [32] |
AKILLI H, SAHIN B, ROCKWELL D. Control of vortex breakdown by a transversely oriented wire[J]. Physics of Fluids, 2001, 13(2): 455. DOI:10.1063/1.1336809 |
| [33] |
GÜLÇAT Ü. Fundamentals of modern unsteady aerodynamics[M]. 2nd ed. Berlin: Springer Press, 2016: 299.
|
| [34] |
CHEN Qingmin, HU Tianxiang, LIU Peiqing, et al. The dynamic vortical flow behaviour on a coplanar canard configuration during large-amplitude-pitching[J]. Aerospace Science and Technology, 2021, 112(4): 106553. DOI:10.1016/j.ast.2021.106553 |
| [35] |
ROCKWELL D. Three-dimensional flow structure on delta wings at high angle-of-attack: experimental concepts and issues [C]//31st Aerospace Sciences Meeting. Reno: AIAA, 1993: 2. DOI: 10.2514/6.1993-550
|
| [36] |
温瑞英. 近耦合鸭式布局鸭翼展向吹气涡控技术实验研究[D]. 北京: 北京航空航天大学, 2008 WEN Ruiying. Experimental study on vortex-control technology of canard-spanwise blowing of close-coupled canard wing configurations[D]. Beijing: Beihang University, 2008 |
| [37] |
DAS A, LONGO J M A. Numerical analysis of the vortical flow around a delta wing-canard configuration[J]. Journal of Aircraft, 1995, 32(4): 724. DOI:10.2514/3.46782 |
 2021, Vol. 53
2021, Vol. 53


